Effective Continuum Approximations for Permeability in Brown-Coal and Other Large-Scale Fractured Media
Abstract
:1. Introduction
2. Model Description
2.1. Effective Fracture-Set Permeability
2.2. Representing Joint Aperture and Separation
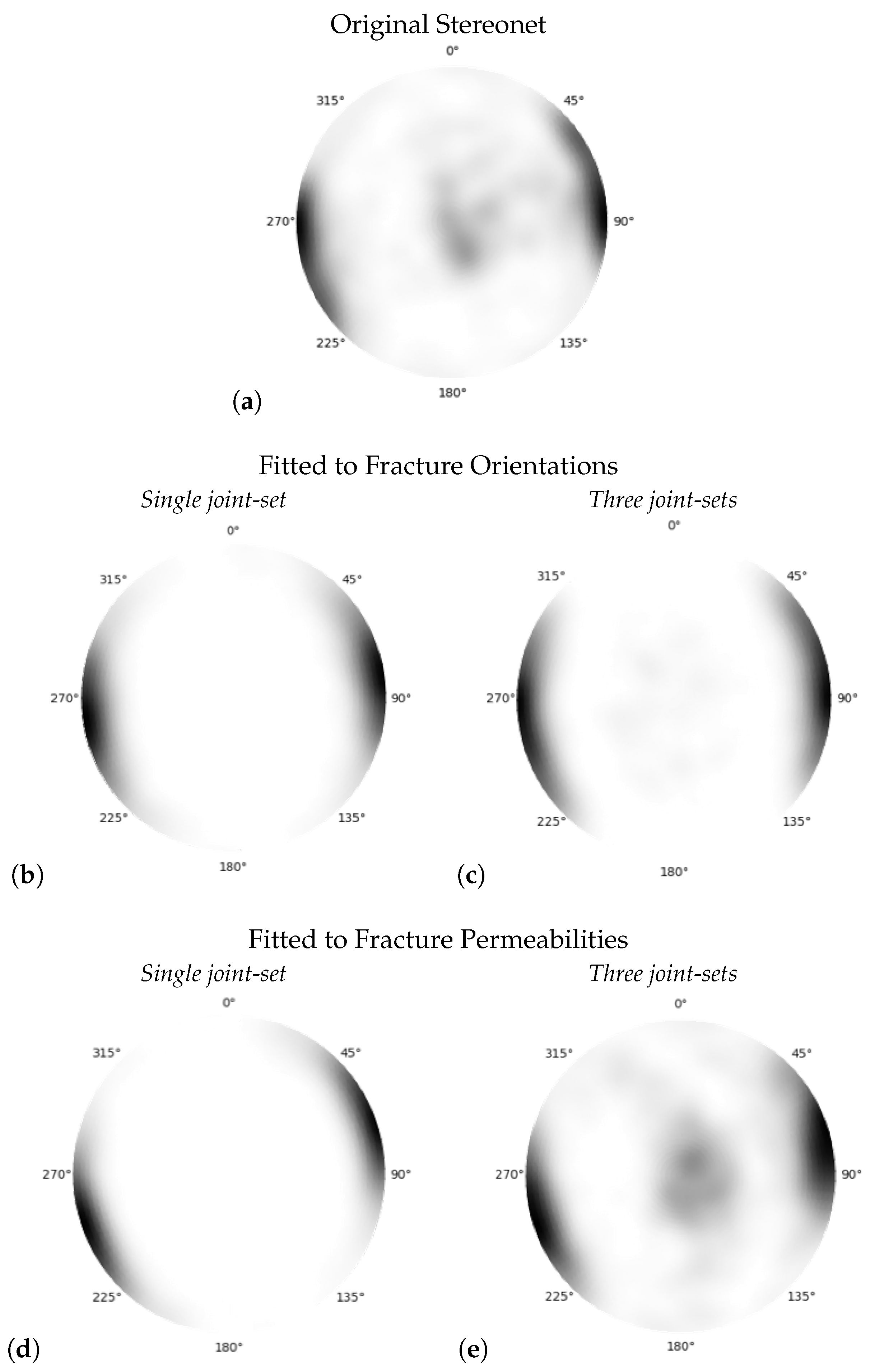
2.3. Representing the Distribution of Joint Orientation
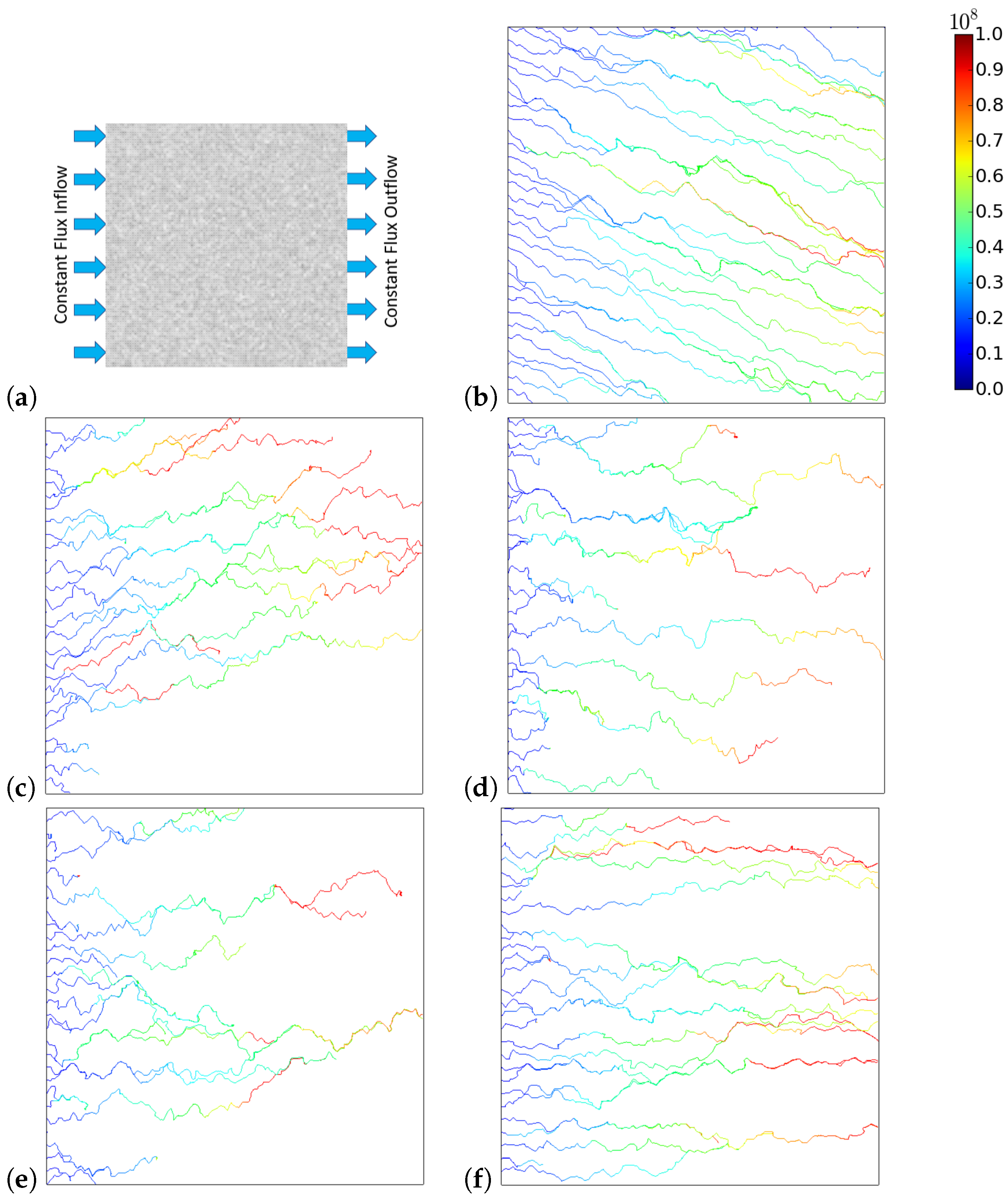
3. Fracture Network Representation
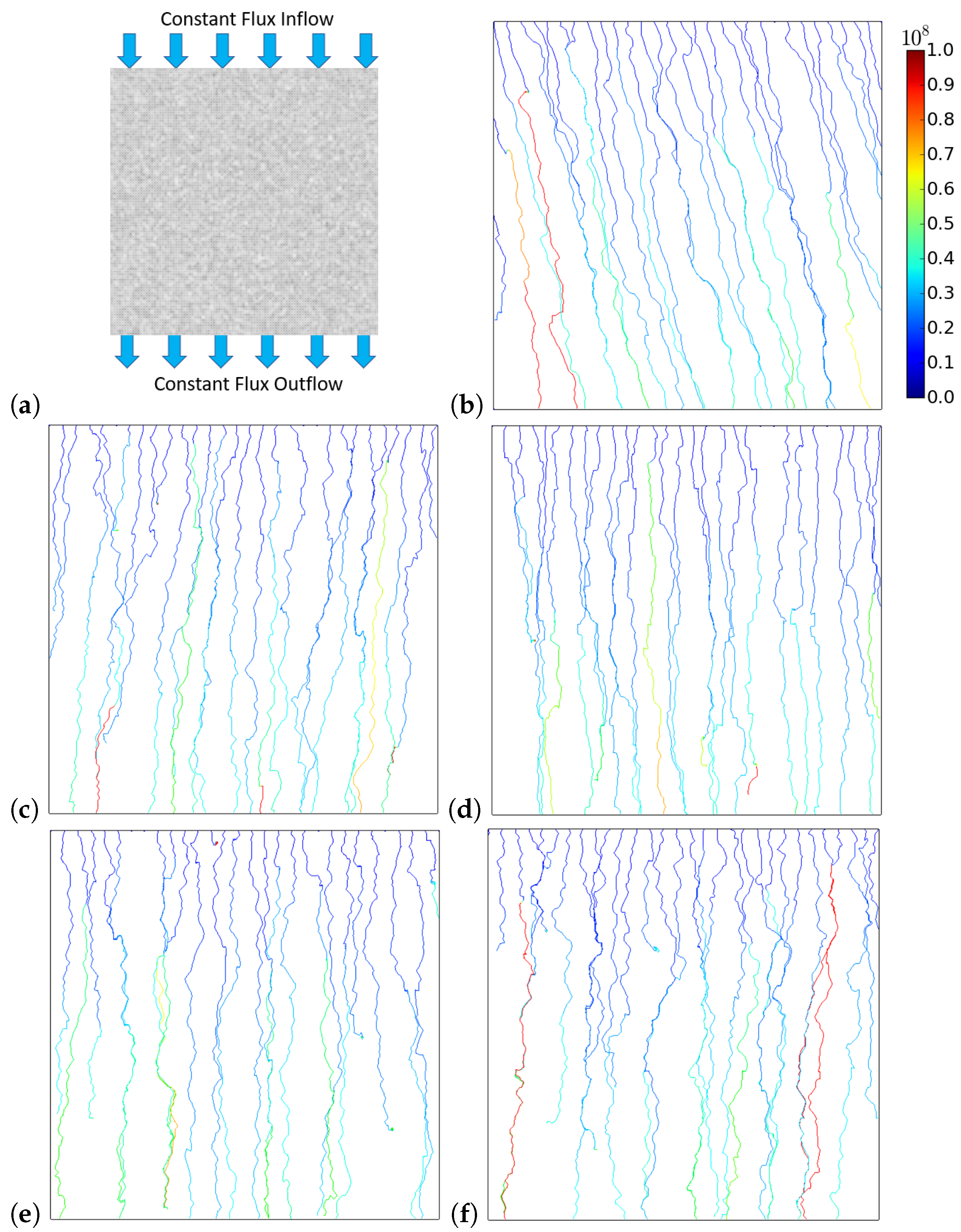
3.1. Fracture Network
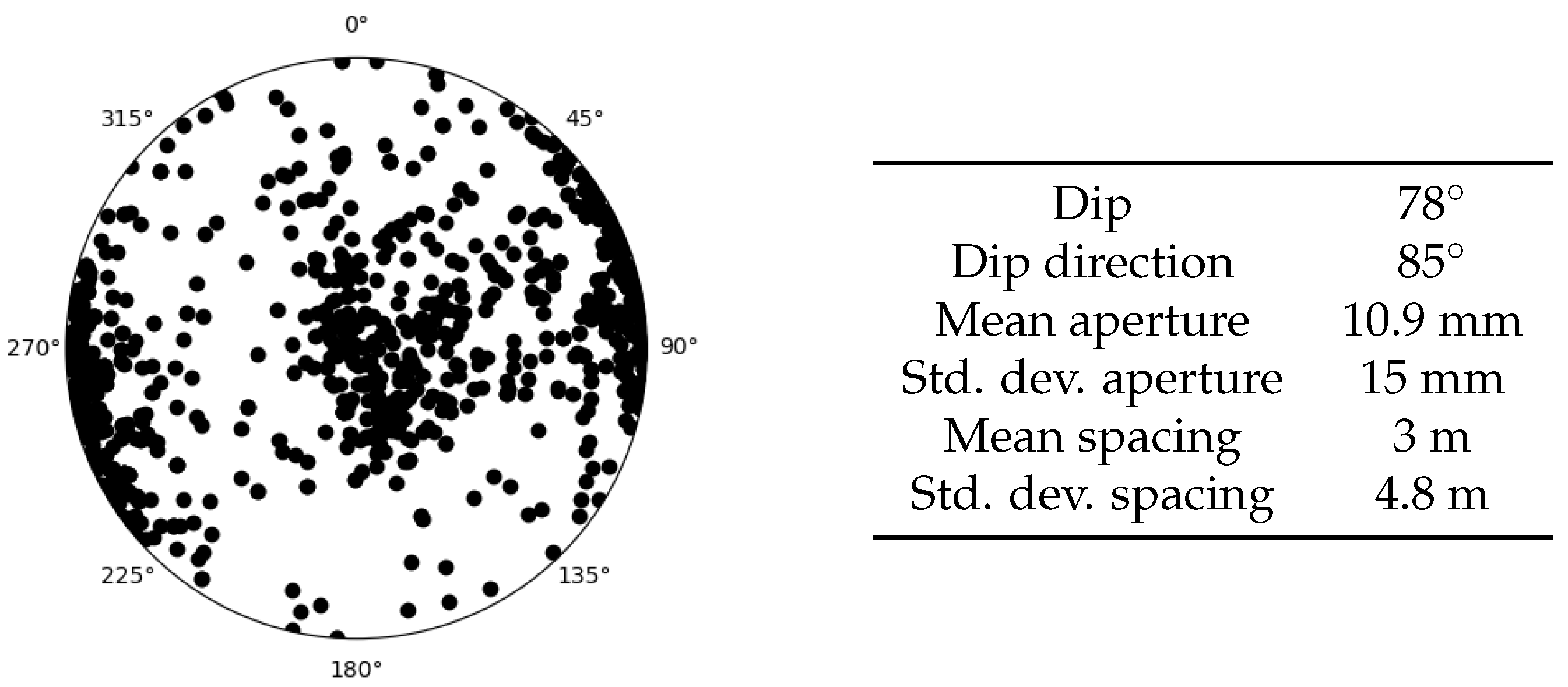
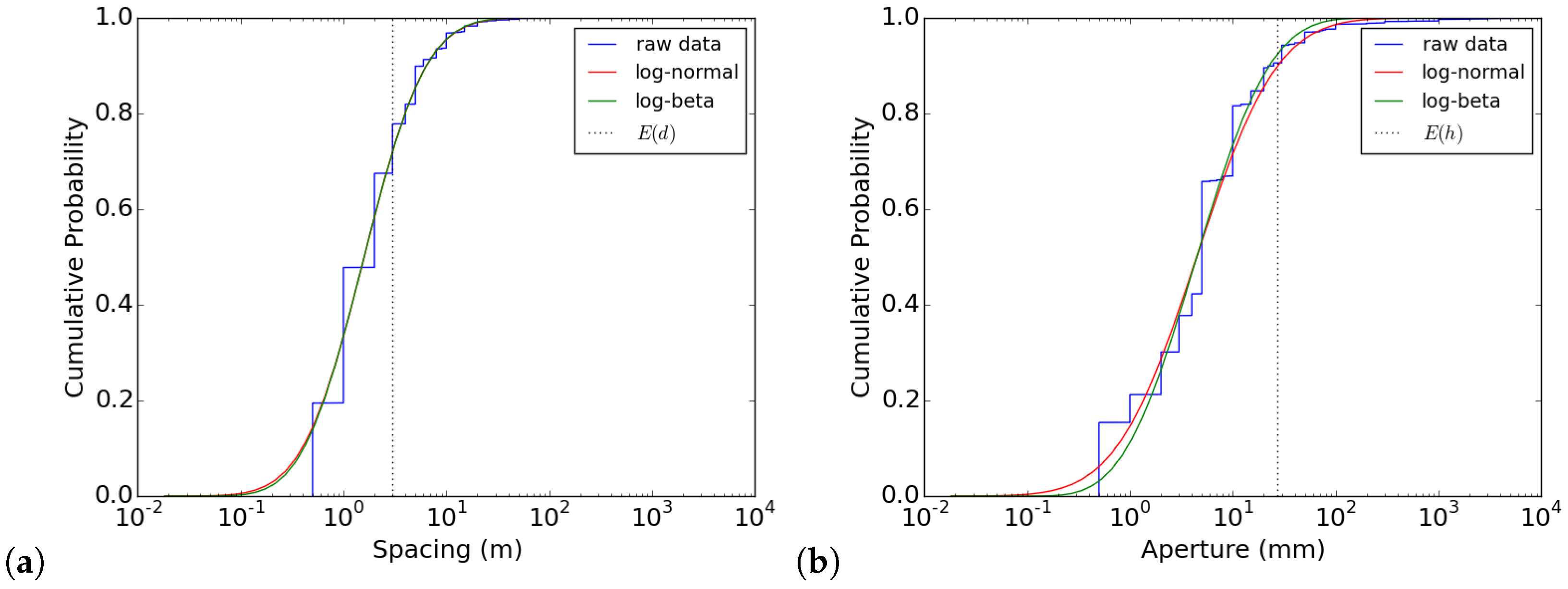
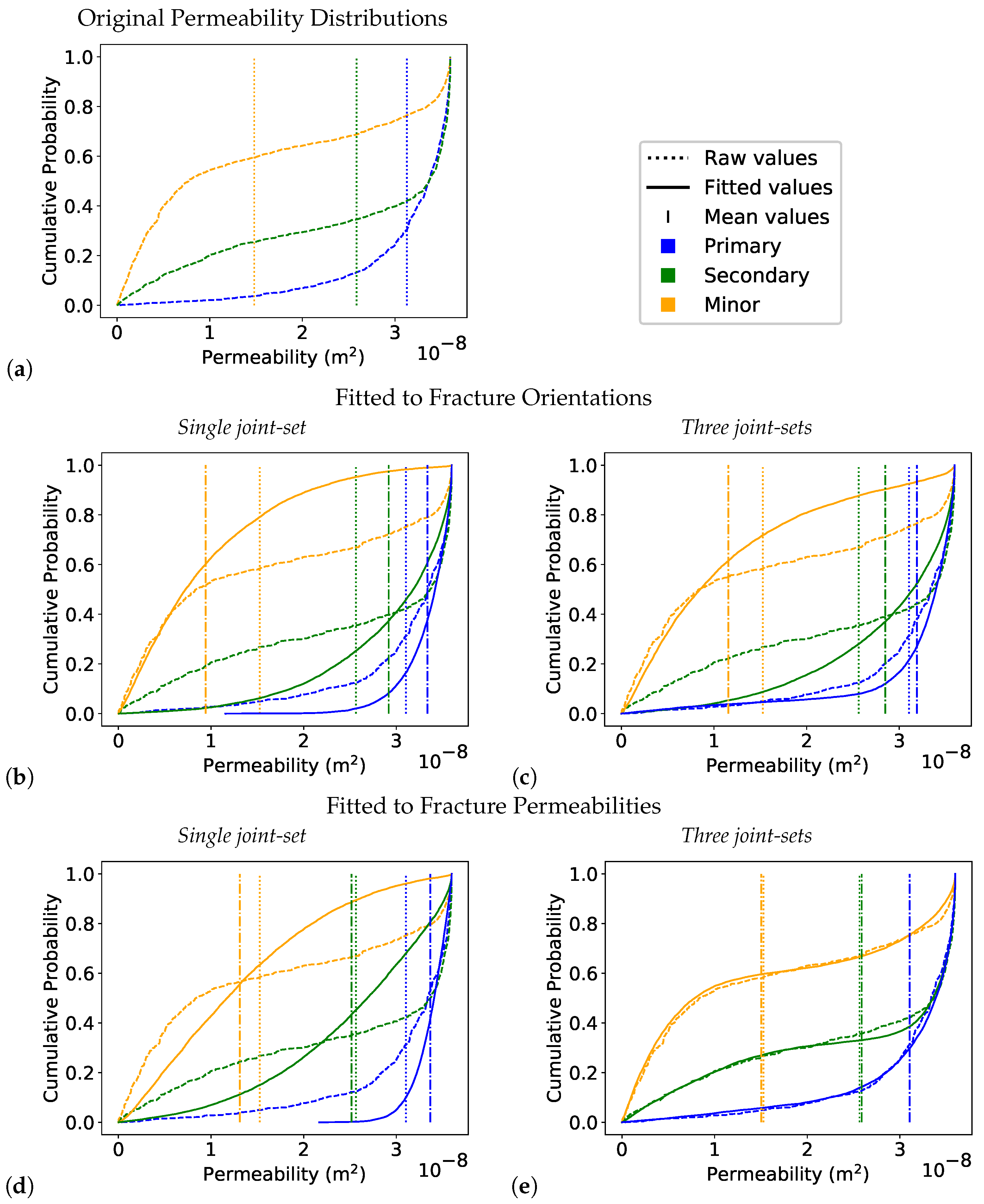
3.2. Fracture Spacing and Aperture
3.3. Fracture Orientation
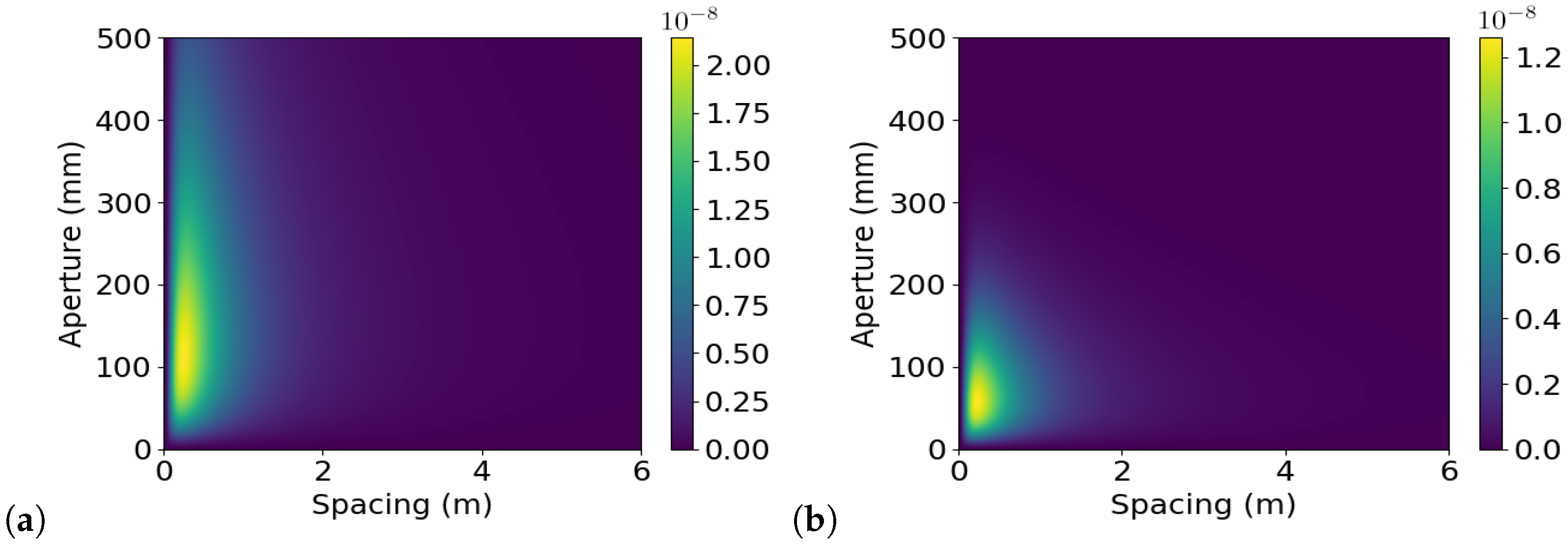
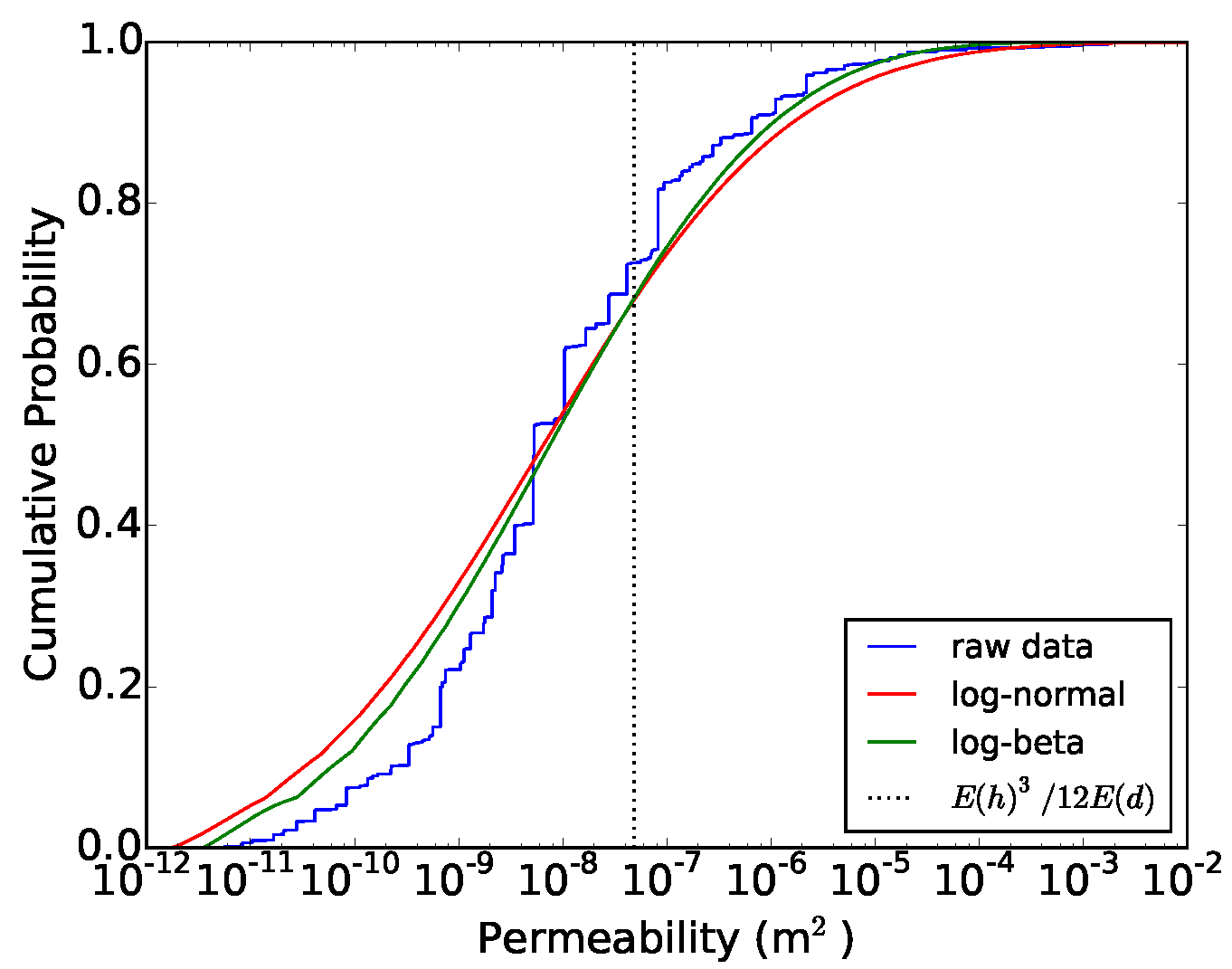
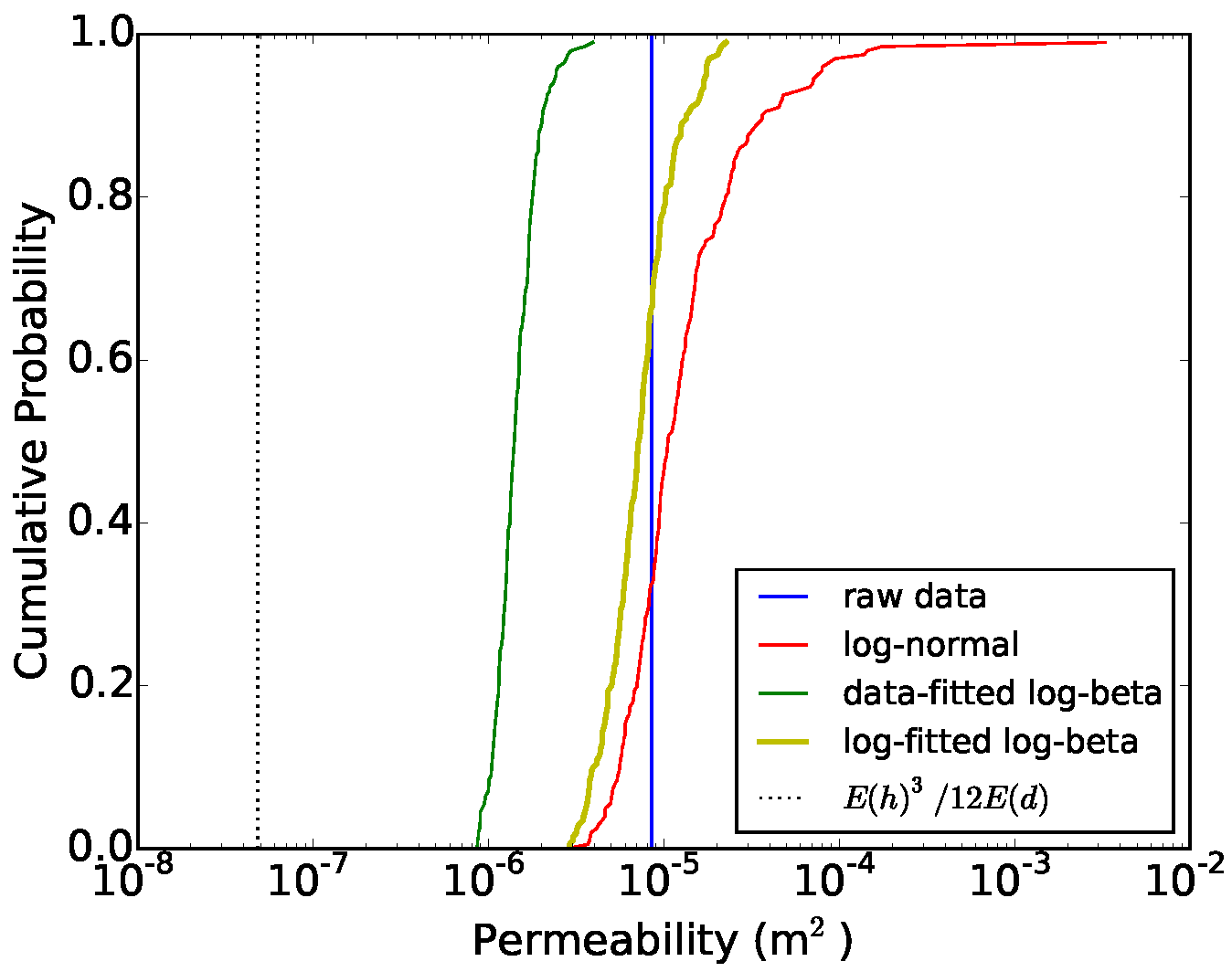
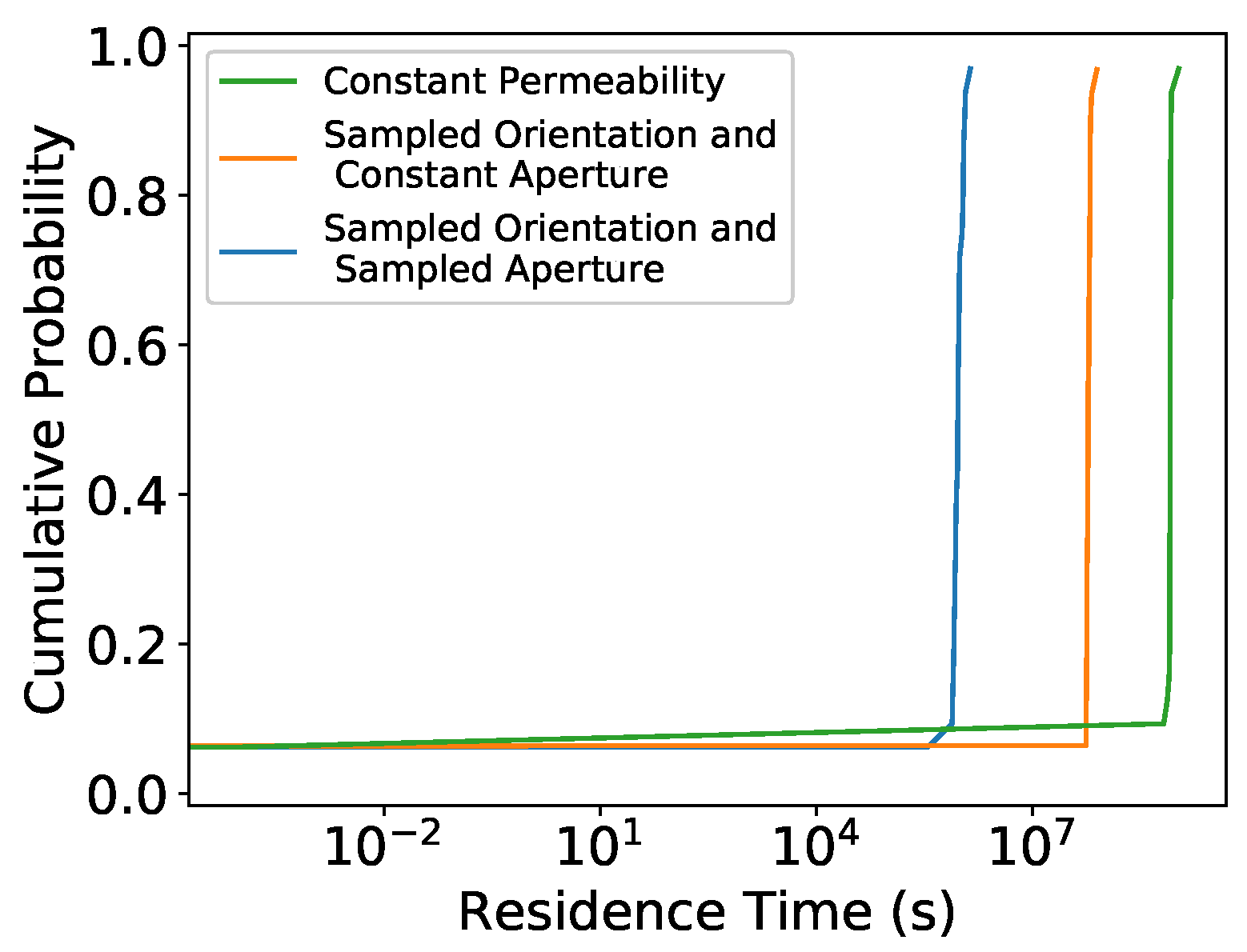
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Pan, Z.; Connell, L.D. Modelling permeability for coal reservoirs: A review of analytical models and testing data. Int. J. Coal Geol. 2012, 92, 1–44. [Google Scholar] [CrossRef]
- Zhang, G.; Ranjith, P.; Liang, W.; Haque, A.; Perera, M.; Li, D. Stress-dependent fracture porosity and permeability of fractured coal: An in-situ X-ray tomography study. Int. J. Coal Geol. 2019, 213, 103279. [Google Scholar] [CrossRef]
- Cai, F.; Ugai, K. Numerical analysis of rainfall effects on slope stability. Int. J. Geomech. 2004, 4, 69–78. [Google Scholar] [CrossRef]
- Cheng-Gang, B. Behavior of unsaturated soil and stability of expansive soil slope. Chin. J. Geotech. Eng. 2004, 26, 1–15. [Google Scholar]
- Osman, N.; Barakbah, S. Parameters to predict slope stability—soil water and root profiles. Ecol. Eng. 2006, 28, 90–95. [Google Scholar] [CrossRef]
- Nguyen, T.S.; Likitlersuang, S. Reliability analysis of unsaturated soil slope stability under infiltration considering hydraulic and shear strength parameters. Bull. Eng. Geol. Environ. 2019, 78, 5727–5743. [Google Scholar] [CrossRef]
- Kim, J.G.; Deo, M.D. Finite element, discrete-fracture model for multiphase flow in porous media. AIChE J. 2000, 46, 1120–1130. [Google Scholar] [CrossRef]
- Maillot, J.; Davy, P.; Le Goc, R.; Darcel, C.; De Dreuzy, J.R. Connectivity, permeability, and channeling in randomly distributed and kinematically defined discrete fracture network models. Water Resour. Res. 2016, 52, 8526–8545. [Google Scholar] [CrossRef] [Green Version]
- Huang, N.; Jiang, Y.; Liu, R.; Li, B. Estimation of permeability of 3-D discrete fracture networks: An alternative possibility based on trace map analysis. Eng. Geol. 2017, 226, 12–19. [Google Scholar] [CrossRef]
- Liu, R.; Li, B.; Yu, L.; Jiang, Y.; Jing, H. A discrete-fracture-network fault model revealing permeability and aperture evolutions of a fault after earthquakes. Int. J. Rock Mech. Min. Sci. 2018, 107, 19–24. [Google Scholar] [CrossRef]
- Huang, N.; Liu, R.; Jiang, Y.; Cheng, Y.; Li, B. Shear-flow coupling characteristics of a three-dimensional discrete fracture network-fault model considering stress-induced aperture variations. J. Hydrol. 2019, 571, 416–424. [Google Scholar] [CrossRef]
- Tavakkoli, M.; Mohammadsadeghi, M.; Shahrabadi, A.; Khajoee, S.; Malakooti, R.; Beidokhti, M.S. Deterministic versus stochastic discrete fracture network (DFN) modeling, application in a heterogeneous naturally fractured reservoir. In Proceedings of the Kuwait International Petroleum Conference and Exhibition, Kuwait City, Kuwait, 14–16 December 2009. [Google Scholar]
- Merrien-Soukatchoff, V.; Korini, T.; Thoraval, A. Use of an integrated discrete fracture network code for stochastic stability analyses of fractured rock masses. Rock Mech. Rock Eng. 2012, 45, 159–181. [Google Scholar] [CrossRef]
- Li, L.; Jiang, H.; Li, J.; Wu, K.; Meng, F.; Xu, Q.; Chen, Z. An analysis of stochastic discrete fracture networks on shale gas recovery. J. Pet. Sci. Eng. 2018, 167, 78–87. [Google Scholar] [CrossRef]
- Styles, T.; Coggan, J.; Pine, R. Stability analysis of a large fractured rock slope using a DFN-based mass strength approach. In Proceedings of the International Symposium on Rock Slope Stability in Open Pit Mining and Civil Engineering, Vancouver, BC, Canada, 18 September 2011; Volume 21, p. 2011. [Google Scholar]
- Leung, C.; Hoch, A.; Zimmerman, R. Comparison of discrete fracture network and equivalent continuum simulations of fluid flow through two-dimensional fracture networks for the DECOVALEX–2011 project. Mineral. Mag. 2012, 76. [Google Scholar] [CrossRef]
- Elmouttie, M.; Krähenbühl, G.; Soliman, A. A new excavation analysis method for slope design using discrete fracture network based polyhedral modelling. Comput. Geotech. 2016, 76, 93–104. [Google Scholar] [CrossRef]
- Meng, Z.; Zhang, J.; Wang, R. In-situ stress, pore pressure and stress-dependent permeability in the Southern Qinshui Basin. Int. J. Rock Mech. Min. Sci. 2011, 48, 122–131. [Google Scholar] [CrossRef]
- Adhikary, D.; Wilkins, A.; Reducing the impact of longwall extraction on groundwater systems. ACARP Report C18016 2012. Available online: https://www.acarp.com.au/abstracts.aspx?repId=C18016 (accessed on 10 October 2021).
- Wilkins, A.; Qu, Q. A formalism to compute permeability changes in anisotropic fractured rocks due to arbitrary deformations. Int. J. Rock Mech. Min. Sci. 2020, 125, 104159. [Google Scholar] [CrossRef]
- Peters, R.; Klavetter, E.A. A continuum model for water movement in an unsaturated fractured rock mass. Water Resour. Res. 1988, 24, 416–430. [Google Scholar] [CrossRef]
- Wang, J.G.; Kabir, A.; Liu, J.; Chen, Z. Effects of non-Darcy flow on the performance of coal seam gas wells. Int. J. Coal Geol. 2012, 93, 62–74. [Google Scholar] [CrossRef]
- Suresh Kumar, G. Mathematical modeling of groundwater flow and solute transport in saturated fractured rock using a dual-porosity approach. J. Hydrol. Eng. 2014, 19, 04014033. [Google Scholar] [CrossRef]
- Cao, P.; Liu, J.; Leong, Y.K. A fully coupled multiscale shale deformation-gas transport model for the evaluation of shale gas extraction. Fuel 2016, 178, 103–117. [Google Scholar] [CrossRef]
- Pruess, K. On water seepage and fast preferential flow in heterogeneous, unsaturated rock fractures. J. Contam. Hydrol. 1998, 30, 333–362. [Google Scholar] [CrossRef] [Green Version]
- De Dreuzy, J.R.; Méheust, Y.; Pichot, G. Influence of fracture scale heterogeneity on the flow properties of three-dimensional discrete fracture networks (DFN). J. Geophys. Res. Solid Earth 2012, 117. [Google Scholar] [CrossRef] [Green Version]
- Santillán, D.; Mosquera, J.C.; Cueto-Felgueroso, L. Fluid-driven fracture propagation in heterogeneous media: Probability distributions of fracture trajectories. Phys. Rev. E 2017, 96, 053002. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Tang, C.; Zhu, W.; Liang, Z. Numerical analysis of slope stability based on the gravity increase method. Comput. Geotech. 2009, 36, 1246–1258. [Google Scholar] [CrossRef]
- Srivastava, A.; Babu, G.S.; Haldar, S. Influence of spatial variability of permeability property on steady state seepage flow and slope stability analysis. Eng. Geol. 2010, 110, 93–101. [Google Scholar] [CrossRef]
- Kumar, A.; Hu, R.; Walsh, S.D. Development of Reduced Order Hydro-mechanical Models of Fractured Media. Rock Mech. Rock Eng. 2021, 1–14. [Google Scholar] [CrossRef]
- Berkowitz, B.; Scher, H. Anomalous transport in random fracture networks. Phys. Rev. Lett. 1997, 79, 4038. [Google Scholar] [CrossRef]
- Fu, P.; Hao, Y.; Walsh, S.D.; Carrigan, C.R. Thermal drawdown-induced flow channeling in fractured geothermal reservoirs. Rock Mech. Rock Eng. 2016, 49, 1001–1024. [Google Scholar] [CrossRef]
- Kang, P.K.; Lei, Q.; Dentz, M.; Juanes, R. Stress-induced anomalous transport in natural fracture networks. Water Resour. Res. 2019, 55, 4163–4185. [Google Scholar] [CrossRef] [Green Version]
- N∄tinger, B. The effective permeability of a heterogeneous porous medium. Transp. Porous Media 1994, 15, 99–127. [Google Scholar]
- Baek, S.H.; Kim, C.Y.; Kim, K.Y.; Hong, S.W.; Moon, H.K. A numerical study on the effect of heterogeneous/anisotropic nature of rock masses on displacement behavior of tunnel. Tunn. Undergr. Space Technol. 2006, 21, 391. [Google Scholar] [CrossRef]
- Kong, P.; Jiang, L.; Shu, J.; Sainoki, A.; Wang, Q. Effect of fracture heterogeneity on rock mass stability in a highly heterogeneous underground roadway. Rock Mech. Rock Eng. 2019, 52, 4547–4564. [Google Scholar] [CrossRef]
- Long, J.C.S.; Remer, J.S.; Wilson, C.R.; Witherspoon, P.A. Porous media equivalents for networks of discontinuous fractures. Water Resour. Res. 1982, 18, 645–658. [Google Scholar] [CrossRef] [Green Version]
- Cesano, D.; Bagtzoglou, A.C.; Olofsson, B. Quantifying fractured rock hydraulic heterogeneity and groundwater inflow prediction in underground excavations: The heterogeneity index. Tunn. Undergr. Space Technol. 2003, 18, 19–34. [Google Scholar] [CrossRef]
- Farhadian, H.; Katibeh, H.; Huggenberger, P. Empirical model for estimating groundwater flow into tunnel in discontinuous rock masses. Environ. Earth Sci. 2016, 75, 471. [Google Scholar] [CrossRef]
- Zeng, J.; Wang, X.; Guo, J.; Zeng, F. Composite linear flow model for multi-fractured horizontal wells in heterogeneous shale reservoir. J. Nat. Gas Sci. Eng. 2017, 38, 527–548. [Google Scholar] [CrossRef]
- You, X.T.; Liu, J.Y.; Jia, C.S.; Li, J.; Liao, X.Y.; Zheng, A.W. Production data analysis of shale gas using fractal model and fuzzy theory: Evaluating fracturing heterogeneity. Appl. Energy 2019, 250, 1246–1259. [Google Scholar] [CrossRef]
- Pruess, K.; Wang, J.; Tsang, Y. On thermohydrologic conditions near high-level nuclear wastes emplaced in partially saturated fractured tuff: 2. Effective continuum approximation. Water Resour. Res. 1990, 26, 1249–1261. [Google Scholar]
- Witherspoon, P.A.; Wang, J.S.; Iwai, K.; Gale, J.E. Validity of cubic law for fluid flow in a deformable rock fracture. Water Resour. Res. 1980, 16, 1016–1024. [Google Scholar] [CrossRef] [Green Version]
- Zimmerman, R.W.; Bodvarsson, G.S. Hydraulic conductivity of rock fractures. Transp. Porous Media 1996, 23, 1–30. [Google Scholar] [CrossRef] [Green Version]
- Waite, M.E.; Ge, S.; Spetzler, H.; Bahr, D.B. The effect of surface geometry on fracture permeability: A case study using a sinusoidal fracture. Geophys. Res. Lett. 1998, 25, 813–816. [Google Scholar] [CrossRef]
- Teng, T.; Gao, F.; Ju, Y.; Xue, Y. How moisture loss affects coal porosity and permeability during gas recovery in wet reservoirs? Int. J. Min. Sci. Technol. 2017, 27, 899–906. [Google Scholar] [CrossRef]
- Wang, K.; Liu, A.; Zhou, A. Theoretical analysis of influencing factors on resistance in the process of gas migration in coal seams. Int. J. Min. Sci. Technol. 2017, 27, 315–319. [Google Scholar] [CrossRef]
- Javanmard, H.; Ebigbo, A.; Walsh, S.D.; Saar, M.O.; Vogler, D. No-Flow Fraction (NFF) permeability model for rough fractures under normal stress. Water Resour. Res. 2021, 57, e2020WR029080. [Google Scholar] [CrossRef]
- Iwai, K. Fundamental Studies of Fluid Flow through a Single Fracture. Ph.D. Thesis, University of California, Berkeley, CA, USA, 1976. [Google Scholar]
- Barton, N.; Bandis, S.; Bakhtar, K. Strength, deformation and conductivity coupling of rock joints. In International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts; Elsevier: Amsterdam, The Netherlands, 1985; Volume 22, pp. 121–140. [Google Scholar]
- Chen, M.; Bai, M.; Roegiers, J.C. Permeability tensors of anisotropic fracture networks. Math. Geol. 1999, 31, 335–373. [Google Scholar] [CrossRef]
- Snow, D.T. Anisotropie permeability of fractured media. Water Resour. Res. 1969, 5, 1273–1289. [Google Scholar] [CrossRef]
- Seidle, J.; Jeansonne, M.; Erickson, D. Application of matchstick geometry to stress dependent permeability in coals. In Proceedings of the SPE Rocky Mountain Regional Meeting. Society of Petroleum Engineers, Casper, Wyoming, 18–21 May 1992. [Google Scholar]
- Liu, H.H.; Rutqvist, J. A new coal-permeability model: Internal swelling stress and fracture–matrix interaction. Transp. Porous Media 2010, 82, 157–171. [Google Scholar] [CrossRef] [Green Version]
- Chen, D.; Pan, Z.; Ye, Z. Dependence of gas shale fracture permeability on effective stress and reservoir pressure: Model match and insights. Fuel 2015, 139, 383–392. [Google Scholar] [CrossRef]
- Yan, Z.; Wang, K.; Zang, J.; Wang, C.; Liu, A. Anisotropic coal permeability and its stress sensitivity. Int. J. Min. Sci. Technol. 2019, 29, 507–511. [Google Scholar] [CrossRef]
- Zheng, G.; Pan, Z.; Chen, Z.; Tang, S.; Connell, L.D.; Zhang, S.; Wang, B. Laboratory study of gas permeability and cleat compressibility for CBM/ECBM in Chinese coals. Energy Explor. Exploit. 2012, 30, 451–476. [Google Scholar] [CrossRef] [Green Version]
- Lei, G.; Cao, N.; McPherson, B.J.; Liao, Q.; Chen, W. A novel Analytical Model for pore Volume compressibility of fractal porous Media. Sci. Rep. 2019, 9, 1–11. [Google Scholar]
- Tan, Y.; Pan, Z.; Feng, X.T.; Zhang, D.; Connell, L.D.; Li, S. Laboratory characterisation of fracture compressibility for coal and shale gas reservoir rocks: A review. Int. J. Coal Geol. 2019, 204, 1–7. [Google Scholar] [CrossRef]
- Renshaw, C.E. On the relationship between mechanical and hydraulic apertures in rough-walled fractures. J. Geophys. Res. Solid Earth 1995, 100, 24629–24636. [Google Scholar] [CrossRef]
- Monsalve, J.J.; Baggett, J.; Bishop, R.; Ripepi, N. Application of laser scanning for rock mass characterization and discrete fracture network generation in an underground limestone mine. Int. J. Min. Sci. Technol. 2019, 29, 131–137. [Google Scholar] [CrossRef]
- Tonks, M.R.; Gaston, D.; Millett, P.C.; Andrs, D.; Talbot, P. An object-oriented finite element framework for multiphysics phase field simulations. Comput. Mater. Sci. 2012, 51, 20–29. [Google Scholar] [CrossRef]
- Podgorney, R.; Huang, H.; Gaston, D. Massively Parallel Fully Coupled Implicit Modeling of Coupled Thermal-Hydrological-Mechanical Processes for Enhanced Geothermal System Reservoirs; Stanford Geothermal Workshop: Stanford, CA, USA, 2010. [Google Scholar]
- Wilkins, A.; Green, C.P.; Ennis-King, J. PorousFlow: A multiphysics simulation code for coupled problems in porous media. J. Open Source Softw. 2020, 5, 2176. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, R.; Walsh, S.D.C. Effective Continuum Approximations for Permeability in Brown-Coal and Other Large-Scale Fractured Media. Geosciences 2021, 11, 511. https://doi.org/10.3390/geosciences11120511
Hu R, Walsh SDC. Effective Continuum Approximations for Permeability in Brown-Coal and Other Large-Scale Fractured Media. Geosciences. 2021; 11(12):511. https://doi.org/10.3390/geosciences11120511
Chicago/Turabian StyleHu, Roger, and Stuart D. C. Walsh. 2021. "Effective Continuum Approximations for Permeability in Brown-Coal and Other Large-Scale Fractured Media" Geosciences 11, no. 12: 511. https://doi.org/10.3390/geosciences11120511
APA StyleHu, R., & Walsh, S. D. C. (2021). Effective Continuum Approximations for Permeability in Brown-Coal and Other Large-Scale Fractured Media. Geosciences, 11(12), 511. https://doi.org/10.3390/geosciences11120511




