Modeling and Simulation of Tsunami Impact: A Short Review of Recent Advances and Future Challenges
Abstract
1. Introduction
2. State of the Field in Tsunami Forward Modeling
3. Mathematical Representations and Assumptions
3.1. The 3D Navier–Stokes Equations
3.2. Depth-Averaged Models
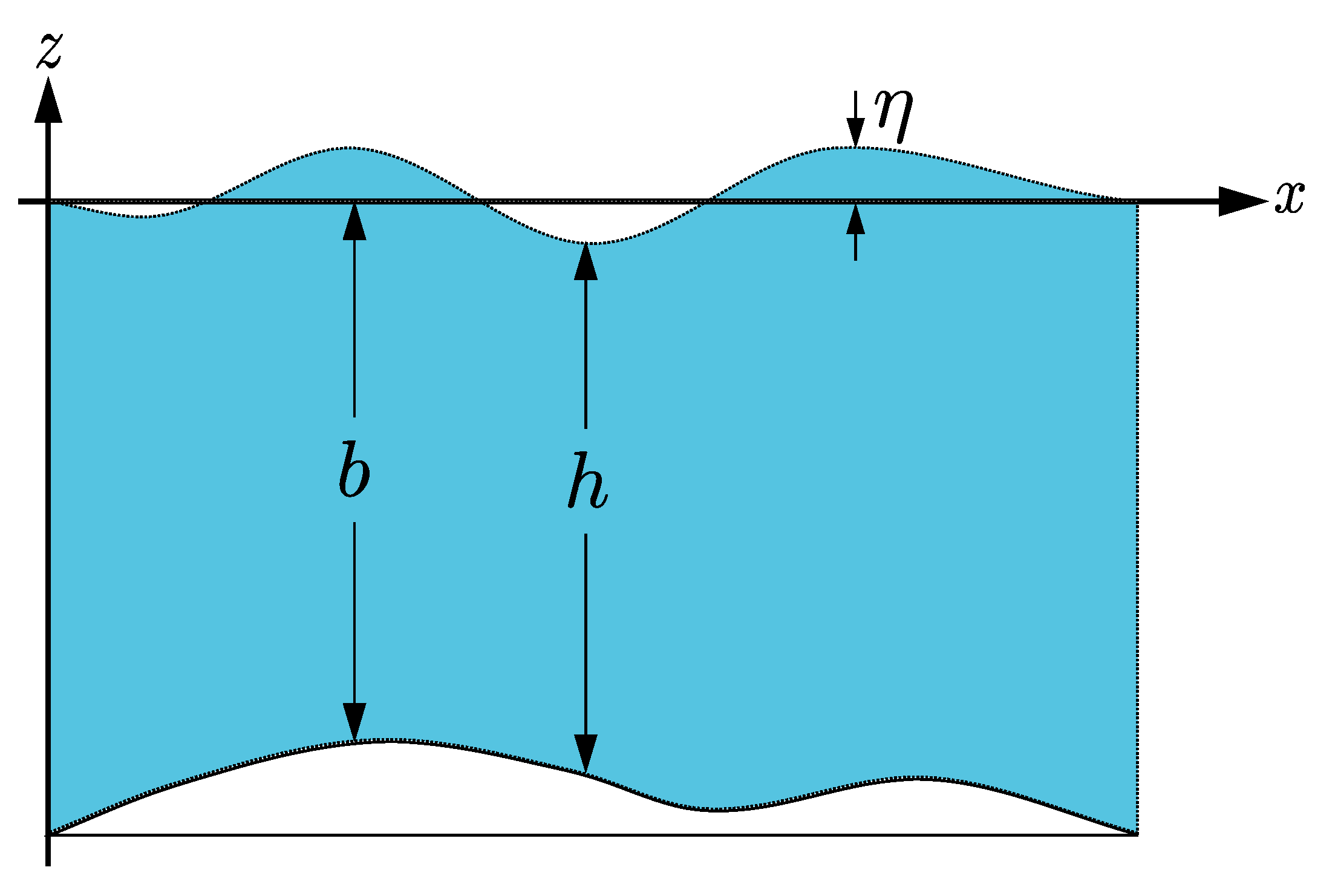
3.2.1. Scaled Equations
3.2.2. Depth Integration
3.2.3. Approximations
3.2.4. Shallow Water
3.2.5. Not So Shallow Equations
3.3. Mathematical Conclusions
4. Numerical Solution and Computational Considerations
- Flow scale and régime. For example, are we modeling breaking waves in the vicinity of the shore or linear waves propagating in the ocean basin? Is turbulence an important factor?
- Complexity of the physics needed. Here the difference between using a wall boundary condition at the shore and doing true wetting and drying may be significant as does the representation of true turbulent flow.
- Performance on the computing architecture being considered.
- Overall size of the problem considered. Is one interested in a single simulation or a large ensemble in order to account for uncertainty?
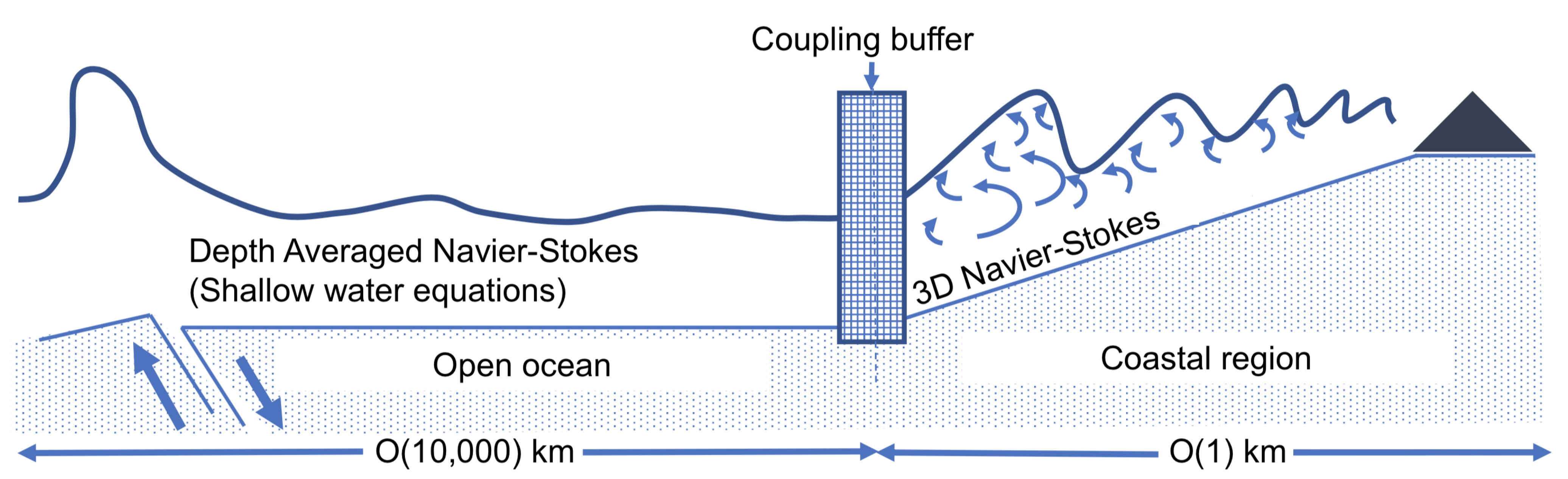
5. Towards a Multi-Scale Framework from Source to Impact
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Model | Space Dim. | Equations | Turbul. | Wave Break. | FSI | MP | SD |
|---|---|---|---|---|---|---|---|
| GeoCLAW [56] | 1D/2D/2D | No | No | No | No | FV | |
| NUMA2D [125,126] | 1D/2D | No | No | No | No | SE/DG | |
| MOST [92] | 1D/2D | No | No | No | No | FD | |
| Cliffs [92,127] | 1D/2D | No | No | No | No | FD | |
| Tsunami-HySEA [128,129,130] | 1D/2D | No | Yes | No | No | FV | |
| Multilayer-HySEA [131,132] | 1D/2D(1/2) | No | Yes | No | Yes | FV | |
| TUNAMI [133,134] | 1D/2D | No | No | No | No | FD | |
| NAMI-DANCE [135] | 1D/2D | No | No | No | No | FD | |
| COMCOT [136] | 1D/2D | No | No | No | No | FD | |
| SELFE [96] | 1D/2D | No | No | No | No | FE | |
| TsunAWI [97] | 1D/2D | No | No | No | No | FE | |
| TsunaFlash [137] | 1D/2D | No | No | No | No | FE/DG | |
| VOLNA [94,138] | 1D/2D | No | No | No | No | FV | |
| Delft3D [139] | 1D/2D | No | No | No | Yes | FD | |
| Basilisk [140,141,142] | 2D/3D | No | Yes | No | Yes | FV | |
| BOSZ [143] | 1D/2D | B | No | No | No | No | FV/FD |
| Celeris [144] | 1D/2D | B | No | No | No | No | FV |
| FUNWAVE [145,146] | 1D/2D | B | No | No | No | No | FV/FD |
| pCOULWAVE [147,148] | 2D/3D | B | Yes | No | No | No | FV |
| NEOWAVE [149] | 2D | B | No | No | No | No | FD |
| GPUSPH [98] | 3D | No | Yes | No | No | SPH | |
| SCHISM [111] | 1D/2D/3D | Yes | No | No | FE/FV | ||
| COBRAS [108,109] | 2D/3D | Yes | No | No | FD | ||
| TSUNAMI3D [110,150] | 2D/3D | Yes | No | No | FD | ||
| waves2FOAM [17,18,112] | 2D (tsunami) | Yes | No | No | FV | ||
| NHWAVE [151] | 2D/3D | LES | Yes | Yes | Yes | FV/FD | |
| Alya [90,152] | 2D/3D | Yes | Yes | Yes | FE |
References
- Ishiwatari, M.; Sagara, J. Structural Measures against Tsunamis; World Bank: Washington, DC, USA, 2012; Available online: http://hdl.handle.net/10986/16160 (accessed on 21 December 2020).
- Reuters. Seven Years after Tsunami, Japanese Live Uneasily with Seawalls. 2018. Available online: https://www.reuters.com/article/us-japan-disaster-seawalls/seven-years-after-tsunami-japanese-live-uneasily-with-seawalls-idUSKCN1GL0DK (accessed on 21 December 2020).
- Guardian, T. After the Tsunami: Japan’s Sea Walls–in Pictures. 2018. Available online: https://www.theguardian.com/world/gallery/2018/mar/09/after-the-tsunami-japan-sea-walls-in-pictures (accessed on 21 December 2020).
- Economist, T. The Great Wall of Japan. 2014. Available online: https://www.economist.com/asia/2014/06/14/the-great-wall-of-japan (accessed on 21 December 2020).
- Times, N.Y. Seawalls Offered Little Protection against Tsunami’s Crushing Waves. 2011. Available online: https://www.nytimes.com/2011/03/14/world/asia/14seawalls.html (accessed on 21 December 2020).
- Wired, W. Ominous Views of Japan’s New Concrete Seawalls. 2018. Available online: https://www.wired.com/story/photo-gallery-japan-seawalls/ (accessed on 21 December 2020).
- Peterson, M.; Lowe, M. Implications of Cumulative Impacts to Estuarine and Marine Habitat Quality for Fish and Invertebrate Resources. Rev. Fish. Sci. 2009, 17, 505–523. [Google Scholar] [CrossRef]
- Dugan, J.; Hubbard, D. Ecological Effects of Coastal Armoring: A Summary of Recent Results for Exposed Sandy Beaches in Southern California. In Puget Sound Shorelines and the Impacts of Armoring; US Geological Survey Scientific Investigations Report; Shipman, H., Dethier, M., Gelfenbaum, G., Fresh, K., Dinicola, R., Eds.; USGS: Reston, VA, USA, 2010. [Google Scholar]
- Bulleri, F.; Chapman, M. The introduction of coastal infrastructure as a driver of change in marine environments. J. Appl. Ecol. 2010, 47, 26–35. [Google Scholar] [CrossRef]
- Dean, R.G.; Dalrymple, R.A. Coastal Processes with Engineering Applications; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Komar, P. Beach Processes and Sedimentation; Prantice Hall: Upper Saddle River, NJ, USA, 1998. [Google Scholar]
- Lunghino, B.; Santiago Tate, A.; Mazereeuw, M.; Muhari, A.; Giraldo, F.; Marras, S.; Suckale, J. The protective benefits of tsunami mitigation parks and ramifications for their strategic design. Proc. Nat. Acad. Sci. USA 2020, 117, 10740–10745. [Google Scholar] [CrossRef] [PubMed]
- Renew Yamada. 2011. Available online: http://renewyamada.org (accessed on 10 July 2020).
- Behrens, J.; Dias, F. New computational methods in tsunami science. Philos. Trans. R. Soc. A 2015, 373, 20140382. [Google Scholar] [CrossRef]
- Qin, X.; Motley, M.; LeVeque, R.; González, F.; Mueller, K. A comparison of a two-dimensional depth-averaged flow model and a three-dimensional RANS model for predicting tsunami inundation and fluid forces. Nat. Hazards Earth Syst. Sci. 2018, 18, 2489–2506. [Google Scholar] [CrossRef]
- Prasetyo, A.; Yasuda, T.; Miyashita, T.; Mori, N. Physical Modeling and Numerical Analysis of Tsunami Inundation in a Coastal City. Front. Built Environ. 2019, 5, 46. [Google Scholar] [CrossRef]
- Larsen, B.; Fuhrman, D. Full-scale CFD simulation of tsunamis. Part 1: Model validation and run-up. Coast. Eng. 2019, 151, 22–41. [Google Scholar] [CrossRef]
- Larsen, B.; Fuhrman, D. Full-scale CFD simulation of tsunamis. Part 2: Boundary layers and bed shear stresses. Coast. Eng. 2019, 151, 42–57. [Google Scholar] [CrossRef]
- Bernard, E.; Mofjeld, H.; Titov, V.; Synolakis, C.; González, F. Tsunami: Scientific frontiers, mitigation, forecasting and policy implications. Philos. Trans. Roy. Soc. A Math. Phys. Eng. Sci. 2006, 364, 1989–2007. [Google Scholar] [CrossRef]
- NHERI. Natural Hazards Research Infrastructure: Five-Year Science Plan, 2nd ed.; Technical Report; NHERI: Salem, OR, USA, 2020.
- Chen, J.; Huang, Z.; Jiang, C.; Deng, B.; Long, Y. An experimental study of changes of beach profile and mean grain size caused by tsunami-like waves. J. Coast. Res. 2012, 28, 1303–1312. [Google Scholar] [CrossRef]
- Jiang, C.; Chen, J.; Yao, Y.; Liu, J.; Deng, Y. Study on threshold motion of sediment and bedload transport by tsunami waves. Ocean Eng. 2015, 100, 97–106. [Google Scholar] [CrossRef]
- Aida, I. Numercal experiments for the tsunami propagation of the 1964 Niigata tsunami and 1968 Tokachi-Oki tsunami. Bull. Earthq. Res. Int. Univ. Tokyo 1969, 47, 673–700. [Google Scholar]
- Aida, I. Numerical computational of a tsunami based on a fault origin model of an earthquake. J. Seismol. Soc. Jpn. 1974, 27, 141–154. [Google Scholar]
- Borrero, J.C.; Legg, M.R.; Synolakis, C.E. Tsunami sources in the southern California bight. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef]
- Pelties, C.; de la Punte, P.; Ampuero, J.P.; Brietzke, G.; Käser, M. Three-dimensional dynamic rupture simulation with a high-order discontinuous Galerkin method on unstructured tetrahedral meshes. J. Geophys. Res. 2012, 117, 2156–2202. [Google Scholar] [CrossRef]
- López-Venegas, A.; Horrillo, J.; Pampell-Manis, A.; Huérfano, V.; Mercado, A. Advanced Tsunami Numerical Simulations and Energy Considerations by use of 3D-2D coupled Models: The October 11, 1918, Mona Passage Tsunami. Pure App. Geophys. 2014, 171, 2863–3174. [Google Scholar] [CrossRef]
- Gálvez, P.; Ampuero, J.P.; Dalguer, L.; Somala, S.N.; Nissen-Meyer, T. Dynamic earthquake rupture modelled with an unstructured 3-D spectral element method applied to the 2011 M9 Tohoku earthquake. Geophys. J. Int. 2014, 198, 1222–1240. [Google Scholar]
- Ulrich, T.; Vater, S.; Madden, E.; Behrens, J.; van Dinther, Y.; van Zelst, I.; Fielding, J.; Liang, C.; Gabriel, A.A. Coupled, Physics-Based Modeling Reveals Earthquake Displacements are Critical to the 2018 Palu, Sulawesi Tsunami. Pure Appl. Geophys. 2019, 176, 4069–4109. [Google Scholar] [CrossRef]
- Titov, V.; González, F.; Bernard, E.; Eble, M.C.; Mofjeld, H.; Newman, J.C.; Venturato, A. Real-Time Tsunami Forecasting: Challenges and Solutions. Nat. Hazards 2005, 35, 41–58. [Google Scholar] [CrossRef]
- LeVeque, R.; George, D.; Berger, M. Tsunami modelling with adaptively refined finite volume methods. Acta Numer. 2011, 20, 211–289. [Google Scholar] [CrossRef]
- Bonev, B.; Hesthaven, J.S.; Giraldo, F.X.; Kopera, M.A. Discontinuous Galerkin scheme for the spherical shallow water equations with applications to tsunami modeling and prediction. J. Comput. Phys. 2018, 362, 425–448. [Google Scholar] [CrossRef]
- Lynett, P.J. Effect of a shallow water obstruction on long wave runup and overland flow velocity. J. Waterw. Port Coastal Ocean Eng. 2007, 133, 455–462. [Google Scholar] [CrossRef]
- Park, H.; Cox, D.T.; Lynett, P.J.; Wiebe, D.M.; Shin, S. Tsunami inundation modeling in constructed environments: A physical and numerical comparison of free-surface elevation, velocity, and momentum flux. Coast. Eng. 2013, 79, 9–21. [Google Scholar] [CrossRef]
- Oishi, Y.; Imamura, F.; Sugawara, D. Near-field tsunami inundation forecast using the parallel TUNAMI-N2 model: Application to the 2011 Tohoku-Oki earthquake combined with source inversions. Geo. Res. Lett. 2015, 42, 1083–1091. [Google Scholar] [CrossRef]
- Vater, S.; Beisiegel, N.; Behrens, J. A limiter-based well-balanced discontinuous Galerkin method for shallow-water flows with wetting and drying: One-dimensional case. Adv. Water Resour. 2015, 85, 1–13. [Google Scholar] [CrossRef]
- Vater, S.; Beisiegel, N.; Behrens, J. A limiter-based well-balanced discontinuous Galerkin method for shallow-water flows with wetting and drying: Triangular grids. Int. J. Numer. Methods Fluids 2019, 91, 395–418. [Google Scholar] [CrossRef]
- Ayog, J.; Kesserwani, G.; Shaw, J.; Sharifian, M.; Bau, D. Second-order discontinuous Galerkin flood model: Comparison with industry-standard finite volume models. arXiv 2020, arXiv:2010.02003. [Google Scholar]
- Lin, P. A numerical study of solitary wave interaction with rectangular obstacles. Coast. Eng. 2004, 51, 35–51. [Google Scholar] [CrossRef]
- Apotsos, A.; Jaffe, B.; Gelfenbaum, G. Wave characteristic and morphologic effects on the onshore hydrodynamic response of tsunamis. Coast. Eng. 2011, 58, 1034–1048. [Google Scholar] [CrossRef]
- Okal, E.; Synolakis, C. Sequencing of tsunami waves: Why the first wave is not always the largest. Geophys. J. Int. 2015, 204, 719–735. [Google Scholar] [CrossRef]
- Lynett, P.; Borrero, J.; Weiss, R.; Greer, D.; Renteria, W. Observations and modeling of tsunami-induced currents in ports and harbors. Earth Planet. Sci. Lett. 2012, 327–328, 68–74. [Google Scholar] [CrossRef]
- Borrero, J.; Lynett, P.; Kalligeris, N. Tsunami currents in ports. Phil. Trans. R. Soc. A 2015, 373, 20140372. [Google Scholar] [CrossRef] [PubMed]
- Borrero, J.; Synolakis, C.; Fritz, H. Northern Sumatra field survey after the December 2004 Great Sumatra Earthquake and Indian Ocean tsunami. Earthq. Spectra 2006, 22, S93–S104. [Google Scholar] [CrossRef]
- Paris, R.; Wassmer, P.; Sartohadi, J.; Lavigne, F.; Barthomeuf, B.; Desgages, E.; Grancher, D.; Baumert, P.; Vautier, F.; Brunstein, D.; et al. Tsunamis as geomorphic crises: Lessons from the december 26, 2004 tsunami in Lhok Nga, West Banda Aceh (Sumatra, Indonesia). Geomorphology 2009, 104, 59–72. [Google Scholar] [CrossRef]
- Kato, F.; Noguchi, K.; Suwa, Y.; Sakagami, T.; Sato, Y. Field survey on tsunami induced topographical change. J. Jpn. Soc. Civil Engrs. Ser. B3 2012, 68, 174–179. [Google Scholar]
- Kuriyama, Y.; Takahashi, K.; Yanagishima, S.; Tomita, T. Beach profile change at Hasaki, Japan caused by 5-m-high tsunami due to the 2011 off the Pacific coast of Tohoku earthquake. Mar. Geol. 2014, 355, 234–243. [Google Scholar] [CrossRef]
- Yamashita, K.; Sugawara, D.; Takahashi, T.; Imamura, F.; Saito, Y.; Imato, Y.; Kai, T.; Uehara, H.; Kato, T.; Nakata, K.; et al. Numerical simulations of large-scale sediment transport caused by the 2011 Tohoku earthquake tsunami in Hirota Bay. Southern Sanriku Coast. Coast. Eng. 2016, 58, 1640015. [Google Scholar] [CrossRef]
- Udo, K.; Takeda, Y.; Tanaka, H. Coastal morphology change before and after 2011 off the Pacific coast of Tohoku earthquake tsunami at Rikuzen-Takata coast. Coast. Eng. 2016, 58, 1640016. [Google Scholar] [CrossRef]
- Levin, B.; Nosov, M. Physics of Tsunamis; Springer: Amsterdam, The Netherlands, 2016. [Google Scholar]
- Li, L.; Qiu, Q.; Huang, Z. Numerical modeling of the morphological change in Lhok Nga, West Banda Aceh, during the 2004 Indian Ocean tsunami: Understanding tsunami deposits using a forward modeling method. Nat. Hazards 2012, 64, 1549–1574. [Google Scholar] [CrossRef]
- Ontowirjo, B.; Paris, R.; Mano, A. Modeling of coastal erosion and sediment deposition during the 2004 Indian Ocean tsunami in Lhok Nga, Sumatra, Indonesia. Nat. Hazards 2013, 65, 1967–1979. [Google Scholar] [CrossRef]
- Sugawara, D.; Takahashi, T.; Imamura, F. Sediment transport due to the 2011 Tohoku-Oki tsunami at Sendai: Results from numerical modeling. Mar. Geol. 2014, 358, 18–37. [Google Scholar] [CrossRef]
- Garres-Díaz, J.; Castro Díaz, M.; Koellermeier, J.; Morales de Luna, T. Shallow Water Moment models for bedload transport problems. arXiv 2020, arXiv:2008.08449. [Google Scholar]
- OpenFOAM v2.3.1. 2014. Available online: https://openfoam.org/release/2-3-1/ (accessed on 21 December 2020).
- Berger, M.; George, D.; LeVeque, R.; Mandli, K. The GeoClaw software for depth-averaged flows with adaptive refinement. Adv. Water Res. 2011, 34, 1195–1206. [Google Scholar] [CrossRef]
- Hsiao, S.C.; Lin, T.C. Tsunami-like solitary waves impinging and overtopping an impermeable seawall: Experiment and RANS modeling. Coast. Eng. 2010, 57, 1–8. [Google Scholar] [CrossRef]
- Larsen, B.; Fuhrman, D. On the over-production of turbulence beneath surface waves in Reynold-averaged Navier-Stokes models. J. Fluid Mech. 2018, 853, 419–460. [Google Scholar] [CrossRef]
- Christensen, E. Large eddy simulation of spilling and plunging breakers. Coast. Eng. 2006, 53, 463–485. [Google Scholar] [CrossRef]
- Meiburg, E.; Radhakrishnan, S.; Nasr-Azadani, M. Modeling Gravity and Turbidity Currents: Computational Approaches and Challenges. Appl. Mech. Rev. 2015, 67, 40802. [Google Scholar] [CrossRef]
- Yu, X.; Ozdemir, C.E.; Hsu, T.J.; Balachandar, S. Numerical Investigation of Turbulence Modulation by Sediment-Induced Stratification and Enhanced Viscosity in Oscillatory Flows. J. Waterw. Port Coast. Ocean Eng. 2014, 140, 160–172. [Google Scholar] [CrossRef]
- Uhlmann, M. An immersed boundary method with direct forcing for the simulation of particulate flows. J. Comput. Phys. 2005, 209, 448–476. [Google Scholar] [CrossRef]
- Lynett, P.J.; Gately, K.; Wilson, R.; Montoya, L.; Arcas, D.; Aytore, B.; Bai, Y.; Bricker, J.D.; Castro, M.J.; Cheung, K.F.; et al. Inter-model analysis of tsunami-induced coastal currents. Ocean Model. 2017, 114, 14–32. [Google Scholar] [CrossRef]
- USACE. Interim Survey Report, Morgan City, Louisiana and Vicinity; Technical Report 63; US Army Engineer District: New Orleans, LA, USA, 1963.
- Fosberg, F.R.; Chapman, V. Mangroves v. tidal waves. Biol. Conserv. 1971, 4, 38–39. [Google Scholar] [CrossRef]
- Mazda, Y.; Magi, M.; Kogo, M.; Hong, P.N. Mangroves as a coastal protection from waves in the Tong King Delta, Vietnam. Mangroves Salt Marshes 1997, 1, 127–135. [Google Scholar] [CrossRef]
- Möller, I.; Spencer, T.; French, J.R.; Leggett, D.J.; Dixon, M. Wave transformation over salt marshes: A field and numerical modeling study from North Norfolk, England. Estuar Coast Shelf Sci. 1999, 49, 411–426. [Google Scholar] [CrossRef]
- Harada, K.; Imamura, F. Effects of coastal forest on tsunami hazard mitigation—A preliminary investigation. In Tsunamis; Springer: Berlin/Heidelberg, Germany, 2005; pp. 279–292. [Google Scholar]
- Tanaka, N.; Sasaki, Y.; Mowjood, M.; Jinadasa, K.; Homchuen, S. Coastal vegetation structures and their functions in tsunami protection: Experience of the recent Indian Ocean tsunami. Landsc. Ecol. Eng. 2007, 3, 33–45. [Google Scholar] [CrossRef]
- Tanaka, N.; Nandasena, N.; Jinadasa, K.; Sasaki, Y.; Tanimoto, K.; Mowjood, M. Developing effective vegetation bioshield for tsunami protection. Civ. Eng. Environ. Syst. 2009, 26, 163–180. [Google Scholar] [CrossRef]
- Stoesser, T.; Palau Salavador, G.; Rodi, W.; Diplas, P. Large eddy simulation of flow through submerged vegetation. Transp. Porous. Med. 2009, 78, 347–365. [Google Scholar] [CrossRef]
- Iimura, K.; Tanaka, N. Numerical simulation estimating effects of tree density distribution in coastal forest on tsunami mitigation. Ocean Eng. 2012, 54, 223–232. [Google Scholar] [CrossRef]
- Tanaka, N.; Jinadasa, K.; Mowjood, M.; Fasly, M. Coastal vegetation planting projects for tsunami disaster mitigation: Effectiveness evaluation of new establishments. Landsc. Ecol. Eng. 2011, 7, 127–135. [Google Scholar] [CrossRef]
- Tanaka, N. Effectiveness and limitations of vegetation bioshield in coast for tsunami disaster mitigagation. In The Tsunami Threat-Research and Technology; BoD-Books: Norderstedt, Germany, 2011. [Google Scholar]
- Thuy, N.B.; Tanaka, N.; Tanimoto, K. Tsunami mitigation by coastal vegetation considering the effect of tree breaking. J. Coast. Conserv. 2012, 16, 111–121. [Google Scholar] [CrossRef]
- Muhammad, R.; Tanaka, N. Energy Reduction of a Tsunami Current through a Hybrid Defense System Comprising a Sea Embankment Followed by a Coastal Forest. Geosciences 2019, 247, 1–27. [Google Scholar]
- Nepf, H. Drag, turbulence, and diffusion in flow through emergent vegetation. Water Resour. Res. 1999, 35, 479–489. [Google Scholar] [CrossRef]
- Bayas, J.; Marohn, C.; Dercon, G.; Dewi, S.; Piepho, H.; Joshi, L.; van Noordwijk, M.; Cadisch, G. Influence of coastal vegetation on the 2004 tsunami wave impact in West Aceh. Proc. Natl. Acad. Sci. USA 2011, 108, 18612–18617. [Google Scholar] [CrossRef]
- Westerink, J.; Luettich, R.; Baptista, A.; Scheffner, N.; Farrar, P. Tide and storm surge predictions using finite element model. ASCE J. Hydraul. Eng. 1992, 118, 1373–1390. [Google Scholar] [CrossRef]
- Kânoğlu, U.; Synolakis, C. Long wave runup on piecewise linear topographies. J. Fluid Mech. 1998, 374, 1–28. [Google Scholar] [CrossRef]
- Westerink, J.; Luettich, R.; Feyen, J.; Atkinson, J.; Dawson, C.; Roberts, H.; Powell, M.; Dunion, J.; Kubatko, E.; Pourtaheri, H. A basin-to-channel-scale unstructured grid hurricane storm surge model applied to southern Louisiana. Mon. Weather Rev. 2008, 136, 833–864. [Google Scholar] [CrossRef]
- Sun, F.; Carson, R. Coastal wetlands reduce property damage during tropical cyclones. Proc. Natl. Acad. Sci. USA 2020, 117, 5719–5725. [Google Scholar] [CrossRef] [PubMed]
- Jackson, N.; Nordstrom, K.; Feagin, R.; Smith, W. Coastal geomorphology and restoration. Geomorphology 2013, 199, 1–7. [Google Scholar] [CrossRef]
- Day, J.; Boesch, D.; Clairain, E.E.A. Restoration of the Mississippi Delta: Lessons from Hurricanes Katrina and Rita. Science 2007, 315, 1679–1684. [Google Scholar] [CrossRef]
- Gedan, K.; Kirwan, M.; Wolanski, E.; Barbier, E.; Silliman, B. The present and future role of coastal wetland vegetation in protecting shorelines: Answering recent challenges to the paradigm. Clim. Chang. 2011, 106, 7–29. [Google Scholar] [CrossRef]
- Shephard, C.; Crain, C.; Beck, M. The protective role of coastal marshes: A systematic review and meta-analysis. PLoS ONE 2012, 6, e27374. [Google Scholar]
- Horstman, E.; Dohmen-Janssen, C.; Narra, P.; van den Berg, N.; Siemerink, M.; Hulscher, S. Wave attenuation in mangroves: A quantitative approach to field observations. Coast. Eng. 2014, 94, 47–62. [Google Scholar] [CrossRef]
- Mattis, S.; Dawson, C.; Kees, C.; Farthing, M. An immersed structure approach for fluid-vegetation interaction. Adv. Water Res. 2015, 80, 1–6. [Google Scholar] [CrossRef]
- Mattis, S.; Kees, C.; Wei, M.; Dimakopoulos, A.; Dawson, C.N. Computational Model for Wave Attenuation by Flexible Vegetation. J. Waterw. Port Coast. Ocean Eng. 2019, 145, 04018033. [Google Scholar] [CrossRef]
- Mukherjee, A.; Cajas, J.; Houzeaux, G.; Lehmkuhl, O.; Vázquez, M.; Suckale, J.; Marras, S. Using fluid-structure interaction to evaluate the energy dissipation of a tsunami run-up through idealized flexible trees. In Proceedings of the ParCFD’2020 32nd International Conference on Parallel Computational Fluid Dynamics, Nice, France, 11–13 May 2020. [Google Scholar]
- Synolakis, C.; Bernard, E. Tsunami science before and beyond boxing day. Philos. Trans. Roy. Soc. Lond. 2006, 364, 2231–2265. [Google Scholar]
- Titov, V.V.; González, F. Implementation and Testing of the Method Of Splitting Tsunami (MOST) Model; NOAA Technical Memorandum ERL PMEL-112 1927; Technical Report; NOAA: Seattle, WA, USA, 1997.
- George, D.L.; LeVeque, R.L. Finite volume methods and adaptive refinement for global tsunami propagation and local inundation. Sci. Tsunami Hazards 2006, 24, 319–328. [Google Scholar]
- Dutykh, D.; Poncet, R.; Dias, F. The VOLNA code for the numerical modeling of tsunami waves: Generation, propagation and inundation. Eur. J. Mech. B/Fluids 2011, 30, 598–615. [Google Scholar] [CrossRef]
- Mandli, K. A numerical method for the two layer shallow water equations with dry states. Ocean Model. 2013, 72, 80–91. [Google Scholar] [CrossRef]
- Zhang, Y.; Baptista, A. An efficient and robust tsunami model on unstructured grids. Part I: Inundation benchmarks. Pure Appl. Geophys. 2008, 165, 2229–2248. [Google Scholar] [CrossRef]
- Harig, S.; Chaeroni, X.; Pranowo, W.; Behrens, J. Tsunami simulations on several scales: Comparison of approaches with unstructured meshes and nested grids. Ocean Dyn. 2008, 58, 429–440. [Google Scholar] [CrossRef]
- Wei, Z.; Dalrympl, R.; Hérault, A.; Bilotta, G.; Rustico, E.; Yeh, H. SPH modeling of dynamic impact of tsunami bore on bridge pier. Coast. Eng. 2015, 104, 26–42. [Google Scholar] [CrossRef]
- Klapp, J.; Areu-Rangel, O.; Cruchaga, M.; Aranguiz, R.; Bonasia, R.; Godoy, M.; Silva-Casarín, R. Tsunami hydrodynamic force on a building using a SPH real-scale numerical simulation. Nat. Hazards 2020, 110, 89–109. [Google Scholar] [CrossRef]
- Behrens, J. Adaptive Atmospheric Modeling. Key Techniques in Grid Generation, Data Structures, and Numerical Operations with Applications; Springer: Berlin/Heidelberg, Germany, 2006; p. 207. [Google Scholar]
- Müller, A.; Kopera, M.; Marras, S.; Wilcox, L.; Isaac, T.; Giraldo, F. Strong scaling for numerical weather prediction at petascale with the atmospheric model NUMA. Int. J. High Perform. Comput. 2018, 33, 411–426. [Google Scholar] [CrossRef]
- Castro, M.; Ferreiro Ferreiro, A.; García-Rodriguez, J.; González-Vida, J.; Macías, J.; Parés, C.; Elena Vázquez-Cendón, M. The numerical treatment of wet/dry fronts in shallow flows: Application to one-layer and two-layer systems. Math. Comput. Model. 2005, 42, 419–439. [Google Scholar] [CrossRef]
- Bunya, S.; Kubatko, E.J.; Westerink, J.J.; Dawson, C. A wetting and drying treatment for the Runge–Kutta discontinuous Galerkin solution to the shallow water equations. Comput. Methods Appl. Mech. Eng. 2009, 198, 1548–1562. [Google Scholar] [CrossRef]
- Kesserwani, G.; Liang, Q. Well-balanced RKDG2 solutions to the shallow water equations over irregular domains with wetting and drying. Comput. Fluids 2010, 39, 2040–2050. [Google Scholar] [CrossRef]
- Berthon, C.; Marche, F.; Turpault, R. An efficient scheme on wet/dry transitions for shallow water equations with friction. Comput. Fluids 2011, 48, 192–201. [Google Scholar] [CrossRef]
- Le, H.; Lambrechts, J.; Ortleb, S.; Gratiot, N.; Deleersnijder, E.; Ao, S.F. An implicit wetting–drying algorithm for the discontinuous Galerkin method: Application to the Tonle Sap, Mekong River Basin. Environ. Fluid Mech. 2020, 20, 923–951. [Google Scholar] [CrossRef]
- Pope, S.B. Turbulent Flows; Cambridge University Press: Cambridge, UK, 2000; pp. 1–771. [Google Scholar]
- Lin, P.; Liu, P. A numerical study of breaking waves in the surf zone. J. Fluid Mech. 1998, 358, 239–264. [Google Scholar] [CrossRef]
- Lin, P.; Liu, P. Turbulence transport, vorticity dynamics, and solute mixing under plunging breaking waves in surf zone. J. Geophys. Res. 1998, 103, 15677–15694. [Google Scholar] [CrossRef]
- Horrillo, J.; Wood, A.; Kim, G.; Parambath, A. A simplified 3-D/Navier–Stokes numerical model for landslide tsunami: Application to the Gulf of Mexico. J. Geophys. Res./Oceans 2013, 118, 6934–6950. [Google Scholar] [CrossRef]
- Zhang, Y.; Ye, F.; Stanev, E.; Grashorn, S. Seamless cross-scale modeling with SCHISM, Ocean Modelling. Ocean Model. 2016, 102, 64–81. [Google Scholar] [CrossRef]
- Jacobsen, N.; Fuhrman, D.; Fredsoe, J. A wave generation toolbox for the open-source CFD library: OpenFOAM (R). Int. J. Numer. Methods Fluids 2012, 70, 1073–1088. [Google Scholar] [CrossRef]
- Ghosh, D.; Mittal, A.; Bhattacharyya, S. Multiphase modeling of tsunami impact on building with openings. J. Comput. Multiph. Flows 2016, 8, 85–94. [Google Scholar] [CrossRef][Green Version]
- Owen, H.; Houzeaux, G.; Samaniego, C.; Cucchietti, F.; Marin, G.; Tripiana, C.; Hadrien, C.; Vázquez, M. Two Fluids Level Set: High Performance Simulation and Post Processing. In Proceedings of the 2012 SC Companion: High Performance Computing, Networking Storage and Analysis, Salt Lake City, UT, USA, 10–16 November 2012. [Google Scholar]
- Madden, E.; Bader, M.; Behrens, J.; van Dinther, Y.; Gabriel, A.A.; Rannabauer, L.; Ulrich, T.; Uphoff, C.; Vater, S.; Wollherr, S.; et al. Linked 3D modeling of megathrust earthquake-tsunami events: From subduction to tsunami run up. Geophys. J. Int. 2020. [Google Scholar] [CrossRef]
- Pelinovscky, E.N. Non-linear hyperbolic equations and run-up of Huge sea waves. Appl. Anal. 1995, 57, 63–84. [Google Scholar] [CrossRef]
- Rivera, P. Modeling the Asian tsunami evolution and propagation with a new generation mechanism and non-linear dispersive wave model. Sci. Tsunami Hazards 2006, 25, 18–33. [Google Scholar]
- Baba, T.; Allgeyer, S.; Hossen, J.; Cummins, P.R.; Tsushima, H.; Imai, K.; Yamashita, K.; Kato, T. Accurate numerical simulation of the far-field tsunami caused by the 2011 Tohoku earthquake, including the effects of Boussinesq dispersion, seawater density stratification, elastic loading, and gravitational potential change. Ocean Model. 2017, 111, 46–54. [Google Scholar] [CrossRef]
- Chen, X. Dynamic coupling of a three-dimensional hydrodynamic model with a laterally averaged, two-dimensional hydrodynamic model. J. Geophys. Res. Ocean. 2007, 112. [Google Scholar] [CrossRef]
- Chen, X.J. Coupling an Unstructured Grid three-dimensional Model with a Laterally Averaged two-dimensional Model for Shallow Water Hydrodynamics and Transport Processes. Int. J. Numer. Methods Fluids 2020. [Google Scholar] [CrossRef]
- Bungartz, H.; Lindner, F.; Gatzhammer, B.; Mehl, M.; Scheufele, K.; Shukaev, A.; Uekermann, B. preCICE–a fully parallel library for multi-physics surface coupling. Comput. Fluids 2016, 141, 250–258. [Google Scholar] [CrossRef]
- Mehl, M.; Uekermann, B.; Bijl, H.; Blom, D.; Gatzhammer, B.; Van Zuijlen, A. Parallel coupling numerics for partitioned fluid–structure interaction simulations. Comput. Math. Appl. 2016, 71, 869–891. [Google Scholar] [CrossRef]
- Lotto, G.; Jeppson, T.; Dunham, E. Fully Coupled Simulations of Megathrust Earthquakes and Tsunamis in the Japan Trench, Nankai Trough, and Cascadia Subduction Zone. Pure Appl. Geophys. 2019, 176, 4009–4041. [Google Scholar] [CrossRef]
- ASCETE. Advanced Simulation of Coupled Earthquake and Tsunami Events. Available online: https://t3projects.cen.uni-hamburg.de/index.php?id=2099 (accessed on 21 December 2020).
- Marras, S.; Kopera, M.; Giraldo, F.X. Simulation of Shallow Water Jets with a Unified Element-based Continuous/Discontinuous Galerkin Model with Grid Flexibility on the Sphere. Q. J. Roy. Meteor. Soc. 2015, 141, 1727–1739. [Google Scholar] [CrossRef]
- Marras, S.; Kopera, M.; Constantinescu, E.; Suckale, J.; Giraldo, F. A Residual-based Shock Capturing Scheme for the Continuous/Discontinuous Spectral Element Solution of the 2D Shallow Water Equations. Adv. Water Res. 2018, 114, 45–63. [Google Scholar] [CrossRef]
- Tolkova, E. Land–water boundary treatment for a tsunami model with dimensional splitting. Pure Appl. Geophys. 2014, 171, 2289–2314. [Google Scholar] [CrossRef]
- Macías, J.; Castro, M.; Ortega, S.; Escalante, C.; González-Vida, J. Performance Benchmarking of Tsunami-HySEA Model for NTHMP’s Inundation Mapping Activities. Pure Appl. Geophys. 2017, 174, 3147–3183. [Google Scholar] [CrossRef]
- Macías, J.; Castro, M.; Ortega, S.; González-Vida, J. Performance assessment of Tsunami-HySEA model for NTHMP tsunami currents benchmarking. Field cases. Ocean Model. 2020, 152, 101645. [Google Scholar] [CrossRef]
- Macías, J.; Castro, M.; Escalante, C. Performance assessment of the Tsunami-HySEA model for NTHMP tsunami currents benchmarking. Laboratory data. Coast. Eng. 2020, 158, 103667. [Google Scholar] [CrossRef]
- Macías, J.; Escalante, C.; Castro, M.J. Multilayer-HySEA model validation for landslide generated tsunamis. Part I Rigid slides. Nat. Hazards Earth Syst. Sci. Discuss. 2020, 2020, 1–33. [Google Scholar] [CrossRef]
- Macías, J.; Escalante, C.; Castro, M.J. Multilayer-HySEA model validation for landslide generated tsunamis. Part II Granular slides. Nat. Hazards Earth Syst. Sci. Discuss. 2020, 2020, 1–34. [Google Scholar] [CrossRef]
- Imamura, F. Tsunami Numerical Simulation with the Staggered Leap-frog Scheme (Numerical Code of TUNAMI-N1 and N2); Disaster Control Res. Center Tohoku Univ.: Miyagi, Japan, 1989. [Google Scholar]
- Imamura, F.; Yalciner, A.; Ozyurt, G. Tsunami Modelling Manual; Technical Report; IOC: Lausanne, Switzerland, 2006. [Google Scholar]
- Yalciner, A.; Pelinovsky, E.; Zaytsev, A.; Kurkin, A.; Ozer, C.; Karakus, H. NAMI DANCE Manual; Technical Report; METU, Civil Engineering Department, Ocean Engineering Research Center: Ankara, Turkey, 2006. [Google Scholar]
- Wang, X. User Manual for COMCOT Version 1.7; Technical Report; Cornell University: New York, NY, USA, 2009. [Google Scholar]
- Pranowo, W.; Behrens, J.; Schlicht, J.; Ziemer, C. Adaptive mesh refinement applied to tsunami modeling: TsunaFLASH. In Proceedings of the the International Conference on Tsunami Warning (ICTW), Denpasar, Bali, Indonesia, 12–14 November 2008; Adrianto, H., Ed.; State Ministry of Research and Technology, Republic of Indonesia (RISTEK): Jakarta, Indonesia, 2008. Available online: http://hdl.handle.net/10013/epic.32425.d001 (accessed on 21 December 2020).
- Reguly, I.Z.; Giles, D.; Gopinathan, D.; Quivy, L.; Beck, J.H.; Giles, M.B.; Guillas, S.; Dias, F. The VOLNA-OP2 tsunami code (version 1.5). Geosci. Model Dev. 2018, 11, 4621–4635. [Google Scholar] [CrossRef]
- Roelvink, J.; Van Banning, G. Design and development of DELFT3D and application to coastal morphodynamics. Oceanogr. Lit. Rev. 1995, 42, 925. [Google Scholar]
- Popinet, S. Basilisk: Simple abstractions for octree-adaptive scheme. In Proceedings of the SIAM Conference on Parallel Processing for Scientific Computing, Boston, MA, USA, 12–15 April 2016. [Google Scholar]
- Popinet, S. A quadtree-adaptive multigrid solver for the Serre–Green–Naghdi equations. J. Comput. Phys. 2015, 302, 336–358. [Google Scholar] [CrossRef]
- Popinet, S. A vertically-Lagrangian, non-hydrostatic, multilayer model for multiscale free-surface flows. J. Comput. Phys. 2020, 418, 109609. [Google Scholar] [CrossRef]
- Roeber, V.; Cheung, K. Boussinesq-type model for energetic breaking waves in fringing reef environment. Coast. Eng. 2012, 70, 1–20. [Google Scholar] [CrossRef]
- Tavakkol, S.; Lynett, P. Celeris: A GPU-accelerated open source software with a Boussinesq-type wave solver for real-time interactive simulation and visualization. Comput. Phys. Commun. 2017, 217, 117–127. [Google Scholar] [CrossRef]
- Kennedy, A.; Chen, Q.; Kirby, J.; Dalrymple, R. Boussinesq modeling of wave transformation, breaking and runup, part I: 1D. J. Waterw. Port Coast. Ocean Eng. 2000, 126, 39–47. [Google Scholar] [CrossRef]
- Shi, F.; Kirby, J.; Harris, J.; Geiman, J.; Grilli, S. A high-order adaptive time-stepping TVD solver for Boussinesq modeling of breaking waves and coastal inundation. Ocean Model. 2012, 43–44, 36–51. [Google Scholar] [CrossRef]
- Lynett, P.J.; Wu, T.R.; Liu, P.L.F. Modeling wave runup with depth-integrated equations. Coast. Eng. 2002, 46, 89–107. [Google Scholar] [CrossRef]
- Kim, D.; Lynett, P. Turbulent mixing and passive scalar transport in shallow flows. Phys. Fluids 2011, 23, 16603. [Google Scholar] [CrossRef]
- Yamazaki, Y.; Kowalik, Z.; Cheung, K. Depth-integrated, non-hydrostatic model for wave breaking and run-up. Int. J. Numer. Meth. Fluids 2009, 61, 473–497. [Google Scholar] [CrossRef]
- Horrillo, J.; Grilli, S.; Nicolsky, D.; Roeber, V.; Zhang, J. Performance benchmarking tsunami models for NTHMP’s inundation mapping activities. Pure Appl. Geophys. 2015, 172, 869–884. [Google Scholar] [CrossRef]
- Ma, G.; Shi, F.; Kirby, J. Shock-capturing non-hydrostatic model for fully dispersive surface wave processes. Ocean Model. 2012, 43–44, 22–35. [Google Scholar] [CrossRef]
- Vázquez, M.; Houzeaux, G. Alya: Multiphysics Engineering Simulation Towards Exascale. J. Comput. Sci 2016, 14, 15–27. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marras, S.; Mandli, K.T. Modeling and Simulation of Tsunami Impact: A Short Review of Recent Advances and Future Challenges. Geosciences 2021, 11, 5. https://doi.org/10.3390/geosciences11010005
Marras S, Mandli KT. Modeling and Simulation of Tsunami Impact: A Short Review of Recent Advances and Future Challenges. Geosciences. 2021; 11(1):5. https://doi.org/10.3390/geosciences11010005
Chicago/Turabian StyleMarras, Simone, and Kyle T. Mandli. 2021. "Modeling and Simulation of Tsunami Impact: A Short Review of Recent Advances and Future Challenges" Geosciences 11, no. 1: 5. https://doi.org/10.3390/geosciences11010005
APA StyleMarras, S., & Mandli, K. T. (2021). Modeling and Simulation of Tsunami Impact: A Short Review of Recent Advances and Future Challenges. Geosciences, 11(1), 5. https://doi.org/10.3390/geosciences11010005






