A Geospatial Approach for Mapping the Earthquake-Induced Liquefaction Risk at the European Scale
Abstract
1. Introduction
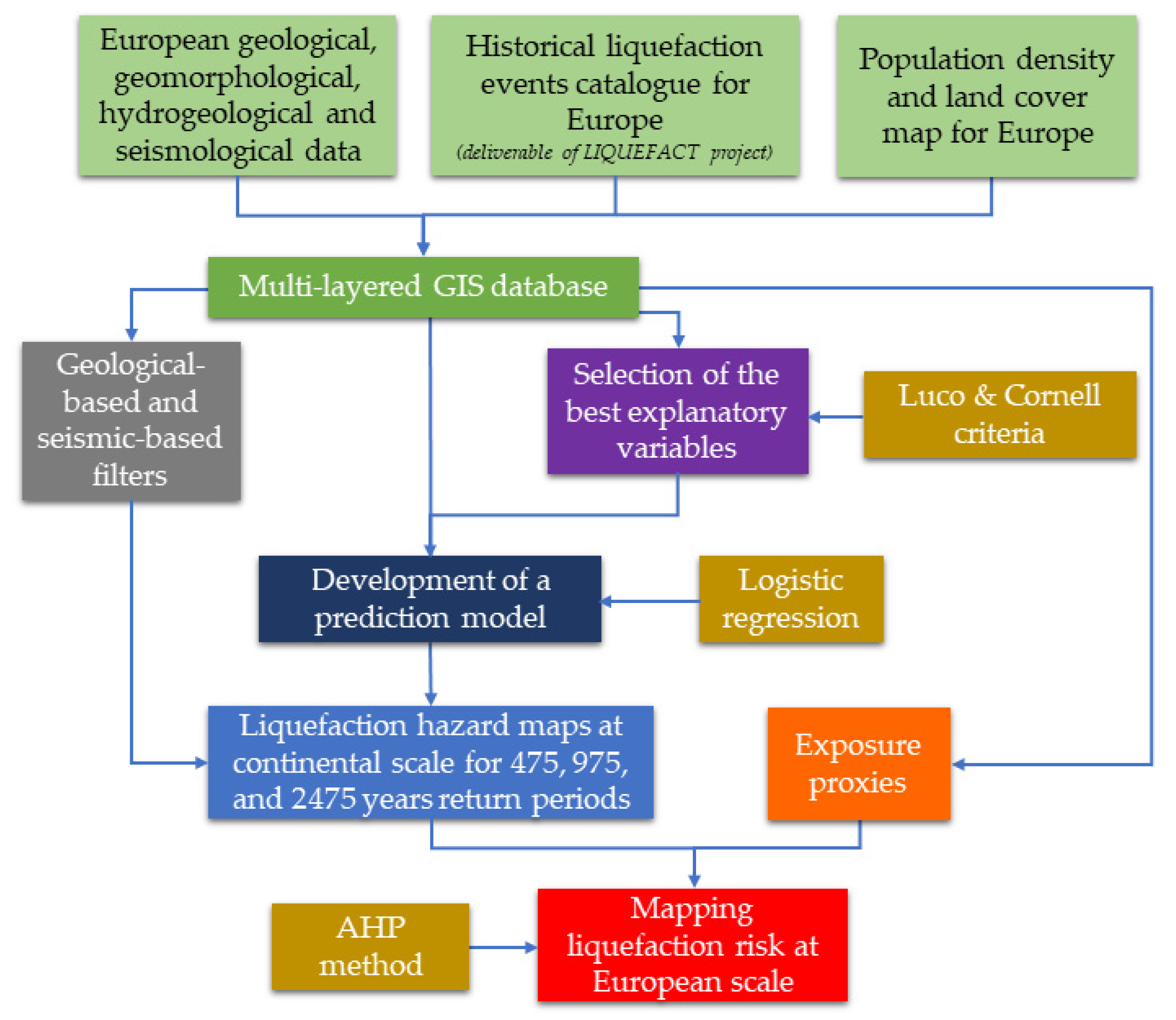
2. Overview of the Methodology
3. Mega-Zonation of the Earthquake-Induced Liquefaction Risk in Continental Europe
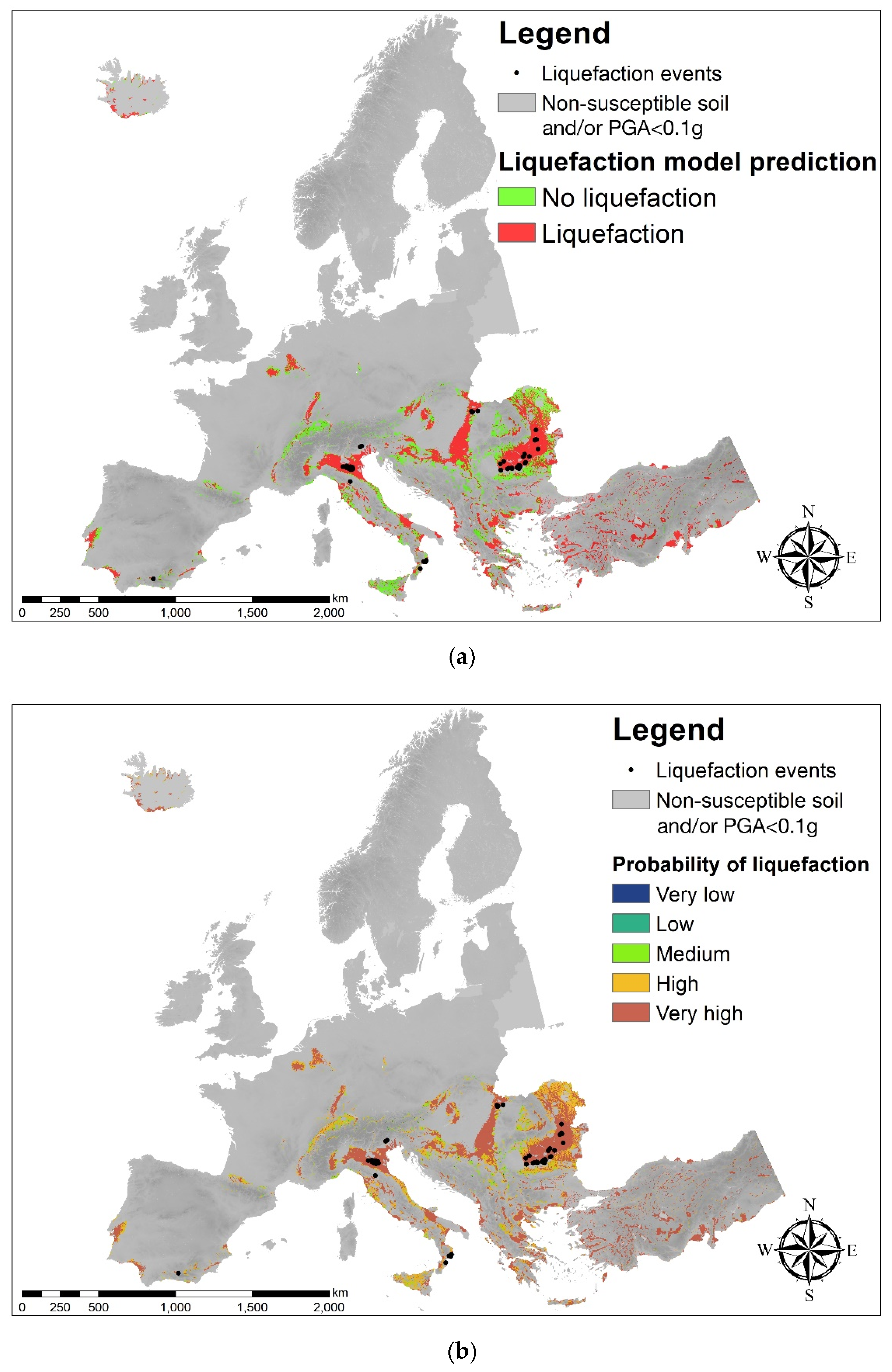
3.1. Mapping the Probability of Liquefaction by Applying A European Prediction Model
- The weighted-mean shear-wave velocity in the top 30 m (VS30), which was adopted as a proxy of soil stiffness since soft sandy soils are more susceptible to liquefaction (they are looser). The US Geological Survey (https://earthquake.usgs.gov/data/vs30/) provided the global topographic-slope based VS30 map and such a map was adopted for Europe;
- The weighted-magnitude peak ground acceleration (PGAm), which was computed as
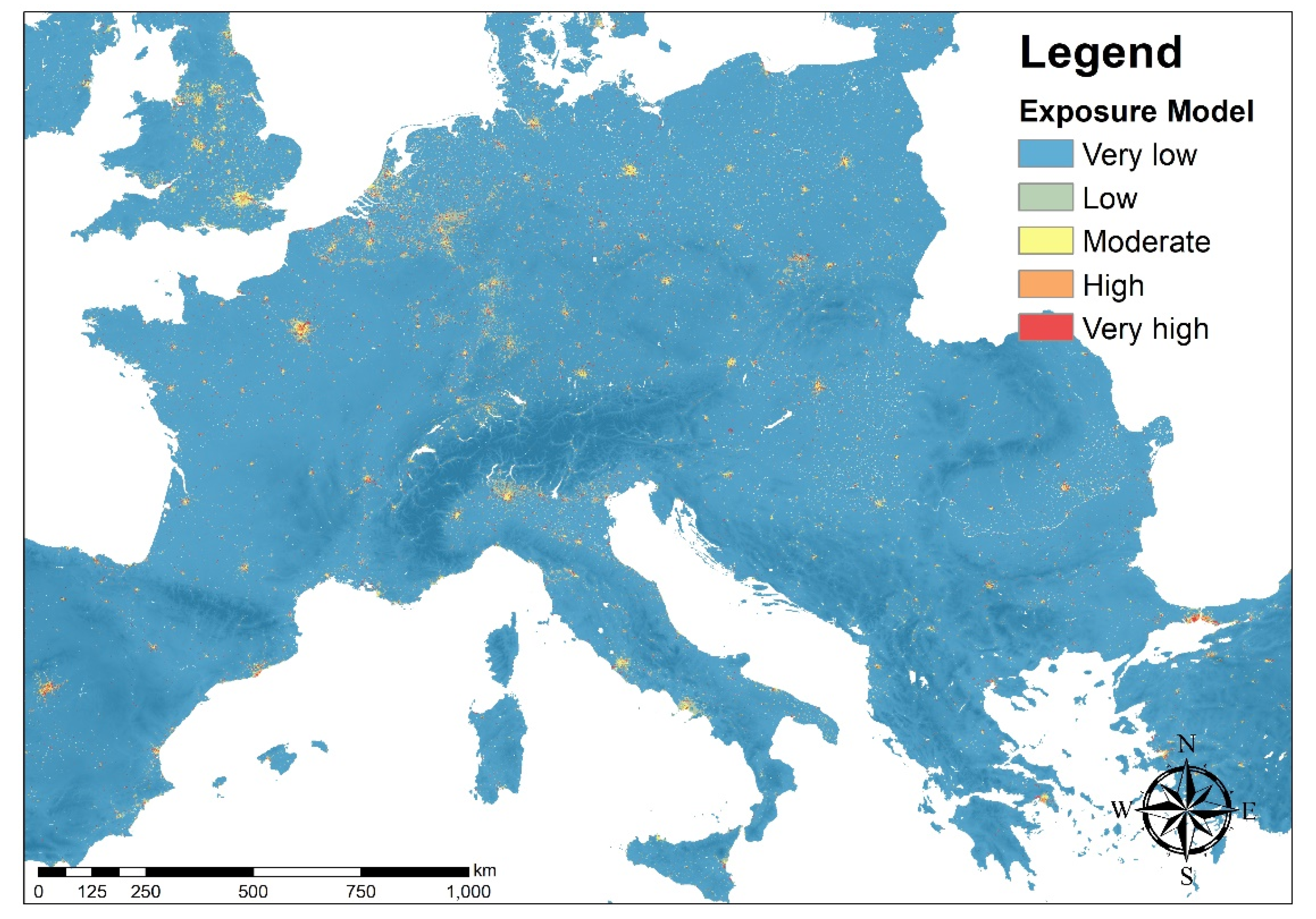
3.2. Exposure Model for Europe
- very low: Pd < 400 inhab./km2;
- low: 400 ≤ Pd 800 inhab./km2;
- medium: 800 ≤ Pd < 2000 inhab./km2;
- high: 2000 ≤ Pd < 5000 inhab./km2;
- very high: Pd ≥ 5000 inhab./km2.
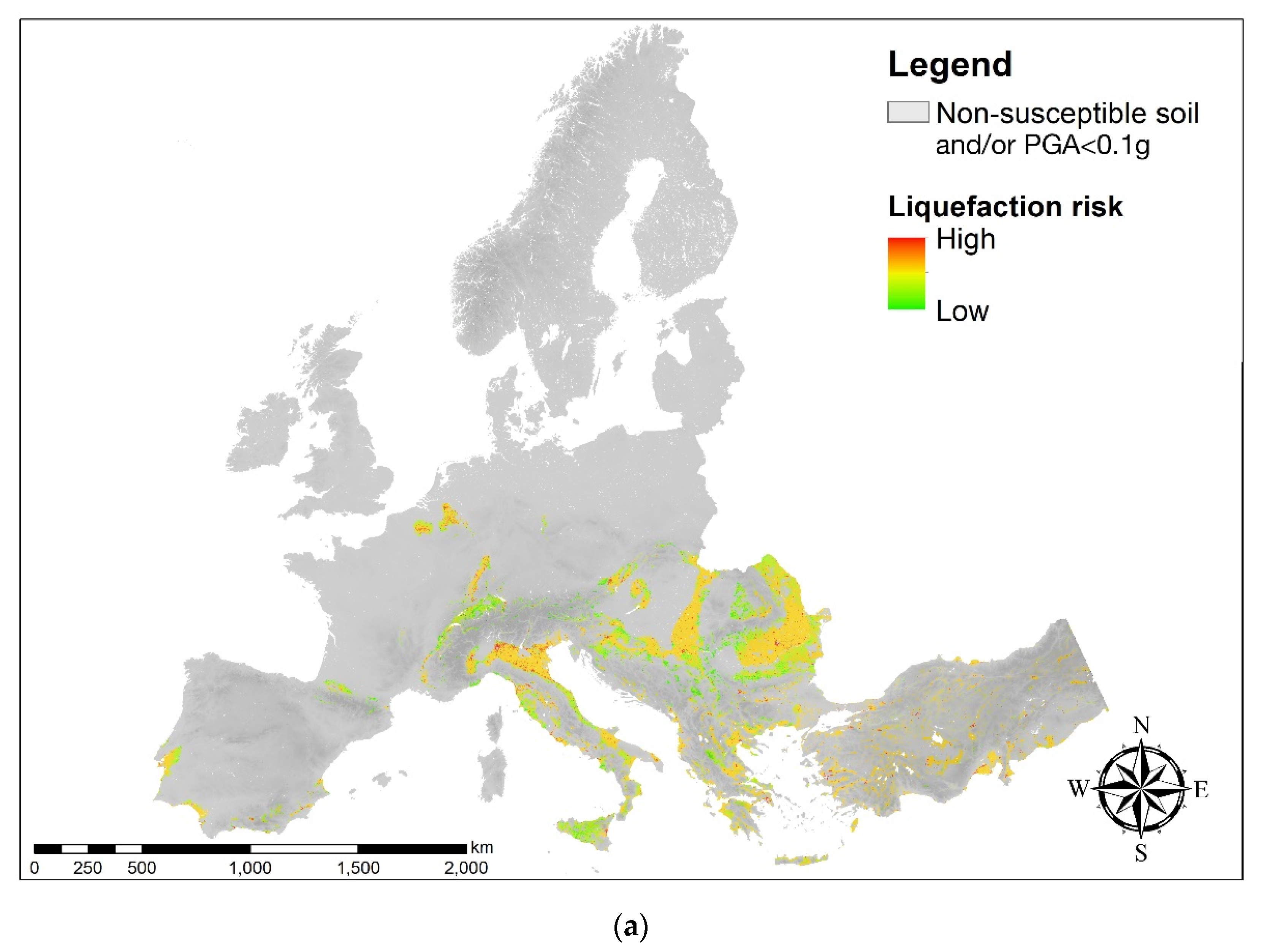
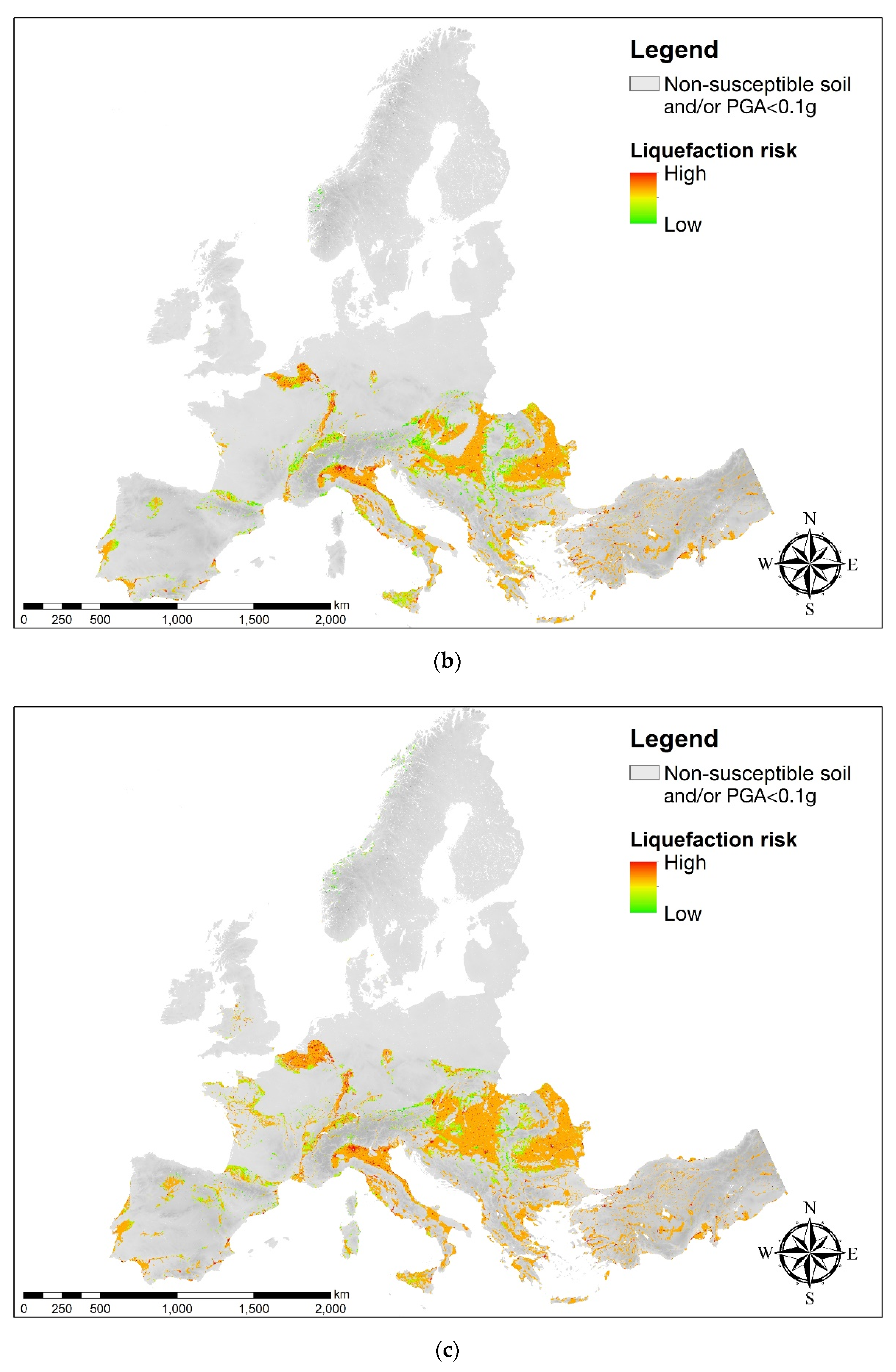
3.3. Assessment of the Liquefaction Risk at the European Scale by Using the AHP Technique
3.4. European Charts for Earthquake-Induced Liquefaction Risk
4. Discussion and Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- National Academies of Sciences, Engineering, and Medicine. State of the Art and Practice in the Assessment of Earthquake-Induced Soil Liquefaction and Its Consequences; The National Academies Press: Washington, DC, USA, 2016. [Google Scholar] [CrossRef]
- Zhu, J.; Daley, D.; Baise, L.; Thompson, E.; Wald, D.; Knudsen, K. A Geospatial Liquefaction Model for Rapid Response and Loss Estimation. Earthq. Spectra 2015, 31, 1813–1837. [Google Scholar] [CrossRef]
- Matsuoka, M.; Wakamatsu, K.; Hashimoto, M.; Senna, S.; Midorikawa, S. Evaluation of liquefaction potential for large areas based on geomorphologic classification. Earthq. Spectra 2015, 31, 2375–2395. [Google Scholar] [CrossRef]
- Zhu, J.; Baise, L.; Thompson, E. An Updated Geospatial Liquefaction Model for Global Application. Bull. Seismol. Soc. Am. 2017, 107, 1365–1385. [Google Scholar] [CrossRef]
- Rashidian, V.; Baise, L.G. Regional efficacy of a global geospatial liquefaction model. Eng. Geol. 2020, 272. [Google Scholar] [CrossRef]
- Yilmaz, C.; Silva, V.; Weatherill, G. Probabilistic framework for regional loss assessment due to earthquake-induced liquefaction including epistemic uncertainty. Soil Dyn. Earthq. Eng. 2020, in press. [Google Scholar] [CrossRef]
- Bozzoni, F.; Bonì, R.; Conca, D.; Lai, C.G.; Zuccolo, E.; Meisina, C. Megazonation of earthquake-induced soil liquefaction hazard in continental Europe. Bull. Earthq. Eng. 2020, in press. [Google Scholar] [CrossRef]
- Saaty, T.L. The Analytic Hierarchy Process; McGraw-Hill: New York, NY, USA, 1980. [Google Scholar]
- Karimzadeh, S.; Miyajima, M.; Hassanzadeh, R.; Amiraslanzadeh, R.; Kamel, B. A GIS-based seismic hazard, building vulnerability and human loss assessment for the earthquake scenario in Tabriz. Soil Dyn. Earthq. Eng. 2014, 66, 263–280. [Google Scholar] [CrossRef]
- Panahi, M.; Rezaie, F.; Meshkani, S. Seismic vulnerability assessment of school buildings in Tehran city based on AHP and GIS. Nat. Hazards Earth Syst. Sci. 2015, 15, 461–474. [Google Scholar] [CrossRef]
- Moustafa, S.S.R. Application of the Analytic Hierarchy Process for Evaluating Geo-Hazards in the Greater Cairo Area, Egypt. Electron. J. Geotech. Eng. 2015, 20, 1921–1938. Available online: http://www.ejge.com/2015/Ppr2015.0207sb.pdf (accessed on 18 December 2020).
- Lai, C.G.; Conca, D.; Bozzoni, F.; Bonì, R.; Meisina, C. Earthquake-induced soil liquefaction risk: Macrozonation of the European territory taking into account exposure. In Proceedings of the IABSE Symposium 2019 Guimarães. Towards a Resilient Built Environment—Risk and Asset Management, Guimarães, Portugal, 27–29 March 2019. [Google Scholar]
- UNESCO. Report of Consultative Meeting of Experts on the Statistical Study of Natural Hazards and Their Consequences; United Nations Educational Scientific and Cultural Organizations Document SC/WS/500; UNESCO: Paris, France, 1972. [Google Scholar]
- Lai, C.G.; Meisina, C.; Bozzoni, F.; Conca, D.; Bonì, R. Report to Describe the Adopted Procedure for the Development of the European Liquefaction Potential Map; Deliverable D2.6. V 1.0. Liquefact Project, H2020-DRA-2015, GA No. 700748; 2019; Available online: http://www.liquefact.eu/wp-content/uploads/2020/03/D2.6.pdf (accessed on 18 December 2020).
- Meisina, C.; Bonì, R.; Bozzoni, F.; Conca, D.; Perotti, C.; Persichillo, P.; Lai, C.G. Assessment of the soil liquefaction susceptibility across Europe using Analytic Hierarchy Process (AHP). Eng. Geol. 2020, submitted. [Google Scholar]
- Cornell, C.A.; Luco, N. Ground motion intensity measures for structural performance assessment at near-fault sites. In Proceedings of the Proceedings U.S.-Japan Joint Workshop and Third Grantees Meeting, Seattle, WA, USA, 15–16 August 2001. [Google Scholar]
- Luco, N.; Cornell, C.A. Structure-specific scalar intensity measures for near-source and ordinary earthquake ground motions. Earthq. Spectra 2007, 23, 357–392. [Google Scholar] [CrossRef]
- Padgett, J.E.; Nielson, B.G.; DesRoches, R. Selection of optimal intensity measures in probabilistic seismic demand models of highway bridge portfolios. Earthq. Eng. Struct. Dyn. 2008, 37, 711–725. [Google Scholar] [CrossRef]
- Wang, X.; Shafieezadeh, A.; Ye, A. Optimal intensity measures for probabilistic seismic demand modeling of extended pile-shaft-supported bridges in liquefied and laterally spreading ground. Bullettin Earthq. Eng. 2018, 16, 229–257. [Google Scholar] [CrossRef]
- Jarvis, A.; Reuter, H.I.; Nelson, A.; Guevara, E. Hole-Filled SRTM for the Globe. Version 4. 2008. Available online: http://srtm.csi.cgiar.org (accessed on 18 December 2020).
- Beven, K.J.; Kirkby, M.J. A physically based, variable contributing area model of basin hydrology. Hydrol. Sci. Bull. 1979, 24, 43–69. [Google Scholar] [CrossRef]
- Eurocode 8. Design of Structures for Earthquake Resistance, Part 1: General Rules, Seismic Actions and Rules for Buildings; Pr-EN1998-1; European Committee for Standardization (CEN): Brussels, Belgium, 2004.
- Chen, R.; Harmsen, S. Probabilistic Ground Motion Calculations and Implementation of PGA Scaling by Magnitude for Assessing Liquefaction Potential, Technical Document 2012-1, Seismic Hazard Zonation Program. 2012.
- Youd, T.L.; Idriss, I.M.; Andrus, R.D.; Arango, I.; Castro, G.; Christian, J.T.; Dobry, R.; Finn, W.D.L.; Harder, L.F.; Hynes, M.E.; et al. Liquefaction resistance of soils: Summary report from the 1996. NCEER and 1998 NCEER/NSF workshops on the evaluation of liquefaction resistance of soils. J. Geotech. Geoenviron. Eng. 2001, 127, 817–833. [Google Scholar] [CrossRef]
- Yen, S.J.; Lee, Y.S. Under-Sampling Approaches for Improving Prediction of the Minority Class in an Imbalanced Dataset. In Intelligent Control and Automation. Lecture Notes in Control and Information Sciences; Huang, D.S., Li, K., Irwin, G.W., Eds.; Springer: Berlin/Heidelberg, Germany, 2006; Volume 344. [Google Scholar] [CrossRef]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic Minority Over-sampling Technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- He, H.; Bai, Y.; Garcia, E.A.; Li, S. ADASYN: Adaptive Synthetic Sampling Approach for Imbalanced Learning. In Proceedings of the 2008 IEEE International Joint Conference on Neural Networks (IEEE World Congress on Computational Intelligence), Hong Kong, China, 1–8 October 2008. [Google Scholar]
- Fawcett, T. An introduction to ROC analysis. Pattern Recognit. Lett. 2005, 27, 861–874. [Google Scholar] [CrossRef]
- Sousa, L.; Silva, V.; Bazzurro, P. Using Open-Access Data in the Development of Exposure Data Sets of Industrial Buildings for Earthquake Risk Modeling. Earthq. Spectra 2017, 33, 63–84. [Google Scholar] [CrossRef]
| Weight/Rank | Relative Importance |
|---|---|
| 1 | equal |
| 3 | moderately dominant |
| 5 | strongly dominant |
| 7 | very strongly dominant |
| 9 | extremely dominant |
| 2, 4, 6, 8 | intermediate values |
| Reciprocals | for inverse judgements |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bozzoni, F.; Bonì, R.; Conca, D.; Meisina, C.; Lai, C.G.; Zuccolo, E. A Geospatial Approach for Mapping the Earthquake-Induced Liquefaction Risk at the European Scale. Geosciences 2021, 11, 32. https://doi.org/10.3390/geosciences11010032
Bozzoni F, Bonì R, Conca D, Meisina C, Lai CG, Zuccolo E. A Geospatial Approach for Mapping the Earthquake-Induced Liquefaction Risk at the European Scale. Geosciences. 2021; 11(1):32. https://doi.org/10.3390/geosciences11010032
Chicago/Turabian StyleBozzoni, Francesca, Roberta Bonì, Daniele Conca, Claudia Meisina, Carlo G. Lai, and Elisa Zuccolo. 2021. "A Geospatial Approach for Mapping the Earthquake-Induced Liquefaction Risk at the European Scale" Geosciences 11, no. 1: 32. https://doi.org/10.3390/geosciences11010032
APA StyleBozzoni, F., Bonì, R., Conca, D., Meisina, C., Lai, C. G., & Zuccolo, E. (2021). A Geospatial Approach for Mapping the Earthquake-Induced Liquefaction Risk at the European Scale. Geosciences, 11(1), 32. https://doi.org/10.3390/geosciences11010032







