1. Introduction
Near-fault effects are able to cause large seismic demand to structures compared to ground motion in far-field and thus their identification and characterization is fundamental for proper assessment of shaking for several engineering applications and seismic hazard analyses. These effects are related to a particular class of near-fault records characterized by pulses in the velocity traces, which can provide considerable input energy to sites located in the direction of propagation of the rupture (i.e., forward-directivity), when the rupture velocity is close to the shear-wave velocity [
1]. Near-fault pulse-like motions may also be caused by fling-step [
1,
2,
3]. Nevertheless, the two phenomena (i.e., fling-step and forward-directivity) implicate distinct characteristics on the time-series: directivity is associated with idealized full-cycle velocity pulses, while the fling-step is related to half-cycle pulses [
1]. Moreover, directivity pulses show acceleration response spectra with larger narrow-band amplitudes and unusual shape; fling-step determines an offset at the end of the displacement record due to permanent tectonic deformation at the site. The latter causes amplifications in long-period spectral ordinates, while showing negligible effects on the acceleration response [
4].
In this paper, we focus on forward-directivity effects identified by selecting the full-cycle pulses in the velocity time series, with the aim of investigating the pulse-like ground motion on spectral demand. These effects have been widely studied by many authors from the phenomenological point of view [
1,
2,
3,
4,
5,
6]; however, they are not yet fully included in the context of Probabilistic Seismic Hazard Analyses (PSHA) and consequently, the current seismic design codes do not provide a proper representation of these effects. In this framework, several authors have proposed simplified empirical approaches to adjust the ground-motion model (GMM) prediction with narrow-band amplification factors dependent on the pulse period [
7,
8,
9,
10,
11,
12]. This approach is currently the most practical one, and is different from the prior studies that proposed GMMs explicitly including directivity effects in the functional form [
13] or models adjusted through broadband scaling factors [
5].
However, the majority of these literature studies are based on limited near-fault datasets, so there is a need to investigate more extensively the pulse-like ground motion properties to calibrate statistically robust models.
In this paper, we explore the main statistical features and amplification effects of the impulsive records identified within a large dataset of near-fault records, i.e., the Near-Source Strong Motion flat-file (NESS1;
https://doi.org/10.13127/NESS.1.0 [
14,
15]) to assess their impact on response spectra and calibrating an empirical corrective factor.
We thus modelled the narrow-band directivity factor based on the within-event part of the model residuals (i.e., the logarithmic difference between the observations and the model predictions) computed on a reference GMM specifically calibrated on the no-pulse (ordinary) records of the same dataset.
2. Near-Source Dataset
The present study takes advantage of the availability of a large number of high-quality waveforms collected within the NESS1 flat-file and containing the related intensity measures, event and station metadata. All the records of pan-European events in NESS1 are also available in the web portals of ITACA (Italian ACcelerometric Archive:
http://itaca.mi.ingv.it; [
16]) and ESM (Engineering Strong Motion:
https://esm-db.eu; [
17]). The NESS1 flat-file consists of about 800 three-component waveforms relative to 700 accelerometric stations, caused by 74 events with moment magnitude larger than 5.5 recorded in the 1933–2016 period. The NESS1 ground-motion data were selected to have a maximum source-to-site distance within one fault length, defined through seismological scaling relations. The accelerometric records were manually and uniformly processed, by using the ESM tool [
18] that entails the application of a second-order acausal time-domain Butterworth filter. Most of the digital waveforms, which constitute about 70% of the dataset, were filtered with high-pass frequencies ≤ 0.1 Hz, whereas analog data were, on average, filtered at frequencies around 0.2 Hz, due to their lower quality [
15]. The application of this type of filtering scheme, as known, does not allow recovery of the information about permanent displacement present in the time-series. Although such static deformation may be significant for near-source records, its estimation entails the adoption of baseline correction procedures (without band-pass filters), the details of which are beyond the scope of this work.
On these bases, an extensive investigation was performed on the NESS1 data by Pacor et al. [
15], allowing recognition of the typical near-source effects, including velocity pulses. In particular, about 30% of the records were found to exhibit pulse-like characteristics, possibly due to forward-rupture directivity.
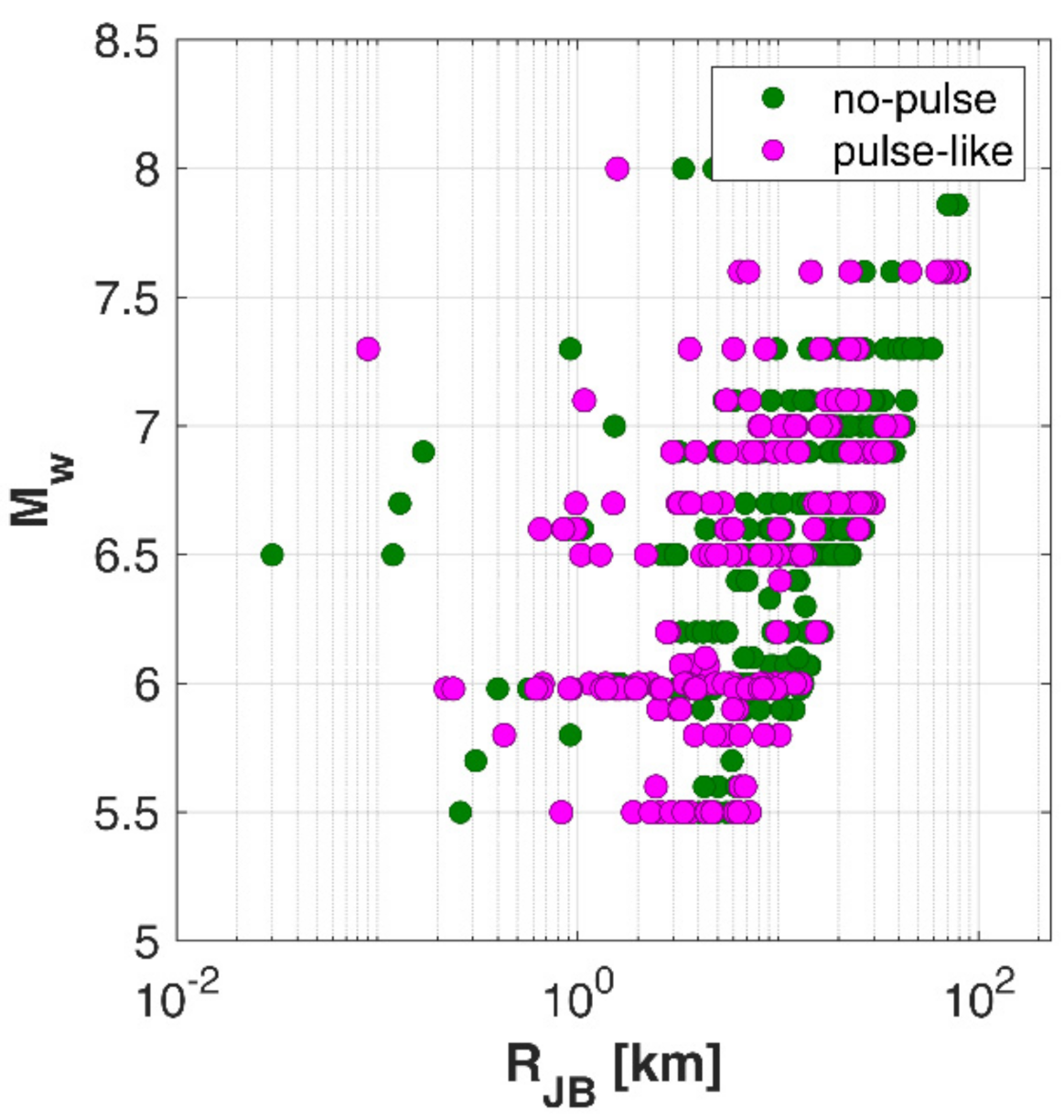
Figure 1 shows the moment magnitude M
w vs Joyner–Boore distance R
JB distribution of NESS1 data grouped into pulse-like (230 records from which we excluded 29 waveforms, having pulses potentially related to geotechnical effects) and no-pulse data (430 records). Both pulse-like and ordinary data are uniformly distributed over the magnitude-distance range of the dataset. The best sampled magnitude range is around M
w 6.0, due to the preponderance of highly sampled Italian data recorded during the seismic sequences of Northern Italy (2012) and Central Italy (2016), where relevant near-fault effects, also related to the presence of pulses, are observed.
3. Pulses Identification
For the investigation of pulse-like effects within the NESS1 dataset, the identification algorithm proposed by Baker [
19] and Shashi and Baker [
10] is herein applied. This procedure is largely adopted in the literature and is based on the use of a continuous wavelet transform of a single-component’s velocity time-history to extract the pulse from the horizontal orientations of each station’s records. In the algorithm implementation, a Pulse-Indicator (PI) score, as well as a lateness indicator (to exclude records with late-arriving pulse) are jointly assessed for each waveform without imposing any limits on peak ground velocity (PGV). The PI comprises a real number between 0 and 1: the larger the score, the more likely the record shows a pulse. Then, the criterion introduced by Shahi and Baker [
10] is applied to each pair of horizontal components. Schematically, in a first step, ground motions with a PI > 0.85 according to [
19] and that also exhibit PGV > 20 cm/s and/or trigger both criteria are flagged as pulse-like. In a second stage, all remaining ground motions that either trigger the Shahi and Baker [
10] criterion alone or exhibit a PI > 0.50 are pooled together. These motions are then subjected to visual inspection of their velocity traces in the relevant orientations as well as of the azimuthal variation of their PI score. The pulse-like flag is also attributed to some of the ground motions in the second pool based on expert judgment and this represents an additional criterion to the original method.
The above procedure was systematically applied to all waveforms in the NESS1 flat-file, leading to a subset of 230 records identified and tagged as impulsive [
15] along with the corresponding pulse period T
p (i.e., the pseudo-period of the wavelet extracted from the velocity signal) and pulse azimuthal orientation α
pulse.
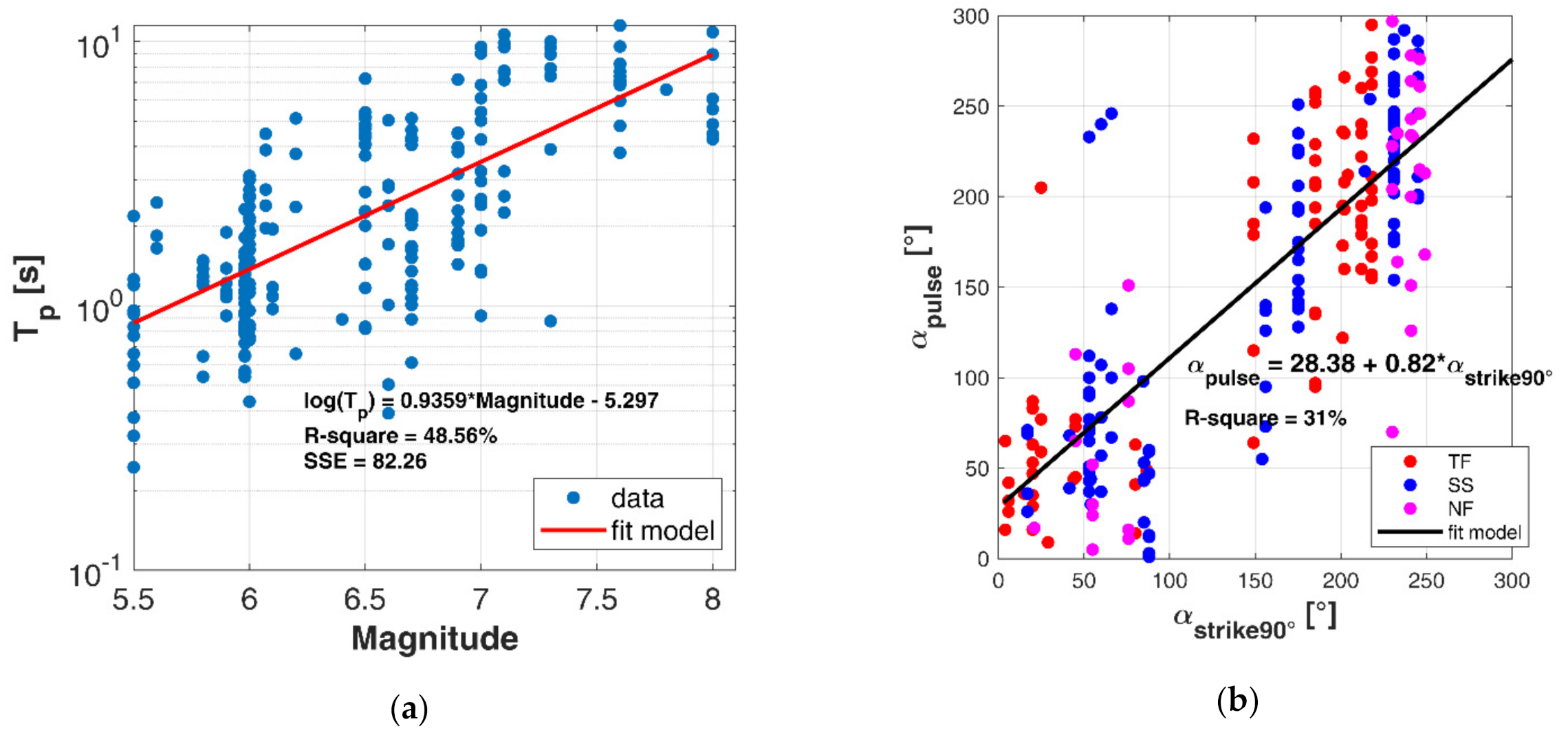
A scatter plot of the extracted pulse periods T
p versus magnitude of the causal events in NESS1 is reported in
Figure 2a along with the corresponding least-squares linear regression model. As expected, we find that the logarithm of the mean of the pulse periods linearly depends on the event magnitude (M), according to the following empirical relationship:
This result is consistent with the fact that the period T
p is related to the rise time (i.e., duration of the slip at a single point on the fault) and the fault dimensions, tending to increase with magnitude; e.g., [
5,
6]. With reference to the pulse orientation (α
pulse), we observe that it correlates with the normal direction (90°) to the strike of the fault (α
strike90°) over all possible orientations of the strike angle, meaning that the pulses occur mainly on the fault normal (FN) direction, with no relevant differences for both Strike-Slip (SS) and dip-slip faults, that are Normal-Faulting (NF) and Thrust-Faulting (TF)—
Figure 2b. On these data, we found the following relationship:
4. Effect of Pulses on Elastic Spectral Response
As the main goal of the present study is to investigate the effect of the impulsive records on the response spectral shape, the NESS1 dataset is analyzed separately for pulse-like and ordinary waveforms to capture the most relevant differences in terms of spectral amplitudes and shapes.
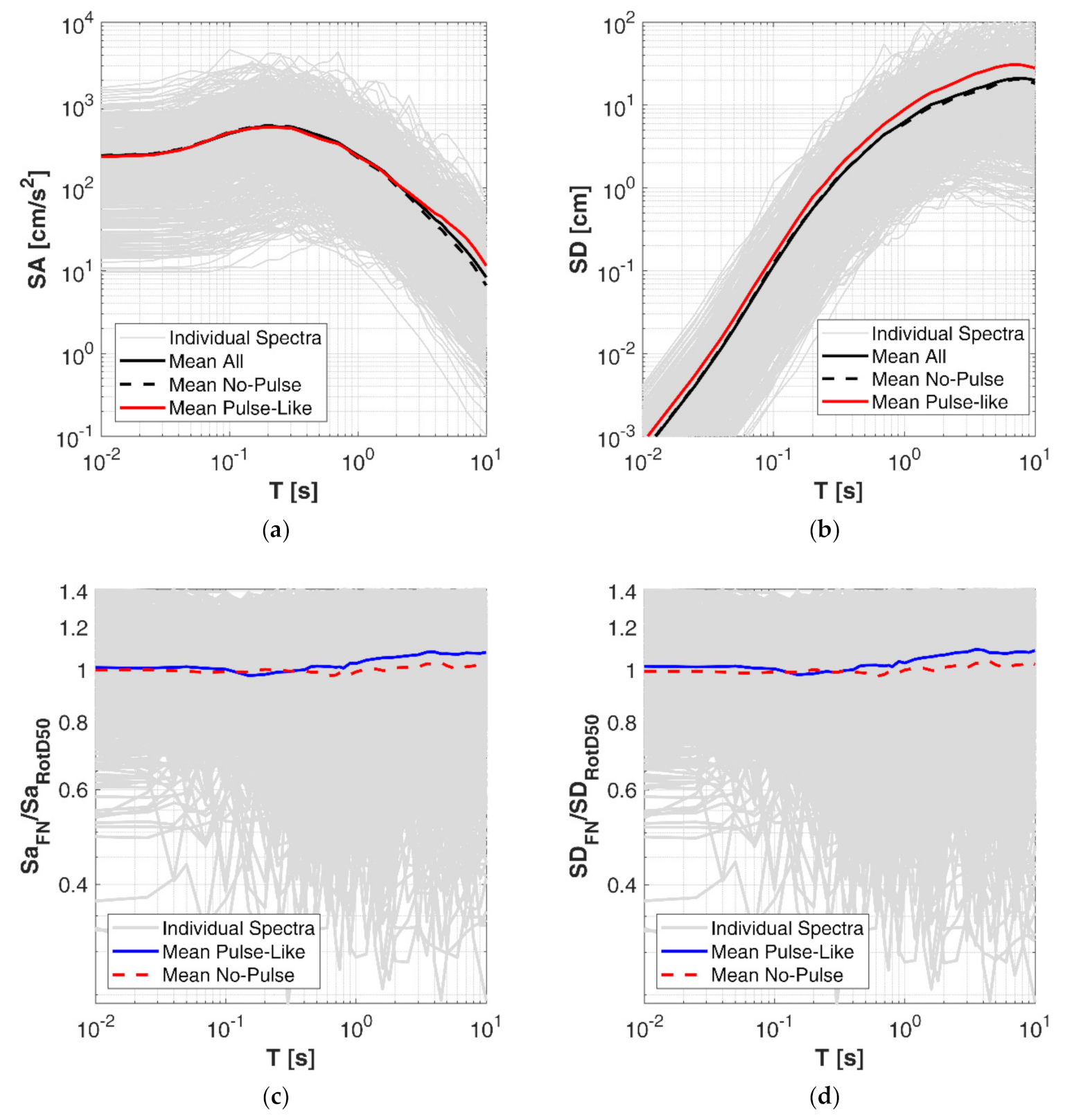
In
Figure 3, we compare the pulse-like and no-pulse average elastic response spectra of 5%-damped acceleration SA (a) and displacement SD (b), with the aim of recognizing the overall effect of pulses on spectral shapes. It can be noted that SA response spectra are affected by pulse-like data at longer periods (T), mainly at T larger than 2 s, whereas on SD the amplification effect of the spectral ordinates is distributed over the whole period range from 0.01 s to 10 s. In this regard, we point out that, although the application of a high-pass filtering to the waveforms instead of a baseline correction procedure may affect the displacement response, it was found by D’Amico et al. [
4] that the results obtained from the two schemes start to diverge only at very long periods (T > 5 s), causing underestimates of the spectral ordinates in case of filtering. Therefore, the above findings on the overall impact of impulsive records on displacement spectra remain still valid.
In the reported plots, the orientation independent component RotD50 [
20] is considered; a comparison of the mean ratio between RotD50 and FN spectral ordinates is given in
Figure 3 both for acceleration (c) and displacement (d) response spectra. The plots show that the mean ratio between the two components is practically near unity at all periods, with slightly larger differences at medium-longer periods (T > 0.5 s) where the ratio is, as expected, higher than 1, being the FN component more energetic. In the following analyses, we choose to show the FN components, being slightly larger than the RotD50 and more frequently used for calibration of directive GMMs. However, the main findings of this work are applicable to both types of components with small differences.
Previous studies on near-fault pulse-like motions showed the dependencies of: (i) the response spectra on the pulse period T
p [
21,
22] and (ii) the pulse period on earthquake magnitude [
2,
5,
6,
23]. To investigate this dependency on spectral ordinates, in
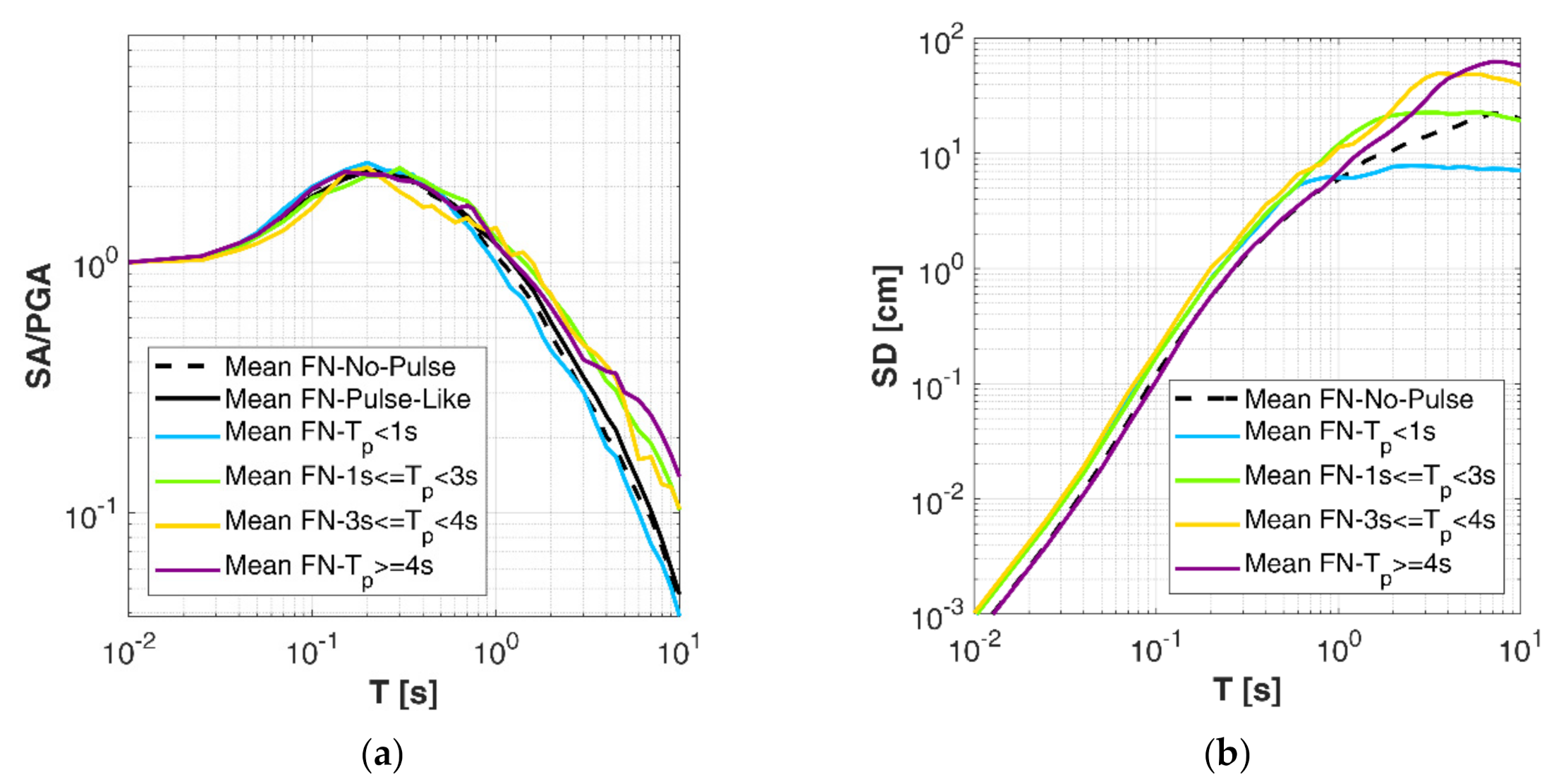
Figure 4 we show a sensitivity analysis of normalized SA, i.e., divided by the PGA value (
Figure 4a), and SD (
Figure 4b) to different bins of the pulse period T
p, showing that spectral amplitudes become larger at longer periods as T
p increases, starting to deviate from the ordinary mean trend in correspondence of the average value of T
p in the bin. However, this effect is not visible for pulse periods shorter than 1 s. The SD (
Figure 4b) are also markedly affected by T
p, showing broadband amplifications at period pulses larger than 1 s.
The effect of the style of faulting on pulse-like spectra is illustrated for the FN components on SA normalized to the PGA (a) and SD (b) in
Figure 5.
This effect is investigated for ground motions related to NF, TF and SS earthquakes for some pulse period Tp bins. In these figures, the SA curves are plotted for pulse-like records with Tp larger than 1 s in order to enhance the shape differences of the normalized SA. It can be noted that SS earthquakes show systematically higher spectral ordinates, both for SA and SD than the other styles of faulting, particularly above a period of 2 s. This effect may achieve about 40% of amplification for SD with respect to ground motions from dip-slip earthquakes. Among the latter, the TF earthquakes provide larger ordinates compared to NF and no-pulse ground motion.
A possible physical explanation of this observation may be related to the correlation that lies between the rise time and the pulse period, which thus implies a correlation of T
p with the style of faulting. Indeed, according to [
23,
24], the rise time for dip-slip earthquakes is, on average, about half the rise time for SS earthquakes. As a result, the pulse period for an SS earthquake is expected to be longer than that for a dip-slip earthquake, thus producing more significant spectral amplifications at longer periods, as evidenced by our analysis.
5. Calibration of the Empirical Corrective Factor
5.1. Reference GMM of No-Pulse Records
The estimation of an empirical corrective factor accounting for pulse-like features is computed on the residuals of the subset of impulsive ground motions with respect to a reference GMM expressed in terms of SA(T). The latter is specifically calibrated for this aim on ground motions (both horizontal FN and RotD50 components) classified as no-pulse, in order to remove any bias from the mean. The 430 no-pulse records selected within NESS1 are within distances RJB ≤ 50 km.
The functional form of the reference GMM is given in Equation (3) and includes the terms related to the source (F
M, Equation (4)), the distance attenuation, also describing the magnitude-dependent geometrical spreading (F
D, Equation (5)), the site (F
S, Equation (6)), the style of faulting (F
SOF, Equation (7)) and the error e (Equation (8)). The explanatory variables are the moment magnitude M
w, the source-to-site distance R, the shear wave velocity in the uppermost 30 m, V
S,30 and the styles of faulting SOF
j, which are dummy variables, introduced to specify SS (j = 1) and dip-slip, i.e., TF/NF (j = 2), fault types.
where:
The hinge magnitude Mh, the reference magnitude Mref and the pseudo-depth h are constants, which have been assumed as follows: Mh = 6.75; Mref = 5.5 and h = 6 km according to the average values in the dataset.
The coefficients a, b
1, b
2, c
1, c
2, k and f
j (f
1 for SS, f
2 for TF and NF) are derived by a mixed-effect linear regression [
25]. The predicted value by the model is a 10-base logarithm of the spectral acceleration SA (i.e., the peak ground acceleration, PGA and SA at 36 ordinates) at 5% damping in the period range 0.01–10 s. The model residuals r
es are partitioned into between-event (δB
e) and within-event (δWS
es) terms of error (Equation (8), thus the total variability σ associated to the GMM (Equation (9) is obtained through the combination of between-event (τ) and within-event (ϕ) standard deviations [
26]:
During the calibration stage, we derive different sets of coefficients for the different source-to-site metrics in order to select the most appropriate one for the GMM description: Joyner–Boore (R = R
JB); rupture (R = R
rup); rupture normalized to the fault length (R = R
norm); line (R = R
line) and nucleation-point (R = R
np) distances (for a detailed description on these distance metrics definitions, see [
15]). We find that the model prediction (
Figure 6a) and the total standard deviation σ (
Figure 6b) computed as mean over all the ordinary records are almost insensitive to the adopted distance metric. In light of this, we decide to adopt the R
JB metric according to the majority of GMMs.
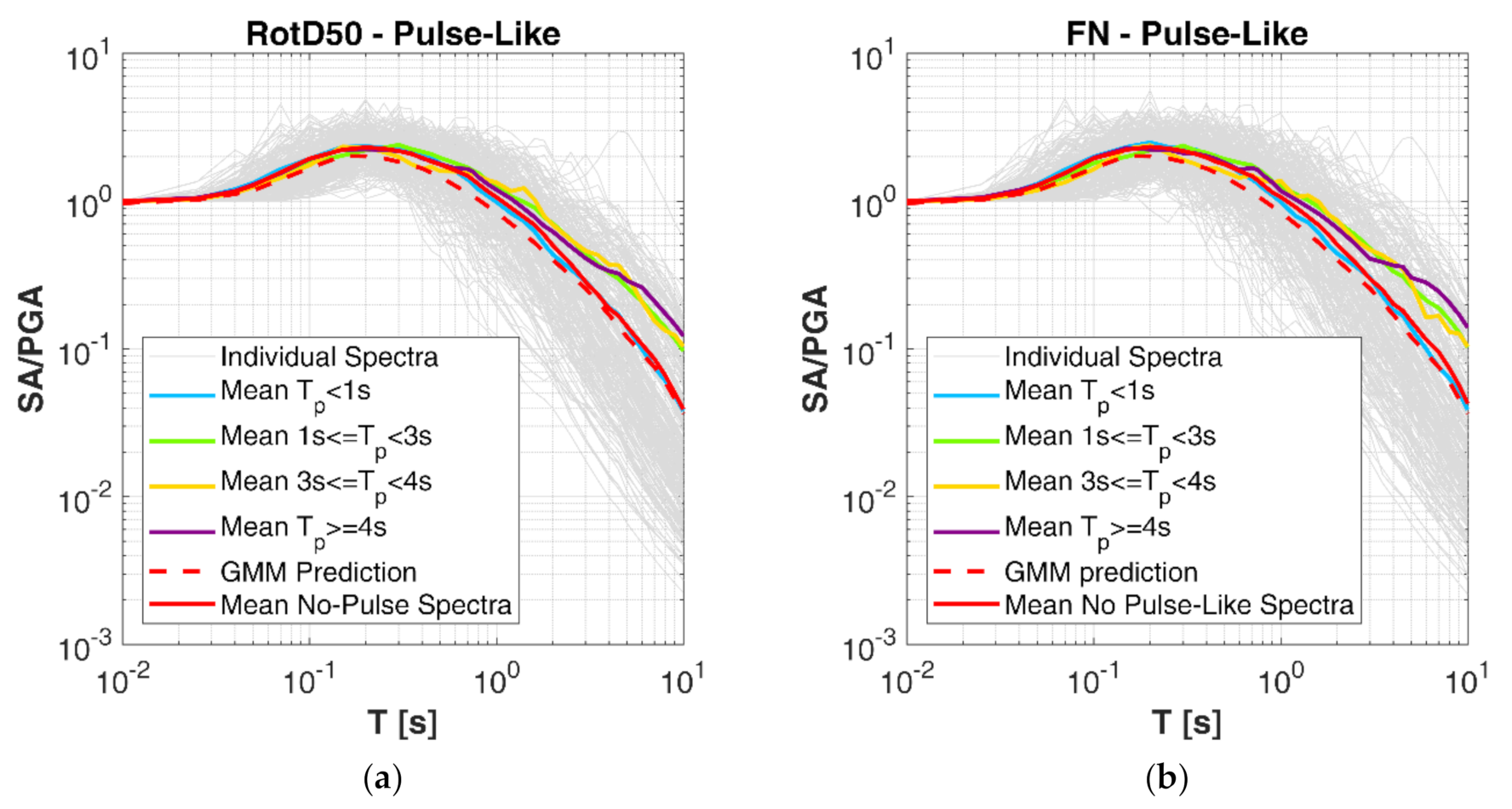
Figure 7 shows the GMM prediction (dashed line) compared to the mean of observed no-pulse and pulse-like data (solid lines), grouped by pulse periods. As expected, the GMM prediction is in good agreement with the mean of no-pulse motions, whereas a significant bias is noticeable for pulse-like records, especially at longer periods. No relevant differences between RotD50 (
Figure 7a) and FN-based (
Figure 7b) predictions can be observed.
5.2. Narrowband Amplification Factor
As discussed in the introduction, a practical approach to estimate spectral accelerations of impulsive records consists in using a GMM to predict ordinary motions (not impulsive) and then add an amplification factor around the pulse period to account for the contribution of the pulse [
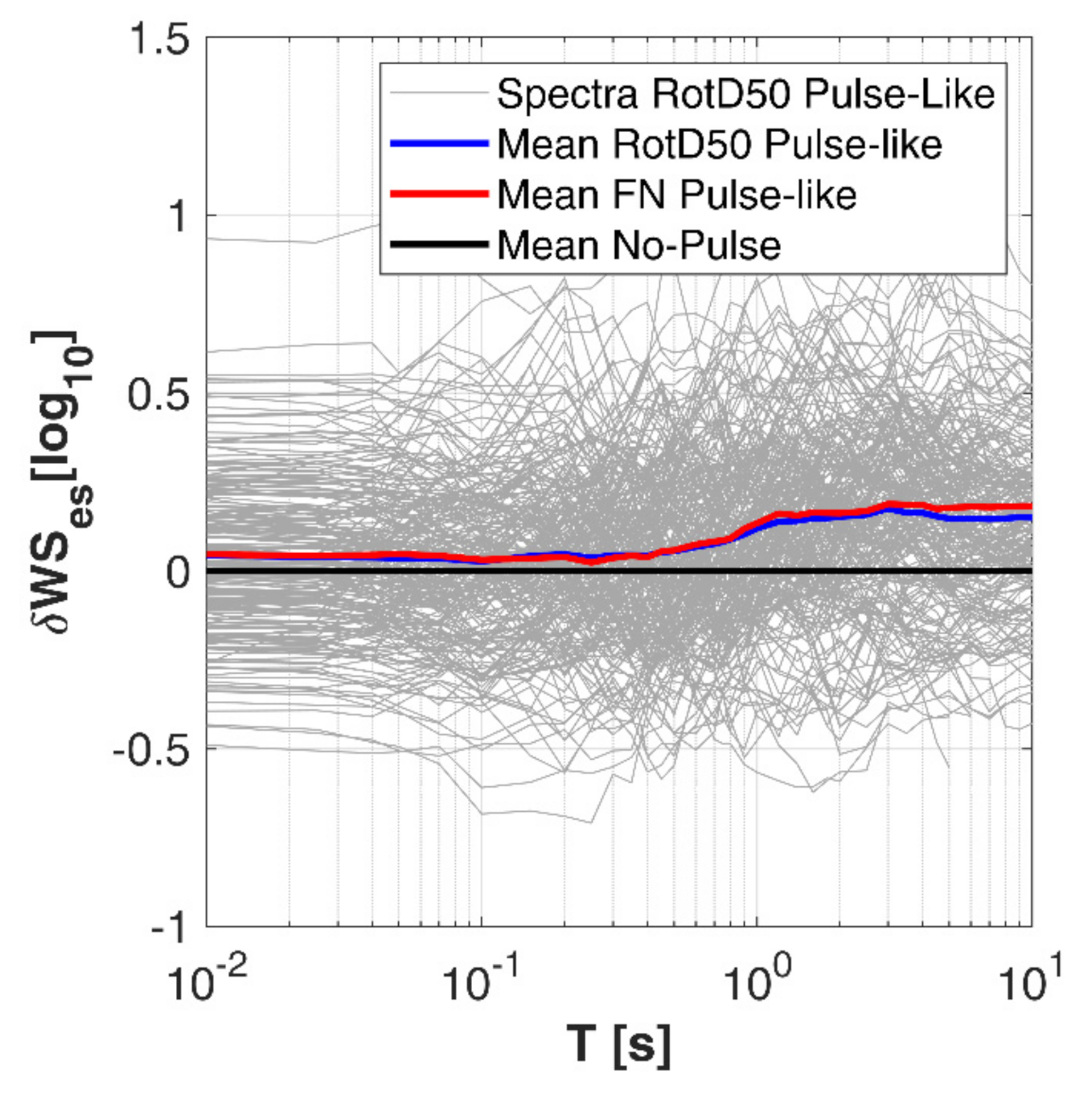
10]. To quantify this amplification effect on SA, we studied the within-event residuals of the observed acceleration spectral amplitudes with respect to that predicted by the GMM calibrated on no-pulse data. The residuals δWS
es versus period T are plotted in
Figure 8.
The black thick line indicates that the mean of the residuals of no-pulse records is close to zero, suggesting that, on average, the calibrated GMM is good for SA prediction and thus can be used to model ordinary near-fault ground motions. The blue and red lines, instead, indicate the mean of the pulse-like residuals, respectively, in terms of RotD50 and FN components. These latter show systematic bias especially at longer periods (T > 0.6 s).
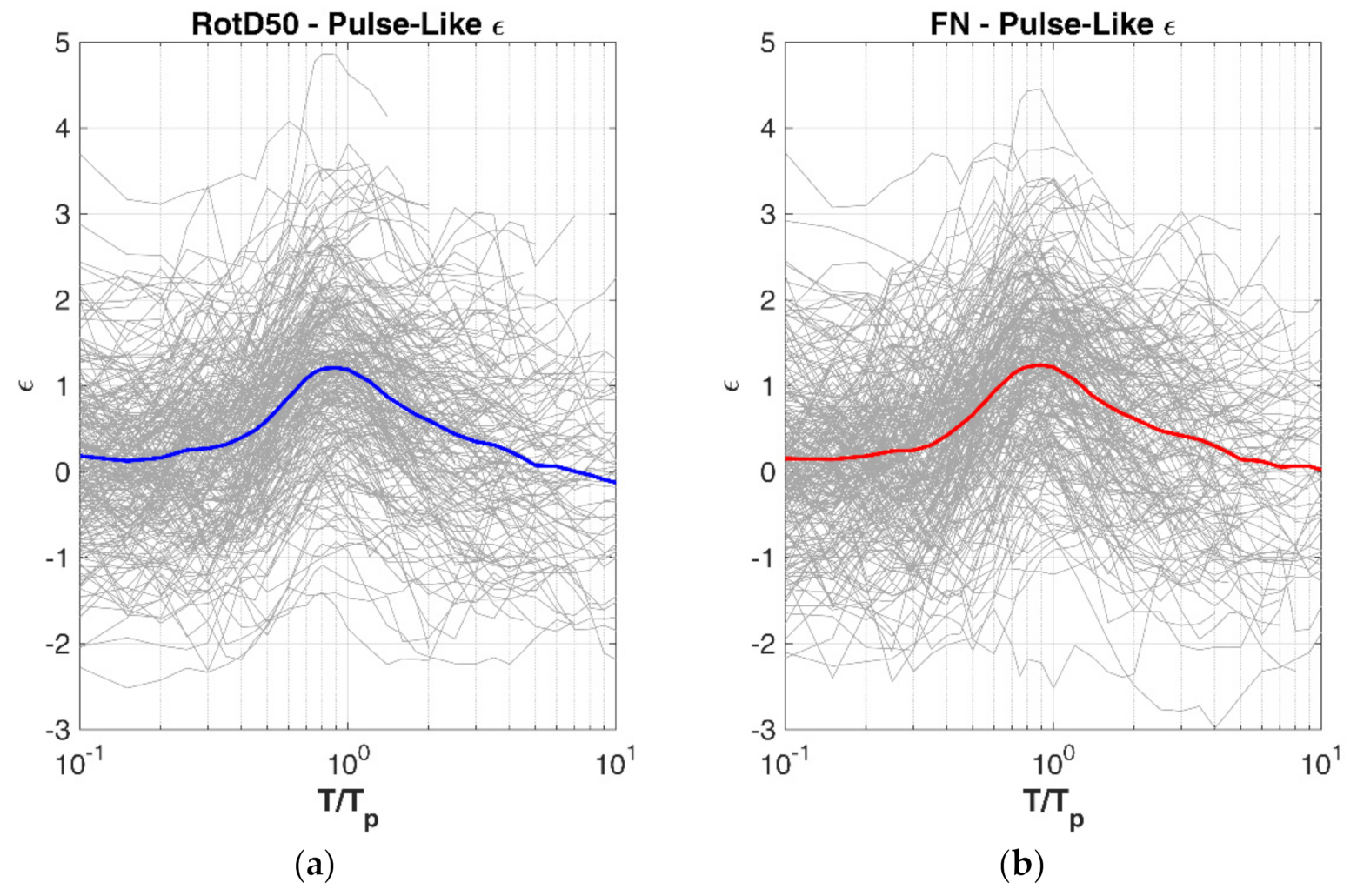
A more convenient form to check the amplification effect of impulsive data is obtained by plotting the within-event residuals normalized to the corresponding standard deviation (ε), as follows:
This quantity is plotted versus the ratio T/T
p, as shown in
Figure 9 for RotD50 (a) and FN (b) pulse-like waveforms. This approach to represent the residuals was also adopted by many authors [
27,
28,
29,
30,
31].
The introduction of the ratio T/T
p leads evident that the mean curve of the residuals has the typical bell-curve shape with a “bump” centered close to ratio T/T
p = 1. This shape of the mean amplification factor µ
Af is well approximated by Equations (11) and (12), respectively for RotD50 and FN components, calibrated through the curve fitting toolbox provided by Mathworks-Matlab
® environment:
For Equation (11), the estimated goodness of fit in terms of RMSE is 0.055 (coefficient of determination R-squared 98.3%), whereas for Equation (12) the RMSE is equal to 0.077 (R-squared 97.4%).
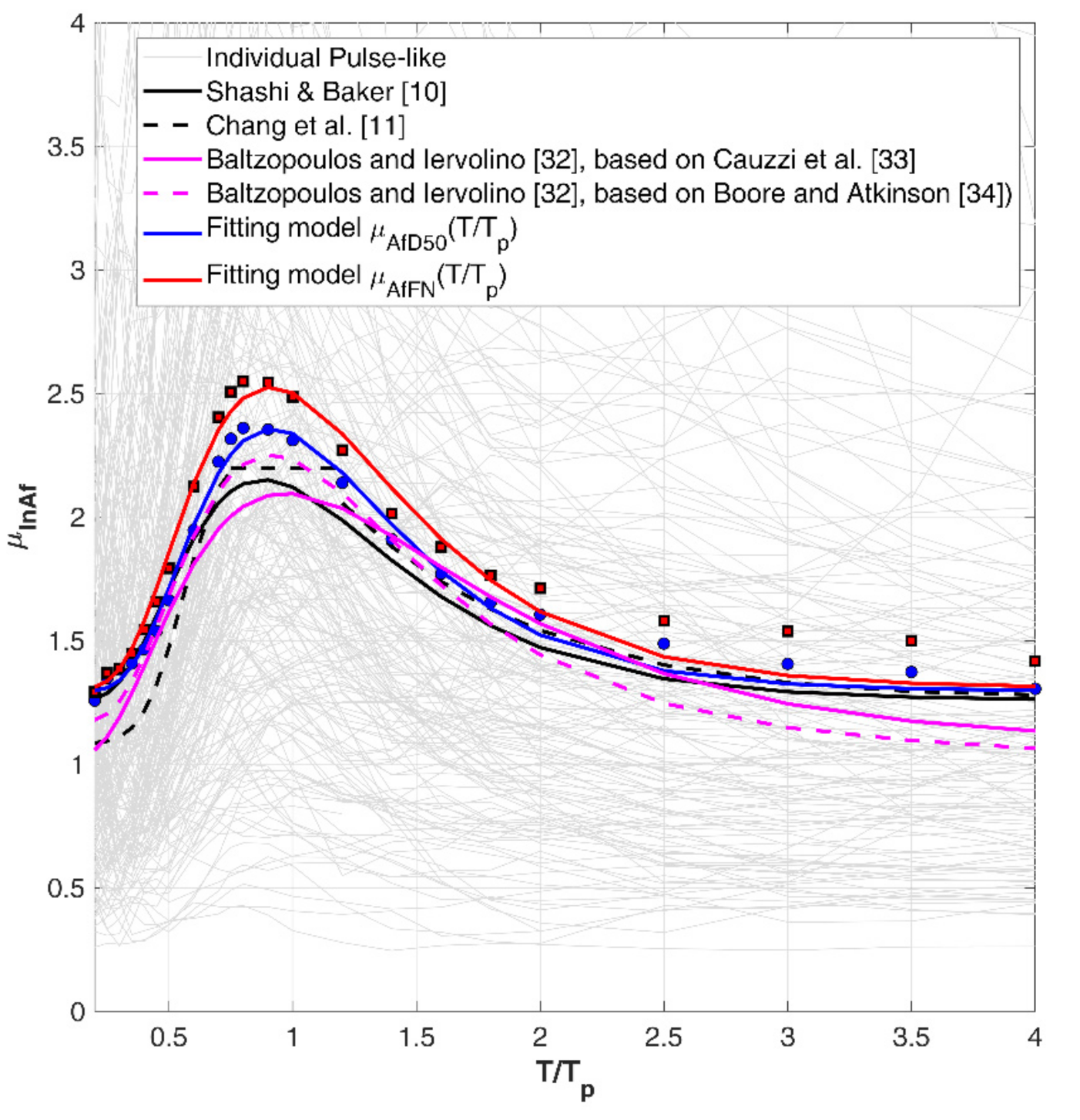
Figure 10 shows that the calibrated amplification factors, in terms of the ratio between the spectral accelerations SA normalized to the GMM prediction, is consistent with those proposed by other authors [
10,
11,
32,
33,
34]. The proposed models estimate systematically higher spectral amplifications compared to previous studies, probably due to the fact that they are calibrated on the residuals referred to an
ad hoc GMM, thus without any prediction bias. In this regard, we add that as all the previous models used for this comparison are based on the same pulse identification criteria introduced by Baker [
7], we do not expect that the observed differences in the amplification function lie in the pulse identification algorithms.
The estimated mean amplification factor µ
lnAf (obtained by Equation (11) or Equation (12)) can thus be used in conjunction with the reference GMM µ
lnSA,GMM (converted in natural logarithm units) to compute the mean ground motion prediction corrected for the pulse-like effects (µ
lnSA,pulse) as follows:
Regarding uncertainty, we did not perform a quantification of the total variability associated to the proposed GMM adjusted for the directivity pulse (σ
lnSA,pulse); thus, for eventual applications we suggest it is conservatively assumed equal to the σ(T) of Equation (7). Indeed, according to the findings of Shashi and Baker [
10], the σ
lnSA,pulse is always lower than the standard deviation of the reference GMM, by a reduction factor dependent on the pulse-period.
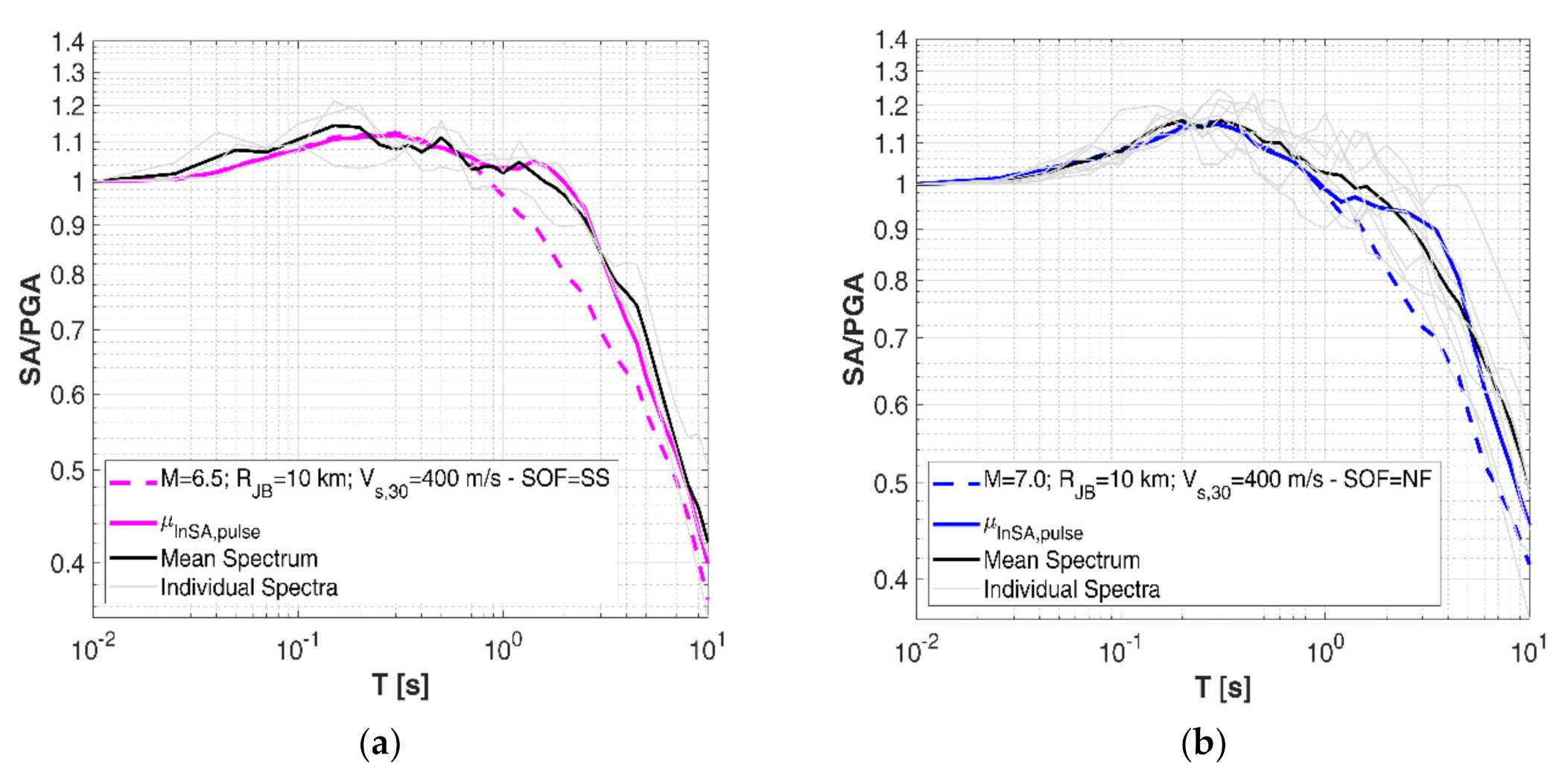
5.3. Application Example
An example of model application for prediction adjustment is illustrated in
Figure 11, which shows the average GMM (dashed lines) and the one modified by the amplification factor µ
lnAf,D50 (solid-colored lines) according to Equation (12) for two scenarios, compared to the observed spectral valuesfrom NESS1 dataset and divided by their PGA.
The first example scenario refers to M6.5 from SS faulting and site characterized by V
S,30 = 400 m/s and R
JB 10 km (
Figure 11a); the second scenario is identical to the first one, except for the event that is M7.0 from NF rupture (
Figure 11b).
The real observed SA values used for comparison are selected according to the same model parameters (magnitude and SOF) but with varying distance RJB < 20 km and site properties VS,30 = 400 ± 50 m/s. In these examples, the values of Tp used to calculate µlnAf,FN are estimated from Equation (1) calibrated on the pulse-like waveforms of NESS1 dataset.
Looking at
Figure 11, it can be noted that the adjusted GMM is able to capture the peculiar mean shape of the selected spectra, in particular the characteristic “bump” that occurs on impulsive spectra at a period close to T
p.
6. Conclusions
In this paper we have shown the most relevant features of spectral response related to records affected by forward-directivity effects and calibrated a model for impulsive ground motions based on an empirical corrective factor.
In detail, the main findings of the presented study include: (i) observations on the statistical features of pulse-like acceleration and displacement elastic spectra, (ii) a new near-source ground-motion model (GMM) of ordinary (no pulse) near-fault records and (iii) a new narrow-band amplification factor of elastic acceleration response that accounts for the increased seismic demand due to pulse-like effects. The analysis and the models here proposed have been calibrated on a comprehensive and high-quality public dataset collecting metadata of near-source waveforms from moderate-to-large worldwide events (NESS1).
Our results confirm that pulse-like effects on acceleration response spectra are not negligible, particularly at higher periods close to the pulse-period. The effect is also evident on displacement spectra, both in terms of amplitudes and period range. The proposed near-source GMM is specifically calibrated on the subset of not-impulsive records, in order to remove any potential bias. The proposed model, used in conjunction with the amplification factor calibrated on the within-event part of the model residuals, allows predicting acceleration spectral response accounting for near-fault pulse-like directivity effects. The model could then be used in combination with contour maps of the probability of pulse occurrence of sites near fault ruptures (e.g., Shahi and Baker [
10]; Chioccarelli and Iervolino [
9]; Iervolino and Cornell [
35]) for PSHA purposes, depending on source-to-site geometrical parameters [
23].
The authors are currently investigating deeper the significance of pulse motions on displacement spectra to calibrate new models and adjustment factors, by using processed waveforms with a baseline correction scheme. Such a modeling could be usefully applied in the framework of performance-based design applications.