Flood Hazard Estimation under Nonstationarity Using the Particle Filter
Abstract
1. Introduction
2. Materials and Methods
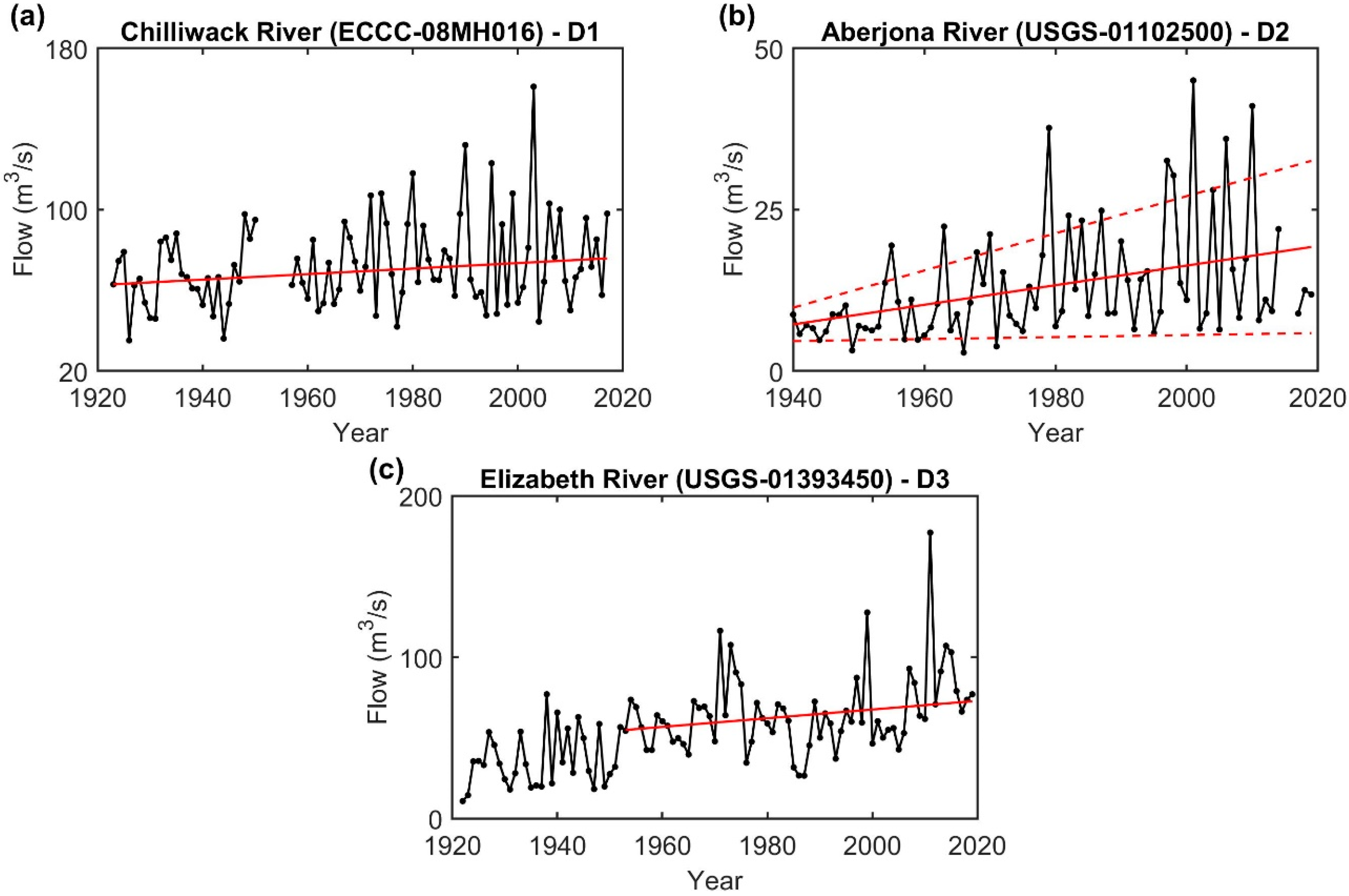
2.1. Nonstationary Datasets
2.2. Distribution and Nonstationary Structure in the Nonstationary Frequency Analysis
2.3. Particle Filtering for the Nonstationary Frequency Analysis
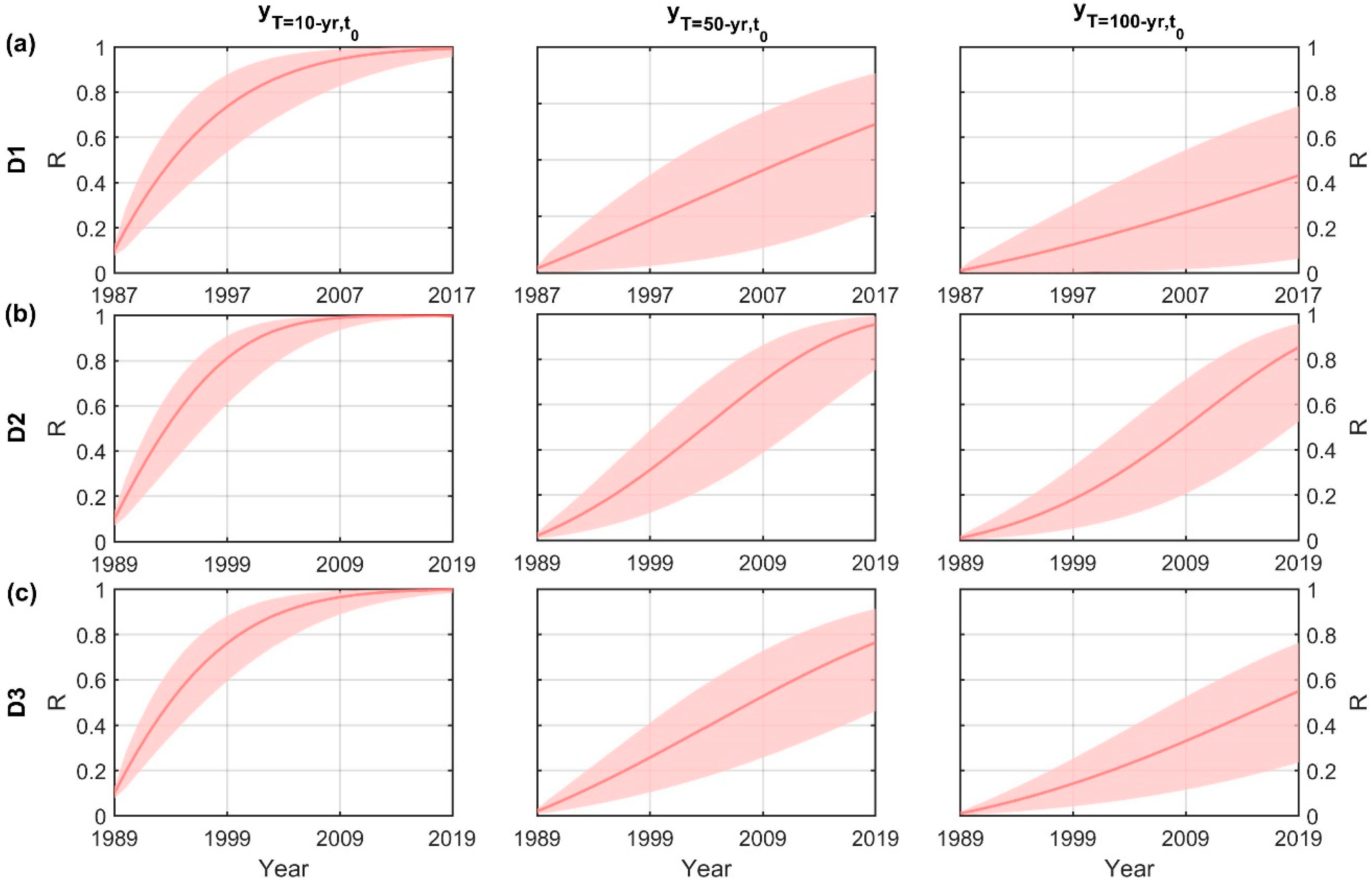
2.4. Flood Hazard Metrics
2.5. Model Evaluation and Uncertainty Metrics
3. Results and Discussion
3.1. Optimal Nonstationary Model
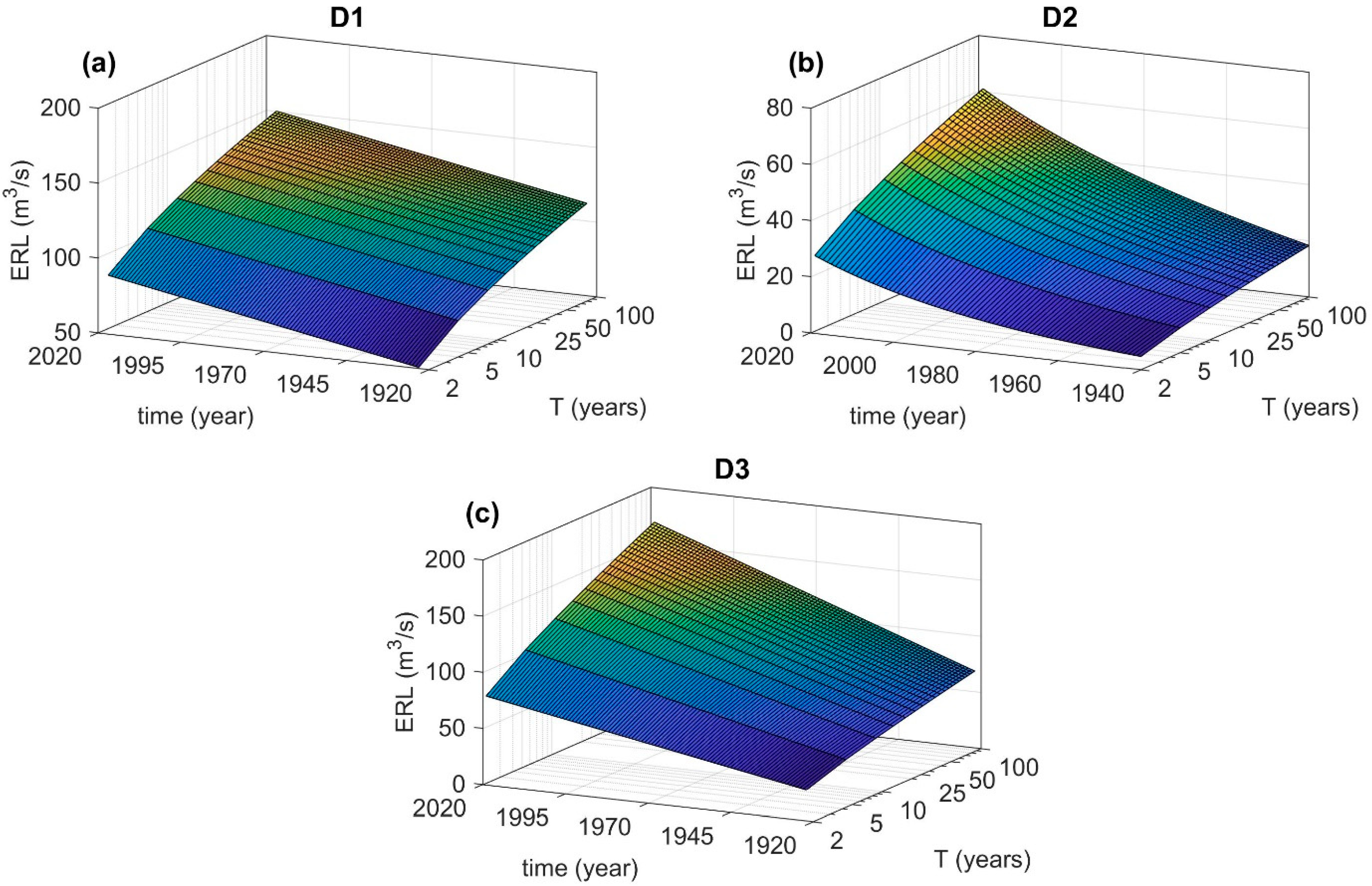
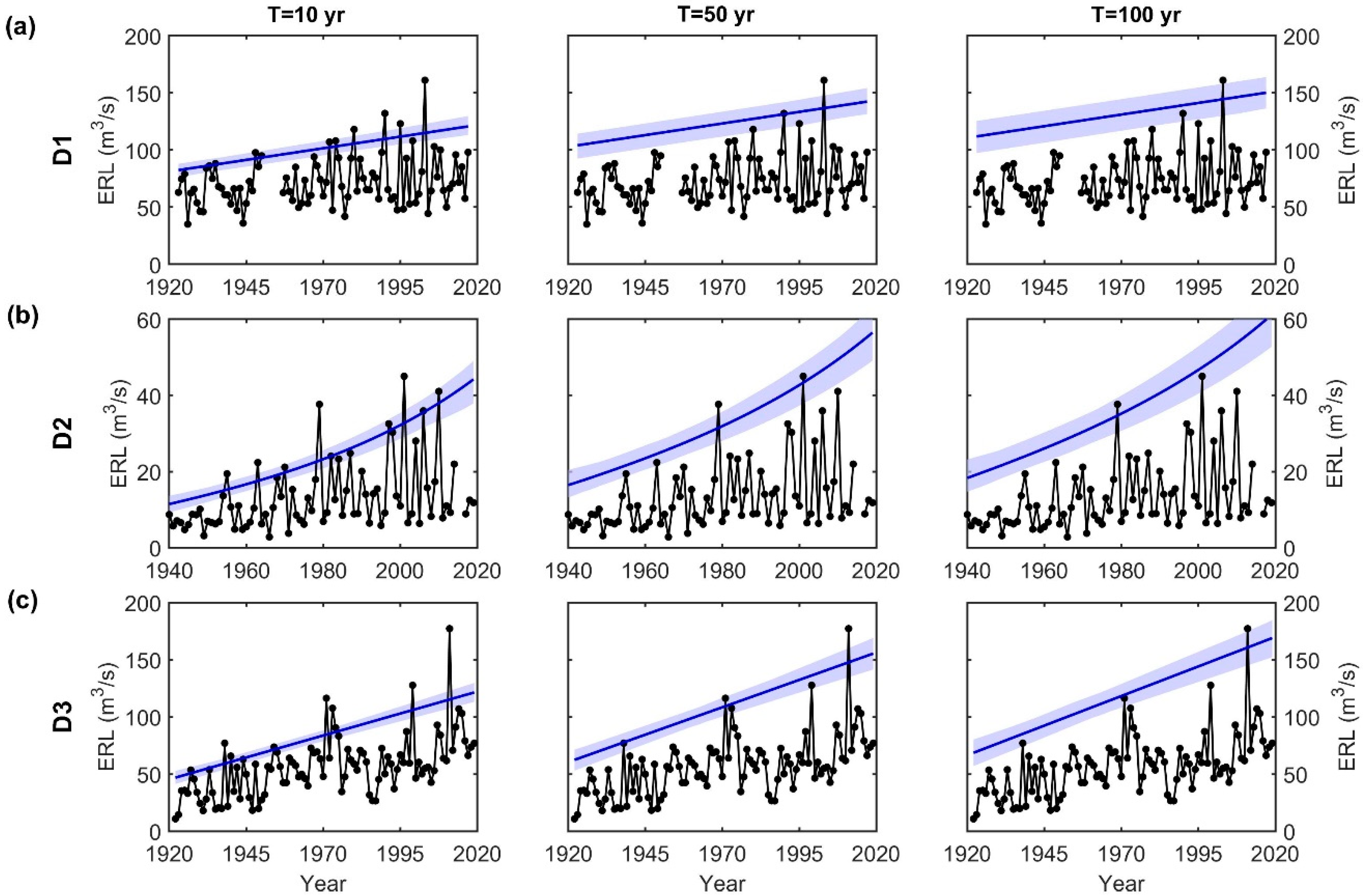
3.2. Flood Hazard Assessment under Nonstationarity
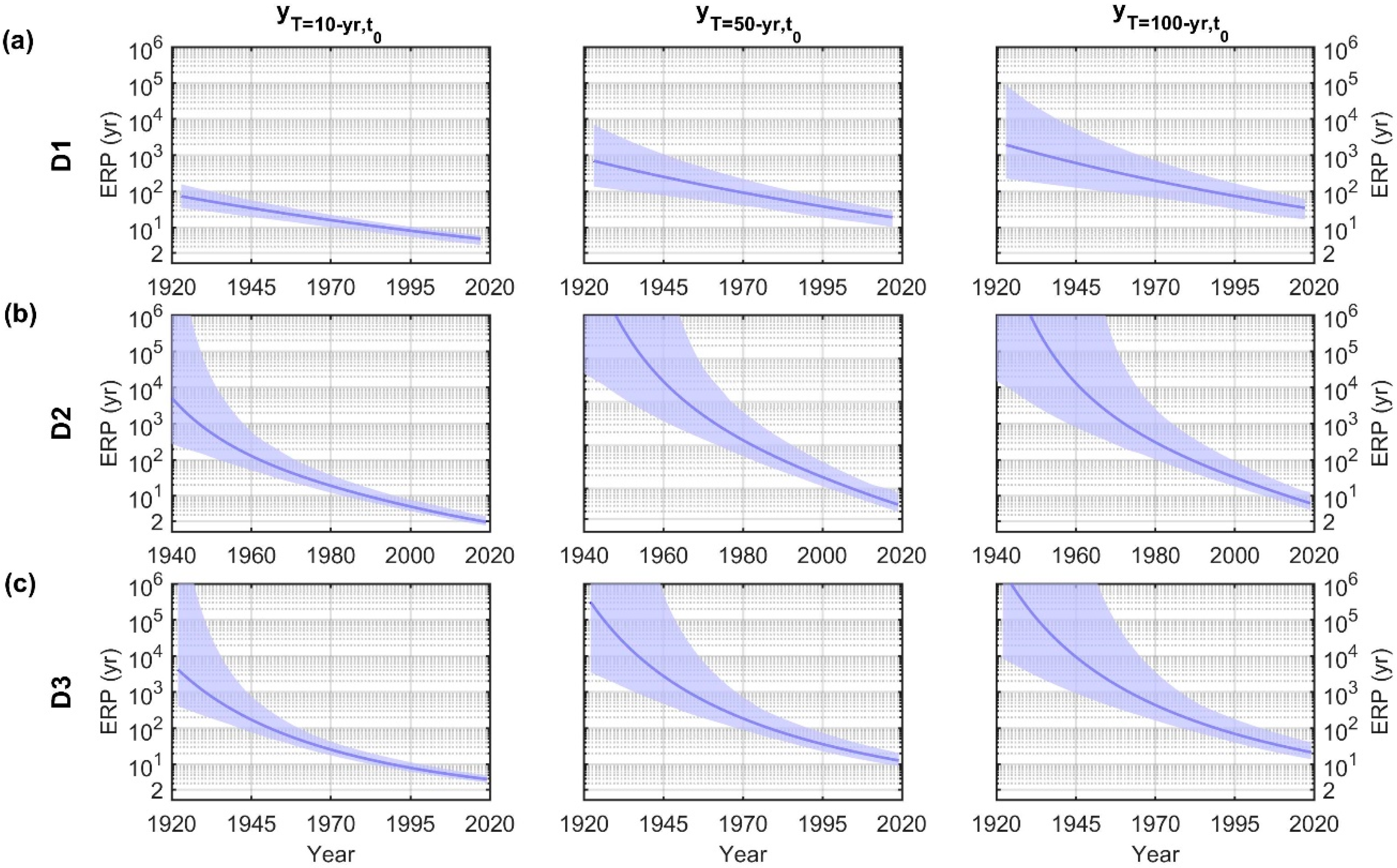
3.3. Uncertainty in the Flood Hazard Assessment
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tessler, Z.D.; Vorosmarty, C.J.; Grossberg, M.; Gladkova, I.; Aizenman, H.; Syvitski, J.P.M.; Foufoula-Georgiou, E. Profiling Risk and Sustainability in Coastal Deltas of the World. Science 2015, 349, 638–643. [Google Scholar] [CrossRef] [PubMed]
- IPCC. Global Warming of 1.5 °C: Summary for Policymakers; World Meteorological Organization: Geneva, Switzerland, 2018. [Google Scholar]
- Brooks, N.; Adger, W.N.; Kelly, P.M. The Determinants of Vulnerability and Adaptive Capacity at the National Level and the Implications for Adaptation. Glob. Environ. Chang. 2005, 15, 151–163. [Google Scholar] [CrossRef]
- Milly, A.P.C.D.; Betancourt, J.; Falkenmark, M.; Hirsch, R.M.; Zbigniew, W.; Lettenmaier, D.P.; Stouffer, R.J.; Milly, P.C.D. Stationarity Is Dead: Whither Water Management? Science 2008, 319, 573–574. [Google Scholar] [CrossRef] [PubMed]
- Faulkner, D.; Warren, S.; Spencer, P.; Sharkey, P. Can We Still Predict the Future from the Past? Implementing Non-Stationary Flood Frequency Analysis in the UK. J. Flood Risk Manag. 2020, 13, 1–15. [Google Scholar] [CrossRef]
- Ray, L.K.; Goel, N.K. Flood Frequency Analysis of Narmada River Basin in India under Nonstationary Condition. J. Hydrol. Eng. 2019, 24, 1–15. [Google Scholar] [CrossRef]
- Mondal, A.; Daniel, D. Return Levels under Nonstationarity: The Need to Update Infrastructure Design Strategies. J. Hydrol. Eng. 2019, 24, 1–11. [Google Scholar] [CrossRef]
- Coles, S. An Introduction to Statistical Modeling of Extreme Values; Springer: London, UK, 2001. [Google Scholar]
- Salas, J.D.; Obeysekera, J.; Vogel, R.M. Techniques for Assessing Water Infrastructure for Nonstationary Extreme Events: A Review. Hydrol. Sci. J. 2018, 63, 325–352. [Google Scholar] [CrossRef]
- Cheng, L.; Aghakouchak, A. Nonstationary Precipitation Intensity-Duration-Frequency Curves for Infrastructure Design in a Changing Climate. Sci. Rep. 2014, 4, 1–6. [Google Scholar] [CrossRef]
- Gado, T.A.; Van Nguyen, V.T. An At-Site Flood Estimation Method in the Context of Nonstationarity I. A Simulation Study. J. Hydrol. 2016, 535, 710–721. [Google Scholar] [CrossRef]
- Villarini, G.; Smith, J.A. Flood Peak Distributions for the Eastern United States. Water Resour. Res. 2010, 46, 1–17. [Google Scholar] [CrossRef]
- Sun, X.; Lall, U.; Merz, B.; Dung, N.V. Hierarchical Bayesian Clustering for Nonstationary Flood Frequency Analysis: Application to Trends of Annual Maximum Flow in Germany. Water Resour. Res. 2015, 51, 6586–6601. [Google Scholar] [CrossRef]
- Mondal, A.; Mujumdar, P.P. Detection of Change in Flood Return Levels under Global Warming. J. Hydrol. Eng. 2016, 21, 1–12. [Google Scholar] [CrossRef]
- Serago, J.M.; Vogel, R.M. Parsimonious Nonstationary Flood Frequency Analysis. Adv. Water Resour. 2018, 112, 1–16. [Google Scholar] [CrossRef]
- Ouarda, T.B.M.J.; Yousef, L.A.; Charron, C. Non-Stationary Intensity-Duration-Frequency Curves Integrating Information Concerning Teleconnections and Climate Change. Int. J. Climatol. 2018, 2306–2323. [Google Scholar] [CrossRef]
- Lu, F.; Song, X.; Xiao, W.; Zhu, K.; Xie, Z. Detecting the Impact of Climate and Reservoirs on Extreme Floods Using Nonstationary Frequency Models. Stoch. Environ. Res. Risk Assess. 2020, 34, 169–182. [Google Scholar] [CrossRef]
- Dong, Q.; Zhang, X.; Lall, U.; Sang, Y.F.; Xie, P. An Improved Nonstationary Model for Flood Frequency Analysis and Its Implication for the Three Gorges Dam, China. Hydrol. Sci. J. 2019, 64, 845–855. [Google Scholar] [CrossRef]
- Um, M.J.; Kim, Y.; Markus, M.; Wuebbles, D.J. Modeling Nonstationary Extreme Value Distributions with Nonlinear Functions: An Application Using Multiple Precipitation Projections for U.S. Cities. J. Hydrol. 2017, 552, 396–406. [Google Scholar] [CrossRef]
- Olsen, J.R.; Lambert, J.H.; Haimes, Y.Y. Risk of Extreme Events under Nonstationary Conditions. Risk Anal. 1998, 18, 497–510. [Google Scholar] [CrossRef]
- Wigley, T.M.L. The Effect of Changing Climate on the Frequency of Absolute Extreme Events. Clim. Chang. 2009, 97, 67–76. [Google Scholar] [CrossRef]
- Parey, S.; Malek, F.; Laurent, C.; Dacunha-Castelle, D. Trends and Climate Evolution: Statistical Approach for Very High Temperatures in France. Clim. Chang. 2007, 81, 331–352. [Google Scholar] [CrossRef]
- Parey, S.; Hoang, T.T.H.; Dacunha-Castelle, D. Different Ways to Compute Temperature Return Levels in the Climate Change Context. Environmetrics 2010, 21, 698–718. [Google Scholar] [CrossRef]
- Katz, R.W.; Parlange, M.B.; Naveau, P. Statistics of Extremes in Hydrology. Adv. Water Resour. 2002, 25, 1287–1304. [Google Scholar] [CrossRef]
- Serinaldi, F.; Kilsby, C.G. Stationarity Is Undead: Uncertainty Dominates the Distribution of Extremes. Adv. Water Resour. 2015, 77, 17–36. [Google Scholar] [CrossRef]
- Read, L.K.; Vogel, R.M. Reliability, Return Periods, and Risk under Nonstationarity. Water Resour. Res. 2015, 6381–6398. [Google Scholar] [CrossRef]
- Klemeš, V. Risk Analysis: The Unbearable Cleverness of Bluffing; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Aven, T.; Pörn, K. Expressing and Interpreting the Results of Quantitative Risk Analyses. Review and Discussion. Reliab. Eng. Syst. Saf. 1998, 61, 3–10. [Google Scholar] [CrossRef]
- Borgomeo, E.; Mortazavi-Naeini, M.; Hall, J.W.; Guillod, B.P. Risk, Robustness and Water Resources Planning Under Uncertainty. Earth’s Futur. 2018, 6, 468–487. [Google Scholar] [CrossRef]
- Obeysekera, J.; Salas, J.D. Quantifying the Uncertainty of Design Floods under Nonstationary Conditions. J. Hydrol. Eng. 2014, 19, 1438–1446. [Google Scholar] [CrossRef]
- Renard, B.; Sun, X.; Lang, M. Bayesian Methods for Non-Stationary Extreme Value Analysis. In Extremes in a Changing Climate; Springer: Berlin/Heidelberg, Germany, 2013; pp. 39–95. [Google Scholar]
- Sen, S.; He, J.; Kasiviswanathan, K.S. Uncertainty Quantification Using the Particle Filter for Non-Stationary Hydrological Frequency Analysis. J. Hydrol. 2020, 584. [Google Scholar] [CrossRef]
- Vidrio-Sahagún, C.T.; He, J.; Kasiviswanathan, K.S.; Sen, S. Stationary Hydrological Frequency Analysis Coupled with Uncertainty Assessment under Nonstationary Scenarios. J. Hydrol. 2020, 125725. [Google Scholar] [CrossRef]
- Salamon, P.; Feyen, L. Assessing Parameter, Precipitation, and Predictive Uncertainty in a Distributed Hydrological Model Using Sequential Data Assimilation with the Particle Filter. J. Hydrol. 2009, 376, 428–442. [Google Scholar] [CrossRef]
- Moradkhani, H.; Hsu, K.-L.; Gupta, H.; Sorooshian, S. Uncertainty Assessment of Hydrologic Model States and Parameters: Sequential Data Assimilation Using the Particle Filter. Water Resour. Res. 2005, 41, 1–17. [Google Scholar] [CrossRef]
- Shrestha, D.L.; Solomatine, D.P. Machine Learning Approaches for Estimation of Prediction Interval for the Model Output. Neural Netw. 2006, 19, 225–235. [Google Scholar] [CrossRef] [PubMed]
- Alvisi, S.; Franchini, M. Fuzzy Neural Networks for Water Level and Discharge Forecasting with Uncertainty. Environ. Model. Softw. 2011, 26, 523–537. [Google Scholar] [CrossRef]
- Doucet, A.; de Freitas, N.; Gordon, N. An Introduction to Sequential Monte Carlo Methods; Springer: New York, NY, USA, 2001. [Google Scholar] [CrossRef]
- Gordon, N.J.; Salmond, D.J.; Smith, A.F.M. Novel Approach to Nonlinear/Non-Gaussian Bayesian State Estimation. IEE Proc. F Radar Signal Process. 1993, 140, 107. [Google Scholar] [CrossRef]
- Milly, P.C.D.; Betancourt, J.; Falkenmark, M.; Hirsch, R.M.; Kundzewicz, Z.W.; Lettenmaier, D.P.; Stouffer, R.J.; Dettinger, M.D.; Krysanova, V. On Critiques of “Stationarity Is Dead: Whither Water Management?”. Water Resour. Res. 2015. [Google Scholar] [CrossRef]
- Bayazit, M. Nonstationarity of Hydrological Records and Recent Trends in Trend Analysis: A State-of-the-Art Review. Environ. Process. 2015, 2, 527–542. [Google Scholar] [CrossRef]
- Matalas, N.C. Comment on the Announced Death of Stationarity. J. Water Resour. Plan. Manag. 2012, 138, 311–312. [Google Scholar] [CrossRef]
- Lindgren, G.; Rootzén, H.; Sandsten, M. Stationary Stochastic Processes for Scientists and Engineers; Chapman and Hall/CRC: Boca Raton, FL, USA, 2013. [Google Scholar]
- Liu, J.; Zhang, Q.; Singh, V.P.; Gu, X.; Shi, P. Nonstationarity and Clustering of Flood Characteristics and Relations with the Climate Indices in the Poyang Lake Basin, China. Hydrol. Sci. J. 2017, 62, 1809–1824. [Google Scholar] [CrossRef]
- Yan, L.; Xiong, L.; Liu, D.; Hu, T.; Xu, C.Y. Frequency Analysis of Nonstationary Annual Maximum Flood Series Using the Time-Varying Two-Component Mixture Distributions. Hydrol. Process. 2017, 31, 69–89. [Google Scholar] [CrossRef]
- Gado, T.A.; Nguyen, V.T. Van. An At-Site Flood Estimation Method in the Context of Nonstationarity II. Statistical Analysis of Floods in Quebec. J. Hydrol. 2016, 535, 722–736. [Google Scholar] [CrossRef]
- Byun, K.; Hamlet, A.F. A Risk-Based Analytical Framework for Quantifying Non-Stationary Flood Risks and Establishing Infrastructure Design Standards in a Changing Environment. J. Hydrol. 2020, 584, 124575. [Google Scholar] [CrossRef]
- Vu, T.M.; Mishra, A.K. Nonstationary Frequency Analysis of the Recent Extreme Precipitation Events in the United States. J. Hydrol. 2019, 575, 999–1010. [Google Scholar] [CrossRef]
- Yan, L.; Li, L.; Yan, P.; He, H.; Li, J.; Lu, D. Nonstationary Flood Hazard Analysis in Response to Climate Change and Population Growth. Water 2019, 11, 1811. [Google Scholar] [CrossRef]
- El Adlouni, S.; Ouarda, T.B.M.J.; Zhang, X.; Roy, R.; Bobée, B. Generalized Maximum Likelihood Estimators for the Nonstationary Generalized Extreme Value Model. Water Resour. Res. 2007, 43, 1–13. [Google Scholar] [CrossRef]
- Ouarda, T.B.M.J.; Charron, C.; St-Hilaire, A. Uncertainty of Stationary and Nonstationary Models for Rainfall Frequency Analysis. Int. J. Climatol. 2019, 1–20. [Google Scholar] [CrossRef]
- Arulampalam, M.S.; Maskell, S.; Gordon, N.; Clapp, T. A Tutorial on Particle Filters for Online Nonlinear/Non-Gaussian Bayesian Tracking. IEEE Trans. Signal Process. 2002, 50, 174–188. [Google Scholar] [CrossRef]
- Sarhadi, A.; Soltani, S.; Modarres, R. Probabilistic Flood Inundation Mapping of Ungauged Rivers: Linking GIS Techniques and Frequency Analysis. J. Hydrol. 2012, 458–459, 68–86. [Google Scholar] [CrossRef]
- Sun, P.; Wen, Q.; Zhang, Q.; Singh, V.P.; Sun, Y.; Li, J. Nonstationarity-Based Evaluation of Flood Frequency and Flood Risk in the Huai River Basin, China. J. Hydrol. 2018, 567, 393–404. [Google Scholar] [CrossRef]
- Hsu, K.-L.; Gupta, H.V.; Sorooshian, S. Artificial Neural Network Modeling of the Rainfall-Runoff Process. Water Resour. Res. 1995, 31, 2517–2530. [Google Scholar] [CrossRef]
- Akaike, H. A New Look at the Statistical Model Identification. IEEE Trans. Automat. Contr. 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Hosking, J.R.M. L-Moments: Analysis and Estimation of Distributions Using Linear Combinations of Order Statistics. J. R. Stat. Soc. 1990, 52, 105–124. [Google Scholar] [CrossRef]
- Xiong, L.; Wan, M.; Wei, X.; O’connor, K.M. Indices for Assessing the Prediction Bounds of Hydrological Models and Application by Generalised Likelihood Uncertainty Estimation/Indices Pour Évaluer Les Bornes de Prévision de Modèles Hydrologiques et Mise En Œuvre Pour Une Estimation d’incertitude. Hydrol. Sci. J. 2009, 54, 852–871. [Google Scholar] [CrossRef]

| Model ID | GEV Parameters |
|---|---|
| , and | |
| , and | |
| , and | |
| , , and | |
| , , and | |
| , , and | |
| , , and |
| RMSE (m3/s) | Bias (m3/s) | R2 | AIC | BIC | |
|---|---|---|---|---|---|
| 1.54 | <−0.01 | >0.99 | 46.43 | 56.39 | |
| 1.54 | 0.02 | >0.99 | 46.63 | 56.59 | |
| 1.51 | <−0.01 | >0.99 | 46.52 | 58.97 | |
| 1.65 | −0.01 | 0.99 | 54.82 | 67.27 | |
| 1.64 | 0.01 | 0.99 | 53.79 | 66.23 | |
| 1.61 | 0.01 | 0.99 | 52.29 | 64.73 | |
| 1.63 | 0.04 | 0.99 | 53.70 | 66.15 | |
| D2 | |||||
| 0.79 | <−0.01 | 0.99 | −10.67 | −1.24 | |
| 1.16 | −0.08 | 0.98 | 19.25 | 28.68 | |
| 0.73 | −0.01 | 0.99 | −14.85 | −3.07 | |
| 0.83 | −0.01 | 0.99 | −4.26 | 7.52 | |
| 0.69 | −0.01 | 0.99 | −19.10 | −7.31 | |
| 0.91 | −0.18 | 0.99 | 3.01 | 14.80 | |
| 1.30 | −0.09 | 0.98 | 30.21 | 41.99 | |
| D3 | |||||
| 2.37 | −0.01 | 0.99 | 92.57 | 102.91 | |
| 2.45 | 0.05 | 0.99 | 95.99 | 106.33 | |
| 2.27 | −0.01 | 0.99 | 90.35 | 103.28 | |
| 1.43 | <0.01 | >0.99 | 44.86 | 57.79 | |
| 1.58 | 0.03 | >0.99 | 54.64 | 67.57 | |
| 1.48 | 0.01 | >0.99 | 48.50 | 61.43 | |
| 2.58 | −0.21 | 0.99 | 102.96 | 115.88 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vidrio-Sahagún, C.T.; He, J. Flood Hazard Estimation under Nonstationarity Using the Particle Filter. Geosciences 2021, 11, 13. https://doi.org/10.3390/geosciences11010013
Vidrio-Sahagún CT, He J. Flood Hazard Estimation under Nonstationarity Using the Particle Filter. Geosciences. 2021; 11(1):13. https://doi.org/10.3390/geosciences11010013
Chicago/Turabian StyleVidrio-Sahagún, Cuauhtémoc Tonatiuh, and Jianxun He. 2021. "Flood Hazard Estimation under Nonstationarity Using the Particle Filter" Geosciences 11, no. 1: 13. https://doi.org/10.3390/geosciences11010013
APA StyleVidrio-Sahagún, C. T., & He, J. (2021). Flood Hazard Estimation under Nonstationarity Using the Particle Filter. Geosciences, 11(1), 13. https://doi.org/10.3390/geosciences11010013






