Ice-Cliff Morphometry in Identifying the Surge Phenomenon of Tidewater Glaciers (Spitsbergen, Svalbard)
Abstract
1. Introduction
2. Materials and Methods
3. Results
3.1. Geometric Parameters of the Glacier Ice-Cliffs in Spitsbergen (1936–2017)
3.2. Frontal Zone Morphometry of the Retreating Glaciers
3.3. Frontal Zone Morphometry of the Advancing Glaciers
3.4. Application of CfD and CfE Indicators in the Classification of Spitsbergen Tidewater Glaciers in Terms of Dynamics
- At the beginning of “the active phase of the glacier surge” both CfD and CfE indicators increase rapidly by 3–5 times during approximately 1–5 years. For larger glaciers, the rate of increase can reach a maximum of a 10× increase (I quadrant in Figure 7 and Figure 8). In this phase, the frontal zone protrudes (convex shape) and the glacier moves forward. Then the ice-cliff position is marked by slight fluctuations or “stagnates”, and numerous inflexion points associated with intensive calving appear in the cliff line.
- After the active phase, the glacier first loses its frontal zone convexity, mainly as a result of intensive calving, and it is subject to “recession” (including the quiescent phase of the glacier surge). At this point, CfD and CfE values decrease interannually to an average of 0.05–0.06 (for CfE the sign changes to negative; III quadrant).
- Subsequently, the glacier can enter a “deep recession phase”, when its frontal zone is strongly concave, especially for the largest glaciers (IV quadrant). “Glacier buttresses” are also observed, i.e., parts of the glacier front anchored on land, from which the ice-cliff bends into an arch. During the quiescent phase, CfD and CfE values change very little interannually and are ca. 0.015–0.025. The value of CfD decreases the most (it can even be negative), with the CfE value slowly increasing from −1 to approximately −0.5.
- The glacier begins to lose its maximum ice-cliff concavity at the end of the recession with “the frontal zone filling and the slow forward movement” beginning (II quadrant). At this point, the CfD value slowly increases and CfE value slowly decreases (from −0.5 to −1) until the protrusion of the glacier front and the value changes to plus sign.
4. Discussion
4.1. The Role of the Ice-Cliffs Morphometry in the Glacier Surge Triggering
4.2. Duration of the Active Phase During the Glacier Surge
5. Conclusions
Supplementary Materials
Funding
Acknowledgments
Conflicts of Interest
References
- Rachlewicz, G.; Szczuciński, W.; Ewertowski, M. Post-“Little Ice Age” retreat rates of glaciers around Billefjorden in central Spitsbergen, Svalbard. Pol. Polar Res. 2007, 28, 159–186. [Google Scholar]
- Ziaja, W.; Pipała, R. Glacial recession 2001–2006 and its landscape effects in the Lindströmfjellet-Håbergnuten mountain ridge, Nordenskiöld Land, Spitsbergen. Pol. Polar Res. 2007, 28, 237–247. [Google Scholar]
- Małecki, J. Elevation and volume changes of seven Dickson Land glaciers, Svalbard, 1960–1990–2009. Polar Res. 2013, 32, 18400. [Google Scholar] [CrossRef]
- Martín-Moreno, R.; Álvarez, F.A.; Hagen, J.O. “Little Ice Age” glacier extent and subsequent retreat in Svalbard archipelago. Holocene 2017, 27, 1379–1390. [Google Scholar] [CrossRef]
- Szafraniec, J.E. Deglaciation rate on southern and western Spitsbergen in the conditions of Arctic amplification. Pol. Polar Res. 2018, 39, 77–98. [Google Scholar] [CrossRef]
- Błaszczyk, M.; Jania, J.A.; Kolondra, L. Fluctuations of tidewater glaciers in Hornsund Fjord (Southern Svalbard) since the beginning of the 20th century. Pol. Polar Res. 2013, 34, 327–352. [Google Scholar] [CrossRef]
- Błaszczyk, M.; Ignatiuk, D.; Uszczyk, A.; Cielecka-Nowak, K.; Grabiec, M.; Jania, J.A.; Moskalik, M.; Walczowski, W. Freshwater input to the Arctic fjord Hornsund (Svalbard). Polar Res. 2019, 38, 3506. [Google Scholar] [CrossRef]
- Nuth, C.; Kohler, J.; König, M.; von Deschwanden, A.; Hagen, J.O.M.; Kääb, A.; Moholdt, G.; Pettersson, R. Decadal changes from a multi-temporal glacier inventory of Svalbard. Cryosphere 2013, 7, 1603–1621. [Google Scholar] [CrossRef]
- Serreze, M.C.; Francis, J.A. The Arctic Amplification Debate. Clim. Chang. 2006, 76, 241–264. [Google Scholar] [CrossRef]
- Francis, J.A.; Vavrus, S.J. Evidence linking Arctic amplification to extreme weather in mid-latitudes. Geophys. Res. Lett. 2012, 39, L06801. [Google Scholar] [CrossRef]
- Meier, W.N.; Gerland, S.; Granskog, M.A.; Key, J.R. Sea ice. In Snow, Water, Ice and Permafrost in the Arctic (SWIPA): Climate Change and Cryosphere; Arctic Monitoring and Assessment Programme (AMAP): Oslo, Norway, 2011; pp. 357–443. [Google Scholar]
- Overland, J.E.; Wang, M.; Walsh, J.E.; Christensen, J.H.; Kattsov, V.M.; Chapman, W.L. Climate Model projections for the Artcic. In Snow, Water, Ice and Permafrost in the Arctic (SWIPA): Climate Change and Cryosphere; Arctic Monitoring and Assessment Programme (AMAP): Oslo, Norway, 2011; pp. 37–54. [Google Scholar]
- Isaksen, K.; Nordli, Ø.; Førland, E.J.; Łupikasza, E.; Eastwood, S.; Niedźwiedź, T. Recent warming on Spitsbergen–Influence of atmospheric circulation and sea ice cover. J. Geophys. Res. D Atmos. 2016, 121, 11–913. [Google Scholar] [CrossRef]
- Dowdeswell, J.A.; Hamilton, G.S.; Hagen, J.O. The duration of the active phase on surge-type glaciers: Contrasts between Svalbard and other regions. J. Glaciol. 1991, 37, 388–400. [Google Scholar] [CrossRef]
- Lefauconnier, B.; Hagen, J.O. Surging and Calving Glaciers in Eastern Svalbard; Meddelelser, 116: Oslo, Norway, 1991; p. 130. [Google Scholar]
- Hagen, J.O.; Liestøl, O.; Roland, E.; Jorgensen, T. Glacier atlas of Svalbard and Jan Mayen; Meddelelser, 129: Oslo, Norway, 1993; p. 169. [Google Scholar]
- Hamilton, G.S.; Dowdeswell, J.A. Controls on glacier surging in Svalbard. J. Glaciol. 1996, 42, 157–168. [Google Scholar] [CrossRef]
- Jiskoot, H.; Murray, T.; Boyle, P. Controls on the distribution of surge-type glaciers in Svalbard. J. Glaciol. 2000, 46, 412–422. [Google Scholar] [CrossRef]
- Sund, M.; Eiken, T.; Hagen, J.O.; Kääb, A. Svalbard surge dynamics derived from geometric changes. Ann. Glaciol. 2009, 50, 50–60. [Google Scholar] [CrossRef]
- Błaszczyk, M.; Jania, J.A.; Hagen, J.O. Tidewater glaciers of Svalbard: Recent changes and estimates of calving fluxes. Pol. Polar Res. 2009, 30, 85–142. [Google Scholar]
- Farnsworth, W.R.; Ingólfsson, Ó.; Retelle, M.; Schomacker, A. Over 400 previously undocumented Svalbard surge-type glaciers identified. Geomorphology 2016, 264, 52–60. [Google Scholar] [CrossRef]
- Sevestre, H.; Benn, D.I.; Luckman, A.; Nuth, C.; Kohler, J.; Lindbäck, K.; Pettersson, R. Tidewater glacier surges initiated at the terminus. J. Geophys. Res. Earth Surf. 2017, 123, 1035–1051. [Google Scholar] [CrossRef]
- Sevestre, H.; Benn, D.I. Climatic and geometric controls on the global distribution of surge-type glaciers: Implications for a unifying model of surging. J. Glaciol. 2015, 61, 646–662. [Google Scholar] [CrossRef]
- Nuth, C.; Moholdt, G.; Kohler, J.; Hagen, J.O.; Kääb, A. Svalbard glacier elevation changes and contribution to sea level rise. J. Geophys. Res. 2010, 115. [Google Scholar] [CrossRef]
- Małecki, J.; Faucherre, S.; Strzelecki, M.C. Post-surge geometry and thermal structure of Hørbyebreen, central Spitsbergen. Pol. Polar Res. 2013, 34, 305–321. [Google Scholar] [CrossRef]
- Benn, D.I.; Fowler, A.C.; Hewitt, I.; Sevestre, H. General theory of glacier surges. J. Glaciol. 2019, 65, 701–716. [Google Scholar] [CrossRef]
- Mansell, D.; Luckman, A.; Murray, T. Dynamics of tidewater surge-type glaciers in northwest Svalbard. J. Glaciol. 2012, 58, 110–118. [Google Scholar] [CrossRef]
- McMillan, M.; Shepherd, A.; Gourmelen, N.; Dehecq, A.; Leeson, A.; Ridout, A.; Flament, T.; Hogg, A.; Gilbert, L.; Benham, T.; et al. Rapid dynamic activation of a marine-based Arctic ice cap. Geophys. Res. Lett. 2014, 41, 8902–8909. [Google Scholar] [CrossRef]
- Aschwanden, A.; Bueler, E.; Khroulev, C.; Blatter, H. An enthalpy formulation for glaciers and ice sheets. J. Glaciol. 2012, 58, 441–457. [Google Scholar] [CrossRef]
- Dunse, T.; Schellenberger, T.; Hagen, J.O.; Kääb, A.; Schuler, T.V.; Reijmer, C.H. Glacier-surge mechanisms promoted by a hydro-thermodynamic feedback to summer melt. Cryosphere 2015, 9, 197–215. [Google Scholar] [CrossRef]
- Benn, D.I.; Warren, C.R.; Mottram, R.H. Calving processes and the dynamics of calving glaciers. Earth Sci. Rev. 2007, 82, 143–179. [Google Scholar] [CrossRef]
- Benn, D.I.; Åström, J.A. Calving glaciers and ice shelves. Adv. Phys. X 2018, 3, 1513819. [Google Scholar] [CrossRef]
- Hagen, J.O.; Kohler, J.; Melvold, K.; Winther, J.-G. Glaciers in Svalbard: Mass balance, runoff and freshwater flux. Polar Res. 2003, 22, 145–159. [Google Scholar] [CrossRef]
- Benn, D.I.; Kristensen, L.; Gulley, J.D. Surge propagation constrained by a persistent subglacial conduit, Bakaninbreen–Paulabreen, Svalbard. Ann. Glaciol. 2009, 50, 81–86. [Google Scholar] [CrossRef]
- Bougamont, M.; Christoffersen, P.; Hubbard, A.L.; Fitzpatrick, A.A.; Doyle, S.H.; Carter, S.P. Sensitive response of the Greenland Ice Sheet to surface melt drainage over a soft bed. Nat. Commun. 2014, 5, 5052. [Google Scholar] [CrossRef]
- Pfeffer, W.T.; Bretherton, C.S. The effect of crevasses on the solar heating of a glacier surface. In IAHS Publ. 170, Proceedings of the an International Symposium Held during the XlXth General Assembly of the International Union of Geodesy and Geophysics–The Physical Basis of Ice Sheet Modelling, Vancouver, BC, Canada, 9–22 August 1987; Waddington, E.D., Walder, J.S., Eds.; IAHS Press, Institute of Hydrology: Wallingford, UK, 1987; pp. 191–205. [Google Scholar]
- Brown, C.S.; Meier, M.F.; Post, A. Calving Speed of Alaska Tidewater Glaciers, with Application to Columbia Glacier; U.S. Geological Survey Professional Paper 1258-C; United States Government Printing Office: Washington, WA, USA, 1982.
- Meier, M.F.; Post, A. Fast Tidewater Glaciers. J. Geophys. Res. 1987, 92, 9051–9058. [Google Scholar] [CrossRef]
- Moskalik, M.; Tęgowski, J.; Głowacki, P.; Żulichowska, M. Principal Component and Cluster Analysis for determining diversification of bottom morphology based on bathymetric profiles from Brepollen (Hornsund, Spitsbergen). Oceanologia 2014, 56, 59–84. [Google Scholar] [CrossRef][Green Version]
- Walczowski, W.; Piechura, J. Influence of the West Spitsbergen Current on the local climate. Int. J. Climatol. 2011, 31, 1088–1093. [Google Scholar] [CrossRef]
- EarthExplorer. Available online: https://earthexplorer.usgs.gov/ (accessed on 12 May 2020).
- Kartserie: Svalbard (S100)–the Svalbard Coverage by the Topographic Maps, Norwegian Polar Institute. Available online: https://www.npolar.no/produkt/svalbard-s100/ (accessed on 12 May 2020).
- TopoSvalbard Portal, Norwegian Polar Institute. Available online: https://toposvalbard.npolar.no/ (accessed on 12 May 2020).
- Norwegian Meteorological Institute (2020). Air Temperature in Svalbard, Annual Mean. Environmental Monitoring of Svalbard and Jan Mayen (MOSJ). Available online: http://www.mosj.no/en/climate/atmosphere/temperature-precipitation.html (accessed on 12 May 2020).
- Murray, T.; Strozzi, T.; Luckman, A.; Jiskoot, H.; Christakos, P. Is there a single surge mechanism? Contrasts in dynamics between glacier surges in Svalbard and other regions. J. Geophys. Res. 2003, 108. [Google Scholar] [CrossRef]
- Sund, M.; Lauknes, T.R.; Eiken, T. Surge dynamics in the Nathorstbreen glacier system, Svalbard. Cryosphere 2014, 8, 623–638. [Google Scholar] [CrossRef]
- Rolstad, C.; Amlien, J.; Hagen, J.O.; Lundén, B. Visible and near-infrared digital images for determination of ice velocities and surface elevation during a surge on Osbornebreen, a tidewater glacier in Svalbard. Ann. Glaciol. 1997, 24, 255–261. [Google Scholar] [CrossRef]
- Flink, A.E.; Noormets, R.; Kirchner, N.; Benn, D.I.; Luckman, A.; Lovell, H. The evolution of a submarine landform record following recent and multiple surges of Tunabreen glacier, Svalbard. Quat. Sci. Rev. 2015, 108, 37–50. [Google Scholar] [CrossRef]
- Sevestre, H.; Benn, D.I.; Hulton, N.R.J.; Bælum, K. Thermal structure of Svalbard glaciers and implications for thermal switch models of glacier surging. J. Geophys. Res. Earth Surf. 2015, 120, 2220–2236. [Google Scholar] [CrossRef]
- Burton, D.J.; Dowdeswell, J.A.; Hogan, K.A.; Noormets, R. Marginal Fluctuations of a Svalbard Surge-Type Tidewater Glacier, Blomstrandbreen, Since the Little Ice Age: A Record of Three Surges. Arct. Antarct. Alp. Res. 2016, 48, 411–426. [Google Scholar] [CrossRef]
- Dowdeswell, J.A.; Benham, T.J. A surge of Perseibreen, Svalbard, examined using aerial photography and ASTER high resolution satellite imagery. Polar Res. 2003, 22, 373–383. [Google Scholar] [CrossRef]
- Murray, T.; James, T.D.; Macheret, Y.; Lavrentiev, I.; Glazovsky, A.; Sykes, H. Geometric Changes in a Tidewater Glacier in Svalbard during its Surge Cycle. Arct. Antarct. Alp. Res. 2012, 44, 359–367. [Google Scholar] [CrossRef]
- Lønne, I. Low-velocity glacial surges–Processes unlocked by modern surge on Svalbard. Geology 2006, 34, 553–556. [Google Scholar] [CrossRef]
- Clarke, G.K.C. Length, width and slope influences on glacier surging. J. Glaciol. 1991, 37, 236–246. [Google Scholar] [CrossRef][Green Version]
- Grant, K.L.; Stokes, C.R.; Evans, I.S. Identification and characteristics of surge-type glaciers on Novaya Zemlya, Russian Arctic. J. Glaciol. 2009, 55, 960–972. [Google Scholar] [CrossRef]
- Kienholz, C.; Rich, J.L.; Arendt, A.A.; Hock, R. A new method for deriving glacier centerlines applied to glaciers in Alaska and northwest Canada. Cryosphere 2014, 8, 503–519. [Google Scholar] [CrossRef]
- Dobra, D.; Jambrożek, S.; Komosa, M.; Mikołajczak, E.; Przybylska, P.; Sysak, A.; Wdowska, A. Metoda sił –łuki (Force method–arches). In Mechanika Budowli (Building Mechanics); Part, I., Pawlak, Z., Eds.; 2003/2004; Poznań University of Technology: Poznań, Poland; Available online: http://www.se.put.poznan.pl/almamater/wyklady/mechanika_budowli_03-04/czesc1/12.pdf (accessed on 12 May 2020). (In Polish)
- Thom, R. Structural Stability and Morphogenesis: An Outline of a General Theory of Models; CRC Press, Taylor & Francis Group LLC: Boca Raton, FL, USA; London, UK; New York, NY, USA, 2018; p. 348. [Google Scholar]
- Grabiec, M.; Leszkiewicz, J.; Głowacki, P.; Jania, J. Distribution of snow accumulation on some glaciers of Spitsbergen. Pol. Polar Res. 2006, 27, 309–326. [Google Scholar]
- Pętlicki, M.; Ciepły, M.; Jania, J.A.; Promińska, A.; Kinnard, C. Calving of tidewater glacier driven by melting at the waterline. J. Glaciol. 2015, 61, 851–863. [Google Scholar] [CrossRef]
- Ziaja, W.; Dudek, J.; Ostafin, K. Landscape transformation under the Gåsbreen glacier recession since 1899, southwestern Spitsbergen. Pol. Polar Res. 2016, 37, 155–172. [Google Scholar] [CrossRef][Green Version]
- Szafraniec, J.E.; Dobiński, W. Deglaciation rate of the selected nunataks in Spitsbergen, Svalbard–potential for the permafrost expansion above glacial environment. Geosciences 2020, 10, 202. [Google Scholar] [CrossRef]
- Lundstrom, S.C.; McCafferty, A.E.; Coe, J.A. Photogrammetric analysis of 1984–89 surface altitude change of the partially debris-covered Eliot Glacier, Mount Hood, Oregon, U.S.A. Ann. Glaciol. 1993, 17, 167–170. [Google Scholar] [CrossRef][Green Version]
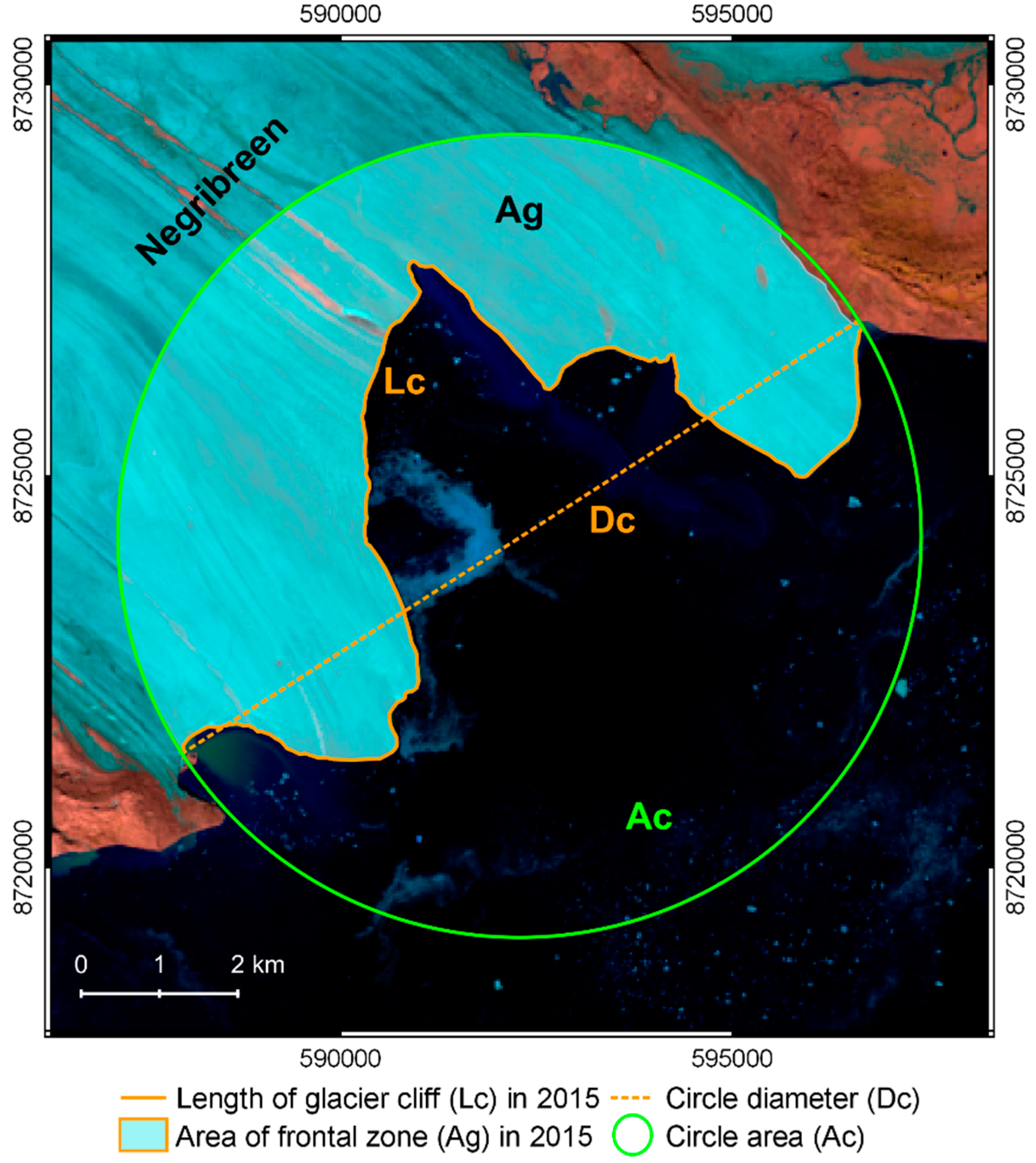
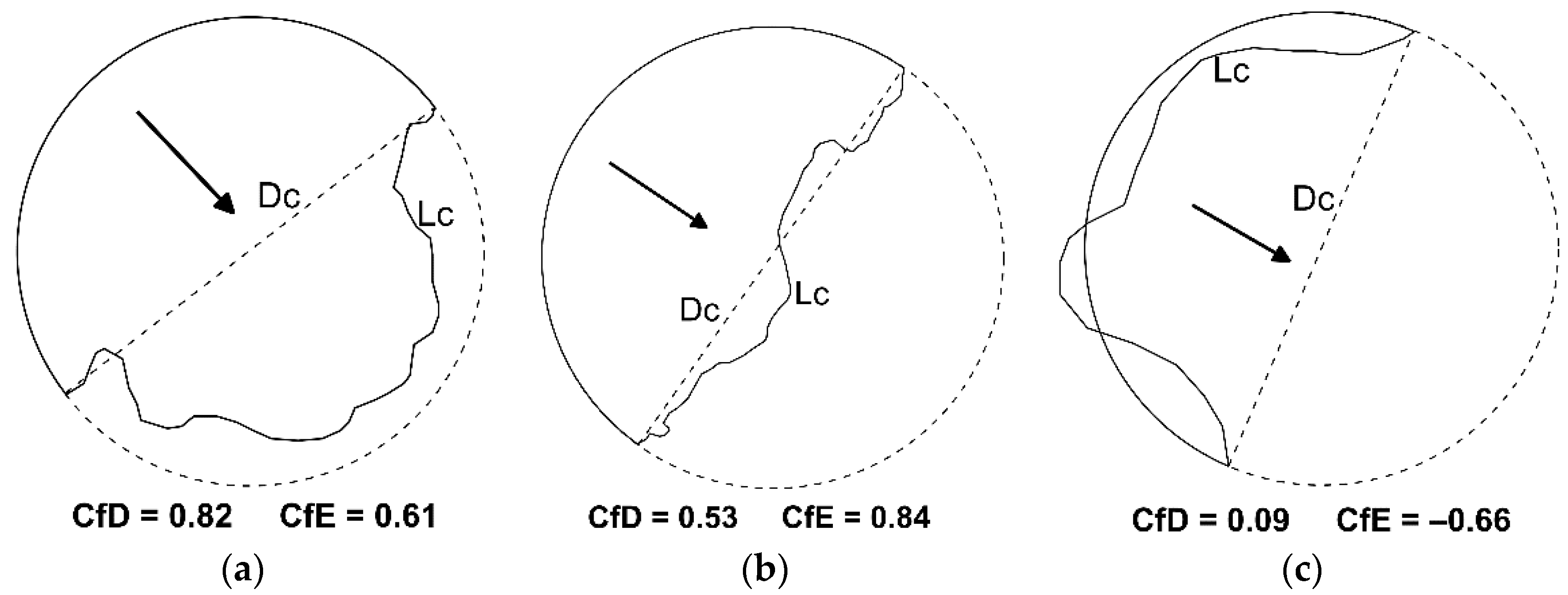

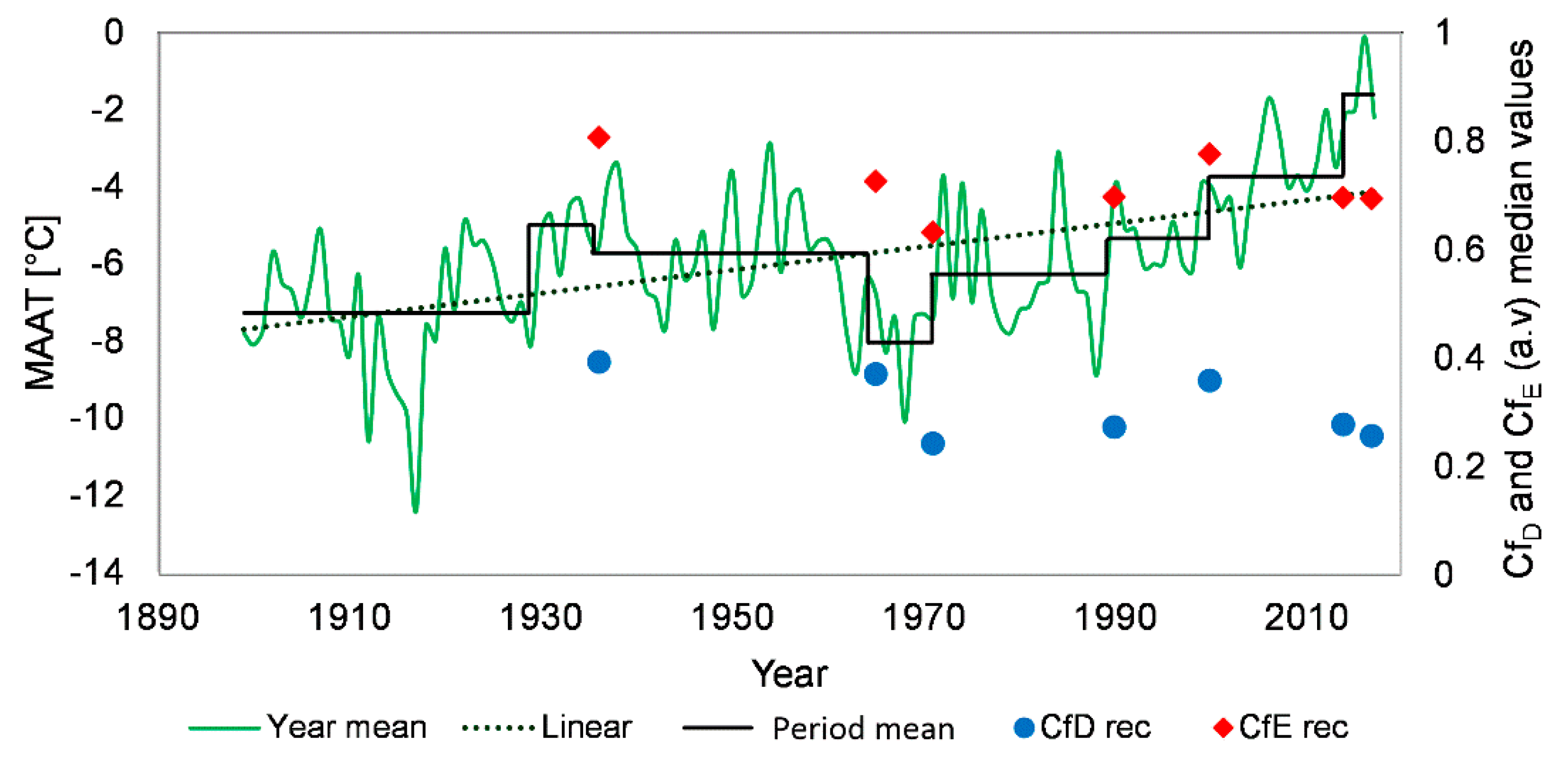
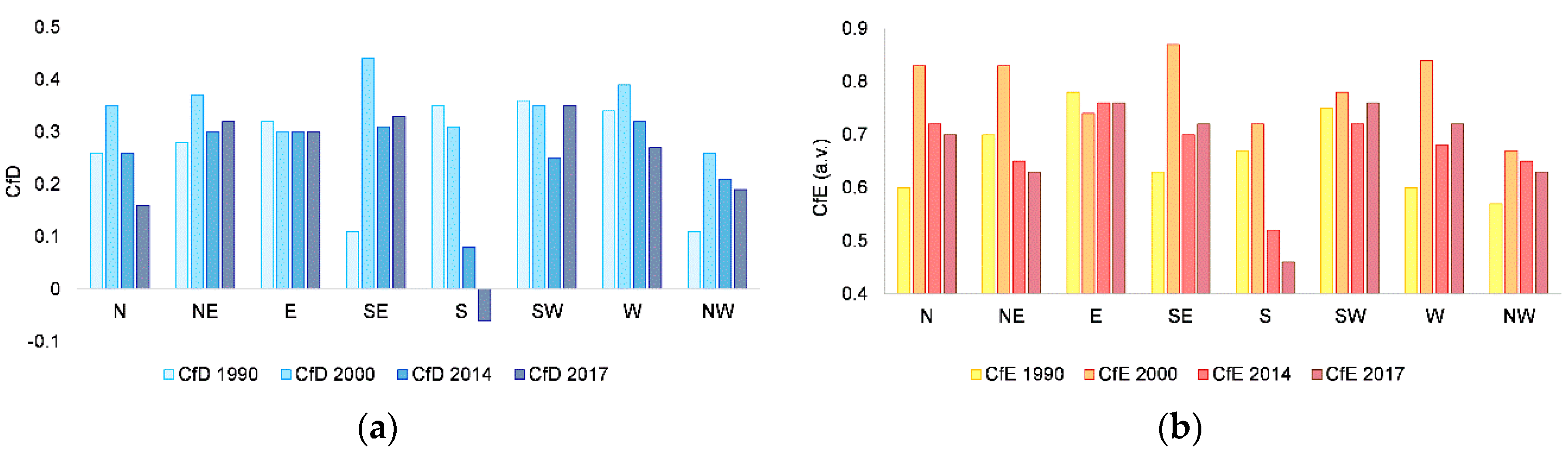
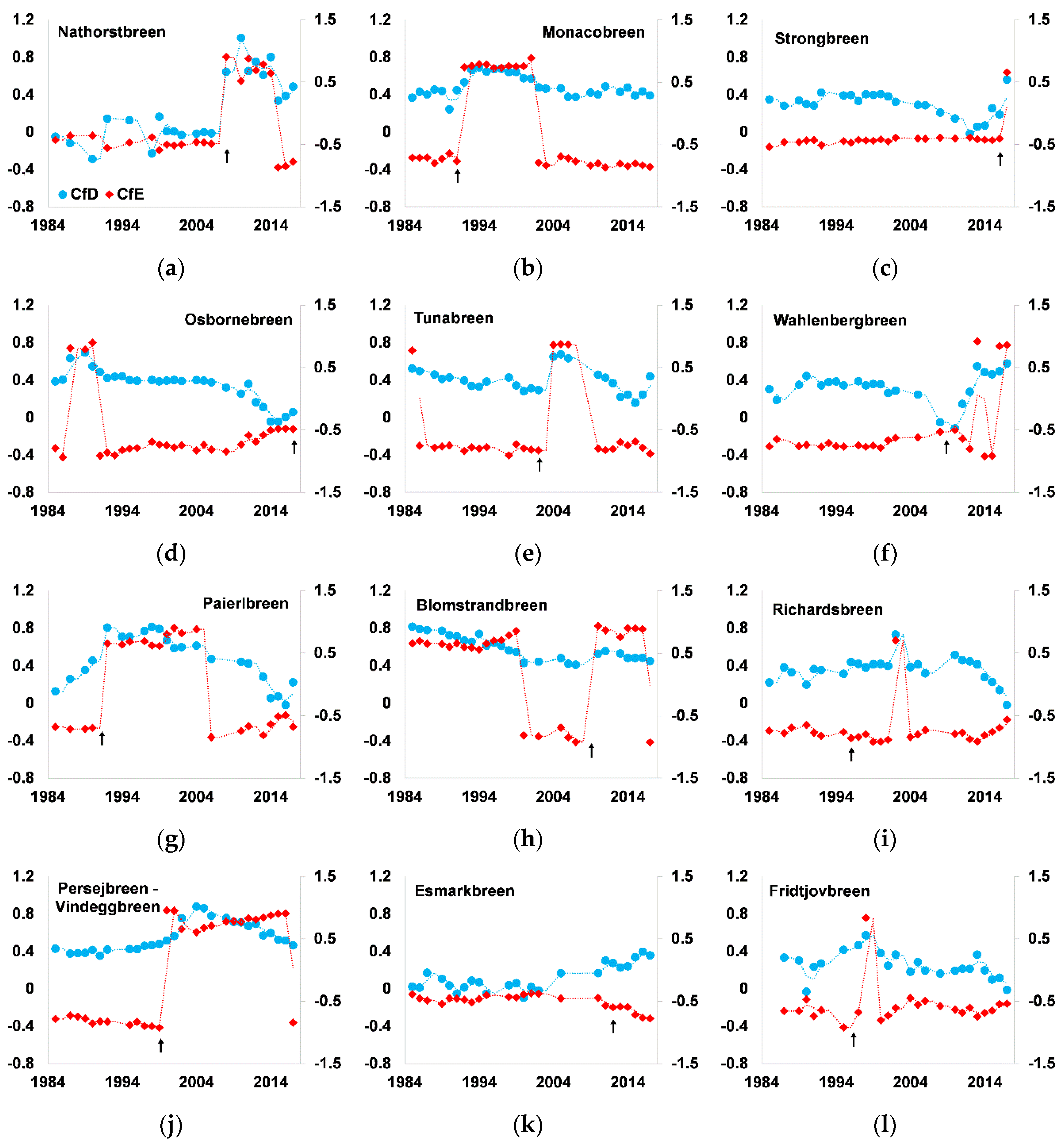
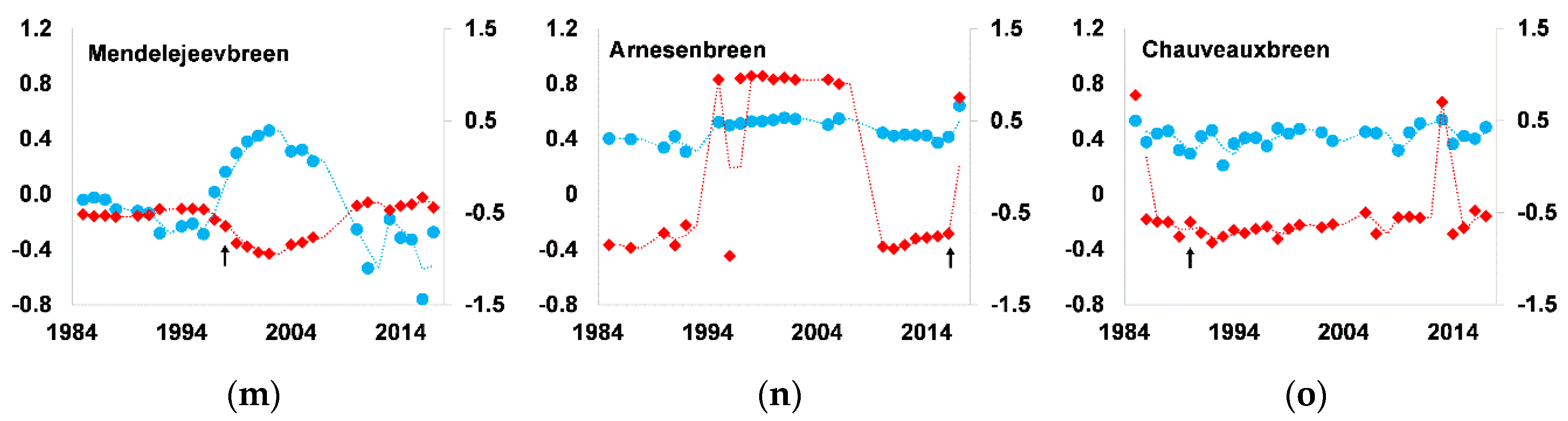
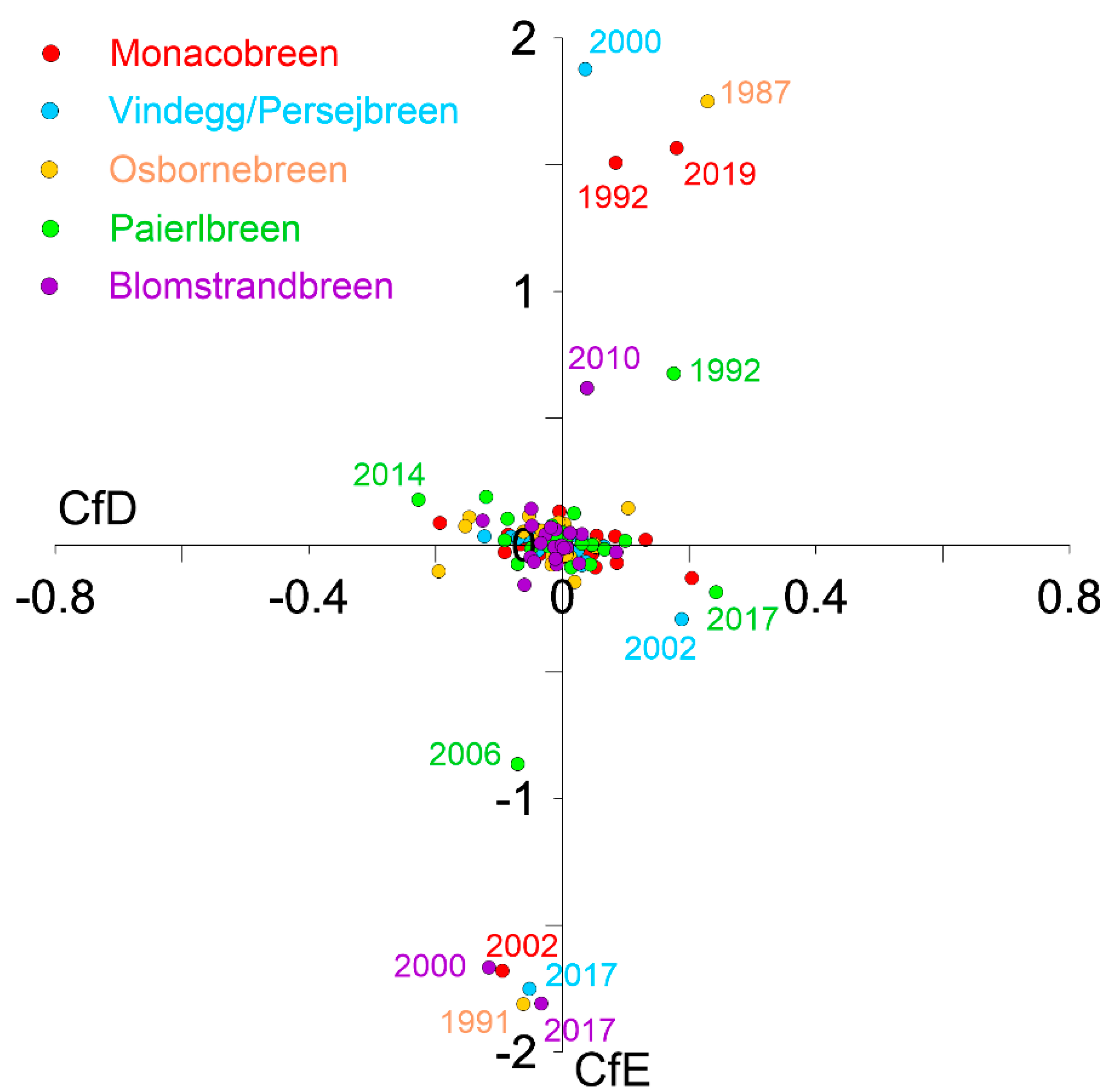
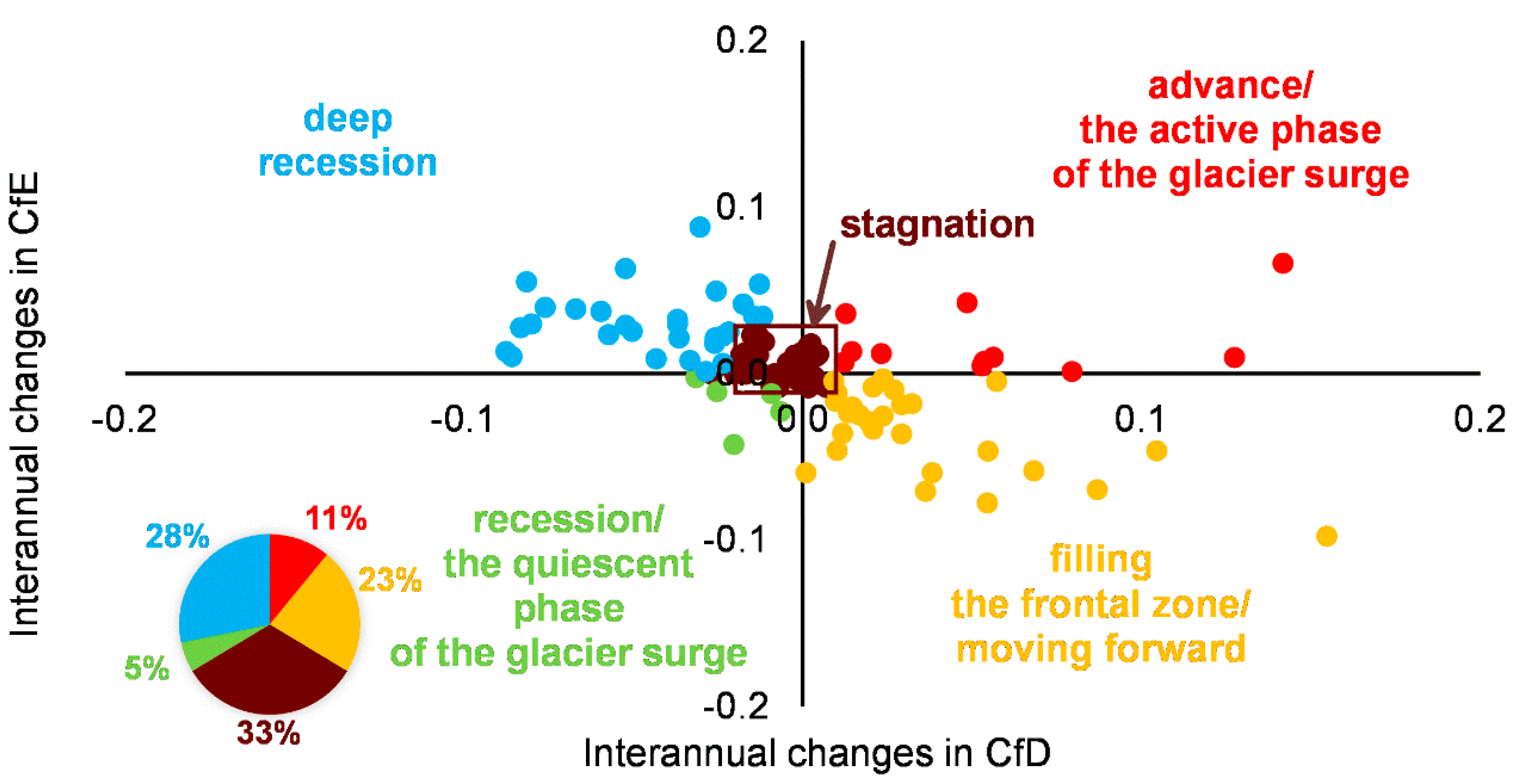
| Year | Lc [km] | Dc [km] | Ag [km2] | Ac [km2] | CfD | CfE (a.v.) |
|---|---|---|---|---|---|---|
| 1936 (28 glaciers) | 4.24 (3.43–5.74) | 3.35 (2.31–4.10) | 3.62 (1.01–6.24) | 8.82 (4.18–13.26) | 0.40 (0.35–0.45) | 0.79 (0.71–0.87) |
| 1960–1966 (35) | 2.47 (1.93–4.71) | 1.85 (1.43–3.05) | 0.91 (0.43–1.92) | 2.67 (1.60–7.24) | 0.37 (0.30–0.43) | 0.75 (0.63–0.81) |
| 1969–1977 (17) | 5.58 (4.38–6.61) | 3.03 (2.39–3.43) | 2.71 (–0.87–4.57) | 7.21 (4.47–9.19) | 0.38 (–0.20–0.48) | 0.61 (0.40–0.81) |
| 1990 (73) | 3.16 (2.28–5.09) | 2.24 (1.44–3.12) | 0.93 (0.11–2.46) | 3.93 (1.62–7.69) | 0.30 (0.16–0.40) | 0.60 (0.30–0.80) |
| 2000 (110) | 2.71 (1.17–3.73) | 1.71 (1.00–2.66) | 0.74 (0.20–1.92) | 2.30 (0.79–5.55) | 0.39 (0.27–0.47) | 0.79 (0.66–0.87) |
| 2014 (110) | 2.78 (1.39–4.38) | 1.72 (1.00–2.89) | 0.59 (0.19–1.89) | 2.34 (0.78–6.59) | 0.30 (0.18–0.40) | 0.71 (0.57–0.79) |
| 2017 (110) | 2.61 (1.46–4.23) | 1.86 (1.04–3.01) | 0.69 (0.08–1.95) | 2.70 (0.85–7.12) | 0.29 (0.13–0.44) | 0.70 (0.57–0.80) |
| Surging Glaciers | Source of Data (Published) | According to Published Data | According to the Ice-Cliff Morphometry | ||
|---|---|---|---|---|---|
| Start of the Active Phase | End (and Duration—in Brackets) of the Active Phase | Start of the Active Phase | End (and Duration—in Brackets) of the Active Phase | ||
| Nathorstbreen system | Sund et al. [46] | 2003–stage 1 2008–stage 2 | 2013 (?) (~5–10 years) | 2006–2008 | 2014–2015 (6–9 years) |
| Monacobreen | Murray et al. [45] Mansell et al. [27] | 1990–1992 1993–1995 | 1997 (2–7 years) | 1991–1992 | 2001–2002 (9–10 years) |
| Osbornebreen | Dowdeswell et al. [14]; Rolstad et al. [47] | 1986–1987 | ? | 1986–1987 | 1990–1991 (3–5 years) |
| Tunabreen | Flink et al. [48]; Sevestre et al. [49] | 2002–2003 2003 | 2004–2005 2005 (1–3 years) | 2002–2004 | 2006–2010 (2–8 years) |
| Wahlenbergbreen | Sevestre at al. [22] | 2009 | – | 2012–2013 | – |
| Paierlbreen | Błaszczyk et al. [6] | 1993 (?) | 1999 (?) (6 years?) | 1990–1992 | 2004–2006 (12–16 years) |
| Blomstrandbreen | Mansell et al. [27]; Burton et al. [50] | 2007 2009 | 2010 (?) 2013 (1–6 years) | 2007–2010 | 2016–2017 (6–10 years) |
| Persejbreen | Dowdeswell and Benham [51] | 2000–2001 | ? | 1999–2000 | 2015–2016 (5–17 years) |
| Fridtjovbreen | Murray et al. [45]; Murray et al. [52]; Lønne [53] | 1994–1995 and re-advance in 1998–1999 | 1997 (2–3 years or 3–5 years) | 1995–1996 | 1998–1999 (2–4 years) |
| Mendeleevbreen | Błaszczyk et al. [6] | between 1995–2002 | between 2002–2010 (up to 15 years?) | 1996–1997 | 2006–2010 (9–14 years) |
| Year Before Surge | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Coeff. of corr. | −0.84 | −0.73 | −0.76 | −0.77 * | −0.80 |
| Year | The Ice-Cliff Shape | Indicators | Interannual Changes in Indicators Value | Dynamics | |||
|---|---|---|---|---|---|---|---|
| CfD | CfE | Ch. of CfD | Ch. of CfE | ||||
| 1985 |  | 0.367 | −0.713 | ? | ? | ? | ? |
| 1986 |  | 0.428 | −0.711 | 0.061 | 0.002 | Frontal zone filling/stagnation | |
| 1987 | 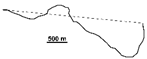 | 0.402 | −0.711 | −0.026 | 0.000 | ||
| 1988 | 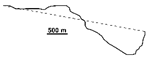 | 0.454 | −0.799 | 0.052 | −0.088 | ||
| 1989 | 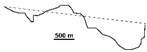 | 0.437 | −0.729 | −0.017 | 0.070 | Deep recession stage—strongly concave ice-cliff shape | |
| 1990 |  | 0.244 | −0.641 | −0.193 | 0.088 | ||
| 1991 | 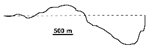 | 0.448 | −0.770 | 0.204 | −0.129 | Entering the active phase (I) of the glacier phase—an advance, convex shape of the ice-cliff | |
| 1992 |  | 0.532 | 0.738 | 0.084 | 1.508 | ||
| 1993 | 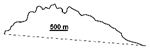 | 0.663 | 0.758 | 0.131 | 0.020 | ||
| 1994 |  | 0.691 | 0.789 | 0.028 | 0.031 | Stagnation—convex ice-cliff, many inflexion points | |
| 1995 |  | 0.646 | 0.783 | −0.045 | −0.006 | ||
| 1996 |  | 0.670 | 0.724 | 0.024 | −0.059 | ||
| 1997 | 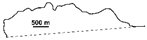 | 0.675 | 0.732 | 0.005 | 0.008 | ||
| 1998 |  | 0.640 | 0.759 | −0.035 | 0.027 | ||
| 1999 |  | 0.641 | 0.750 | 0.001 | −0.009 | ||
| 2000 |  | 0.575 | 0.753 | −0.066 | 0.003 | Deep recession by calving and melting | |
| 2001 |  | 0.570 | 0.885 | −0.005 | 0.132 | ||
| 2002 |  | 0.475 | −0.794 | −0.095 | −1.679 | Entering the quiescent phase of the glacier stage—retreat, few inflexion points on the ice-cliff line | |
| 2003 |  | 0.463 | −0.837 | −0.012 | −0.043 | ||
| 2004 | – | – | – | – | – | – | |
| 2005 |  | 0.466 | −0.695 | ? | ? | ? | |
| 2006 | 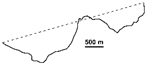 | 0.375 | −0.722 | –0.091 | −0.027 | ||
| 2007 |  | 0.375 | −0.770 | 0.000 | −0.048 | ||
| 2008 | – | – | – | – | – | – | |
| 2009 |  | 0.420 | −0.839 | ? | ? | ? | |
| 2010 | 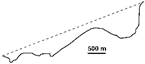 | 0.402 | −0.801 | −0.018 | 0.038 | ||
| 2011 |  | 0.488 | −0.870 | 0.086 | −0.069 | Small interannual fluctuations and stagnation—filling the frontal zone balanced by the ice-cliff retreating | |
| 2012 | – | – | – | – | – | – | |
| 2013 |  | 0.427 | −0.809 | ? | ? | ? | |
| 2014 |  | 0.474 | −0.845 | 0.047 | −0.036 | ||
| 2015 |  | 0.388 | −0.804 | −0.086 | 0.041 | ||
| 2016 |  | 0.431 | −0.835 | 0.043 | −0.031 | ||
| 2017 |  | 0.390 | −0.858 | −0.041 | −0.023 | ||
| 2018 |  | 0.473 | −0.823 | 0.083 | 0.035 | Entering the active phase (II) of the glacier phase—an advance, convex shape of the ice-cliff | |
| 2019 | 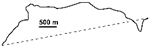 | 0.653 | 0.743 | 0.180 | 1.566 | ||
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Szafraniec, J.E. Ice-Cliff Morphometry in Identifying the Surge Phenomenon of Tidewater Glaciers (Spitsbergen, Svalbard). Geosciences 2020, 10, 328. https://doi.org/10.3390/geosciences10090328
Szafraniec JE. Ice-Cliff Morphometry in Identifying the Surge Phenomenon of Tidewater Glaciers (Spitsbergen, Svalbard). Geosciences. 2020; 10(9):328. https://doi.org/10.3390/geosciences10090328
Chicago/Turabian StyleSzafraniec, Joanna Ewa. 2020. "Ice-Cliff Morphometry in Identifying the Surge Phenomenon of Tidewater Glaciers (Spitsbergen, Svalbard)" Geosciences 10, no. 9: 328. https://doi.org/10.3390/geosciences10090328
APA StyleSzafraniec, J. E. (2020). Ice-Cliff Morphometry in Identifying the Surge Phenomenon of Tidewater Glaciers (Spitsbergen, Svalbard). Geosciences, 10(9), 328. https://doi.org/10.3390/geosciences10090328





