Mass Balance of Austre Grønfjordbreen, Svalbard, 2006–2020, Estimated by Glaciological, Geodetic and Modeling Aproaches
Abstract
1. Introduction
2. Data and Methods
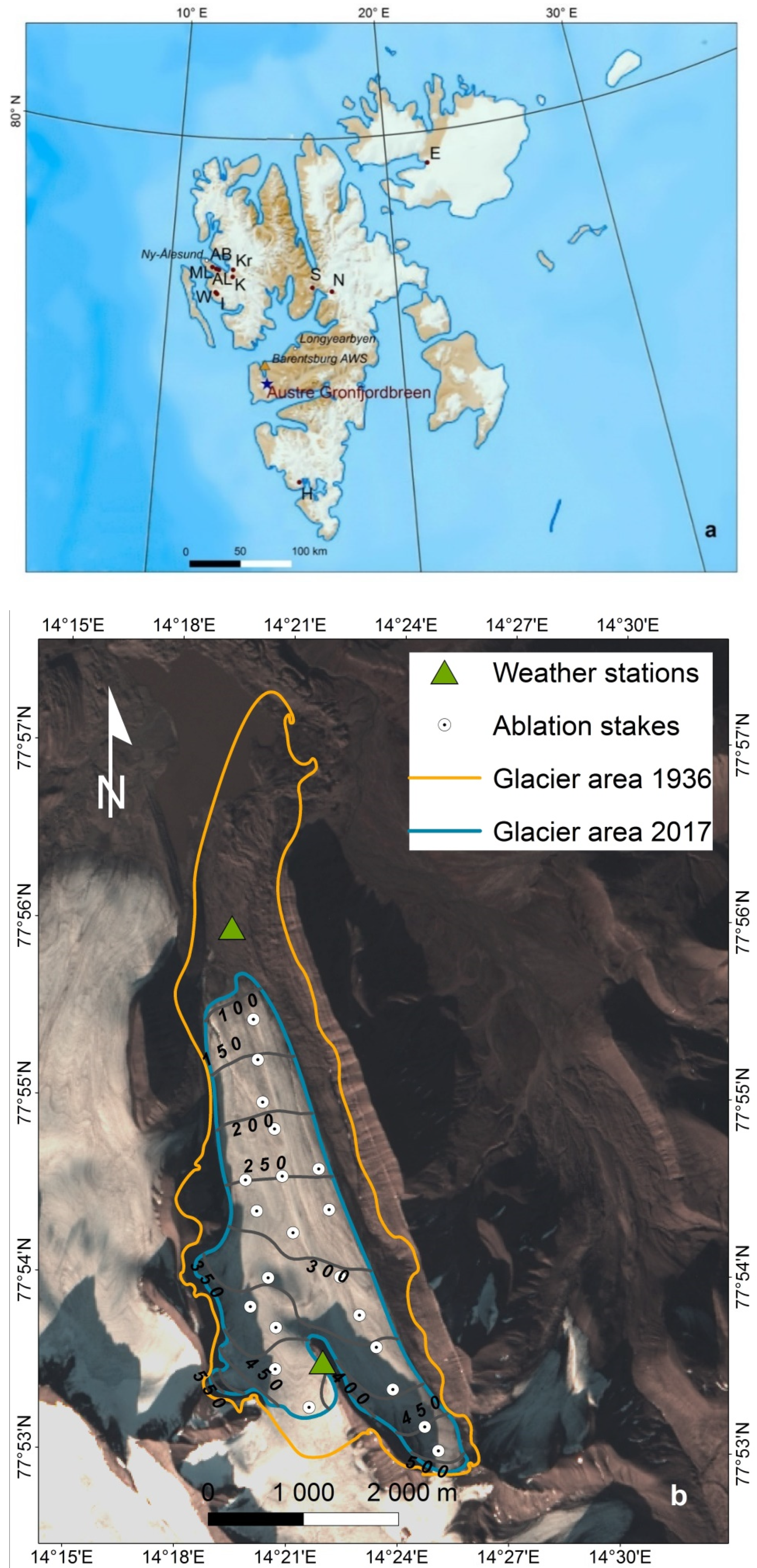
2.1. Field Measurements and Data
2.2. Glaciological Method
2.3. Geodetic Mass Balance
2.4. Temperature-Index Modeling
2.5. Energy-Malance Model A-Melt
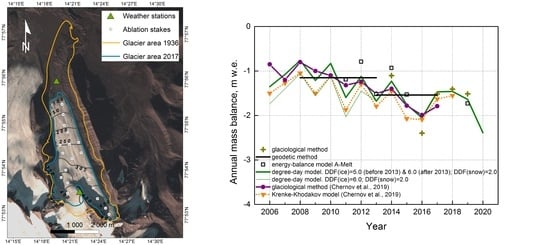
3. Results
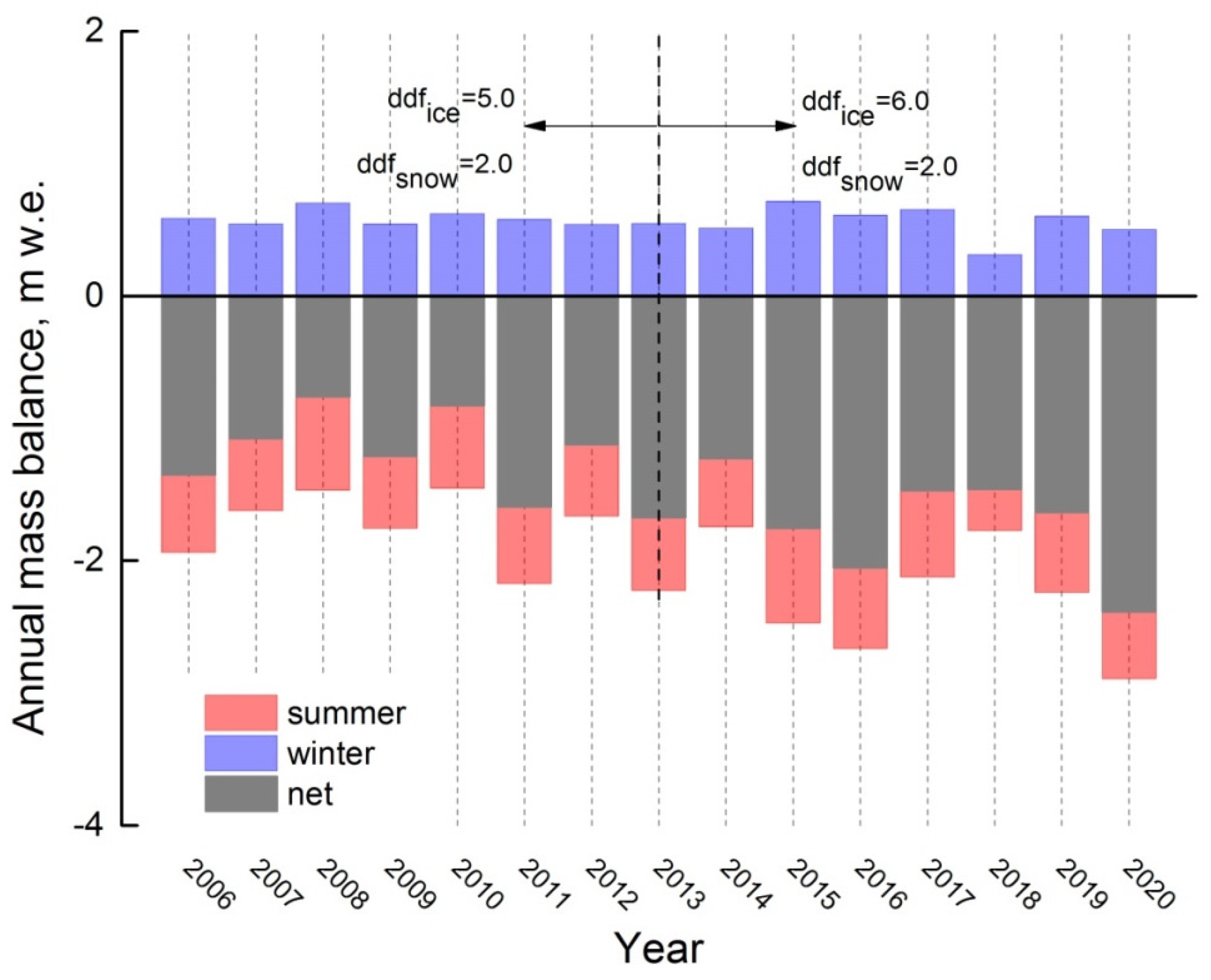
3.1. Surface Mass Balance Estimated by the Glaciological Method
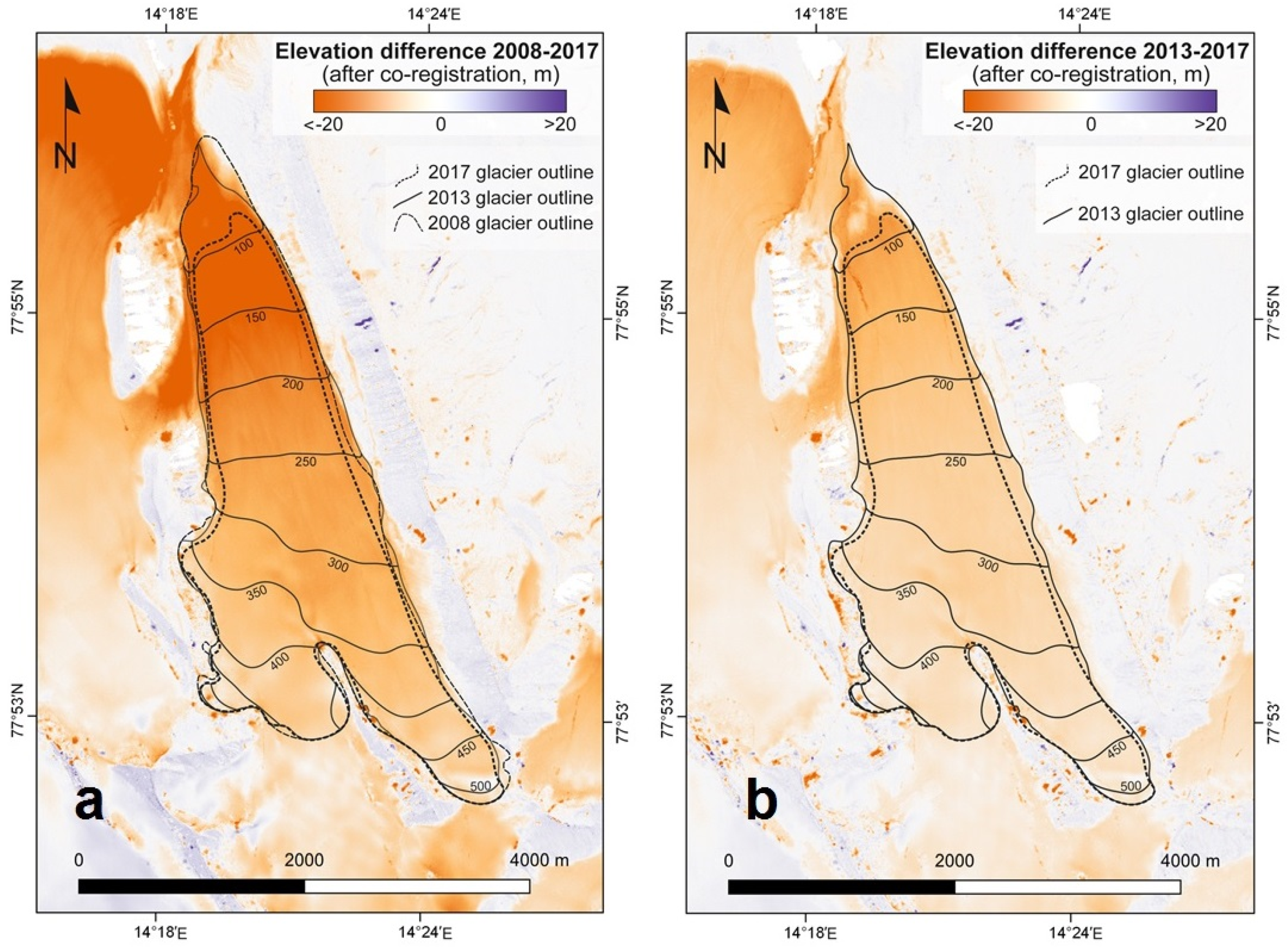
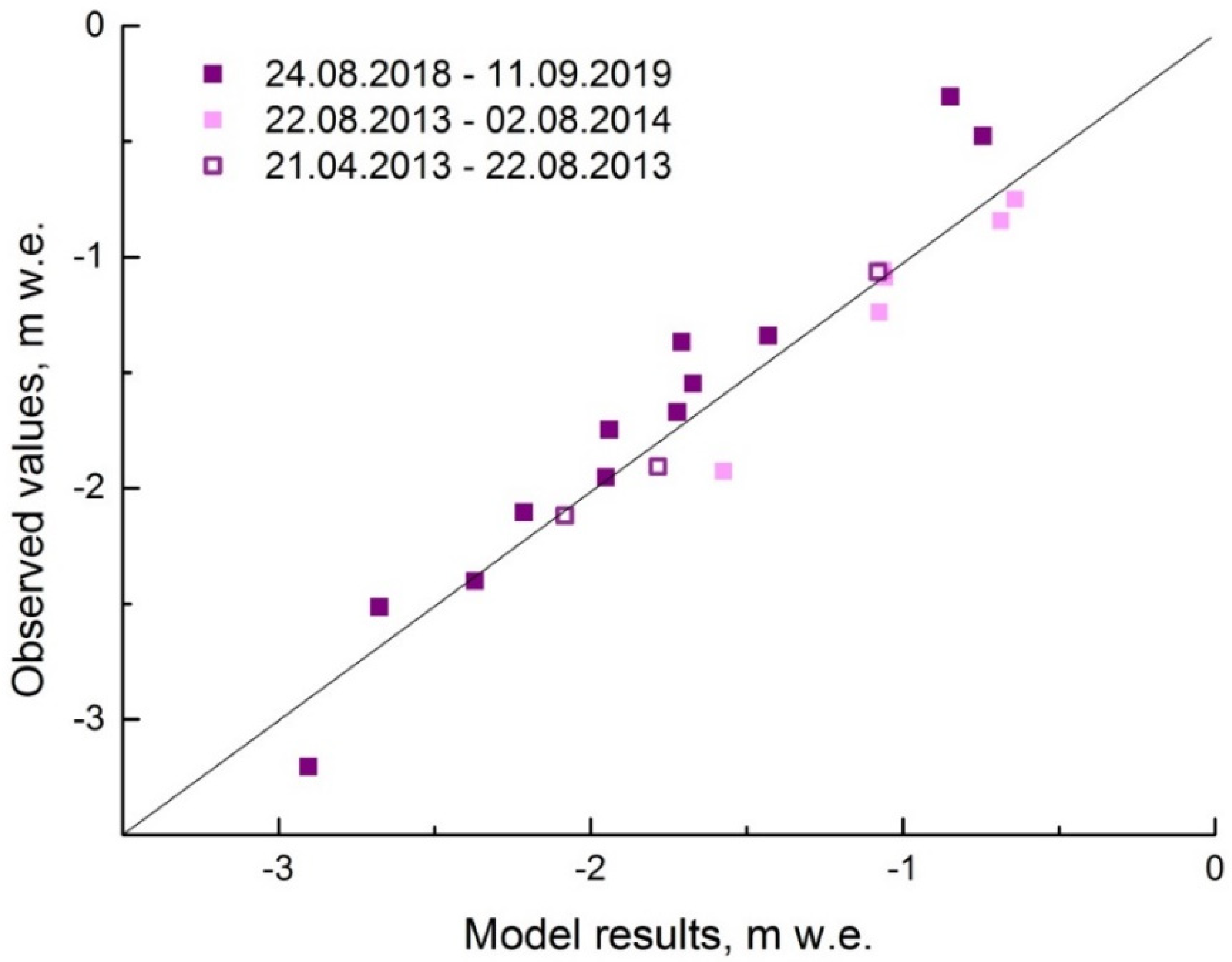
3.2. Geodetic Mass Balance
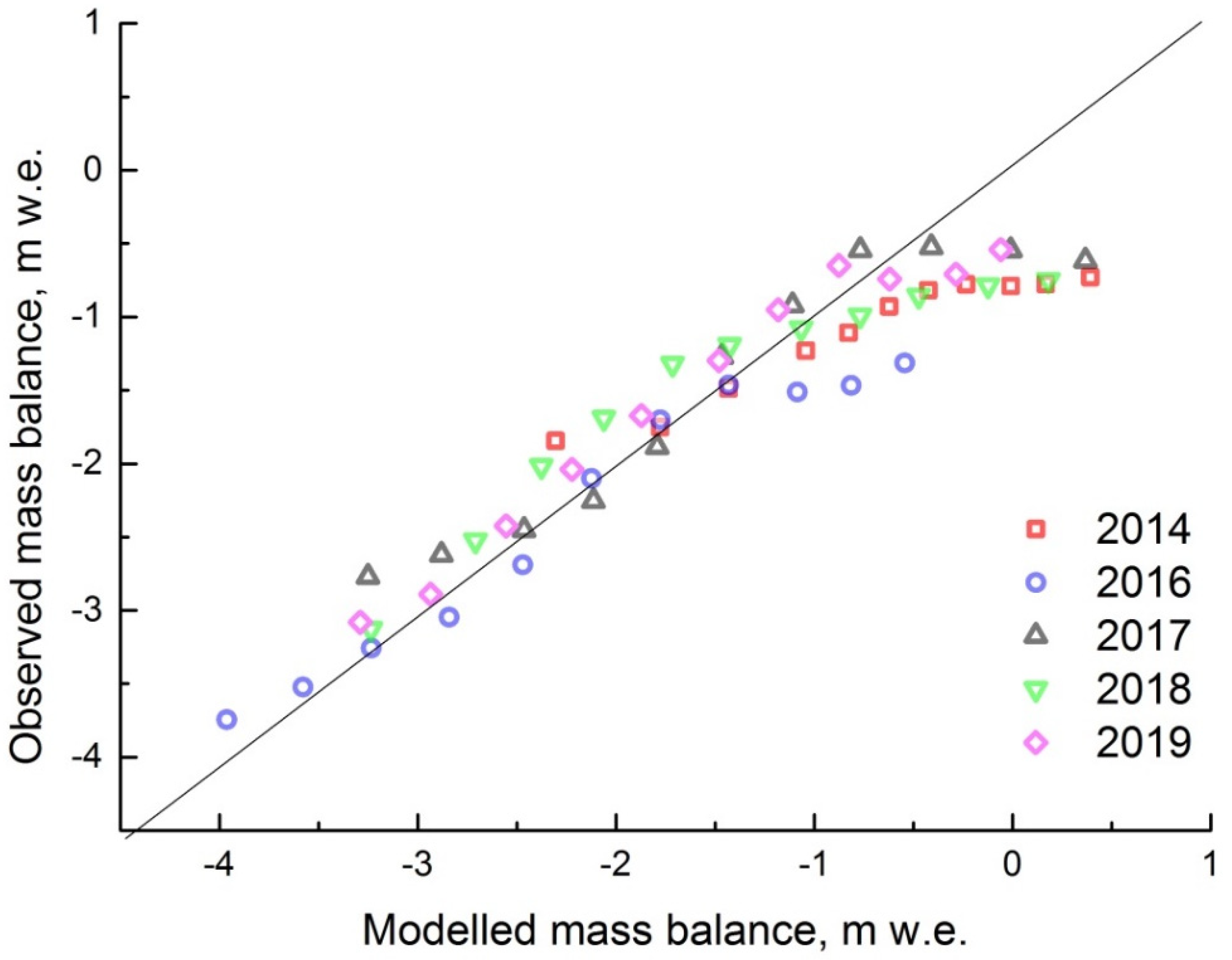
3.3. Mass-Balance Reconstruction by DDF Model
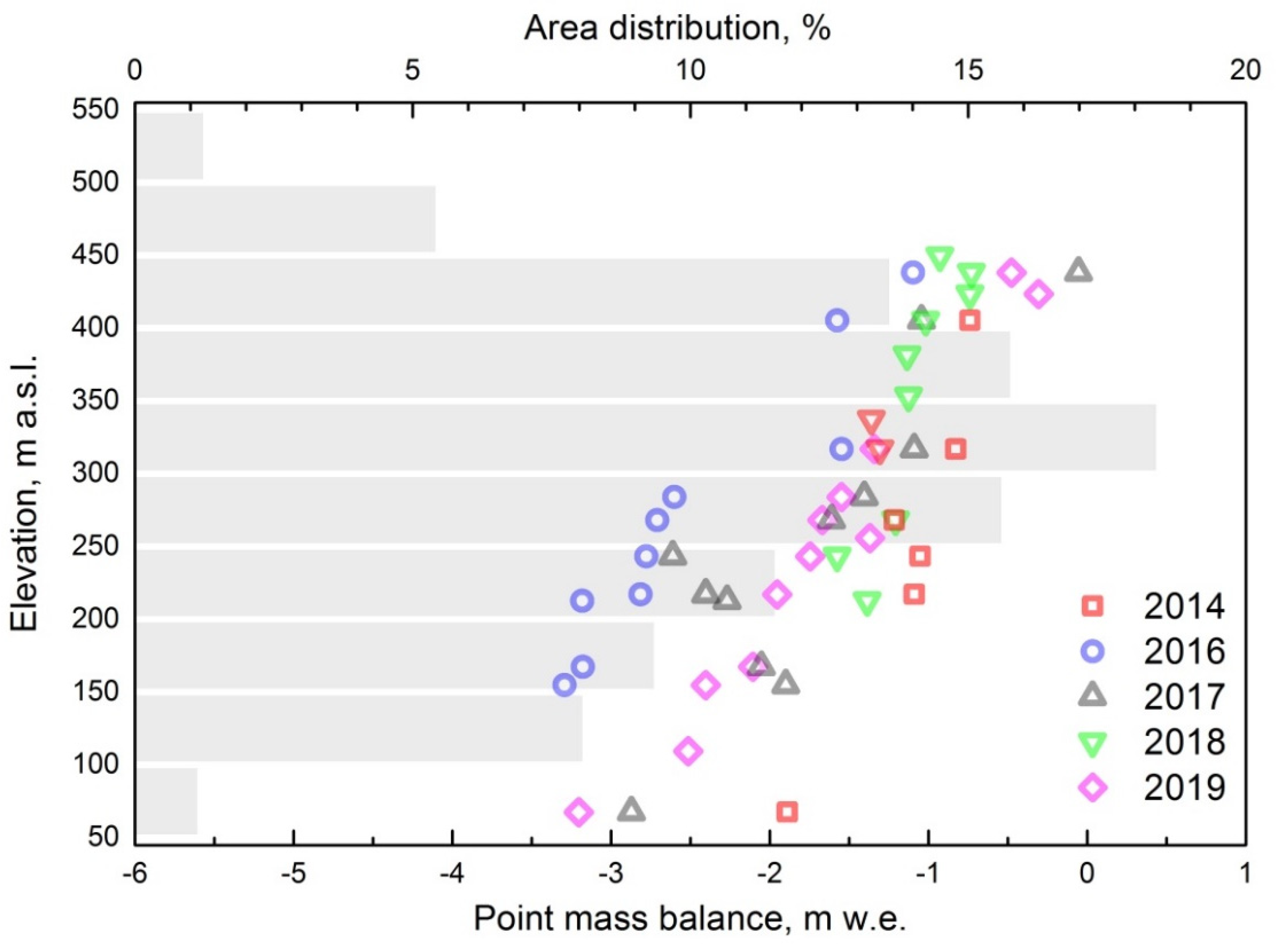
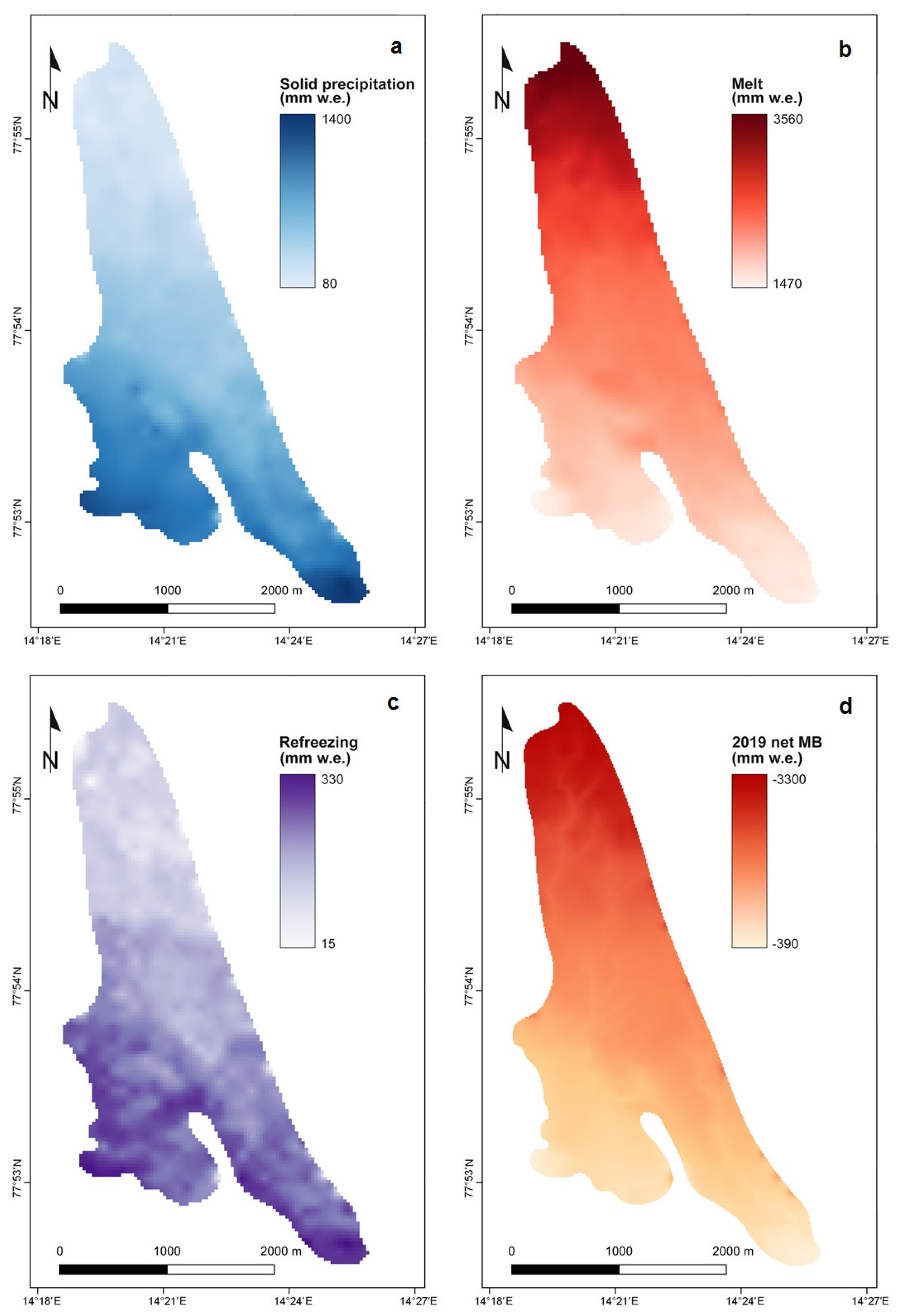
3.4. Spatially Distributed Mass Balance and its Components
4. Discussion
4.1. Differences in Mass Balance Assessment Approaches
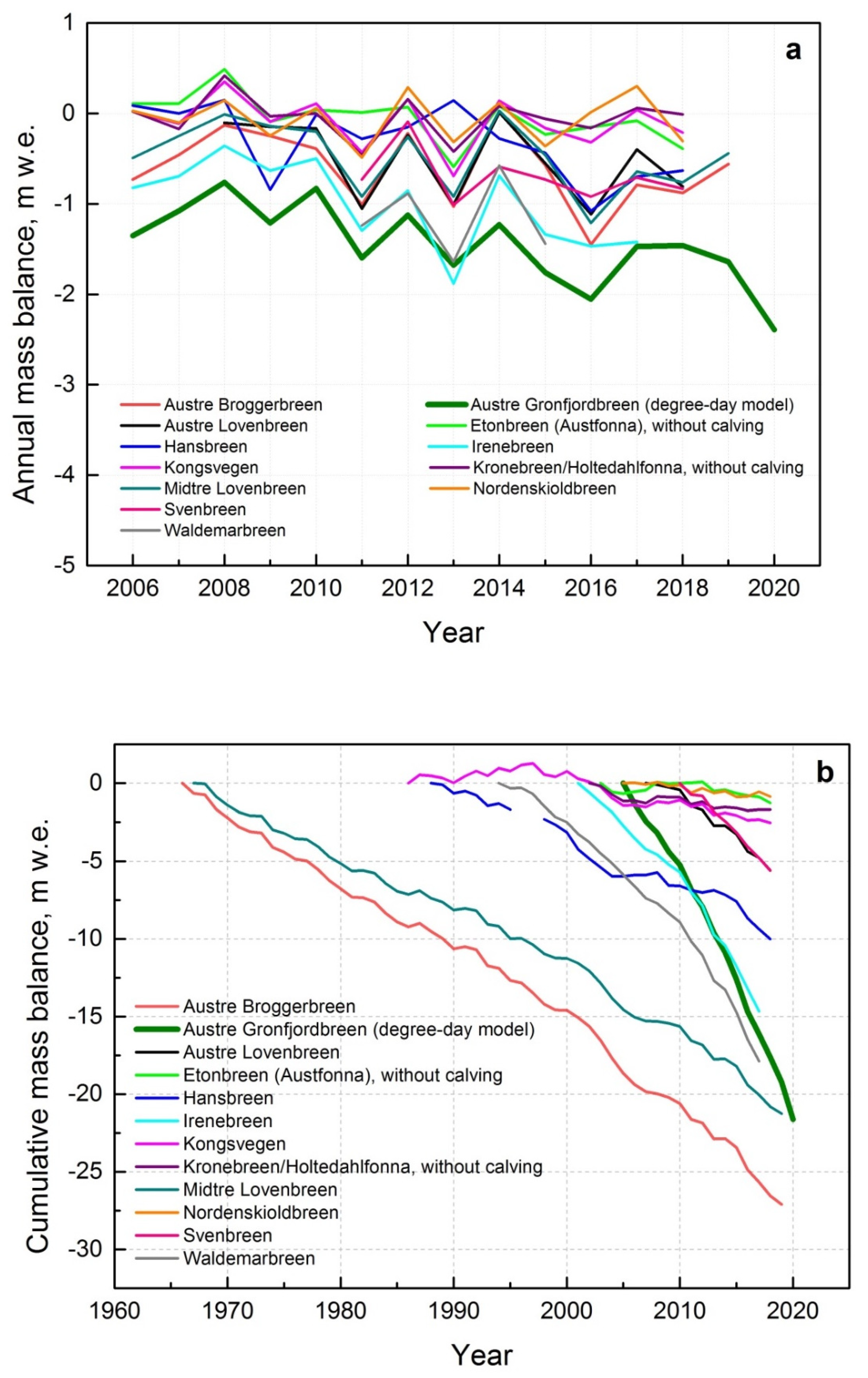
4.2. Comparison with the Other Olaciers of the Archipelago
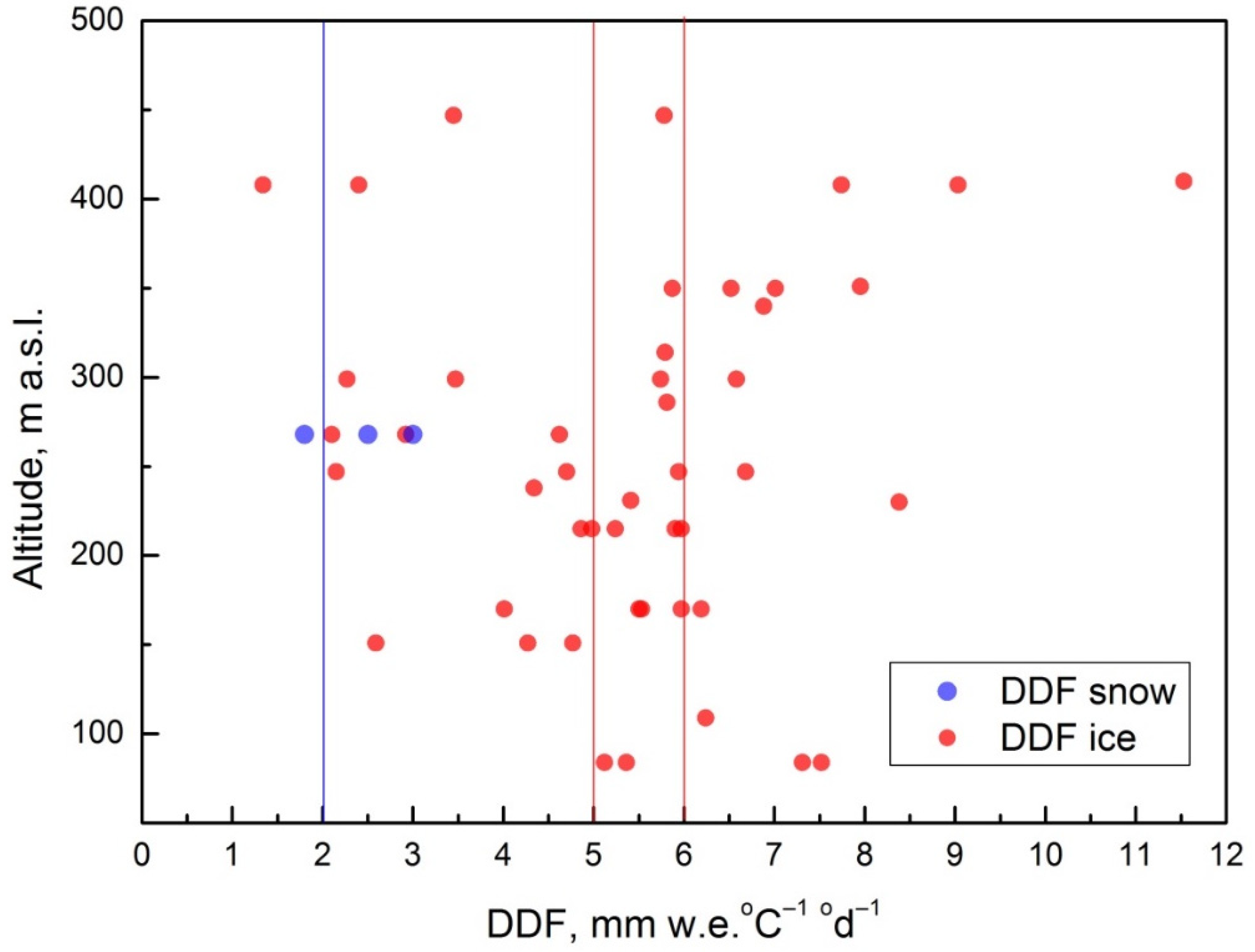
4.3. Degree-Day Factors Variations
4.4. Sensitivity Tests
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zemp, M.; Huss, M.; Thibert, E.; Eckert, N.; McNabb, R.; Huber, J.; Barandun, M.; Machguth, H.; Nussbaumer, S.U.; Gärtner-Roer, I. Global glacier mass changes and their contributions to sea-level rise from 1961 to 2016. Nature 2019, 568, 382–386. [Google Scholar] [CrossRef]
- Dyurgerov, M.B.; Meier, M.F. Twentieth century climate change: Evidence from small glaciers. Proc. Natl. Acad. Sci. USA 2000, 97, 1406–1411. [Google Scholar] [CrossRef]
- Kaser, G.; Cogley, J.G.; Dyurgerov, M.B.; Meier, M.F.; Ohmura, A. Mass balance of glaciers and ice caps: Consensus estimates for 1961–2004. Geophys. Res. Lett. 2006, 33, L19501. [Google Scholar] [CrossRef]
- Hock, R.; Bliss, A.; Marzeion, B.; Giesen, R.H.; Hirabayashi, Y.; HUSS, M.; Radic, V.; Slangen, A.B.A. GlacierMIP–A model intercomparison of global-scale glacier mass-balance models and projections. J. Glaciol. 2019, 65, 453–467. [Google Scholar] [CrossRef]
- IPCC Special Report: The Ocean and Cryosphere in a Changing Climate (final draft). IPCC Summ. Policymalers 2019. Available online: https://www.ipcc.ch/report/srocc/ (accessed on 12 December 2019).
- Nuth, C.; Kohler, J.; König, M.; von Deschwanden, A.; Hagen, J.O.; Kääb, A.; Moholdt, G.; Pettersson, R. Decadal changes from a multi-temporal glacier inventory of Svalbard. Cryosphere 2013, 7, 1603–1621. [Google Scholar] [CrossRef]
- Martín-Español, A.; Navarro, F.J.; Otero, J.; Lapazaran, J.J.; Błaszczyk, M. Estimate of the total volume of Svalbard glaciers, and their potential contribution to sea-level rise, using new regionally based scaling relationships. J. Glaciol. 2015, 61, 29–41. [Google Scholar] [CrossRef]
- Jania, J.; Hagen, J.O. Mass Balance of Arctic Glaciers; International Arctic Science Committee: Katowice, Poland, 1996; ISBN 8390564343. [Google Scholar]
- Hagen, J.O.; Melvold, K.; Pinglot, F.; Dowdeswell, J.A. On the net mass balance of the glaciers and ice caps in Svalbard, Norwegian Arctic. Arct. Antarct. Alp. Res. 2003, 35, 264–270. [Google Scholar] [CrossRef]
- Schuler, T.V.; Kohler, J.; Elagina, N.; Hagen, J.O.M.; Hodson, A.J.; Jania, J.A.; Kääb, A.M.; Luks, B.; Małecki, J.; Moholdt, G. Reconciling Svalbard Glacier Mass Balance. Front. Earth Sci. 2020, 8, 1–31. [Google Scholar] [CrossRef]
- WGMS (World Glacier Monitoring Service) Fluctuations of Glaciers Database. Available online: http://dx.doi.org/10.5904/wgms-fog-2020-08 (accessed on 1 March 2020).
- Möller, M.; Kohler, J. Differing Climatic Mass Balance Evolution Across Svalbard Glacier Regions Over 1900–2010. Front. Earth Sci. 2018, 6, 1–20. [Google Scholar] [CrossRef]
- Troitsky, L.S. On the mass balance of different types of glaciers in Spitsbergen. Mater. Glyatsiologicheskikh Issled. Data Glaciol. Stud. 1988, 1, 117–121. [Google Scholar]
- Mavlyudov, B.; Savatyugin, L.; Solovyanova, I. The reaction of the glaciers of the Nordenskiold Land (Spitsbergen) to climate change. Probl. Arct. Antarct. 2012, 1, 67–77. [Google Scholar]
- Chernov, R.A.; Kudikov, A.V.; Vshivtseva, T.V.; Osokin, N.I. Estimation of the surface ablation and mass balance of Austre Grønfjordbreen (Spitsbergen). Ice Snow 2019, 59, 59–66. [Google Scholar] [CrossRef]
- Sosnovsky, A.V.; Macheret, Y.Y.; Glazovsky, A.F.; Lavrentiev, I.I. Influence of snow cover on the thermal regime of a polythermal glacier in Western Spitsbergen. Ice Snow 2015, 131, 27. [Google Scholar] [CrossRef][Green Version]
- Lavrentiev, I.I.; Kutuzov, S.S.; Glazovsky, A.F.; Macheret, Y.Y.; Osokin, N.I.; Sosnovsky, A.V.; Chernov, R.A.; Cherniakov, G.A. Snow thickness on Austre Grønfjordbreen, Svalbard, from radar measurements and standard snow surveys. Ice Snow 2018, 58, 5–20. [Google Scholar] [CrossRef]
- Rets, E.; Kireeva, M. Hazardous hydrological processes in mountainous areas under the impact of recent climate change: Case study of Terek River basin. IAHS-AISH Publ. 2010, 340, 126–134. [Google Scholar]
- Belozerov, E.; Rets, E.; Petrakov, D.; Popovnin, V. Modelling glaciers’ melting in Central Caucasus (the Djankuat and Bashkara Glacier case study). E3S Web Conf. 2020, 163, 01002. [Google Scholar] [CrossRef]
- Rets, E.; Barandun, M.; Belozerov, E.; Petrakov, D.; Shpuntova, A. Mass-balance modelling of Ak-Shyirak massif Glaciers, Inner Tian Shan.; EGU General Assembly: Vienna, Austria, 2017; p. 10327. [Google Scholar]
- Rets, E.P.; Petrakov, D.A.; Belozerov, E.V.; Shpuntova, A.M. Sary-Tor glaier mass balance modelling (the Ak-Shiyrak massif, inner Tien Shan). Earth’s Cryoshpere 2021, in press. [Google Scholar]
- Chernov, R.A.; Muraviev, A.Y. Contemporary changes in the area of glaciers in the western part of the Nordenskjold Land (Svalbard). Led i Sneg 2018, 462–472. [Google Scholar] [CrossRef]
- Norwegian Polar Institute (npolar.no) TopoSvalbard Map Service. Available online: https://toposvalbard.npolar.no/ (accessed on 18 November 2020).
- König, M.; Kohler, J.; Nuth, C. Glacier Area Outlines - Svalbard [Data set]. Norwegian Polar Institute. Available online: https://data.npolar.no/dataset/89f430f8-862f-11e2-8036-005056ad0004 (accessed on 25 January 2020).
- Nuth, C.; Kääb, A. Co-registration and bias corrections of satellite elevation data sets for quantifying glacier thickness change. Cryosphere 2011, 5, 271–290. [Google Scholar] [CrossRef]
- ArcticDEM. Available online: https://www.pgc.umn.edu/data/arcticdem (accessed on 17 October 2020).
- Norwegian Polar Institute. Terrengmodell Svalbard (S0 Terrengmodell) [Data Set]. Available online: https://doi.org/10.21334/npolar.2014.dce53a47 (accessed on 17 October 2020).
- Braithwaite, R.J.; Zhang, Y. Sensitivity of mass balance of five Swiss glaciers to temperature changes assessed by tuning a degree-day model. J. Glaciol. 2000, 46, 7–14. [Google Scholar] [CrossRef]
- Hock, R. Temperature index melt modelling in mountain areas. J. Hydrol. 2003, 282, 104–115. [Google Scholar] [CrossRef]
- Kuzmin, P.P. The Process of Snow Melting; Gidrometizdat: Leningrad, Russia, 1961. [Google Scholar]
- The University Centre in Svalbard UNIS Weather stations and CTD stations. Available online: https://www.unis.no/resources/weather-stations/ (accessed on 3 March 2020).
- Institute of Applied Astronomy of the Russian Academy of Sciences Online Ephemeris Service. Available online: http://iaaras.ru/dept/ephemeris/online/ (accessed on 4 March 2020).
- Terekhov, A.V.; Tarasov, G.V.; Sidorova, O.R.; Demidov, V.E.; Anisimov, M.A.; Verkulich, S.R. Estimation of mass balance of Aldegondabreen (Spitsbergen) in 2015–2018 based on ArcticDEM, geodetic and glaciological measurements. Ice Snow 2020, 192–200. [Google Scholar] [CrossRef]
- Terekhov, A.V.; Demidov, V.E.; Kazakov, E.E.; Anisimov, M.A.; Verkulich, S.R. Geodetic mass balance of Vöring Glacier, Western Spitsbergen, in 2013–2019. Kriosf. Zemli 2020, 14, 55–63. [Google Scholar] [CrossRef]
- Van Pelt, W.; Kohler, J. Modelling the long-term mass balance and firn evolution of glaciers around Kongsfjorden, Svalbard. J. Glaciol. 2015, 61, 731–744. [Google Scholar] [CrossRef]
- Pramanik, A.; Van Pelt, W.; Kohler, J.; Schuler, T.V. Simulating climatic mass balance, seasonal snow development and associated freshwater runoff in the Kongsfjord basin, Svalbard (1980–2016). J. Glaciol. 2018, 64, 943–956. [Google Scholar] [CrossRef]
- Krenke, A.M.; Khodakov, V.G. Connection of the surface melting glaciers and air temperature. Mater. Glyatsiologicheskikh Issled. Data Glaciol. Stud. 1966, 1, 153–164. [Google Scholar]
- Schuler, T.V.; Glazovsky, A.; Hagen, J.O.; Hodson, A.; Jania, J.; Kohler, J.; Malecki, J.; Moholdt, G.; Pohjola, V.; Van Pelt, W.; et al. New data, new techniques and new challenges for updating the state of Svalbard glaciers (SvalGlac). 2019, 4, 1–22. [Google Scholar]
- Kohler, J. Mass balance for glaciers near Ny-Ålesund [Data set]. Norwegian Polar Institute. Available online: https://doi.org/10.21334/npolar.2013.ad6c4c5a (accessed on 1 March 2020).
- Malecki, J. Annual mass balance of Svenbreen, Central Spitsbergen, Svalbard [Data set]. Adam Mickiewicz University. Available online: https://doi.org/10.21334/npolar.2020.b3bb4ee2 (accessed on 1 March 2020).
- Walczowski, W.; Piechura, J. Influence of the West Spitsbergen Current on the local climate. Int. J. Climatol. 2011, 31, 1088–1093. [Google Scholar] [CrossRef]
- Van Pelt, W.J.J.; Kohler, J.; Liston, G.E.; Hagen, J.O.; Luks, B.; Reijmer, C.H.; Pohjola, V.A. Multidecadal climate and seasonal snow conditions in Svalbard. J. Geophys. Res. Earth Surf. 2016, 121, 2100–2117. [Google Scholar] [CrossRef]
- Hagen, J.O.; Liestøl, O.; Roland, E.; Jørgensen, T. Glacier atlas of Svalbard and Jan Mayen. Norwegian Polar Institue: Oslo, Norway, 1993; ISBN 8276660665. [Google Scholar]
- Haeberli, W.; Bösch, H.; Scherler, K.; Østrem, G.; Wallén, C.C. WGMS (1989): World glacier inventory – Status 1988; World Glacier Monitoring Service: Zurich, Switzerland, 1989. [Google Scholar]
- Huss, M.; Bauder, A.; Funk, M. Homogenization of long-term mass-balance time series. Ann. Glaciol. 2009, 50, 198–206. [Google Scholar] [CrossRef]
- Nuth, C.; Schuler, T.V.; Kohler, J.; Altena, B.; Hagen, J.O. Estimating the long-term calving flux of Kronebreen, Svalbard, from geodetic elevation changes and mass-balance modeling. J. Glaciol. 2012, 58, 119–133. [Google Scholar] [CrossRef]
- Reveillet, M.; Vincent, C.; Six, D.; Rabatel, A. Which empirical model is best suited to simulate glacier mass balances? J. Glaciol. 2017, 63, 39–54. [Google Scholar] [CrossRef]
- Xu, M.; Yan, M.; Kang, J.; Ren, J. Comparative studies of glacier mass balance and their climatic implications in Svalbard, Northern Scandinavia, and Southern Norway. Environ. Earth Sci. 2012, 67, 1407–1414. [Google Scholar] [CrossRef]
- Van Pelt, W.J.J.; Oerlemans, J.; Reijmer, C.H.; Pohjola, V.A.; Pettersson, R.; van Angelen, J.H. Simulating melt, runoff and refreezing on Nordenskiöldbreen, Svalbard, using a coupled snow and energy balance model. Cryosphere 2012, 6, 641–659. [Google Scholar] [CrossRef]
- Østby, T.I.; Schuler, T.V.; Hagen, J.O.; Hock, R.; Kohler, J.; Reijmer, C.H. Diagnosing the decline in climatic mass balance of glaciers in Svalbard over 1957–2014. Cryosphere 2017, 11, 191–215. [Google Scholar] [CrossRef]



| Balance Year | Number of Stake Measurements | Beginning of Survey Period (dd.mm.yyyy) | End of Winter Season (dd.mm.yyyy) | End of Survey Period (dd.mm.yyyy) | Method of Winter Measurements | Number of Snow Pits | Number of Manual Snow Probings |
|---|---|---|---|---|---|---|---|
| 2019 | 12 | 24.08.2018 | 08.04.2019 | 11.09.2019 | Snow pits; manual snow probings; GPR | 6 | 58 |
| 2018 | 11 | 10.09.2017 | 24.08.2018 | ||||
| 2017 | 11 | 06.09.2016 | 10.09.2017 | ||||
| 2016 | 10 | 06.08.2015 | 06.09.2016 | ||||
| 2015 | 12.04.2015 | Snow pits; GPR | 12 | ||||
| 2014 | 6 | 22.08.2013 | 17.04.2014 | 02.08.2014 | Snow pits; manual snow probings; GPR | 13 | 77 |
| 2013 | 21.04.2013 | Snow pits; manual snow probings | 10 | 44 |
| Parameter | Value | Unit |
|---|---|---|
| DDF ice | 6.0; 5.0 | mm °C−1 d−1 |
| DDF snow | 2.0 | mm °C−1 d−1 |
| Threshold temperature for snow/rain | 1 | °C |
| Threshold temperature for melting | 0 | °C |
| Temperature lapse rate | 0.6 | °C /100 m |
| Precipitation coefficient | 0.95 | - |
| Input Data | Data Source |
|---|---|
| Glacier area | Landsat imagery |
| Glacier topography | ArcticDEM (Release 7) |
| The type of surface (ice/firn/snow/debris) | Landsat imagery |
| Snow thickness/snowline dynamics | Field snow measurements/Landsat imagery |
| Meteorological parameters (temperature/wind speed/relative humidity/precipitation) | Barentsburg weather station |
| Longwave and shortwave radiation (downwards) | Adventdalen weather station (© The University Centre in Svalbard) [31] |
| Albedo (ice/firn/snow) | The pyranometric data provided by Arctic and Antarctic Research Institute (Russian Scientific Arctic Expedition on the Spitsbergen Archipelago) |
| Solar ephemeris | © Institute of Applied Astronomy of the Russian Academy of Sciences [32] |
| Surface Mass Balance, m w.e. | |||
|---|---|---|---|
| Year | Net | Summer | Winter |
| 2019 | −1.51 | −2.04 | 0.53 |
| 2018 | −1.41 | ||
| 2017 | −1.51 | ||
| 2016 | −2.40 | ||
| 2015 | 0.77 | ||
| 2014 | −1.10 | −1.65 | 0.54 |
| 2013 | 0.62 | ||
| Balance Year | Net Mass Balance, m w.e. | Solid Precipitation, m w.e. | Melt, m w.e. | Refreezing, m w.e. |
|---|---|---|---|---|
| 2019 | −1.73 | 0.66 | 2.38 | 0.18 |
| 2015 | −1.53 | 0.86 | 1.87 | 0.25 |
| 2014 | −0.93 | 0.64 | 1.65 | 0.12 |
| 2013 | −1.52 | 0.81 | 2.37 | 0.21 |
| 2012 | −1.19 | 0.81 | 1.59 | 0.18 |
| 2011 | −1.56 | 0.73 | 1.91 | 0.31 |
| Abbreviation | Elevation Range, m a.s.l. | Area, km2 | Investigation Period | Mass Balance Data Reference | |
|---|---|---|---|---|---|
| Austre Brøggerbreen | AB | 50–600 | 6.1 | 1967–2018 | [39] |
| Austre Grønfjordbreen | AG | 70–550 | 6.2 | 2013–2019 | this study |
| Austre Lovénbreen | AL | 100–550 | 4.5 | 2008–2018 | [11] |
| Etonbreen (Austfonna) | E | 0–800 | 880.0 | 2004–2018 | [39] |
| Hansbreen | H | 0–510 | 56.7 | 1989–2018 | [11] |
| Irenebreen | I | 125–650 | 4.0 | 2002–2017 | [11] |
| Kongsvegen | K | 0–1050 | 101.9 | 1987–2018 | [39] |
| Kronebreen/Holtedalsfonna | Kr | 0–1361 | 370 | 2003–2018 | [39] |
| Midtre Lovénbreen | ML | 50–600 | 5.4 | 1968–2018 | [39] |
| Nordenskiöldbreen 2 | N | 0–1200 | 206 | 2006–2018 | [11] |
| Svenbreen | S | 155–757 | 4.5 | 2010–2018 | [40] |
| Waldemarbreen | W | 100–570 | 2.4 | 1995–2017 | [11] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elagina, N.; Kutuzov, S.; Rets, E.; Smirnov, A.; Chernov, R.; Lavrentiev, I.; Mavlyudov, B. Mass Balance of Austre Grønfjordbreen, Svalbard, 2006–2020, Estimated by Glaciological, Geodetic and Modeling Aproaches. Geosciences 2021, 11, 78. https://doi.org/10.3390/geosciences11020078
Elagina N, Kutuzov S, Rets E, Smirnov A, Chernov R, Lavrentiev I, Mavlyudov B. Mass Balance of Austre Grønfjordbreen, Svalbard, 2006–2020, Estimated by Glaciological, Geodetic and Modeling Aproaches. Geosciences. 2021; 11(2):78. https://doi.org/10.3390/geosciences11020078
Chicago/Turabian StyleElagina, Nelly, Stanislav Kutuzov, Ekaterina Rets, Andrei Smirnov, Robert Chernov, Ivan Lavrentiev, and Bulat Mavlyudov. 2021. "Mass Balance of Austre Grønfjordbreen, Svalbard, 2006–2020, Estimated by Glaciological, Geodetic and Modeling Aproaches" Geosciences 11, no. 2: 78. https://doi.org/10.3390/geosciences11020078
APA StyleElagina, N., Kutuzov, S., Rets, E., Smirnov, A., Chernov, R., Lavrentiev, I., & Mavlyudov, B. (2021). Mass Balance of Austre Grønfjordbreen, Svalbard, 2006–2020, Estimated by Glaciological, Geodetic and Modeling Aproaches. Geosciences, 11(2), 78. https://doi.org/10.3390/geosciences11020078