Laboratory and Physical Prototype Tests for the Investigation of Hydraulic Hysteresis of Pyroclastic Soils
Abstract
1. Introduction
2. Materials and Methods
2.1. The Test Site and the Soil Physical Properties
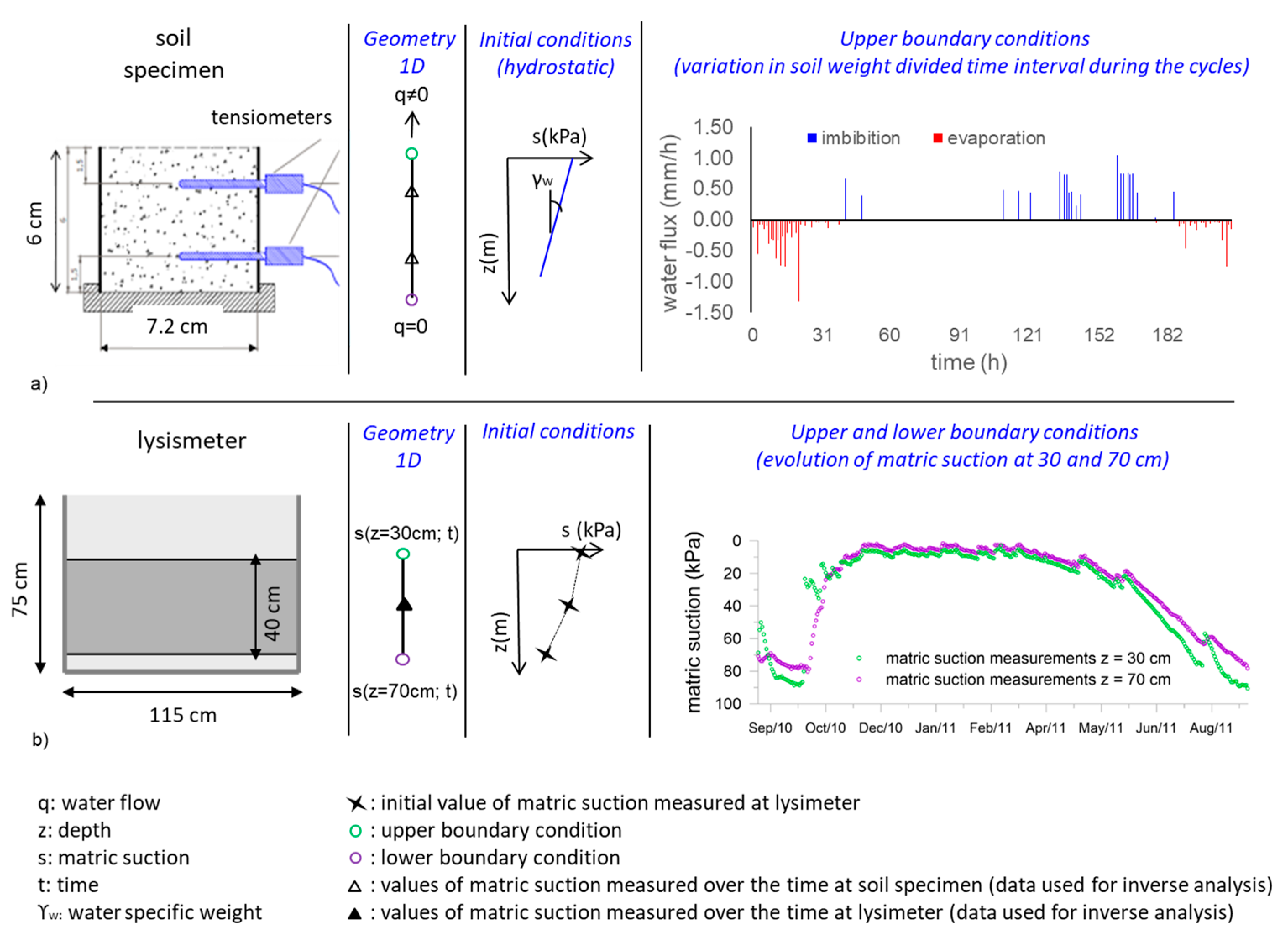
2.2. Investigation at the Small Scale: Laboratory Test
2.3. Investigation at the Medium Scale: Lysimeter
- the uppermost surface, where there are inward (rainfall infiltration) and outward (evaporation) water flows due to the interaction between the atmosphere and topsoil; both flows were monitored by regularly weighing the tank through three load cells that were used to quantify water storage changes, which, in turn, corresponded to rainfall infiltration amounts during periods without drainage and actual evaporation during periods without drainage or rainfall;
- the bottom, where there is a seepage surface due to the capillary barrier effect regulated by a geotextile interposed between the layer and the holed tank base; the seepage surface behaves as an impervious surface, while negative pore water pressures act near the surface and as a free draining surface otherwise; in this regard, the experimental results can be retrieved in [34]; and
- the lateral faces, where surfaces are impervious to water flow.
2.4. Modeling Methods
2.4.1. Fitting of the Experimental Data from Laboratory Tests
2.4.2. Fitting of the Experimental Data from the Physical Prototype
- (1)
- were obtained by the experimental main drying curve determined by Nicotera et al. [19];
- (2)
- was assumed to be 0.5; and
- (3)
- were determined by numerically interpreting data recorded during the first year in the bare soil and were validated through the data collected in the remaining three years.
3. Results
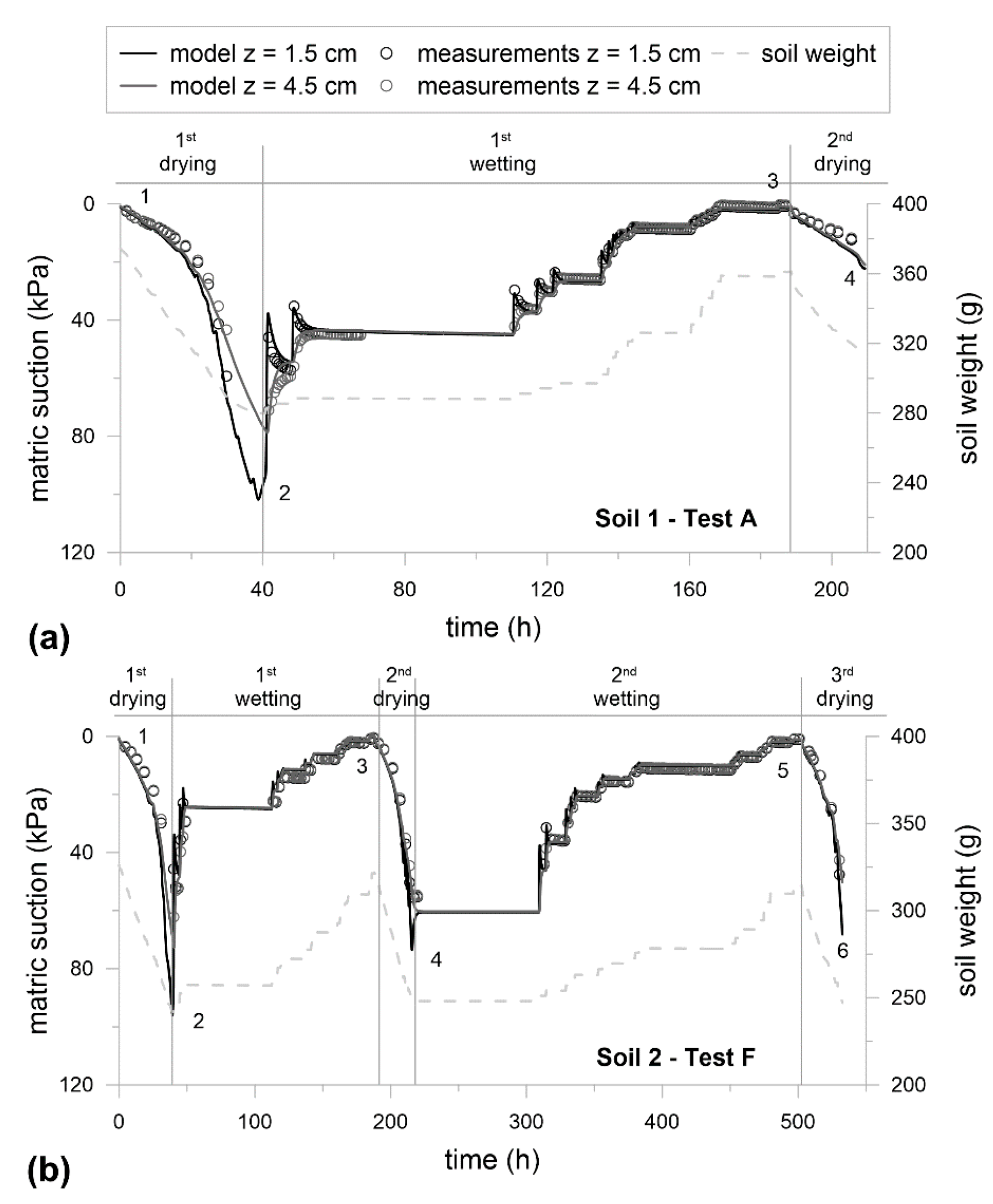
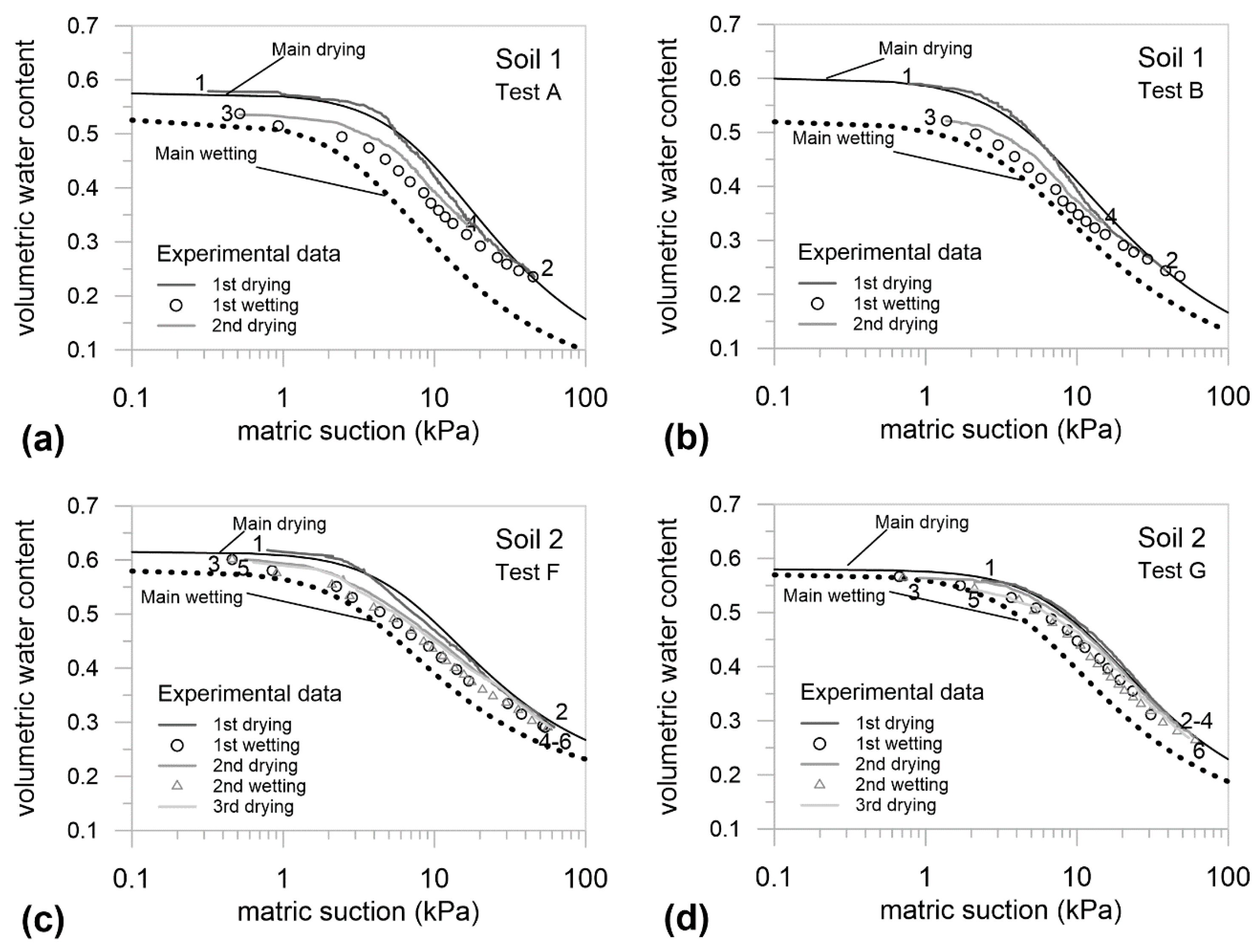
3.1. Investigation at the Small Scale: Laboratory Test
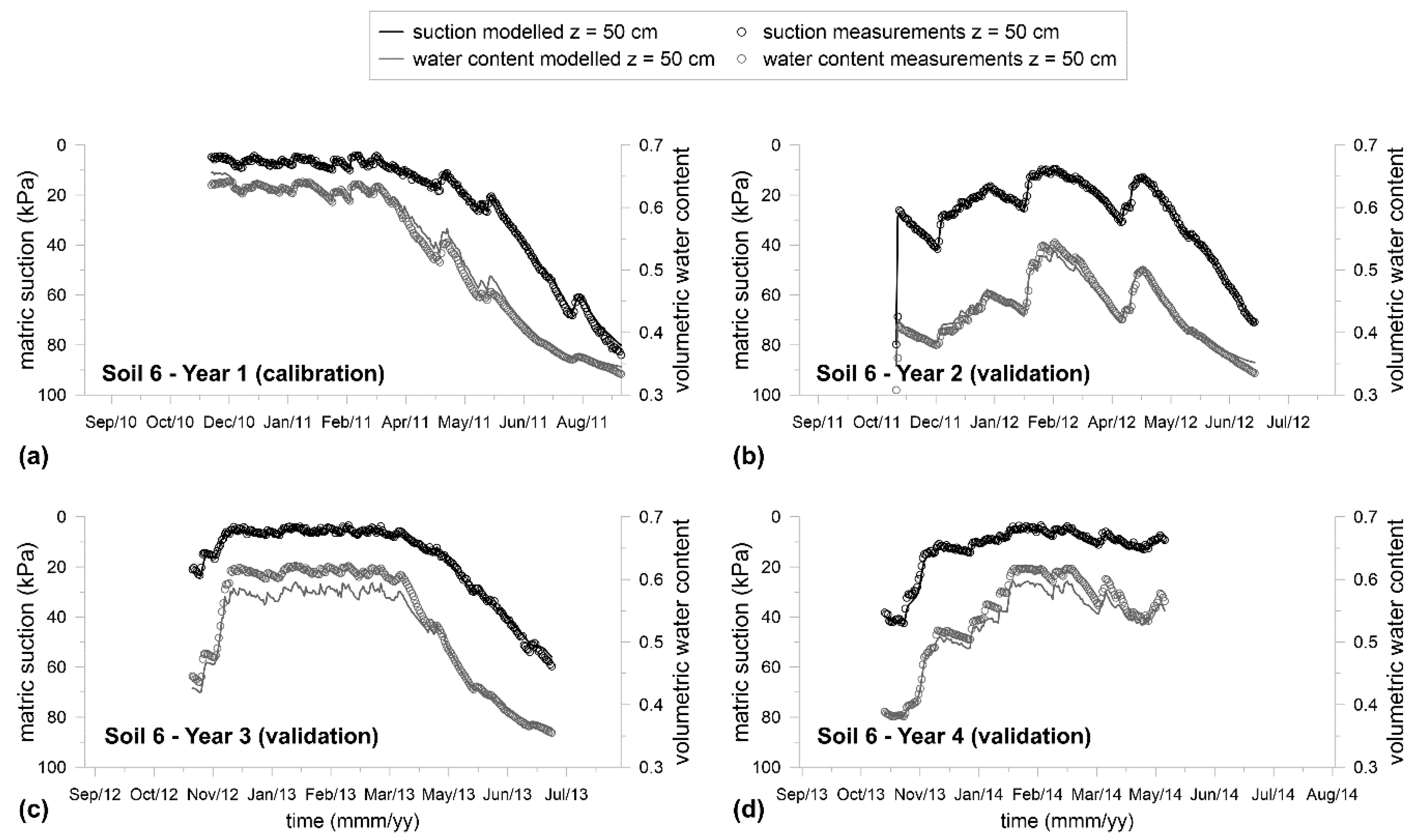
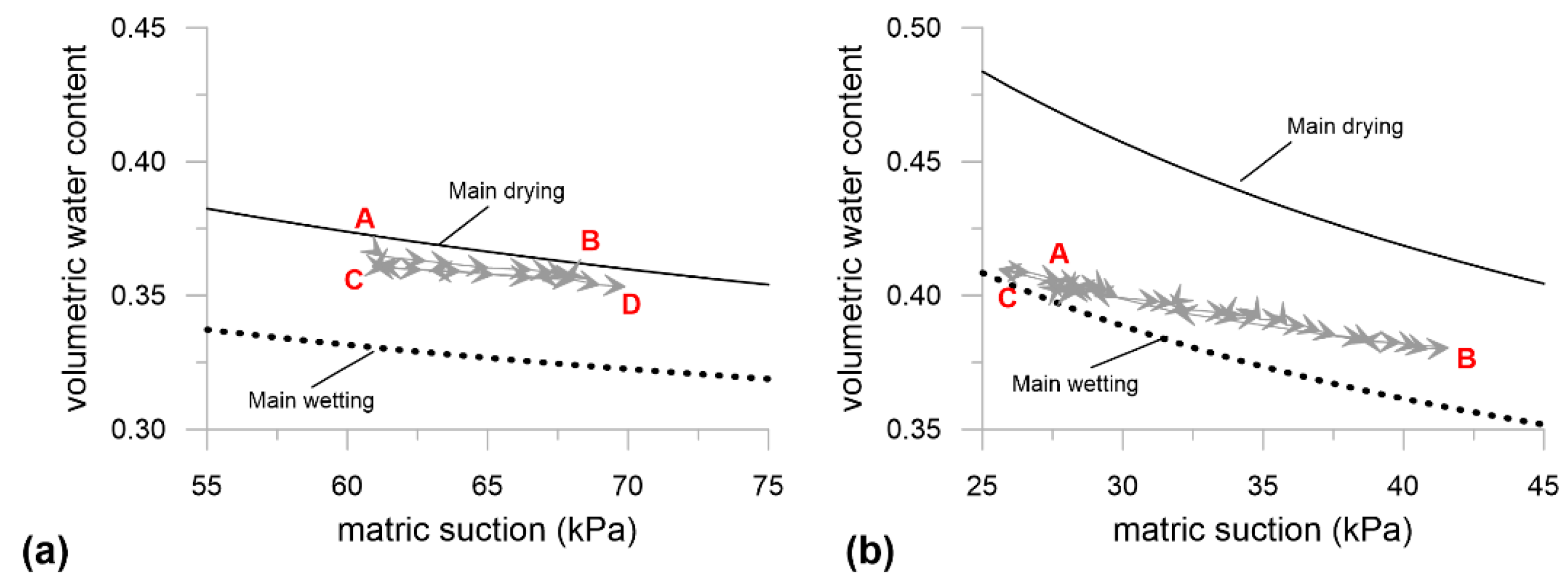
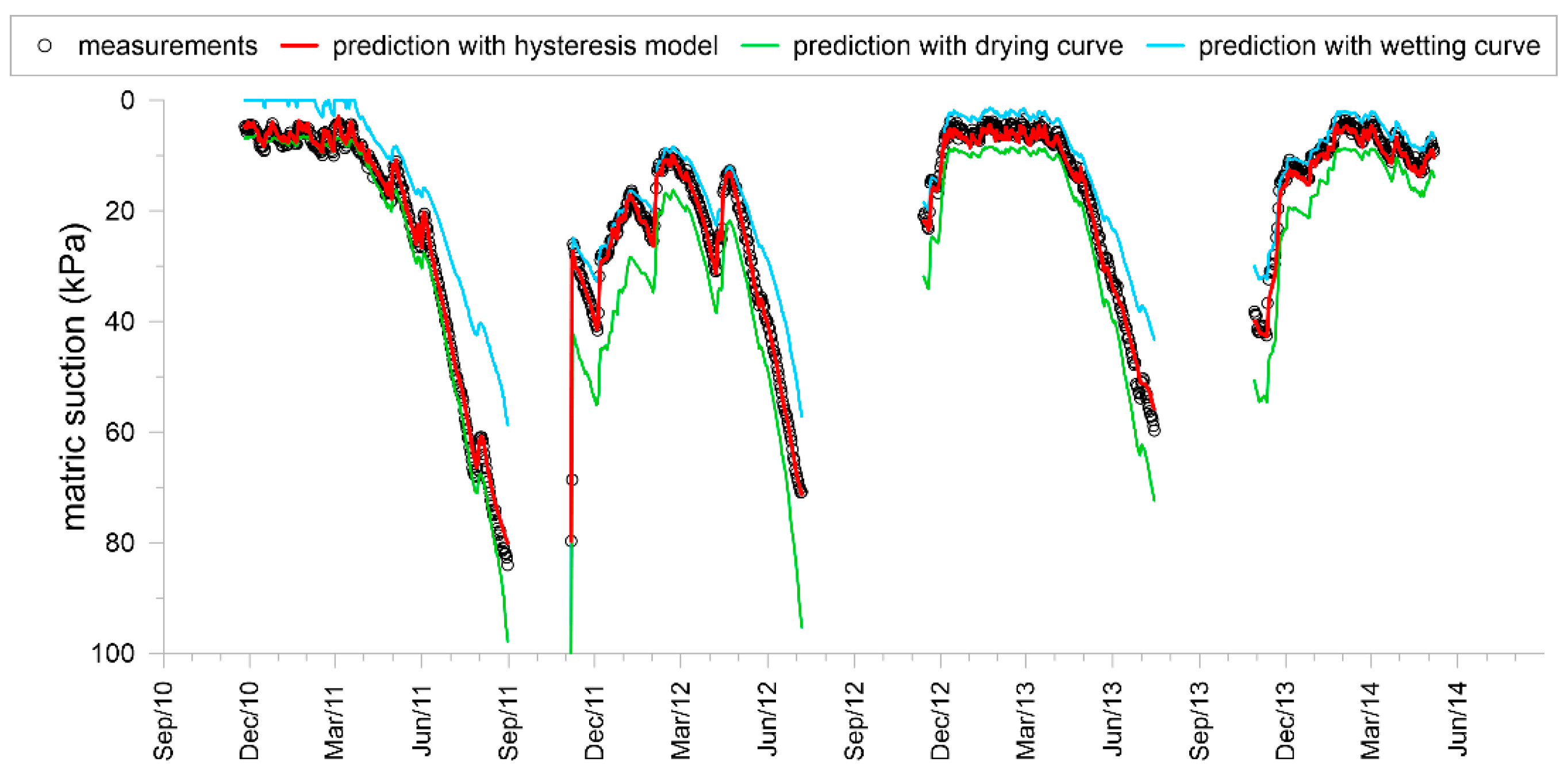
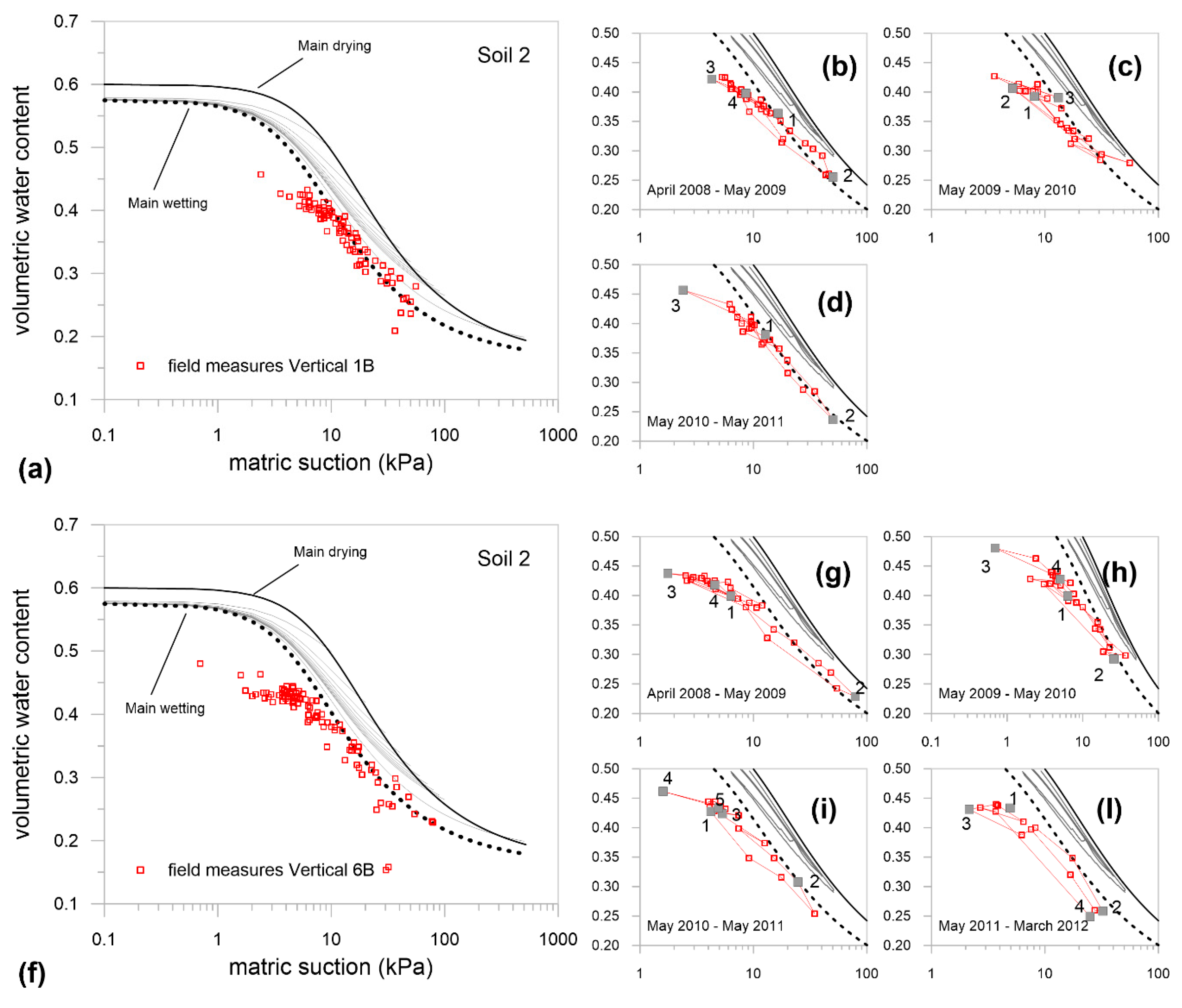
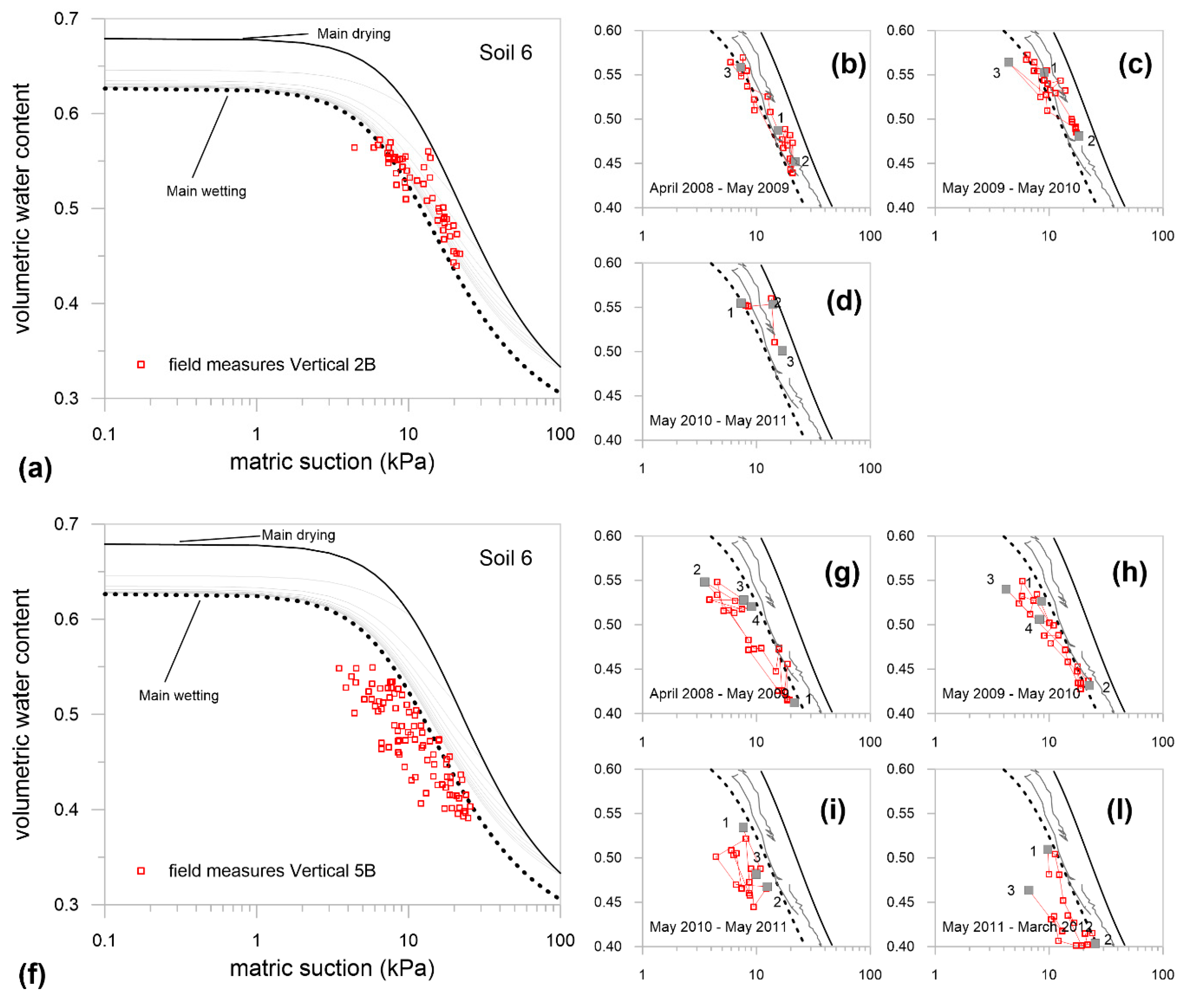
3.2. Investigation at the Medium Scale: Lysimeter
4. Discussion
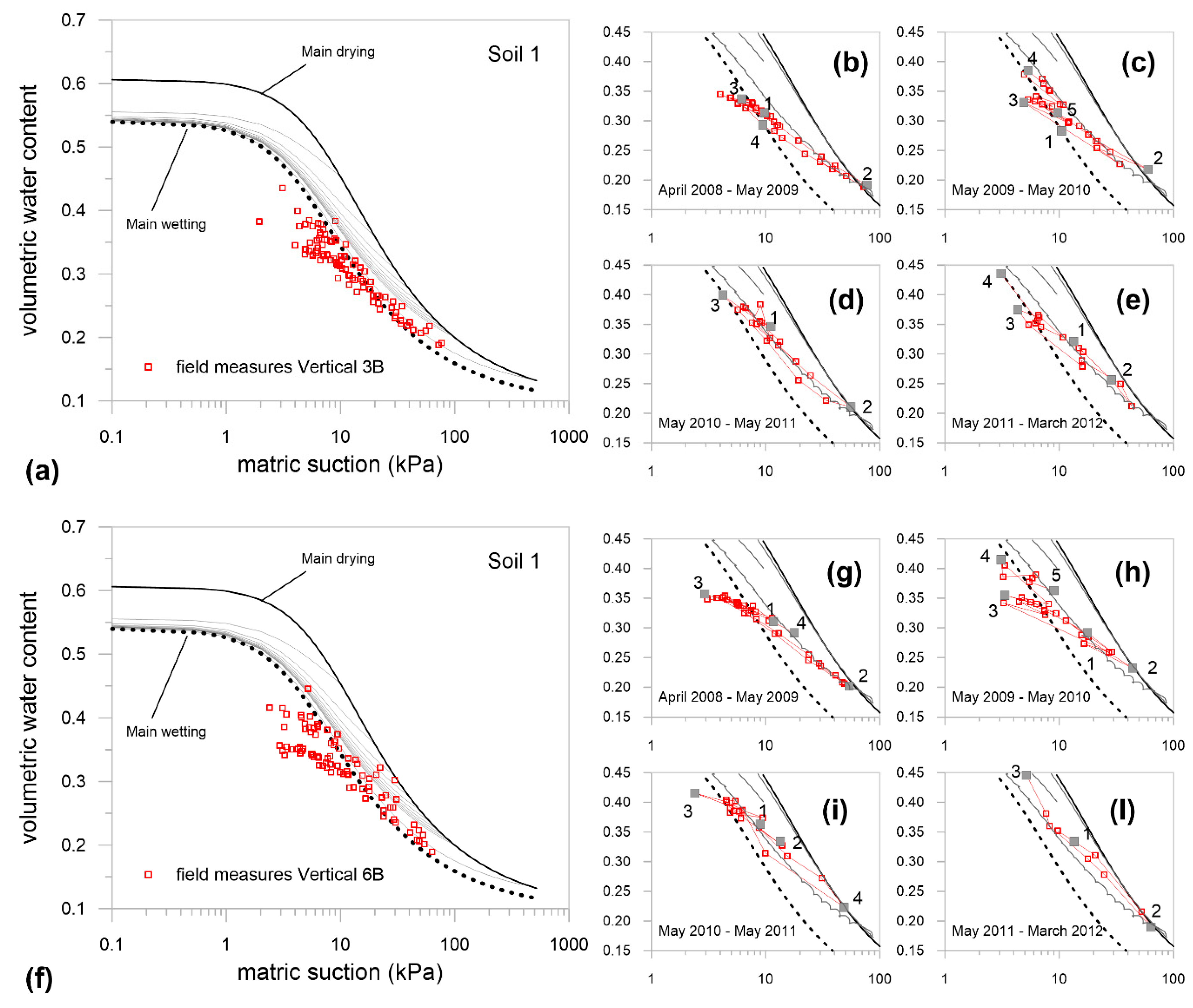
4.1. Comparison between the LP Parameters Determined at Small/Medium Scales
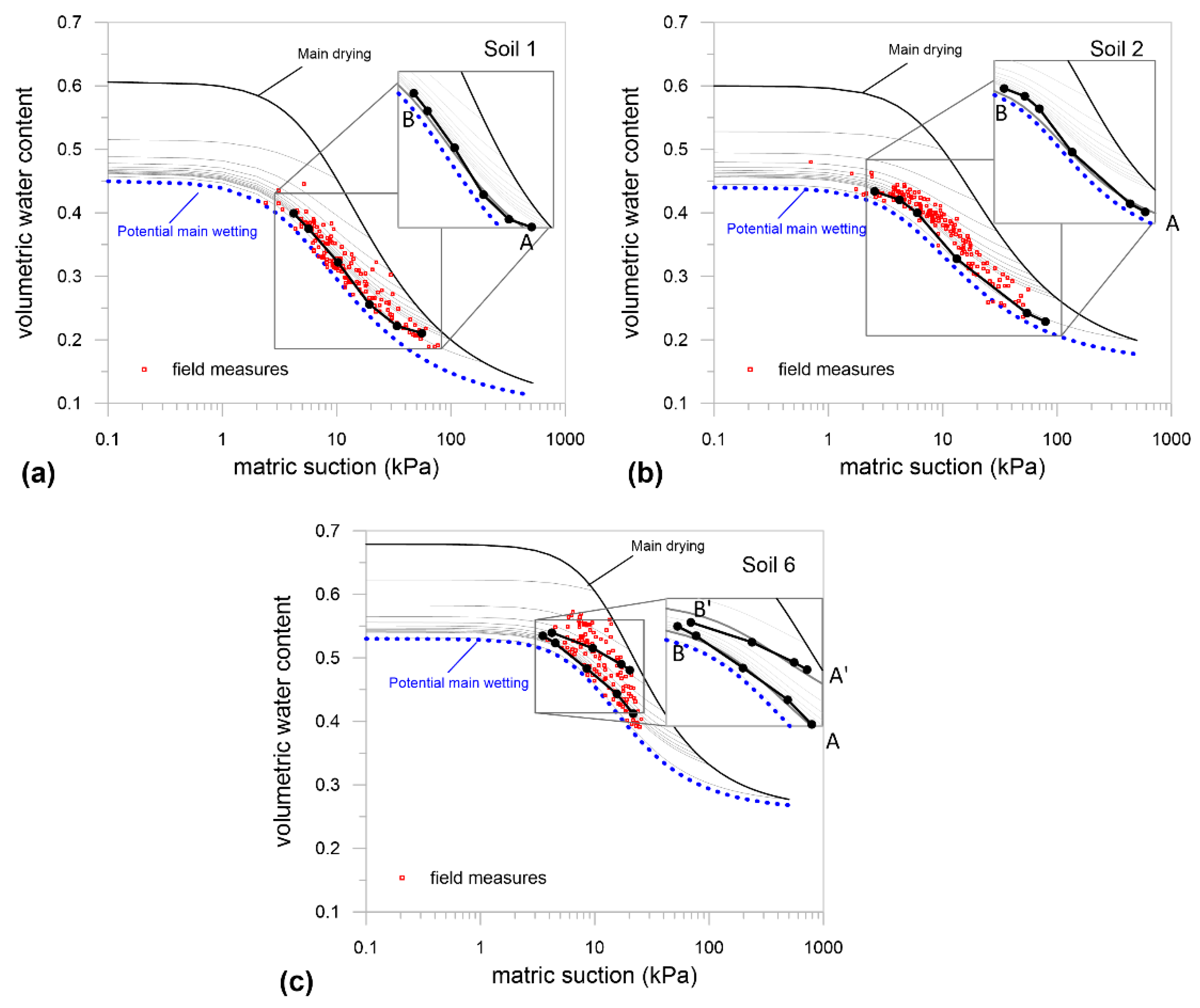
4.2. Reliability of the Hydraulic Characterization Determined at Small/Medium Scales
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Toll, D.G.; Hughes, P.N.; Asquith, J.D. Soil water retention behaviour for an instrumented embankment. In Proceedings of the 3rd European Conference on Unsaturated Soils (E-UNSAT), Paris, France, 12–14 September 2016. [Google Scholar] [CrossRef]
- Pirone, M.; Papa, R.; Nicotera, M.V.; Urciuoli, G. Hydraulic Behaviour of Unsaturated Pyroclastic Soil Observed at Different Scales. In Proceedings of the VI Italian Conference of Researchers in Geotechnical Engineering (CNRIG)—Geotechnical Engineering in Multidisciplinary Research: From Microscale to Regional Scale, Bologna, Italy, 22–23 September 2016. [Google Scholar]
- Pirone, M.; Rianna, G.; Reder, A.; Pagano, L.; Urciuoli, G. Two Applications of Soil Water Balance in Unsaturated Pyroclastic Soils. In Proceedings of the VI Italian Conference of Researchers in Geotechnical Engineering, (CNRIG)—Geotechnical Engineering in Multidisciplinary Research: From Microscale to Regional Scale, Bologna, Italy, 22–23 September 2016. [Google Scholar]
- Nielsen, D.R.; Van Genuchten, M.T.; Biggar, J.W. Water flow and solute transport process in the unsaturated zone. Water Resour. Res. 1986, 22, 89–108. [Google Scholar] [CrossRef]
- De Rooij, G.H. Averaging hydraulic head, pressure head, and gravitational head in subsurface hydrology, and implications for averaged fluxes, and hydraulic conductivity. Hydrol. Earth Syst. Sci. 2009, 13, 1123–1132. [Google Scholar] [CrossRef]
- Hopmans, J.W.; Nielsen, D.R. How useful are small-scale soil hydraulic property measurements for large-scale vadose zone modeling? In Environmental Mechanics: Water, Mass and Energy Transfer in the Biosphere Geophysical Monograph; American Geophysical Union: Washington, DC, USA, 2002. [Google Scholar] [CrossRef]
- Papa, R.; Pirone, M.; Nicotera, M.V.; Urciuoli, G. Seasonal groundwater regime in an unsaturated pyroclastic slope. Geotechnique 2013, 63, 420–426. [Google Scholar] [CrossRef]
- Comegna, L.; Damiano, E.; Greco, R.; Guida, A.; Olivares, L.; Picarelli, L. Field hydrological monitoring of a sloping shallow pyroclastic deposit. Can. Geotech. J. 2016, 53, 1125–1137. [Google Scholar] [CrossRef]
- Durner, W.; Schultze, B.; Zurmühl, T. State-of-the-Art in Inverse Modeling of Inflow/Outflow Experiments. In Proceedings of the International Workshop on Characterization and Measurement of the Hydraulic Properties of Unsaturated Porous Media, University of California, Riverside, CA, USA, 22–24 October 1997; pp. 661–681. [Google Scholar]
- Diamantopoulos, E.; Iden, I.C.; Durner, W. Inverse modeling of dynamic non- equilibrium in water flow with an effective approach. Water Resour. Res. 2012, 48, W03503. [Google Scholar] [CrossRef]
- Pirone, M.; Papa, R.; Nicotera, M.V.; Urciuoli, G. In situ monitoring of the groundwater field in an unsaturated pyroclastic slope for slope stability evaluation. Landslides 2015, 12, 259–276. [Google Scholar] [CrossRef]
- Pirone, M.; Papa, R.; Nicotera, M.V.; Urciuoli, G. Soil water balance in an unsaturated pyroclastic slope for evaluation of soil hydraulic behaviour and boundary conditions. J. Hydrol. 2015, 528, 63–83. [Google Scholar] [CrossRef]
- Rianna, G.; Pagano, L.; Urciuoli, G. Investigation of soil–atmosphere interaction in pyroclastic soils. J. Hydrol. 2014, 510, 480–492. [Google Scholar] [CrossRef]
- Reder, A.; Rianna, G.; Pagano, L. Physically based approaches incorporating evaporation for early warning predictions of rainfall–induced landslides. Nat. Hazards Earth Syst. Sci. 2018, 18, 613–631. [Google Scholar] [CrossRef]
- Reder, A.; Rianna, G.; Pagano, L. Some aspects of water and energy budget of a pyroclastic cover. Environ. Geotech. 2019, 6, 406–419. [Google Scholar] [CrossRef]
- Pagano, L.; Reder, A.; Rianna, G. Effects of vegetation on hydrological response of silty volcanic covers. Can. Geotech. J. 2019, 56, 1261–1277. [Google Scholar] [CrossRef]
- Parker, J.C.; Lenhard, R.J. A Model for Hysteretic Constitutive Relations Governing Multiphase Flow 1. Saturation Pressure Relations. Water Resour. Res. 1987, 23, 2187–2196. [Google Scholar] [CrossRef]
- Van Genuchten, M.T. A Closed-Form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Nicotera, M.V.; Papa, R.; Urciuoli, G. An experimental technique for determining the hydraulic properties of unsaturated pyroclastic soils. Geotech. Test. J. 2010, 33, 263–285. [Google Scholar] [CrossRef]
- Pirone, M.; Urciuoli, G. Cyclical suction characteristics in unsaturated slopes. In Proceedings of the International Workshop on Volcanic Rocks and Soils, Ischia Island, Italy, 24–25 September 2015; pp. 183–185. [Google Scholar]
- Schaap, M.G.; Van Genuchten, M.T. A Modified Mualem–van Genuchten Formulation for Improved Description of the Hydraulic Conductivity Near Saturation. Vadose Zone J. 2006, 5, 27–34. [Google Scholar] [CrossRef]
- Tarantino, A. A water retention model for deformable soils. Geotechnique 2009, 59, 751–762. [Google Scholar] [CrossRef]
- Pasha, A.Y.; Khoshghalb, A.; Khalili, N. Hysteretic model for the evolution of water retention curve with void ratio. ASCE’s J. Eng. Mech. 2017, 143. [Google Scholar] [CrossRef]
- Gallipoli, D.; Wheeler, S.J.; Karstunen, M. Modelling the variation of degree of saturation in a deformable unsaturated soil. Geotechnique 2003, 53, 105–112. [Google Scholar] [CrossRef]
- Pasha, A.Y.; Khoshghalb, A.; Khalili, N. Can degree of saturation decrease during constant suction compression of an unsaturated soil? Comput. Geotech. 2019, 106, 199–204. [Google Scholar] [CrossRef]
- Khoshghalb, A.; Pasha, A.Y.; Khalili, N. A Fractal Model for Volume Change Dependency of the Water Retention Curve. Géotechnique 2015, 62, 141–146. [Google Scholar] [CrossRef]
- Nuth, M.; Laloui, L. Advances in modelling hysteretic water retention curve in deformable soils. Comput. Geotech. 2008, 35, 835–844. [Google Scholar] [CrossRef]
- Pasha, A.; Khoshghalb, A.; Khalili, N. Evolution of isochoric water retention curve with void ratio. Comput. Geotech. 2020, 122, 103536. [Google Scholar] [CrossRef]
- Pasha, A.Y.; Khoshghalb, A.; Khalili, N. Pitfalls in Interpretation of Gravimetric Water Content–Based Soil-Water Characteristic Curve for Deformable Porous. Int. J. Geomech. 2016, 16, D4015004. [Google Scholar] [CrossRef]
- Nicotera, M.V.; Papa, R.; Urciuoli, G. The Hydro-Mechanical Behaviour of Unsaturated Pyroclastic Soils: An Experimental Investigation. Eng. Geol. 2015, 195, 70–84. [Google Scholar] [CrossRef]
- Papa, R. Indagine Sperimentale sulla Coltre Piroclastica di un Versante della Campania [Experimental investigation on the pyroclastic cover of a slope in Campania (Italy)]. Ph.D. Thesis, Università di Napoli Federico II, Napoli, Italy, 2007; p. 367. [Google Scholar]
- Pagano, L.; Picarelli, L.; Rianna, G.; Urciuoli, G. A simple numerical procedure for timely prediction of precipitation-induced landslides in unsaturated pyroclastic soils. Landslides 2010, 7, 273–289. [Google Scholar] [CrossRef]
- Lo Presti, D.C.F.; Pedroni, S.; Crippa, V. Maximum dry density of cohesionless soil by pluviation and by ASTM D 4253–83: A comparative study. Geotech. Test. J. 1992, 15, 180–189. [Google Scholar]
- Reder, A.; Pagano, L.; Picarelli, L.; Rianna, G. The role of the lowermost boundary conditions in the hydrological response of shallow sloping covers. Landslides 2017, 14, 861–873. [Google Scholar] [CrossRef]
- Lenhard, R.J.; Parker, J.C.; Kaluarachchi, J.J. Comparing Simulated and Experimental Hysteretic Two-Phase Transitent Fluid Phenomena. Water Resour. Res. 1991, 27, 2113–2124. [Google Scholar] [CrossRef]
- Lenhard, R.J.; Parker, J.C. A Model for Hysteretic Constitutive Relations Governing Multiphase Flow 2. Permeability-Saturation Relations. Water Resour. Res. 1987, 23, 2187–2196. [Google Scholar] [CrossRef]
- Dias, A.S. The Effect of Vegetation on Slope Stability of Shallow Pyroclastic Soil Covers. Ph.D. Thesis, University of Montpellier, Montpellier, France, 2019. Available online: https://tel.archives-ouvertes.fr/tel-02045922 (accessed on 25 January 2019).
- Ippisch, O.; Vogel, H.-J.; Bastian, P. Validity limits for the van Genuchten–Mualem model and implications for parameter estimation and numerical simulation. Adv. Water Resour. 2006, 29, 1780–1789. [Google Scholar] [CrossRef]
- Madi, R.; De Rooij, G.H.; Mielenz, H.; Mai, J. Parametric soil water models: A critical evaluation of expressions for the full moisture range. Hydrol. Earth Syst. Sci. 2018, 22, 1193–1219. [Google Scholar] [CrossRef]
- Scott, P.S.; Farquhar, G.J.; Kouwen, N. Hysteretic effects on net infiltration. Advances in Infiltration. Am. Soc. Agric. Eng. Publ. 1983, 11–83, 163–170. [Google Scholar]
- Kool, J.B.; Parker, J.C. Development and Evaluation of Closed-form Expressions for Hysteretic Soil Hydraulic Properties. Water Resour. Res. 1987, 23, 105–114. [Google Scholar] [CrossRef]
- Werner, A.D.; Lockington, D.A. Artificial pumping errors in the Kool—Parker scaling model of soil moisture hysteresis. J. Hydrol. 2006, 325, 118–133. [Google Scholar] [CrossRef]
- Land, C.S. Calculation of Imbibition Relative Permeability for Two-and Three-Phase Flow from Rock Properties. Soc. Pet. Eng. J. 1968, 8, 149–156. [Google Scholar] [CrossRef]
- Mualem, Y. A modified dependent-domain theory of hysteresis. Soil Sci. 1984, 137, 283–291. [Google Scholar] [CrossRef]
- Šimůnek, J.; Šejna, M.; Saito, H.; Sakai, M.; Van Genuchten, M.T. The HYDRUS-1D Software Package for Simulating the One-Dimensional Movement of Water, Heat, and Multiple Solutes in Variably-Saturated Media 2013, Technical manual, version 4.16; Department of Environmental Science University of California Riverside: Riverside, CA, USA, 2013. [Google Scholar]
- Marquard, D.W. An Algorithm for Least-Squares Estimation of Nonlinear Parameters. J. Soc. Ind. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Rianna, G.; Comegna, L.; Pagano, L.; Picarelli, L.; Reder, A. The Role of Hydraulic Hysteresis on the Hydrological Response of Pyroclastic Silty Covers. Water 2019, 11, 628. [Google Scholar] [CrossRef]
- Basile, A.; Ciollaro, G.; Coppola, A. Hysteresis in Soil Water Characteristics as a Key to Interpreting Comparisons of Laboratory and Field Measured Hydraulic Properties. Water Resour. Res. 2003, 39, 1355. [Google Scholar] [CrossRef]
- Askarinejad, A.; Casini, F.; Kienzler, P.; Springman, S.M. Comparison of the in situ and laboratory water retention curves for a silty sand. In Proceedings of the 5th International Conference of Unsaturated Soils (UNSAT), Barcelona, Spain, 6–9 September 2011. [Google Scholar]
- Ng, C.W.W.; Wong, H.N.; Tse, Y.M.; Pappin, J.W.; Sun, H.W.; Millis, S.W.; Leung, A.K. A field study of stress-dependent soil–water characteristic curves and permeability of a saprolitic slope in Hong Kong. Geotechnique 2011, 61, 511–521. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models, Part I: A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Knoben, W.J.M.; Freer, J.E.; Woods, R.A. Technical note: Inherent benchmark or not? Comparing Nash–Sutcliffe and Kling–Gupta efficiency scores. Hydrol. Earth Syst. Sci. 2019, 23, 4323–4331. [Google Scholar] [CrossRef]
- Gebrenegus, T.; Ghezzehei, T.A. An index for degree of hysteresis in water retention. Soil Sci. Soc. Am. J. 2011, 75, 2122–2127. [Google Scholar] [CrossRef]
- Yang, C.; Sheng, D.; Carter, J.P. Effect of Hydraulic Hysteresis on Seepage Analysis for Unsaturated Soils. Comput. Geotech. 2012, 41, 36–56. [Google Scholar] [CrossRef]
- Huang, H.C.; Tan, Y.C.; Liu, C.W.; Chen, C.H. A novel hysteresis model in unsaturated soil. Hydrol. Process. 2005, 19, 1653–1665. [Google Scholar] [CrossRef]
- Capparelli, G.; Spolverino, G. An Empirical Approach for Modeling Hysteresis Behavior of Pyroclastic Soils. Hydrology 2020, 7, 14. [Google Scholar] [CrossRef]
- Greco, R.; Comegna, L.; Damiano, E.; Guida, A.; Olivares, L.; Picarelli, L. Hydrological modelling of a slope covered with shallow pyroclastic deposits from field monitoring data. Hydrol. Earth Syst. Sci. 2013, 17, 4001–4013. [Google Scholar] [CrossRef]
- Santo, A.; Di Crescenzo, G.; Forte, G.; Papa, R.; Pirone, M.; Urciuoli, G. Flow-type landslides in pyroclastic soils on flysch bedrock in southern Italy: The Bosco de’ Preti case study. Landslides 2018, 15, 63–82. [Google Scholar] [CrossRef]
- Forte, G.; Pirone, M.; Santo, A.; Nicotera, M.V.; Urciuoli, G. Triggering and predisposing factors for flow-like landslides in pyroclastic soils: The case study of the Lattari Mts. (southern Italy). Eng. Geol. 2019, 257, 105137. [Google Scholar] [CrossRef]
- Pirone, M.; Papa, R.; Nicotera, M.V.; Urciuoli, G. Analysis of Safety Factor in unsaturated pyroclastic slope. In Landslides and Engineered Slopes. Experience, Theory and Practice; CRC Press: Naples, Italy, 2016; Volume 3, pp. 1647–1654. [Google Scholar] [CrossRef]

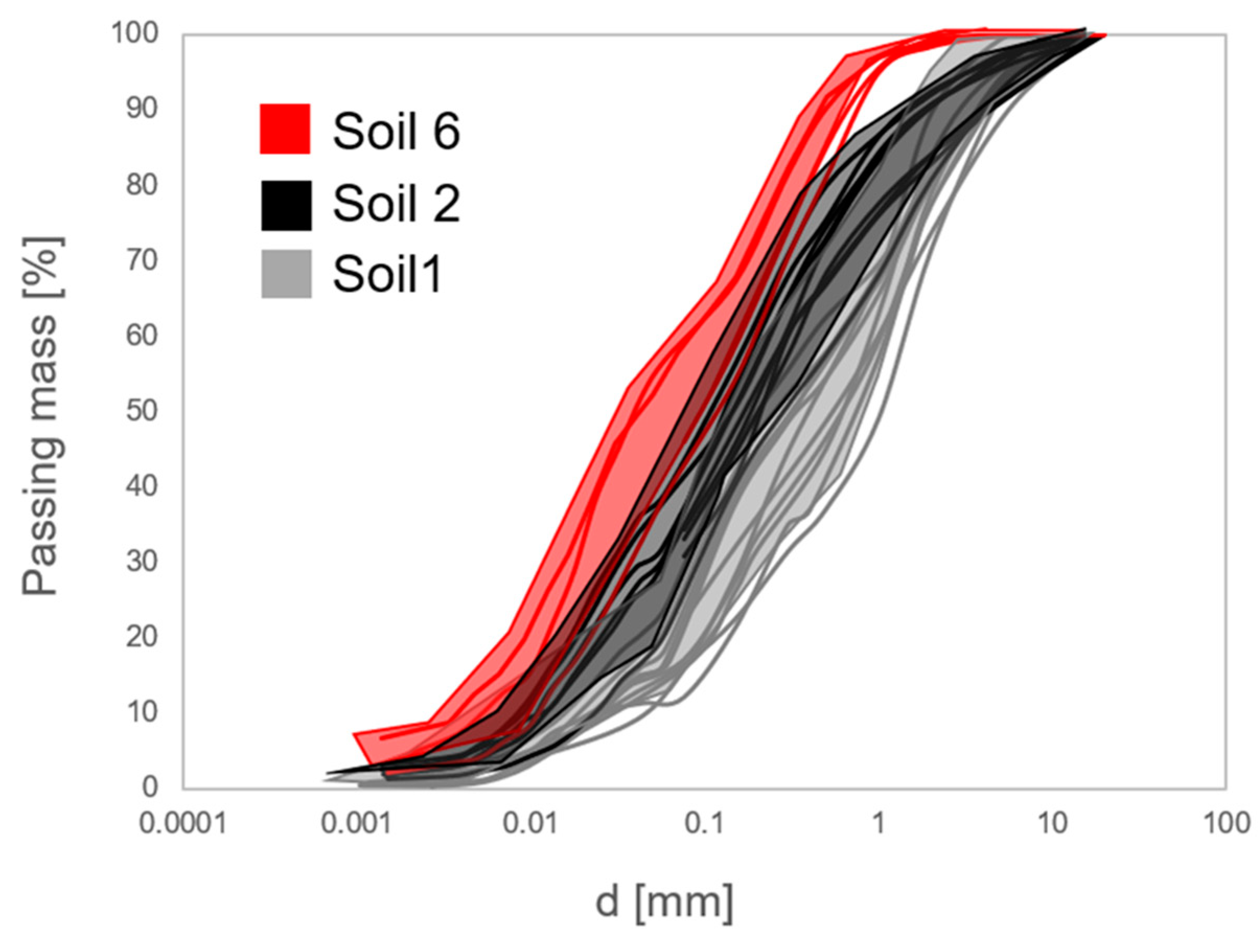



| Soil | n | Gs | Size of Sample (d *; h **) (cm) | Testing Method | |
|---|---|---|---|---|---|
| 1 (topsoil) | 0.66 | 7.90 | 2.65 | soil specimen (d: 7.2; h: 6) | evaporation/imbibition test |
| 2 (topsoil) | 0.69 | 7.90 | 2.55 | soil specimen (d: 7.2; h: 6) | evaporation/imbibition test |
| 6 (deep soil) | 0.72 | 7.13 | 2.57 | physical prototype (d: 115; h: 75) | monitoring of soil hydraulic behavior under actual weather forcing [13,14,15,16] |
| Experimental Data | |||||||
|---|---|---|---|---|---|---|---|
| Soil | Test | Porosity | Phase | Final State | |||
| # | N | # | n Step° | s (kPa) | Theta | ||
| 0–1 | saturation | 0.3 | 0.58 | ||||
| 1–2 | evaporation | 44.7 | 0.24 | ||||
| 1 | A | 0.63 | 2–3 | wetting | 17 | 0.5 | 0.54 |
| 3–4 | evaporation | 16.6 | 0.33 | ||||
| 4–5 | drying | 1000.0 | 0.18 | ||||
| 0–1 | saturation | 0.8 | 0.59 | ||||
| 1–2 | evaporation | 39.0 | 0.25 | ||||
| 1 | B | 0.64 | 2–3 | wetting | 17 | 1.4 | 0.52 |
| 3–4 | evaporation | 14.8 | 0.33 | ||||
| 4–5 | drying | 1000.0 | 0.16 | ||||
| 0–1 | saturation | 1.7 | 0.58 | ||||
| 1–2 | evaporation | 41.1 | 0.31 | ||||
| 1 | C | 0.68 | 2–3 | wetting | 18 | 1.71 | 0.57 |
| 3–4 | evaporation | 22.3 | 0.37 | ||||
| 4–5 | drying | 1000.0 | 0.20 | ||||
| 0–1 | saturation | 0.8 | 0.63 | ||||
| 1–2 | evaporation | 45.0 | 0.31 | ||||
| 1 | D | 0.67 | 2–3 | wetting | 18 | 0.6 | 0.60 |
| 3–4 | evaporation | 21.89 | 0.38 | ||||
| 4–5 | drying | 1000.0 | 0.22 | ||||
| 0–1 | saturation | 0.6 | 0.58 | ||||
| 1–2 | evaporation | 57.0 | 0.28 | ||||
| 2 | E | 0.71 | 2–3 | wetting | 31 | 1.0 | 0.56 |
| 3–4 | evaporation | 56.0 | 0.29 | ||||
| 4–5 | wetting | 0.6 | 0.57 | ||||
| 5–6 | evaporation | 58.1 | 0.28 | ||||
| 6–7 | drying | 1000.0 | 0.18 | ||||
| 0–1 | saturation | 0.8 | 0.62 | ||||
| 1–2 | evaporation | 61.8 | 0.29 | ||||
| 2 | F | 0.72 | 2–3 | wetting | 38 | 0.5 | 0.60 |
| 3–4 | evaporation | 57.0 | 0.29 | ||||
| 4–5 | wetting | 0.5 | 0.60 | ||||
| 5–6 | evaporation | 58.0 | 0.29 | ||||
| 6–7 | drying | 1000 | 0.20 | ||||
| 0–1 | saturation | 2.4 | 0.56 | ||||
| 1–2 | evaporation | 46.9 | 0.29 | ||||
| 2 | G | 0.64 | 2–3 | wetting | 31 | 0.7 | 0.57 |
| 3–4 | evaporation | 58.2 | 0.27 | ||||
| 4–5 | wetting | 0.7 | 0.56 | ||||
| 5–6 | evaporation | 54.9 | 0.27 | ||||
| 6–7 | drying | 1000.0 | 0.12 | ||||
| Soil | Test | Ksat | R2 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| m/s | ||||||||||
| 1 | A | 5.56∙× 10−6 | 0.575 | 0.027 | 0.108 | 1.600 | −0.500 | 0.526 | 0.250 | 0.994 |
| 1 | B | 5.56∙× 10−6 | 0.600 | 0.033 | 0.180 | 1.500 | −0.500 | 0.520 | 0.240 | 0.990 |
| 1 | C | 4.28∙× 10−6 | 0.600 | 0.200 | 0.105 | 1.860 | −0.500 | 0.560 | 0.180 | 0.994 |
| 1 | D | 4.65∙× 10−6 | 0.650 | 0.107 | 0.134 | 1.450 | 1.000 | 0.570 | 0.200 | 0.994 |
| mean | 5.0∙× 10−6 | 0.61 | 0.09 | 0.13 | 1.60 | −0.1 | 0.5 | 0.22 | 0.99 | |
| std | 6.5∙× 10−7 | 0.03 | 0.08 | 0.03 | 0.18 | 0.75 | 0.02 | 0.03 | ||
| 2 | E | 5.53∙× 10−6 | 0.589 | 0.19 | 0.095 | 1.8 | 1 | 0.58 | 0.2 | 0.705 |
| 2 | F | 5.60∙× 10−6 | 0.615 | 0.173 | 0.13 | 1.6 | 1 | 0.58 | 0.25 | 0.963 |
| 2 | G | 9.72∙× 10−7 | 0.59 | 0.103 | 0.099 | 1.59 | 1 | 0.57 | 0.18 | 0.945 |
| mean | 4.0∙× 10−6 | 0.60 | 0.16 | 0.11 | 1.66 | 1.0 | 0.8 | 0.21 | 0.87 | |
| std | 2.6∙× 10−6 | 0.01 | 0.05 | 0.02 | 0.12 | 0.00 | 0.01 | 0.04 | ||
| 6 | Year 1 | 1.0∙× 10−6 | 0.68 | 0.26 | 0.07 | 1.90 | 0.50 | 0.63 | 0.10 | 0.99 |
| NSE | KGE | ||||
|---|---|---|---|---|---|
| Hysteresis | Main Drying | Main Wetting | Hysteresis | Main Drying | Main Wetting |
| 0.99 | 0.82 | 0.78 | 0.97 | 0.67 | 0.61 |
| Material | Path | NSE | KGE |
|---|---|---|---|
| Soil 1 | A–B | 0.99 | 0.94 |
| Soil 2 | A–B | 0.97 | 0.89 |
| Soil 6 | A–B | 0.99 | 0.98 |
| Soil 6 | A’–B’ | 0.90 | 0.69 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pirone, M.; Reder, A.; Rianna, G.; Pagano, L.; Nicotera, M.V.; Urciuoli, G. Laboratory and Physical Prototype Tests for the Investigation of Hydraulic Hysteresis of Pyroclastic Soils. Geosciences 2020, 10, 320. https://doi.org/10.3390/geosciences10080320
Pirone M, Reder A, Rianna G, Pagano L, Nicotera MV, Urciuoli G. Laboratory and Physical Prototype Tests for the Investigation of Hydraulic Hysteresis of Pyroclastic Soils. Geosciences. 2020; 10(8):320. https://doi.org/10.3390/geosciences10080320
Chicago/Turabian StylePirone, Marianna, Alfredo Reder, Guido Rianna, Luca Pagano, Marco Valerio Nicotera, and Gianfranco Urciuoli. 2020. "Laboratory and Physical Prototype Tests for the Investigation of Hydraulic Hysteresis of Pyroclastic Soils" Geosciences 10, no. 8: 320. https://doi.org/10.3390/geosciences10080320
APA StylePirone, M., Reder, A., Rianna, G., Pagano, L., Nicotera, M. V., & Urciuoli, G. (2020). Laboratory and Physical Prototype Tests for the Investigation of Hydraulic Hysteresis of Pyroclastic Soils. Geosciences, 10(8), 320. https://doi.org/10.3390/geosciences10080320







