Abstract
Groundwater has supported 70% of the water supply at the Lower Kelantan River Basin (LKRB) since the 1930s and demand for groundwater increases annually. Groundwater has been abstracted from shallow and deep aquifers. However, a comprehensive study on groundwater recharge estimation has never been reported. This study evaluated various methods to quantify recharge rate using chloride mass balance (CMB), water table fluctuation (WTF), temperature–depth profiles (TDP), and groundwater modelling coupled with water balance (GM(WB)). Recharge estimation using CMB, WTF, TDP, and GM(WB) showed high variability within 8% to 68% of annual rainfall. CMB is range from 16% to 68%, WTF 11% to 19%, TDP 8% to 11%, and GM(WB) 7% to 12% of annual rainfall, respectively. At 11%, recharge from GM(WB) was the best method for estimation because the model was constructed and calibrated using locally derived input parameters. GM(WB) is the only method involved with calibration and validation process to reduce the uncertainty. The WTF method based on long-term hydrological records gives a reasonable recharge value, in good agreement with GM(WB) and these methods can be paired to ensure the reliability of recharge value approximation in the same ranges. Applying various methods has given insight into methods selection to quantify recharge at LKRB and it is recommended that a lysimeter is installed as a direct method to estimate recharge.
1. Introduction
Groundwater resources are used by approximately 2.5 billion people in the world to support their daily needs [1]. Groundwater has been abstracted ~986 km3/year (60%) worldwide and most of this for agricultural, domestic, and industrial uses [2]. Over exploitation of groundwater has introduced unprecedented groundwater stress problems in some regions. The greatest stress on groundwater occurred mostly in arid and semi-arid areas of the world [3,4,5,6]. In the tropical region, groundwater stress has triggered or exacerbated land subsidence, aquifer compaction, groundwater depletion, salt water intrusion, arsenic contamination, and groundwater quality deterioration, as reported for the Chao Phraya River Basin, Mekong River Basin, the Greater Jakarta Basin, Irrawaddy Delta, Bengal Mega Delta, and others [7,8,9,10]. The stress becomes worse especially during periods of drought. The projection of global groundwater depletion during the twenty first century according to the influence of groundwater extraction costs and resources, ranges from 180 km3/year to 480 km3/year (restricted renewable water) and 110 km3/year to 210 km3/year (expanded renewable water), which is lower than the 2050 prediction and also less than models predicted by [11,12] detailed in [13]. The stresses on groundwater are still increasing and present considerable risk and uncertainty. Whether there will be a sufficient groundwater in the future with good quality is still undetermined.
One of the key elements for sustainable groundwater resource management is groundwater recharge. Groundwater recharge is the process where water infiltrates into subsurface until it reaches the water tables forming an addition to the groundwater reservoir [14,15,16]. Recharge processes can occur either as diffused recharge or focused recharge [16]. It is challenging to measure the natural recharge directly and accurately because the processes vary in spatial and temporal variability, climate, soil and geology, surface topography, hydrology, vegetation, and land use of the study area [17,18,19,20,21]. Climate change and urbanization are the main factors that can reduce the groundwater recharge rate [6,22,23,24]. Information related to groundwater recharge will help to manage an over extraction of groundwater and prevent groundwater stress in order to sustain the resources. In some regions, managed aquifer recharge (MAR) has successfully overcome and improved the quantity and quality of groundwater [25,26].
Numerous methods or techniques have been applied and developed to estimate the recharge either using water budget, surface water data, modelling, physical (unsaturated and saturated), and tracers (chemical, isotopes, or heat) [19,20,27,28,29,30,31,32,33]. Reference [16] has compiled and provided detailed explanation on critical evaluation or understanding of the theory and assumption that underlie each method for estimating groundwater recharge in various hydrologic zones and climates. Through reviews, methods are widely applied in arid and semi-arid regions but less in humid and sub-humid regions. In addition to the methods described above, and not included by [16], the application of remote sensing and geographic information system (GIS) for estimates of groundwater dynamics has gained much interest and attention from researches [4,5,6,34,35]. References [4,6] utilized water manager data along with satellite information from GRACE (NASA) and model simulations to predict groundwater fluctuations and to estimate how the cascading effect of the hydrologic cycle results in groundwater depletion and recharge, respectively. Reference [5] monitored the land subsidence caused from both short-term and long-term groundwater depletion and recharge based on satellite data. Spatial decision-making technique, which is a combination of remote sensing, GIS, and analytic hierarchy process (AHP), has been applied in groundwater management studies to solve complex groundwater related problems (e.g., mapping the groundwater recharge suitability zones) [34,35]. Most of the studies applied multi-methods to quantify the recharge rate. The use of various methods enables us to improve understanding of recharge in the hydrogeological system locally and regionally that can provide a more reliable recharge estimation even though different methods have their own assumptions and limitations. Consideration of data availability for method selection is important as many regions often have insufficient data on record from either primary or secondary sources [16,18,36].
In Malaysia, the utilization of groundwater is relatively low at only 3% [37] because surface water is the main source of water supply. Therefore, there are no comprehensive studies related to groundwater recharge estimation for Malaysia except using water balance study. In Kelantan, especially at LKRB, groundwater resources have been utilised since 1935 [37] and the groundwater demand has risen till the present time with 70% utilization. In order to meet the increase in water demand usage, water operator, Air Kelantan Sdn. Bhd. (AKSB), has constructed a river bank filtration (RBF) system in a few places and is planning to construct river barrage and subsurface storage dam (groundwater dam) within the basin in the future [38]. The aim of this study was to apply and compare various methods to quantify recharge rate using chloride mass balance (CMB), water table fluctuation (WTF), temperature–depth profiles (TDP), and groundwater modelling coupled with water balance (GM(WB)) and to evaluate the best methods to be applied to quantify the recharge rate that is suitable for tropical humid areas. The paper comprehensively contributes to the field of hydrogeological research justifying the confidence level regarding the rates of recharge component into the regional aquifer. The detailed studies on the groundwater recharge are essential to improve the understanding and estimation of this climatic variable. These results will be valuable as a baseline study to enlighten the understanding of groundwater recharge rate for sustainable groundwater resources management at LKRB and throughout Malaysia.
2. Study Area
2.1. Location and Climate Condition
Lower Kelantan River Basin (LKRB) is situated in the northeast coast of the Malaysian Peninsula with an area of approximately 1450 km2. The basin is bounded by Thailand at the northwest, South China Sea in the north and east, and Southern Kelantan area in the south as shown in Figure 1a. LKRB has flat topography with mean elevation of 7 m above sea level (ASL). The maximum elevation in the basin of the hilly area is located at the southwest with an elevation about 40 m ASL while the elevation is approximately 100 and 192 m ASL at the southeast. LKRB experiences a humid tropical climate, controlled by two monsoon seasons. The southwest Monsoon occurs between April to October often bringing less rainfall whereas the northeast Monsoon from November to March frequently generates high rainfall intensity over the study area. The annual rainfall recorded from 22 rainfall stations varies between 2400–3110 mm with mean annual of 2774 mm. The mean annual temperature (1968–2013) is 27 °C ranging from 26.2 °C to 27.9 °C, while the mean relative humidity (1968–2013) is 82% ranging from 79% to 85%. The mean surface wind speed (1979–2013) is 2.2 m/s ranging from 1.3 m/s to 2.7 m/s. The river discharge of Kelantan River is estimated from Gulliemard Bridge station about 22 km along the reaches outside the study area boundary. This is the only station close to the LKRB. The mean annual river discharge from 1979 to 2013 was 478 m3/s ranging from 308 m3/s to 679 m3/s.
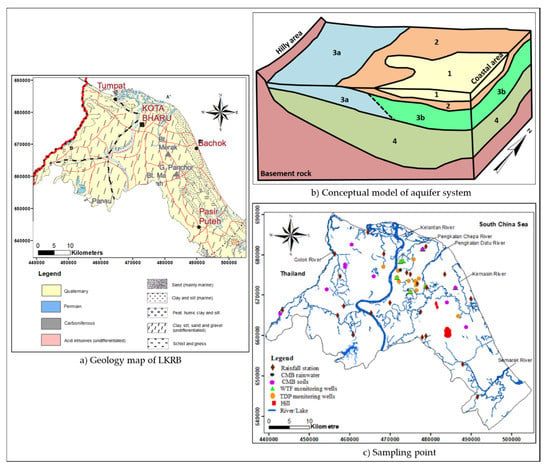
Figure 1.
(a) Geology map of Lower Kelantan River Basin (LKRB) (modified from [47]); (b) Conceptual model of aquifer system [46]; and (c) Sampling point.
2.2. Geology and Hydrogeology Conditions
The study area is covered by alluvium deposits of Quaternary age as shown in Figure 1a and underlain by granite and metamorphic as bedrock. The deposits of Pleistocene and Holocene mainly consist of unconsolidated to semi consolidated gravel, sand, clay, and silts that occupy in the north of Kelantan state and along the river valley [39]. The first 13 to 15 m deposit is recent in age [40,41] and composed of silty to clay. Towards the coast, the thickness of alluvium may reach up to more than 200 m [42] and it forms a shape like a thick wedge towards the sea. This sediment is complicated and made up of interstratified and intercalated deposit with marine and non-marine strata [43]. The mixtures of marine and non-marine sediment build of due to sea level changes during the Quaternary age [44].
According to the hydrogeological map, this area is indicated as fresh water and classified as a very high aquifer potential area [45]. The aquifer system consists of four aquifer units [46] as shown in Figure 1b. This conceptual model aquifer system is proposed in groundwater modelling (see Section 3.4 and Section 4.4). The aquifer system consists of four aquifer units [46] as shown in Figure 1b. Unit 1 is the shallow unconfined aquifer, followed by Unit 2, which is the protective clay layer, Unit 3a and 3b which are the gravely sand and sandy silty clay, respectively, and then Unit 4, which is the coarse sand confined aquifer. The hydraulic conductivity ranges from 10−2 to 10−3 m/s, 10−6 to 10−8 m/s, 10−4 to 10−6 m/s, 10−5 to 10−7 m/s, and 10−4 m/s, for units 1, 2, 3a, 3b, and 4 [46].
3. Materials and Methods
This study applied four methods to quantify groundwater recharge, which are chloride mass balance, water table fluctuation, temperature–depth profiles, and groundwater modelling coupled with water balance. The following section will briefly explain sampling, analysis, and data collection related to each method.
3.1. Chloride Mass Balance, CMB
CMB has been widely applied especially in arid and semi-arid areas [48,49,50,51,52,53] because of its simplicity and inexpensiveness. Chloride ion is known as a conservative natural tracer because of its property, which neither leaches from, nor is absorbed by, the sediment particles, is highly soluble (high solubility) in water, and is rarely found in solid phase. It does not react with geochemical or biochemical reaction processes during its movements through an unsaturated zone to at saturated zone and is not taken up by plants (root zones) during evapotranspiration process that will contributes to an accumulation of chloride in soil moisture [16,54,55,56]. The sources of atmospheric chloride are from wet and dry deposition in which wet deposition occurs when chloride ions are entrained in rainwater or snow while dry deposition is from the sea breeze [16,57]. Chloride ions from dry deposition are able to deposit up to 100 km inland from coastal area and can be negligible or low in effect because the aerosol size are washed out by precipitation especially in tropical areas with high rainfall intensity [57,58,59]. The only source of chloride in soil and groundwater is assumed from precipitation and not from weathering or anthropogenic sources [60]. If this assumption is valid, it follows that the chloride ion can adequately trace groundwater recharge processes and can thus provide reasonable estimates of groundwater recharge for understanding of the hydrological system. Its reliability therefore, hinges on the compatibility of the precipitation event that recharged the system under the study and recent precipitation [61]. Equation (1) was used to estimate recharge (R) using CMB method.
where R is recharge (mm/year), P is annual average rainfall (mm/year), ClP is the weighted average of chloride concentration (mg/L) in rainfall, and Cluz is the average chloride concentration in pore water of the unsaturated zone profile (mg/L) and/or in groundwater. The weighted average chloride in rainfall (ClP) was calculated according to the following equation:
where P1 is the first rainfall event (mm) and C1 is the corresponding chloride concentration in the rainfall (mg/L) in the area for 1 to n events. To determine the weighted chloride average for each hydrological year, the chloride concentration of each rainfall event is first multiplied by the amount of rainfall. The summation of these individual components is then divided by the total annual rainfall. There are several potential limitations of the CMB application [62]. The mass flux of chloride flowing on or off the terrain feature at the sampling area is uncertainly quantified. The aquifer system is probably not in the steady-state condition for input mass flux of chloride. CMB does not measure the total recharge as the unmeasured component that possibly occurs through leakages from other aquifers.
R = P × (ClP/Cluz)
ClP = P1 × C1+.......+ Pn × Cn / (P1 +.........+ Pn)
A total of 11 samples were collected for chloride analysis: 1 sample of rainwater and 10 samples of soil from the unsaturated zone within the basin as shown in Figure 1c. The data were collected between 2012 and 2015. Rainwater was collected at LRA Kg. Puteh using simple and temporary rain gauge of 25 L and 500 mL with paraffin oil used to prevent evaporation of rainwater. Chloride concentration in rainwater was measured at LRA Kg. Puteh laboratory and at the Department of Geology, University of Malaya. The soil samples were collected using hand auger and soil cores until reaching the water table. The soil samples were removed from steel cores at the Department of Civil Engineering, University of Malaya, then were sliced at 10 cm each and dried at 105 °C for 48 h. Dry soil samples were separated for 1) grain size analysis and 2) chloride concentration analysis [63]. Grain size analysis was performed according to the BS1377 (1990) method using a mechanical sieve apparatus to determine the distribution of the coarser particles. The fine particle (<63 micron) content was analyzed using a MALVERN MasterSizer (Malvern Instruments Ltd., UK). For chloride analysis, the dry soils needed to be grained to produce homogenised samples using pestel and mortar and automatic grinder (Retsch, Germany). Ultra-pure water (UPW) was added to the grained soil samples in a 1:1 or 2:1 ratio. Samples then were agitated on a reciprocal shaker table for 8 h. This was followed by samples centrifugation at 5000 rpm for 10 min at the Department of Mechanical Engineering, University of Malaya. The supernatant was filtered through 0.45 μm filters and chloride concentration was analyzed using ion chromatography (Metrohm, Switzerland).
3.2. Water Level Fluctuation, WTF
WTF has been applied by many researchers and modified in time series analysis for estimating groundwater recharge [64,65,66,67,68,69] within different climate conditions. The application of the WTF method requires knowledge of the specific yield and changes in groundwater levels caused by recharging aquifer [16,70]. Because of the abundance of available groundwater level data and the simplicity of estimating recharge rates from temporal or spatial patterns of water level, [70] had attributed a wide use of this method. The WTF method is best applied in estimating recharge over a short time period in an area with shallow unconfined aquifer that shows a sharp rise and fall of groundwater levels [18,69,70] due to rainfall events. This method is simple, easy to use, and there is no assumption made on the mechanism of water movement through the unsaturated zone. The occurrence of preferential flow path does not limit the application and the estimated recharge rates are able to represent an area of several to thousand square meters. The recharge estimate using WTF method gives the actual value and it is more reliable compared to potential recharge estimation by other methods [68]. Because of the simplicity of the method, many approaches for WTF have been studied and modified in time series analysis for estimating groundwater recharge [67,71,72,73] in order to improve the accuracy of the estimation. The WTF was applied to estimate groundwater recharge in saturated zones from groundwater level time series data. WTF is based on the premise that rises in groundwater levels in unconfined aquifers are due to recharge water arriving at the water tables [16]. The recharge was calculated as below:
where ΔSgw: changes in storage, R: recharge, Sy: specific yield, Δh: changes in water table, and Δt: period of time interval. The graphical approach was used to determine the groundwater level rise (Δh). The equation assumes that the water arriving at the water table goes immediately into storage and all other water-budget components are zero during the period of recharge. For each individual water level rise an estimation of total or gross recharge will generated. To determine the total recharge, Δh is set equal to the difference between the peak of the rise and low point of the extrapolated antecedent recession curve at the time of peak. The difference between recharge and net recharge in subsurface storage is equal to the sum of evapotranspiration from groundwater, baseflow and net subsurface flow from the site. The antecedent recession curves are extrapolated manually based on visual inspection of the entire data set. This approach involves more subjectivity and different users no doubt would produce slightly different recession curves [65]. The application of WTF has a few limitations [74]. The WTF method generally quantifies the recharge under a natural condition without considering changes of water table from pumping activities. The specific yield (Sy) of aquifer has to be known beforehand. The process to acquire the parameter is related to pumping tests.
ΔSgw = R = SyΔhΔt
In total, 14 monitoring wells (Figure 1c) belonging to the Mineral and Geosciences Department (MGD) were selected to quantify the recharge. All monitoring well sites were in shallow aquifer (Layer 1) with depth ranging from 9.4 m to 17 m. The wells were selected based on long-term groundwater level data availability within 1991 to 2008. Only monitoring wells with 96% and 100% of available data were used to estimate the groundwater recharge. Seven water years (WY) were identified; 1991–1992, 1992–1993, 1993–1994, 1994–1995, 2000–2001, 2004–2005, and 2007–2008, each from May until the following April, respectively.
3.3. Temperature-Depth Profiles, TDP
Research on the use of temperature started way back in the 1960s [75,76,77,78]. Since then, the number of studies has increased in the application of temperature to study groundwater–surface interaction within the streambed [79,80,81], climate (past and future), and land use (deforestation/urbanization) changes [82,83,84,85,86] and groundwater flow (recharge and discharge) [31,87,88,89]. Heat flow in the subsurface is closely related with the movement of water because groundwater transports thermal energy and disturbs the subsurface thermal regime not only by conduction but also by advection caused by the groundwater movement [90,91]. Various analytical solution such as 1-dimensional (1D), 2-dimensional (2D), and 3-dimensional (3D) and groundwater modelling have been applied and improved to examine the behavior of subsurface temperature profiles [76,78,86,90].
Heat in subsurface layers is principally distributed by conduction and advection caused by recharging or discharging water flow. The upward heat from the interior is influenced by the high aquifer temperature compared to the ground surface temperature. The governing equation representing the heat exchange of subsurface in response to an incompressible fluid flow through homogenous porous media is expressed as Equation (4) [88,92,93].
where T denotes the temperature, z represents the depth below the ground surface (positive downward), t signifies the time, α is the thermal diffusivity of the aquifer, and , in which v is the vertical groundwater flux and and are the heat capacity of water and aquifer, respectively. Under the condition of a linear increase in subsurface temperature, the analytical solution for one-dimensional heat conduction–convection found in [78] was applied as Equation (5). The modelling is limited to semi-infinite layers with only vertical conduction and convection, and vertical groundwater flux is assumed to be constant with depth [88].
The T0 is set as 27 °C and this is considered as the mean annual surface air temperature because there is no available long-term data on ground surface temperature at LKRB. Surface temperature usually changes according to the change in air temperature [88]. The geothermal gradient, TG, of 0.045 °C/m is used in the calculation based on the ranges of geothermal gradient at Penyu basin 0.036 °C/m to 0.055 °C/m [94]. The thermal diffusivity, α is 6.5 × 10−7 m2s−1 is adapted from [95]. One hundred years (t) is considered as the time after semi equilibrium and the increase in surface temperature at LKRB; b is 0.0162 °C/year. U = vc0ρ0/cρ where v is the vertical groundwater flux, c0ρ0 is the heat capacity of water, and cρ is the heat capacity of aquifer while erfc is the complementary error function. Different U values were used to compute the calculated TDP. The positive U value will show the downward movement of groundwater flow (recharge) while the negative U value will represent the upward movement of groundwater flow (discharge). The limitations of the TDP method are notified [96]. The vertical groundwater flux is constant throughout the unlimited depth. The assumption does not take into account that the flux along the vertical direction is decreasingly reduced in depth and along high-hydraulic-conductivity aquifer materials. The groundwater flux is set at the steady state even if the subsurface temperature is in the transient condition. The assumption does not consider the fact that the groundwater flux seasonally varies leading to the limitation of heat transfer application. The TDP method constrains the vertical heat transfer; however, the lateral heat advection and diffusion due to groundwater flow or fracture flow significantly invalidate the application. The thermal properties of subsurface media are homogenously generalized, but the vertical thermal properties of aquifer materials are varied. Therefore, the accuracy of TDP method is possibly affected by the assumption.
In total, 21 MGD monitoring wells were used for subsurface temperature profile studies as shown in Figure 1c. The temperature within wells was measured at a depth interval of 1 m. The well depth ranged from 15 m to 150 m with screen length ranging from 1 m to 9 m and well diameter of 2” to 6”. A small diameter of wells will ensure that there is no significant occurrence of free convective flow [87]. Most of the monitoring wells were drilled before the 1980s and included wells lid. Therefore, the water temperature in the wells represents the temperature of groundwater surrounding the wells.
3.4. Groundwater Modelling, GM(WB)
The groundwater flow model has been widely applied as a useful tool for professional hydrogeologists to solve the governing partial differential equations of groundwater flow, salute transport, and heat transport processes for the past three decades [97,98,99,100]. The application of groundwater flow models has been tested in this study. The groundwater model of Visual MODFLOW Classic Interface 4.6.0.168 from Waterloo Hydrogeologic was applied to analyze the recharge. The modular finite-different flow model (MODFLOW) established by the United States Geological Survey (USGS) is one of the components of the software. MODFLOW was developed based on the principle equations of Darcy’s Law and conservation mass equations. The governing partial-differential equation for the groundwater movement with constant density in a confined aquifer is described as Equation (6) [101].
where h is the groundwater head in (L); t is the time (T); Ss is the specific storage of the aquifer material (L−1); W represents volumetric flux per unit volume of sources and/sinks of water as W < 0 for outflow from the groundwater system and W > 0 for inflow into the system (T−1); and Kxx, Kyy, and Kzz are the hydraulic conductivity along x, y, and z coordinate axes (L/T), respectively. Equation (6) is developed into the finite-difference form based on the aquifer domain discretised into rows, columns, and layers [101]. Waterloo Hydrogeologic Solver (WHS) iteratively approximates the solution of the finite-difference equation of groundwater flow through a Bi-Conjugate Gradient Stabilized (Bi-CGSTAB) acceleration routine [102]. In GM(WB) application, there are several limitations to implement the method. Hydrogeological variables are comprehensively considered; however, GM(WB) depends significantly on a complexity of groundwater flow equation representing the groundwater flux in the system. For the MODFLOW code, the groundwater recharge is predefined as an input parameter. The justified rate contributes to the calibrated and validated simulation. On the other hand, MODFLOW-SURFACT improved code of MODFLOW is able to handle the groundwater flow in unsaturated and saturated zones, i.e., the groundwater recharge is spatially and temporally quantified [103,104].
The regional LKRB boundary (Figure 1a) was used as a model area in the simulation. The model area discretization consisted of 155 columns and 144 rows as shown in Figure 2a. The general grid size was 1000 m × 1000 m. The grid was refined into 250 m uniform spacing between nodes around the active pumping wellfields and 10.5 m uniform spacing between nodes in the area around Kg. Chap and Pintu Geng wellfields. The grid spacing was refined into smaller grid size especially near the area of interest. The 3D distribution of aquifer stratigraphic units representing the natural heterogeneous condition of the aquifer system in the numerical simulation is presented in Figure 2b (see Section 2.2).
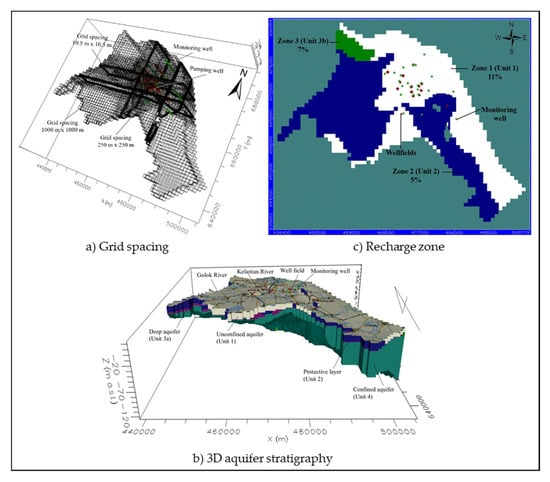
Figure 2.
Model simulation (a) grid spacing; (b) 3D aquifer system; (c) and recharge zone.
In the numerical simulation, two types of boundary conditions (BC) were assigned: Dirichlet-type BC (Constant head BC) and Neumann-type BC (Recharge BC, river BC, and no-flow BC). As in Figure 1a, the South China Sea in the north-eastern boundary of the modelled area was assigned as constant head BC as well as Lemal River connected to Tok’ Uban Lake. River BCs were assigned at the western side of the study area (Golok River) and rivers in the area, e.g., Kelantan River, Pengkalan Chepa River, Pengkalan Datu River, Kemasin River, Mulong River, Ketereh River, Semarak River, Lemal River, and Meranti River. All riverbed materials were suggested to have the hydraulic conductivity (Kr = 10−4 m/s). Tok’ Uban Lake has been assigned as River BC with the different value of riverbed conductivity (Kr = 10−6 m/s) because it is an artificial reservoir where the bed materials are the protective unit (Unit 2). The southern part of the modelled area and both mountains were assigned as no-flow BC.
For the recharge BC, it is recommended that a value between 5 to 20% of the annual rainfall is a reasonable percentage for the groundwater recharge [105]. Recharge BC was assigned accordingly on the available aquifer units that were exposed on the ground surface which were zone 1 of Unit 1, zone 2 of Unit 2, and zone 3 of Unit 3b, respectively, as shown in Figure 2c. The recharge used in this groundwater modelling is estimated from a water balance study [106] by considering 11% of annual rainfall. The mean annual rainfall recorded from 22 rainfall station (1989–2000) was 2708.95 mm/yr. 11% of recharge was assigned for zone 1, while for zone 2 and zone 3 the percentages of recharge were lower than for zone 1, depending on the hydraulic conductivity (see Section 2.2).
The location of monitoring wells and well fields is shown in Figure 2b. In total, forty-nine (49) piezometer head of MGD monitoring wells were with long-term records from 1989 to 2000. The total withdrawal of groundwater from 14 wellfields was approximately 256,777 m3/d. The accumulated pumping rates were used in the model calibration processes.
Model calibration was carried out under steady-state condition resulting in changes or refinement in the conceptual model. Model input parameters were changed to achieve a better representation of the physical system [107] or in other words, to match the field conditions at a site so it was properly characterized. Calibration was run repeatedly following the standard trial-and-error method [108]. After the model was calibrated, it was validated using a new data set to test the calibrated model. Sensitivity analysis was performed on calibrated model to determine the effect of parameter variation on the model results by quantifying the uncertainty in the calibrated model caused by uncertainty in the estimates of aquifer parameters, stresses, and boundary conditions. This is a method to identify the most influenced parameters on the model simulation and helps to achieve better calibration results that give satisfaction to the modeller themself. This analysis will provide a modeller with an understanding of the level of confidence in model results and is used to identify data deficiencies [107]. The performance of calibrated and validated model and sensitivity analysis were considered through the graphical fit between calculated heads and observed heads or statistical comparison of root mean squared (RMS), correlation coefficient (R2), residual mean (RM), and absolute residual mean (ARM) [108].
4. Results
4.1. Chloride Mass Balance, CMB
The only source of chloride deposition is from the rainwater. No data of chloride via dry deposition has been recorded at LKRB. It is believed that with the high amount of rainfall in the basin, dry chloride deposition (aerosol) can be rained out from the cloud or washed out by the falling rain drops [58]. The highest chloride deposition was measured in the month of April with 10.33 mg/L and the lowest was measured in November with 1.77 mg/L. It can be said that chloride deposition is high during the dry season and vice-versa, which indicated that circulation of the south-west monsoon brings along high chloride aerosol to be deposited at LKRB. The weighted average of chloride concentration in rainwater (ClP) was calculated using Equation (2). The weighted mean annual chloride, ClP concentration in rainwater was 1.18 mg/L. This value was used as an input parameter to estimate the groundwater recharge using Equation (1).
Table 1 summarises the soil profiles of depth to water level, chloride concentration, and percentage of particle size. The depth to water level of soil profiles, ranging from 0.65 m to 1.71 m, were recorded in a 2013 sampling campaign while 0.51 m to 1.96 m were recorded in 2015. In 2013, the sand particle ranges were from 48% to 99%, silt from 0.3% to 17%, and clay from 0.12% to 35%, while in 2015, the particle size can be divided into two groups: Group 1 had sand particle between 39% and 99%, silt between 0.10% and 19%, and clay between 0.40% and 42%. For group 2, sand particle were between 7% and 99%, silt between 0.02% and 35%, and clay between 0.2% and 82%, respectively. Group 1 is considered as an unsaturated soil profiles that contains more sandy texture covering the area of the eastern part (S1–S4) and upper (S5) and lower (S10) western parts of the LKRB. Group 2 contains more clayey silt in texture that covers the middle area of the western part (S6–S9) of the basin. This texture will slow the process of infiltrating rainfall into deeper zones in soil profiles [109]. Chloride concentration was between 1.66 mg/L to 17.12 mg/L in 2013, while in 2015 the range was from 0.21 mg/L to 17.60 mg/L. The variation of chloride concentration in soil profiles could be related to the changes of chloride input due to chloride deposition or man-made influenced [60]. The anthropogenic effects were not considered in this study. During rainfall events, chloride ions percolate with infiltrating water into unsaturated zones. The chloride ions in porewater tend to increase with depth through the root zone as a result of evapotranspiration because plants will exclude the chloride during the process and water will return to the atmosphere through bare-soil evaporation that is pure [16]. The concentrated chloride in the root zone later will be flushed downward by infiltrating rainfall which increases the chloride in the deeper profiles [110]. The downward movement and accumulation of chloride ions is influenced by the soil textures where profiles comprised of predominantly clay and silt will have slow process [109,110].

Table 1.
Summary of soil samples depth to water level, chloride concentration and percentage of particle size.
Recharge values were quantified using Equation (1). The percentage of annual recharge varies within the LKRB ranging from 13% to 68% of annual rainfall with a mean of 36% as presented in Table 2. The distribution of recharge can be separated into the centre area of the western part that shows high recharge percentage ranging from 40% to 68% of rainfall while the eastern part, that includes the upper and lower area of western part, shows a low recharge percentage with 13% to 32% of annual rainfall, respectively. The mean recharge estimated in this study is within the range of humid tropical of 15% to 47% of the annual rainfall as studied by [111] at Phuket, Thailand, and Takounjou, Ndam Ngoupayou, Riotte, Takem, Mafany, Maréchal and Ekodeck [30], at Yaounde, Cameroon.

Table 2.
Recharge estimated using chloride mass balance (CMB) at different location.
4.2. Water Level Fluctuation, WTF
The fluctuation of groundwater in monitoring wells corresponds well with the monthly amount of rainfall received in the basin within 1991 to 2008 (Figure 3a). High groundwater levels can be seen through when rainfall is high and vice-versa. In general, the range of each groundwater level at sites was between −5.36 m to 5.53 m with a mean of −2.20 m to 3.18 m. The highest monthly rainfall is usually received in November and December when the north-east monsoon begins and causes flooding in several area within the basin. During the rainfall infiltration through the unsaturated zone, possible entrapment of air within the unsaturated zone can cause the “Lisse” effect at a depth of less than 1.3 m [67,70,112]. However, this effect can be negligible within the basin as most of the groundwater fluctuations are above 1.3 m below the ground surface and the effect is less in the coastal sandy environment.
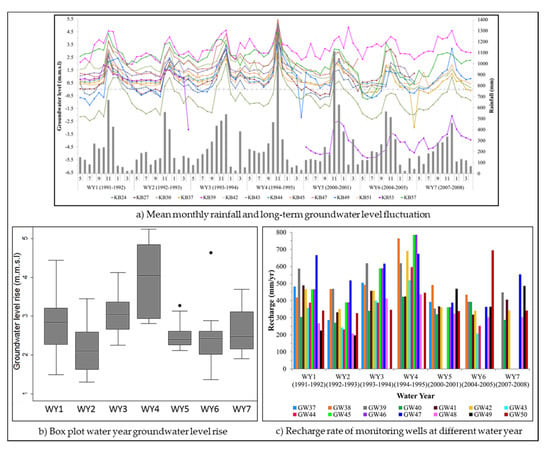
Figure 3.
(a) Mean monthly rainfall and long-term groundwater level fluctuation; (b) box plot water year level rise; and (c) recharge rate of monitoring wells at different water year.
Box plots of groundwater level rise (Δh) for each water cycle (Figure 3b), after having been extrapolated using graphical approach [65] (see Section 3.2), show ranges of groundwater level rise (Δh) for WY1, WY2, WY3, WY4, WY5, WY6, and WY7 of 1.50 m to 4.44 m with a mean of 2.80 ± 0.80 m, 1.31 m to 3.45 m with a mean of 2.18 ± 0.67 m, 2.26 m to 4.12 m with a mean of 3.12 ± 0.63 m, 2.81 m to 5.24 m with a mean of 3.97 ± 0.96 m, 2.12 m to 3.27 m with a mean of 2.52 ± 0.37 m, 1.37 m to 4.63 m with a mean of 2.46 ± 0.84 m, and 1.91 to 3.69 m with a mean of 2.63 ± 0.63 m, respectively. The annual rainfall of WY1, WY2, WY3, WY4, WY5, WY6, and WY7 was 2382 mm, 2297 mm, 2895 mm, 3521 mm, 3509 mm, 2590 mm and 2426 mm, respectively, with mean of a 2803 mm. Specific yield, Sy, value reported at LKRB ranges from 0.06 to 0.3 [41,46,113]. A constant Sy value of 0.15 was used to represent the LKRB to estimate the recharge. Using Equation (3) (see Section 3.2), the estimated recharge ranges were between 225 to 666 mm/yr representing 11% to 28% of annual rainfall, 197 to 518 mm/yr representing 9% to 23% of annual rainfall, 339 to 618 mm/yr representing 12% to 21% of annual rainfall, 422 to 786 mm/yr representing 12% to 22% of annual rainfall, 319 to 490 mm/yr representing 9% to 14% of annual rainfall, 206 to 694 mm/yr representing 8% to 27% of annual rainfall, and 287 to 554 mm/yr representing 12% to 23% of annual rainfall, respectively, for W1 to WY7 as shown in Figure 3c. The average recharge estimated according to monitoring wells ranged from 321 mm/yr to 540 mm/yr with a mean recharge of 425 ± 79 mm/yr representing 11% to 19% with 15% of the long term mean annual rainfall (2790 mm), as tabulated in Table 3.

Table 3.
Summary of estimated groundwater recharge (mm/yr and %).
The finding of a mean recharge of 15% annual rainfall is considered within the ranges reported for part of a humid area of Pampa plain, Argentina, with a range of 4% to 33% of annual rainfall and a mean of 14% and 18% at different Sy of 0.07 and 0.09, respectively [72]. [30] at Younde, Cameroon, which has a recharge that ranges from 1.4% to 12.3% with a mean 5.7% of annual rainfall and with the mean recharge of 20% annual rainfall was estimated for both Holocene and Pleistocene aquifer at Hanoi, Vietnam [73].
4.3. Temperature–Depth Profiles, TDP
The long-term mean annual air temperature recorded from 1968 to 2015 at Kota Bharu station has shown a linear increased trend of 0.76 °C/47 years (R2 of 0.431) as shown in Figure 4a. This long-term record shows a warming trend following the general trend of global warming [114]. The increase of local warming trends is influenced by the urbanization process, especially in the Kota Bharu area where the growth of the urban population has resulted in redevelopment of agricultural land for urban use. There was no significant trend in the annual rainfall (mean annual 2619 mm) with increase of air temperature (Figure 4a). However, any anomalous annual rainfall amount might disturb the subsurface temperature by changing the groundwater recharge/discharge rates [85].
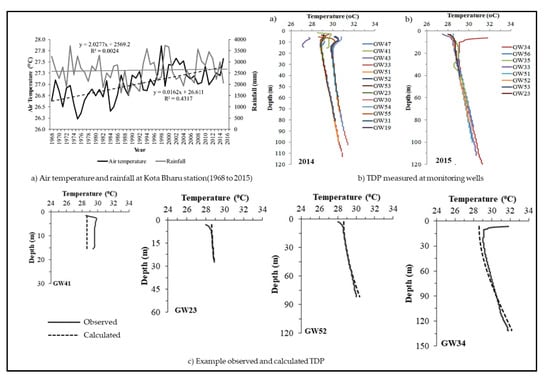
Figure 4.
(a) Mean annual air temperature and rainfall at Kota Bharu station; (b) measured temperature–depth profiles (TDP) during sampling campaign; and (c) examples observed and calculated TDP.
The depth to water level (bgl) was measured at sites in 2014 and 2015 and ranged from 1.60 m to 8.97 m with Layer 1 ranging from 1.60 m to 8.97 m, Layer 2 ranging from 2.86 m to 4.70 m, and Layer 3 ranging from 2.95 m to 5.50 m, respectively. According to the literature, most of the groundwater flux studies from steady state temperature–depth profiles are from deep aquifers with a depth of more than 200 m [31,82,90,115,116]. Therefore, the same concept is applied even though the maximum depth at LKRB is only up to 150 m and wells are not spatially distributed within the basin. The measured TDP is presented in Figure 4b with a range of subsurface temperature from 27.0 °C to 32 °C. An increase in temperature trend as the depth increases can be seen from the Figure 4b. This similar trend can be found in studies related to subsurface temperature [31,117,118]. The changes in the slope of the temperature–depth profile can possibly be attributed to the different thermal of aquifer layer [86].
Figure 4c shows examples of calculated TDP with the observed TDP. The calculated profiles represent the best shape of the observed profiles at shallow and deep aquifer. The misfit in the profiles may result from a difference of thermal properties (thermal conductivity and thermal diffusivity) of the aquifer materials which may affect heat convection within the aquifer [31,86]. Table 4 list the best-calculated U values for monitoring well profiles in 2014 and 2015, which ranges from 100 mm/yr to 300 mm/yr with RMSE value of 0.10 to 1.43. The positive U values indicates all monitoring wells are recharge type with downward groundwater flow system in the basin [119]. The root mean square error (RMSE) of the observed and calculated profiles ranged from 0.10 to 1.43. Considering the long-term mean annual rainfall of 2619 mm, the percentage of rainfall for Layer 1 ranged from 8% to 11% with a mean of 10%, whereas for Layer 2, the percentage ranged from 4% to 8% with a mean of 6%, while for Layer 3 it was from 2% to 7% with a mean of 5%. In general, the average values for percentage of rainfall show a decreasing trend from Layer 1 to Layer 3 from 10% to 6%, respectively. This study has indicated the spatial variation of subsurface temperature at LKRB by the presence of shallow and deep groundwater flow systems.

Table 4.
Groundwater recharge estimated using TDP method.
The effects of surface air temperature were not considered during groundwater recharge interpretation. Groundwater temperatures down to the depth of ~25 m was strongly affected by seasonal variations in surface temperature [120]. The fluctuation of surface temperature creates a temperature wave which propagates down into the subsurface rather than the heat convection caused by groundwater flow [88,121,122]. Reference [115] have shown that shallow subsurface temperature (up to 75 m) is closely related to the surface air temperature during non-seasonal ground freezing and this correlation was confirmed by modelling results using synthetic transient temperature–depth profiles at the northern plain of USA [123]. Reference [90] stated that groundwater fluxes in shallow aquifers are more complex as they are influenced by changes in surface air temperature and aquifers are actively used as resources.
4.4. Groundwater Modelling, GM(WB)
The water balance of the aquifer system studied by [106] considered rainfall, potential evapotranspiration and river discharge of 3.09 × 1010 m3/yr, 1.23 × 1010 m3/yr, and 1.53 × 1010 m3/yr, respectively. The estimated value of change in storage was 3.26 × 109 m3/yr (11%). This 11% value, which is equivalent to recharge into the basin, was used in the model simulation. The model was successfully converged after maximum outer and inner iterations of 100 and 50 with head change and residual criterion of 0.01. A scatter plot of the best fit between the observed heads and calculated heads of the calibration simulation is shown in Figure 5a with RM, RMSE, NRMSE, and R2 of 0.003 m, 1.460 m, 13.54% and 79.2%, respectively. Then, the model was validated with RM, RMSE, NRMSE, and R2 of 0.806 m, 2.097 m, 15.841% and 78.8%, respectively (Figure 5b). The RMSE of the validated simulation was higher (at 0.637 m) than the calibrated simulation, it remains within the 2–3 m acceptable ranges of heads decreased.
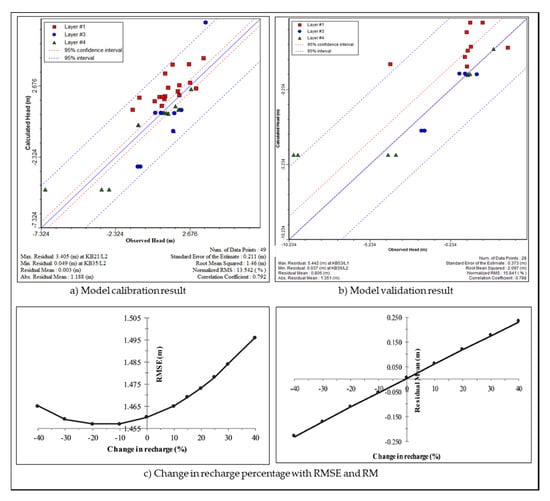
Figure 5.
(a) Model calibration result; (b) model validation result; and (c) change in recharge percentage with RMSE and RM.
To further determine the acceptable water balance recharge value, a sensitivity analysis was performed manually by standardising the 10% increment and decrement of each recharge zone. The results for the sensitivity analysis are presented in Figure 5c. The relationship between RMSE and change in recharge shows a slight decrease from 1.457 m to 1.465 m when the percentage of recharge decreased from 10% to 40%, while RMSE values increased from 1.465 m to 1.496 m when the percentage of recharge increased from 10% to 40%. The relationship between residual mean (RM) and change in recharge shows a linear increasing and decreasing trend of residual mean (RM) as the recharge percentage is increased and decreased within 10% to 40%. This indicates that recharge is a sensitive parameter and the value selection, or its representation, is very crucial in the model calibration processes. Sensitivity analysis is a good measure to quantify the uncertainty of the calibrated model especially when the model was developed with limited data [124]. This is caused by the uncertainty of the aquifer parameters and sometimes by the model boundary conditions (e.g., hydraulic conductivity and recharge).
5. Discussion
Various method of recharge estimation using CMB, WTF, TDP, and GM(WB) have been used at LKRB. Selection of these methods was dependent on the existing and accessible data that were available within the period of study. Explanation on the comparison of methods is based on percentage of annual rainfall because each method that was applied in this study has a different range of annual rainfall. The ranges of recharge estimation are summarised in Table 5.

Table 5.
Summary of recharge estimation using different methods.
CMB method shows a large variation in recharge estimation ranging from 13% to 68% with a mean of 36% of annual rainfall, as tabulated in Table 5. In the CMB method, rainfall amount and chloride concentration measured in rainfall, and unsaturated zone (soils) are used to estimate the recharge. An assumption that the primary source of recharge is rainfall has met CMB’s application criteria at LKRB, with rainfall recorded at over 1000 mm annually. Uncertainty arises when determining the concentration of chloride in rainfall and soils. The available data of rainfall chloride was collected only for a short period of less than three years. The rainfall chloride data should be for a period of at least five years monitoring [125] and should provide the most representative rainfall chloride data for the basin which is not available in the study area. Rainfall chloride of wet deposition is the only source of chloride: the atmospheric chloride of dry deposition was not accounted because no data has been recorded within the basin. Dry deposition can be neglected because heavy rainfall will wash out the dry deposition [58,59]. Even though it can be negligible, determination of dry deposition will be a good practice as the dry deposition has potential to be deposited within 100 km from the coastal area [58,59]. Consideration of both wet and dry chloride can improve the recharge estimates.
Caution during soil sample preparation to extract the chloride and to conduct particles size analysis [126] will reduce the error level. Following the assumption in CMB method, chloride in soils are not from weathering or anthropogenic sources. Soil texture play a significant role in holding chloride concentration [109,110] along the soil profiles. Infiltrated rainfall will flush and take the chloride ions deeper downward. Changes of soil texture from clay silt materials to coarse materials are expected to result in high recharge value [53,54]. The variation in chloride concentration and soil texture in the soil profiles has shown the heterogeneity within the basin. Therefore, to have a good recharge estimation using CMB, rainfall and soil samples must spatially represent the basin and repeated sampling data is a must to reduce the uncertainty of the method.
The recharge estimation using the WTF method ranges from 11% to 19% with a mean of 15% of annual rainfall, as tabulated in Table 5. In the WTF method, components of specific yield, Sy, and groundwater level rise are used to calculate recharge. The availability of long-term groundwater water level data at LKRB gives an advantage in using WTF. The groundwater level data shows a quick response of recharge as the fluctuation of water level corresponds well with the rainfall events (Figure 3a). The Lisse effect [67,70,112] at LKRB can be said to be negligible or minimal within the basin because the depth to water table in shallow aquifer is more than 1.30 m and LKRB itself is coastal sandy aquifer. Currently, LKRB is actively pumping but there is no indication of a sharp difference in water level fluctuation based on the long-term data [127] or that ground settlement has occurred in the basin [128]. The uncertainty may come during the extrapolation of water cycle hydrograph via graphical approach [65] to identify the groundwater level rise. An Sy value of 0.15 was set to be constant throughout the aquifer following a common practice of researchers [65] because the Sy value is difficult to determine even with proper planning [16]. Sy values actually vary with depth and location [129] and this applies to LKRB as well as a heterogeneous aquifer. Assumption of a constant Sy value may lead to either overestimates or underestimates of recharge. The scarcity of monitoring wells that are not spatially distributed within the basin has influenced the Sy value and groundwater level data with incomplete temporal record.
Like the WTF method, the TDP method also give a small range of recharge estimation from 8% to 11% with mean of 10% of annual rainfall as shown in Table 5. TDP results indicate that LKRB is dominated by the downward movement groundwater flux of recharge type for both shallow and deep aquifer systems. Recharge area is recognised to have a low thermal gradient [130]. In the TDP method, recharge estimation was calculated using Equation (5). The uncertainty is induced by input parameters of the equation in the initial condition [86]. To apply this TDP method, some of the parameter values were adopted from the literature [94,95] due to unavailable data related to LKRB, which might give an overestimation or underestimation of recharge. The effect of surface air temperature in wells caused by seasonal changes was not accounted [88,90,120,121], especially in shallow aquifer which can reflect the recharge quantification. Lacking in the number of monitoring wells that represent the basin and aquifer layer has limited the interpretation of temporal and spatial variation of recharge estimation and also an understanding the groundwater flow pattern. The need for repeated measurement of temperature–depth profiles and measurement of the local thermal properties perhaps will also improve the recharge estimation and reduce the uncertainty.
GM(WB) applied 11% of recharge from the water balance (WB) study [106]. The steady state model was constructed using available local data input for the basin. The model was successfully calibrated and validated with correlation coefficients of 79.2% and 78.8%. The calibration processes reduced the uncertainty within the model. The sensitivity analysis result indicates that recharge WB is sensitive during parameter adjustment of 10% increment and decrement in the model. The model is sensitive to recharge because rainfall is the primary input source of the model. Uncertainty in GM(WB) usually arises during the construction of the conceptual model. The model input parameters still need to be improved or updated because a lack in data inputs will produce an unreasonable model. Modeller knowledge is also important as this helps to increase understanding of the model. The advantages of using GM(WB) are that it can be used to predict future recharge that will help in groundwater resources management and that the model can be used to represent a range of scales from point to regionally [131,132].
Table 5 summarised the recharge estimations quantified using four methods. Generally, recharge ranges showed high variability within 6.6% to 68% of annual rainfall. CMB ranged from 16% to 68%, WTF ranged from 11% to 19%, TDP ranged from 8% to 11%, and GM(WB) based on WB value of 11% of annual rainfall, giving a range 6.6% to 12.1% (sensitivity analysis) of annual rainfall, respectively. The average recharge of CMB, WTF, and TDP methods is 20% of annual rainfall with diversion as compared to average values ranging from 12% to 48%. A wide range of recharge is evidenced to different factors subject to inherent principles and assumptions in the methods applied, data quality and quantity, and geological condition. All methods are sensitive to the input parameters; therefore, it is essential to reduce the uncertainty and errors inherent in quantifying recharge estimation from any single method as discussed above.
Based on results of the four methods applied at LKRB, 11% of recharge shows GM(WB) to be the best method to estimate groundwater recharge for this humid tropical basin. The 11% derived from WB quantified the potential recharge considering the basic information of inflow and outflow. By coupling the WB recharge with GM, the value become model-generated recharge, which is actual recharge, as the GM(WB) model has constructed and calibrated using locally derived data input parameters. GM(WB) is the only method that involved a calibration process by comparing the observed and calculated values. Recharge is sensitive to the adjustment of parameters as rainfall is the primary source in steady-state model simulation. WTF gives a reasonable recharge value to be used together with GM(WB) to ensure the reliability of recharge value approximately in the same range. WTF based on long-term hydrological data records and the method itself, quantify potential recharge of change in aquifer storage. The recharge fluctuates accordingly to the fluctuation of water table in shallow aquifer due to seasonal rainfall input at LKRB. Even though TDP gave a mean recharge of 10% close to that from GM(WB), this method is not suitable to be paired together. The recharge quantified by TDP is potential recharge that is dependent on temperature, as temperature fluctuates in response to the heat flows. Since there is no thermal aquifer property information for LKRB, the adopted values from the literatures were used, which were from an area with active volcanic activity which differs from LKRB. Thus, the recharge may not be appropriate to represent the basin. In an area with active volcanism, the thermal properties always represent the current state of heat flow in the aquifer. A value of 36% for mean recharge by CMB does not mean this value is inaccurate because CMB is point estimation; therefore, different areas will have different recharge values, as the basin is not homogenised. CMB based on chloride as a conservative tracer quantifies the potential recharge in an unsaturated zone. The heterogeneity of the aquifer and data points should be considered to provide spatial information of recharge in the basin so that the recharge estimates are more reliable.
6. Conclusions
This study has highlighted the importance of applying various methods in quantification of recharge estimation. The variability of recharge range is evidenced by different factors subject to inherent principles and assumptions in the methods applied, data quality and quantity, and geological conditions within the basin. The reliability and suitability of recharge estimates can be improved by obtaining reliable and spatiotemporal data within LKRB that are applicable to the method used. The comparison of groundwater recharge applications in the study area leads to a recommendation of the WTF method, complementing GW(WB), as the best method to enable quantification of actual recharge at LKRB. Methods can be accepted as long as climate and land use are not changing dramatically in the basin. Spatial distribution of recharge can imply better recharge proxy that is good for future urban planning at LKRB, which was limited in this study as data were lacking in number of representative points of sampling or monitoring wells to represent the aquifer layer and basin area. In addition, there is the need for repeated sampling and frequency of measurement. This study has provided insight into quantification of groundwater recharge and method selection for humid tropical areas of LKRB and is useful as a baseline study for groundwater resources management at LKRB, in particular and for Malaysia as a whole. Lysimeter as a direct and best method to quantify groundwater recharge was unable to be installed during the studies due to difficulty in obtaining approval and permission from the land-owner.
Author Contributions
Conceptualization, I.Y. and N.H.H.; methodology, I.Y. and N.H.H.; software, N.H.H. and M.R.; validation, H.N.H. and M.R.; formal analysis, I.Y., N.H.H., and M.R.; investigation, N.H.H. and I.Y.; resources, I.Y. and H.N.H.; data curation, N.H.H., I.Y., and M.R.; writing—original draft preparation, N.H.H.; writing—review and editing, N.H.H. and I.Y.; visualization, N.H.H. and M.R.; supervision, I.Y. and M.R.; project administration, I.Y. and N.H.H.; and funding acquisition, I.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by University of Malaya, grant number PV112/2012A and PG132-2014A and Malaysian Nuclear Agency in collaboration with International Atomic Energy Agency (IAEA), grant number IAEA/RAC-RAS/7/022.
Acknowledgments
We would like to thank Dr. Wan Zakaria W Muhd Tahir, a retired officer at Nuclear Malaysia Agency, who has helping in providing funding, supervision, and assisted in fieldwork of this research study. We also like to thank Dr. Ratan Kumar Majumder for giving us the TDP spreadsheet. Special thanks to Civil Engineering Department, Mechanical Department, and Geology Department of University of Malaya, Air Kelantan Sdn. Bhd., Department of Mineral and Geoscience Malaysia (Kelantan), Department of Irrigation and Drainage Malaysia, Malaysian Meteorological Department for providing data, helping in fieldwork and laboratory analysis. We also thank to the reviewers for giving us constructive comments to improve this manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- UNESCO. Water for a Sustainable World: Facts and Figures. In The United Nations World Water Development Report 2015; Franek, E.K.A., Connor, R., Hunziker, D., Eds.; United Nations World Water Assessment Programme: Perugia, Italy, 2015. [Google Scholar]
- NGWA. Facts about Global Groundwater Usage. National Groundwater Association, 2016. Available online: http://www.ngwa.org/Fundamentals/Documents/global-groundwater-use-fact-sheet.pdf (accessed on 20 April 2018).
- Famiglietti, J.S. The Global Groundwater Crisis. Nat. Clim. Chang. 2014, 4, 945–948. [Google Scholar] [CrossRef]
- Elias, M.; Turmon, M.; Reager, J.; Hobbs, J.; Liu, Z.; David, C.H. Cascading Dynamics of the Hydrologic Cycle in California Explored through Observations and Model Simulations. Geosciences 2020, 10, 71. [Google Scholar]
- Zhen, L.; Liu, P.W.; Massoud, E.; Farr, T.G.; Lundgren, P.; Famiglietti, J.S. Monitoring Groundwater Change in California’s Central Valley Using Sentinel-1 and Grace Observations. Geosciences 2019, 9, 436. [Google Scholar]
- Massoud, E.C.; Purdy, A.J.; Miro, M.E.; Famiglietti, J.S. Projecting Groundwater Storage Changes in California’s Central Valley. Sci. Rep. 2018, 8, 12917. [Google Scholar] [CrossRef] [PubMed]
- Babel, M.S.; Gupta, A.D.; Domingo, N.D.S. Land Subsidence: A Consequence of Groundwater over-Exploitation in Bangkok, Thailand. Int. Rev. Environ. Strateg. 2006, 6, 307–328. [Google Scholar]
- Delinom, R.M. Groundwater Management Issues in the Greater Jakarta. In Proceedings of the International Workshop on Integrated Watershed Management for Sustainable Water Use in a Humid Tropical Region, JSPS-DGHE Joint Research Project, University of Tsukuba, Tsukuba, Japan, 31 October 2007. [Google Scholar]
- Taylor, R.G.; Burgess, W.G.; Shamsudduha, M.; Zahid, A.; Lapworth, D.J.; Ahmed, K.; Mukherjee, A.; Nowreen, S. Deep Groundwater in the Bengal Mega Delta: New Evidence of Aquifer Hydraulics and the Influence of Intensive Abstraction. In Groundwater Science Programme; British Geological Survey: Nottingham, UK, 2014; Volume 14. [Google Scholar]
- Ha, K.C.; Ngoc, N.T.M.; Lee, E.H.; Jayakumar, R. Current Status and Issues of Groundwater in the Mekong River Basin; Korea Institute of Geoscience and Mineral Resources: Daejeon, Korea, 2016; Volume 121. [Google Scholar]
- Wada, Y.; Bierkens, M.F. Sustainability of Global Water Use: Past Reconstruction and Future Projections. Environ. Res. Lett. 2014, 9, 104003. [Google Scholar] [CrossRef]
- Kim, S.H.; Hejazi, M.; Liu, L.; Calvin, K.; Clarke, L.; Edmonds, J. Balancing Global Water Availability and Use at Basin Scale in an Integrated Assessment Model. Clim. Chang. 2016, 136, 217–231. [Google Scholar] [CrossRef]
- Turner, S.W.D.; Hejazi, M.; Yonkofski, C.; Kim, S.H.; Kyle, P. Influence of Groundwater Extraction Costs and Resource Depletion Limits on Simulated Global Nonrenewable Water Withdrawals over the Twenty-First Century. Earth’s Future 2019, 7, 123–135. [Google Scholar] [CrossRef]
- de Vries, J.J.; Simmers, I. Groundwater Recharge: An Overview of Processes and Challenges. Hydrogeol. J. 2002, 10, 5–17. [Google Scholar] [CrossRef]
- Nimmo, J.R.; Healy, R.W.; Stonestrom, D.A. Aquifer Recharge. In Encyclopedia of Hydrological Science: Part 13. Groundwater; Anderson, M.G., Bear Anderson, J., Eds.; Wiley: Chichester, UK, 2005; pp. 2229–2246. [Google Scholar]
- Healy, R.W. Estimating Groundwater Recharge; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Simmers, I. Groundwater Recharge Principles, Problems and Developments. In Recharge of Phreatic Aquifers in (Semi-)Arid Areas; Simmers, I., Ed.; A.A. Balkema: Rotterdam, The Netherlands, 1997; pp. 1–18. [Google Scholar]
- Scanlon, B.R.; Healy, R.W.; Cook, P.G. Choosing Appropriate Techniques for Quantifying Groundwater Recharge. Hydrogeol. J. 2002, 10, 18–39. [Google Scholar] [CrossRef]
- Dripps, W.R.; Bradbury, K.R. A Simple Daily Soil–Water Balance Model for Estimating the Spatial and Temporal Distribution of Groundwater Recharge in Temperate Humid Areas. Hydrogeol. J. 2007, 15, 433–444. [Google Scholar] [CrossRef]
- Barron, O.V.; Crosbie, R.S.; Dawes, W.R.; Charles, S.P.; Pickett, T.; Donn, M.J. Climatic Controls on Diffuse Groundwater Recharge across Australia. Hydrol. Earth Syst. Sci. 2012, 16, 4557–4570. [Google Scholar] [CrossRef]
- Moeck, C.; Grech-Cumbo, N.; Podgorski, J.; Bretzler, A.; Gurdak, J.J.; Berg, M.; Schirmer, M. A Global-Scale Dataset of Direct Natural Groundwater Recharge Rates: A Review of Variables, Processes and Relationships. Sci. Total Environ. 2020, 717, 137042. [Google Scholar] [CrossRef] [PubMed]
- Jayakumar, R.; Lee, E. Climate Change and Groundwater Conditions in the Mekong Region–a Review. J. Groundw. Sci. Eng. 2017, 5, 14–30. [Google Scholar]
- Hepburn, E.; Cendón, D.I.; Bekele, D.; Currell1, M. Environmental Isotopes as Indicators of Groundwater Recharge, Residence Times and Salinity in a Coastal Urban Redevelopment Precinct in Australia. Hydrogeol. J. 2019, 28, 503–520. [Google Scholar] [CrossRef]
- Minnig, M.; Moeck, C.; Radny, D.; Schirmer, M. Impact of Urbanization on Groundwater Recharge Rates in Dübendorf, Switzerland. J. Hydrol. 2018, 563, 1135–1146. [Google Scholar] [CrossRef]
- Dillon, P.; Stuyfzand, P.; Grischek, T.; Lluria, M.; Pyne, R.D.G.; Jain, R.C.; Bear, J.; Schwarz, J.; Wang, W.; Fernandez, E.; et al. Sixty Years of Global Progress in Managed Aquifer Recharge. Hydrogeol. J. 2019, 27, 1–30. [Google Scholar] [CrossRef]
- Sallwey, J.; Valverde, J.P.B.; López, F.V.; Junghanns, R.; Stefan, C. Suitability Maps for Managed Aquifer Recharge: A Review of Multi-Criteria Decision Analysis Studies. Environ. Rev. 2019, 27, 138–150. [Google Scholar] [CrossRef]
- Lerner, D.N.; Issar, A.; Simmers, I. Groundwater Recharge; a Guide to Understanding and Estimating Natural Recharge; International Contributions to Hydrogeology; Heise: Hannover, Germany, 1990; Volume 8. [Google Scholar]
- Hendrickx, J.M.H.; Walker, G.R. Recharge from Precipitation. In Recharge of Phreatic Aquifers in (Semi-) Arid Areas; Simmers, I., Ed.; A.A. Belkema: Rotterdam, The Netherlands; Brookfield, VT, USA, 1997. [Google Scholar]
- Delin, G.N.; Risser, D.W. Ground-Water Recharge in Humid Areas of the United States—A Summary of Ground-Water Resources Program Studies, 2003–2006; U.S. Department of the Interior, U.S. Geological Survey, Eds.; U.S. Geological Survey: Reston, VA, USA, 2007.
- Takounjou, A.F.; Ngoupayou, J.R.N.; Riotte, J.; Takem, G.E.; Mafany, G.; Maréchal, J.C.; Ekodeck, G.E. Estimation of Groundwater Recharge of Shallow Aquifer on Humid Environment in Yaounde, Cameroon Using Hybrid Water-Fluctuation and Hydrochemistry Methods. Environ. Earth Sci. 2011, 64, 107–118. [Google Scholar] [CrossRef]
- Majumder, R.K.; Shimada, J.; Taniguchi, M. Groundwater Flow Systems in the Bengal Delta, Bangladesh, Inferred from Subsurface Temperature Readings. Songklanakarin J. Sci. Technol. 2013, 35, 99–106. [Google Scholar]
- Vishal, V.; Kumar, S.; Singhal, D.C. Estimation of Groundwater Recharge in National Capital Territory, Delhi Using Groundwater Modeling. J. Indian Water Resour. Soc. 2014, 34, 15–23. [Google Scholar]
- Flint, A.L.; Flint, L.E.; Kwicklis, E.M.; Fabryka-Martin, J.T.; Bodvarsson, G.S. Estimating Recharge at Yucca Mountain, Nevada, USA: Comparison of Methods. Hydrogeol. J. 2002, 10, 180–204. [Google Scholar] [CrossRef]
- Verma, P.; Singh, P.; Srivastava, S.K. Development of Spatial Decision-Making for Groundwater Recharge Suitability Assessment by Considering Geoinformatics and Field Data. Arabian J. Geosci. 2020, 13, 306. [Google Scholar] [CrossRef]
- Senthilkumar, M.; Gnanasundar, D.; Arumugam, R. Identifying Groundwater Recharge Zones Using Remote Sensing & Gis Techniques in Amaravathi Aquifer System, Tamil Nadu, South India. Sustain. Environ. Res. 2019, 29, 15. [Google Scholar]
- Walker, D.; Parkin, G.; Schmitter, P.; Gowing, J.; Tilahun, S.A.; Haile, A.T.; Yimam, A.Y. Insights from a Multi-Method Recharge Estimation Comparison Study. Groundwater 2018, 57, 245–258. [Google Scholar] [CrossRef]
- DID. National Water Resources Study 2000–2050 (Malaysian Peninsula). Groundwater Studies; Department of Irrigation and Drainage Malaysia: Kuala Lumpur, Malaysia, 2000. [Google Scholar]
- Wan Ismail, W.M.Z. Groundwater for Public Water Supply. In Proceedings of the National Groundwater Conference 2019, Concarde Hotel, Shah Alam, Selangor, Malaysia, 2–3 July 2019. [Google Scholar]
- Md Hashim, M.A. Geologi Dan Geomorfologi Kawasan Kuala Besar Hingga Kuala Pengkalan Besar Dengan Penekanan Permatang-Permatang Holosen Dan Perubahan Pantai. Ph.D. Thesis, University of Malaya, Kuala Lumpur, Malaysia, 2002. [Google Scholar]
- Soh, Z.A. The Geomorphology of Kelantan Delta, Malaysia. Ph.D. Thesis, University of Malaya, Kuala Lumpur, Malaysia, 1972. [Google Scholar]
- Noor, I.M. Prefeasibility Study of Potential Groundwater Development in Kelantan, Malaysia. Ph.D. Thesis, University of Birmingham, Birmingham, UK, 1980. [Google Scholar]
- Suratman, S. Groundwater Protection in North Kelantan, Malaysia: An Integrated Mapping Approach Using Modeling and Gis. Ph.D. Thesis, University of Upon Tyne, Newcastle Upon Tyne, UK, 1997. [Google Scholar]
- Udie Lmasudin, M.I. Kajian Taburan Enapan Resen Dan Perubahan Pesisir Pantai, Kota Bharu—Kuala Telong, Kelantan Darul Naim. Ph.D. Thesis, University of Malaya, Kuala Lumpur, Malaysia, 2000. [Google Scholar]
- Tjia, H.D. Quaternary. In Geology of Peninsular Malaysia; Hutchison, C.S., Tan, D.N.K., Eds.; University of Malaya and Geological Society of Malaysia: Kuala Lumpur, Malaysia, 1973. [Google Scholar]
- MGD. Hydrogeological Map; Minerals and Geoscience Deaprtment, Malaysia (Ministry of Natural Resources and Environment): Kuala Lumpur, Malaysia, 2008. [Google Scholar]
- Sofner, B. Groundwater Monitoring and Groundwater Protection at the Geological Survey Department (Gsd) of Malaysia; Geological Survey Department of Malaysia: Kuala Lumpur, Malaysia, 1992. [Google Scholar]
- MGD. Geological Map of Peninsular Malaysia, 9th ed.; Minerals and Geoscience Malaysia: Kuala Lumpur, Malaysia, 2014. [Google Scholar]
- Bazuhair, A.S.; Wood, W.W. Chloride Mass-Balance Method for Estimating Ground Water Recharge in Arid Areas: Examples from Western Saudi Arabia. J. Hydrol. 1996, 186, 153–159. [Google Scholar] [CrossRef]
- Wood, W.W.; Sanford, W.E. Chemical and Isotopic Methods for Quantifying Groundwater Recharge in a Regional, Semiarid Environment. Ground Water 1995, 33, 458–468. [Google Scholar] [CrossRef]
- Subyani, A.M. Use of Chloride-Mass Balance and Environmental Isotopes for Evaluation of Groundwater Recharge in the Alluvial Aquifer, Wadi Tharad, Western Saudi Arabia. Environ. Geol. 2004, 46, 741–749. [Google Scholar] [CrossRef]
- Dassi, L. Use of Chloride Mass Balance and Tritium Data for Estimation of Groundwater Recharge and Renewal Rate in an Unconfined Aquifer from North Africa: A Case Study from Tunisia. Environ. Earth Sci. 2010, 60, 861–871. [Google Scholar] [CrossRef]
- Eriksson, E.; Khunakasem, V. Chloride Concentration in Groundwater, Recharge Rate and Rate of Deposition of Chloride in Israel Coastal Plain. J. Hydrol. 1969, 7, 178–197. [Google Scholar] [CrossRef]
- Ifediegwu, I.S. Groundwater Recharge Estimation Using Chloride Mass Balance: A Case Study of Nsukka Local Government Area of Enugu State, Southeastern, Nigeria. Model. Earth Syst. Environ. 2020, 6, 799–810. [Google Scholar] [CrossRef]
- Ting, C.S.; Kerh, T.; Liao, C.J. Estimation of Groundwater Recharge Using the Chloride Mass-Balance Method, Pingtung Plain, Taiwan. Hydrogeol. J. 1998, 6, 282–292. [Google Scholar] [CrossRef]
- Carrier, M.A.; Lefebvre, R.; Asare, E.B. Groundwater Recharge Assessment in Northern Ghana Using Soil Moisture Balance and Chloride Mass Balance. In Proceedings of the 61st Canadian Geotechnical Conference and 9th Joint CGS/IAH-CNC Groundwater Conference, Edmonton, AB, Canada, 21–24 September 2008. [Google Scholar]
- Scanlon, B.R.; Stonestrom, D.A.; Reedy, R.C.; Leaney, F.W.; Gates, J.; Cresswell, R.G. Inventories and Mobilization of Unsaturated Zone Sulfate, Fluoride, and Chloride Related to Land Use Change in Semiarid Regions, Southwestern United States and Australia. Water Resour. Res. 2009, 45, W00A18. [Google Scholar] [CrossRef]
- Bresciani, E.; Ordens, C.M.; Werner, A.D.; Batelaan, O.; Guan, H.; Post, V.E.A. Spatial Variability of Chloride Deposition in a Vegetated Coastal Area: Implications for Groundwater Recharge Estimation. J. Hydrol. 2014, 519, 1177–1191. [Google Scholar] [CrossRef]
- Guan, H.D.; Love, A.J.; Simmons, C.T.; Makhnin, O.; Kayaalp, A.S. Factors Influencing Chloride Deposition in a Coastal Hilly Area and Application to Chloride Deposition Mapping. Hydrol. Earth Syst. Sci. 2010, 14, 801–813. [Google Scholar] [CrossRef]
- Gobinddass, M.L.; Molinie, J.; Richard, S.; Panechou, K.; Jeannot, A.; Jean-Louis, S. Coastal Sea Salt Chlorine Deposition Linked to Intertropical Convergence Zone (Itcz) Oscillation in French Guiana. J. Atmos. Sci. 2020, 77, 1723–1731. [Google Scholar] [CrossRef]
- Gaye, C.B.; Edmunds, W.M. Groundwater Recharge Estimation Using Chloride, Stable Isotopes and Tritium Profiles in the Sands of Northwestern Senegal. Environ. Geol. 1996, 27, 246–251. [Google Scholar] [CrossRef]
- Mensah, F.O.; Alo, C.; Yidana, S.M. Evaluation of Groundwater Recharge Estimates in a Partially Metamorphosed Sedimentary Basin in a Tropical Environment: Application of Natural Tracers. Sci. World J. 2014, 2014, 419508. [Google Scholar]
- Wood, W. Interactive Comment on “Theory of the Generalized Chloride Mass Balance Method for Recharge Estimation in Groundwater Basins Characterised by Point and Diffuse Recharge” by N. Somaratne and K. R. J. Smettem. Hydrol. Earth Syst. Sci. Discuss. 2014, 11, C19–C21. [Google Scholar]
- Scanlon, B. Evaluation of Moisture Flux from Chloride Data in Desert Soils. J. Hydrol. 1991, 128, 137–156. [Google Scholar] [CrossRef]
- Meinzer, O.E. The Occurence of Groundwater in the United States with a Discussion of Principles. (Water Supply Paper 489); United States Government Printing Office: Washington, DC, USA, 1923. [Google Scholar]
- Delin, G.N.; Healy, R.W.; Lorenz, D.L.; Nimmo, J.R. Comparison of Local- to Regional-Scale Estimates of Ground-Water Recharge in Minnesota, USA. J. Hydrol. 2007, 334, 231–249. [Google Scholar] [CrossRef]
- Hall, B.; Currell, M.; Webb, J. Using Multiple Lines of Evidence to Map Groundwater Recharge in a Rapidly Urbanising Catchment: Implications for Future Land and Water Management. J. Hydrol. 2020, 580, 124265. [Google Scholar] [CrossRef]
- Crosbie, R.S.; Binning, P.; Kalma, J.D. A Time Series Approach to Inferring Groundwater Recharge Using the Water Table Fluctuation Method. Water Resour. Res. 2005, 41, 1–21. [Google Scholar] [CrossRef]
- Obuobie, E.; Diekkrueger, B.; Agyekum, W.; Agodzo, S. Groundwater Level Monitoring and Recharge Estimation in the White Volta River Basin of Ghana. J. Afr. Earth Sci. 2012, 71–72, 80–86. [Google Scholar] [CrossRef]
- Moon, S.K.; Woo, N.C.; Lee, K.S. Statistical Analysis of Hydrographs and Water-Table Fluctuation to Estimate Groundwater Recharge. J. Hydrol. 2004, 292, 198–209. [Google Scholar] [CrossRef]
- Healy, R.W.; Cook, P.G. Using Groundwater Levels to Estimate Recharge. Hydrogeol. J. 2002, 10, 91–109. [Google Scholar] [CrossRef]
- Labrecque, G.; Chesnaux, R.; Boucher, M. Water-Table Fluctuation Method for Assessing Aquifer Recharge: Application to Canadian Aquifers and Comparison with Other Methods. Hydrogeol. J. 2020, 28, 521–533. [Google Scholar] [CrossRef]
- Varni, M.R. Application of Several Methodologies to Estimate Groundwater Recharge in the Pampeano Aquifer, Argentina. Tecnol. Y Cienc. Del Agua 2013, 4, 67–85. [Google Scholar]
- Hung Vu, V.; Merkel, B.J. Estimating Groundwater Recharge for Hanoi, Vietnam. Sci. Total Environ. 2019, 651, 1047–1057. [Google Scholar] [CrossRef]
- Yang, L.; Qi, Y.; Zheng, C.; Andrews, C.B.; Yue, S.; Lin, S.; Li, Y.; Wang, C.; Xu, Y.; Li, H.A. A Modified Water-Table Fluctuation Method to Characterize Regional Groundwater Discharge. Water 2018, 10, 503. [Google Scholar] [CrossRef]
- Suzuki, K. Percolation Measurements Based on Heat Flow through Soil with Special Reference to Paddy Fields. J. Geophys. Res. 1960, 65, 2883–2885. [Google Scholar] [CrossRef]
- Bredehoeft, J.D.; Papadopulos, I.S. Rates of Vertical Groundwater Movement Estimated from Earth’s Thermal Profile. Water Resour. Res. 1965, 1, 325–328. [Google Scholar] [CrossRef]
- Stallman, R.W. Steady One Dimensional Fluid Flow in the Semi-Infinate Porous Medium with Sinusoidal Surface Temperature. J. Geophys. Res. 1965, 70, 2821–2827. [Google Scholar] [CrossRef]
- Carslaw, H.S.; Jaeger, J.C. Conduction of Heat in Solids, 2nd ed.; Oxford University Press: Oxford, UK, 1959. [Google Scholar]
- Constantz, J. Interaction between Streambed Temperature, Streamflow, and Groundwater Exchanges in Alpine Streams. Water Resour. Res. 1998, 34, 1609–1615. [Google Scholar] [CrossRef]
- Hatch, C.E.; Fischer, A.T.; Revenaugh, J.S.; Constantz, J.; Ruehl, C. Quantifying Surface Water/Groundwater Interaction Using Time Series Analysis of Streambed Thermal Records: Method Development. Water Resour. Res. 2006, 42, W10410. [Google Scholar] [CrossRef]
- Glose, T.J.; Lowry, C.S.; Hausner, M.B. Limits on Groundwater-Surface Water Fluxes Derived from Temperature Time Series: Defining Resolution-Based Thresholds. Water Resour. Res. 2019, 55, 1–12. [Google Scholar] [CrossRef]
- Taniguchi, M. Estimations of the Past Groundwater Recharge Rate from Deep Borehole Temperature Data. Catena 2002, 48, 39–51. [Google Scholar] [CrossRef]
- Taniguchi, M.; Shimada, J.; Tanaka, T.; Kayane, I.; Sakura, Y.; Shimano, Y.; Dapaah-Siakwan, S.; Kawashima, S. Disturbances of Temperature-Depth Profilesdue to Surface Climate Change and Subsurface Water Flow: (1) an Effect of Linear Increase in Surface Temperature Caused by Global Worming and Urbanization in the Tokyo Metropolitan Area, Japan. Water Resour. Res. 1999, 35, 1507–1517. [Google Scholar] [CrossRef]
- Taniguchi, M.; Williamson, D.R.; Peck, A.J. Disturbances of Temperature–Depth Profiles Due to Surface Climate-Change and Subsurface Water Flow: (2) an Effect of Step Increase in Surface Temperature Caused by Forest Clearing in Southwest of Western Australia. Water Resour. Res. 1999, 35, 1519–1529. [Google Scholar] [CrossRef]
- Dong, L.; Fu, C.; Liu, J.; Wang, Y. Disturbances of Temperature-Depth Profiles by Surface Warming and Groundwater Flow Convection in Kumamoto Plain, Japan. Geofluids 2018, 2018, 8451276. [Google Scholar] [CrossRef]
- Irvine, D.J.; Kurylyk, B.L.; Cartwright, I.; Bonham, M.; Post, V.E.A.; Banks, E.W.; Simmons, C.T. Groundwater Flow Estimation Using Temperature-Depth Profiles in a Complex Environment and a Changing Climate. Sci. Total Environ. 2017, 574, 272–281. [Google Scholar] [CrossRef] [PubMed]
- Dapaah-Siakwan, S.; Kayane, I. Estimation of Vertical Water and Heat Fluxes in the Semi-Confined Aquifers in Tokyo Metropolitan Area, Japan. Hydrol. Process. 1995, 9, 143–160. [Google Scholar] [CrossRef]
- Taniguchi, M.; Shimada, J.; Uemura, T. Transient Effects of Surface Temperature Anf Groundwater Flow on Subsurface Temperature in Kumamoto Plain, Japan. Phys. Chem. Earth 2003, 28, 477–486. [Google Scholar] [CrossRef]
- Li, S.; Dong, L.; Chen, J.; Li, R.; Yang, Z.; Liang, Z. Vertical Groundwater Flux Estimation from Borehole Temperature Profiles by a Numerical Model, Rflux. Hydrol. Process. 2019, 33, 1542–1552. [Google Scholar] [CrossRef]
- Taniguchi, M. Evaluation of Vertical Groundwater Fluxes and Thermal Properties of Aquifer Based on Transient Temperature-Depth Profiles. Water Resour. Res. 1993, 29, 2021–2026. [Google Scholar] [CrossRef]
- Ingebritsen, S.E.; Sanford, W.E.; Neuzil, C.E. Groundwater in Geological Processes, 2nd ed.; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Kurylyk, B.L.; Irvine, D.J.; Carey, S.K.; Briggs, M.A.; Werkema, D.D.; Bonham, M. Heat as a Groundwater Tracer in Shallow and Deep Heterogeneous Media: Analytical Solution, Spreadsheet Tool, and Field Applications. Hydrol. Process. 2017, 31, 2648–2661. [Google Scholar] [CrossRef]
- Suzuki, A.; Ikhwanda, F.; Yamaguchi, A.; Hashida, T. Estimations of Fracture Surface Area Using Tracer and Temperature Data in Geothermal Fields. Geosciences 2019, 9, 425. [Google Scholar] [CrossRef]
- Madon, M. Regional Tectonics and Sedimentary Basins of Malaysia: Basin Types, Tectono-Stratigraphy Provinces, Structural Styles. In The Petroleum Geology and Resorces of Malaysia; PETRONAS, Ed.; PETRONAS: Kuala Lumpur, Malaysia, 1999; pp. 79–111. [Google Scholar]
- Taniguchi, M.; Shimano, Y.; Kayane, I. Groundwater Flow Analysis Using the Temperature in the Upland Areas at the Western Foot of Aso Volcanoes. Journal of Japan Assoc. Hydrol. Sci. 1989, 19, 171–179. [Google Scholar]
- Kurylyk, B.L.; Irvine, D.J.; Bense, V.F. Theory, Tools, and Multidisciplinary Applications for Tracing Groundwater Fluxes from Temperature Profiles. WIREs Water 2019, 6, 1329. [Google Scholar] [CrossRef]
- Sudhakar, S.; Verma, M.K.; Soumya, S. Application of Gis and Modflow to Ground Water Hydrology—A Review. Int. J. Eng. Res. Appl. 2016, 6, 36–42. [Google Scholar]
- Hariharan, V.; Shankar, M.U. A Review of Visual Modflow Applications in Groundwater Modelling. In IOP Conf. Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2017; p. 032025. [Google Scholar]
- Pathak, R.; Awasthi, M.K.; Sharma, S.K.; Hardaha, M.K.; Nema, R.K. Ground Water Flow Modelling Using Modflow—A Review. Int. J. Curr. Microbiol. Appl. Sci. 2018, 7, 83–88. [Google Scholar] [CrossRef]
- Panda, P.; Narasimham, M.L. A Review on Modelling and Simulation of Ground Water Resources in Urban Regions. Infokara Res. 2020, 9, 235–244. [Google Scholar]
- Harbaugh, A.W. Modflow-2005: The U.S. Geological Survey Modular Ground-Water Model—The Ground-Water Flow Process. In Techniques and Methods 6–A16; US Geological Survey: Reston, VA, USA, 2005. [Google Scholar]
- Waterloo Hydrogeologic. Visual Modflow Help. Waterloo Hydrogeologic. Available online: https://www.waterloohydrogeologic.com/help/vmod/ (accessed on 27 June 2020).
- Thompson, C.E. Hydrologic Functioning of Glacial Moraine Landscapes within Alberta’s Boreal Plains. Ph.D. Thesis, University of Alberta, Edmonton, AB, Canada, 2019. [Google Scholar]
- Hydrogeologic Inc. (HGL). Modhms/Modflow-Surfact: A Comprehensive Modflow-Based Hydrologic Modeling System; HydroGeoLogic, Inc.: Reston, VA, USA, 2015. [Google Scholar]
- Waterloo Hydrogeologic. Visual Modflow V. 4.1 User’s Manual; Waterloo Hydrogeologic: Waterloo, ON, Canada, 2005. [Google Scholar]
- Hussin, N.H. Hydrogeochemical Study and Iron Removal of Groundwater in North Kelantan. Ph.D. Thesis, University of Malaya, Kuala Lumpur, Malaysia, 2011. [Google Scholar]
- ASTM. Standard Guide for Application of a Groundwater Flow Model to a Site-Specific Problem. In Astm Standards Related to Environment Site Characterization, 3rd ed.; Arendt, S.A., Bailey, S.J., Baldini, N.C., Eds.; ASTM: Baltimore, MD, USA, 2006. [Google Scholar]
- Anderson, M.P.; Woessner, W.W. Applied Groundwater Modelling: Simulation of Flow and Advective Transport; Academic Press: San Diego, CA, USA, 1992. [Google Scholar]
- Liu, G.Q.; Wang, Y.S.; Zhang, Y.F.; Song, T. Application of Chloride Profile and Water Balance Methods in Estimating Groundwater Recharge in Luanjing Irrigation Area, Inner Mongolia. Hydrol. Sci. J. 2009, 54, 961–973. [Google Scholar] [CrossRef]
- Huang, T.M.; Pang, Z.H. Estimating Groundwater Recharge Following Land-Use Change Using Chloride Mass Balance of Soil Profiles: A Case Study at Guyuan and Xifeng in the Loess Plateau of China. Hydrogeol. J. 2011, 19, 177–186. [Google Scholar] [CrossRef]
- Tesfaldet, Y.T.; Puttiwongrak, A.; Arpornthip, T. Spatial and Temporal Variation of Groundwater Recharge in Shallow Aquifer in the Thepkasattri of Phuket, Thailand. J. Groundw. Sci. Eng. 2019, 8, 10–19. [Google Scholar]
- Weeks, E.P. The Lisse Effect Revisited. Groundwater 2002, 40, 652–656. [Google Scholar] [CrossRef]
- Awadalla, S.; Noor, I.B.M.; Ibrahim, I. Comparative Model Study for Groundwater Resources Evaluation in Kelantan Malaysia; Part 1: Model Evaluation. In Proceedings of the International Workshop on Appropriate Methodologies for Development and Management of Groundwater Resources in Developing Countries, Hyderabad, India, 28 February–4 March 1989. [Google Scholar]
- Hansen, J.; Ruedy, R.; Sato, M.; Lo, K. Global Surface Temperature Change. Rev. Geophys. 2010, 48, 1–29. [Google Scholar] [CrossRef]
- Gosnold, W.D.; Todhunter, P.E.; Schmidt, W. The Borehoe Temperature Record of Climate Warming in the Mid-Continent of North America. Glob. Planet. Chang. 1997, 15, 33–45. [Google Scholar] [CrossRef]
- Gunawardhana, L.N.; Kazama, S. Statistical and Numerical Analyses of the Influence of Climate Variability on Aquifer Water Levels and Groundwater Temperatures: The Impacts of Climate Change on Aquifer Thermal Regimes. Glob. Planet. Chang. 2012, 86–87, 66–78. [Google Scholar] [CrossRef]
- Taniguchi, M.; Turner, J.V.; Smith, A.J. Evaluation of Groundwater Discharge Rates from Subsurface Temperature in Cockburn Sound, Western Australia. Biogeochemistry 2003, 66, 111–124. [Google Scholar] [CrossRef]
- Salem, Z.E.-S. Subsurface Thermal Regime to Delineate the Paleo-Groundwater Flow System in an Arid Area, Al Kufra, Libya. J. Astron. Geophys. 2016, 5, 451–462. [Google Scholar] [CrossRef]
- Domenico, A.P.; Palciauskus, V.V. Theoretical Analysis of Forced Convective Heat Transfer in Regional Groundwater Flow. Geol. Soc. Am. Bull. 1973, 84, 3803–3814. [Google Scholar] [CrossRef]
- Hiscock, K.M.; Bense, V.F. Hydrogeology: Principles and Practice, 2nd ed.; John Wiley & Sons, Ltd.: West Sussex, UK, 2014. [Google Scholar]
- Colombani, N.; Giambastiani, B.M.S.; Mastrocicco, M. Use of Shallow Groundwater Temperature Proflies to Infer Climate and Land Use Change: Interpretation and Measurement Challenges. Hydrol. Process. 2016, 30, 10805. [Google Scholar] [CrossRef]
- Bense, V.F.; Kooi, H. Temporal and Spatial Variations of Shallow Subsurface Temperature as a Record of Lateral Variations in Groundwater Flow. J. Geophys. Res. 2004, 9, B04103. [Google Scholar] [CrossRef]
- Harris, R.N.; Gosnold, W.D. Comparisons of Borehole Temperature-Depth Profiles and Surface Air Temperatures in the Northern Plain of the USA. Geophys. J. Int. 1999, 138, 541–548. [Google Scholar] [CrossRef]
- Lenhart, T.; Eckhardt, K.; Fohrer, N.; Frede, H.-G. Comparison of Two Different Approaches of Sensitivity Analysis. Phys. Chem. Earth Part B-Hydrol. Oceans Atmos. 2002, 27, 645–654. [Google Scholar] [CrossRef]
- Sukhija, B.S.; Reddy, D.V.; Nagabhushanam, P.; Hussain, S. Recharge Processes: Piston Flow Vs Preferential Flow in Semi-Arid Aquifers of India. Hydrogeol. J. 2003, 11, 387–395. [Google Scholar] [CrossRef]
- Deng, L.; Wang, W.; Hu, A. Estimation of Groundwater Recharge by Chloride Mass Balance (Cmb) Method in a Typical Semiarid Climate of China. In Proceedings of the International Symposium on Water Resource and Environmental Protection, Xi’an, China, 20–22 May 2011. [Google Scholar]
- MGD. Groundwater Modelling for Lower Kelantan River Basin. In 10th Malaysian Plan of National Groundwater Resources Study; Minerals and Geoscience Department of Malaysia: Kelantan, Malaysia, 2014. [Google Scholar]
- Che Sulaiman, M.Y. Pemantauan Pemendapan Tanah Di Kawasan Lembangan Sungai Kelantan. In Rancangan Malaysia Ke Sembilan Kajian Sumber Air Tanah Negara. Kementerian Sumber Asli dan Alam Sekitar; Jabatan Mineral dan Geosains Malaysia: Kota Bharu, Kelantan, Malaysia, 2010. [Google Scholar]
- Song, J.; Chen, X. Variation of Specific Yield with Depth in an Alluvial Aquifer of the Platte River Valley, USA. Int. J. Sediment Res. 2010, 25, 185–193. [Google Scholar] [CrossRef]
- Uchida, Y.; Hayashi, T. Effects of Hydrogeological and Climate Change on the Subsurface Thermal Regime in the Sendai Plain. Phys. Earth Planet. Inter. 2005, 152, 292–304. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, W. A Review of Regional Groundwater Flow Modeling. Geosci. Front. 2011, 2, 205–214. [Google Scholar] [CrossRef]
- Scanlon, B.R.; Keese, K.E.; Flint, A.L.; Flint, L.E.; Gaye, C.B.; Edmunds, W.M.; Simmers, I. Global Synthesis of Groundwater Recharge in Semiarid and Arid Regions. Hydrol. Process. 2006, 20, 3335–3370. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).