Integrating Point Process Models, Evolutionary Ecology and Traditional Knowledge Improves Landscape Archaeology—A Case from Southwest Madagascar
Abstract
1. Introduction
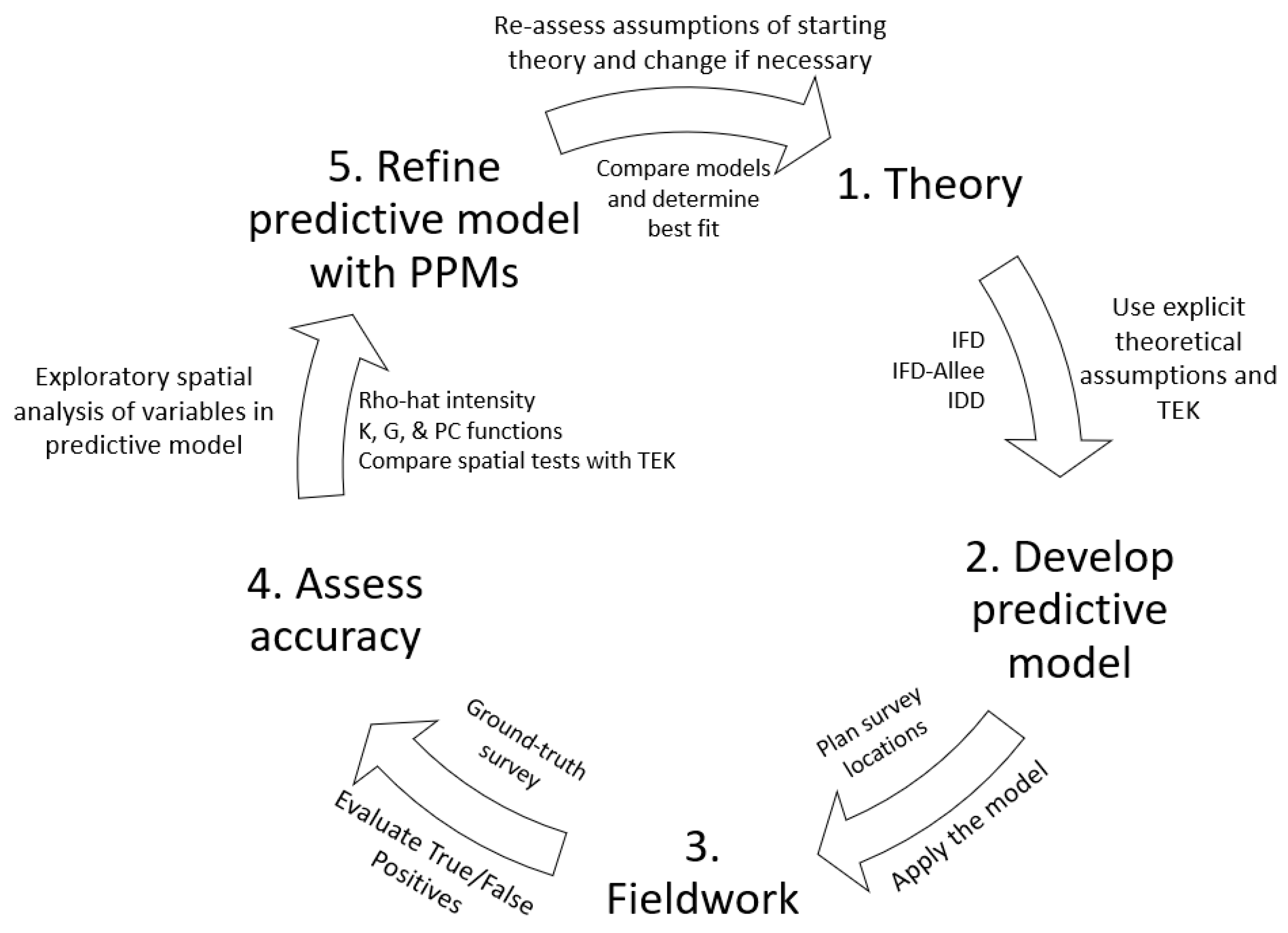
2. Materials and Methods
2.1. Point Process Modeling for First-Order Properties
2.2. GIS Analysis
2.3. Point Process Modeling for Second-Order Properties
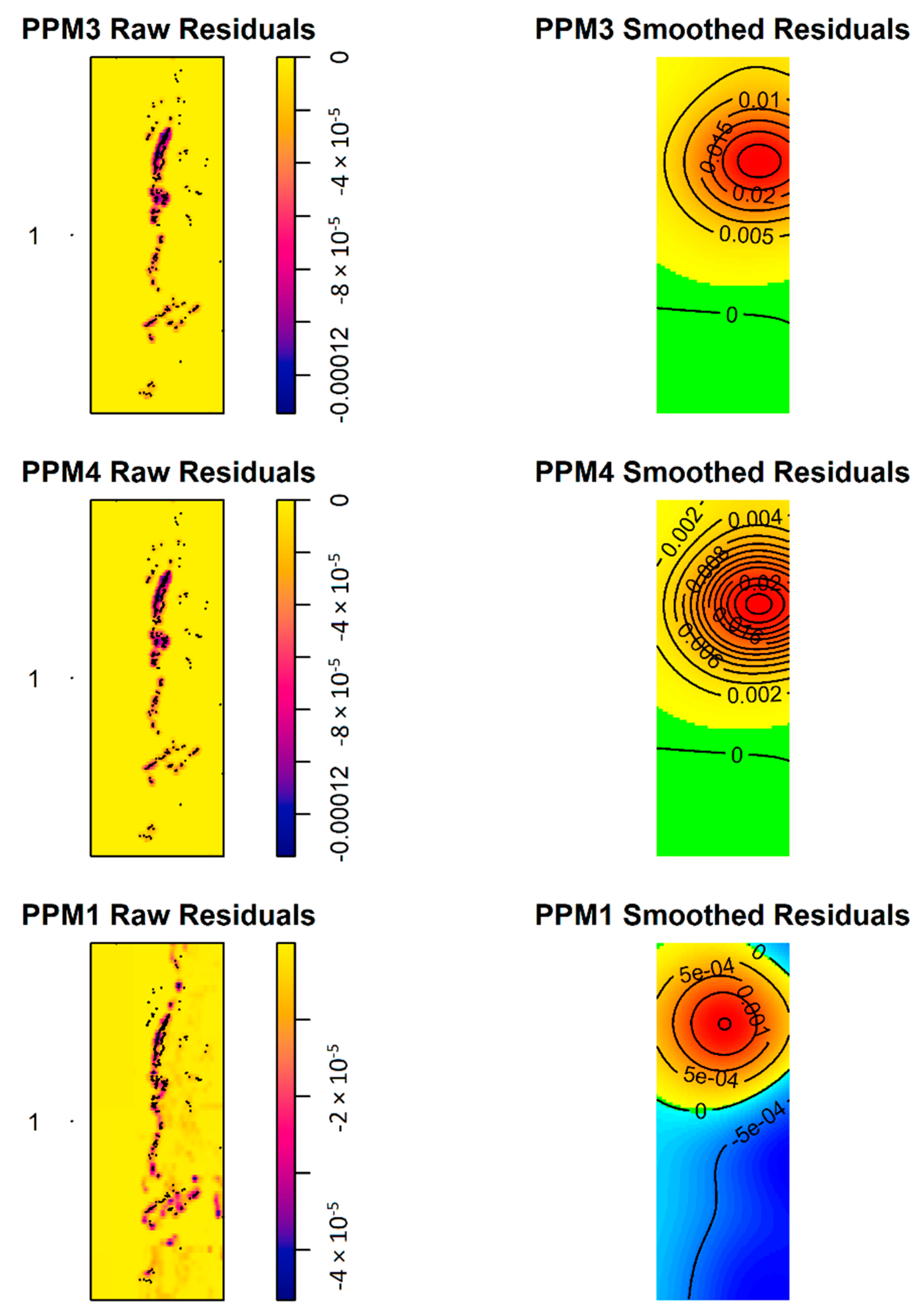
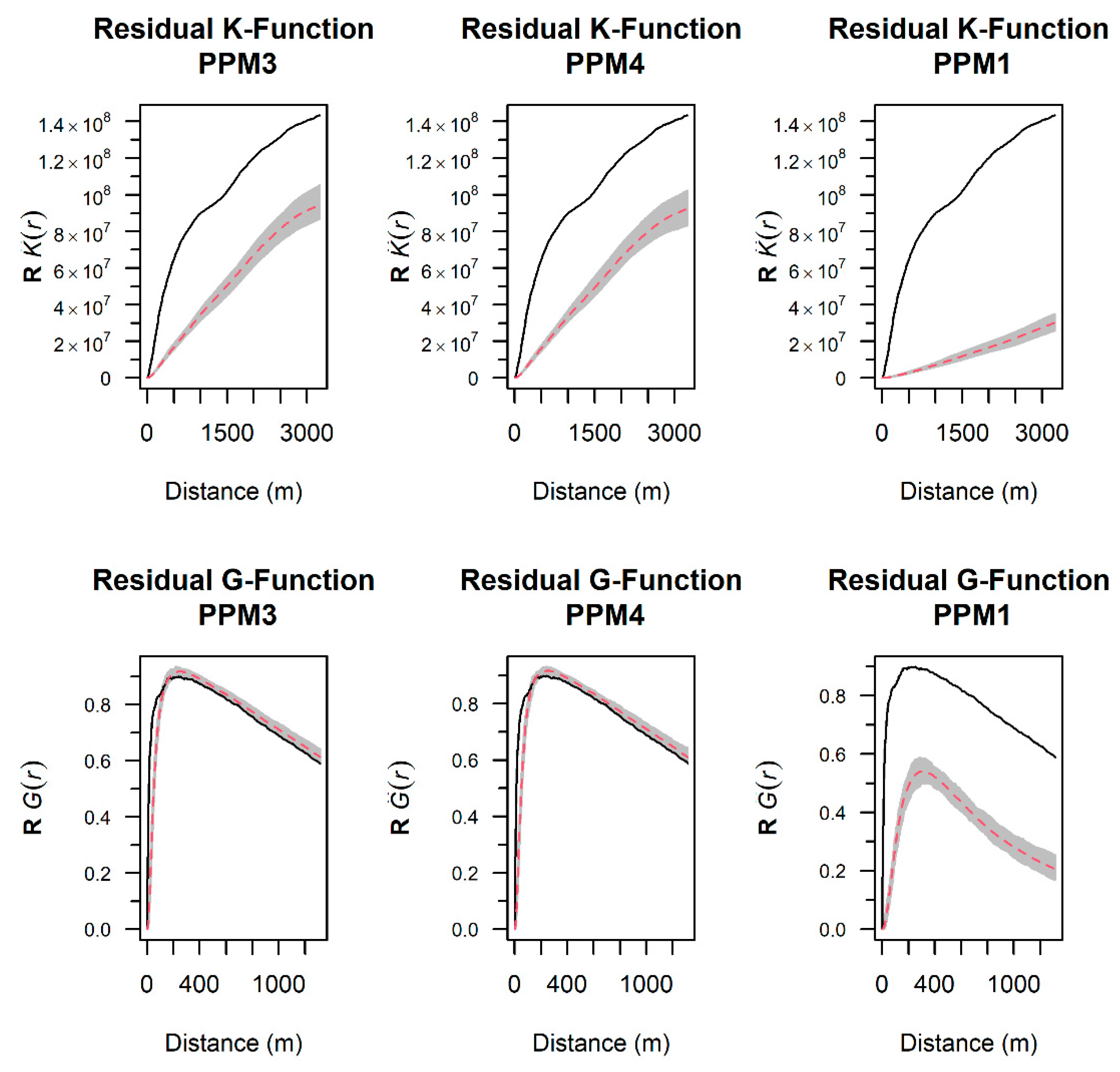
3. Results
3.1. Point Process Modeling of First-Order Properties
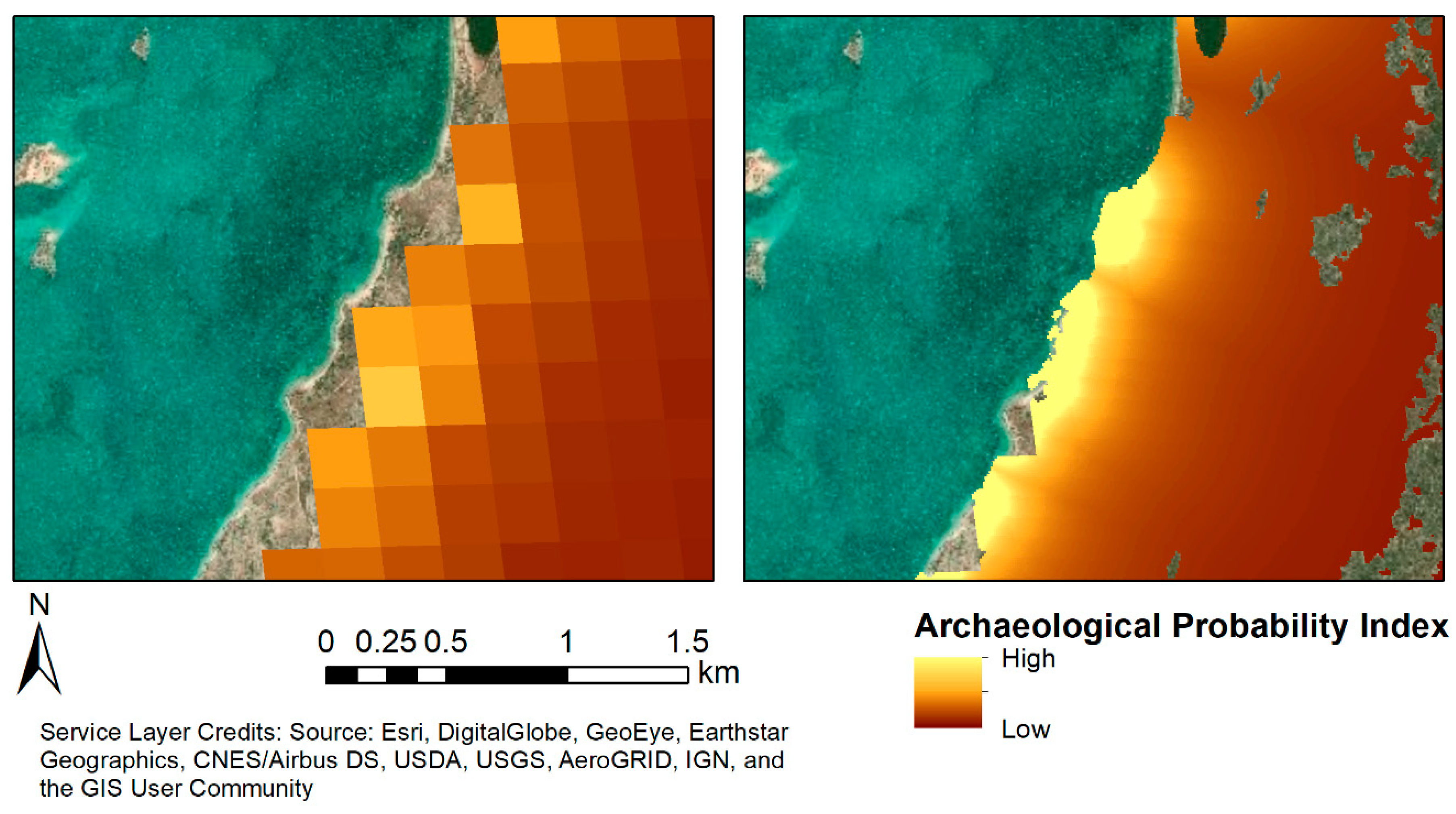
3.2. GIS Analysis
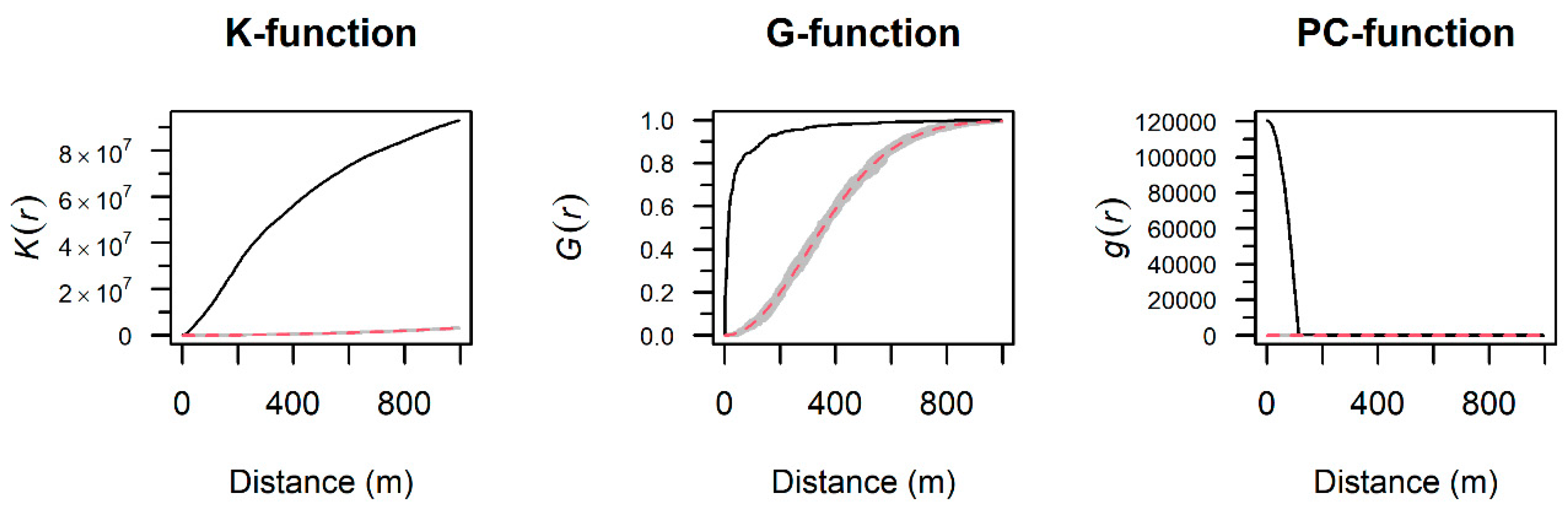
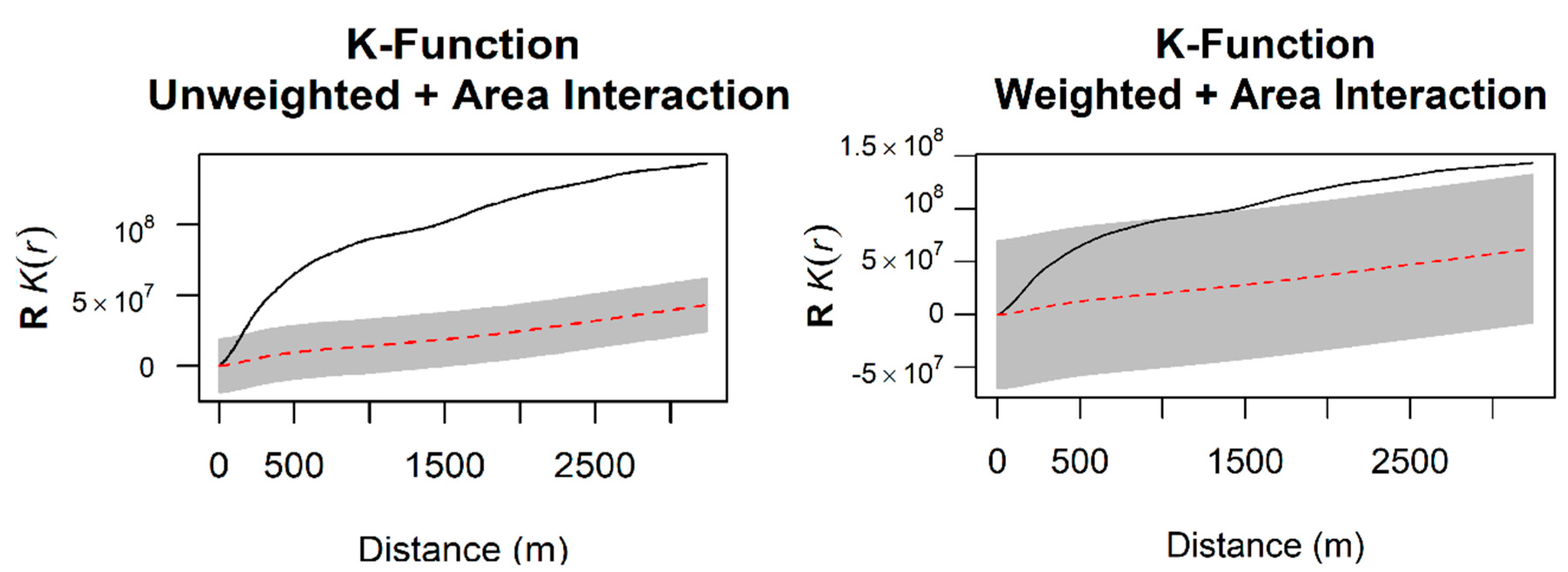
3.3. Point Process Modeling of Second-Order Properties
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bettinger, R.L. Explanatory/predictive models of hunter–gatherer adaptation. In Advances in Archaeological Method and Theory; Elsevier: Amsterdam, Netherlands, 1980; pp. 189–255. [Google Scholar]
- Custer, J.F.; Eveleigh, T.; Klemas, V.; Wells, I. Application of Landsat Data and Synoptic Remote Sensing to Predictive Models for Prehistoric Archaeological Sites: An Example from the Delaware Coastal Plain. Am. Antiq. 1986, 51, 572–588. [Google Scholar] [CrossRef]
- Quantifying the Present and Predicting the Past: Theory, Method, and Application of Archaeological Predictive Modeling; U.S. Department of the Interior, Judge, W.J., Sebastian, L., Eds.; Bureau of Land Management: Denver, CO, USA, 1988.
- Jochim, M.A. Hunter-Gatherer Subsistence and Settlement: A Predictive Model; Academic Press: New York, NY, USA, 1976. [Google Scholar]
- Plog, F.; Hill, J.N. Explaining variability in the distribution of sites. Distrib. Prehist. Popul. Aggreg. 1971, 1, 7. [Google Scholar]
- Verhagen, P.; Whitley, T.G. Integrating Archaeological Theory and Predictive Modeling: A Live Report from the Scene. J. Archaeol. Method Theory 2012, 19, 49–100. [Google Scholar] [CrossRef]
- Kirk, S.D.; Thompson, A.E.; Lippitt, C.D. Predictive Modeling for Site Detection Using Remotely Sensed Phenological Data. Adv. Archaeol. Pract. 2016, 4, 87–101. [Google Scholar] [CrossRef]
- Klehm, C.; Barnes, A.; Follett, F.; Simon, K.; Kiahtipes, C.; Mothulatshipi, S. Toward archaeological predictive modeling in the Bosutswe region of Botswana: Utilizing multispectral satellite imagery to conceptualize ancient landscapes. J. Anthr. Archaeol. 2019, 54, 68–83. [Google Scholar] [CrossRef]
- Alexakis, D.; Sarris, A.; Astaras, T.; Albanakis, K. Integrated GIS, remote sensing and geomorphologic approaches for the reconstruction of the landscape habitation of Thessaly during the neolithic period. J. Archaeol. Sci. 2011, 38, 89–100. [Google Scholar] [CrossRef]
- Parker, S. Predictive modeling of site settlement systems using multivariate logistics. In For Concordance in Archaeological Analysis: Bridging Data Structure, Quantitative Technique and Theory; Waveland Press: New York, NY, USA, 1985; pp. 173–207. [Google Scholar]
- Warren, R.E. Predictive modelling in archaeology: A primer. In Interpreting Space: GIS and Archaeology; Allen, K.M., Green, S.W., Zubrow, E.B.W., Eds.; Taylor and Francis: London, UK, 1990; pp. 90–111. [Google Scholar]
- van Leusen, M.; Deeben, J.; Hallewas, D.; Zoetbrood, P.; Kamermans, H.; Verhagen, P. A baseline for predictive modelling in the Netherlands. In Predictive modelling for archaeological heritage management: A research agenda; van Leusen, M., Kamermans, H., Eds.; Rijksdienst v/h Oudheidkundig: Amsterdam, The Netherlands, 2005; pp. 25–93. [Google Scholar]
- Howey, M.C.L.; Palace, M.W.; McMichael, C.H. Geospatial modeling approach to monument construction using Michigan from A.D. 1000–1600 as a case study. Proc. Natl. Acad. Sci. USA 2016, 113, 7443–7448. [Google Scholar] [CrossRef]
- Davis, D.S.; Douglass, K. Aerial and Spaceborne Remote Sensing in African Archaeology: A Review of Current Research and Potential Future Avenues. Afr. Archaeol. Rev. 2020, 37, 9–24. [Google Scholar] [CrossRef]
- Baddeley, A.; Rubak, E.; Turner, R. Spatial Point Patterns: Methodology and Applications with R; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- O’Sullivan, D.; Perry, G.L. Spatial Simulation: Exploring Pattern and Process; Wiley-Blackwell: Oxford, UK, 2013. [Google Scholar]
- DiNapoli, R.J.; Lipo, C.P.; Brosnan, T.; Hunt, T.L.; Hixon, S.; Morrison, A.E.; Becker, M. Rapa Nui (Easter Island) monument (ahu) locations explained by freshwater sources. PLoS ONE 2019, 14, e0210409. [Google Scholar] [CrossRef]
- Bevan, A.; Crema, E.; Palmisano, A. Intensities, interactions and uncertainties: Some new approaches to archaeological distributions. In Computational Approaches to Archaeological Spaces; Bevan, A., Lake, M., Eds.; Left Coast Press: Walnut Creek, CA, USA, 2013; pp. 27–52. [Google Scholar]
- Carrero-Pazos, M.; Bevan, A.; Lake, M.W. The spatial structure of Galician megalithic landscapes (NW iberia): A case study from the Monte Penide region. J. Archaeol. Sci. 2019, 108, 104968. [Google Scholar] [CrossRef]
- Davis, D.S.; DiNapoli, R.J.; Sanger, M.C.; Lipo, C.P. The integration of lidar and legacy datasets provides improved explanations for the spatial patterning of shell rings in the American Southeast. Adv. Archaeol. Pract. 2020, in press. [Google Scholar] [CrossRef]
- Brandolini, F.; Carrer, F. Terra, Silva et Paludes Assessing the Role of Alluvial Geomorphology for Late-Holocene Settlement Strategies (Po Plain – N Italy) Through Point Pattern Analysis. Environ. Archaeol. 2020, 1–15. [Google Scholar] [CrossRef]
- Eve, S.J.; Crema, E.R. A house with a view? Multi-model inference, visibility fields and point process analysis of a Bronze Age settlement on Leskernick Hill (Cornwall, UK). J. Archaeol. Sci. 2014, 43, 267–277. [Google Scholar] [CrossRef]
- Bevan, A.; Conolly, J. Terraced fields and Mediterranean landscape structure: An analytical case study from Antikythera, Greece. Ecol. Model. 2011, 222, 1303–1314. [Google Scholar] [CrossRef]
- Bevan, A.; Jobbová, E.; Helmke, C.; Awe, J.J. Directional layouts in central lowland Maya settlement. J. Archaeol. Sci. 2013, 40, 2373–2383. [Google Scholar] [CrossRef][Green Version]
- Bevan, A.; Lake, M. Intensities, interactions and uncertainties: Some new approaches to archaeological distributions. In Computational Approaches to Archaeological Spaces; Routledge: Abingdon, UK, 2016; pp. 27–52. [Google Scholar]
- Bevan, A.; Wilson, A. Models of settlement hierarchy based on partial evidence. J. Archaeol. Sci. 2013, 40, 2415–2427. [Google Scholar] [CrossRef]
- Carrero-Pazos, M. Density, intensity and clustering patterns in the spatial distribution of Galician megaliths (NW Iberian Peninsula). Archaeol. Anthr. Sci. 2019, 11, 2097–2108. [Google Scholar] [CrossRef]
- Carrero-Pazos, M.; Bustelo-Abuín, J.; Barbeito-Pose, V.; Rodríguez-Rellán, C. Locational preferences and spatial arrangement in the barrow landscape of Serra do Barbanza (North-western Iberia). J. Archaeol. Sci. Rep. 2020, 31, 102351. [Google Scholar] [CrossRef]
- Spencer, C.; Bevan, A. Settlement location models, archaeological survey data and social change in Bronze Age Crete. J. Anthr. Archaeol. 2018, 52, 71–86. [Google Scholar] [CrossRef]
- Vernon, K.B.; Yaworsky, P.M.; Spangler, J.; Brewer, S.; Codding, B.F. Decomposing Habitat Suitability Across the Forager to Farmer Transition. Environ. Archaeol. 2020, 1–14, in press. [Google Scholar] [CrossRef]
- Knitter, D.; Nakoinz, O. Point Pattern Analysis as Tool for Digital Geoarchaeology: A Case Study of Megalithic Graves in Schleswig-Holstein, Germany. In Digital Geoarchaeology: New Techniques for Interdisciplinary Human-Environmental Research; Siart, C., Forbriger, M., Bubenzer, O., Eds.; Natural Science in Archaeology; Springer International Publishing: Cham, Switzerland, 2018; pp. 45–64. ISBN 978-3-319-25316-9. [Google Scholar]
- Hamer, W.B.; Knitter, D.; Grimm, S.B.; Serbe, B.; Eriksen, B.V.; Nakoinz, O.; Duttmann, R. Location Modeling of Final Palaeolithic Sites in Northern Germany. Geosciences 2019, 9, 430. [Google Scholar] [CrossRef]
- Beaujard, P. East Africa, the Comoros Islands and Madagascar before the sixteenth century: On a neglected part of the world system. Azania Archaeol. Res. Afr. 2007, 42, 15–35. [Google Scholar] [CrossRef]
- Beaujard, P. The first migrants to Madagascar and their introduction of plants: Linguistic and ethnological evidence. Azania Archaeol. Res. Afr. 2011, 46, 169–189. [Google Scholar] [CrossRef]
- Boivin, N.; Crowther, A.; Helm, R.; Fuller, D.Q. East Africa and Madagascar in the Indian Ocean world. J. World Prehistory 2013, 26, 213–281. [Google Scholar] [CrossRef]
- Radimilahy, C.M.; Crossland, Z. Situating Madagascar: Indian Ocean dynamics and archaeological histories. Azania Archaeol. Res. Afr. 2015, 50, 495–518. [Google Scholar] [CrossRef]
- Mitchell, P. Settling Madagascar: When Did People First Colonize the World’s Largest Island? J. Isl. Coast. Archaeol. 2019, 1–20. [Google Scholar] [CrossRef]
- Hansford, J.; Wright, P.C.; Rasoamiaramanana, A.; Pérez, V.R.; Godfrey, L.R.; Errickson, D.; Thompson, T.; Turvey, S.T. Early Holocene human presence in Madagascar evidenced by exploitation of avian megafauna. Sci. Adv. 2018, 4, eaat6925. [Google Scholar] [CrossRef]
- Anderson, A.; Clark, G.; Haberle, S.; Higham, T.; Nowak-Kemp, M.; Prendergast, A.; Radimilahy, C.; Rakotozafy, L.M.; Virah-Sawmy, M.; Schwenninger, J.-L.; et al. New evidence of megafaunal bone damage indicates late colonization of Madagascar. PLoS ONE 2018, 13, e0204368. [Google Scholar] [CrossRef]
- Douglass, K.; Hixon, S.; Wright, H.T.; Godfrey, L.R.; Crowley, B.E.; Manjakahery, B.; Rasolondrainy, T.; Crossland, Z.; Radimilahy, C. A critical review of radiocarbon dates clarifies the human settlement of Madagascar. Quat. Sci. Rev. 2019, 221, 105878. [Google Scholar] [CrossRef]
- Astuti, R. The People of the Sea: Identity and Decent among the Vezo of Madagascar; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Iida, T. The past and present of the coral reef fishing economy in Madagascar: Implications for self-determination in resource use. Senri Ethnol. Stud. 2005, 67, 237–258. [Google Scholar]
- Koechlin, B. Es Vezo du Sud-Ouest de Madagascar: Contribution à l’étude de l’éco-système de Semi-Nomades Marins; Mouton & Co: Paris, France, 1975. [Google Scholar]
- Yount, J.W.; Tucker, B.T. Constructing Mikea Identity: Past or Present Links to Forest and Foraging. Ethnohistory 2001, 48, 257–291. [Google Scholar] [CrossRef]
- Tucker, B.; Tsimitamby, M.; Humber, F.; Benbow, S.; Iida, T. Foraging for Development: A Comparison of Food Insecurity, Production and Risk among Farmers, Forest Foragers and Marine Foragers in Southwestern Madagascar. Hum. Organ. 2010, 69, 375–386. [Google Scholar] [CrossRef]
- Dewar, R.E.; Radimilahy, C.; Wright, H.T.; Jacobs, Z.; Kelly, G.O.; Berna, F. Stone tools and foraging in northern Madagascar challenge Holocene extinction models. Proc. Natl. Acad. Sci. USA 2013, 110, 12583–12588. [Google Scholar] [CrossRef] [PubMed]
- Parker Pearson, M.; Godden, K.; Ramilisonina, R.; Schwenninger, J.; Heurtebize, G.; Radimilahy, C.; Smith, H. Pastoralists, Warriors and Colonists: The Archaeology of Southern Madagascar; BAR International Series; Archaeopress: Oxford, UK, 2010. [Google Scholar]
- Douglass, K. An Archaeological Investigation of Settlement and Resource Exploitation Patterns in the Velondriake Marine Protected Area, Southwest Madagascar, Ca. 900 BC to AD 1900. Ph.D. Thesis, Yale University, New Haven, CT, USA, 2016. [Google Scholar]
- Davis, D.S.; Andriankaja, V.; Carnat, T.L.; Chrisostome, Z.M.; Colombe, C.; Fenomanana, F.; Hubertine, L.; Justome, R.; Lahiniriko, F.; Léonce, H.; et al. Satellite-based remote sensing rapidly reveals extensive record of Holocene coastal settlement on Madagascar. J. Archaeol. Sci. 2020, 115, 105097. [Google Scholar] [CrossRef]
- Charnov, E.L. Optimal Foraging, the Marginal Value Theorem. Theor. Popul. Biol. 1976, 9, 129–136. [Google Scholar] [CrossRef]
- Fretwell, S.D.; Lucas, H.L. On territorial behavior and other factors influencing habitat distribution in birds: I. Theoretical development. Acta Biotheor. 1969, 19, 16–36. [Google Scholar] [CrossRef]
- MacArthur, R.H.; Pianka, E.R. On Optimal Use of a Patchy Environment. Am. Nat. 1966, 100, 603–609. [Google Scholar] [CrossRef]
- Douglass, K.; Quintana Morales, E.M.; Rasolondrainy, T.; Manahira, G.; Manjakahery, B.; Rosily; Ediedy, A.; Mampibay, F.; Rabekoto, H.; Rasoafiavy, P.; et al. The Vezo Ecological Knowledge Exchange. J. Ethnobiol. in preparation.
- Lane, P.J. Archaeology in the age of the Anthropocene: A critical assessment of its scope and societal contributions. J. Field Archaeol. 2015, 40, 485–498. [Google Scholar] [CrossRef]
- Huntington, H.; Callaghan, T.; Fox, S.; Krupnik, I. Matching Traditional and Scientific Observations to Detect Environmental Change: A Discussion on Arctic Terrestrial Ecosystems. AMBIO 2004, 33, 18–23. [Google Scholar] [CrossRef]
- Cooper, J.; Sheets, P. Surviving Sudden Environmental Change: Answers from Archaeology; University Press of Colorado: Boulder, CT, USA, 2012. [Google Scholar]
- Lefale, P.F. Ua ‘afa le Aso Stormy weather today: Traditional ecological knowledge of weather and climate. The Samoa experience. Clim. Chang. 2010, 100, 317–335. [Google Scholar] [CrossRef]
- Cooper, J.; Duncan, L. Applied Archaeology in the Americas: Evaluating Archaeological Solutions to the Impacts of Global Environmental Change. In The Oxford Handbook of Historical Ecology and Applied Archaeology; Isendahl, C., Stump, D., Eds.; Oxford University Press: Oxford, UK, 2019; pp. 440–458. ISBN 978-0-19-967269-1. [Google Scholar]
- Winterhalder, B.; Kennett, D.J.; Grote, M.N.; Bartruff, J. Ideal free settlement of California’s Northern Channel Islands. J. Anthr. Archaeol. 2010, 29, 469–490. [Google Scholar] [CrossRef]
- Bliege Bird, R.; McGuire, C.; Bird, D.W.; Price, M.H.; Zeanah, D.; Nimmo, D.G. Fire mosaics and habitat choice in nomadic foragers. Proc. Natl. Acad. Sci. USA 2020, 117, 201921709. [Google Scholar] [CrossRef] [PubMed]
- Jazwa, C.S.; Kennett, D.J.; Winterhalder, B.; Joslin, T.L. Territoriality and the rise of despotic social organization on western Santa Rosa Island, California. Quat. Int. 2017, 518, 41–56. [Google Scholar] [CrossRef]
- Summers, K. The evolutionary ecology of despotism. Evol. Hum. Behav. 2005, 26, 106–135. [Google Scholar] [CrossRef]
- Bell, A.V.; Winterhalder, B. The Population Ecology of Despotism. Hum. Nat. 2014, 25, 121–135. [Google Scholar] [CrossRef][Green Version]
- Huete, A.R. A soil-adjusted vegetation index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- Tucker, B. Où vivre sans boire revisited: Water and political-economic change among Mikea hunter-gatherers of southwestern Madagascar. Econ. Anthr. 2020, 7, 22–37. [Google Scholar] [CrossRef]
- Langley, J.M. Vezo Knowledge: Traditional Ecological Knowledge in Andavadoaka, southwest Madagascar; Blue Ventures: London, UK, 2006; p. 73. [Google Scholar]
- Douglass, K.; Walz, J.; Quintana-Morales, E.; Marcus, R.; Myers, G.; Pollini, J. Historical perspectives on contemporary human-environment dynamics in southeast Africa. Conserv. Biol. 2019, 33, 260–274. [Google Scholar] [CrossRef]
- Fishman, R.M.; Siegfried, T.; Raj, P.; Modi, V.; Lall, U. Over-extraction from shallow bedrock versus deep alluvial aquifers: Reliability versus sustainability considerations for India’s groundwater irrigation. Water Resour. Res. 2011, 47, 6. [Google Scholar] [CrossRef]
- Gabrielli, C.P.; McDonnell, J.J.; Jarvis, W.T. The role of bedrock groundwater in rainfall–runoff response at hillslope and catchment scales. J. Hydrol. 2012, 450, 117–133. [Google Scholar] [CrossRef]
- Hengl, T.; Heuvelink, G.B.; Kempen, B.; Leenaars, J.G.; Walsh, M.G.; Shepherd, K.D.; Sila, A.; MacMillan, R.A.; de Jesus, J.M.; Tamene, L. Mapping soil properties of Africa at 250 m resolution: Random forests significantly improve current predictions. PLoS ONE 2015, 10, e0125814. [Google Scholar] [CrossRef] [PubMed]
- Appels, W.M.; Graham, C.B.; Freer, J.E.; McDonnell, J.J. Factors affecting the spatial pattern of bedrock groundwater recharge at the hillslope scale. Hydrol. Process. 2015, 29, 4594–4610. [Google Scholar] [CrossRef]
- Hopp, L.; McDonnell, J.J. Connectivity at the hillslope scale: Identifying interactions between storm size, bedrock permeability, slope angle and soil depth. J. Hydrol. 2009, 376, 378–391. [Google Scholar] [CrossRef]
- Brosnan, T.; Becker, M.W.; Lipo, C.P. Coastal groundwater discharge and the ancient inhabitants of Rapa Nui (Easter Island), Chile. Hydrogeol. J. 2018, 27, 519–534. [Google Scholar] [CrossRef]
- Brenan, P. The Geology of Madagascar. In Biogeography and Ecology in Madagascar; Battistini, R., Richard-Vindard, G., Eds.; Springer Netherlands: Dordrecht, The Netherlands, 1972; Volume 21, pp. 27–86. ISBN 978-94-015-7161-6. [Google Scholar]
- Douglass, K. The Diversity of Late Holocene Shellfish Exploitation in Velondriake, Southwest Madagascar. J. Isl. Coast. Archaeol. 2017, 12, 333–359. [Google Scholar] [CrossRef]
- Douglass, K.; Morales, E.Q.; Manahira, G.; Fenomanana, F.; Samba, R.; Lahiniriko, F.; Chrisostome, Z.M.; Vavisoa, V.; Soafiavy, P.; Justome, R.; et al. Toward a just and inclusive environmental archaeology of southwest Madagascar. J. Soc. Archaeol. 2019, 19, 307–332. [Google Scholar] [CrossRef]
- Ripley, B.D. Modelling spatial patterns. J. R. Stat. Soc. Ser. B Methodol. 1977, 39, 172–192. [Google Scholar] [CrossRef]
- Stoyan, D.; Stoyan, H. Fractals, Random Shapes and Point Fields: Methods of Geometrical Statistics; John Wiley & Sons Inc.: Hoboken, NJ, USA, 1994; Volume 302. [Google Scholar]
- Akaike, H. A New Look at the Statistical Model Identification. In Selected Papers of Hirotugu Akaike; Parzen, E., Tanabe, K., Kitagawa, G., Eds.; Springer: New York, NY, USA, 1974; pp. 215–222. ISBN 978-1-4612-7248-9. [Google Scholar]
- Burnham, K.P.; Anderson, D.R. Model Selection and Multimodel inference: A Practical Information-Theoretic Approach, 2nd ed.; Springer: New York, NY, USA, 2002. [Google Scholar]
- Schwarz, G. Estimating the Dimension of a Model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Venables, W.N.; Ripley, B.D. Modern Applied Statistics with S, 4th ed.; Springer: New York, NY, USA, 2002; ISBN 0-387-95457-0. [Google Scholar]
- Baddeley, A.; Turner, R.; Møller, J.; Hazelton, M. Residual analysis for spatial point processes (with discussion). J. R. Stat. Soc. Ser. B Stat. Methodol. 2005, 67, 617–666. [Google Scholar] [CrossRef]
- Baddeley, A.; Rubak, E.; Møller, J. Score, pseudo-score and residual diagnostics for spatial point process models. Stat. Sci. 2011, 26, 613–646. [Google Scholar] [CrossRef]
- ESRI ArcGIS. Environmental Systems Research Institute; ESRI ArcGIS: Redlands, CA, USA, 2019. [Google Scholar]
- QGIS Development Team. QGIS Geographic Information System; Open Source Geospatial Foundation Project; 2018. Available online: https://qgis.org/en/site/ (accessed on 27 July 2020).
- Jenks, G.F. The data model concept in statistical mapping. Int. Yearb. Cartogr. 1967, 7, 186–190. [Google Scholar]
- R Core Team R. A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2019. [Google Scholar]
- Barton, K. MuMIn: Multi-Model Inference; 2019. Available online: https://r-forge.r-project.org/R/?group_id=346 (accessed on 27 July 2020).
- Bivand, R.; Lewin-Koh, N. Maptools: Tools for Handling Spatial Objects; 2019. Available online: https://cran.r-project.org/web/packages/maptools/index.html (accessed on 27 July 2020).
- Hijmans, R.J. Raster: Geographic Data Analysis and Modeling; 2019. Available online: https://cran.r-project.org/web/packages/raster/index.html (accessed on 27 July 2020).
- Bivand, R.; Keitt, T.; Rowlingson, B. Rgdal: Bindings for the “Geospatial” Data Abstraction Library; 2019. Available online: https://cran.r-project.org/web/packages/rgdal/index.html (accessed on 27 July 2020).
- Bivand, R.; Rundel, C. Rgeos: Interface to Geometry Engine—Open Source (‘GEOS’); 2019. Available online: https://cran.r-project.org/web/packages/rgeos/index.html (accessed on 27 July 2020).
- Bivand, R.S.; Pebesma, E.J.; Gomez-Rubio, V.; Pebesma, E.J. Applied Spatial Data Analysis with R, 2nd ed.; Springer: New York, NY, USA, 2013. [Google Scholar]
- Pebesma, E.J.; Bivand, R.S. Classes and methods for spatial data in R. R News 2005, 5, 9–13. [Google Scholar]
- Baddeley, A.J.; van Lieshout, M.N.M. Area-interaction point processes. Ann. Inst. Stat. Math. 1995, 47, 601–619. [Google Scholar] [CrossRef]
- Angulo, E.; Luque, G.M.; Gregory, S.D.; Wenzel, J.W.; Bessa-Gomes, C.; Berec, L.; Courchamp, F. Review: Allee effects in social species. J. Anim. Ecol. 2018, 87, 47–58. [Google Scholar] [CrossRef] [PubMed]
- Plekhov, D.; Levine, E.I. Defining Suitability in Mixed Agropastoral Societies: A Case Study from Bactria in Northern Afghanistan. Environ. Archaeol. 2020, 1–16. [Google Scholar] [CrossRef]
- Green, L.F.; Green, D.R.; Neves, E.G. Indigenous Knowledge and Archaeological Science: The Challenges of Public Archaeology in the Reserva Uaçá. J. Soc. Archaeol. 2003, 3, 366–398. [Google Scholar] [CrossRef]
- Moser, S.; Glazier, D.; Phillips, J.E.; el Nemr, L.N.; Mousa, M.S.; Aiesh, R.N.; Richardson, S.; Conner, A.; Seymour, M. Transforming archaeology through practice: Strategies for collaborative archaeology and the Community Archaeology Project at Quseir, Egypt. World Archaeol. 2002, 34, 220–248. [Google Scholar] [CrossRef]
- Gallivan, M.; Moretti-Langholtz, D.; Woodard, B. Collaborative archaeology and strategic essentialism: Native empowerment in Tidewater Virginia. Hist. Archaeol. 2011, 45, 10–23. [Google Scholar] [CrossRef]
- Davis, D.S. Studying human responses to environmental change: Trends and trajectories of archaeological research. Environ. Archaeol. 2019, 1–15, in press. [Google Scholar] [CrossRef]
- d’Alpoim Guedes, J.A.; Crabtree, S.A.; Bocinsky, R.K.; Kohler, T.A. Twenty-first century approaches to ancient problems: Climate and society. Proc. Natl. Acad. Sci. USA 2016, 113, 14483–14491. [Google Scholar] [CrossRef] [PubMed]
- Contreras, D.A. Correlation is not enough: Building better arguments in the archaeology of human-environment interactions. In The Archaeology of Human-Environment Interactions; Routledge: Abingdon, UK, 2016; pp. 17–36. [Google Scholar]
- Virah-Sawmy, M.; Willis, K.J.; Gillson, L. Evidence for drought and forest declines during the recent megafaunal extinctions in Madagascar. J. Biogeogr. 2010, 37, 506–519. [Google Scholar] [CrossRef]
- Burney, D.A. Rates, Patterns and Processes of Landscape Transformation and Extinction in Madagascar. In Extinctions in Near Time; MacPhee, R.D.E., Ed.; Springer US: Boston, MA, USA, 1999; pp. 145–164. ISBN 978-1-4419-3315-7. [Google Scholar]
- Hixon, S.W.; Elliott Smith, E.A.; Crowley, B.E.; Perry, G.H.; Randrianasy, J.; Ranaivoarisoa, J.F.; Kennett, D.J.; Newsome, S.D. Nitrogen isotope (δ 15 N) patterns for amino acids in lemur bones are inconsistent with aridity driving megafaunal extinction in south-western Madagascar: Megafaunal Extinction in South-Western Madagascar. J. Quat. Sci. 2018, 33, 958–968. [Google Scholar] [CrossRef]
- Godfrey, L.R.; Scroxton, N.; Crowley, B.E.; Burns, S.J.; Sutherland, M.R.; Pérez, V.R.; Faina, P.; McGee, D.; Ranivoharimanana, L. A new interpretation of Madagascar’s megafaunal decline: The “Subsistence Shift Hypothesis”. J. Hum. Evol. 2019, 130, 126–140. [Google Scholar] [CrossRef] [PubMed]
- Kvamme, K.L. A Manual for Predictive Site Location Models: Examples from the Grand Junction District, Colorado; Bureau of Land Management: Grand Junction District, CO, USA, 1983.
- Altschul, J.H. Models and the Modeling Process. In Quantifying the Present and Predicting the Past: Theory, Method, and Application of Archaeological Predictive Modeling; Judge, W.J., Sebastian, L., Eds.; US Department of the Interior, Bureau of Land Management: Denver, CO, USA, 1988; pp. 61–96. [Google Scholar]
- Green, E.L. Location analysis of prehistoric Maya sites in Northern British Honduras. Am. Antiq. 1973, 38, 279–293. [Google Scholar] [CrossRef]

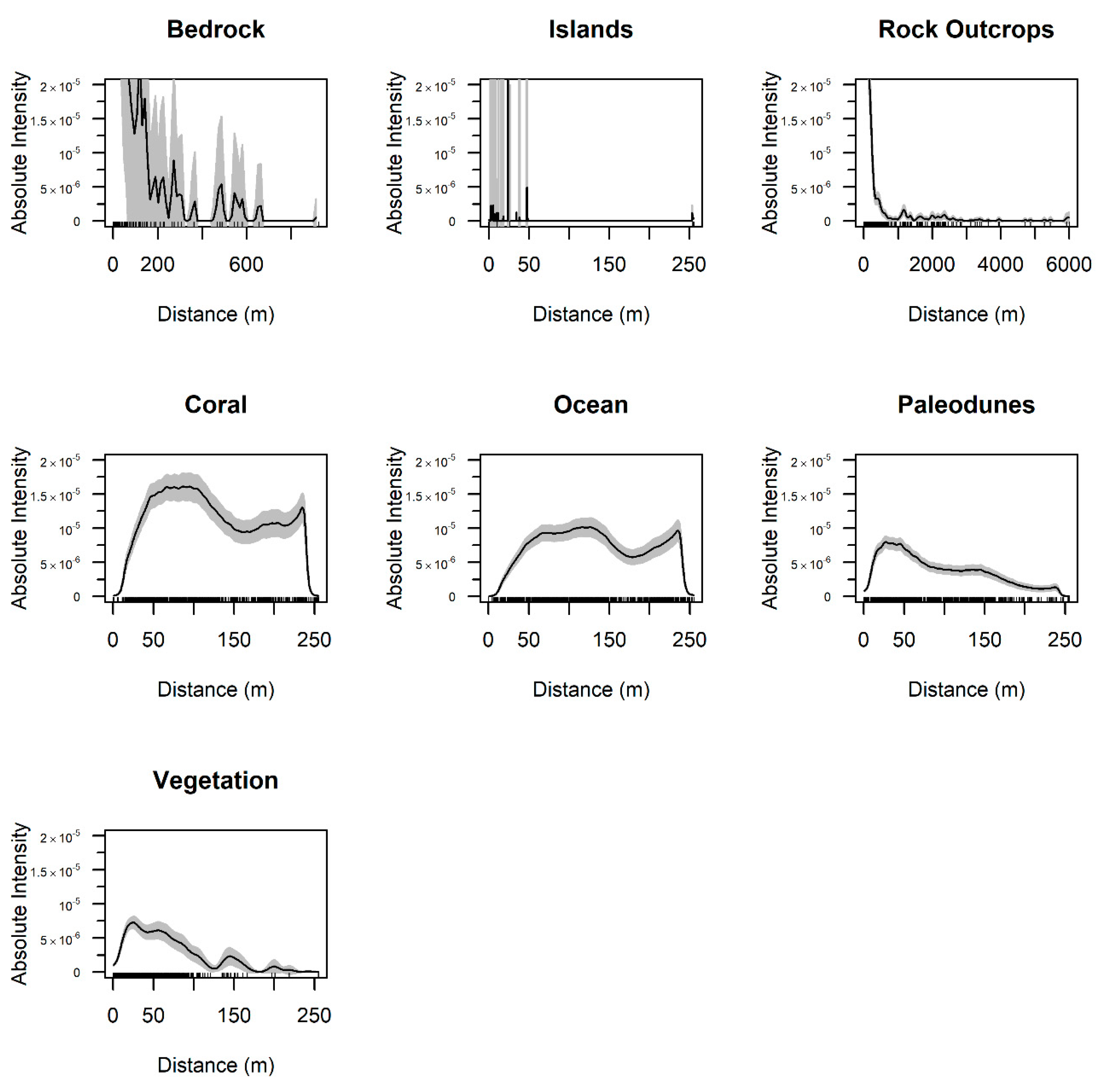

| Variable | Davis et al. [49] | This Study |
|---|---|---|
| Vegetative Productivity | Yes | Yes |
| Coral Reefs | Yes | Yes |
| Offshore Islands | Yes | Yes |
| Distance to the Ocean | Yes | Yes |
| Paleodunes | Yes | Yes |
| Rocky outcrops | No | Yes |
| Depth to bedrock | No | Yes |
| Model | Variables | Df | ΔAIC | Wi | ΔBIC | Wi |
|---|---|---|---|---|---|---|
| PPM3 | coral, water, islands, rocky shoreline, depth to bedrock | 6 | 1.13 | 0.256 | 0 | 0.848 |
| PPM4 | vegetation, coral, water, islands, rocky shoreline, depth to bedrock | 7 | 0 | 0.452 | 3.55 | 0.143 |
| PPM2 | vegetation, dunes, coral, water, islands, rocky shoreline, depth to bedrock | 8 | 0.88 | 0.292 | 9.12 | 0.009 |
| PPM1 | vegetation, dunes, coral, water, islands | 6 | 3486.97 | 0 | 3485.84 | 0 |
| PPM0 | Complete spatial randomness (Poisson Process) | 1 | 6074.78 | 0 | 6050.20 | 0 |
| Estimate | S.E. | CI95 Low | CI95 Hi | Ztest | Zval | |
|---|---|---|---|---|---|---|
| Intercept | −10.3513 | 0.24798 | −10.8373 | −9.865255 | <0.0001 | −41.7427 |
| Coral | −0.0118 | 0.00133 | −0.014358 | −0.0092 | <0.0001 | −8.8633 |
| Water/Ocean | 0.0112 | 0.001354 | 0.008508 | 0.0138 | <0.0001 | 8.2433 |
| Offshore Islands | 0.0043 | 0.000952 | 0.002429 | 0.0062 | <0.0001 | 4.5132 |
| Rocky outcrops | −0.0004 | 0.000061 | −0.000504 | −0.0003 | <0.0001 | −6.3179 |
| Depth to Bedrock | −0.0205 | 0.001075 | −0.022596 | −0.0184 | <0.0001 | −19.0557 |
| Algorithm | Formula | True Positive (#) 1 | False Positive (#) 1 | # Artifacts (High Prob.) | #Artifacts (Medium Prob.) | # Artifacts (Low Prob.) |
|---|---|---|---|---|---|---|
| Davis et al. [49] | 29 | 7 | 654 | 332 | 141 | |
| Unweighted Model | 28 | 3 | 886 | 102 | 160 | |
| Weighted Model 1 | 31 | 7 | 955 | 144 | 49 | |
| Weighted Model 2 | 23 | 2 | 813 | 136 | 199 | |
| Weighted Model 3 | 32 | 7 | 957 | 138 | 53 | |
| Weighted Model 4 | 32 | 7 | 957 | 138 | 53 |
| Model | Total Average | Median | Mode | Standard Error |
|---|---|---|---|---|
| Unweighted | 0.00924 | 0.00243 | 0.00038 | 0.00024 |
| Weighted 1 | 0.04769 | 0.03150 | 0.01762 | 0.001486 |
| Weighted 2 | 0.03182 | 0.01487 | 0.00106 | 0.000992 |
| Weighted 3 | 0.04769 | 0.03150 | 0.01762 | 0.001486 |
| Weighted 4 | 0.04467 | 0.03148 | 0.01762 | 0.001392 |
| Weighted 5 | 0.02545 | 0.01189 | 0.00085 | 0.000793 |
| Model | Variables | Df | ΔAIC | Wi | ΔBIC | Wi |
|---|---|---|---|---|---|---|
| PPM8 | Area interaction, Weighted Model 3 * | 3 | 0 | 1 | 0 | 1 |
| PPM7 | Area interaction, Unweighted Model ** | 3 | 507.96 | 0 | 508.12 | 0 |
| PPM5 | Weighted Model 3 * | 2 | 2376.92 | 0 | 2371.23 | 0 |
| PPM6 | Unweighted Model Raster ** | 2 | 3230.97 | 0 | 3225.28 | 0 |
| PPM9 | Area interaction, CSR | 2 | 7632.29 | 0 | 7627.76 | 0 |
| PPM0 | Complete Spatial Randomness (CSR) | 1 | 13,174.52 | 0 | 13,164.14 | 0 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Davis, D.S.; DiNapoli, R.J.; Douglass, K. Integrating Point Process Models, Evolutionary Ecology and Traditional Knowledge Improves Landscape Archaeology—A Case from Southwest Madagascar. Geosciences 2020, 10, 287. https://doi.org/10.3390/geosciences10080287
Davis DS, DiNapoli RJ, Douglass K. Integrating Point Process Models, Evolutionary Ecology and Traditional Knowledge Improves Landscape Archaeology—A Case from Southwest Madagascar. Geosciences. 2020; 10(8):287. https://doi.org/10.3390/geosciences10080287
Chicago/Turabian StyleDavis, Dylan S., Robert J. DiNapoli, and Kristina Douglass. 2020. "Integrating Point Process Models, Evolutionary Ecology and Traditional Knowledge Improves Landscape Archaeology—A Case from Southwest Madagascar" Geosciences 10, no. 8: 287. https://doi.org/10.3390/geosciences10080287
APA StyleDavis, D. S., DiNapoli, R. J., & Douglass, K. (2020). Integrating Point Process Models, Evolutionary Ecology and Traditional Knowledge Improves Landscape Archaeology—A Case from Southwest Madagascar. Geosciences, 10(8), 287. https://doi.org/10.3390/geosciences10080287





