A Review of Data Cleaning Approaches in a Hydrographic Framework with a Focus on Bathymetric Multibeam Echosounder Datasets
Abstract
1. Introduction
- the input data;
- the type of outlier;
- the supervision type;
- the output of the detection;
2. MBES Data Features
3. Outlier Characteristics
3.1. Types of Outliers
3.2. Outliers and Robust Statistics
- Able to fully absorb proper measurements;
- Computationally efficient;
- Coming with a fitting algorithm suitable for the internal use of a robust estimator.
3.3. Deeper Insight into Outliers in a Hydrographic Context
- Sensors dysfunctions;
- Bubbles at the head of the transducers;
- Multiple acoustic reflection paths;
- Strong acoustical interfaces in the water column;
- Side lobes effects;
- Bad weather conditions (low signal-to-noise ratio);
- Objects in the water column (e.g., fishes, algae, hydrothermal plume);
- Other equipment operating at the same frequency, etc.
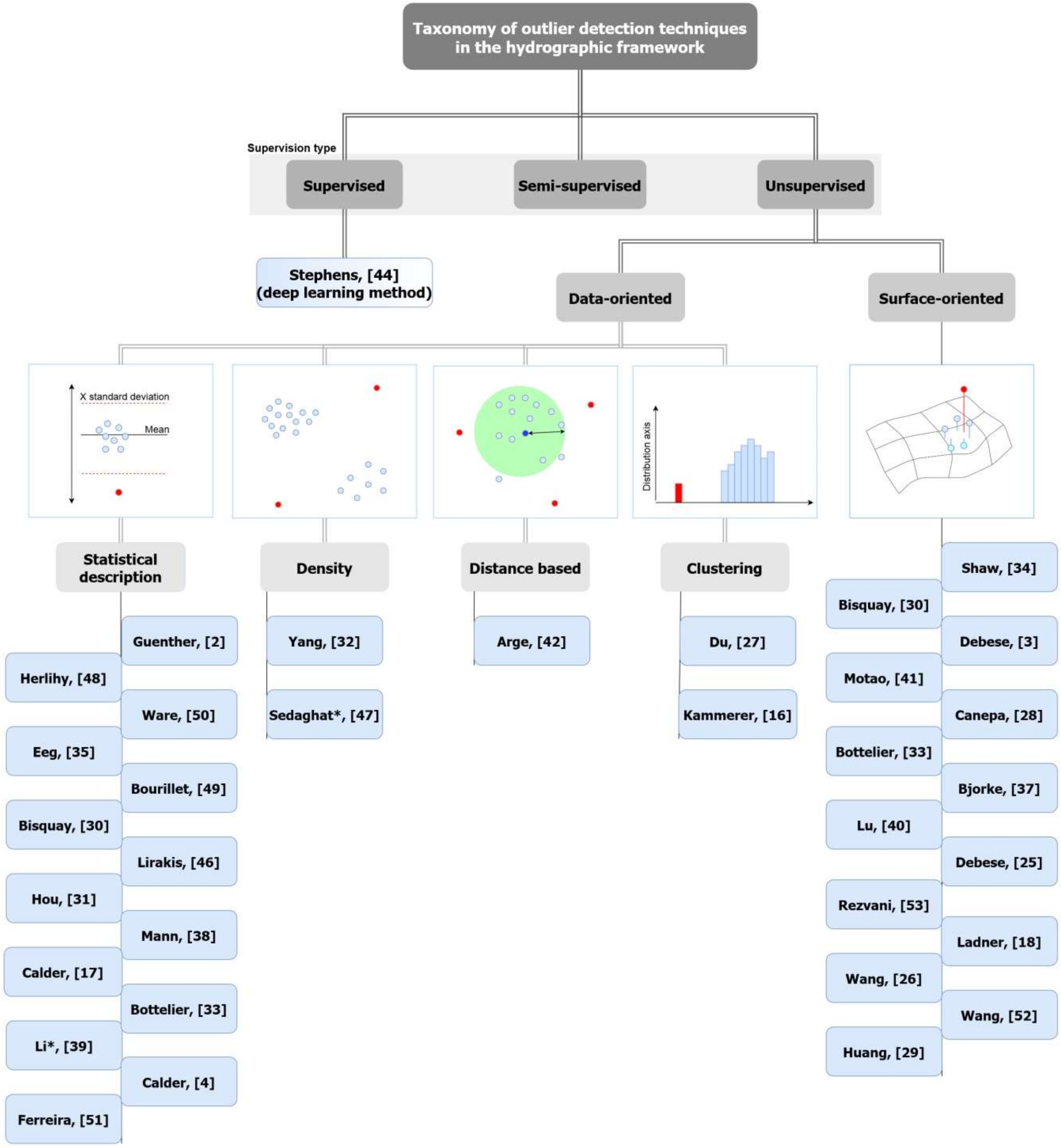
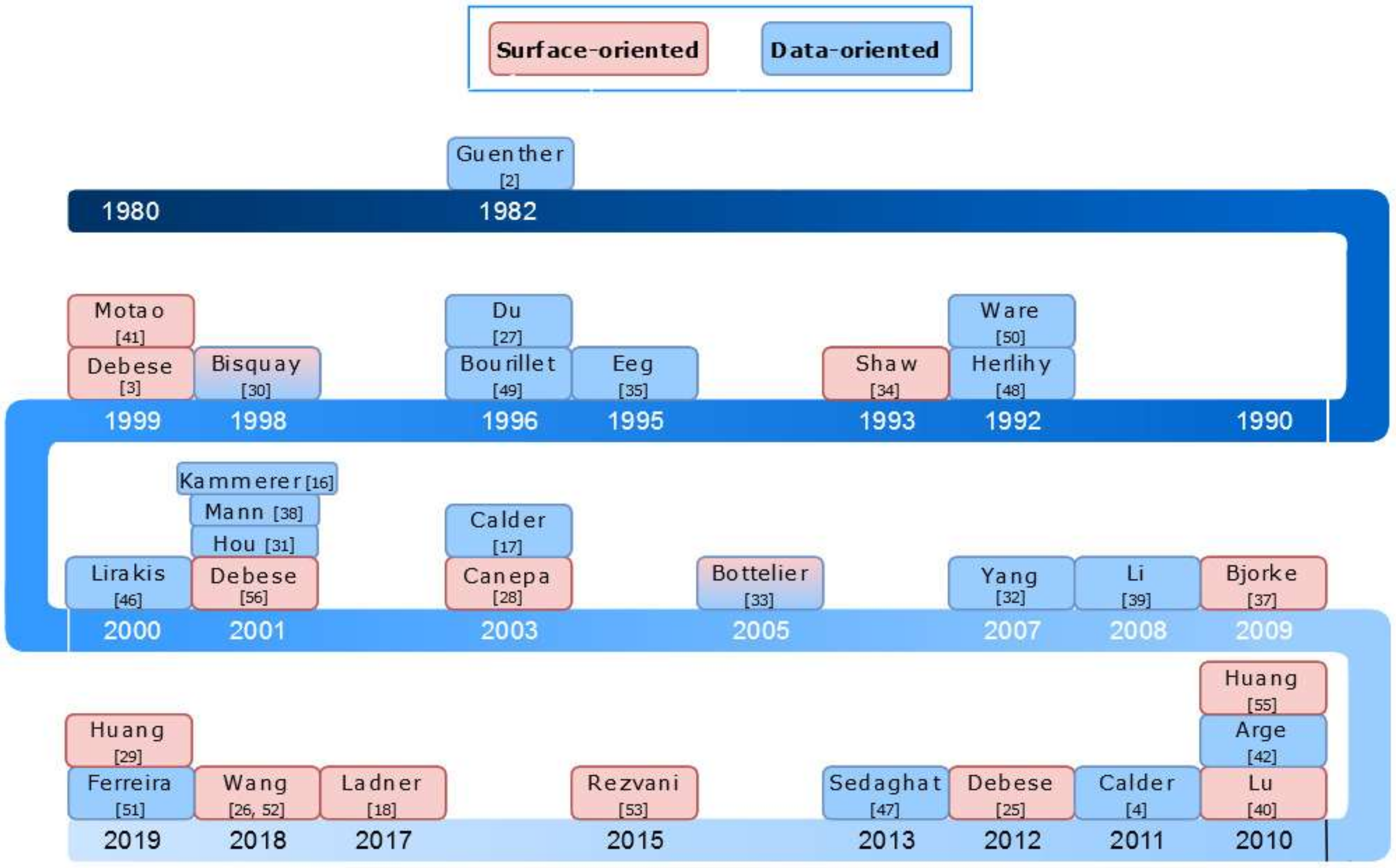
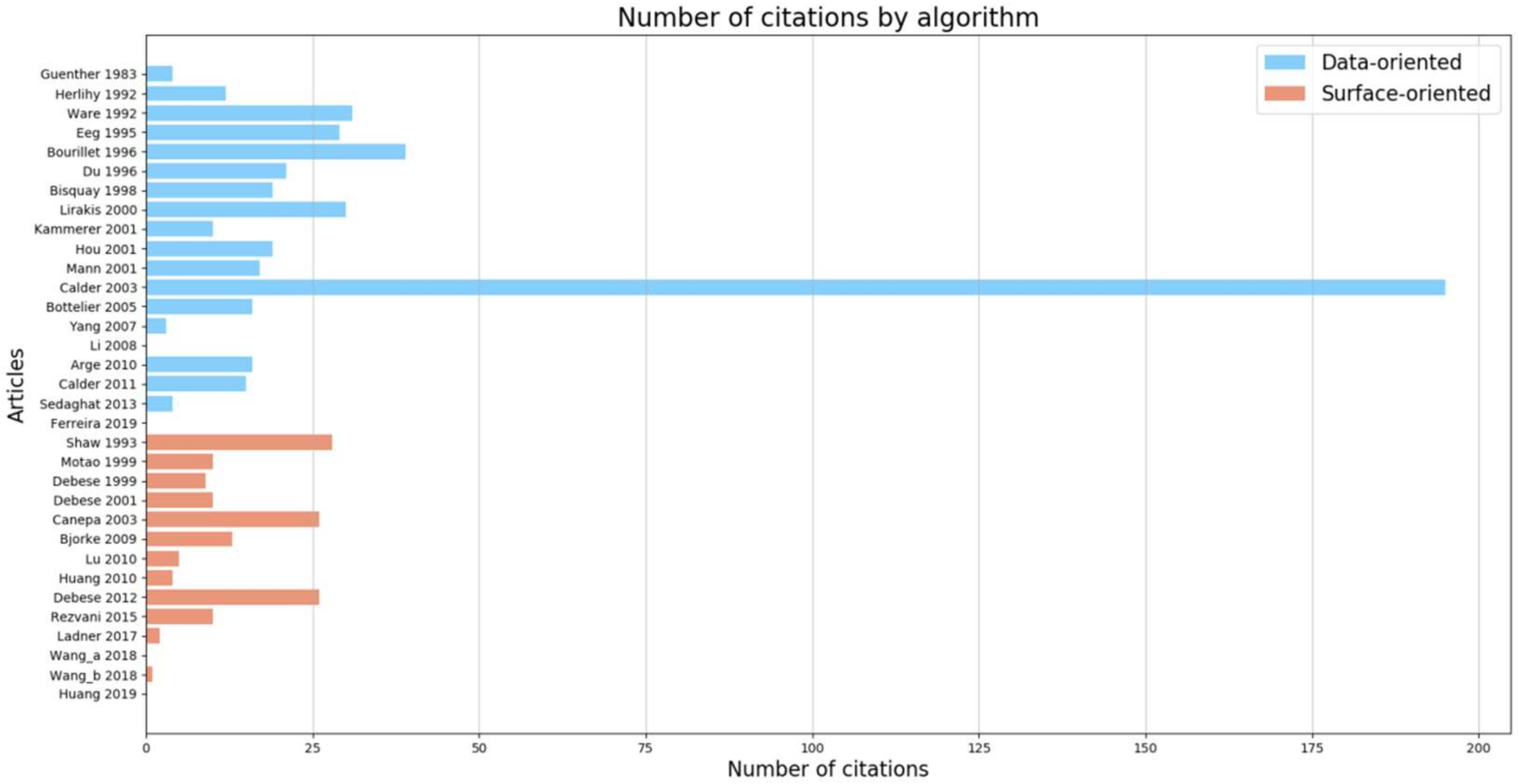
4. Taxonomy of Outlier Detection Techniques
- Supervised: algorithms that generate a predictive function for a set of data from previously labeled data (in relation to the problem to solve);
- Non-supervised: algorithms dealing with unlabeled data, in other words, with no prior knowledge of the data;
- Semi-supervised: algorithms merging these two approaches by determining a prediction function for the learning step with a small amount of labeled data and a great amount of non-labeled data.
4.1. Data-Oriented Approaches
- Statistical-based approaches are generally divided into two classes depending on whether the distribution of the data is assumed to be known or not. Parametric approaches are used to estimate the parameters of the assumed distribution, most of the time the mean and standard deviation of a Gaussian distribution, while non-parametric approaches estimate the density probability from the data, without any assumption about the shape of the distribution. In both cases, outliers are identified as points belonging to the ends of the distribution tails.
- Distance-based approaches, also called nearest neighbor techniques, rely on the spatial correlation by computing the distance from a given point to its vicinity. Points having a higher distance than other normal points are identified as outliers.
- Density-based approaches are quite close to distance-based approaches, as the density of points per unit of surface/volume is inversely linked to the distances between neighbors. Outliers are localized in low-density areas while normal points are aggregated.
- Clustering-based approaches are classical approaches in machine learning. These global approaches consist of grouping similar data into groups called clusters. Since outliers are rare they are either left isolated or if they are grouped into a cluster the latter is far away from the others.
4.1.1. Statistical-Based Approaches
4.1.2. Distance-Based Approach
4.1.3. Density-Based Approach
4.1.4. Clustering-Based Approach
4.2. Surface-Oriented Approaches
- A mathematical model that describes the set of features that are the most representative of the seabed morphology;
- A robust approach that takes into account the presence of outliers and assumes an a priori random noise while estimating the model parameters;
- A strategy that identifies outliers as a subset of distant soundings far from the model.
5. Output of Outlier Detection
- Scores techniques (regression);
- Labeled techniques (classification).
6. Summary and Discussion
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- IHO. Standards for Hydrographic Surveys; International Hydrographic Bureau: Monaco, 2008. [Google Scholar]
- Guenther, G.; Green, J.; Wells, D. Improved Depth Selection in the Bathymetric Swath Survey System (BS3) Combined Offline Processing (COP) Program; NOAA Technical Report OTES 10; National Technical Information Service: Rockville, MD, USA, 1982.
- Debese, N.; Bisquay, H. Automatic detection of punctual errors in multibeam data using a robust estimator. Int. Hydrogr. Rev. 1999, 76, 49–63. [Google Scholar]
- Calder, B.R.; Rice, G. Design and implementation of an extensible variable resolution bathymetric estimator. In Proceedings of the U.S. Hydrographic Conference, Tampa, FL, USA, 25–28 April 2011; p. 15. [Google Scholar]
- Calder, B.; Smith, S. A time/effort comparison of automatic and manual bathymetric processing in real-time mode. Int. Hydrogr. Rev. 2004, 5, 10–23. [Google Scholar]
- Aggarwal, C.C. Outlier Analysis, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2017; ISBN 978-3-319-47577-6. [Google Scholar]
- Kotu, V.; Deshpande, B. Chapter 13—Anomaly Detection. In Data Science, 2nd ed.; Kotu, V., Deshpande, B., Eds.; Morgan Kaufmann: Burlington, MA, USA, 2019; pp. 447–465. ISBN 978-0-12-814761-0. [Google Scholar]
- Hawkins, D.M. Identification of Outliers; Chapman and Hall: London, UK, 1980. [Google Scholar]
- Weatherall, P.; Marks, K.M.; Jakobsson, M.; Schmitt, T.; Tani, S.; Arndt, J.E.; Rovere, M.; Chayes, D.; Ferrini, V.; Wigley, R. A new digital bathymetric model of the world’s oceans. Earth Space Sci. 2015. [Google Scholar] [CrossRef]
- Mayer, L.; Jakobsson, M.; Allen, G.; Dorschel, B.; Falconer, R.; Ferrini, V.; Lamarche, G.; Snaith, H.; Weatherall, P. The Nippon Foundation-GEBCO seabed 2030 project: The quest to see the world’s oceans completely mapped by 2030. Geosciences 2018, 8, 63. [Google Scholar] [CrossRef]
- Chandola, V.; Banerjee, A.; Kumar, V. Anomaly detection: A survey. ACM Comput. Surv. 2009, 41, 3. [Google Scholar] [CrossRef]
- Lurton, X. Chapter 6—Geophysical Sciences. In An Introduction to Underwater Acoustics: Principles and Applications, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2010; Volume 1, ISBN 978-3-540-78480-7. [Google Scholar]
- Clarke, J.E.H. The impact of acoustic imaging geometry on the fidelity of seabed bathymetric models. Geosciences 2018, 8, 109. [Google Scholar] [CrossRef]
- Godin, A. The Calibration of Shallow Water Multibeam Echo-Sounding Systems; UNB Geodesy and Geomatics Engineering: Fredericton, NB, Canada, 1998; pp. 76–130. [Google Scholar]
- Lurton, B.X.; Ladroit, Y. A Quality Estimator of Acoustic Sounding Detection. Int. Hydrogr. Rev. 2010, 4, 35–45. [Google Scholar]
- Kammerer, E.; Charlot, D.; Guillaudeux, S.; Michaux, P. Comparative study of shallow water multibeam imagery for cleaning bathymetry sounding errors. In Proceedings of the MTS/IEEE Oceans 2001, Honolulu, HI, USA, 5–8 November 2001; Volume 4, pp. 2124–2128. [Google Scholar]
- Calder, B.R.; Mayer, L.A. Automatic processing of high-rate, high-density multibeam echosounder data. Geochem. Geophys. Geosyst. 2003, 4. [Google Scholar] [CrossRef]
- Ladner, R.W.; Elmore, P.; Perkins, A.L.; Bourgeois, B.; Avera, W. Automated cleaning and uncertainty attribution of archival bathymetry based on a priori knowledge. Mar. Geophys. Res. 2017, 38, 291–301. [Google Scholar] [CrossRef]
- Mayer, L.; Paton, M.; Gee, L.; Gardner, S.V.; Ware, C. Interactive 3-D visualization: A tool for seafloor navigation, exploration and engineering. In Proceedings of the OCEANS 2000 MTS/IEEE Conference and Exhibition, Providence, RI, USA, 11–14 September 2000; Volume 2, pp. 913–919. [Google Scholar]
- Wölfl, A.C.; Snaith, H.; Amirebrahimi, S.; Devey, C.W.; Dorschel, B.; Ferrini, V.; Huvenne, V.A.I.; Jakobsson, M.; Jencks, J.; Johnston, G.; et al. Seafloor mapping—The challenge of a truly global ocean bathymetry. Front. Mar. Sci. 2019, 6. [Google Scholar] [CrossRef]
- Davies, L.; Gather, U. The Identification of Multiple Outliers. J. Am. Stat. Assoc. 1993, 88, 782–792. [Google Scholar] [CrossRef]
- Hampel, F.R.; Ronchetti, E.M.; Rousseeuw, P.J.; Stahel, W.A. Robust Statistics: The Approach Based on Influence Functions; John Wiley & Sons: Hoboken, NJ, USA, 1986. [Google Scholar]
- Planchon, V. Traitement des valeurs aberrantes: Concepts actuels et tendances générales. Biotechnol. Agron. Soc. Environ. 2005, 9, 19–34. [Google Scholar]
- Burke, R.G.; Forbes, S.; White, K. Processing “Large” Data Sets from 100% Bottom Coverage “Shallow” Water Sweep Surveys A New Challenge for the Canadian Hydrographic Service. Int. Hydrogr. Rev. 1988. Available online: https://journals.lib.unb.ca/index.php/ihr/article/view/23364/27139 (accessed on 1 July 2020).
- Debese, N.; Moitié, R.; Seube, N. Multibeam echosounder data cleaning through a hierarchic adaptive and robust local surfacing. Comput. Geosci. 2012, 46, 330–339. [Google Scholar] [CrossRef]
- Wang, S.; Zhou, P.; Wu, Z.; Li, J.; Wei, Y. Detection and Elimination of Bathymetric Outliers in Multibeam Echosounder System Based on Robust Multi—quadric Method and Median Parameter Model. J. Eng. Sci. Technol. Rev. 2018, 11, 70–78. [Google Scholar] [CrossRef]
- Du, Z.; Wells, D.; Mayer, L.A. An Approach to Automatic Detection of outliers in Multibeam Echo Sounding. Hydrogr. J. 1996, 79, 19–23. [Google Scholar]
- Canepa, G.; Bergem, O.; Pace, N.G. A new algorithm for automatic processing of bathymetric data. IEEE J. Ocean. Eng. 2003, 28, 62–77. [Google Scholar] [CrossRef]
- Huang, X.; Huang, C.; Zhai, G.; Lu, X.; Xiao, G.; Sui, L.; Deng, K. Data Processing Method of Multibeam Bathymetry Based on Sparse Weighted LS-SVM Machine Algorithm. IEEE J. Ocean. Eng. 2019, 1–14. [Google Scholar] [CrossRef]
- Bisquay, H.; Freulon, X.; De Fouquet, C.; Lajaunie, C. Multibeam data cleaning for hydrography using geostatistics. In Proceedings of the IEEE Oceanic Engineering Society (OCEANS’98), Nice, France, 28 September–1 October 1998; Volume 2, pp. 1135–1143. [Google Scholar]
- Hou, T.; Huff, L.C.; Mayer, L.A. Automatic Detection of Outliers in Multibeam Echo Sounding Data; University of New Hampshire, Center for Coastal and Ocean Mapping: Durham, NH, USA, 2001. [Google Scholar]
- Yang, F.; Li, J.; Chu, F.; Wu, Z. Automatic Detecting Outliers in Multibeam Sonar Based on Density of Points. In Proceedings of the OCEANS 2007—Europe, Aberdeen, UK, 18–21 June 2007; pp. 1–4. [Google Scholar]
- Bottelier, P.; Briese, C.; Hennis, N.; Lindenbergh, R.; Pfeifer, N. Distinguishing features from outliers in automatic Kriging-based filtering of MBES data: A comparative study. Geostat. Environ. Appl. 2005, 403–414. [Google Scholar] [CrossRef]
- Arnold, J.; Shaw, S. A surface weaving approach to multibeam depth estimation. In Proceedings of the OCEANS ’93, Victoria, BC, Canada, 18–21 October 1993; Volume 2, pp. II/95–II/99. [Google Scholar]
- Eeg, J. On the identification of spikes in soundings. Int. Hydrogr. Rev. 1995, 72, 33–41. [Google Scholar]
- Ferreira, I.O.; de Paula dos Santos, A.; de Oliveira, J.C.; das Graças Medeiros, N.; Emiliano, P.C. Robust Methodology for Detection Spikes in Multibeam Echo Sounder Data. Bol. Ciênc. Geod. 2019, 25. [Google Scholar] [CrossRef]
- Bjorke, J.T.; Nilsen, S. Fast trend extraction and identification of spikes in bathymetric data. Comput. Geosci. 2009, 35, 1061–1071. [Google Scholar] [CrossRef]
- Mann, M.; Agathoklis, P.; Antoniou, A. Automatic outlier detection in multibeam data using median filtering. In Proceedings of the 2001 IEEE Pacific Rim Conference on Communications, Computers and Signal Processing, Victoria, BC, Canada, 26–28 August 2001; Volume 2, pp. 690–693. [Google Scholar]
- Li, M.; Liu, Y.C.; Lv, Z.; Bao, J. Order Statistics Filtering for Detecting Outliers in Depth Data along a Sounding Line. In Proceedings of the VI Hotine-Marussi Symposium on Theoretical and Computational Geodesy; Xu, P., Liu, J., Dermanis, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 258–262. [Google Scholar]
- Lu, D.; Li, H.; Wei, Y.; Zhou, T. Automatic outlier detection in multibeam bathymetric data using robust LTS estimation. In Proceedings of the 2010 3rd International Congress on Image and Signal Processing, Yantai, China, 16–18 October 2010; Volume 9, pp. 4032–4036. [Google Scholar]
- Motao, H.; Guojun, Z.; Rui, W.; Yongzhong, O.; Zheng, G. Robust Method for the Detection of Abnormal Data in Hydrography. Int. Hydrogr. Rev. 1999, LXXVI. Available online: https://www.semanticscholar.org/paper/Robust-Method-for-the-Detection-of-Abnormal-Data-in-Mo-tao-Guo-jun/16644f7e77104d0383e9224ec330b074e8b8525d (accessed on 1 July 2020).
- Arge, L.; Larsen, L.; Mølhave, T.; van Walderveen, F. Cleaning Massive Sonar Point Clouds. In Proceedings of the 18th ACM SIGSPATIAL International Symposium on Advances in Geographic Information Systems, ACM-GIS 2010, San Jose, CA, USA, 3–5 November 2010; pp. 152–161. [Google Scholar]
- Calder, B.R. Multibeam Swath Consistency Detection and Downhill Filtering from Alaska to Hawaii. In Proceedings of the U.S. Hydrographic Conference (US HYDRO), San Diego, CA, USA, 29–31 March 2005. [Google Scholar]
- Stephens, D.; Smith, A.; Redfern, T.; Talbot, A.; Lessnoff, A.; Dempsey, K. Using three dimensional convolutional neural networks for denoising echosounder point cloud data. Appl. Comput. Geosci. 2020, 5, 100016. [Google Scholar] [CrossRef]
- Hodge, V.J.; Austin, J. A Survey of Outlier Detection Methodologies. Artif. Intell. Rev. 2004, 22, 85–126. [Google Scholar] [CrossRef]
- Lirakis, C.B.; Bongiovanni, K.P. Automated multibeam data cleaning and target detection. In Proceedings of the OCEANS 2000 MTS/IEEE Conference and Exhibition, Providence, RI, USA, 11–14 September 2000; Volume 1, pp. 719–723. [Google Scholar]
- Sedaghat, L.; Hersey, J.; McGuire, M.P. Detecting spatio-temporal outliers in crowdsourced bathymetry data. In Proceedings of the Second ACM SIGSPATIAL Inernational Workshop on Crowdsourced and Volunteered Geographic Information, Orlando, FL, USA, 5 November 2013; pp. 55–62. [Google Scholar] [CrossRef]
- Herlihy, D.R.; Stepka, T.; Rulon, D. Filtering erroneous soundings from multibeam survey data. Int. Hydrogr. Rev. 1992, LXIX. Available online: https://journals.lib.unb.ca/index.php/ihr/article/view/26178/1882518870 (accessed on 1 July 2020).
- Bourillet, J.F.; Edy, C.; Rambert, F.; Satra, C.; Loubrieu, B. Swath mapping system processing: Bathymetry and cartography. Mar. Geophys. Res. 1996, 18, 487–506. [Google Scholar] [CrossRef]
- Ware, C.; Slipp, L.; Wong, K.W.; Nickerson, B.; Wells, D.; Lee, Y.C.; Dodd, D.; Costello, G. A System for Cleaning High Volume Bathymetry. Int. Hydrogr. Rev. 1992, 69, 77–92. [Google Scholar]
- Ferreira, I.O.; de Paula dos Santos, A.; de Oliveira, J.C.; das Graças Medeiros, N.; Emiliano, P.C. Spatial outliers detection algorithm (soda) applied to multibeam bathymetric data processing. Bol. Ciênc. Geod. 2019, 25. [Google Scholar] [CrossRef]
- Wang, S.; Dai, L.; Wu, Z.; Li, J.; Wei, Y. Multibeam Bathymetric Data Quality Control based on Robust Least Square Collocation of Improved Multi-quadric Function. J. Eng. Sci. Technol. Rev. 2018, 11, 139–146. [Google Scholar] [CrossRef]
- Rezvani, M.-H.; Sabbagh, A.; Ardalan, A.A. Robust Automatic Reduction of Multibeam Bathymetric Data Based on M-estimators. Mar. Geod. 2015, 38, 327–344. [Google Scholar] [CrossRef]
- Debese, N. Multibeam Echosounder Data Cleaning Through an Adaptive Surface-Based Approach; IEEE: Piscataway, NJ, USA, 2007; pp. 1–18. [Google Scholar]
- Huang, X.; Zhai, G.; Sui, L.; Huang, M.; Huang, C. Application of least square support vector machine to detecting outliers of multi-beam data. Geomat. Inf. Sci. 2010, 35, 1188–1191. [Google Scholar]
- Debese, N. Use of a robust estimator for automatic detection of isolated errors appearing in the bathymetry data. Int. Hydrogr. Rev. 2001, 2, 32–44. [Google Scholar]
- Lecun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-Based Learning Applied to Document Recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Calder, B.B. Multi-Algorithm Swath Consistency Detection for Multibeam Echosounder Data. Int. Hydrogr. Rev. 2007, 8, 9–24. [Google Scholar]
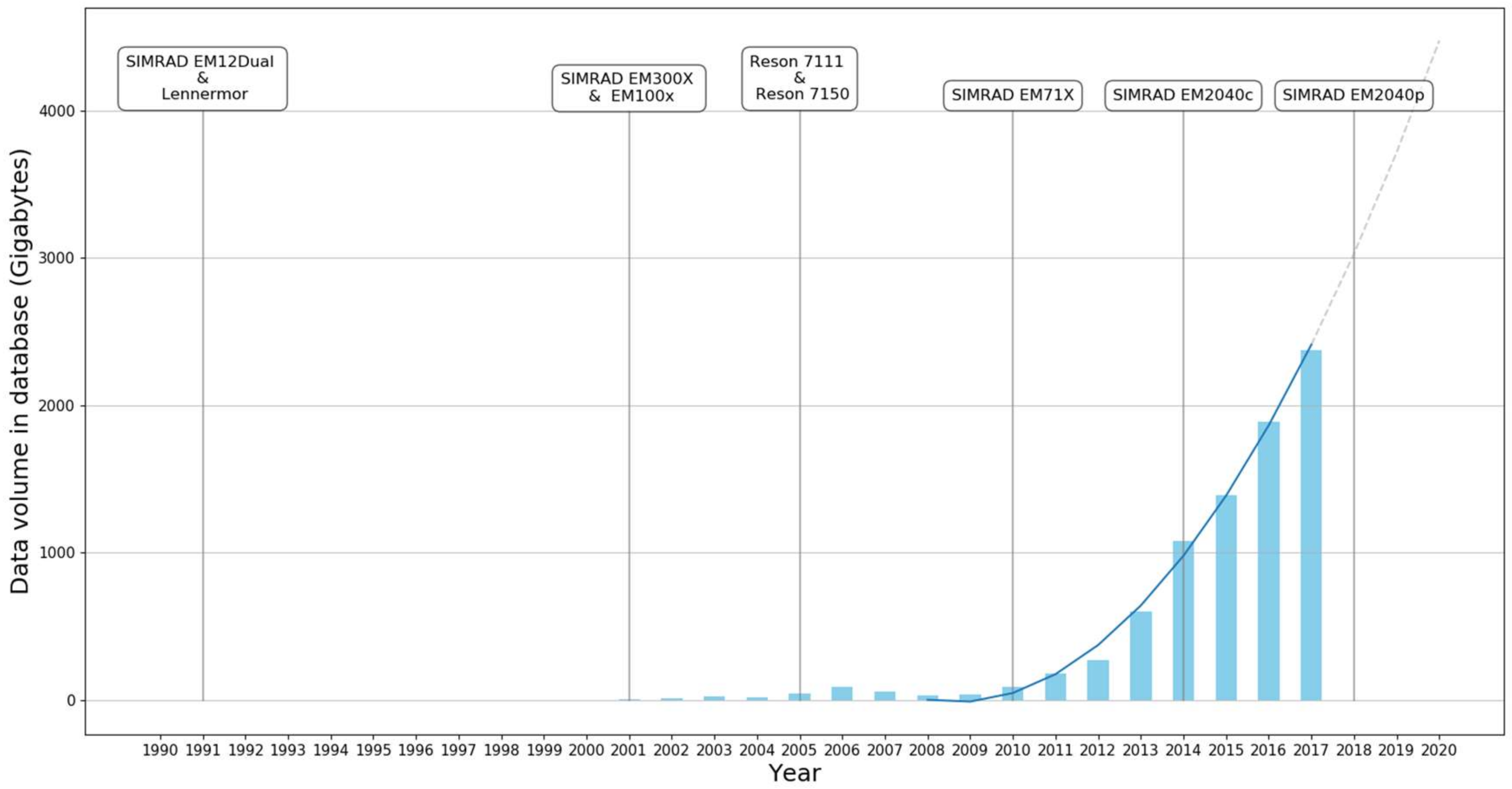
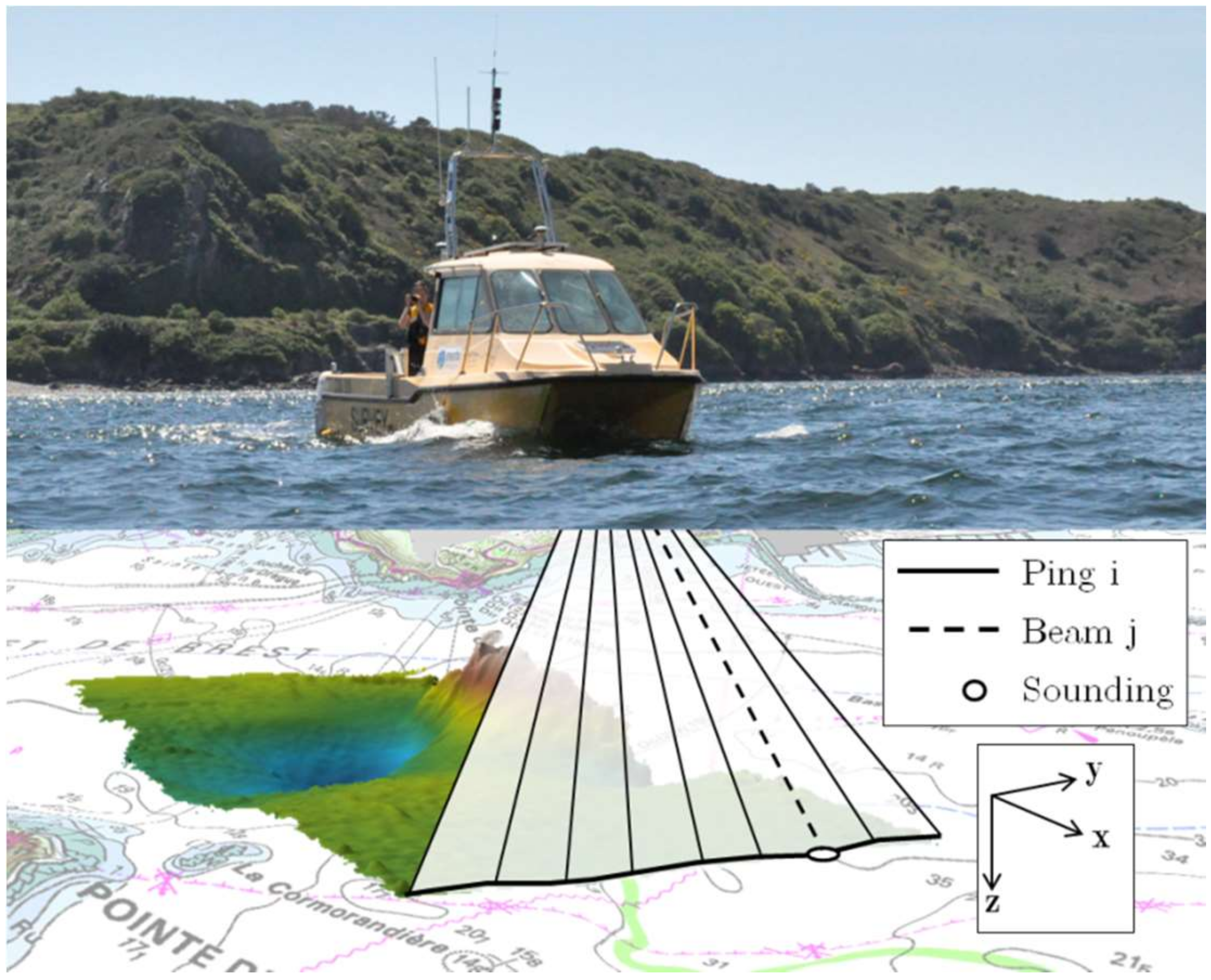
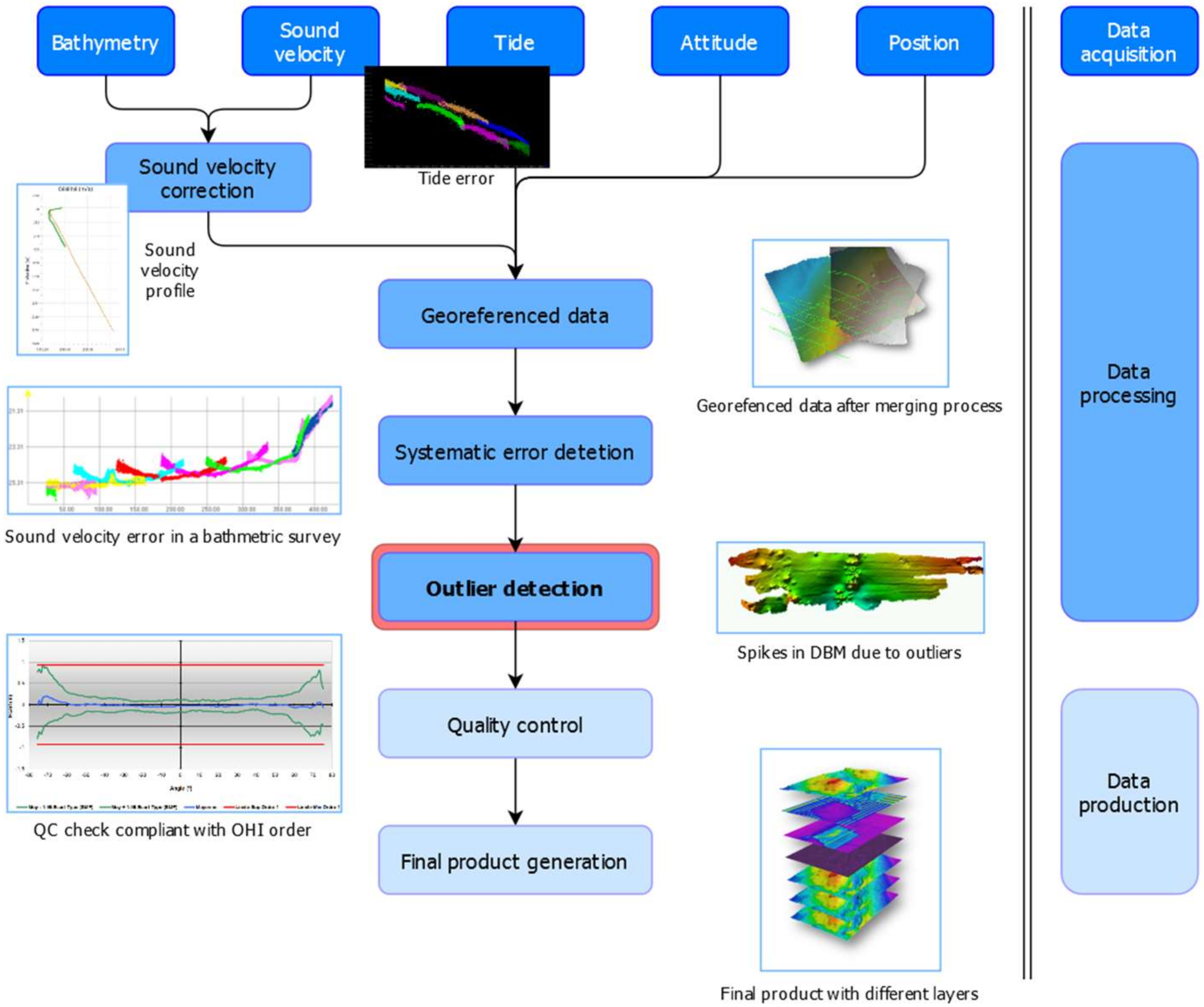
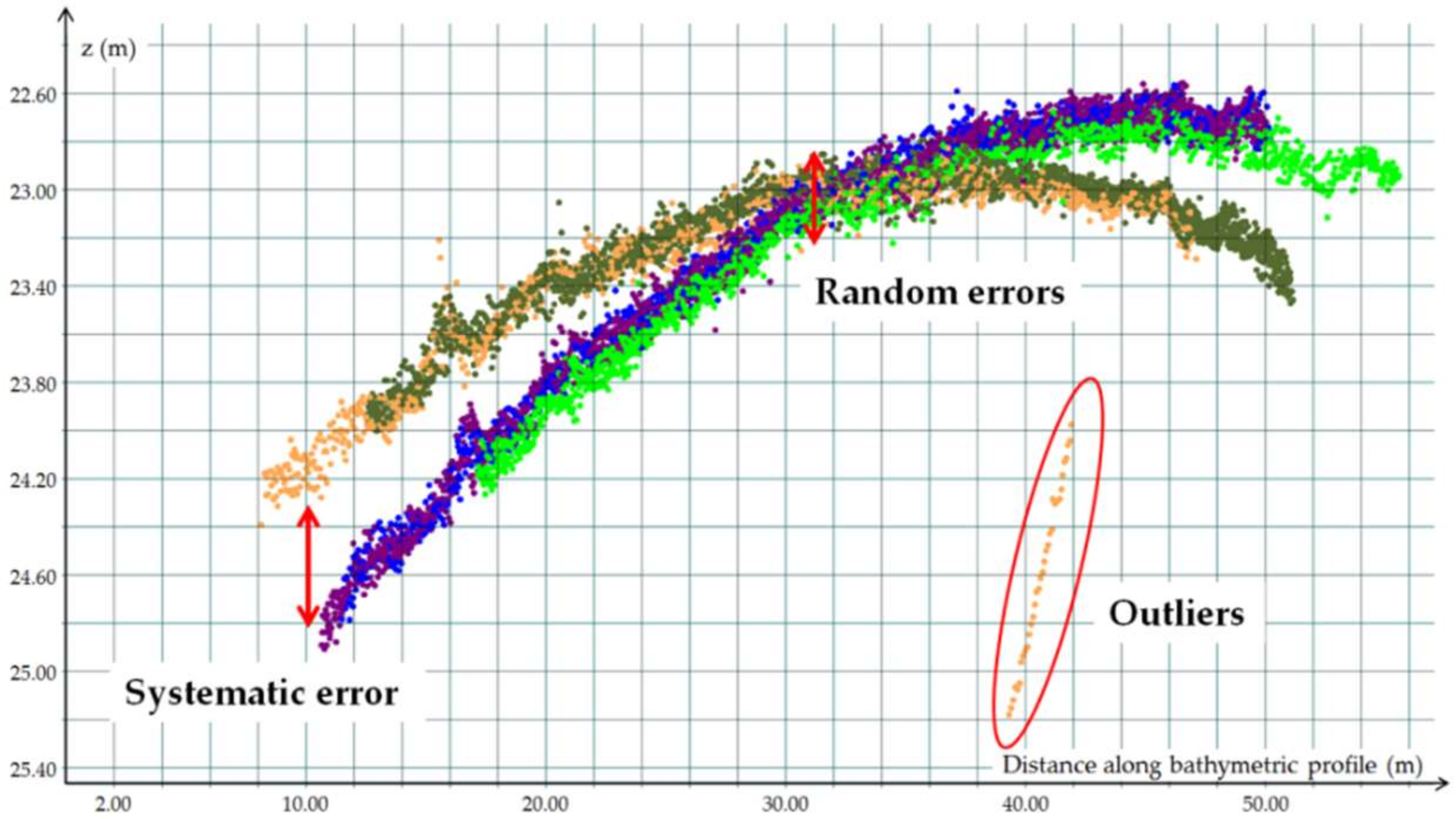
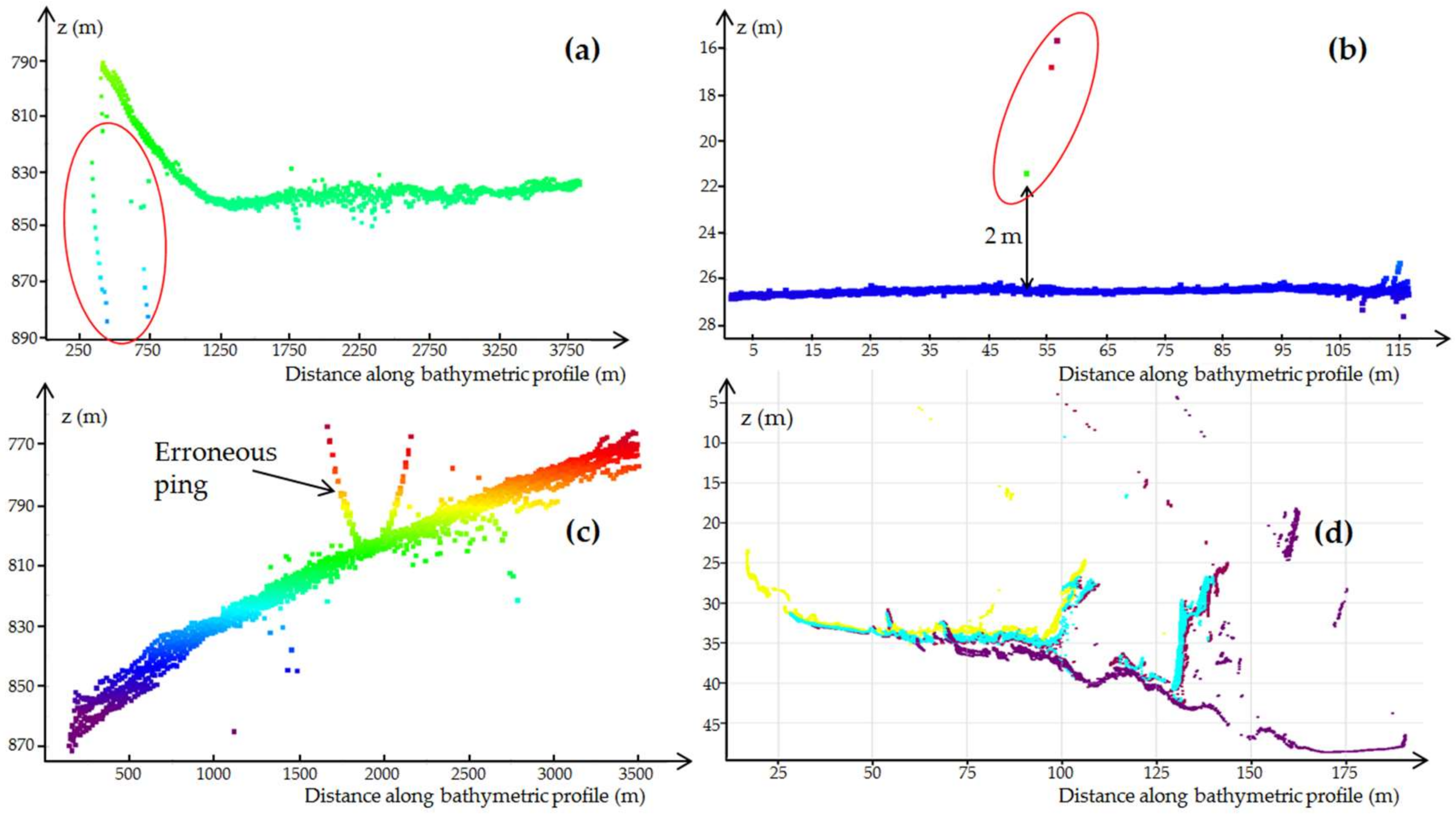

| Year | MBES | Area 1 | Number of Soundings | Angular Sector | Covered Area |
|---|---|---|---|---|---|
| 2012 | EM3002 | CR | 2,608,853 | 150° maximum | 0.100 km2 |
| 2017 | EM1002 | PN | 693,417 | 150° maximum | 3.270 km2 |
| 2019 | EM2040c | CR | 4,376,801 | 150° maximum | 0.104 km2 |
| 2016 | EM710 | PN | 7,160,800 | 150° maximum | 2.753 km2 |
| 2020 | EM712 | PN | 6,455,200 | 150° maximum | 3.227 km2 |
| Approach | Class 1 | Overall Structure 2 | Description Mode 3 | Neighborhood 4 | Techniques 5 |
|---|---|---|---|---|---|
| [2] Guenther | S | 1 | T | Fa | Statistical filter: mean, multiple of standard deviation on windows of 3 beams × 5 pings |
| [48] Herlihy | S | 3 C | T | Fau(1) |
|
| [50] Ware | S | 1 | S | Fu(1) | Classification of soundings according into 8 classes based on a linear combination of weighted average and standard deviation Weighted average, applied to each cell of a base surface (3) |
| [35] Eeg | S | 1 | S | Fau(1) | Inspection of a reduced list of soundings sorted by a quotient (i.e., outlierness score) (1). |
| [49] Bourillet | S | 4 C | B | Fau(1) |
|
| [27] Du | C | 3 C | T | Fau(2) |
|
| [30] Bisquay | S | 2 S | S | Fu(3) |
|
| [46] Lirakis | S | 5 C | B | Fau(1) |
|
| [31] Hou | S | 3 C | T | Fau(1) |
|
| [16] Kammerer | C | 4 S | B | Fau(1) |
|
| [38] Mann | S | 1 | S | Fu(1) | Statistical filter based on median (1); |
| [17] Calder | S | 1 | S | Fu(2) | CUBE (4 *); |
| [33] Bottelier | S | 2 S | T | Fa |
|
| [32] Yang | De | 2 C | T | Fu(1) |
|
| [4] Calder | S | 1 | S | Fu(4) | CHRT (4 *); |
| [42] Arge | Di | 1 | S | Fa | Connected-component of a TIN after edges removing (1); |
| [47] Sedaghat | De/C | 2 S | S | Fu(1) | Combination of LOF and DBSCAN algorithms to find spatio-temporal clusters (3); Hotspot detection from local Moran’I and z-score statistics (1); |
| [51] Ferreira | S | 3 S | S | Fau(1) |
|
| [39] Li | S | 2 C | S | Fa |
|
| Algorithm | Description Mode 1 | Observation Type 2 | Approach Scope 3 | Robust Estimation 4 | Approach Type. In the Case of a Robust Estimation Approach, Type of the Robust Estimator | Initial Step 5 | Surface Type |
|---|---|---|---|---|---|---|---|
| [34] Arnold | S | A | L | 0 | Graduated Non-convexity algorithm | 0 | Weak membrane (first order)/Thin plate (second order) |
| [34] Arnold | S | P | L | 1 | Robust linear prediction involved in an auto-regressive process | 0 | First-order non symmetric half-plane (NSHP) image model/bidirectional vector |
| [30] Bisquay | S | P | L | 0 | 1 | Ordinary kriging—Linear variogram | |
| [41] Motao | G | P | G | 1 | IGIII (M-Estimator) | 1 | IDW |
| [28] Canepa | G | P | G | 1 | Tukey (M-Estimator) | 1 | Local polynomial |
| [33] Bottelier | G | A | G | 1 | M-estimator | 0 | Ordinary kriging—Gaussian model |
| [37] Bjorke | B | A | G | 0 | - | 0 | Biquadratic polynomial |
| [40] Lu | B | A | L | 1 | LTS estimator | 0 | Second/third order polynomial |
| [25] Debese | B | A | L | 1 | Tukey (M-Estimator) | 1 | Polynomial |
| [53] Rezvani | G | A | L | 1 | Huber; IGGIII, Hampel, Tukey (M-estimator) | 1 | Horizontal plane |
| [18] Ladner | G | A | L | 1 | LTS estimator | 0 | Polynomial |
| [52] Wang | B | A | G | 1 | Huber (M-Estimator) | 1 | Improved Multi Quadric model |
| [26] Wang | B | A | G | 1 | IGIII (M-Estimator) | 1 | Multi Quadric model |
| [29] Huang | G | A | G | 0 | Sparse weighted LS-SVM | Polynomial and gauss radial kernel function |
| Algorithm | Depth Range 1 | Sensor Model | Datasets | ||
|---|---|---|---|---|---|
| Number of | Volume | Type 2 | |||
| [2] Guenther | D/VD | BS 3 | - | - | - |
| [48] Herlihy | D/VD | Seabeam Hydro Chart | 2 | 23,735,009; 15,622,682 | - |
| [50] Ware | - | Navitronics 3 | 1 | 200,000 | A |
| [34] Arnold | - | MBES 4 | 1 | - | P |
| [35] Eeg | S | MBES 4 | 1 | 65,000 | S |
| [49] Bourillet | D/VD | SIMRAD EM12D; EM1000 | - | - | - |
| [27] Du | S | SIMRAD EM1000 | 1 | - | - |
| [30] Bisquay | VD | SIMRAD EM12D | 3 | 46,592; 108,297; 189,699 | S |
| [41] Motao | - | Chinese-developed H/HCS-017 | 1 | 198,928 | A |
| [3] Debese | S/D/VD | SIMRAD EM12D EM3000 Lennermor | 5 | 38,000; 46,000; 88,000; 108,000; 178,000 | S |
| [46] Lirakis | S | SIMRAD EM1000 EM3000 EM121 | 5 | 774,400; 300,800; 665,600; 1,251,200; 195,200 | A |
| [16] Kammerer | S | SIMRAD EM1002S Atlas FS20 | 2 | - | A |
| [56] Debese | S/D/VD | SIMRAD EM12D EM3000 | 3 | 108,000; 178,000; 195,200 | S |
| [31] Hou | S | SAX-99 (Destin FL) | - | 6.9 Go 5 | A |
| [38] Mann | S | SIMRAD EM3000 | 1 | 641,421 | A |
| [28] Canepa | S/D | SIMRAD EM3000 HYDROSWEEP MD | 3 | 36,482; 1,220,358; 500,000 | A |
| [17] Calder | S/D | SIMRAD EM3000 SIMRAD EM1002 | 2 | 1,000,153 | A |
| [33] Bottelier | S | Reson8101 mounted on a ROV | 1 | 300,000 | S |
| [54] Debese | S/D | ATLAS Fansweep20 SIMRAD EM3000 EM1002, EM120 | 4 | 550,000 to 3,000,000 | A |
| [32] Yang | VD | - | 1 | (9.6 × 30.2) km2 6 | S |
| [39] Li | S | SDH-13D 7 | 1 | 619 | S |
| [37] Bjorke | S | SIMRAD EM1002 | 1 | 93,424 | A |
| [40] Lu | S | - | 1 | 6,350 | P |
| [42] Arge | - | MBES (4) | 3 | 7,000,000; 7,000,000; 6,000,000 | A |
| [55] Huang | S | Reson 8101 | 1 | 13,300 | A |
| [4] Calder | S | - | 1 | 100 m × 200 m 8 | A |
| [25] Debese | S | SIMRAD EM3002 | 1 | 2,600,000 | A |
| [47] Sedaghat | S | SBES 9 | 1 | 1,500,000 | A |
| [53] Rezvani | S | Atlas Fansweep 20 | 1 | 32,020 | S |
| [18] Ladner | D/VD | - | 2 | 4,318,703; 260,527 | A |
| [52] Wang | S | MBES 4 | 1 | 1045 | P |
| [26] Wang | S | MBES 4 | 1 | 1904 | P |
| [29] Huang | VD | Seabeam 2112 | 1 | 6268 | S |
| [51] Ferreira | S | R2Sonic 2022 | 1 | 8090 | S |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Le Deunf, J.; Debese, N.; Schmitt, T.; Billot, R. A Review of Data Cleaning Approaches in a Hydrographic Framework with a Focus on Bathymetric Multibeam Echosounder Datasets. Geosciences 2020, 10, 254. https://doi.org/10.3390/geosciences10070254
Le Deunf J, Debese N, Schmitt T, Billot R. A Review of Data Cleaning Approaches in a Hydrographic Framework with a Focus on Bathymetric Multibeam Echosounder Datasets. Geosciences. 2020; 10(7):254. https://doi.org/10.3390/geosciences10070254
Chicago/Turabian StyleLe Deunf, Julian, Nathalie Debese, Thierry Schmitt, and Romain Billot. 2020. "A Review of Data Cleaning Approaches in a Hydrographic Framework with a Focus on Bathymetric Multibeam Echosounder Datasets" Geosciences 10, no. 7: 254. https://doi.org/10.3390/geosciences10070254
APA StyleLe Deunf, J., Debese, N., Schmitt, T., & Billot, R. (2020). A Review of Data Cleaning Approaches in a Hydrographic Framework with a Focus on Bathymetric Multibeam Echosounder Datasets. Geosciences, 10(7), 254. https://doi.org/10.3390/geosciences10070254






