Event-Based Landslide Modeling in the Styrian Basin, Austria: Accounting for Time-Varying Rainfall and Land Cover
Abstract
1. Introduction
2. Materials and Methods
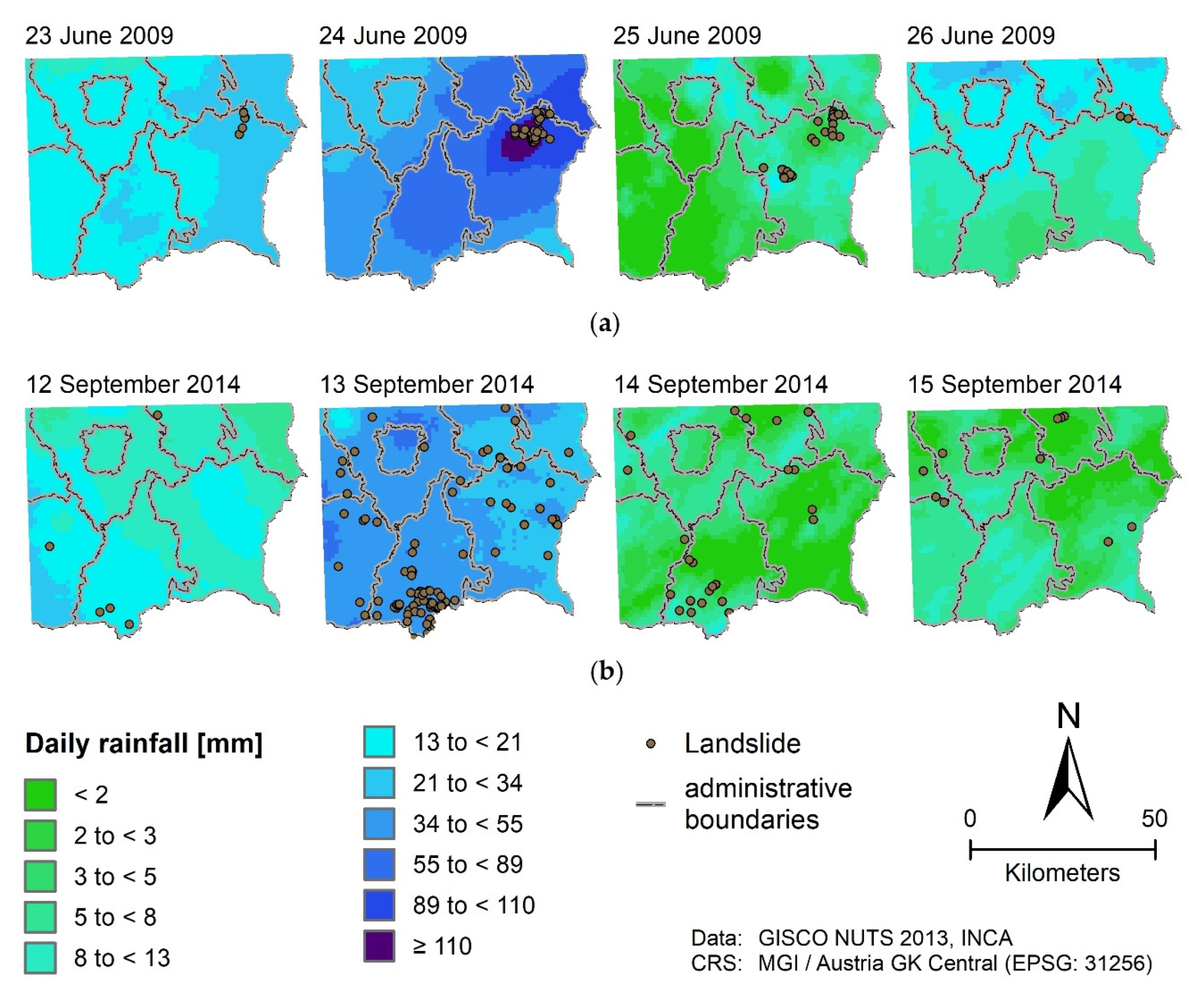
2.1. Study Area and Extreme Rainfall Events
2.2. Data
2.2.1. Climate Data
2.2.2. Land Surface Data
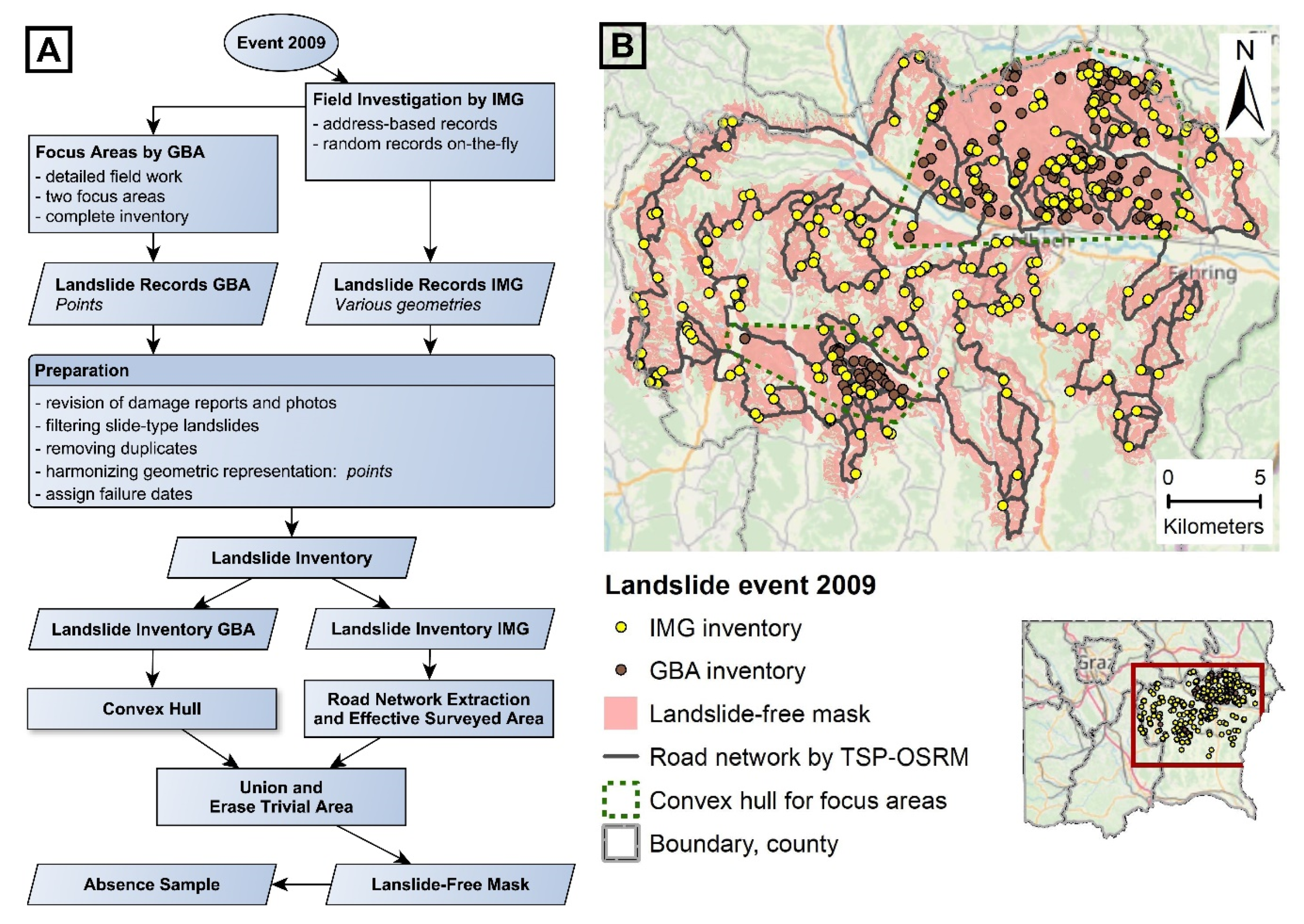
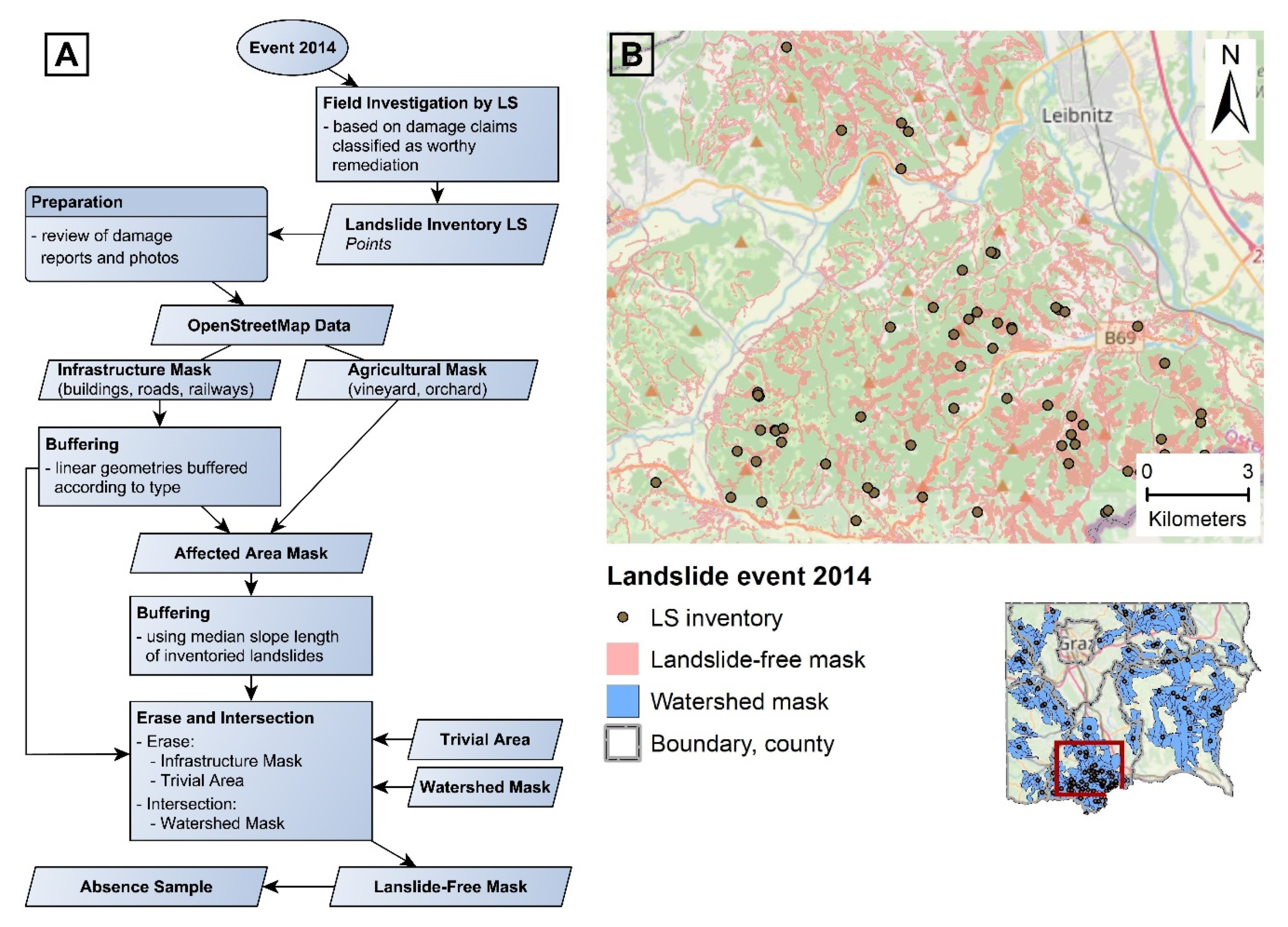
2.2.3. Landslide Data
2.3. Landslide Susceptibility Modeling
2.3.1. Sampling Design
2.3.2. Landslide Models and Input Data
2.3.3. Model Performance and Variable Assessment
3. Results
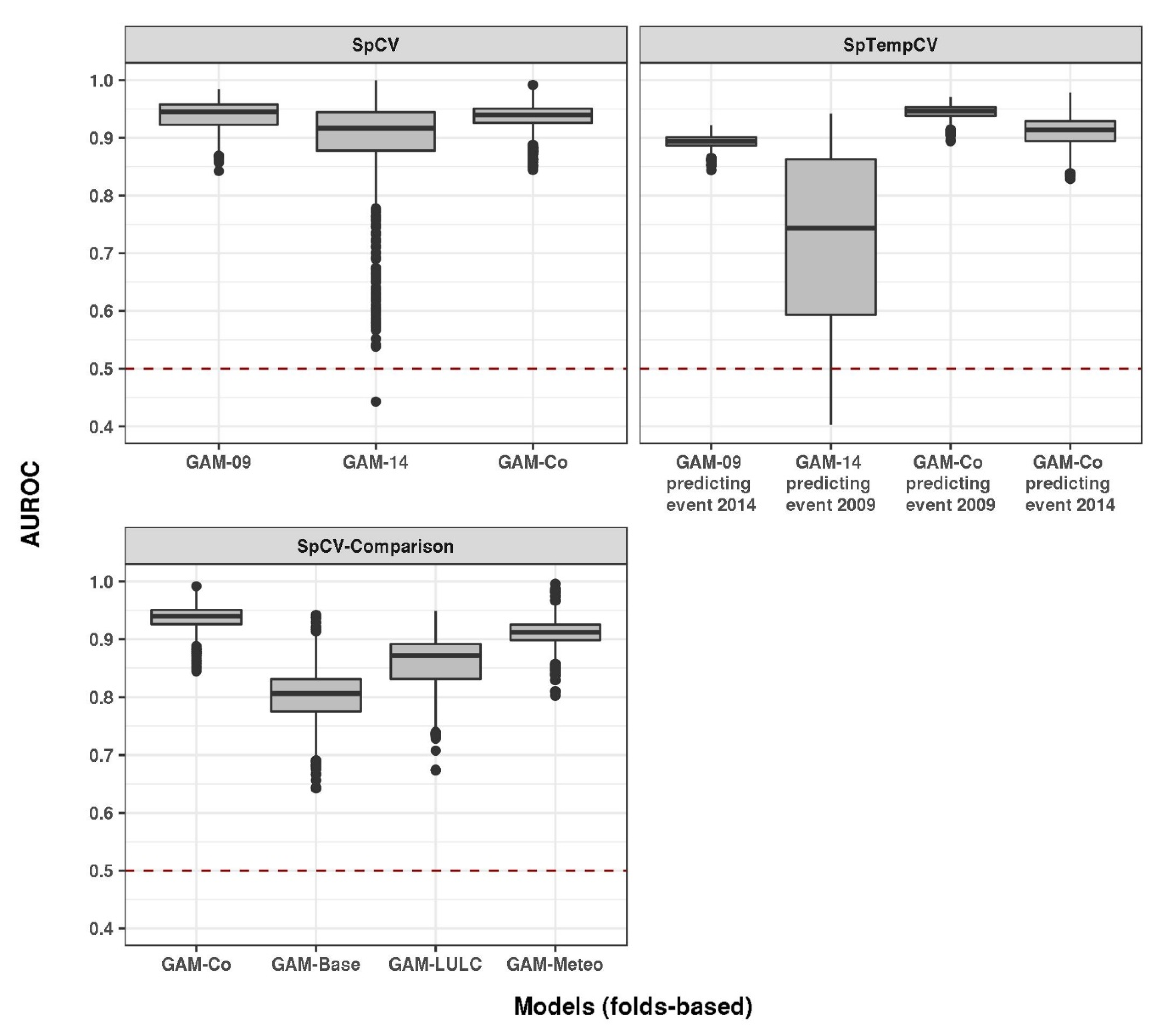
3.1. Performance Assessment
3.2. Variable Importance
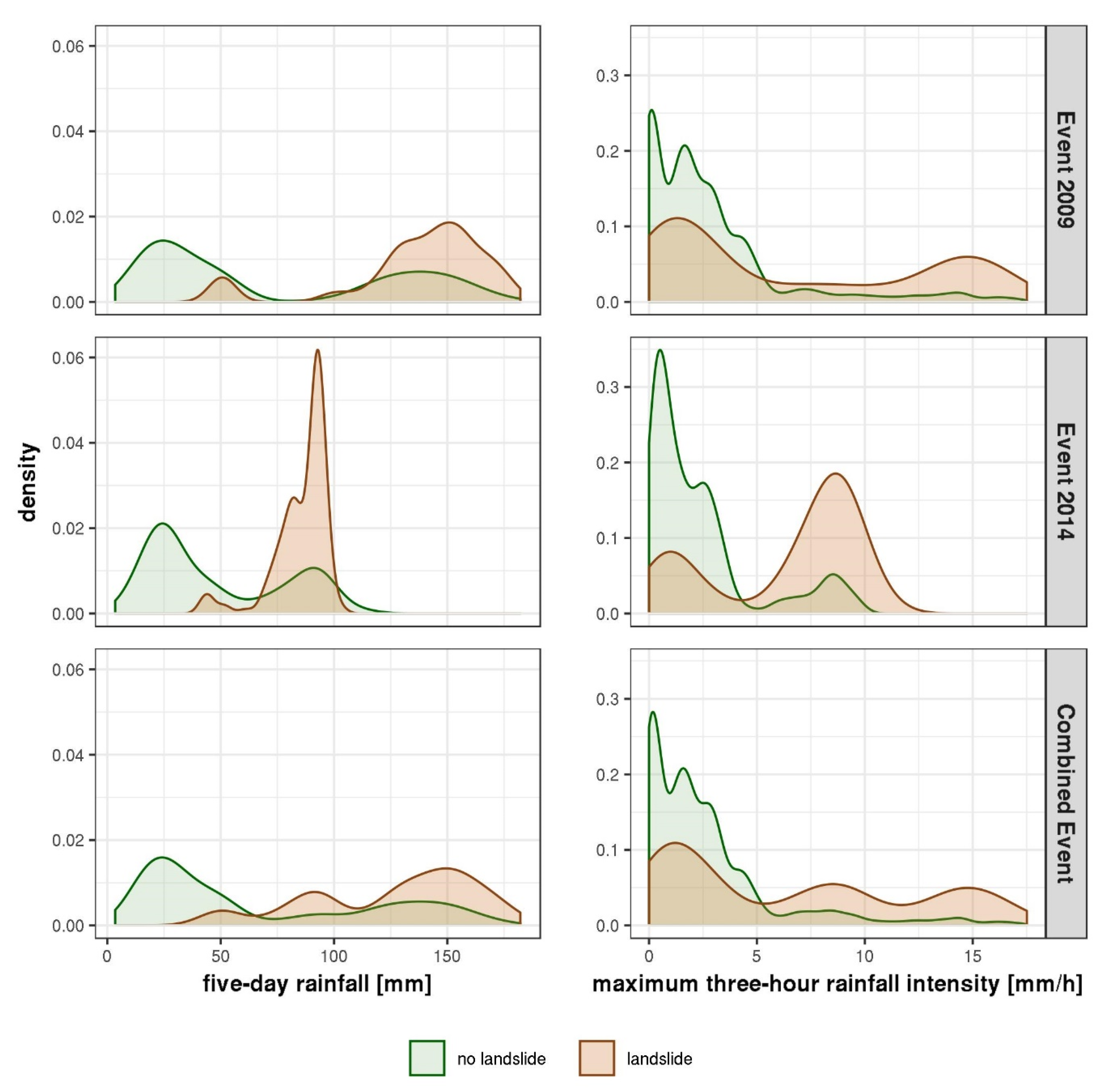
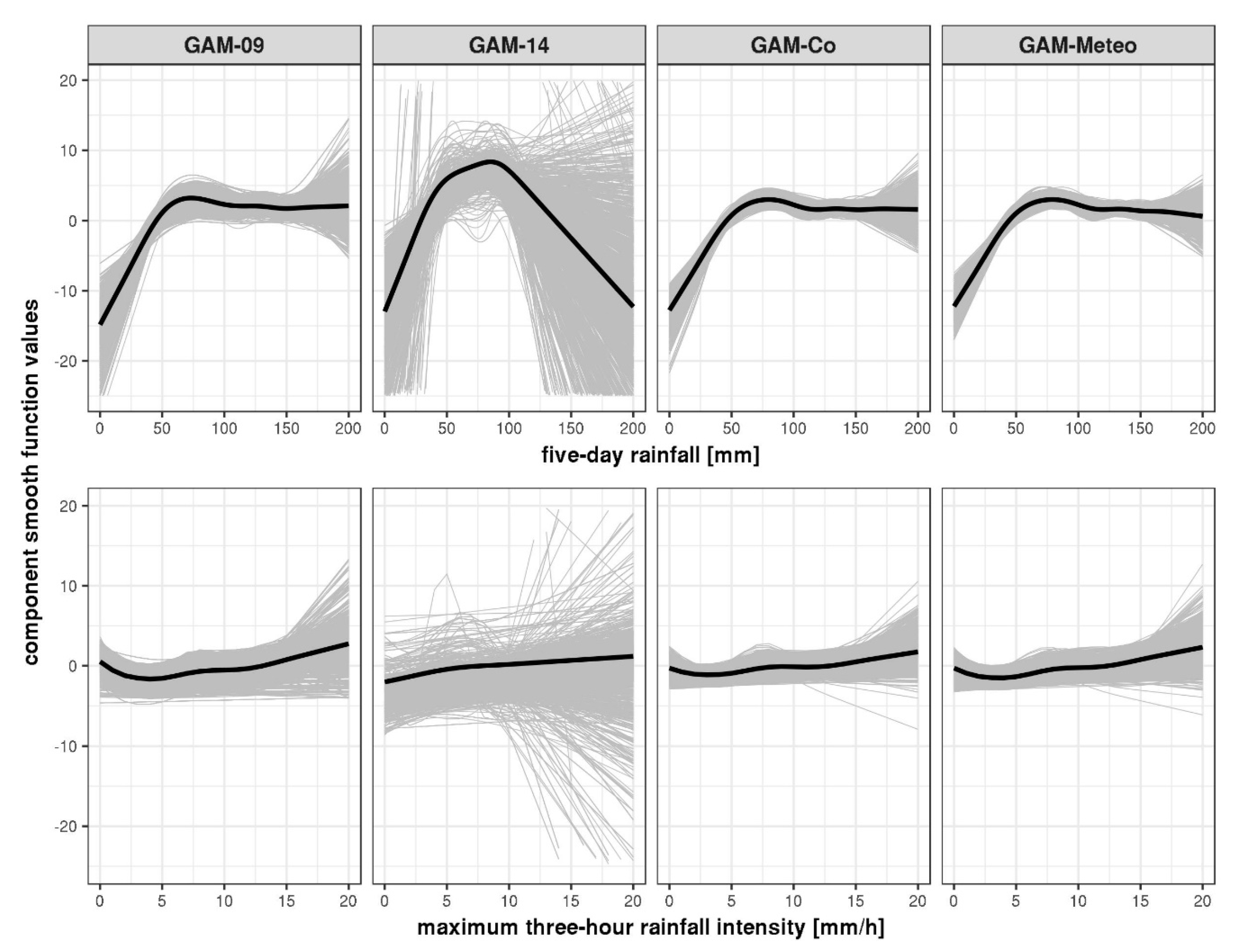
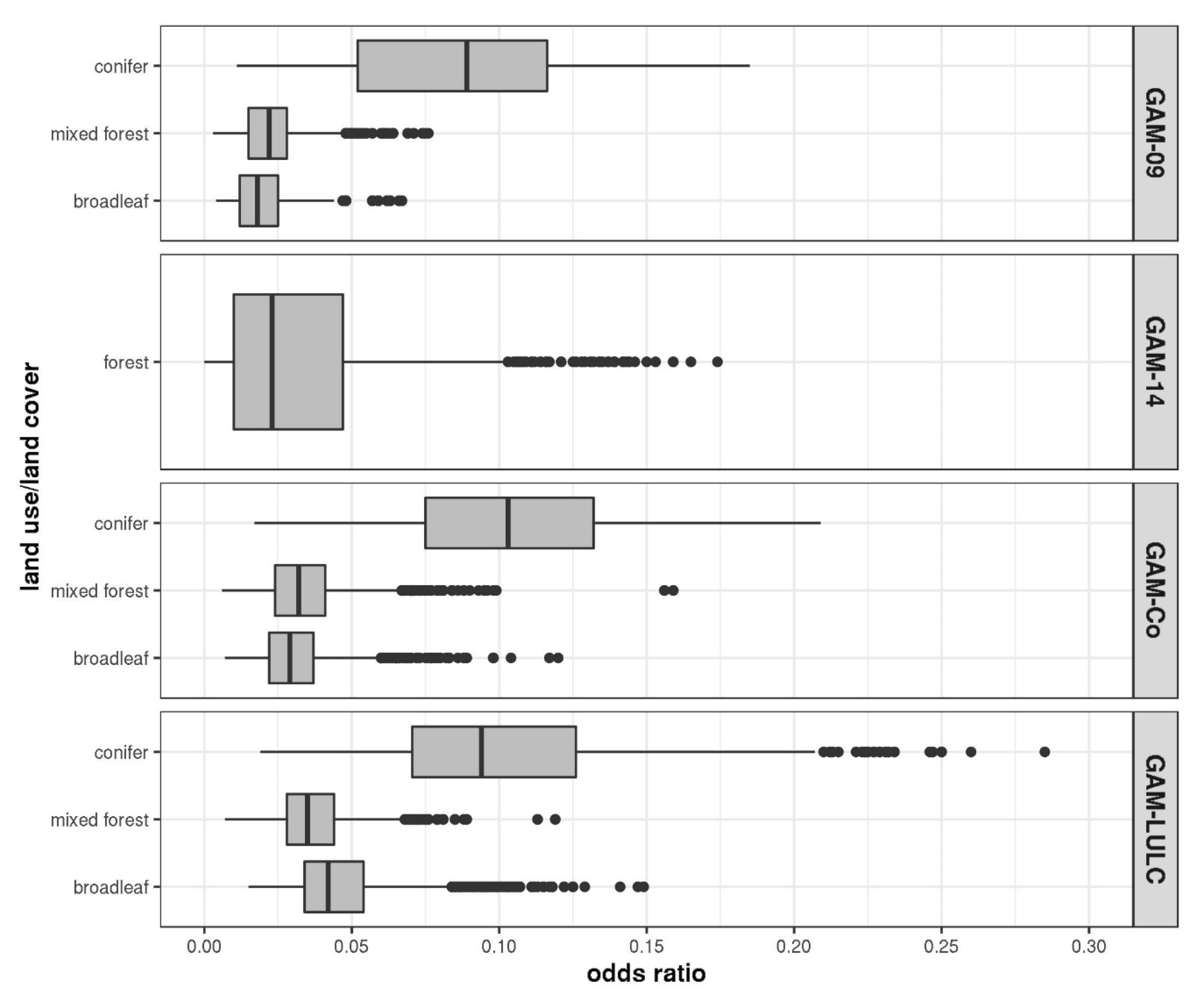
3.3. Relationship between Landslide Occurrence and Time-Varying Variables
3.3.1. Relationship to Meteorological Variables
3.3.2. Relationship to the LULC Variable
4. Discussion
4.1. Model Performance and the Role of Time-Varying Variables
4.2. Challenges and Uncertainties
5. Conclusions and Outlook
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Descriptive Summary of Input Data
| Name | Description | Source |
|---|---|---|
| Climate Data | ||
| INCA | Integrated Nowcasting through Comprehensive Analysis | Central Institute for Meteorology and Geodynamics (ZAMG) |
| Landslide Data | ||
| Event 2009 | rainfall-triggered, 22 to 25 June | Geological Survey of Austria (GBA), Institute of Military Geoinformation (IMG) |
| Event 2014 | rainfall-triggered, 12 to 15 September | Department of Hydrology, Resources and Sustainability of the Styrian Government (LS) |
| Land Surface Data | ||
| HRDTM | airborne LiDAR-derived high resolution digital terrain model | GIS department of Styria (GIS-Steiermark) |
| LULC | forest map with conifer amount; classified in: no forest, broadleaf, mixed forest and conifer | JOANNEUM RESEARCH (JR) |
| Watershed | 1303 catchment areas | GIS department of Styria (GIS-Steiermark) |
| Geological base map | reference scale: 1:50,000; classified in geological units | GIS department of Styria (GIS-Steiermark), alluvial corrected by Austrian Institute of Technology (AIT) |
| OSM | OpenStreetMap data for Styria as of 29.10.2018 | Geofabrik, OpenStreetMap (OSM) |
| Description | Total | Event 2009 | Event 2014 | |
|---|---|---|---|---|
| GBA | IMG | LS | ||
| Landslides | ||||
| presence (raw) | 626 | 218 (680) | 269 (1026) | 139 (508) |
| absence | 3130 | 2435 | 695 | |
| Landslide Type (%) | ||||
| shallow | 421 (67.3) | 414 (85) | 7 (5) | |
| deep-seated | 157 (25.1) | 73 (15) | 84 (60.4) | |
| Failure date (%) | 245 (39.1) | 106 (21.8) | 139 (100) | |
| LULC (%) | ||||
| forest | 78 (12.5) | 68 (14) | 10 (7.2) | |
| OSM | vineyard and orchard (30.8%), farmland (22.2%), urban areas (streets and buildings, 30.3%), meadow and forests (16.8%) | |||
| Description | Dates | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A: Event 2009: 16–26 June | |||||||||||||||||
| D | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | |||||||||
| n | 304 | 313 | 302 | 283 | 325 | 542 | 511 | 342 | |||||||||
| Po | 0 | 0 | 0 | 0 | 8 | 36 | 36 | 4 | |||||||||
| P | 0 | 0 | 0 | 0 | 43 | 225 | 200 | 19 | |||||||||
| A | 304 | 313 | 302 | 283 | 282 | 317 | 311 | 323 | |||||||||
| B: Event 2014: 30 August–15 September | |||||||||||||||||
| D | 30 | 31 | 01 | 02 | 03 | 04 | 05 | 06 | 07 | 08 | 09 | 10 | 11 | 12 | 13 | 14 | 15 |
| n | 4 | 6 | 5 | 9 | 13 | 7 | 7 | 6 | 6 | 3 | 116 | 123 | 96 | 87 | 186 | 125 | 35 |
| P, Po | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 6 | 99 | 24 | 10 |
| A | 4 | 6 | 5 | 9 | 13 | 7 | 7 | 6 | 6 | 3 | 116 | 123 | 96 | 81 | 87 | 101 | 25 |
| Variable | n (%) | Min | q1 | q3 | Max | IQR | ||
|---|---|---|---|---|---|---|---|---|
| land surface variables | ||||||||
| convergence index, 100 m | 3756 | −54.19 | −12.05 | 3.41 | 3.97 | 19.65 | 71.45 | 31.71 |
| convergence index, 500 m | 3756 | −46.46 | −8.84 | 4.1 | 3.91 | 16.89 | 58.79 | 25.73 |
| curvature, plan | 3756 | −0.086 | −0.002 | 0 | 0 | 0.003 | 0.06 | 0.006 |
| curvature, profile | 3756 | −0.072 | −0.003 | 0.001 | 0.001 | 0.005 | 0.051 | 0.007 |
| flow accumulation | 3756 | 4.61 | 5.96 | 6.53 | 6.67 | 7.16 | 16.73 | 1.2 |
| normalized height | 3756 | 0.04 | 0.24 | 0.48 | 0.49 | 0.72 | 0.96 | 0.48 |
| slope angle | 3756 | 0.09 | 7.36 | 12.01 | 12.77 | 17.2 | 42.32 | 9.84 |
| slope angle, catchment | 3756 | 0.2 | 8.83 | 11.87 | 11.82 | 14.48 | 33.53 | 5.65 |
| slope aspect, S-N | 3756 | −1 | −0.69 | −0.11 | −0.06 | 0.54 | 1 | 1.23 |
| slope aspect, W-E | 3756 | −1 | −0.77 | 0.1 | 0.04 | 0.8 | 1 | 1.57 |
| TPI | 3756 | −12.67 | −0.73 | 0.08 | 0.17 | 1.11 | 8.25 | 1.84 |
| SWI | 3756 | 1.21 | 2.92 | 3.29 | 3.44 | 3.8 | 7.98 | 0.89 |
| meteorological variables | ||||||||
| five-day rainfall | 3756 | 3.46 | 27.32 | 52.28 | 76.77 | 131.06 | 182.18 | 103.74 |
| maximum three-hour rainfall intensity | 3756 | 0 | 0.51 | 1.93 | 3.33 | 4.07 | 17.51 | 3.57 |
| geology | ||||||||
| 0 | 575 (15.3) | |||||||
| 1 | 1108 (29.5) | |||||||
| 2 | 1753 (46.7) | |||||||
| 3 | 320 (8.5) | |||||||
| land use/land cover forest type | ||||||||
| no forest | 2527 (68.3) | |||||||
| broadleaf | 503 (13.4) | |||||||
| mixed forest | 590 (15.7) | |||||||
| conifer | 136 (3.6) | |||||||
Appendix B. Descriptive Summary of Processing Results
| Model | Range | Min | Max | IQR | |||
|---|---|---|---|---|---|---|---|
| A: Spatial-Cross Validation (SpCV) | |||||||
| GAM-09 1 | 0.94 | 0.94 | 0.14 | 0.84 | 0.98 | 0.04 | |
| GAM-14 1 | 0.92 | 0.90 | 0.56 | 0.44 | 1.00 | 0.07 | |
| GAM-Co 1,2 | 0.94 | 0.94 | 0.15 | 0.84 | 0.99 | 0.02 | |
| B: Spatio-Temporal Cross Validation (SpTempCV) | |||||||
| GAM-09 predicting 2014 | 0.89 | 0.89 | 0.08 | 0.84 | 0.92 | 0.01 | |
| GAM-14 predicting 2009 | 0.72 | 0.69 | 0.66 | 0.28 | 0.94 | 0.31 | |
| GAM-Co predicting 2009 | 0.95 | 0.94 | 0.08 | 0.89 | 0.97 | 0.02 | |
| GAM-Co predicting 2014 | 0.91 | 0.91 | 0.15 | 0.83 | 0.98 | 0.03 | |
| C: Spatial-Cross Validation Comparison (SpCV-Comparison) | |||||||
| GAM-Base 2 | 0.81 | 0.80 | 0.30 | 0.64 | 0.94 | 0.06 | |
| GAM-LULC 2 | 0.87 | 0.86 | 0.28 | 0.67 | 0.95 | 0.06 | |
| GAM-Meteo 2 | 0.91 | 0.91 | 0.19 | 0.80 | 1.00 | 0.03 | |
| GAM-Co 1,2 | 0.94 | 0.94 | 0.15 | 0.84 | 0.99 | 0.02 | |
| Model | Z | -Values | ) | |
|---|---|---|---|---|
| GAM-Base | 0.81 | |||
| GAM-LULC | 40.91 | <0.001 | 0.87 (0.06) | 0.82 |
| GAM-Meteo | 42.58 | <0.001 | 0.91 (0.04) | 0.85 |
| GAM-Co | 42.48 | <0.001 | 0.94 (0.03) | 0.85 |
| Variable | GAM-09 | GAM-14 | GAM-Co | GAM-LULC | GAM-Meteo | GAM-Base |
|---|---|---|---|---|---|---|
| land surface variables | ||||||
| convergence index, 100 m | 0.39 (12) | 1.37 (10) | 0.34 (10) | 0.46 (8) | 0.34 (11) | 0.39 (10) |
| convergence index, 500 m | 0.43 (10) | 1.46 (8) | 0.3 (11) | 0.15 (12) | 0.28 (12) | 0.14 (13) |
| curvature, plan | 0.25 (14) | 1.23 (12) | 0.21 (14) | 0.4 (9) | 0.24 (14) | 0.31 (11) |
| curvature, profile | 1.67 (4) | 1.43 (9) | 1.21 (4) | 1.41 (3) | 0.92 (4) | 1.35 (2) |
| flow accumulation | 0.39 (13) | 0.94 (14) | 0.27 (13) | 0.32 (11) | 0.28 (13) | 0.54 (9) |
| normalized height | 0.42 (11) | 2.12 (6) | 0.55 (9) | 1.4 (4) | 0.59 (6) | 1.33 (3) |
| slope angle | 7.05 (3) | 2.03 (7) | 5.31 (3) | 7.85 (2) | 3.87 (2) | 5.96 (1) |
| slope angle, catchment area | 0.17 (16) | 0.64 (16) | 0.08 (16) | 0.12 (13) | 0.11 (15) | 0.2 (12) |
| slope aspect, S-N | 0.17 (15) | 1.35 (11) | 0.09 (15) | 0.1 (14) | 0.75 (5) | 1.06 (4) |
| slope aspect, W-E | 0.92 (6) | 0.81 (15) | 0.27 (12) | 0.35 (10) | 0.38 (9) | 0.56 (8) |
| TPI | 0.54 (9) | 2.37 (4) | 0.66 (8) | 1.06 (6) | 0.37 (10) | 0.69 (6) |
| SWI | 0.74 (7) | 0.95 (13) | 0.71 (7) | 0.88 (7) | 0.5 (8) | 0.59 (7) |
| meteorological variables | ||||||
| five-day rainfall | 13.57 (1) | 17.75 (1) | 15.13 (1) | 16.85 (1) | ||
| maximum three-hour rainfall intensity | 1.58 (5) | 2.91 (3) | 1.05 (5) | 1.75 (3) | ||
| geology | ||||||
| geology | 0.55 (8) | 2.27 (5) | 0.73 (6) | 1.18 (5) | 0.57 (7) | 0.77 (5) |
| land use/land cover | ||||||
| forest type | 9.31 (2) | 4.14 (2) | 8.57 (2) | 12.45 (1) |
| Class | Z | N | -Values | ) | OR | |
|---|---|---|---|---|---|---|
| A: GAM-09 | ||||||
| conifer | −2.42 | |||||
| mixed forest | −33.31 | 1484 | <0.001 | −3.86 (−1.44) | 0.24 | −0.86 |
| broadleaf | −14.42 | 2500 | <0.001 | −4.07 (−0.21) | 0.81 | −0.29 |
| B: GAM-Co | ||||||
| conifer | −2.27 | |||||
| mixed forest | −33.29 | 1608 | <0.001 | −3.44 (−1.17) | 0.31 | −0.83 |
| broadleaf | −7.33 | 2500 | <0.001 | −3.61 (−0.17) | 0.84 | −0.14 |
| C: GAM-LULC | ||||||
| conifer | −2.36 | |||||
| broadleaf | −41.23 | 2375 | <0.001 | −3.19 (−0.83) | 0.44 | −0.85 |
| mixed forest | −20.15 | 2500 | <0.001 | −3.32 (−0.14) | 0.87 | −0.4 |


References
- Hornich, R.; Adelwöhrer, R. Landslides in Styria in 2009. Geomech. Tunn. 2010, 3, 455–461. [Google Scholar] [CrossRef]
- ZAMG. Meldungen zu Unwetter und Witterungsbedingten Schäden in der Wirtschaft / September 2014 [Reports on Severe Weather and Weather-Related Losses in the Economy/September 2014]; ZAMG. 2014. Available online: https://www.zamg.ac.at/zamgWeb/klima/klimarueckblick/archive/2014/09/unwetter09-14.pdf (accessed on 30 April 2020).
- Crozier, M.J. Deciphering the effect of climate change on landslide activity: A review. Geomorphology 2010, 124, 260–267. [Google Scholar] [CrossRef]
- Crozier, M.J.; Glade, T. Landslide Hazard and Risk: Issues, Concepts and Approach. In Landslide Hazard and Risk; Glade, T., Anderson, M., Crozier, M.J., Eds.; John Wiley & Sons: Chichester, UK, 2005; pp. 1–40. [Google Scholar]
- Papathoma-Köhle, M.; Glade, T. The role of vegetation cover change for landslide hazard and risk. In The Role of Ecosystems in Disaster Risk Reduction; UNU-Press: Tokyo, Japan, 2013; pp. 293–320. [Google Scholar]
- Promper, C.; Gassner, C.; Glade, T. Spatiotemporal patterns of landslide exposure – a step within future landslide risk analysis on a regional scale applied in Waidhofen/Ybbs Austria. Int. J. Disaster Risk Reduct. 2015, 12, 25–33. [Google Scholar] [CrossRef]
- Kociu, A.; Schwarz, L.; Hagen, K.; Rudolf-Miklau, F. New Perspectives on Landslide Assessment for Spatial Planning in Austria. In Advancing Culture of Living with Landslides; Mikoš, M., Vilímek, V., Yin, Y., Sassa, K., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 45–50. [Google Scholar]
- Malamud, B.D.; Turcotte, D.L.; Guzzetti, F.; Reichenbach, P. Landslide inventories and their statistical properties. Earth Surf. Process. Landf. 2004, 29, 687–711. [Google Scholar] [CrossRef]
- Guzzetti, F.; Reichenbach, P.; Cardinali, M.; Galli, M.; Ardizzone, F. Probabilistic landslide hazard assessment at the basin scale. Geomorphology 2005, 72, 272–299. [Google Scholar] [CrossRef]
- van Westen, C.J.; van Asch, T.W.J.; Soeters, R. Landslide hazard and risk zonation—why is it still so difficult? Bull. Eng. Geol. Environ. 2006, 65, 167–184. [Google Scholar] [CrossRef]
- Reichenbach, P.; Rossi, M.; Malamud, B.D.; Mihir, M.; Guzzetti, F. A review of statistically-based landslide susceptibility models. Earth-Sci. Rev. 2018, 180, 60–91. [Google Scholar] [CrossRef]
- Brabb, E.E. Innovative approaches to landslide hazard and risk mapping. In Proceedings of the Fourth International Symposium on Landslides; Canadian Geotechnical Society: Toronto, ON, Canada, 1984; Volume 1, pp. 307–328. [Google Scholar]
- Fell, R.; Corominas, J.; Bonnard, C.; Cascini, L.; Leroi, E.; Savage, W.Z. Guidelines for landslide susceptibility, hazard and risk zoning for land use planning. Eng. Geol. 2008, 102, 85–98. [Google Scholar] [CrossRef]
- Petschko, H.; Brenning, A.; Bell, R.; Goetz, J.; Glade, T. Assessing the quality of landslide susceptibility maps – case study Lower Austria. Nat. Hazards Earth Syst. Sci. 2014, 14, 95–118. [Google Scholar] [CrossRef]
- Varnes, D.J. International Association of Engineering Geology Commission on Landslides and Other Mass Movements on Slopes. In Landslide Hazard Zonation: A Review of Principles and Practice; United Nations Educational: Paris, France, 1984. [Google Scholar]
- Carrara, A. Uncertainty in Evaluating Landslide Hazard and Risk. In Prediction and Perception of Natural Hazards: Proceedings Symposium, 22–26 October 1990, Perugia, Italy; Nemec, J., Nigg, J.M., Siccardi, F., Eds.; Advances in Natural and Technological Hazards Research; Springer: Dordrecht, The Netherlands, 1993; pp. 101–109. [Google Scholar]
- Reichenbach, P.; Busca, C.; Mondini, A.C.; Rossi, M. The Influence of Land Use Change on Landslide Susceptibility Zonation: The Briga Catchment Test Site (Messina, Italy). Environ. Manag. 2014, 54, 1372–1384. [Google Scholar] [CrossRef]
- Samia, J.; Temme, A.; Bregt, A.K.; Wallinga, J.; Stuiver, J.; Guzzetti, F.; Ardizzone, F.; Rossi, M. Implementing landslide path dependency in landslide susceptibility modelling. Landslides 2018, 15, 2129–2144. [Google Scholar] [CrossRef]
- Gariano, S.L.; Guzzetti, F. Landslides in a changing climate. Earth-Sci. Rev. 2016, 162, 227–252. [Google Scholar] [CrossRef]
- Segoni, S.; Leoni, L.; Benedetti, A.I.; Catani, F.; Righini, G.; Falorni, G.; Gabellani, S.; Rudari, R.; Silvestro, F.; Rebora, N. Towards a definition of a real-time forecasting network for rainfall induced shallow landslides. Nat. Hazards Earth Syst. Sci. 2009, 9, 2119–2133. [Google Scholar] [CrossRef]
- Rossi, G.; Catani, F.; Leoni, L.; Segoni, S.; Tofani, V. HIRESSS: A physically based slope stability simulator for HPC applications. Nat. Hazards Earth Syst. Sci. 2013, 13, 151–166. [Google Scholar] [CrossRef]
- Melillo, M.; Brunetti, M.T.; Peruccacci, S.; Gariano, S.L.; Guzzetti, F. An algorithm for the objective reconstruction of rainfall events responsible for landslides. Landslides 2015, 12, 311–320. [Google Scholar] [CrossRef]
- Rossi, M.; Luciani, S.; Valigi, D.; Kirschbaum, D.; Brunetti, M.T.; Peruccacci, S.; Guzzetti, F. Statistical approaches for the definition of landslide rainfall thresholds and their uncertainty using rain gauge and satellite data. Geomorphology 2017, 285, 16–27. [Google Scholar] [CrossRef]
- Guzzetti, F.; Peruccacci, S.; Rossi, M.; Stark, C.P. The rainfall intensity–duration control of shallow landslides and debris flows: An update. Landslides 2008, 5, 3–17. [Google Scholar] [CrossRef]
- Aleotti, P.; Chowdhury, R. Landslide hazard assessment: Summary review and new perspectives. Bull. Eng. Geol. Environ. 1999, 58, 21–44. [Google Scholar] [CrossRef]
- Monsieurs, E.; Dewitte, O.; Demoulin, A. A susceptibility-based rainfall threshold approach for landslide occurrence. Nat. Hazards Earth Syst. Sci. 2019, 19, 775–789. [Google Scholar] [CrossRef]
- Segoni, S.; Lagomarsino, D.; Fanti, R.; Moretti, S.; Casagli, N. Integration of rainfall thresholds and susceptibility maps in the Emilia Romagna (Italy) regional-scale landslide warning system. Landslides 2015, 12, 773–785. [Google Scholar] [CrossRef]
- Segoni, S.; Tofani, V.; Rosi, A.; Catani, F.; Casagli, N. Combination of Rainfall Thresholds and Susceptibility Maps for Dynamic Landslide Hazard Assessment at Regional Scale. Front. Earth Sci. 2018, 6, 1–11. [Google Scholar] [CrossRef]
- Glade, T. Landslide occurrence as a response to land use change: A review of evidence from New Zealand. CATENA 2003, 51, 297–314. [Google Scholar] [CrossRef]
- Persichillo, M.G.; Bordoni, M.; Meisina, C. The role of land use changes in the distribution of shallow landslides. Sci. Total Environ. 2017, 574, 924–937. [Google Scholar] [CrossRef] [PubMed]
- Pisano, L.; Zumpano, V.; Malek, Ž.; Rosskopf, C.M.; Parise, M. Variations in the susceptibility to landslides, as a consequence of land cover changes: A look to the past, and another towards the future. Sci. Total Environ. 2017, 601–602, 1147–1159. [Google Scholar] [CrossRef] [PubMed]
- Schmaltz, E.M.; Steger, S.; Glade, T. The influence of forest cover on landslide occurrence explored with spatio-temporal information. Geomorphology 2017, 290, 250–264. [Google Scholar] [CrossRef]
- Torizin, J.; Wang, L.; Fuchs, M.; Tong, B.; Balzer, D.; Wan, L.; Kuhn, D.; Li, A.; Chen, L. Statistical landslide susceptibility assessment in a dynamic environment: A case study for Lanzhou City, Gansu Province, NW China. J. Mt. Sci. 2018, 15, 1299–1318. [Google Scholar] [CrossRef]
- Gassner, C.; Promper, C.; Beguería, S.; Glade, T. Climate Change Impact for Spatial Landslide Susceptibility. In Engineering Geology for Society and Territory; Springer International Publishing: Cham, Switzerland, 2015; Volume 1, pp. 429–433. [Google Scholar]
- Shou, K.-J.; Yang, C.-M. Predictive analysis of landslide susceptibility under climate change conditions—A study on the Chingshui River Watershed of Taiwan. Eng. Geol. 2015, 192, 46–62. [Google Scholar] [CrossRef]
- Kim, H.G.; Lee, D.K.; Park, C.; Kil, S.; Son, Y.; Park, J.H. Evaluating landslide hazards using RCP 4.5 and 8.5 scenarios. Environ. Earth Sci. 2015, 73, 1385–1400. [Google Scholar] [CrossRef]
- Proske, H.; Bauer, C. Methodik zur Erstellung einer Gefahrenhinweiskarte für Rutschungen in der Steiermark [Methodology of the generation of an indicative hazard map for landslides in Styria]. Torrent Avalanche Landslide Rock Fall 2012, 11, 184. [Google Scholar]
- Burak, A.; Zepp, H.; Zöller, L. Reliefenergie—Wo die Höhenunterschiede am stärksten sind [Relative relief—where the differences in height are the greatest]. In Relief, Boden und Wasser; Leibniz-Institut für Länderkunde, Ed.; Nationalatlas Bundesrepublik Deutschland; Springer Spektrum: Heidelberg, Germany, 2003; Volume 2, pp. 26–27. [Google Scholar]
- Gasser, D.; Gusterhuber, J.; Krische, O.; Puhr, B.; Scheucher, L.; Wagner, T.; Stüwe, K. Geology of Styria: An overview. Mitteilungen Naturwissenschaftlichen Ver. Für Steiermark 2009, 139, 5–36. [Google Scholar]
- Haiden, T. Meteorologische Analyse des Niederschlags von 22.-25. Juni 2009 [Meteorological Analysis of the Precipitation from 22 to 25 June 2009]; ZAMG: Vienna, Austria, 2009; p. 5. Available online: http://www.zamg.ac.at/docs/aktuell/2009-06-30_Meteorologische%20Analyse%20HOWA2009.pdf (accessed on 30 April 2020).
- Landeswarnzentrale Steiermark Niederschlagswarnung für die Steiermark. Für den Zeitraum: Donnerstag, 11.09.2014 12:00 Uhr MESZ bis Sonntag, 14.09.2014 12:00 Uhr MESZ [Precipitation Warning for Styria. For the Period: Thursday, 11 September 2014 12:00 CEST to Sunday, 14 September 2014 12:00 CEST]; Graz, Austria. 2014. Available online: http://www.katastrophenschutz.steiermark.at/cms/beitrag/12083692/5461/ (accessed on 30 April 2020).
- Landeswarnzentrale Steiermark Update der Niederschlagswarnung für die Steiermark. Für den Zeitraum: Heute bis Sonntag, 14.09.2014 12:00 Uhr MESZ [Update of the Precipitation Warning for Styria. For the Period: Today until Sunday, 14 September 2014 12:00 CEST]; Graz, Austria. 2014. Available online: http://www.katastrophenschutz.steiermark.at/cms/beitrag/12084075/443/ (accessed on 30 April 2020).
- Haiden, T.; Kann, A.; Wittmann, C.; Pistotnik, G.; Bica, B.; Gruber, C. The Integrated Nowcasting through Comprehensive Analysis (INCA) System and Its Validation over the Eastern Alpine Region. Weather Forecast. 2010, 26, 166–183. [Google Scholar] [CrossRef]
- Gräf, W. Naturraumpotentialkarten im Dienste einer umweltbewußten Rohstoffsicherung, dargestellt am Beispiel der Steiermark [Natural Environments Potential maps in the service of an environmentally conscious securing of raw materials, the case study of Styria]. Mitteilungen Österr. Geol. Ges. 1986, 79, 15–29. [Google Scholar]
- Gräf, W.; Niederl, R. Zwanzig Jahre Rohstoffforschung in der Steiermark 1974–1994 [Twenty years of raw materials research in Styria 1974–1994]. Steirische Beitr. Zur Rohst. Energieforschung 1994, 10, 1–96. [Google Scholar]
- Flügel, H.W.; Neubauer, F.R. Geologische Karte der Steiermark 1:200.000 [Geological Map of Styria 1:200,000]; Geologische Bundesanstalt: Vienna, Austria, 1984.
- Kautz, H. Geodatenaufbereitung in einem Assistenzeinsatz des Österreichischen Bundesheeres - am Beispiel Katastrophenregion Feldbach 2009 [Geodata preparation in an assistance mission of the Austrian Armed Forces - the example of the disaster region Feldbach 2009]. In Proceedings of the Angewandte Geoinformatik 2010; Strobl, J., Blaschke, T., Griesebner, G., Eds.; Wichmann: Salzburg, Austria, 2010; Volume 22, pp. 638–640. [Google Scholar]
- Lotter, M.; Schwarz, L.; Haberler, A.; Kociu, A. Erhebung und Dokumentation gravitativer Massenbewegungen in der Katastrophenregion Feldbach im Sommer 2009. Eine vorläufige Bestandsaufnahme [Survey and Documentation of Mass Movements in the Disaster Region Feldbach in Summer 2009. A Preliminary Inventory]. Presented at the Landesgeologentag, Graz, Austria, 12 November 2009. [Google Scholar]
- Cruden, D.M.; Varnes, D.J. Landslide Types and Processes. In Landslides Investigation and Mitigation. Transportation Research Board, US National Research Council; Turner, A.K., Schuster, R.L., Eds.; Special Report 247; U.S. National Academy of Sciences: Washington, DC, USA, 1996; pp. 36–75. [Google Scholar]
- PostGIS Project. PostGIS 2.5.4dev Manual. DEV (Thu 05 Sep 2019 05:11:29 PM UTC rev. 17805). Available online: https://postgis.net/stuff/postgis-2.5.pdf (accessed on 30 April 2020).
- Hastie, T.; Tibshirani, R. Generalized Additive Models. Stat. Sci. 1986, 1, 297–310. [Google Scholar] [CrossRef]
- Wood, S.N. Generalized Additive Models: An Introduction with R, 2nd ed.; Chapman and Hall/CRC: Boca Raton, FL, USA, 2017. [Google Scholar]
- Goetz, J.; Guthrie, R.; Brenning, A. Integrating physical and empirical landslide susceptibility models using generalized additive models. Geomorphology 2011, 129, 376–386. [Google Scholar] [CrossRef]
- Goetz, J.; Brenning, A.; Petschko, H.; Leopold, P. Evaluating machine learning and statistical prediction techniques for landslide susceptibility modeling. Comput. Geosci. 2015, 81, 1–11. [Google Scholar] [CrossRef]
- Brenning, A.; Schwinn, M.; Ruiz-Páez, A.P.; Muenchow, J. Landslide susceptibility near highways is increased by 1 order of magnitude in the Andes of southern Ecuador, Loja province. Nat. Hazards Earth Syst. Sci. 2015, 15, 45–57. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2018; R Version 3.5.2.; Available online: https://www.R-project.org/ (accessed on 30 April 2020).
- Bischl, B.; Lang, M.; Kotthoff, L.; Schiffner, J.; Richter, J.; Studerus, E.; Casalicchio, G.; Jones, Z.M. mlr: Machine Learning in R. J. Mach. Learn. Res. 2016, 17, 1–5. [Google Scholar]
- Neteler, M.; Mitasova, H. Open Source GIS: A GRASS GIS Approach, 3rd ed.; Springer: New York, NY, USA, 2008. [Google Scholar]
- Conrad, O.; Bechtel, B.; Dietrich, H.; Fischer, E.; Gerlitz, L.; Wehberg, J.; Wichmann, V.; Böhner, J. System for Automated Geoscientific Analyses (SAGA) v. 2.1.4. Geosci. Model Dev. 2015, 8, 1991–2007. [Google Scholar] [CrossRef]
- Tarboton, D.G.; Dash, P.; Sazib, N. TauDEM 5.3: Guide to Using the TauDEM Command Line Functions; Utah State University: Logan, UT, USA, 2015. [Google Scholar]
- Bivand, R.S. rgrass7: Interface between GRASS 7 Geographical Information System and R; 2018. R Package Version 0.1-12. Available online: https://CRAN.R-project.org/package=rgrass7 (accessed on 30 April 2020).
- Brenning, A.; Bangs, D.; Becker, M. RSAGA: SAGA Geoprocessing and Terrain Analysis; 2018. R Package Version 1.3.0. Available online: https://CRAN.R-project.org/package=RSAGA (accessed on 30 April 2020).
- Steger, S.; Glade, T. The Challenge of “Trivial Areas” in Statistical Landslide Susceptibility Modelling. In Proceedings of the Advancing Culture of Living with Landslides; Mikos, M., Tiwari, B., Yin, Y., Sassa, K., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 803–808. [Google Scholar] [CrossRef]
- Bornaetxea, T.; Rossi, M.; Marchesini, I.; Alvioli, M. Effective surveyed area and its role in statistical landslide susceptibility assessments. Nat. Hazards Earth Syst. Sci. 2018, 18, 2455–2469. [Google Scholar] [CrossRef]
- Meinhardt, M.; Fink, M.; Tünschel, H. Landslide susceptibility analysis in central Vietnam based on an incomplete landslide inventory: Comparison of a new method to calculate weighting factors by means of bivariate statistics. Geomorphology 2015, 234, 80–97. [Google Scholar] [CrossRef]
- Luxen, D.; Vetter, C. Real-time Routing with OpenStreetMap Data. In Proceedings of the 19th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems, Chicago, IL, USA, 1–4 November 2011; ACM: New York, NY, USA, 2011; pp. 513–516. [Google Scholar] [CrossRef]
- Hahsler, M.; Hornik, K. TSP - Infrastructure for the traveling salesperson problem. J. Stat. Softw. 2007, 23, 1–21. [Google Scholar] [CrossRef]
- Hahsler, M.; Hornik, K. TSP: Traveling Salesperson Problem (TSP); 2019. R Package Version 1.1-7. Available online: https://CRAN.R-project.org/package=TSP (accessed on 30 April 2020).
- Knevels, R. RainSlide: Rainfall-Induced Landslide Analysis Tools; 2020. R Package Version 0.0.0-9000. Available online: https://github.com/raff-k/RainSlide (accessed on 30 April 2020).
- van Westen, C.J.; Castellanos, E.; Kuriakose, S.L. Spatial data for landslide susceptibility, hazard, and vulnerability assessment: An overview. Eng. Geol. 2008, 102, 112–131. [Google Scholar] [CrossRef]
- Koethe, R.; Lehmeier, F. SARA - System zur Automatischen Relief-Analyse. User Manual, 2nd ed.; Department of Geography, University of Göttingen: Göttingen, Germany, 1996. [Google Scholar]
- Zevenbergen, L.W.; Thorne, C.R. Quantitative Analysis of Land Surface Topography. Earth Surf. Process. Landf. 1987, 12, 47–56. [Google Scholar] [CrossRef]
- Tarboton, D.G. A new method for the determination of flow directions and upslope areas in grid digital elevation models. Water Resour. Res. 1997, 33, 309–319. [Google Scholar] [CrossRef]
- Dietrich, H.; Böhner, J. Cold Air Production and Flow in a Low Mountain Range Landscape in Hessia. SAGA–Seconds Hambg. Beitr. Zur Phys. Geogr. Landschaftsökologie 2008, 19, 37–48. [Google Scholar]
- Böhner, J.; Selige, T. Spatial Prediction of Soil Attributes Using Terrain Analysis and Climate Regionalisation. Gött. Geogr. Abh. 2006, 115, 13–27. [Google Scholar]
- Brenning, A.; Trombotto, D. Logistic regression modeling of rock glacier and glacier distribution: Topographic and climatic controls in the semi-arid Andes. Geomorphology 2006, 81, 141–154. [Google Scholar] [CrossRef]
- Guisan, A.; Weiss, S.B.; Weiss, A.D. GLM versus CCA spatial modeling of plant species distribution. Plant Ecol. 1999, 143, 107–122. [Google Scholar] [CrossRef]
- Brenning, A. Improved spatial analysis and prediction of landslide susceptibility: Practical recommendations. In Proceedings of the Landslides and Engineered Slopes: Protecting Society through Improved Understanding, Banff, AB, Canada, 3–8 June 2012; Eberhardt, E., Froese, C., Turner, A.K., Leroueil, S., Eds.; CRC Press/Balkema: Banff, AB, Canada, 2012; Volume 1, pp. 789–794. [Google Scholar]
- Petschko, H.; Bell, R.; Glade, T.; Brenning, A. Landslide susceptibility modeling with generalized additive models—facing the heterogeneity of large regions. In Protecting Society through Improved Understanding; Landslides and Engineered Slopes; CRC Press: Boca Raton, FL, USA, 2012; Volume 1, pp. 769–777. [Google Scholar]
- Zweig, M.H.; Campbell, G. Receiver-operating characteristic (ROC) plots: A fundamental evaluation tool in clinical medicine. Clin. Chem. 1993, 39, 561–577. [Google Scholar] [CrossRef]
- Hosmer, D.W.; Lemeshow, S.; Sturdivant, R.X. Applied Logistic Regression; Wiley Series in Probability and Statistics; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Goetz, J.; Brenning, A.; Marcer, M.; Bodin, X. Modeling the precision of structure-from-motion multi-view stereo digital elevation models from repeated close-range aerial surveys. Remote Sens. Environ. 2018, 210, 208–216. [Google Scholar] [CrossRef]
- Szumilas, M. Explaining Odds Ratios. J. Can. Acad. Child Adolesc. Psychiatry 2010, 19, 227–229. [Google Scholar]
- Hothorn, T.; Hornik, K.; van de Wiel, M.A.; Zeileis, A. A Lego System for Conditional Inference. Am. Stat. 2006, 60, 257–263. [Google Scholar] [CrossRef]
- Demšar, J. Statistical Comparisons of Classifiers over Multiple Data Sets. J. Mach. Learn. Res. 2006, 7, 1–30. [Google Scholar]
- Benjamini, Y.; Hochberg, Y. Controlling the False Discovery Rate: A Practical and Powerful Approach to Multiple Testing. J. R. Stat. Soc. Ser. B Methodol. 1995, 57, 289–300. [Google Scholar] [CrossRef]
- Rosenthal, R. Meta-Analytic Procedures for Social Research; SAGE Publications: Thousand Oaks, CA, USA, 1991. [Google Scholar]
- Guzzetti, F.; Peruccacci, S.; Rossi, M.; Stark, C.P. Rainfall thresholds for the initiation of landslides in central and southern Europe. Meteorol. Atmos. Phys. 2007, 98, 239–267. [Google Scholar] [CrossRef]
- Segoni, S.; Piciullo, L.; Gariano, S.L. A review of the recent literature on rainfall thresholds for landslide occurrence. Landslides 2018, 15, 1483–1501. [Google Scholar] [CrossRef]
- Moser, M.; Hohensinn, F. Geotechnical aspects of soil slips in Alpine regions. Eng. Geol. 1983, 19, 185–211. [Google Scholar] [CrossRef]
- Loibl, W.; Köstl, M.; Züger, J.; Leopold, P. Climate Change Impact on Landslide Risk – Estimating Change in Heavy Precipitation Event Frequencies. In Proceedings of the AGIT. Journal für Angewandte Geoinformatik; Strobl, J., Zagel, B., Griesebner, G., Blaschke, T., Eds.; Wichmann: Salzburg, Austria, 2019; pp. 368–382. [Google Scholar]
- Peruccacci, S.; Brunetti, M.T.; Gariano, S.L.; Melillo, M.; Rossi, M.; Guzzetti, F. Rainfall thresholds for possible landslide occurrence in Italy. Geomorphology 2017, 290, 39–57. [Google Scholar] [CrossRef]
- Marchi, L.; Arattano, M.; Deganutti, A.M. Ten years of debris-flow monitoring in the Moscardo Torrent (Italian Alps). Geomorphology 2002, 46, 1–17. [Google Scholar] [CrossRef]
- Popescu, M. Landslide causal factors and landslide remedial options, Keynote lecture. In Proceedings of the 3rd International Conference on Landslides, Slope Stability and the Safety of Infra-Structures, Singapore, 11–12 July 2002; Ci-Premier Pte Ltd.: Singapore, 2002; Volume 3, pp. 61–81. [Google Scholar]
- Marston, R.A. Geomorphology and vegetation on hillslopes: Interactions, dependencies, and feedback loops. Geomorphology 2010, 116, 206–217. [Google Scholar] [CrossRef]
- Steger, S.; Brenning, A.; Bell, R.; Glade, T. The influence of systematically incomplete shallow landslide inventories on statistical susceptibility models and suggestions for improvements. Landslides 2017, 14, 1767–1781. [Google Scholar] [CrossRef]
- Corominas, J.; Moya, J. Reconstructing recent landslide activity in relation to rainfall in the Llobregat River basin, Eastern Pyrenees, Spain. Geomorphology 1999, 30, 79–93. [Google Scholar] [CrossRef]
- Cardinali, M.; Galli, M.; Guzzetti, F.; Ardizzone, F.; Reichenbach, P.; Bartoccini, P. Rainfall induced landslides in December 2004 in south-western Umbria, central Italy: Types, extent, damage and risk assessment. Nat. Hazards Earth Syst. Sci. 2006, 6, 237–260. [Google Scholar] [CrossRef]
- Stokes, A.; Atger, C.; Bengough, A.G.; Fourcaud, T.; Sidle, R.C. Desirable plant root traits for protecting natural and engineered slopes against landslides. Plant Soil 2009, 324, 1–30. [Google Scholar] [CrossRef]
- Collison, A.; Wade, S.; Griffiths, J.; Dehn, M. Modelling the impact of predicted climate change on landslide frequency and magnitude in SE England. Eng. Geol. 2000, 55, 205–218. [Google Scholar] [CrossRef]
- Glade, T.; Crozier, M.J. A Review of Scale Dependencyin Landslide Hazardand Risk Analysis. In Landslide Hazard and Risk; Glade, T., Anderson, M., Crozier, M.J., Eds.; John Wiley & Sons: Chichester, UK, 2005; pp. 75–138. [Google Scholar]
- Kirschbaum, D.; Stanley, T. Satellite-Based Assessment of Rainfall-Triggered Landslide Hazard for Situational Awareness. Earths Future 2018, 6, 505–523. [Google Scholar] [CrossRef]

| Variable(s) | Software | Setting | Method |
|---|---|---|---|
| land surface variables | |||
| convergence index (100 m, 500 m) | SAGA GIS | r = 100 m, 500 m | [71] |
| curvature (plan, profile) | SAGA GIS | [72] | |
| flow accumulation, D-Infinity | TauDEM | log-transformed | [73] |
| normalized height | SAGA GIS | w = 5; t = 2; e = 2 | [74] |
| slope angle | SAGA GIS | [72] | |
| slope angle, catchment area | SAGA GIS | [75] | |
| slope aspect (S-N, W-E) | SAGA GIS | cosine, sine transformed | [72,76] |
| topographic position index (TPI) | SAGA GIS | r = 500 m | [77] |
| topographic wetness index (SWI) | SAGA GIS | [75] | |
| meteorological variables | |||
| five-day rainfall | R | ||
| maximum three-hour rainfall intensity | R | ||
| geology | |||
| geology | ref: ‘Neogene formations with coarse-grained layers’ | ||
| land use/land cover | |||
| forest type | ref: ‘no forest’ |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Knevels, R.; Petschko, H.; Proske, H.; Leopold, P.; Maraun, D.; Brenning, A. Event-Based Landslide Modeling in the Styrian Basin, Austria: Accounting for Time-Varying Rainfall and Land Cover. Geosciences 2020, 10, 217. https://doi.org/10.3390/geosciences10060217
Knevels R, Petschko H, Proske H, Leopold P, Maraun D, Brenning A. Event-Based Landslide Modeling in the Styrian Basin, Austria: Accounting for Time-Varying Rainfall and Land Cover. Geosciences. 2020; 10(6):217. https://doi.org/10.3390/geosciences10060217
Chicago/Turabian StyleKnevels, Raphael, Helene Petschko, Herwig Proske, Philip Leopold, Douglas Maraun, and Alexander Brenning. 2020. "Event-Based Landslide Modeling in the Styrian Basin, Austria: Accounting for Time-Varying Rainfall and Land Cover" Geosciences 10, no. 6: 217. https://doi.org/10.3390/geosciences10060217
APA StyleKnevels, R., Petschko, H., Proske, H., Leopold, P., Maraun, D., & Brenning, A. (2020). Event-Based Landslide Modeling in the Styrian Basin, Austria: Accounting for Time-Varying Rainfall and Land Cover. Geosciences, 10(6), 217. https://doi.org/10.3390/geosciences10060217






