The Altotiberina Low-Angle Normal Fault (Italy) Can Fail in Moderate-Magnitude Earthquakes as a Result of Stress Transfer from Stable Creeping Fault Area
Abstract
1. Introduction
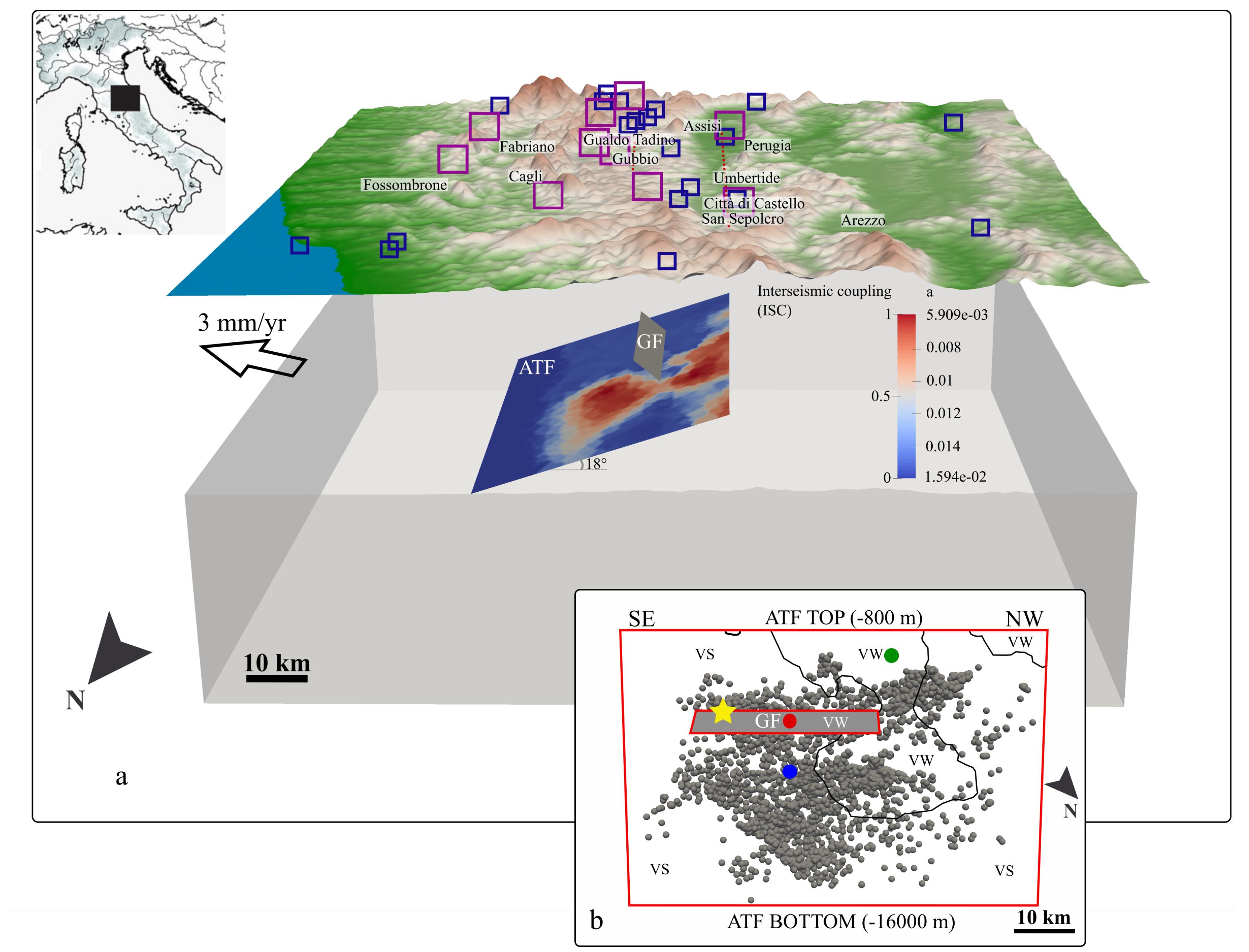
2. Model Set-Up
2.1. Model Geometry and Material Properties
2.2. Rate- and State-Dependent Friction Law
2.3. Modeling the Mixed-Mode Fault Slip Behavior
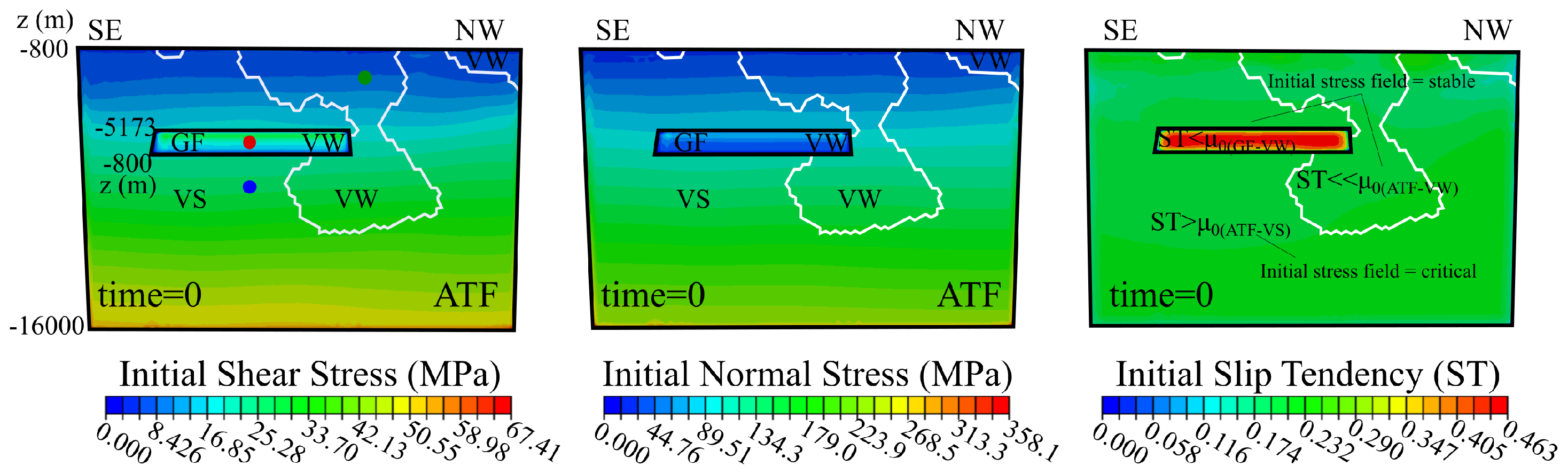
2.4. Initial Stress Field Conditions
2.5. Fault Slip Condition
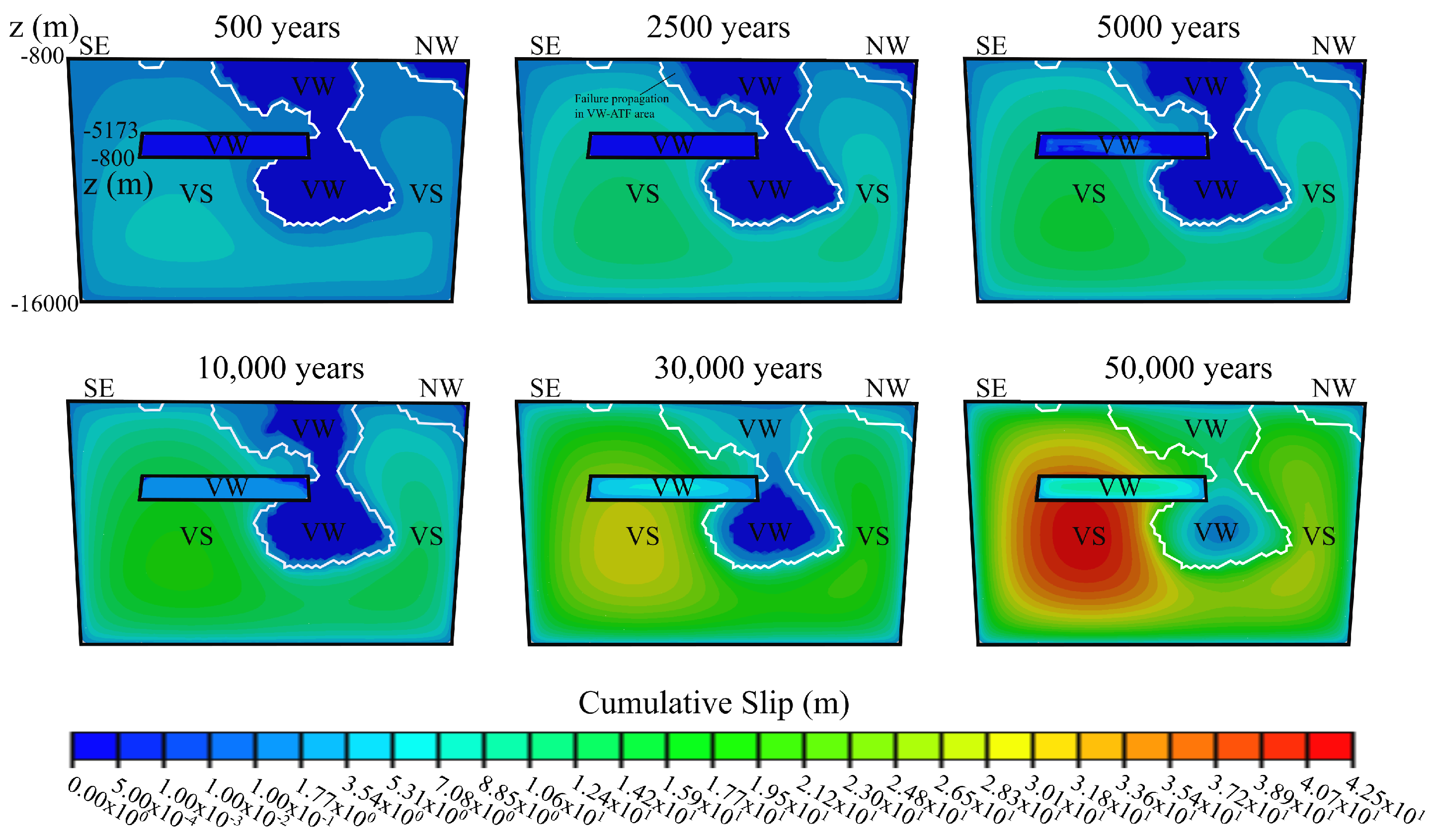
3. Model Results
3.1. Reactivation of Misoriented and Potentially Seismic Fault Patches
3.2. Stick-Slip Versus Creeping Deformation
4. Discussion and Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Serpelloni, E.; Anzidei, M.; Baldi, P.; Casula, G.; Galvani, A. Crustal velocity and strain-rate fields in Italy and surrounding regions: New results from the analysis of permanent and non-permanent GPS networks. Geophys. J. Int. 2005, 161, 861–880. [Google Scholar] [CrossRef]
- Barchi, M.; Minelli, R.; Pialli, G. The crop 03 profile: A synthesis of results on deep structures of the northern Apennines. Mem. Della Soc. Geol. Ital. 1998, 52, 383–400. [Google Scholar]
- Boncio, P.; Brozzetti, F.; Lavecchia, G. Architecture and seismotectonics of a regional low-angle normal fault zone in central Italy. Tectonics 2000, 19, 1038–1055. [Google Scholar] [CrossRef]
- Collettini, C.; Barchi, M.; Chiaraluce, L.; Mirabella, F.; Pucci, S. The Gubbio fault: Can different methods give pictures of the same object? J. Geodyn. 2003, 36, 51–66. [Google Scholar] [CrossRef]
- Chiaraluce, L.; Chiarabba, C.; Collettini, C.; Piccinini, D.; Cocco, M. Architecture and mechanics of an active low-angle normal fault: Alto Tiberina Fault, northern Apennines, Italy. J. Geophys. Res. Solid Earth 2007, 112. [Google Scholar] [CrossRef]
- Valoroso, L.; Chiaraluce, L.; Di Stefano, R.; Monachesi, G. Mixed-Mode Slip Behavior of the Altotiberina Low-Angle Normal Fault System (Northern Apennines, Italy) through High-Resolution Earthquake Locations and Repeating Events. J. Geophys. Res. Solid Earth 2017, 122, 10220–10240. [Google Scholar] [CrossRef]
- Collettini, C.; Holdsworth, R. Fault zone weakening and character of slip along low-angle normal faults: Insights from the Zuccale fault, Elba, Italy. J. Geol. Soc. 2004, 161, 1039–1051. [Google Scholar] [CrossRef]
- D’Agostino, N.; Mantenuto, S.; D’Anastasio, E.; Avallone, A.; Barchi, M.; Collettini, C.; Radicioni, F.; Stoppini, A.; Fastellini, G. Contemporary crustal extension in the Umbria–Marche Apennines from regional CGPS networks and comparison between geodetic and seismic deformation. Tectonophysics 2009, 476, 3–12. [Google Scholar] [CrossRef]
- Hreinsdóttir, S.; Bennett, R.A. Active aseismic creep on the Alto Tiberina low-angle normal fault, Italy. Geology 2009, 37, 683–686. [Google Scholar] [CrossRef]
- Lockner, D.A.; Morrow, C.; Moore, D.; Hickman, S. Low strength of deep San Andreas fault gouge from SAFOD core. Nature 2011, 472, 82–85. [Google Scholar] [CrossRef]
- Collettini, C.; Viti, C.; Holdsworth, R.E.; Smith, S.A.F. Development of interconnected talc networks and weakening of continental low-angle normal faults. Geology 2009, 37, 567–570. [Google Scholar] [CrossRef]
- Smith, S.A.F.; Faulkner, D.R. Laboratory measurements of the frictional properties of the Zuccale low-angle normal fault, Elba Island, Italy. J. Geophys. Res. Solid Earth 2010, 115. [Google Scholar] [CrossRef]
- Collettini, C.; Niemeijer, A.; Viti, C.; Smith, S.A.; Marone, C. Fault structure, frictional properties and mixed-mode fault slip behavior. Earth Planet. Sci. Lett. 2011, 311, 316–327. [Google Scholar] [CrossRef]
- Anderlini, L.; Serpelloni, E.; Belardinelli, M.E. Creep and locking of a low-angle normal fault: Insights from the Altotiberina fault in the Northern Apennines (Italy). Geophys. Res. Lett. 2016, 43, 4321–4329. [Google Scholar] [CrossRef]
- Chiaraluce, L.; Amato, A.; Carannante, S.; Castelli, V.; Cattaneo, M.; Cocco, M.; Collettini, C.; D’Alema, E.; Stefano, R.D.; Latorre, D.; et al. The Alto Tiberina Near Fault Observatory (northern Apennines, Italy). Ann. Geophys. 2014, 57. [Google Scholar] [CrossRef]
- Gualandi, A.; Nichele, C.; Serpelloni, E.; Chiaraluce, L.; Anderlini, L.; Latorre, D.; Belardinelli, M.E.; Avouac, J.P. Aseismic deformation associated with an earthquake swarm in the northern Apennines (Italy). Geophys. Res. Lett. 2017, 44, 7706–7714. [Google Scholar] [CrossRef]
- Vadacca, L.; Casarotti, E.; Chiaraluce, L.; Cocco, M. On the mechanical behaviour of a low-angle normal fault: The Alto Tiberina fault (Northern Apennines, Italy) system case study. Solid Earth 2016, 7, 1537–1549. [Google Scholar] [CrossRef]
- Rovida, A.; Camassi, R.; Gasperini, P.; Stucchi, M.E. CPTI11, the 2011 version of the Parametric Catalogue of Italian Earthquakes. Milano Bologna 2011. [Google Scholar] [CrossRef]
- Byerlee, J. Friction of rocks. Pure Appl. Geophys. 1978, 116, 615–626. [Google Scholar] [CrossRef]
- Collettini, C. The mechanical paradox of low-angle normal faults: Current understanding and open questions. Tectonophysics 2011, 510, 253–268. [Google Scholar] [CrossRef]
- Anderson, E. The dynamics of faulting. Trans. Edinb. Geol. Soc. 1905, 8, 387–402. [Google Scholar] [CrossRef]
- Sibson, R.H. A note on fault reactivation. J. Struct. Geol. 1985, 7, 751–754. [Google Scholar] [CrossRef]
- Collettini, C.; Tesei, T.; Scuderi, M.; Carpenter, B.; Viti, C. Beyond Byerlee friction, weak faults and implications for slip behavior. Earth Planet. Sci. Lett. 2019, 519, 245–263. [Google Scholar] [CrossRef]
- ABAQUS. Theory Manual; Version 6.13; ABAQUS: Providence, RI, USA, 2013. [Google Scholar]
- Mirabella, F.; Brozzetti, F.; Lupattelli, A.; Barchi, M.R. Tectonic evolution of a low-angle extensional fault system from restored cross-sections in the Northern Apennines (Italy). Tectonics 2011, 30. [Google Scholar] [CrossRef]
- Vadacca, L.; Colciago, C.M.; Micheletti, S.; Scotti, A. Effects of the Anisotropy of the Fault Zone Permeability on the Timing of Triggered Earthquakes: Insights from 3D-Coupled Fluid Flow and Geomechanical Deformation Modeling. Pure Appl. Geophys. 2018, 175, 4131–4144. [Google Scholar] [CrossRef]
- Dieterich, J.H. Modeling of rock friction: 1. Experimental results and constitutive equations. J. Geophys. Res. Solid Earth 1979, 84, 2161–2168. [Google Scholar] [CrossRef]
- Ruina, A. Slip instability and state variable friction laws. J. Geophys. Res. Solid Earth 1983, 88, 10359–10370. [Google Scholar] [CrossRef]
- Scholz, C.H. Mechanics of Faulting. Annu. Rev. Earth Planet. Sci. 1989, 17, 309–334. [Google Scholar] [CrossRef]
- Marone, C. Laboratory-derived friction laws and their application to seismic faulting. Annu. Rev. Earth Planet. Sci. 1998, 26, 643–696. [Google Scholar] [CrossRef]
- Aagaard, B.T.; Knepley, M.G.; Williams, C.A. A domain decomposition approach to implementing fault slip in finite-element models of quasi-static and dynamic crustal deformation. J. Geophys. Res. Solid Earth 2013, 118, 3059–3079. [Google Scholar] [CrossRef]
- Aagaard, B.; Knepley, M.; Williams, C. PyLith User Manual; Version 2.2.0; Computational Infrastructure for Geodynamics: Davis, CA, USA, 2017. [Google Scholar]
- Kaneko, Y.; Avouac, J.P.; Lapusta, N. Towards inferring earthquake patterns from geodetic observations of interseismic coupling. Nat. Geosci. 2010, 3, 363–369. [Google Scholar] [CrossRef]
- Mariucci, M.T.; Montone, P. The new release of the Italian contemporary stress map. Geophys. J. Int. 2016, 205, 1525–1531. [Google Scholar] [CrossRef]
- Engelder, T. Stress Regimes in the Lithosphere; Princeton University Press: Princeton, NJ, USA, 1993. [Google Scholar]
- DISS-Working-Group. Database of Individual Seismogenic Sources (DISS), Version 3.2.1: A compilation of potential sources for earthquakes larger than M 5.5 in Italy and surrounding areas. Istituto Nazionale di Geofisica e Vulcanologia 2018. [Google Scholar] [CrossRef]
- Noda, H.; Lapusta, N. Stable creeping fault segments can become destructive as a result of dynamic weakening. Nature 2013, 493, 518–521. [Google Scholar] [CrossRef]
- Tse, S.T.; Dmowska, R.; Rice, J.R. Stressing of locked patches along a creeping fault. Bull. Seismol. Soc. Am. 1985, 75, 709–736. [Google Scholar]


| ATF Friction Parameters | Symbol | Value | Reference |
|---|---|---|---|
| Reference friction coefficient in VW | 0.61 | [11] | |
| Reference friction coefficient in VS | 0.1 | [12] | |
| Reference slip velocity in VW | 100 × 10 m/s | [11] | |
| Reference slip velocity in VS | 30 × 10 m/s | [11] | |
| Rate-and-state parameter A in VW | variable (Figure 1b) | calculated value | |
| Rate-and-state parameter A in VS | variable (Figure 1b) | calculated value | |
| Rate-and-state parameter B in VW | 0.01 | fixed value | |
| Rate-and-state parameter B in VS | 0.01 | fixed value | |
| Characteristic slip distance in VW | 302.15 × 10 m | [11] | |
| Characteristic slip distance in VS | 33.61 × 10 m | [11] | |
| Initial state variable | L/ | calculated value | |
| Linear slip velocity | 1.0 × 10 m/s | calculated value |
| GF Friction Parameters | Symbol | Value | Reference |
|---|---|---|---|
| Reference friction coefficient | 0.61 | [11] | |
| Reference slip velocity | 100 × 10 m/s | [11] | |
| Rate-and-state parameter A | A | 0.008646 | [11] |
| Rate-and-state parameter B | B | 0.01 | [11] |
| Characteristic slip distance | L | 302.15 × 10 m | [11] |
| Initial state variable | L/ | calculated value | |
| Linear slip velocity | 1.0 × 10 m/s | calculated value |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vadacca, L. The Altotiberina Low-Angle Normal Fault (Italy) Can Fail in Moderate-Magnitude Earthquakes as a Result of Stress Transfer from Stable Creeping Fault Area. Geosciences 2020, 10, 144. https://doi.org/10.3390/geosciences10040144
Vadacca L. The Altotiberina Low-Angle Normal Fault (Italy) Can Fail in Moderate-Magnitude Earthquakes as a Result of Stress Transfer from Stable Creeping Fault Area. Geosciences. 2020; 10(4):144. https://doi.org/10.3390/geosciences10040144
Chicago/Turabian StyleVadacca, Luigi. 2020. "The Altotiberina Low-Angle Normal Fault (Italy) Can Fail in Moderate-Magnitude Earthquakes as a Result of Stress Transfer from Stable Creeping Fault Area" Geosciences 10, no. 4: 144. https://doi.org/10.3390/geosciences10040144
APA StyleVadacca, L. (2020). The Altotiberina Low-Angle Normal Fault (Italy) Can Fail in Moderate-Magnitude Earthquakes as a Result of Stress Transfer from Stable Creeping Fault Area. Geosciences, 10(4), 144. https://doi.org/10.3390/geosciences10040144





