Lava Flow Roughness on the 2014–2015 Lava Flow-Field at Holuhraun, Iceland, Derived from Airborne LiDAR and Photogrammetry
Abstract
1. Introduction
2. The Surface Roughness of Lava Flows
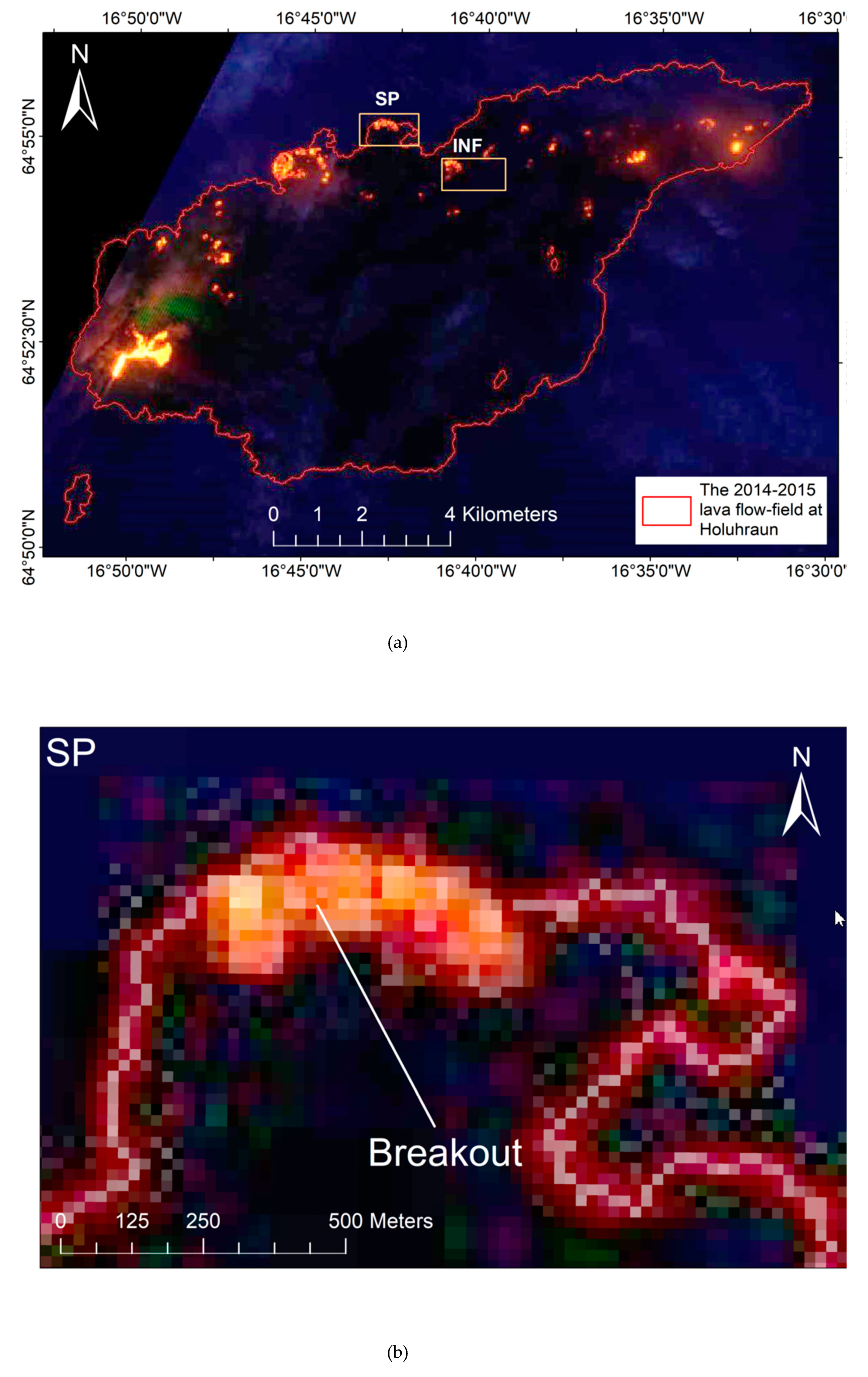
3. Morphology of the 2014–2015 Lava Flow at Holuhraun
4. Datasets and Methods
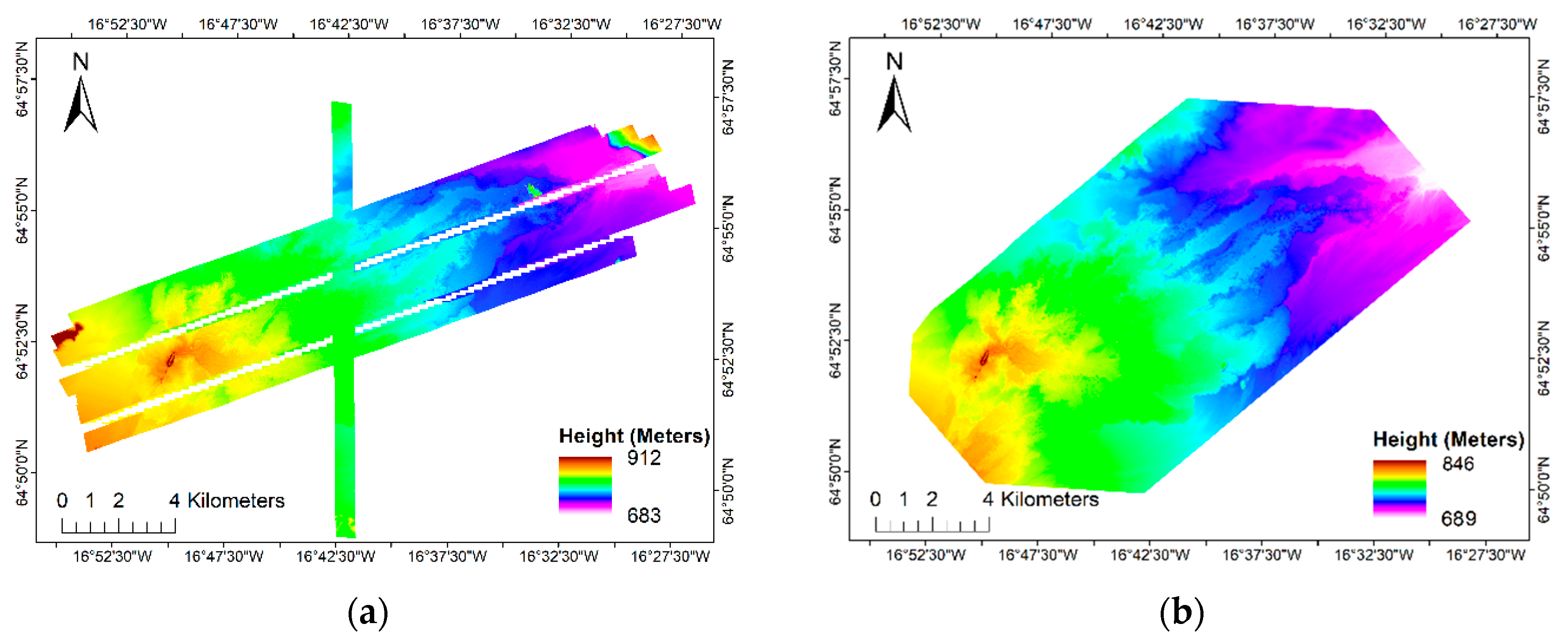
4.1. Airborne LiDAR and Photogrammetry
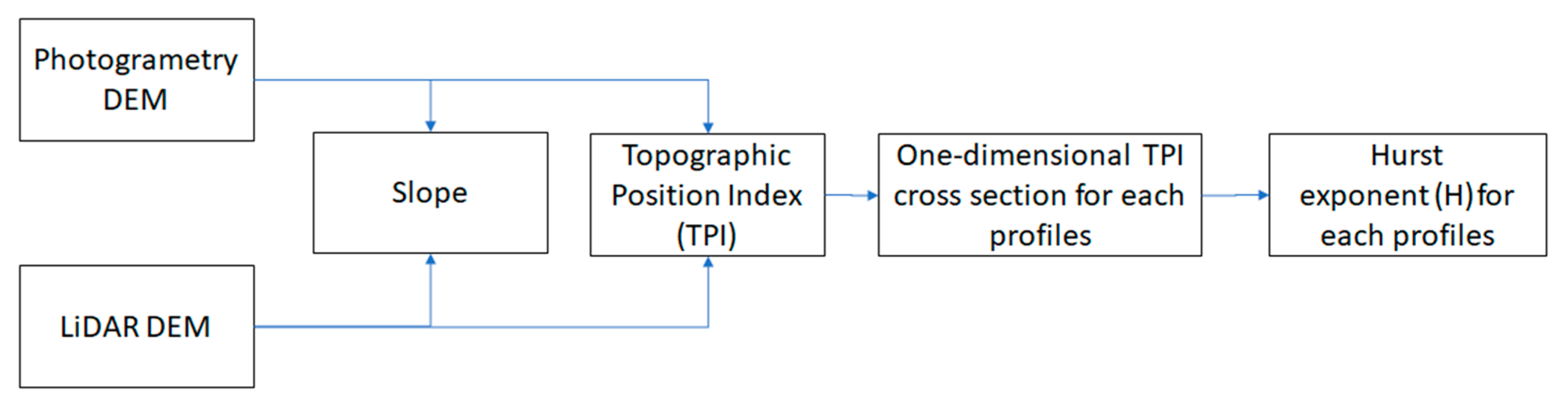
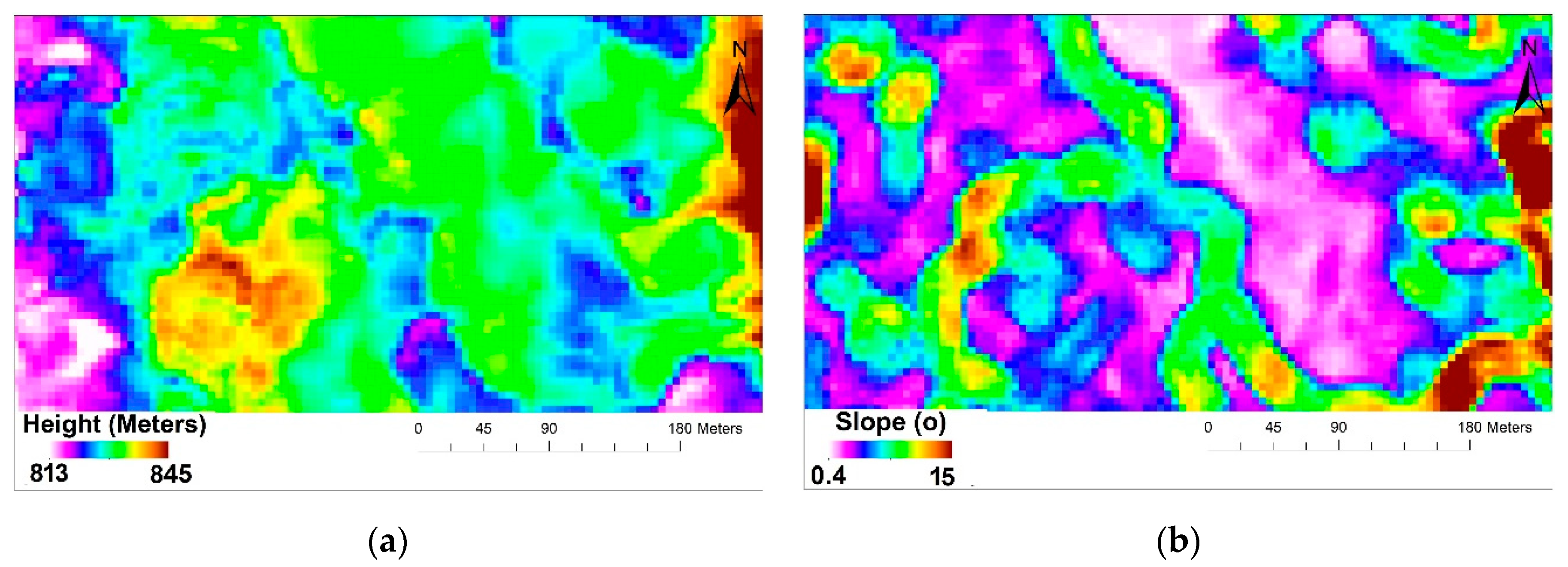
4.2. Deriving Surface Roughness
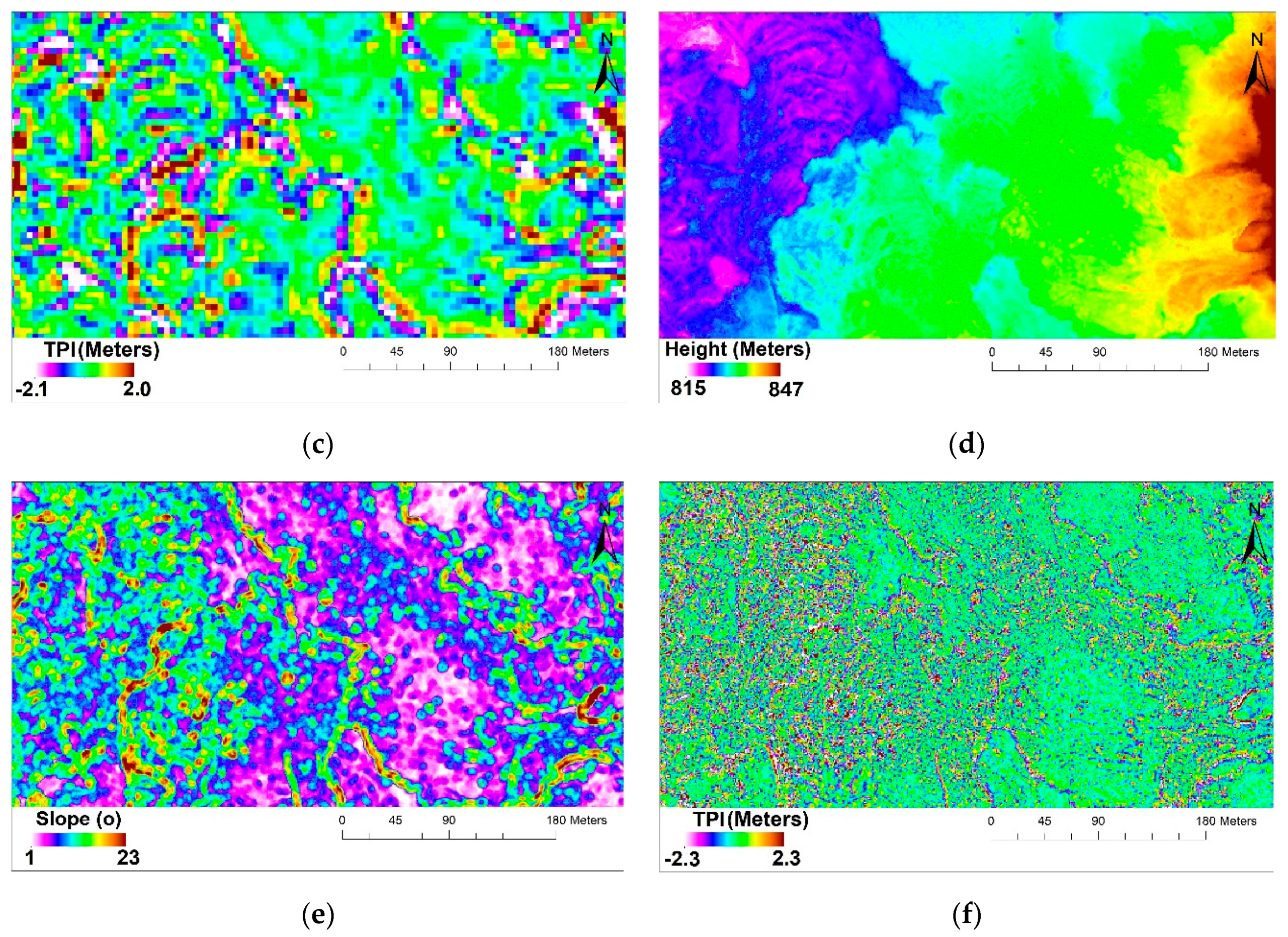
4.2.1. Slope
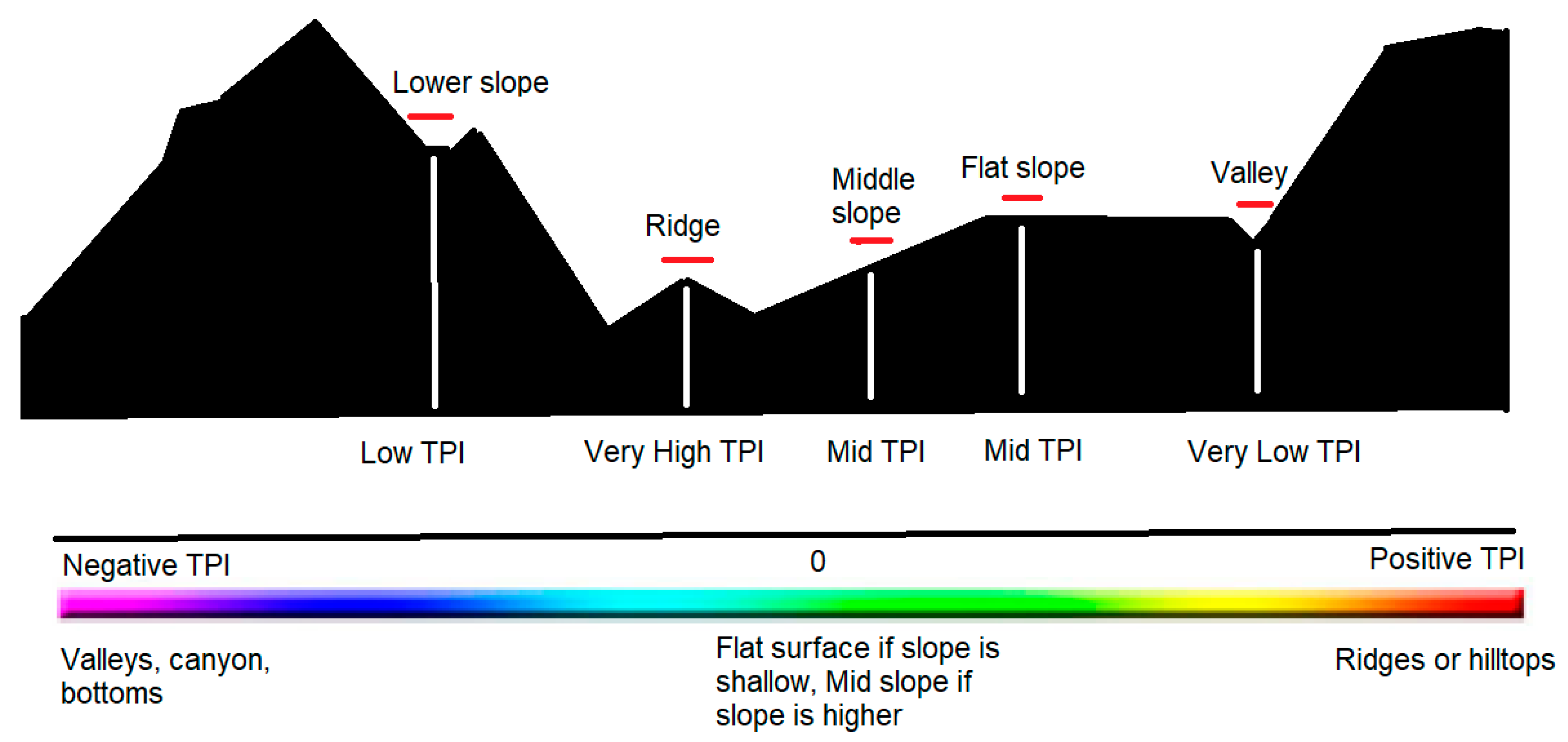
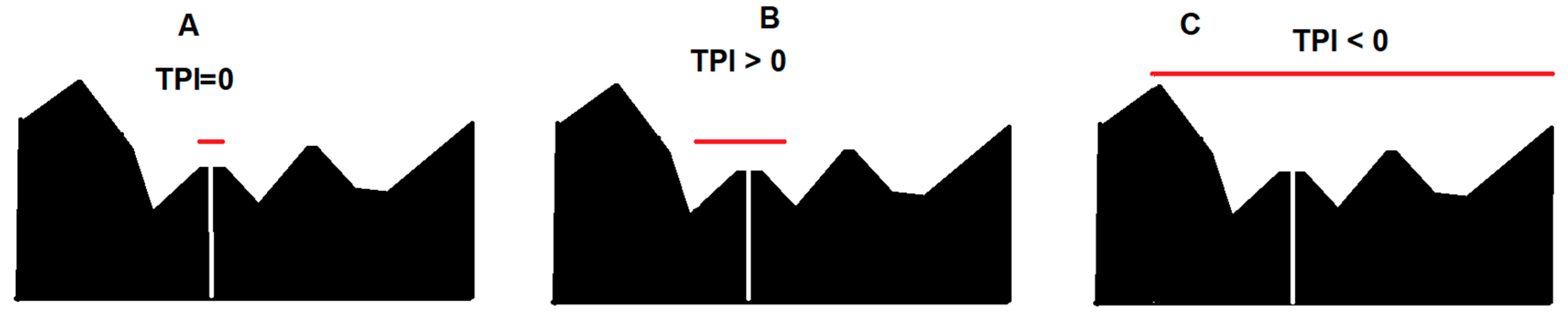
4.2.2. Topographic Position Index
4.2.3. Hurst Exponent
5. Results
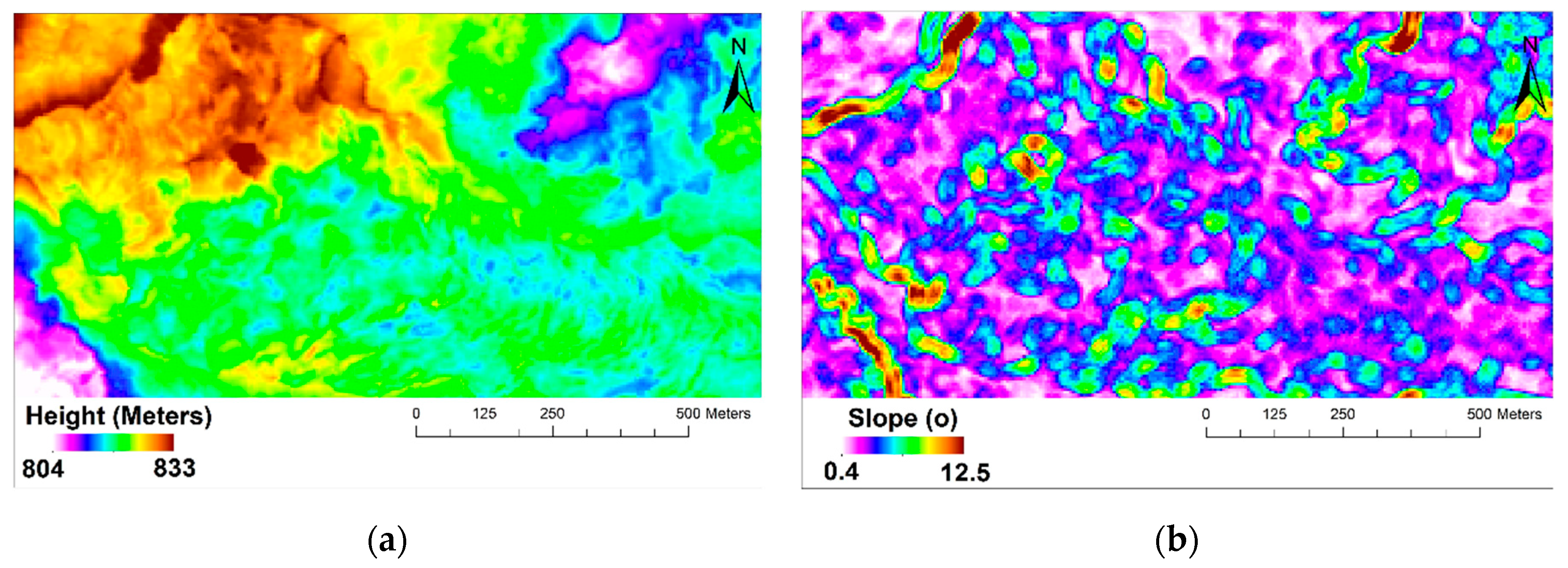
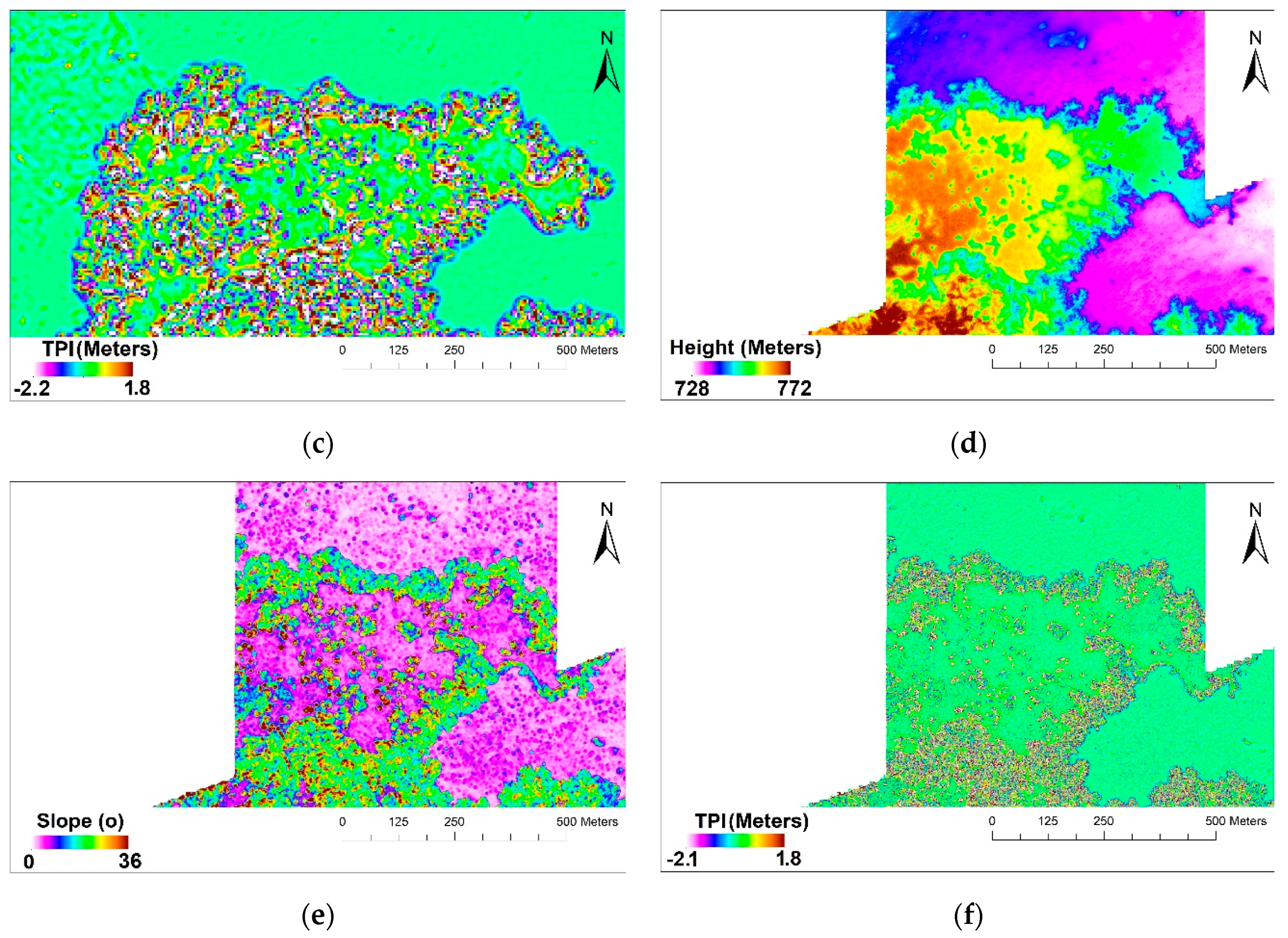
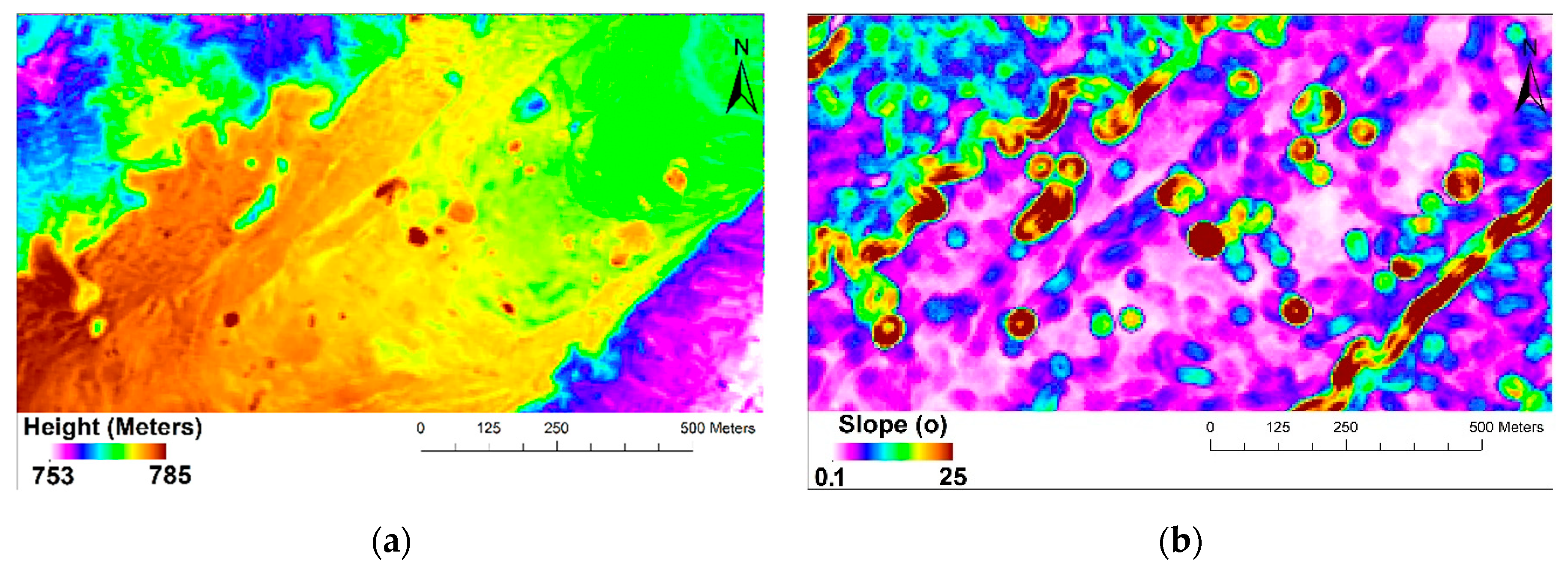
5.1. Lava Pond Roughness
5.2. Spiny Lava Roughness
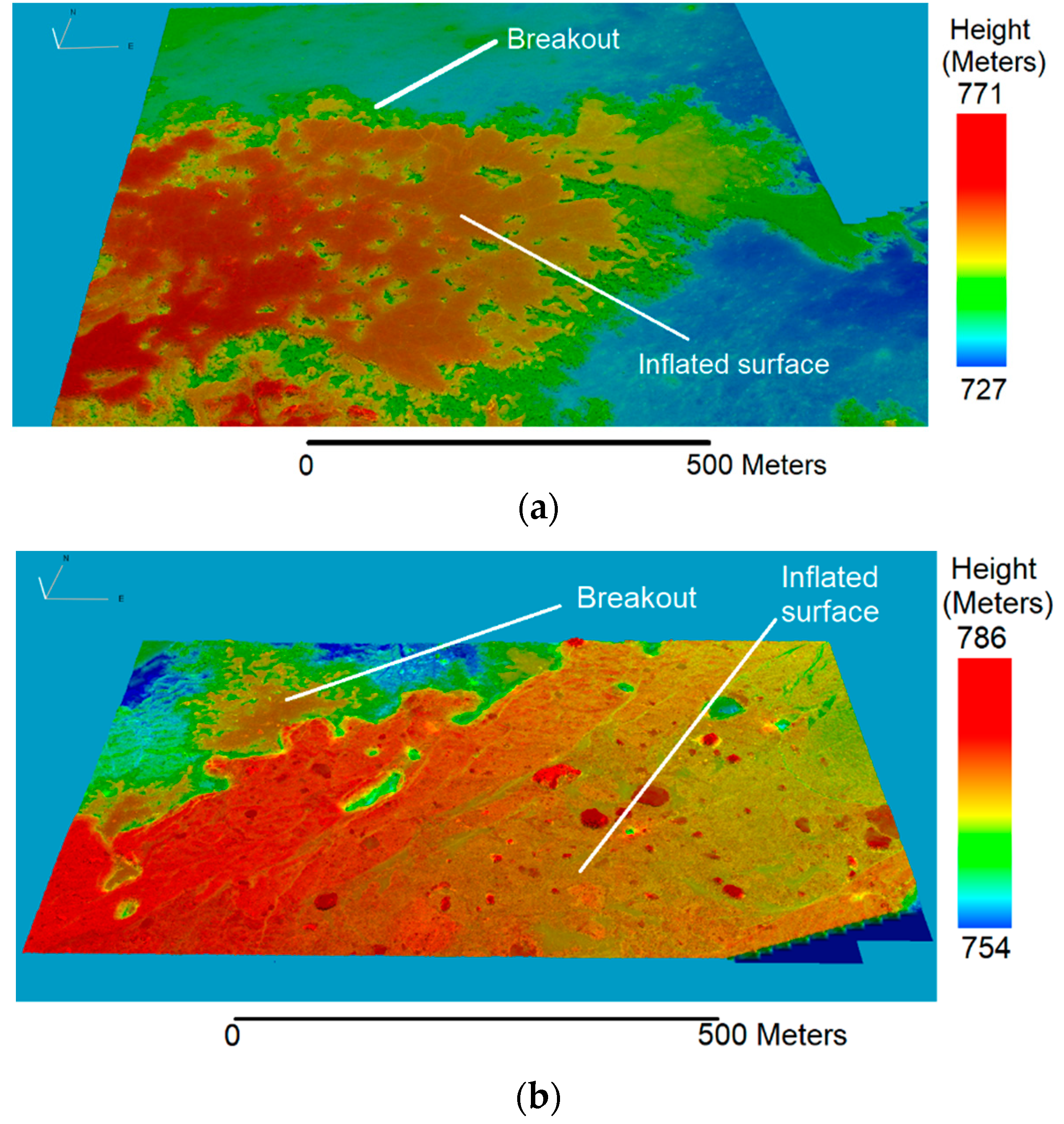
5.3. Inflated Channel Roughness
5.4. Block Surface Roughness
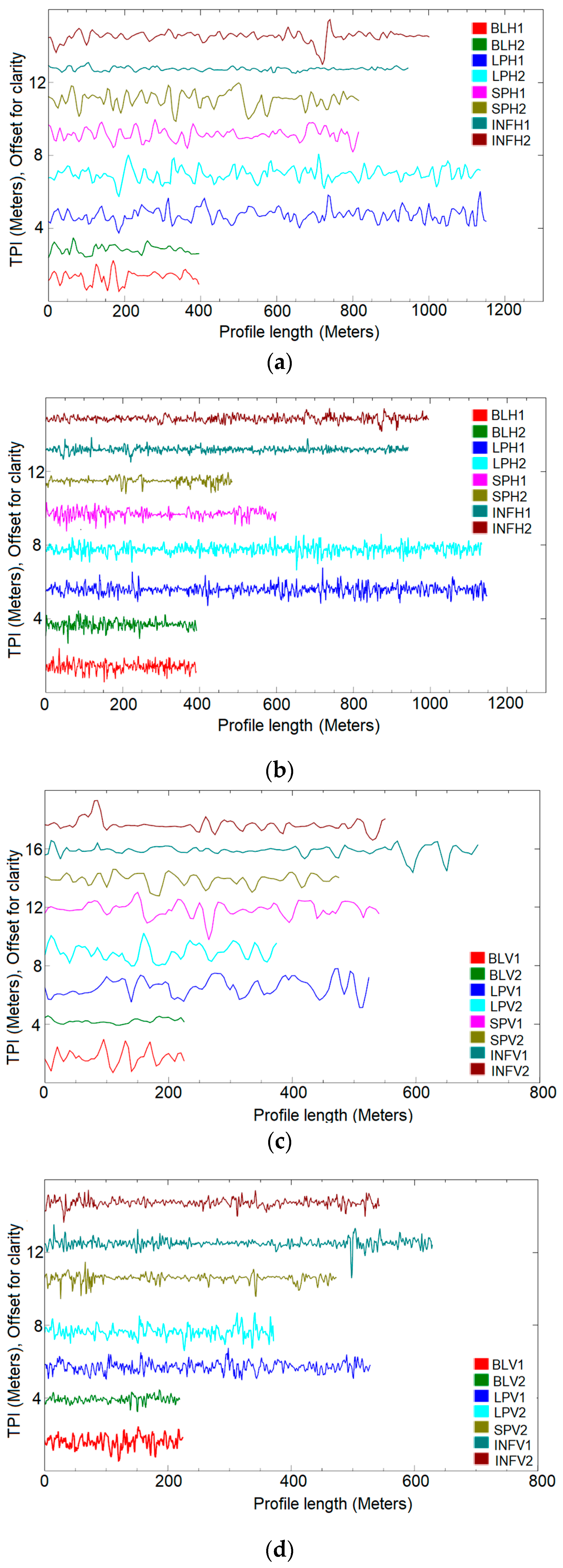
5.5. Hurst Exponent Derived Roughness
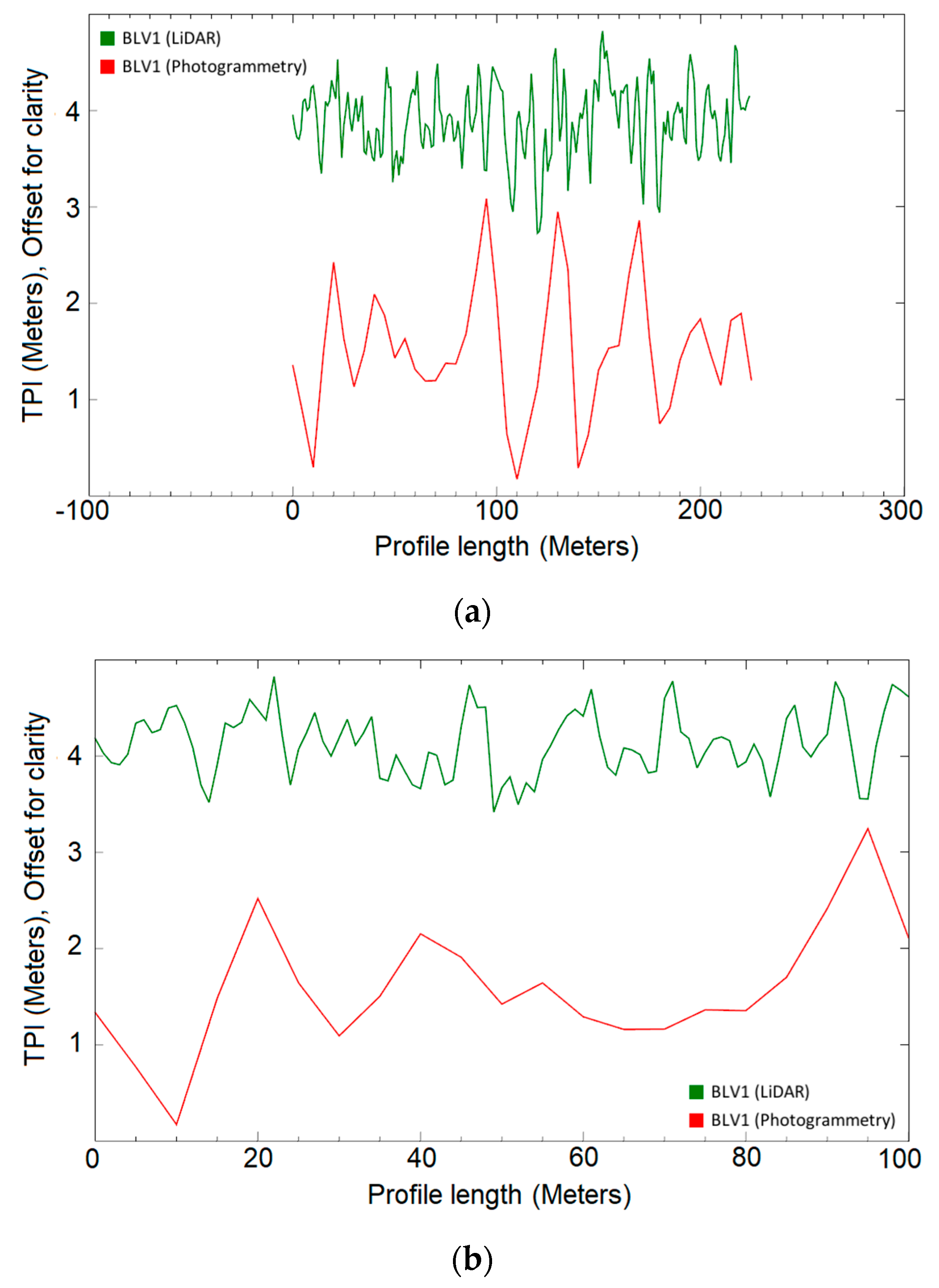
One Dimensional TPI Profiles
6. Discussion
6.1. TPI Neighborhood Size and Profile Length
6.2. Eruption Condition and Link Quantitative Roughness with the Emplacement Style
6.3. Alternative Datasets and Methods for Deriving Roughness
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Mills, G.; Fotopoulos, G. On the estimation of geological surface roughness from terrestrial laser scanner point clouds. Geosphere 2013, 9, 1410–1416. [Google Scholar] [CrossRef]
- Shepard, M.K.; Bulmer, M.H.; Gaddis, L.R.; Plaut, J.J.; Campbell, B.A.; Farr, T. The roughness of natural terrain: A planetary and remote sensing perspective. J. Geophys. Res. Space Phys. 2001, 106, 32777–32795. [Google Scholar] [CrossRef]
- Gaddis, L.R.; Mouginis-Mark, P.J.; Hayashi, J.N. Lava flow surface textures: SIR-B radar image texture, field observations, and terrain measurements. Photogramm. Eng. Remote Sens. 1990, 56, 211–224. [Google Scholar]
- Campbell, B.A.; Shepard, M.K. Lava flow surface roughness and depolarized radar scattering. J. Geophys. Res. Space Phys. 1996, 101, 18941–18951. [Google Scholar] [CrossRef]
- Crown, D.A.; Ramsey, M. Morphologic and thermophysical characteristics of lava flows southwest of Arsia Mons, Mars. J. Volcanol. Geotherm. Res. 2017, 342, 13–28. [Google Scholar] [CrossRef]
- Whelley, P.; Garry, W.B.; Hamilton, C.W.; Bleacher, J. LiDAR-derived surface roughness signatures of basaltic lava types at the Muliwai a Pele Lava Channel, Mauna Ulu, Hawai‘i. Bull. Volcanol. 2017, 79, 79. [Google Scholar] [CrossRef]
- Neish, C.; Hamilton, C.; Hughes, S.; Nawotniak, S.K.; Garry, W.; Skok, J.; Elphic, R.; Schaefer, E.; Carter, L.; Bandfield, J.; et al. Terrestrial analogues for lunar impact melt flows. Icarus 2017, 281, 73–89. [Google Scholar] [CrossRef]
- Morris, A.; Anderson, F.S.; Haldemann, A.F.C.; Brooks, B.A.; Foster, J.; Mouginis-Mark, P.J. Roughness of Hawaiian volcanic terrains. J. Geophys. Res. Space Phys. 2008, 113. [Google Scholar] [CrossRef]
- Anderson, S.W.; Stofan, E.; Plaut, J.J.; Crown, D.A. Block size distributions on silicic lava flow surfaces: Implications for emplacement conditions. GSA Bull. 1998, 110, 1258–1267. [Google Scholar] [CrossRef]
- Byrnes, J.M. Lava Flow Field Emplacement Studies on Mauna Ulu (Kilauea, Volcano, Hawai’i, USA) and Venus, Using Field and Remote Sensing Analyses. Ph.D. Thesis, University of Pittsburgh, Pittsburgh, PA, USA, 2002; pp. 1–212. [Google Scholar]
- James, D.H. Comparing Terrestrial and Extraterrestrial Lava Surface Roughness Using Digital Elevation Models From High Resolution Topography and Structure From Motion. Master’s Thesis, University of Northern Colorado, Greeley, CO, USA, 2019. [Google Scholar]
- Richardson, P.W.; Karlstrom, L. The multi-scale influence of topography on lava flow morphology. Bull. Volcanol. 2019, 81, 21. [Google Scholar] [CrossRef]
- Favalli, M.; Fornaciai, A.; Nannipieri, L.; Harris, A.; Calvari, S.; Lormand, C. UAV-based remote sensing surveys of lava flow fields: A case study from Etna’s 1974 channel-fed lava flows. Bull. Volcanol. 2018, 80, 29. [Google Scholar] [CrossRef]
- Gharechelou, S.; Tateishi, R.; Johnson, B.A. A Simple Method for the Parameterization of Surface Roughness from Microwave Remote Sensing. Remote. Sens. 2018, 10, 1711. [Google Scholar] [CrossRef]
- Aufaristama, M.; Höskuldsson, Á.; Jónsdóttir, I.; Ulfarsson, M.; Thordarson, T. New Insights for Detecting and Deriving Thermal Properties of Lava Flow Using Infrared Satellite during 2014–2015 Effusive Eruption at Holuhraun, Iceland. Remote. Sens. 2018, 10, 151. [Google Scholar] [CrossRef]
- Mallonee, H.C.; Kobs Nawotniak, S.E.; McGregor, M.; Hughes, S.S.; Neish, C.D.; Downs, M.; Delparte, D.; Lim, D.S.S.; Heldmann, J.L.; Team, F. Lava flow morphology classification based on measures of roughness. In Proceedings of the 48th Lunar and Planetary Science Conference, The Woodlands, TX, USA, 20–24 March 2017. [Google Scholar]
- Witt, T.; Walter, T.R.; Müller, D.; Guðmundsson, M.T.; Schöpa, A. The relationship between lava fountaining and vent morphology for the 2014–2015 Holuhraun eruption, Iceland, analyzed by video monitoring and topographic mapping. Front. Earth Sci. 2018, 6, 235. [Google Scholar] [CrossRef]
- Kereszturi, G.; Németh, K.; Moufti, M.R.; Cappello, A.; Murcia, H.; Ganci, G.; Del Negro, C.; Procter, J.; Zahran, H.M.A. Emplacement conditions of the 1256AD Al-Madinah lava flow field in Harrat Rahat, Kingdom of Saudi Arabia—Insights from surface morphology and lava flow simulations. J. Volcanol. Geotherm. Res. 2016, 309, 14–30. [Google Scholar] [CrossRef]
- Jennes, J. Topographic Position Index (tpi_jen.avx) Extension for ArcView 3.x, v. 1.3a; Jenness Enterprises: Flagstaff, AZ, USA, 2006; pp. 1–43. [Google Scholar]
- Swanson, D.A. Pahoehoe Flows from the 1969–1971 Mauna Ulu Eruption, Kilauea Volcano, Hawaii. GSA Bull. 1973, 84, 615. [Google Scholar] [CrossRef]
- Lopes, R.M.C.; Kilburn, C.R.J. Emplacement of lava flow fields: Application of terrestrial studies to Alba Patera, Mars. J. Geophys. Res. Space Phys. 1990, 95, 14383. [Google Scholar] [CrossRef]
- Diniega, S.; Smrekar, S.E.; Anderson, S.; Stofan, E.R. The influence of temperature-dependent viscosity on lava flow dynamics. J. Geophys. Res. Earth Surf. 2013, 118, 1516–1532. [Google Scholar] [CrossRef]
- Ramsey, M.S.; Fink, J.H. Estimating silicic lava vesicularity with thermal remote sensing: A new technique for volcanic mapping and monitoring. Bull. Volcanol. 1999, 61, 32–39. [Google Scholar] [CrossRef]
- Guest, J.E.; Duncan, A.M.; Stofan, E.R.; Anderson, S.W. Effect of slope on development of pahoehoe flow fields: Evidence from Mount Etna. J. Volcanol. Geotherm. Res. 2012, 219, 52–62. [Google Scholar] [CrossRef]
- Kilburn, C.R.J. Lava flows and flow fields. In Encyclopedia of Volcanoes; Sigurdsson, H., Ed.; Academic Press: San Diego, CA, USA, 2000; pp. 291–305. [Google Scholar]
- Hamilton, C.W. Fill and spill” lava flow emplacement: Implications for understanding planetary flood basalt eruptions. In NASA Technical Memorandum: Marshall Space Flight Center Faculty Fellowship Program; Six, N., Karr, G., Eds.; NASA Marshall Space Flight Center: Huntsville, AL, USA, 2019; pp. 47–56. [Google Scholar]
- Byrnes, J.M.; Ramsey, M.S.; Crown, D. A Surface unit characterization of the Mauna Ulu flow field, Kilauea Volcano, Hawai′i, using integrated field and remote sensing analyses. J. Volcanol. Geotherm. Res. 2004, 135, 169–193. [Google Scholar] [CrossRef]
- Griffiths, R.W.; Fink, J.H. The morphology of lava flows in planetary environments: Predictions from analog experiments. J. Geophys. Res. Space Phys. 1992, 97, 19739. [Google Scholar] [CrossRef]
- Anderson, S.W.; Fink, J.H. The Development and Distribution of Surface Textures at the Mount St. Helens Dome; Springer Science and Business Media LLC: Berlin/Heidelberg, Germany, 1990; Volume 2, pp. 25–46. [Google Scholar]
- Fink, J.H.; Fletcher, R.C. Ropy pahoehoe: Surface folding of a viscous fluid. J. Volcanol. Geotherm. Res. 1978, 4, 151–170. [Google Scholar] [CrossRef]
- Byrnes, J.M.; Crown, D.A. Morphology, stratigraphy, and surface roughness properties of Venusian lava flow fields. J. Geophys. Res. Space Phys. 2002, 107, 9-1. [Google Scholar] [CrossRef]
- Moore, R.B.; Clague, D.A.; Rubin, M.; Bohrson, W.A. Volcanism in Hawaii; U.S. Geological Survey Professional Paper 1350; U.S. Geological Survey: Reston, VA, USA, 1987. [Google Scholar]
- Wall, S.; Farr, T.; Muller, J.-P.; Lewis, P.; Leberl, F. Measurement of surface microtopography using helicopter-mounted stereo film cameras and two stereo matching techniques. In Proceedings of the 12th Canadian Symposium on Remote Sensing Geoscience and Remote Sensing Symposium, Vancouver, BC, Canada, 10–14 July 1989. [Google Scholar]
- Cashman, K.V.; Thornber, C.; Kauahikaua, J.P. Cooling and crystallization of lava in open channels, and the transition of Pāhoehoe Lava to ’A’ā. Bull. Volcanol. 1999, 61, 306–323. [Google Scholar] [CrossRef]
- Whelley, P.; Glaze, L.S.; Calder, E.S.; Harding, D.J. LiDAR-Derived Surface Roughness Texture Mapping: Application to Mount St. Helens Pumice Plain Deposit Analysis. IEEE Trans. Geosci. Remote. Sens. 2013, 52, 426–438. [Google Scholar] [CrossRef]
- Bretar, F.; Arab-Sedze, M.; Champion, J.; Pierrot-Deseilligny, M.; Heggy, E.; Jacquemoud, S. An advanced photogrammetric method to measure surface roughness: Application to volcanic terrains in the Piton de la Fournaise, Reunion Island. Remote. Sens. Environ. 2013, 135, 1–11. [Google Scholar] [CrossRef]
- Pedersen, G.B.M.; Höskuldsson, A.; Dürig, T.; Thordarson, T.; Jónsdóttir, I.; Riishuus, M.S.; Óskarsson, B.V.; Dumont, S.; Magnusson, E.; Gudmundsson, M.T.; et al. Lava field evolution and emplacement dynamics of the 2014–2015 basaltic fissure eruption at Holuhraun, Iceland. J. Volcanol. Geotherm. Res. 2017, 340, 155–169. [Google Scholar] [CrossRef]
- Bonny, E.; Thordarson, T.; Wright, R.; Höskuldsson, Á.; Jonsdottir, I. The Volume of Lava Erupted During the 2014 to 2015 Eruption at Holuhraun, Iceland: A Comparison Between Satellite- and Ground-Based Measurements. J. Geophys. Res. Solid Earth 2018, 123, 5412–5426. [Google Scholar] [CrossRef]
- Diego, C.; Ripepe, M.; Marco, L.; Cigolini, C. Modelling satellite-derived magma discharge to explain caldera collapse. Geology 2017, 45, 523–526. [Google Scholar]
- Pedersen, G.; Höskuldsson, A.; Riishuus, M.S.; Jónsdóttir, I.; Thórdarson, T.; Gudmundsson, M.T.; Durmont, S. Emplacement dynamics and lava field evolution of the flood basalt eruption at Holuhraun, Iceland: Observations from field and remote sensing data. In Proceedings of the EGU General Assembly, Vienna, Austria, 17–22 April 2016; Volume 18, p. 13961. [Google Scholar]
- Rowland, S.K.; Walker, G.P. Pahoehoe and aa in Hawaii: Volumetric flow rate controls the lava structure. Bull. Volcanol. 1990, 52, 615–628. [Google Scholar] [CrossRef]
- Gíslason, S.; Stefánsdóttir, G.; Pfeffer, M.A.; Barsotti, S.; Jóhannsson, T.; Galeczka, I.; Bali, E.; Sigmarsson, O.; Stefánsson, A.; Keller, N.S.; et al. Environmental pressure from the 2014–15 eruption of Bárðarbunga volcano, Iceland. Geochem. Perspect. Lett. 2015, 1, 84–93. [Google Scholar] [CrossRef]
- Gudmundsson, M.T.; Jónsdóttir, K.; Hooper, A.; Holohan, E.; Halldórsson, S.A.; Ófeigsson, B.G.; Cesca, S.; Vogfjörd, K.S.; Sigmundsson, F.; Högnadóttir, T.; et al. Gradual caldera collapse at Bárdarbunga volcano, Iceland, regulated by lateral magma outflow. Science 2016, 353, aaf8988. [Google Scholar] [CrossRef] [PubMed]
- Aufaristama, M.; Höskuldsson, Á.; Ulfarsson, M.; Jónsdóttir, I.; Thordarson, T. The 2014–2015 Lava Flow Field at Holuhraun, Iceland: Using Airborne Hyperspectral Remote Sensing for Discriminating the Lava Surface. Remote. Sens. 2019, 11, 476. [Google Scholar] [CrossRef]
- Hargitai, H. Inflated lava flow. In Encyclopedia of Planetary Landforms; Hargitai, H., Kereszturi, Á., Eds.; Springer: New York, NY, USA, 2015; pp. 1029–1034. [Google Scholar]
- Florinsky, I. Accuracy of local topographic variables derived from digital elevation models. Int. J. Geogr. Inf. Sci. 1998, 12, 47–62. [Google Scholar] [CrossRef]
- Zhou, Q.; Liu, X. Analysis of errors of derived slope and aspect related to DEM data properties. Comput. Geosci. 2004, 30, 369–378. [Google Scholar] [CrossRef]
- Guisan, A.; Weiss, S.B. GLM versus CCA spatial modeling of plant species distribution. Plant Ecol. 1999, 143, 107–122. [Google Scholar] [CrossRef]
- Liu, B.; Yao, L.; Fu, X.; He, B.; Bai, L. Application of the Fractal Method to the Characterization of Organic Heterogeneities in Shales and Exploration Evaluation of Shale Oil. J. Mar. Sci. Eng. 2019, 7, 88. [Google Scholar] [CrossRef]
- Hirzel, A.; Guisan, A. Which is the optimal sampling strategy for habitat suitability modelling. Ecol. Model. 2002, 157, 331–341. [Google Scholar] [CrossRef]
- Mokarram, M.; Roshan, G.; Negahban, S. Landform classification using topography position index (case study: Salt dome of Korsia-Darab plain, Iran). Model. Earth Syst. Environ. 2015, 1, 1–7. [Google Scholar] [CrossRef]
- Hamilton, C.W.; Mouginis-Mark, P.J.; Sori, M.M.; Scheidt, S.P.; Bramson, A.M. Episodes of Aqueous Flooding and Effusive Volcanism Associated With Hrad Vallis, Mars. J. Geophys. Res. Planets 2018, 123, 1484–1510. [Google Scholar] [CrossRef]
- Fan, K.; Neish, C.D.; Zanetti, M.; Kukko, A. An improved methodology for 3-dimensional characterization of surface roughness as applied to lava flows. In Proceedings of the 49th Lunar and Planetary Science Conference 2018, The Woodlands, TX, USA, 19–23 March 2018. [Google Scholar]
- Thordarson, T.; Self, S. The Roza Member, Columbia River Basalt Group: A gigantic pahoehoe lava flow field formed by endogenous processes? J. Geophys. Res. Space Phys. 1998, 103, 27411–27445. [Google Scholar] [CrossRef]
- Spinetti, C.; Mazzarini, F.; Casacchia, R.; Colini, L.; Neri, M.; Behncke, B.; Salvatori, R.; Buongiorno, M.F.; Pareschi, M.T. Spectral properties of volcanic materials from hyperspectral field and satellite data compared with LiDAR data at Mt. Etna. Int. J. Appl. Earth Obs. Geoinf. 2009, 11, 142–155. [Google Scholar] [CrossRef]
- Aufaristama, M.; Höskuldsson, Á.; Jonsdottir, I.; Ólafsdóttir, R. Mapping and Assessing Surface Morphology of Holocene Lava Field in Krafla (NE Iceland) Using Hyperspectral Remote Sensing. IOP Conf. Ser. Earth Environ. Sci. 2016, 29, 12002. [Google Scholar] [CrossRef]




| Scale | Flow Features | Common Methods | Resolution | References |
|---|---|---|---|---|
| Millimeter to centimeter | Gas bubble walls and minor folds/cracks | Microscope, Radar backscattering | <1 cm | [33,34] |
| Centimeter to meter | Flow toes and blocks | Hurst exponent, RMS slope | <1 m | [2,7,11,33] |
| Meter | Tumuli, ridges, and crease patterns | Radar backscatter, Hurst exponent | ~1 m | [7,11,16,31] |
| More than decameter | Full flow fields, flow margin | Radar polarization | >10 m | [3,4,15] |
| Platform | Date of Acquisition | Area | Spatial Resolution | Source |
|---|---|---|---|---|
| Airborne LiDAR | 4 September 2015 | 100 km2 (Gap in between lines) | 1 m (processed in ENVI LiDAR 5.3) | NERC |
| Airborne photogrammetry | 30 August 2015 | 167 km2 | 5 m | Loftmyndir ehf |
| Profile | Lava Feature | Length (m) | H (Photogrammetry) | H (LiDAR) | (Mean) |
|---|---|---|---|---|---|
| LPH1 | Lava pond | 1150 | 0.53 ± 0.07 | 0.52 ± 0.05 | 0.55 ± 0.06 |
| LPH2 | Lava pond | 1150 | 0.55 ± 0.06 | 0.43 ± 0.07 | |
| LPV1 | Lava pond | 530 | 0.56 ± 0.06 | 0.6 ± 0.03 | |
| LPV2 | Lava pond | 370 | 0.65 ± 0.05 | 0.57 ± 0.06 | |
| SPH1 | Spiny | 810 | 0.52 ± 0.06 | 0.56 ± 0.05 | 0.58 ± 0.05 |
| SPH2 | Spiny | 810 | 0.65 ± 0.06 | 0.56 ± 0.05 | |
| SPV1 | Spiny | 540 | 0.63 ± 0.04 | - * | |
| SPV2 | Spiny | 480 | 0.63 ± 0.04 | 0.54 ± 0.06 | |
| INFH1 | Inflated channel | 950 | 0.66 ± 0.06 | 0.52 ± 0.04 | 0.61 ± 0.06 |
| INFH2 | Inflated channel | 1000 | 0.69 ± 0.06 | 0.55 ± 0.06 | |
| INFV1 | Inflated channel | 630 | 0.56 ± 0.07 | 0.56 ± 0.06 | |
| INFV2 | Inflated channel | 540 | 0.76 ± 0.04 | 0.60 ± 0.05 | |
| BLH1 | Blocky surface | 390 | 0.61 ± 0.04 | 0.49 ± 0.03 | 0.52 ± 0.04 |
| BLH2 | Blocky surface | 390 | 0.65 ± 0.05 | 0.56 ± 0.03 | |
| BLV1 | Blocky surface | 220 | 0.4 ± 0.05 | 0.30 ± 0.04 | |
| BLV2 | Blocky surface | 220 | 0.65 ± 0.05 | 0.52 ± 0.03 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aufaristama, M.; Höskuldsson, Á.; Ulfarsson, M.O.; Jónsdóttir, I.; Thordarson, T. Lava Flow Roughness on the 2014–2015 Lava Flow-Field at Holuhraun, Iceland, Derived from Airborne LiDAR and Photogrammetry. Geosciences 2020, 10, 125. https://doi.org/10.3390/geosciences10040125
Aufaristama M, Höskuldsson Á, Ulfarsson MO, Jónsdóttir I, Thordarson T. Lava Flow Roughness on the 2014–2015 Lava Flow-Field at Holuhraun, Iceland, Derived from Airborne LiDAR and Photogrammetry. Geosciences. 2020; 10(4):125. https://doi.org/10.3390/geosciences10040125
Chicago/Turabian StyleAufaristama, Muhammad, Ármann Höskuldsson, Magnus Orn Ulfarsson, Ingibjörg Jónsdóttir, and Thorvaldur Thordarson. 2020. "Lava Flow Roughness on the 2014–2015 Lava Flow-Field at Holuhraun, Iceland, Derived from Airborne LiDAR and Photogrammetry" Geosciences 10, no. 4: 125. https://doi.org/10.3390/geosciences10040125
APA StyleAufaristama, M., Höskuldsson, Á., Ulfarsson, M. O., Jónsdóttir, I., & Thordarson, T. (2020). Lava Flow Roughness on the 2014–2015 Lava Flow-Field at Holuhraun, Iceland, Derived from Airborne LiDAR and Photogrammetry. Geosciences, 10(4), 125. https://doi.org/10.3390/geosciences10040125






