Groundwater Storage Changes Derived from GRACE and GLDAS on Smaller River Basins—A Case Study in Poland
Abstract
1. Introduction
- Raw measurement on Level-1 (L1),
- Geopotential in a form of a spherical harmonics coefficients on Level-2 (L2),
- Monthly values of a terrestrial water storage (TWS) on Level-3 (L3).
- Partial representativeness, first of all taking into account the structure and parameters of aquifers/aquifers, location of pressure foci and is mainly relevant for determining the optimal location and depth of the research point;
- Temporal representativeness taking into account the speed of hydrogeological processes, which is combined with determining the appropriate frequency of measurements and tests (sampling). Determination of the structure and density of the observation and research network, as well as indication of locations of monitoring points in the area of a particular JCWPd (in Polish: Jednolite częsci wód podziemnych–Groundwater plain parts) of the selected aquifer, took place so as to obtain spatial representativeness of the network.
- At groundwater level or usable aquifer with unconfined water table (when there is no insulation from the area)—1 point per 500 km2, but not less than 3 points within JCWPd.
2. Data Used for the Study
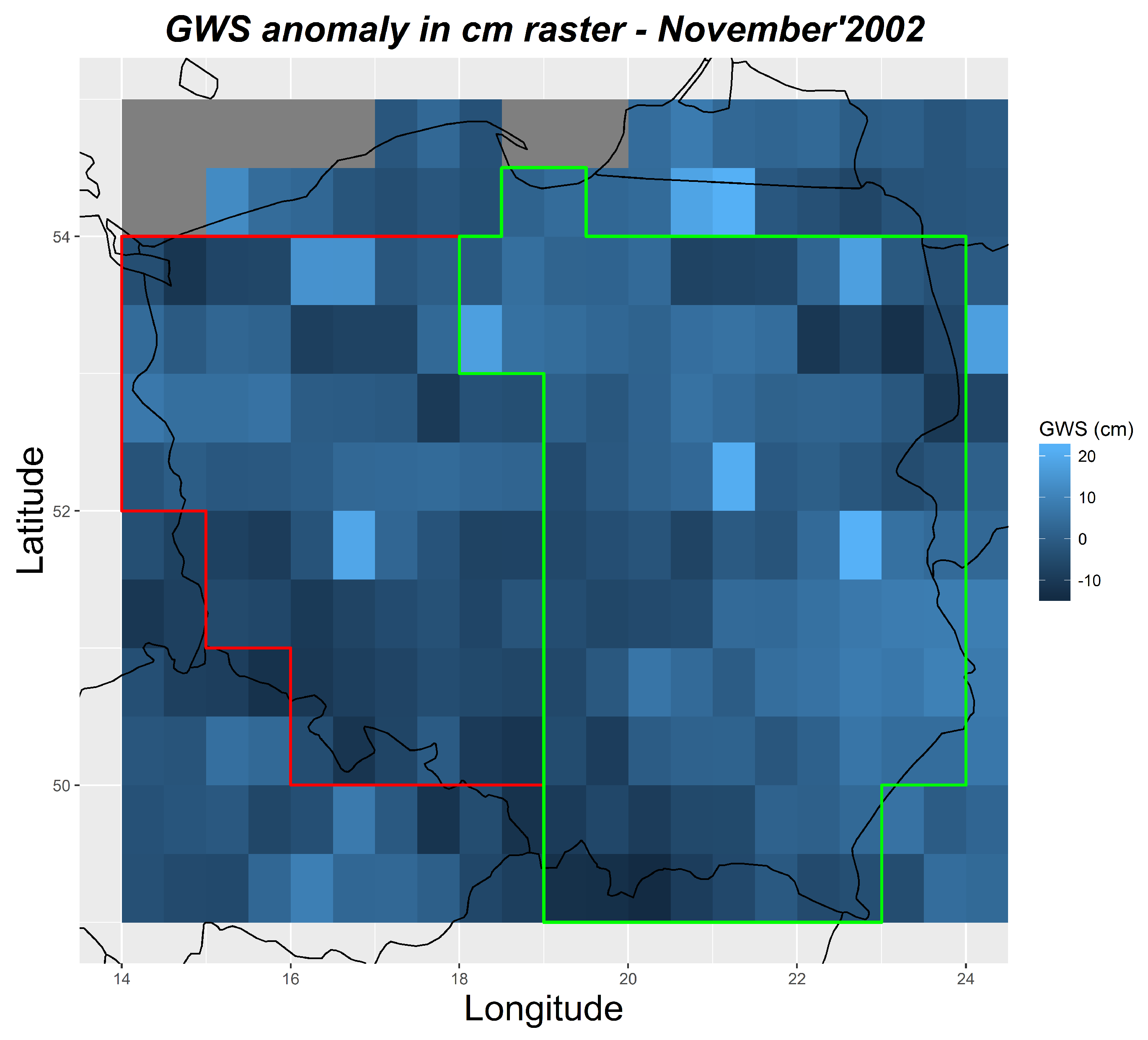
2.1. GRACE Data
2.2. GLDAS Data
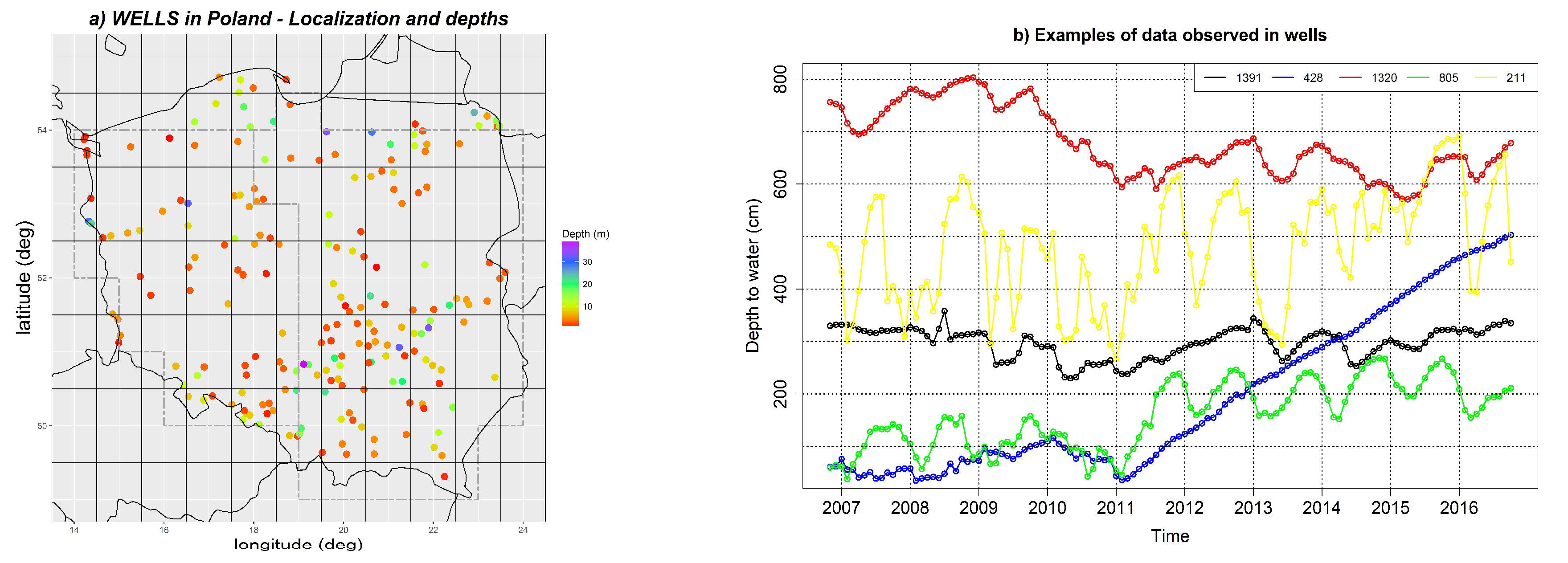
2.3. Polish Wells
3. Methods
4. Analysis of Results
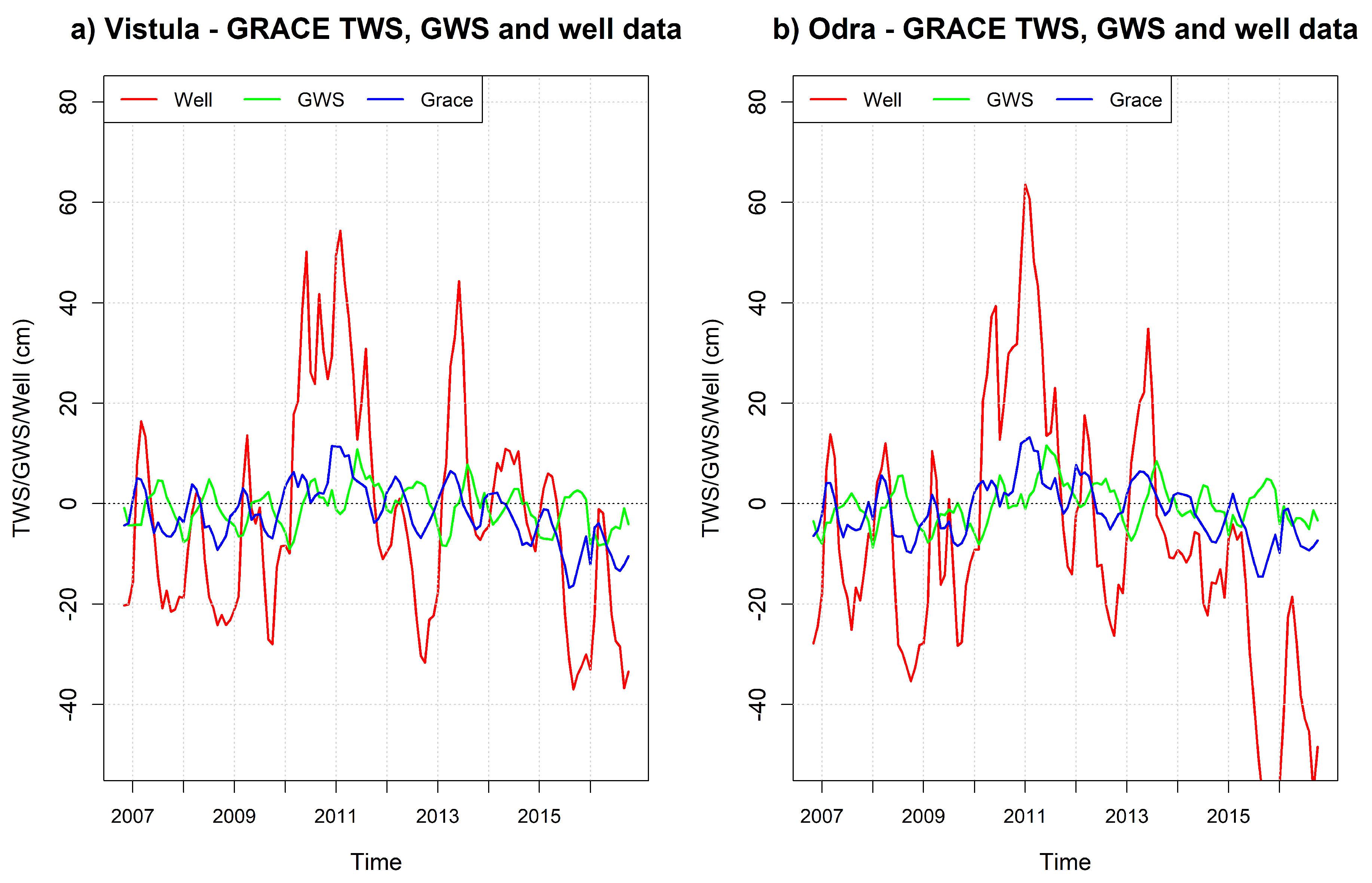
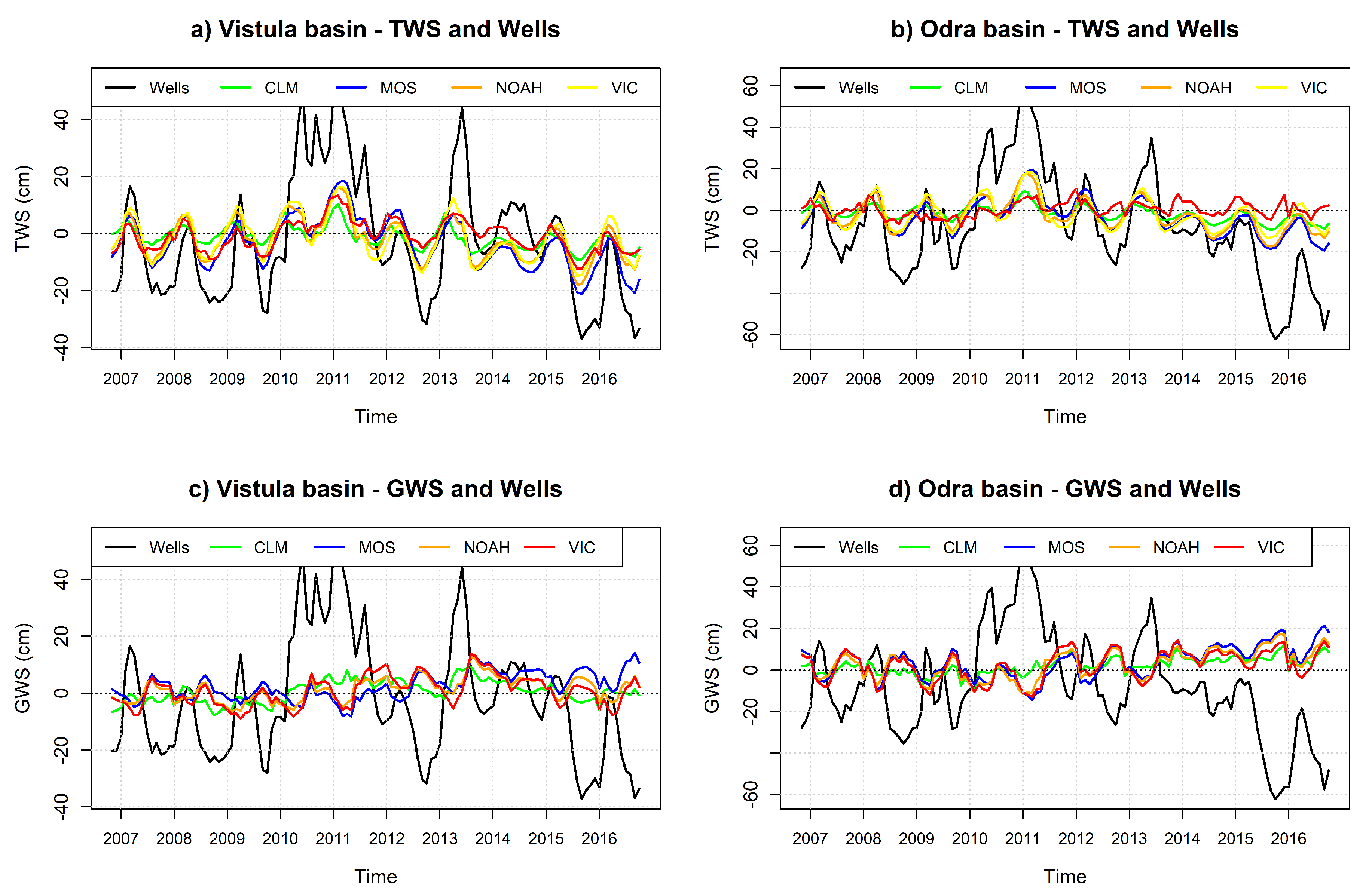
4.1. Comparison of GWS with Polish Well Data in 2006–2016
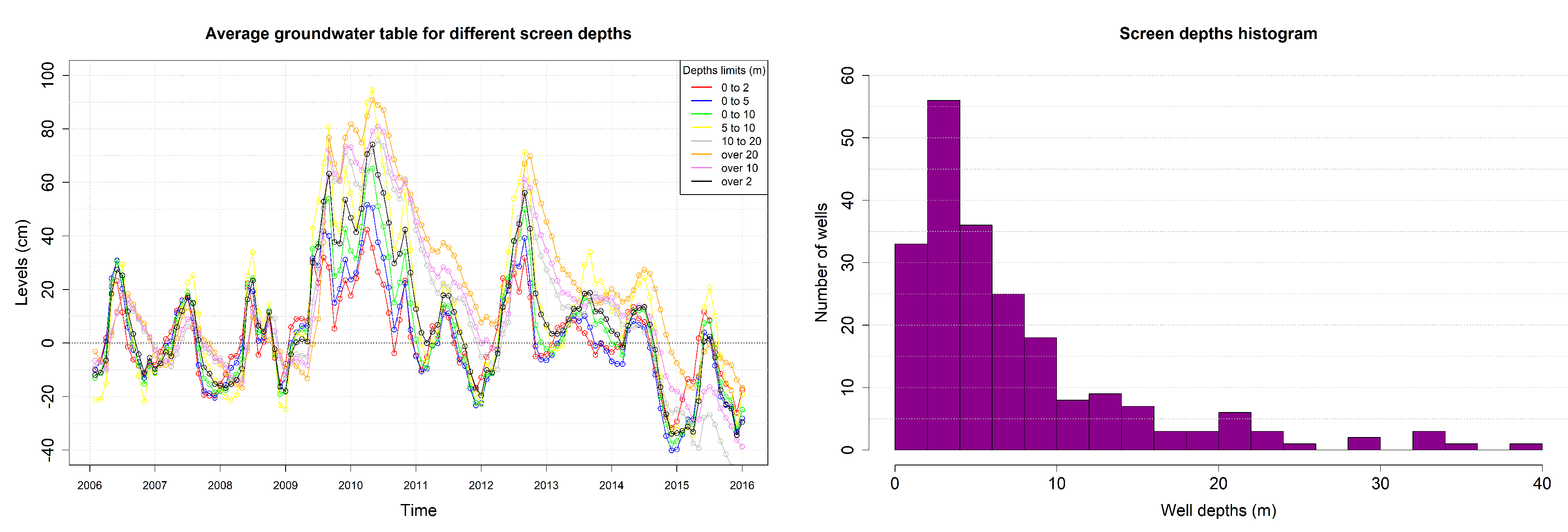
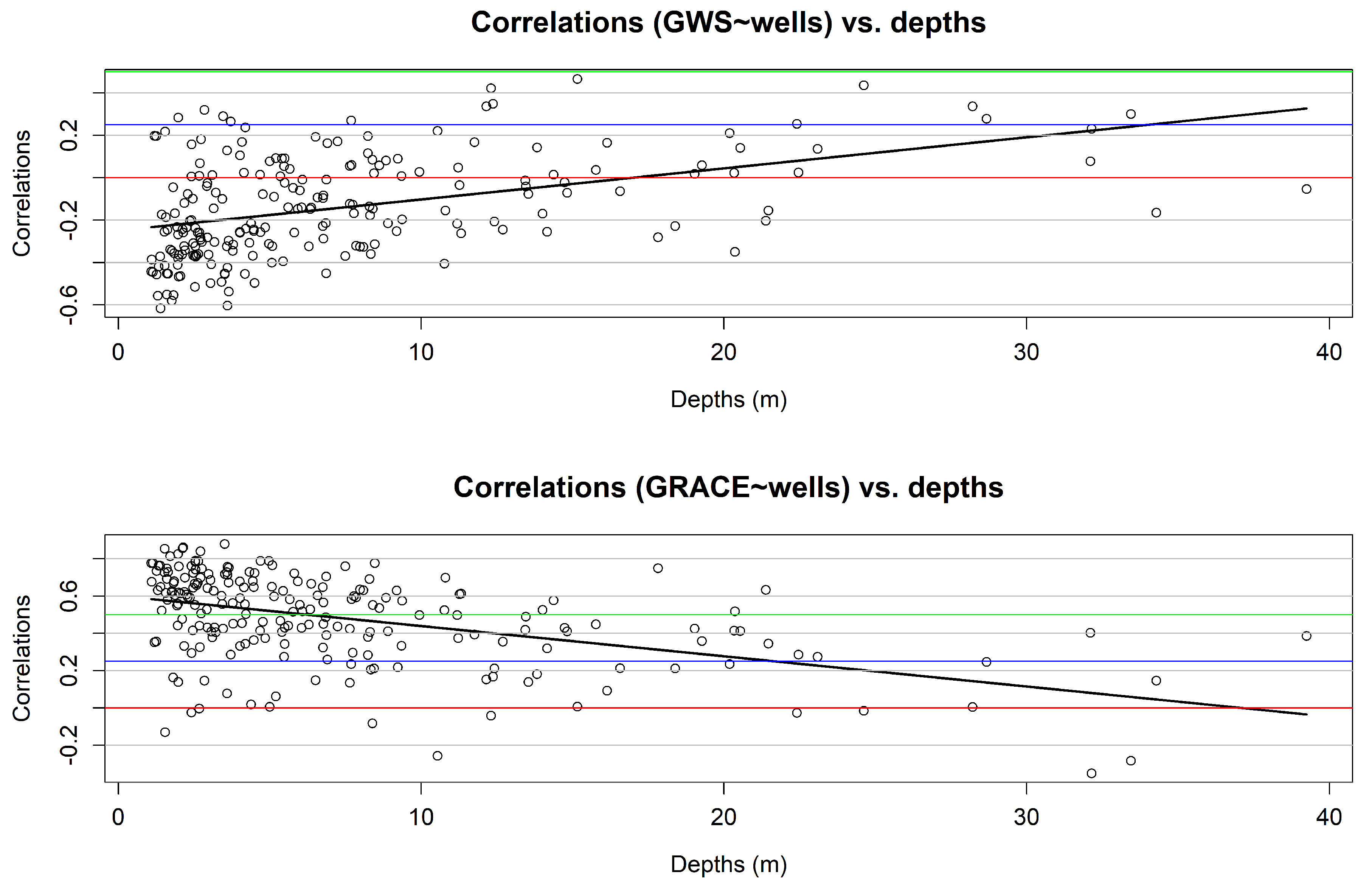
4.2. Analyses Concerning Well Depths
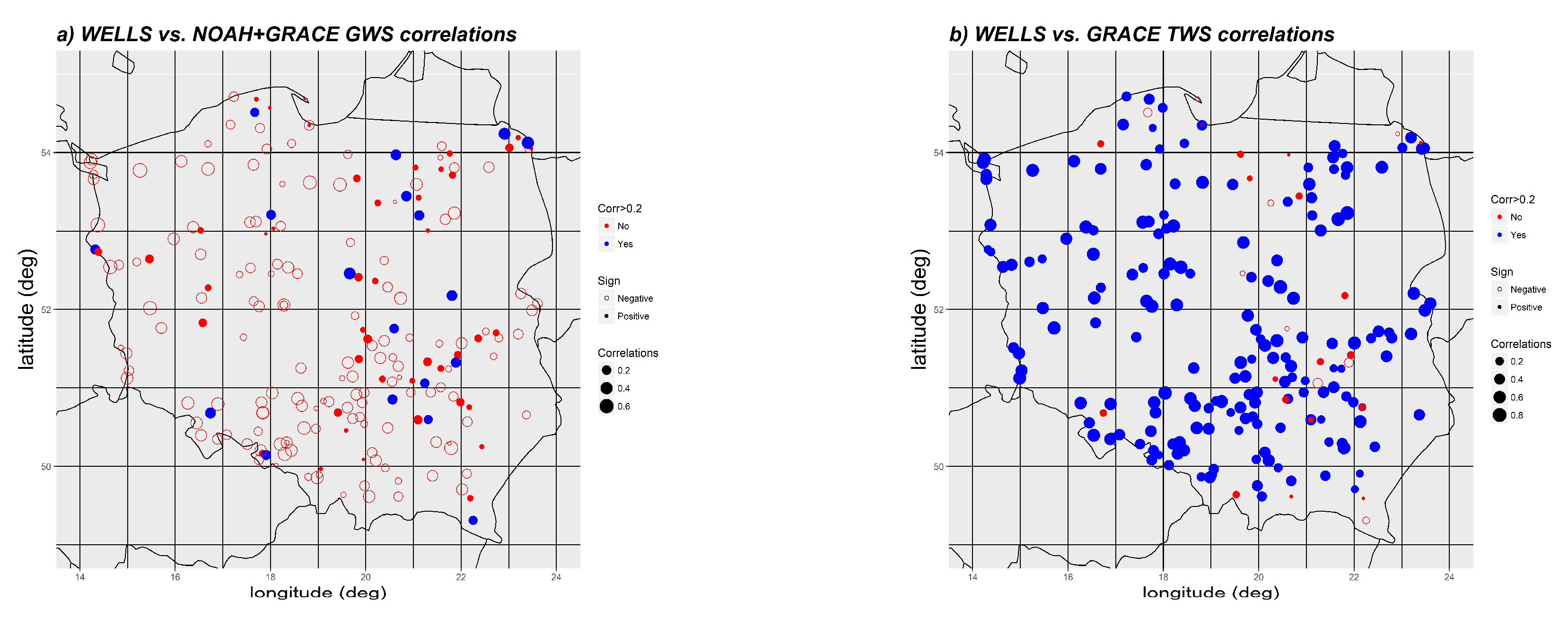
4.3. Dependence on Localization
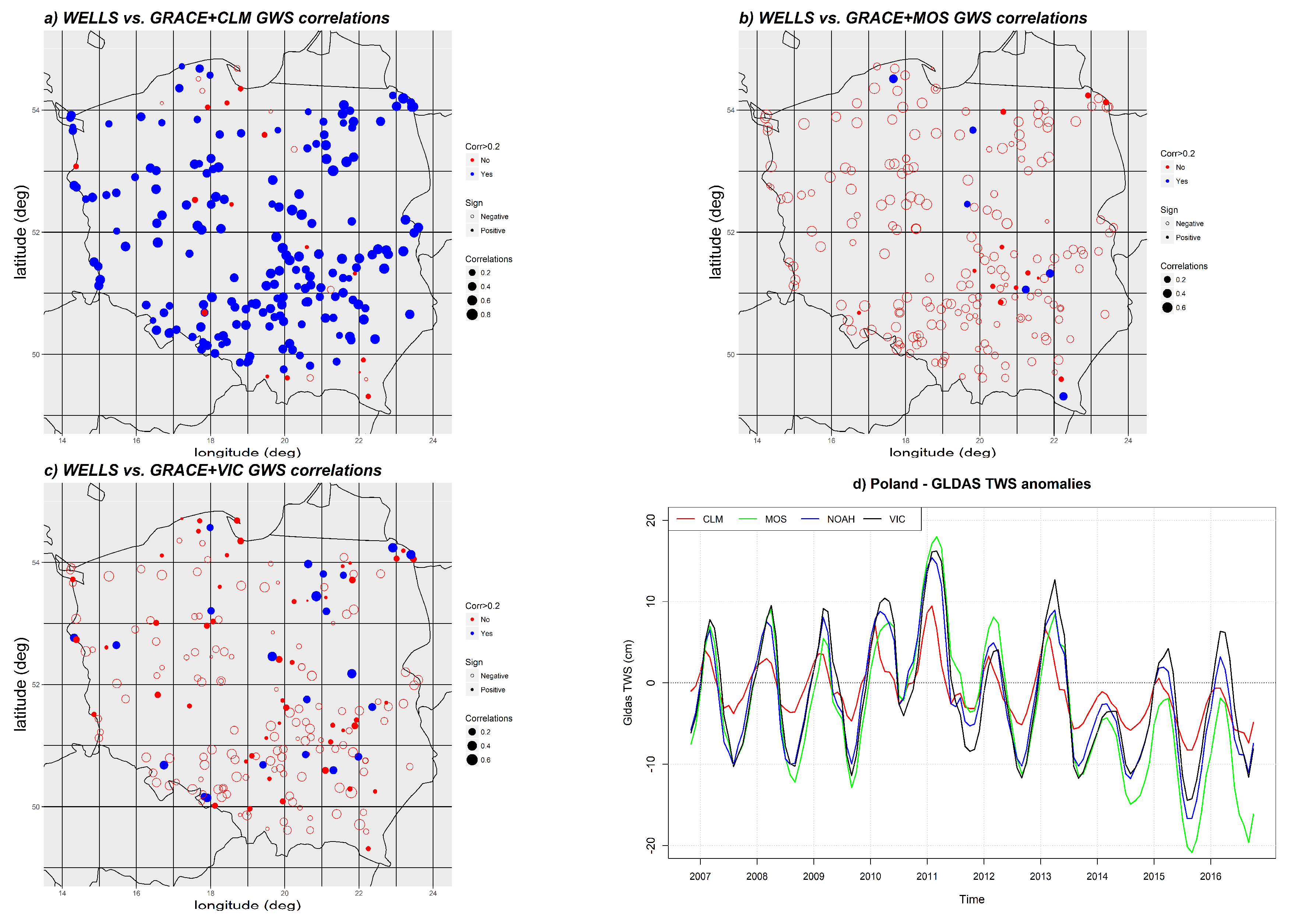
4.4. Dependence on the LDAS Model Admitted
5. Conclusions
- GRACE and the thickness of the unsaturated zone at the location of the well in Poland were highly correlated, wells data were delayed by one month on average. The cross-correlation function values were equal to 0.78 and 0.82 for Vistula and Odra basins at lag = 0, and to 0.82 and 0.90 respectively at lag = −1.
- After applying GLDAS NOAH to GRACE data, the resulting GWS were shifted in respect to direct measurements in wells by three months (GWS was delayed). The achieved values of the cross-correlation function were in this case much smaller (appropriate values were 0.20 and 0.21 for lag = 0, and 0.61 and 0.59 for lag = 3).
- No clear dependence of well depths and locations on the correlations could be observed.
- It seems that the GLDAS NOAH data had too large amplitudes of changes in comparison with the GRACE data on the area of the Polish basins studied.
- It seems that the CLM model fit much better in Poland for computation of groundwater storage variation values. Its annual amplitudes of changes were significantly smaller than the NOAH amplitudes. Due to this, the phase of TWS signal from GRACE did not change when performing differentiating according to Equation (1).
- However, it seems that GRACE data alone, not reduced by any model, when properly shifted, best reflected the behavior of the water level in the wells. The time shifts obtained between the GRACE series and the thickness of the unsaturated zone at the location of the well were logical and easy to interpret.
- It can be seen from the data that the changes in water levels in the wells were much greater than the changes in TWS from GRACE or GWS from GRACE and GLDAS. This is probably due to the mean soil porosity. Since the amplitudes of the thickness of the unsaturated zone at the location of the well changes were generally about four times greater than the amplitudes of the GRACE/NOAH GWS variations consequently a conclusion on the mean soil porosity could be derived: it was approximately equal to 0.25.
Author Contributions
Funding
Conflicts of Interest
References
- Massoud, E.C.; Purdy, A.J.; Miro, M.E.; Famiglietti, J.S. Projecting groundwater storage changes in California’s Central Valley. Sci. Rep. 2018, 8, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Purdy, A.J.; David, C.H.; Sikder, S.; Reager, J.T.; Chandanpurkar, H.A.; Jones, N.L.; Matin, M.A. An Open-Source Tool to Facilitate the Processing of GRACE Observations and GLDAS Outputs: An Evaluation in Bangladesh. Front. Environ. Sci. 2019, 7, 155. [Google Scholar] [CrossRef]
- Tapley, B.D.; Watkins, M.M.; Flechtner, F.; Reigber, C.; Bettadpur, S.; Rodell, M.; Sasgen, I.; Famiglietti, J.S.; Landerer, F.W.; Chambers, D.P.; et al. Contributions of GRACE to understanding climate change. Nat. Clim. Chang. 2009, 9, 358–369. [Google Scholar] [CrossRef] [PubMed]
- Cooley, S.S.; Landerer, F.W. GRACE D-103133 Gravity Recovery and Climate Experiment Follow-on (GRACE-FO) Level-3 Data Product User Handbook; NASA Jet Propulsion Laboratory, California Institute of Technology: Pasadena, CA, USA, 2019.
- Swenson, S.; Wahr, J. Post-processing removal of correlated errors in GRACE data. Hydrol. Land Surf. Stud. 2006, 36. [Google Scholar] [CrossRef]
- Rodell, M.; Houser, P.R.; Jambor, U.; Gottschalck, J.; Mitchell, K.; Meng, C.J.; Arsenault, K.; Cosgrove, B.; Radakovich, J.; Bosilovich, M.; et al. The Global Land Data Assimilation System. Bull. Amer. Meteor. Soc. 2004, 85, 381–394. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, P.W.; Massoud, E.; Farr, T.G.; Lundgren, P.; Famiglietti, J.S. Monitoring Groundwater Change in California’s Central Valley Using Sentinel-1 and GRACE Observations. Geosciences 2019, 9, 436. [Google Scholar] [CrossRef]
- Rodell, M.; Famiglietti, J.S. The potential for satellite-based monitoring of groundwater storage changes using GRACE: The High Plains aquifer, Central US. J. Hydrol. 2002, 263, 245–256. [Google Scholar] [CrossRef]
- Rodell, M.; Famiglietti, J.S. An analysis of terrestrial water storage variations in Illinois with implications for the Gravity Recovery and Climate Experiment (GRACE). Water Resour. Res. 2001, 37, 1327–1339. [Google Scholar] [CrossRef]
- Rodell, M.; Famiglietti, J.S. Detectability of variations in continental water storage from satellite observations of the time dependent gravity field. Water Resour. Res. 1999, 35. [Google Scholar] [CrossRef]
- Li, B.; Rodell, M.; Kumar, S.; Beaudoing, H.K.; Getirana, A.; Zaitchik, B.F.; de Goncalves, L.G.; Cossetin, C.; Bhanja, S.; Mukherjee, A.; et al. Global GRACE Data Assimilation for Groundwater and Drought Monitoring: Advances and Challenges. Water Resour. Res. 2019, 5. [Google Scholar] [CrossRef]
- Huang, J.; Pavlic, G.; Rivera, A.; Palombi, D.; Smerdon, B. Mapping groundwater storage variations with GRACE: A case study in Alberta, Canada. Hydrogeol. J. 2016. [Google Scholar] [CrossRef]
- Meghwal, R.; Shah, D.; Mishra, V. On the Changes in Groundwater Storage Variability in Western India Using GRACE and Well Observations. Remote Sens. Earth Syst. Sci. 2019, 2, 741–755. [Google Scholar] [CrossRef]
- Henry, C.M.; Allen, D.M.; Huang, J. Groundwater storage variability and annual recharge using well-hydrograph and GRACE satellite data. Hydrogeol. J. 2011, 19. [Google Scholar] [CrossRef]
- Watkins, M.M.; Wiese, D.N.; Yuan, D.-N.; Boening, C.; Landerer, F.W. Improved methods for observing Earth’s time variable mass distribution with GRACE using spherical cap mascons. J. Geophys. Res. Solid Earth 2015, 120, 2648–2671. [Google Scholar] [CrossRef]
- Winter, T.C.; Harvey, J.W.; Lehn, O.; William, F.; William, M.A. Ground Water and Surface Water a Single Resource; U.S. Geological Survey Circular: Cantua Creek, CA, USA, 1998; Volume 1139.
- Witczak, S.; Kania, J.; Kmiecik, E. Katalog Wybranych Fizycznych I Chemicznych Wskaźników Zanieczyszczeń Wód Podziemnych I Metod Ich Oznaczania (Published in Polish: Catalog of Selected Types and Chemical Substances Contained in Groundwater and Methods of their Determination); Główny Inspektorat Ochrony Środowiska: Warszawa, Poland, 2013; ISBN 978-83-61227-13-7.
- Wiese, D.N.; Landerer, F.W.; Watkins, M.M. Quantifying and reducing leakage errors in the JPL RL05M GRACE Mascon solution. Water Resour. Res. 2016, 52. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2014; Available online: http://www.R-project.org/ (accessed on 12 December 2019).
- Available online: www.pgi.gov.pl (accessed on 21 December 2019).
- Oleson, K.W.; Lawrence, D.M.; Bonan, G.B.; Flanner, M.G.; Kluzek, E.; Lawrence, P.J.; Levis, S.; Swenson, S.C.; Thornton, P.E. Technical Description of Version 4.0 of the Community Land Model (CLM); NCAR Tech. Note NCAR/TN-478+STR; National Center for Atmospheric Research: Boulder, CO, USA, 2010; Available online: http://www.cesm.ucar.edu/models/cesm1.0/clm/CLM4_Tech_Note.pdf (accessed on 6 December 2019).
- Suarez, M.J.; Bloom, S.; Dee, D. Energy and Water Balance Calculations in the Mosaic LSM; NASA Technical Memorandum 104606; NASA: Greenbelt, MA, USA, 1996. Available online: https://gmao.gsfc.nasa.gov/pubs/docs/Koster130.pdf (accessed on 1 September 2019).
- Rodell, M.; Beaudoing, K.H. GLDAS VIC Land Surface Model L4 Monthly 1.0 x 1.0 degree V001; Goddard Earth Sciences Data and Information Services Center (GES DISC): Greenbelt, MA, USA, 2019. [CrossRef]
- Available online: https://disc.gsfc.nasa.gov/datasets/GLDAS_VIC10_M_001/summary?keywords=gldas%20vic (accessed on 20 December 2019).
- Sadurski, A. Hydrogeological Annual Reports. Polish Hydrological Survey; Hydrological Year 2015; Polish Geological Institute: Gdansk, Poland, 2016.
- Hijmans Robert, J. Introduction to the ’Raster’ Package (Version 3.0-2); 2019. Available online: https://cran.r-project.org/web/packages/raster/vignettes/Raster.pdf (accessed on 8 December 2019).
- Liang, J.; Yang, Z.; Lin, P. Systematic Hydrological Evaluation of the Noah-MP Land Surface Model over China. Adv. Atmos. Sci. 2019, 36, 1171–1187. [Google Scholar] [CrossRef]
- Pennemann, P.C.S.; Rivera, J.A.R.; Saulo, A.C.E.; Penalba, O.C.P. A Comparison of GLDAS Soil Moisture Anomalies against Standardized Precipitation Index and Multisatellite Estimations over South America. J. Hydrometeorol. 2016, 16. [Google Scholar] [CrossRef]
- Sliwinska, J.; Birylo, M.; Rzepecka, Z.; Nastula, J. Analysis of groundwater and total water storage changes in Poland using GRACE observations, in-situ data, and various assimilation models. Remote Sens. 2019, 11, 2949. [Google Scholar] [CrossRef]
- Available online: https://ldas.gsfc.nasa.gov/gldas (accessed on 12 November 2019).
| CCF Values | Vistula Basin | Odra Basin |
|---|---|---|
| CCF(GWS~wells) at lag = 0 | 0.20 | 0.21 |
| Max CCF(GWS~wells) = CCF(GWS~wells) at lag = 3 | 0.61 | 0.59 |
| CCF(GRACE~wells) at lag = 0 | 0.78 | 0.89 |
| Max CCF(GRACE~wells) = CCF(GRACE~wells) at lag = −1 | 0.82 | 0.90 |
| Depths (m) | No. of Wells | Cor(GWL ~well)[0] | Lag[max], Max | Cor(TWS ~well)[0] | Lag[max], Max |
|---|---|---|---|---|---|
| 0 ÷ 2 | 30 | −0.17 | 5 (0.61) | 0.88 | 0 (0.88) |
| Over 2 | 161 | 0.27 | 3 (0.62) | 0.82 | −1 (0.86) |
| 2 ÷ 5 | 68 | 0.06 | 4 (0.61) | 0.86 | −1 (0.86) |
| 5 ÷ 10 | 54 | 0.25 | 3 (0.61) | 0.75 | −1 (0.82) |
| 10 ÷ 20 | 23 | 0.48 | 1 (0.55) | 0.71 | −2 (0.78) |
| Over 20 | 15 | 0.52 | 1 (0.56) | 0.62 | −2 (0.73) |
| 0 ÷ 5 | 99 | 0.02 | 4 (0.62) | 0.87 | 0 (0.87) |
| 0 ÷ 10 | 154 | 0.10 | 3 (0.61) | 0.75 | −1 (0.85) |
| Over 10 | 38 | 0.51 | 1 (0.57) | 0.68 | −2 (0.77) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rzepecka, Z.; Birylo, M. Groundwater Storage Changes Derived from GRACE and GLDAS on Smaller River Basins—A Case Study in Poland. Geosciences 2020, 10, 124. https://doi.org/10.3390/geosciences10040124
Rzepecka Z, Birylo M. Groundwater Storage Changes Derived from GRACE and GLDAS on Smaller River Basins—A Case Study in Poland. Geosciences. 2020; 10(4):124. https://doi.org/10.3390/geosciences10040124
Chicago/Turabian StyleRzepecka, Zofia, and Monika Birylo. 2020. "Groundwater Storage Changes Derived from GRACE and GLDAS on Smaller River Basins—A Case Study in Poland" Geosciences 10, no. 4: 124. https://doi.org/10.3390/geosciences10040124
APA StyleRzepecka, Z., & Birylo, M. (2020). Groundwater Storage Changes Derived from GRACE and GLDAS on Smaller River Basins—A Case Study in Poland. Geosciences, 10(4), 124. https://doi.org/10.3390/geosciences10040124





