Study on Methods to Control Interstory Deflections
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussion
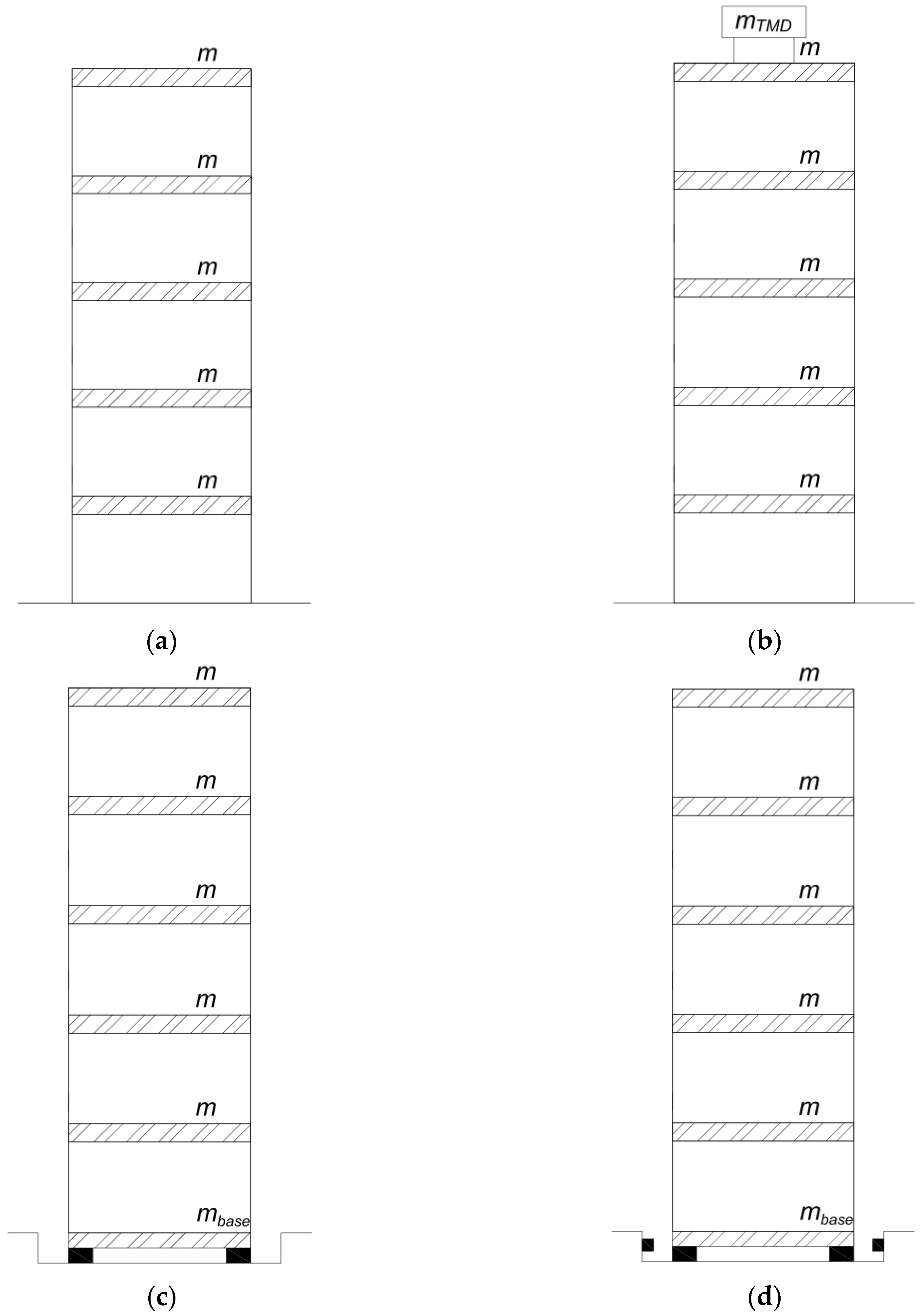
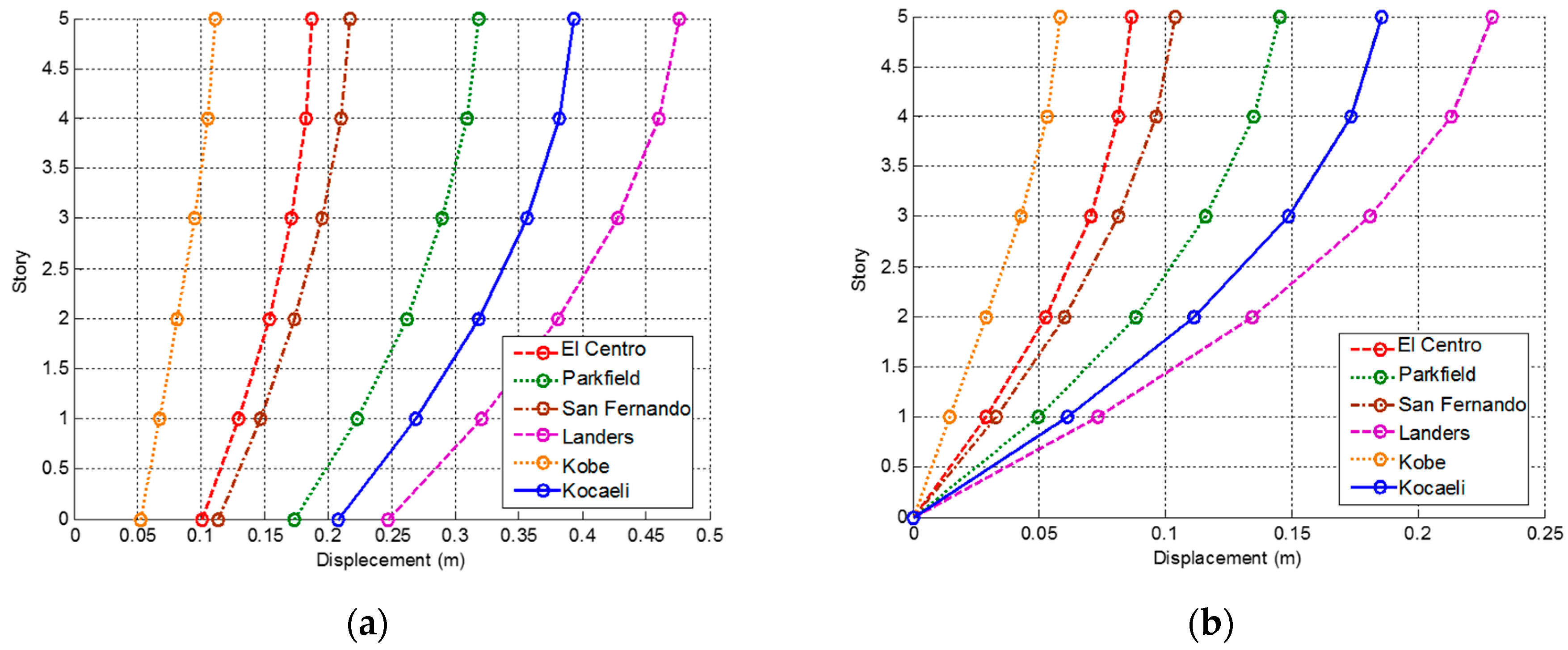
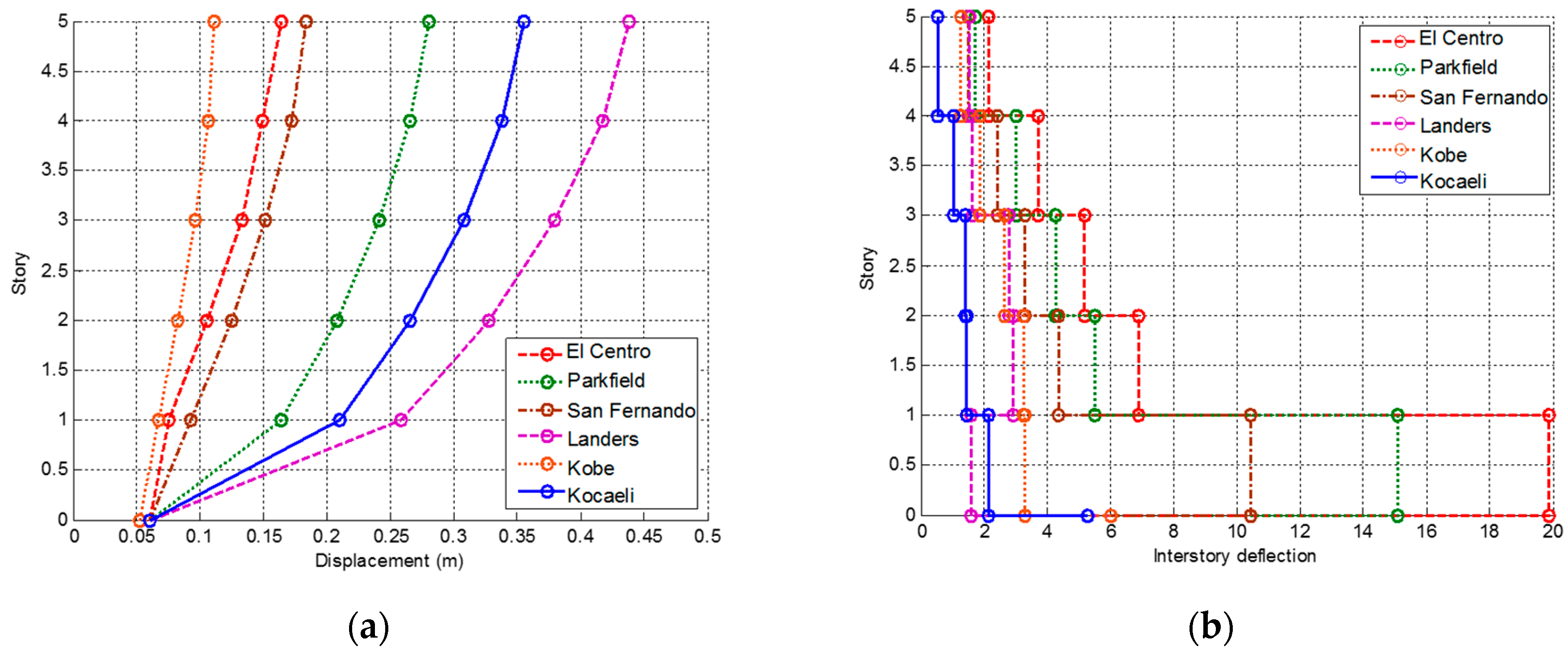
3.1. Original Building
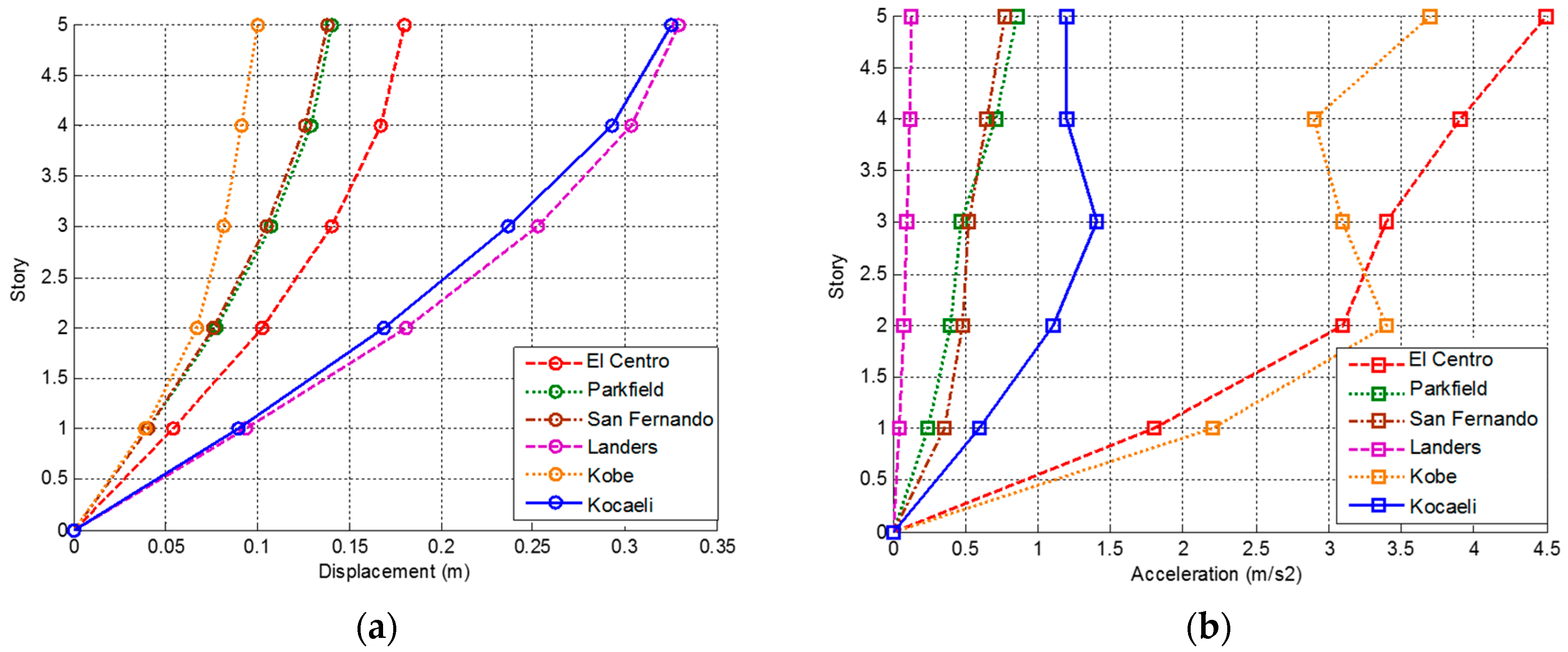
3.1.1. Changing Story Mass
3.1.2. Changing Story Stiffness
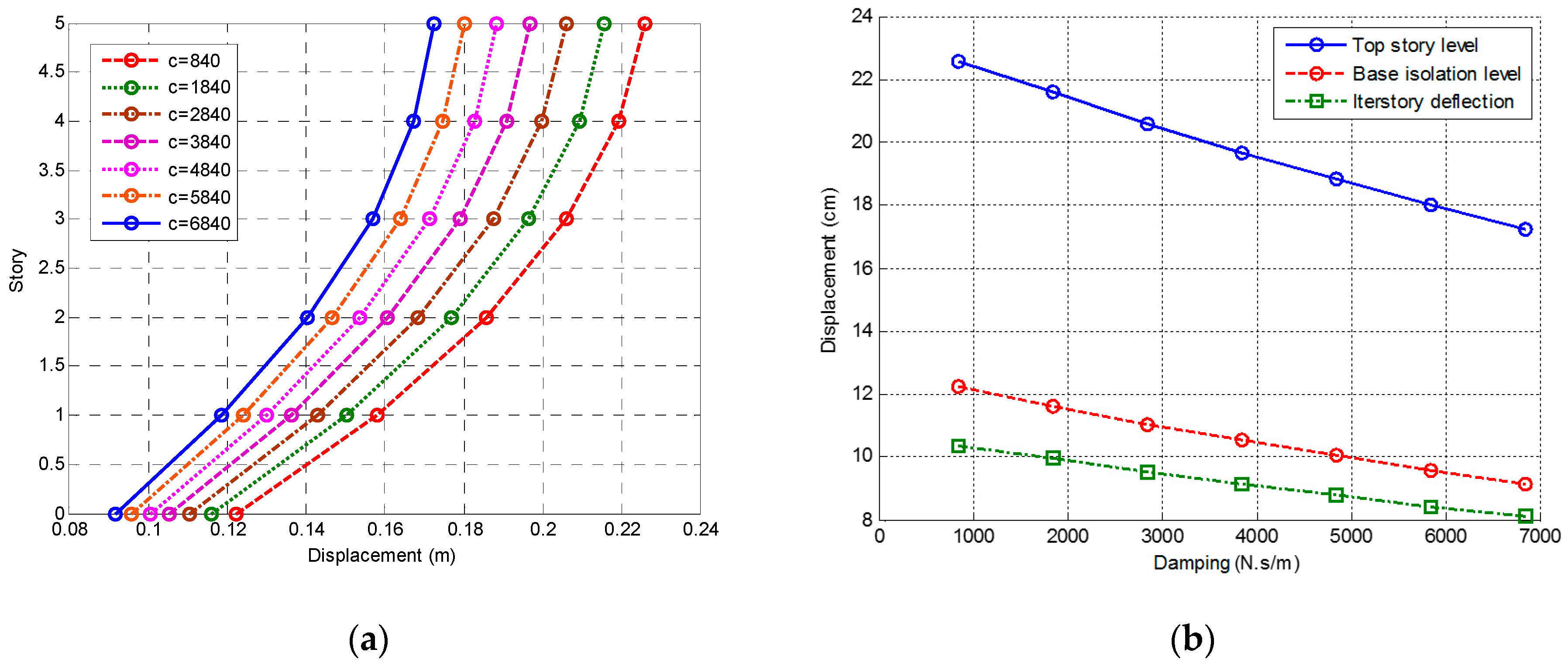
3.1.3. Changing Story Damping
3.2. Building with Additional Devices
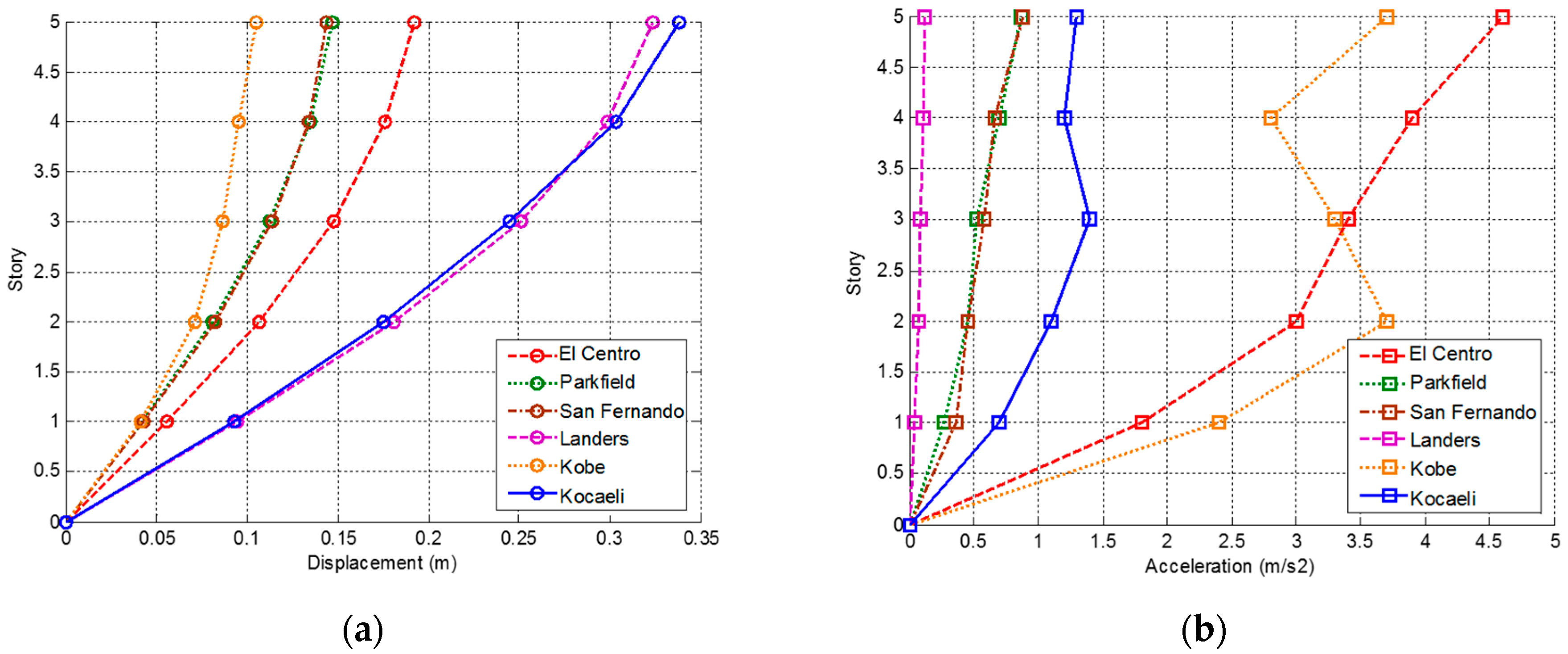
3.2.1. Using TMD
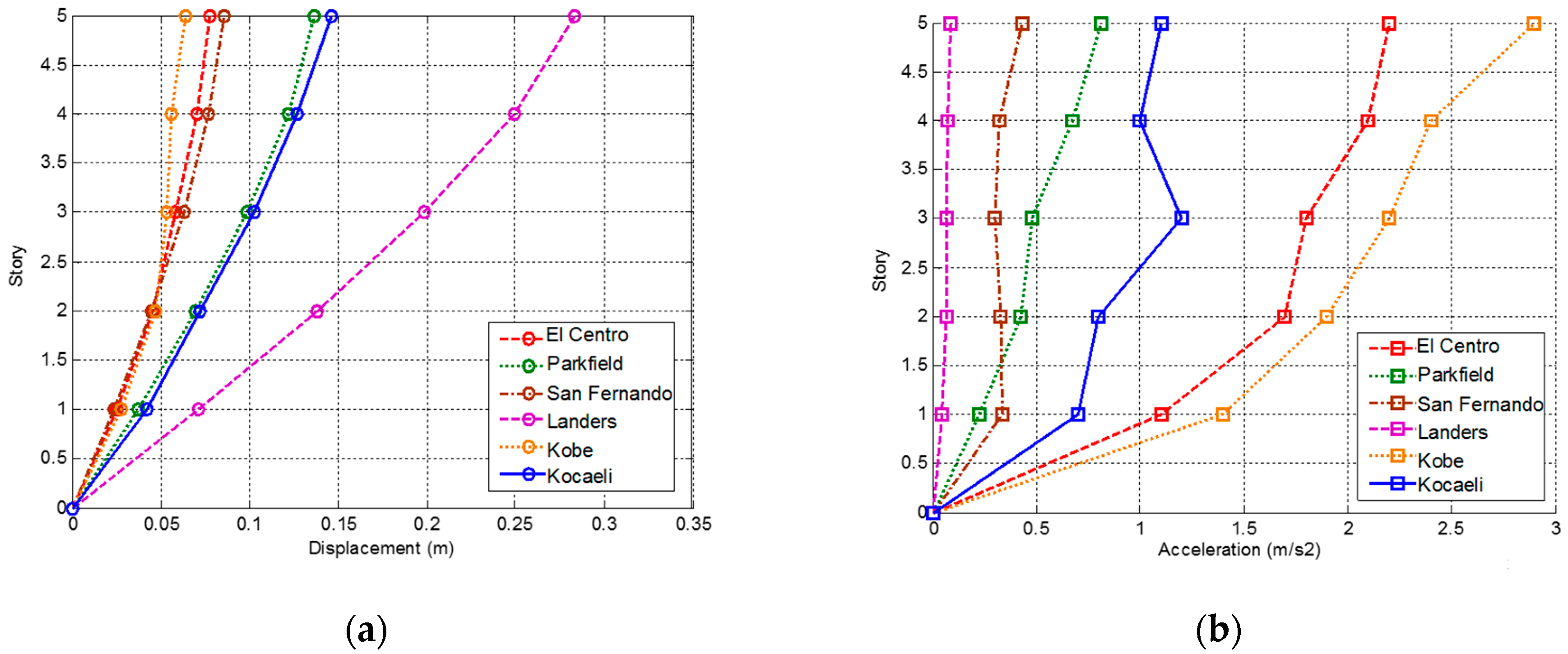
3.2.2. Using the Base Isolation System
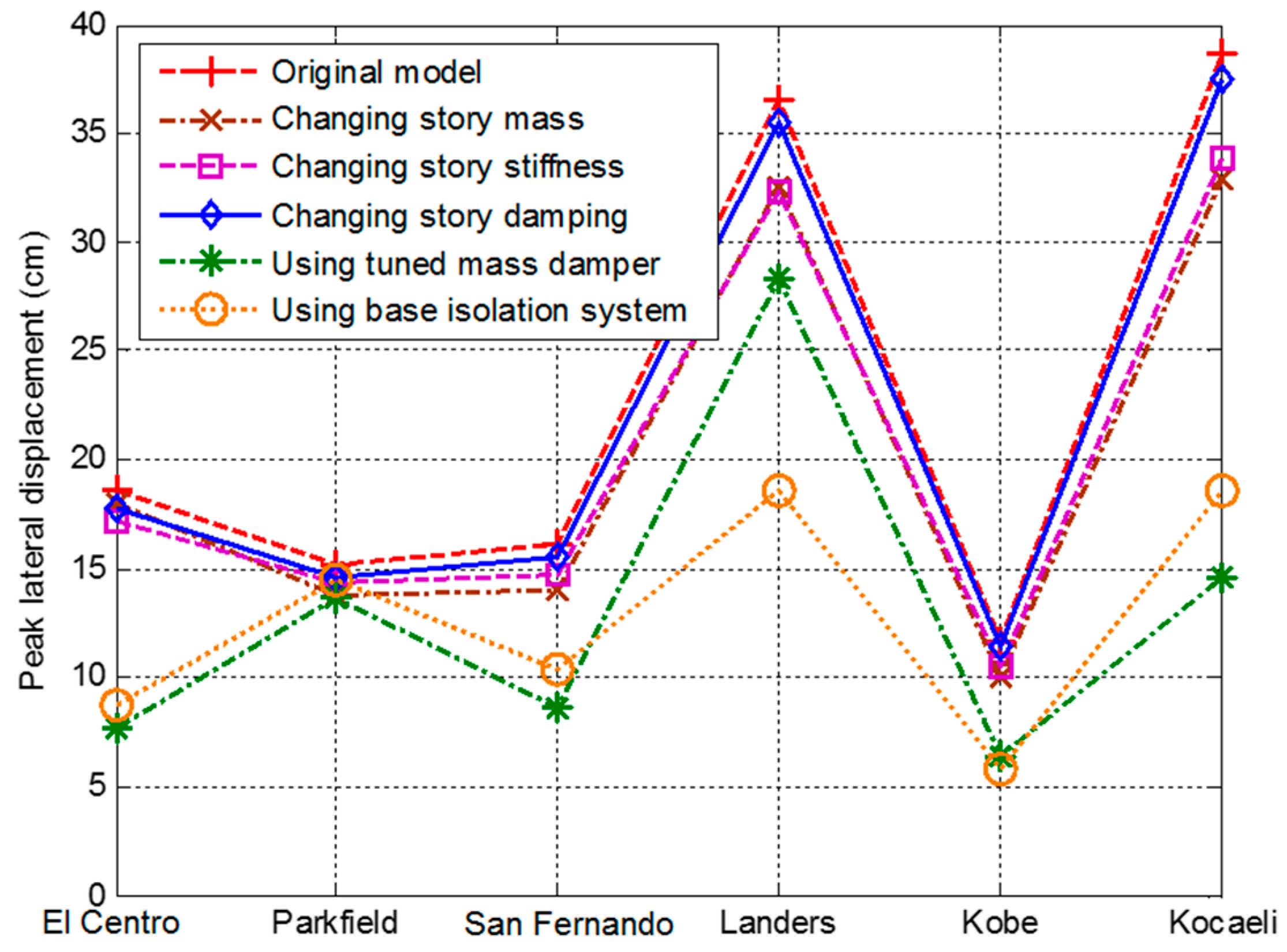
3.2.3. Comparison of Different Approaches
3.3. Base-isolated Building
3.3.1. Changing Initial Stiffness of Base Isolation
3.3.2. Changing the Mass of the Isolated Base
3.3.3. Changing Damping of Base Isolation
3.3.4. Using Rubber Bumpers
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Anagnostopoulos, S.A. Pounding of building in series during earthquakes. Earthq. Eng. Struct. Dyn. 1988, 16, 443–456. [Google Scholar] [CrossRef]
- Sołtysik, B.; Jankowski, R. Non-linear strain rate analysis of earthquake-induced pounding between steel buildings. Int. J. Earth Sci. Eng. 2013, 6, 429–433. [Google Scholar]
- Jankowski, R. Pounding between superstructure segments in multi-supported elevated bridge with three-span continuous deck under 3D non-uniform earthquake excitation. J. Earthq. Tsunami 2015, 9, 1550012. [Google Scholar] [CrossRef]
- Elwardany, H.; Seleemah, A.; Jankowski, R. Seismic pounding behavior of multi-story buildings in series considering the effect of infill panels. Eng. Struct. 2017, 144, 139–150. [Google Scholar] [CrossRef]
- Rezaei, H.; Moayyedi, S.A.; Jankowski, R. Probabilistic seismic assessment of RC box-girder highway bridges with unequal-height piers subjected to earthquake-induced pounding. Bull. Earthq. Eng. 2020, 18, 1547–1578. [Google Scholar] [CrossRef]
- Miari, M.; Choong, K.K.; Jankowski, R. Seismic pounding between adjacent buildings: Identification of parameters, soil interaction issues and mitigation measures. Soil Dyn. Earthq. Eng. 2019, 121, 135–150. [Google Scholar] [CrossRef]
- Anagnostopoulos, S.A.; Karamaneas, C.E. Use of collision shear walls to minimize seismic separation and to protect adjacent buildings from collapse due to earthquake-induced pounding. Earthq. Eng. Struct. Dyn. 2008, 37, 1371–1388. [Google Scholar] [CrossRef]
- Barros, R.C.; Khatami, S.M. Damping ratios for pounding of adjacent building and their consequence on the evaluation of impact forces by numerical and experimental models. Mecânica Exp. 2013, 22, 119–131. [Google Scholar]
- Kelly, J.M. Earthquake-resistant design with rubber; Springe: London, UK, 1993. [Google Scholar]
- Falborski, T.; Jankowski, R. Experimental study on effectiveness of a prototype seismic isolation system made of polymeric bearings. Appl. Sci. 2017, 7, 808. [Google Scholar] [CrossRef]
- Falborski, T.; Jankowski, R.; Kwiecień, A. Experimental study on polymer mass used to repair damaged structures. Key Eng. Mater. 2012, 488–489, 347–350. [Google Scholar] [CrossRef]
- Naderpour, H.; Naji, N.; Burkacki, D.; Jankowski, R. Seismic response of high-rise buildings equipped with base isolation and non-traditional tuned mass dampers. Appl. Sci. 2019, 9, 1201. [Google Scholar] [CrossRef]
- Jankowski, R.; Mahmoud, S. Linking of adjacent three-storey buildings for mitigation of structural pounding during earthquakes. Bull. Earthq. Eng. 2016, 14, 3075–3097. [Google Scholar] [CrossRef]
- Zhang, W.S.; Xu, Y.L. Dynamic characteristics and seismic response of adjacent buildings linked by discrete dampers. Earthq. Eng. Struct. Dyn. 1999, 28, 1163–1185. [Google Scholar] [CrossRef]
- Matsagar, V.A.; Jangid, R.S. Viscoelastic damper connected to adjacent structures involving seismic isolation. J. Civ. Eng. Manag. 2005, 11, 309–322. [Google Scholar] [CrossRef]
- Westermo, B.D. The dynamics of interstructural connection to prevent pounding. Earthq. Eng. Struct. Dyn. 1989, 18, 687–699. [Google Scholar] [CrossRef]
- Khatami, S.M.; Naderpour, H.; Barros, R.C.; Jakubczyk-Gałczyńska, A.; Jankowski, R. Determination of peak impact force for buildings exposed to structural pounding during earthquakes. Geosciences 2020, 10, 18. [Google Scholar] [CrossRef]
- Khatami, S.M.; Naderpour, H.; Barros, R.C.; Jakubczyk-Gałczyńska, A.; Jankowski, R. Effective formula for impact damping ratio for simulation of earthquake-induced structural pounding. Geosciences 2019, 9, 347. [Google Scholar] [CrossRef]
- Kasai, K.; Jeng, V.; Patel, P.C.; Munshi, J.A.; Maison, B.F. Seismic pounding effects—Survey and analysis. In Proceedings of the 10th World Conference on Earthquake Engineering, Madrid, Spain, 19–24 July 1992; pp. 3893–3898. [Google Scholar]
- Polycarpou, P.C.; Komodromos, P. Numerical investigation of potential mitigation measures for pounding of seismically isolated building. Earthq. Struct. 2011, 2, 1–24. [Google Scholar] [CrossRef]
- Polycarpou, P.C.; Komodromos, P.; Polycarpou, A.C. A nonlinear impact model for simulating the use of rubber shock absorbers for mitigating the effects of structural pounding during earthquakes. Earthq. Eng. Struct. Dyn. 2013, 42, 81–100. [Google Scholar] [CrossRef]
- Raheem, S.E.A. Mitigation measures for earthquake induced pounding effects on seismic performance of adjacent buildings. Bull. Earthq. Eng. 2014, 12, 1705–1724. [Google Scholar] [CrossRef]
- Dogruel, S. Application of genetic algorithms for optimal aseismic design of passively damped adjacent structures; State University of New York at Buffalo: Buffalo, NY, USA, 2005. [Google Scholar]
- Braz, C.; Barros, R.C. Semi-active vibration control of buildings using MR dampers: Numerical and experimental verification. In Proceedings of the 14th Earthquake Conference on Earthquake Engineering, Macedonia, Balkans, March 2010. [Google Scholar]
- Lopez-Garcia, D.; Soong, T.T. Evaluation of current criteria in predicting the separation necessary to prevent seismic pounding between nonlinear hysteretic structural systems. Eng. Struct. 2009, 31, 1217–1229. [Google Scholar] [CrossRef]
- Lopez-Garcia, D. Separation between adjacent non-linear structures for prevention of seismic pounding. In Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, BC, Canada, 1–6 August 2004. [Google Scholar]
- Favvata, M.J. Minimum required separation gap for adjacent RC frames with potential inter-story seismic pounding. Eng. Struct. 2017, 152, 643–659. [Google Scholar] [CrossRef]
- Favvata, M.J.; Karayannis, C.G.; Liolios, A.A. Influence of exterior joint effect on the inter-story pounding interaction of structures. Struct. Eng. Mech. 2009, 33, 113–136. [Google Scholar] [CrossRef]
- Favvata, M.J.; Naoum, M.C.; Karayannis, C.G. Limit states of RC structures with first floor irregularities. Structural Engineering and Mechanics 2013, 47, 791–818. [Google Scholar] [CrossRef]
- Karayannis, C.G.; Favvata, M.J.; Kakaletsis, D.J. Seismic behaviour of infilled and pilotis RC frame structures with beam–column joint degradation effect. Eng. Struct. 2011, 33, 2821–2831. [Google Scholar] [CrossRef]







| Earthquake | Date | Magnitude | Station | Component | PGA (cm/s2) |
|---|---|---|---|---|---|
| Kocaeli | 17.08.1999 | 7.6 | Sakarya | EW | 369.28 |
| Kobe | 17.01.1995 | 7.2 | JMA | NS | 817.82 |
| Parkfield | 28.06.1966 | 6.2 | Jennings (CGS) | NS | 462.00 |
| El Centro | 18.05.1940 | 6.9 | El Centro | NS | 307.00 |
| San Fernando | 09.02.1971 | 6.6 | Pacoima Dam | N16° W | 1202.62 |
| Landers | 28.09.1992 | 7.3 | Baker | SS | 853.00 |
| Earthquake | Original Model | Changing Story Mass | Changing Story Stiffness | Changing Story Damping | Using TMD | Using the Base Isolation System |
|---|---|---|---|---|---|---|
| El Centro | 18.65 | 18.02 | 17.21 | 17.76 | 7.7 | 8.72 |
| Parkfield | 15.19 | 13.83 | 14.42 | 14.66 | 13.69 | 14.52 |
| San Fernando | 16.11 | 14.05 | 14.74 | 15.57 | 8.62 | 10.39 |
| Landers | 36.53 | 32.56 | 32.34 | 35.44 | 28.37 | 18.64 |
| Kobe | 11.68 | 10.01 | 10.51 | 11.46 | 6.4 | 5.86 |
| Kocaeli | 38.69 | 32.93 | 33.84 | 37.45 | 14.63 | 18.59 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khatami, S.M.; Naderpour, H.; Razavi, S.M.N.; Barros, R.C.; Jakubczyk-Gałczyńska, A.; Jankowski, R. Study on Methods to Control Interstory Deflections. Geosciences 2020, 10, 75. https://doi.org/10.3390/geosciences10020075
Khatami SM, Naderpour H, Razavi SMN, Barros RC, Jakubczyk-Gałczyńska A, Jankowski R. Study on Methods to Control Interstory Deflections. Geosciences. 2020; 10(2):75. https://doi.org/10.3390/geosciences10020075
Chicago/Turabian StyleKhatami, Seyed Mohammad, Hosein Naderpour, Seyed Mohammad Nazem Razavi, Rui Carneiro Barros, Anna Jakubczyk-Gałczyńska, and Robert Jankowski. 2020. "Study on Methods to Control Interstory Deflections" Geosciences 10, no. 2: 75. https://doi.org/10.3390/geosciences10020075
APA StyleKhatami, S. M., Naderpour, H., Razavi, S. M. N., Barros, R. C., Jakubczyk-Gałczyńska, A., & Jankowski, R. (2020). Study on Methods to Control Interstory Deflections. Geosciences, 10(2), 75. https://doi.org/10.3390/geosciences10020075






