Numerical Evaluation of Natural Periods and Mode Shapes of Earth Dams for Probabilistic Seismic Hazard Analysis Applications
Abstract
1. Introduction
2. Methodology and Data
3. Results
4. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Penman, A.D.M. On the embankment dam. Geotechnique 1986, 36, 301–348. [Google Scholar] [CrossRef]
- Zimmaro, P. Seismic Response of the Farneto del Principe Dam in Italy Using Hazard-consistent and Site-specific Ground Motions. Ph.D. Thesis, University Mediterranea, Reggio Calabria, Italy, March 2015. [Google Scholar]
- Norme Tecniche per la Progettazione e la Costruzione Degli Sbarramenti di Ritenuta (Dighe e Traverse); Ministry of Infrastructures and Transport of Italy: Rome, Italy, 14 June 2014. (In Italian)
- Aggiornamento delle Norme Tecniche per le Costruzioni; Ministry of Infrastructures and Transport of Italy: Rome, Italy, 17 January 2018. (In Italian)
- Verifiche Sismiche delle Grandi dighe, degli Scarichi e delle opere Complementari e Accessorie; Ministry of Infrastructures and Transport of Italy: Rome, Italy, 3 July 2019. (In Italian)
- Baker, J.W. Conditional Mean Spectrum: Tool for ground motion selection. J. Struct. Eng. 2011, 137, 322–331. [Google Scholar] [CrossRef]
- Baker, J.W.; Cornell, C.A. Spectral shape, epsilon and record selection. Earthq. Eng. Struct. Dyn. 2006, 35, 1077–1095. [Google Scholar] [CrossRef]
- Dakoulas, P.; Gazetas, G. A class of inhomogeneous shear models for seismic response of dams and embankments. Soil Dyn. Earthq. Eng. 1985, 4, 166–182. [Google Scholar] [CrossRef]
- Watanabe, H.; Kikuchi, K.; Cao, Z. Vibration Modes of Rockfill Dam Based on the Observations of Microtremors and an Earthquake; Research report; Thammasat Univ. Rangsit Campus: Pathum Thani, Thailand, 1995. [Google Scholar]
- Castro, R.R.; Mucciarelli, M.; Pacor, F.; Federici, P.; Zaninetti, A. Determination of the characteristic frequency of two dams located in the region of Calabria. Bull. Seismol. Soc. Am. 1998, 88, 503–511. [Google Scholar]
- Rainieri, C.; Fabbrocino, G. Operational Modal Analysis of Civil Engineering Structures; Springer: New York, NY, USA, 2014. [Google Scholar]
- Aloisio, A.; Di Pasquale, A.; Alaggio, R.; Fragiacomo, M. Assessment of seismic retrofitting interventions of a masonry palace using operational modal analysis. Int. J. Archit. Herit. 2020, 1–13. [Google Scholar] [CrossRef]
- Chugh, A.K. Natural vibration characteristics of gravity structures. Int. J. Numer. Anal. Methods Geomech. 2007, 31, 607–648. [Google Scholar] [CrossRef]
- Chakraborty, S.; Das, J.T.; Puppala, A.J.; Banerjee, A. Natural frequency of earthen dams at different induced strain levels. Eng. Geol. 2019, 248, 330–345. [Google Scholar] [CrossRef]
- Yaseri, A.; Konrad, J.M. Estimation of natural periods of earth dam-flexible canyon systems with 3D coupled FEM-SBFEM. Comput. Geotech. 2020, 123, 103546. [Google Scholar] [CrossRef]
- Zimmaro, P.; Stewart, J.P. Site-specific seismic hazard analysis for Calabrian dam site using regionally customized seismic source and ground motion models. Soil Dyn. Earthq. Eng. 2017, 94, 179–192. [Google Scholar] [CrossRef]
- CSI Analysis Reference Manual for SAP2000, ETABS and SAFE; Computers and Structures, Inc.: Berkeley, CA, USA, 2013.
- Ambraseys, N.N. A note on the response of an elastic overburden of varying rigidity to an arbitrary ground motion. Bull. Seismol. Soc. Am. 1959, 49, 211–220. [Google Scholar]
- Seed, H.B.; Idriss, I.M. The influence of ground conditions on ground motions during earthquakes. J. Soil Mech. Found. Div. 1969, 94, 93–137. [Google Scholar]
- Dobry, R.; Whitman, R.; Roesset, J.M. Soil Properties and the One-dimensional Theory of Earthquake Amplification; Research Report R71-18; M.I.T.: Cambridge, MA, USA, May 1971. [Google Scholar]
- Schreyer, H. One-dimensional elastic waves in inhomogeneous media. J. Eng. Mech. Div. 1977, 103, 979–990. [Google Scholar]
- Gazetas, G. Vibrational characteristics of soil deposits with variable wave velocity. Int. J. Numer. Anal. Methods Geomech. 1982, 6, 1–20. [Google Scholar] [CrossRef]
- Towhata, I. Seismic wave propagation in elastic soil with continuous variation of shear modulus in the vertical direction. Soil. Found. 1996, 36, 61–72. [Google Scholar] [CrossRef]
- Rovithis, E.; Parashakis, C.; Mylonakis, G. 1D harmonic response of layered inhomogeneous soil: Analytical investigation. Soil Dyn. Earthq. Eng. 2011, 31, 879–890. [Google Scholar] [CrossRef]
- Durante, M.G.; Karamitros, D.; Di Sarno, L.; Sica, S.; Taylor, C.A. Characterisation of shear wave velocity profiles of non-uniform bi-layer soil deposits: Analytical evaluation and experimental validation. Soil Dyn. Earthq. Eng. 2015, 75, 44–54. [Google Scholar] [CrossRef]
- Bishop, A.W.; Height, D.W. The value of Poisson’s ratio in saturated soils and rocks stressed under undrained conditions. Geotechnique 1977, 27, 369–384. [Google Scholar] [CrossRef]
- Ausilio, E.; Dente, G.; Zimmaro, P. Geotechnical Investigation and Field Performance of a Zoned Earth Dam in Italy. In Proceedings of the 1st IMEKO TC4 International Workshop on Metrology for Geotechnics, Benevento, Italy, 16–18 March 2016. [Google Scholar]
- Richart, F.E.; Hall, J.R.; Woods, R.D. Vibrations of Soils and Foundations; Prentice-Hall, Inc.: Upper Saddle River, NJ, USA, 1970. [Google Scholar]
- Hardin, B.O.; Drnevich, V.P. Shear modulus and damping in soils: Measurement and parameter effects, Terzaghi Lecture. J. Soil Mech. Found. Div. 1972, 98, 603–624. [Google Scholar]
- Mancuso, C. Aspetti Metodologici ed Applicazione della Tecnica Sperimentale SASW. Riv. Ital. Geotec. 1995, 4, 271–288. [Google Scholar]
- Pagano, L.; Mancuso, C.; Sica, S. Prove in sito sulla diga del Camastra: Tecniche sperimentali e risultati. Riv. Ital. Geotec. 2008, 3, 11–28. [Google Scholar]
- Jacobsen, L.S. Motion of a soil subjected to a simple harmonic ground vibration. Bull. Seismol. Soc. Am. 1930, 20, 160–195. [Google Scholar]
- Idriss, I.M.; Mathr, J.M.; Seed, H.B. Earth Dam-foundation interaction during earthquakes. Earthq. Eng. Struct. Dyn. 1973, 2, 313–323. [Google Scholar] [CrossRef]
- Carlton, B.; Abrahamson, N. Issues and approaches for implementing conditional mean spectra in practice. Bull. Seismol. Soc. Am. 2014, 104, 503–512. [Google Scholar] [CrossRef]
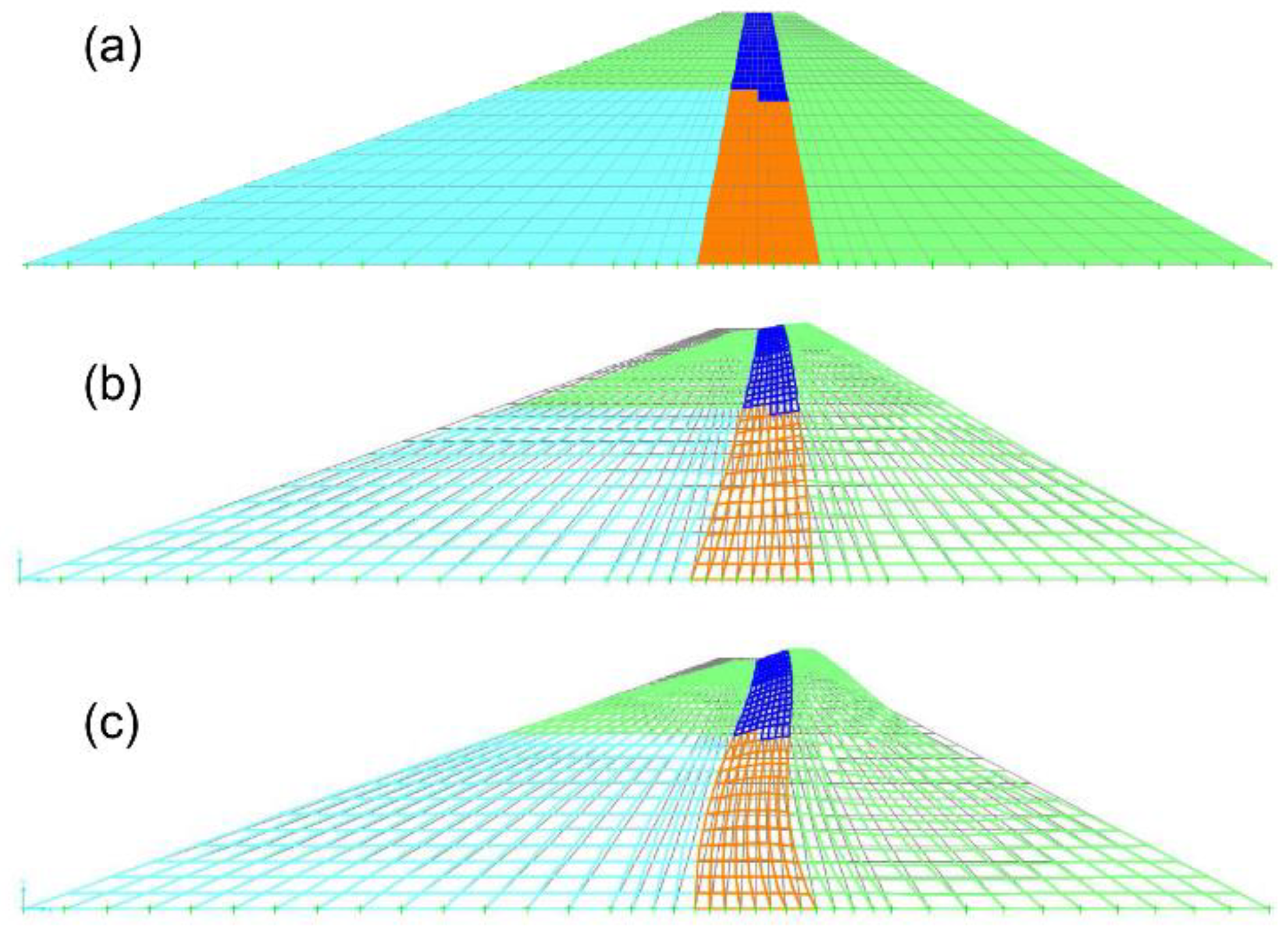
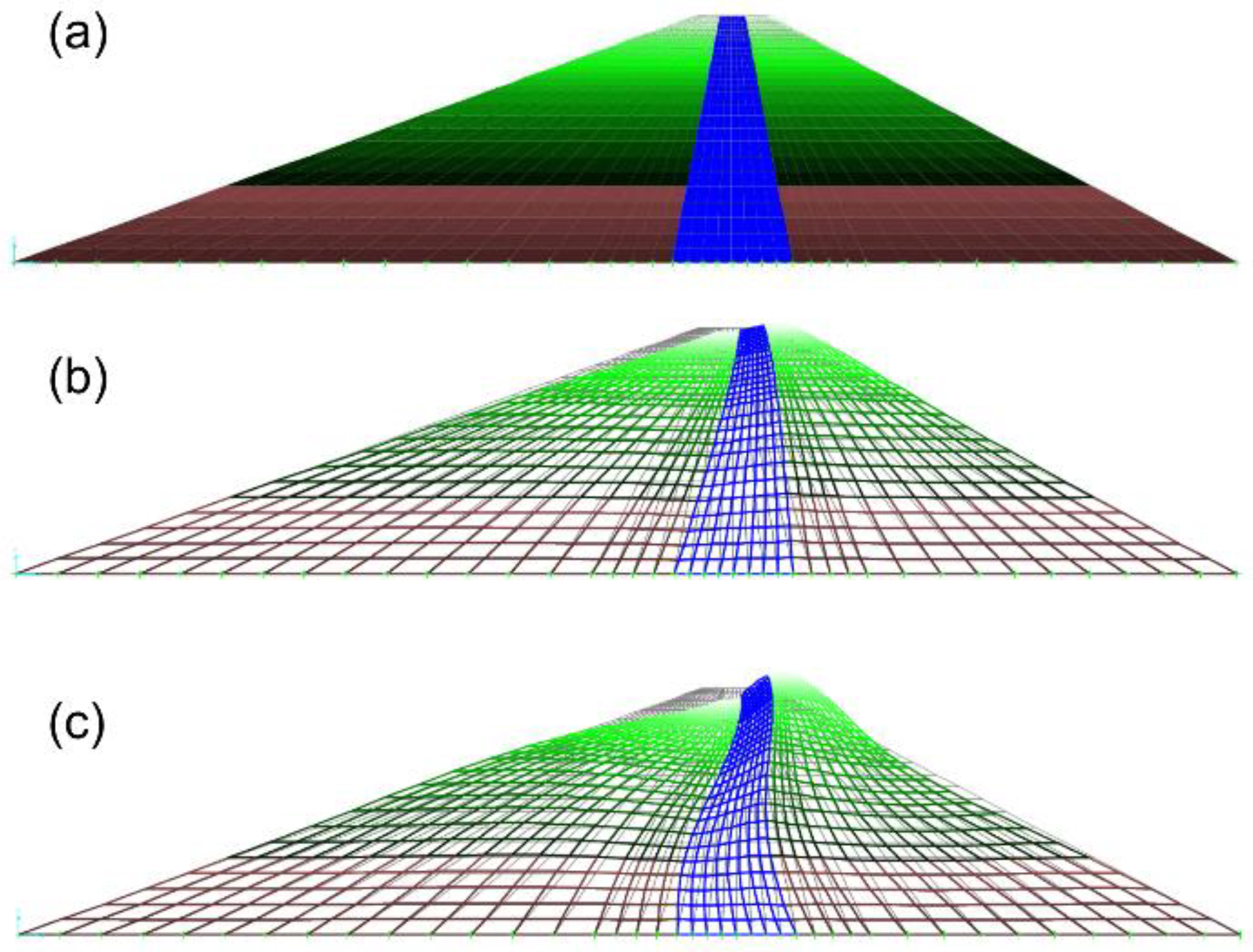
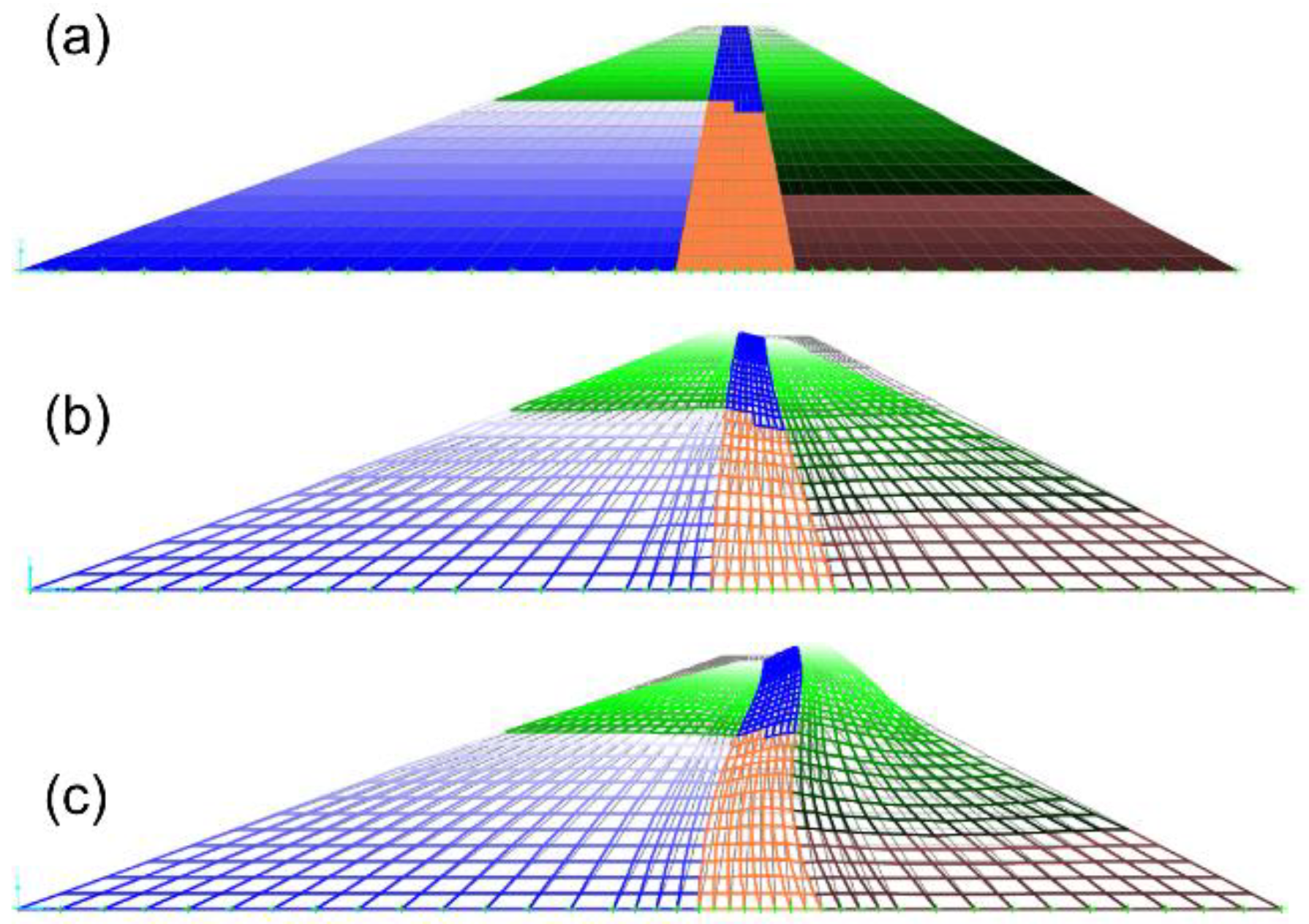
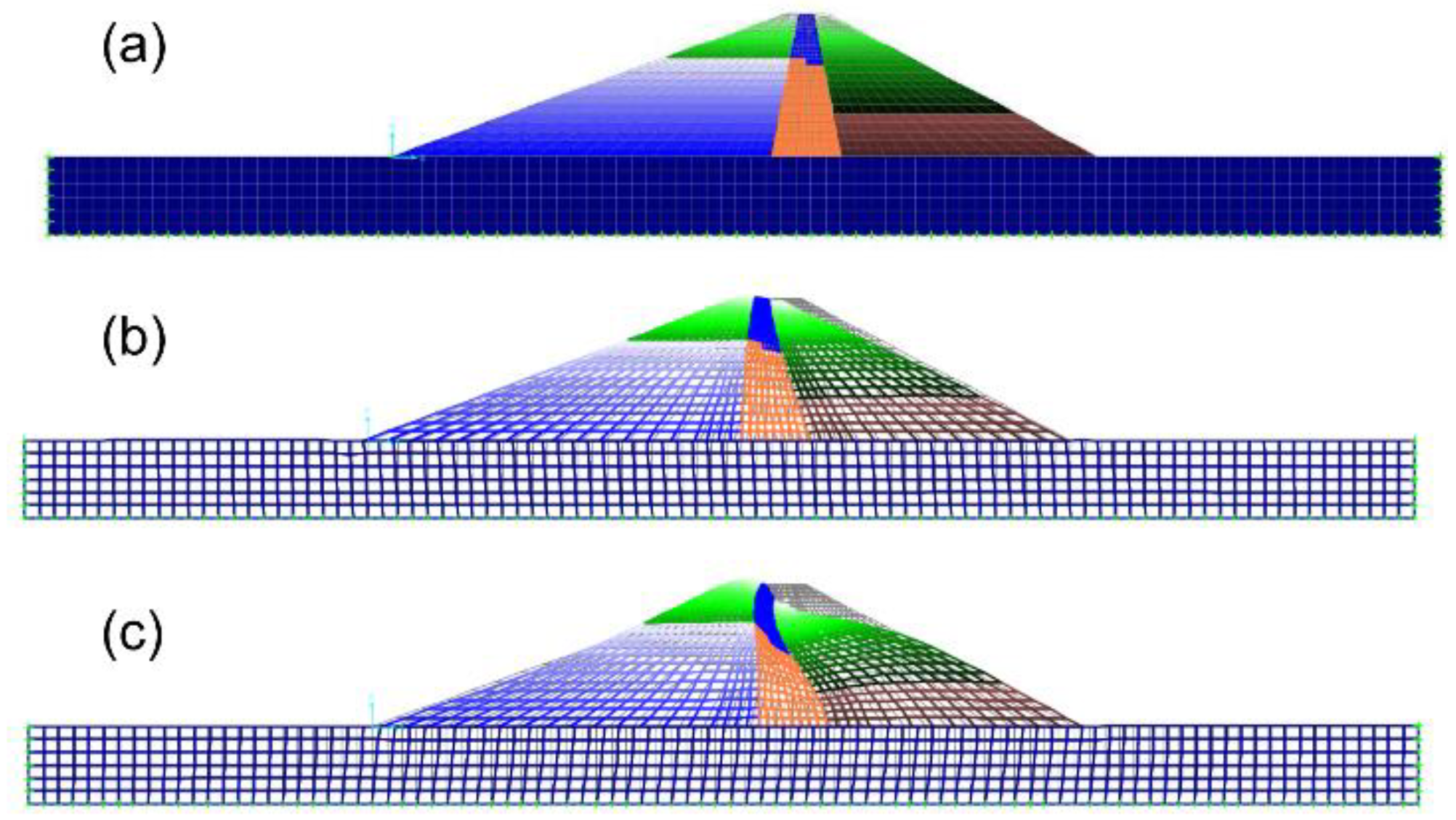
| Model # | Rigid Base | Flexible Base | Presence of Water | VS Variable with Depth |
|---|---|---|---|---|
| 1 | ✓ | ✗ | ✗ | ✗ |
| 2 | ✓ | ✗ | ✓ | ✗ |
| 3 | ✓ | ✗ | ✗ | ✓ |
| 4 | ✓ | ✗ | ✓ | ✓ |
| 5 | ✗ | ✓ | ✓ | ✓ |
| Parameter | Above the Phreatic Surface | Below the Phreatic Surface | Foundation | ||
|---|---|---|---|---|---|
| Core | Shells | Core | Shells | ||
| γ (kN/m3) | 18 | 24 | 21.3 | 25.1 | 24.1 |
| Poisson’s ratio | 0.35 | 0.33 | 0.49 | 0.49 | 0.33 |
| VS (m/s) | 250 | Variable with depth (models 4 and 5) | 250 | Variable with depth models 4 and 5) | 650 |
| Mode | Model 1 | Model 2 | Model 3 | Model 4 | ||||
|---|---|---|---|---|---|---|---|---|
| Period (s) | MPMR (%) | Period (s) | MPMR (%) | Period (s) | MPMR (%) | Period (s) | MPMR (%) | |
| 1 | 0.213 | 63 | 0.205 | 65 | 0.205 | 60 | 0.197 | 62 |
| 2 | 0.102 | 14 | 0.099 | 10 | 0.099 | 16 | 0.097 | 12 |
| 3 | 0.059 | 2 | 0.055 | 2 | 0.062 | 2 | 0.063 | 2 |
| 4 | 0.045 | 1 | 0.040 | 2 | 0.004 | 1 | 0.038 | 2 |
| Model | Period (s) | Period Elongation (%) | ||
|---|---|---|---|---|
| T1 | T2 | ΔT1 | ΔT2 | |
| 4 (fixed base) | 0.197 | 0.097 | - | - |
| 5 (flexible base) | 0.240 | 0.126 | 22 | 29 |
| Mode | Homogeneous Shear Beam [8] | Inhomogeneous Shear Beam [8] | One-Dimensional Solution [32] | Model 4 (FEM, Fixed Base) |
|---|---|---|---|---|
| Period (s) | Period (s) | Period (s) | Period (s) | |
| 1 | 0.168 | 0.169 | 0.257 | 0.197 |
| 2 | 0.073 | 0.080 | 0.086 | 0.097 |
| 3 | 0.047 | 0.052 | 0.051 | 0.063 |
| 4 | 0.034 | 0.038 | 0.037 | 0.038 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zimmaro, P.; Ausilio, E. Numerical Evaluation of Natural Periods and Mode Shapes of Earth Dams for Probabilistic Seismic Hazard Analysis Applications. Geosciences 2020, 10, 499. https://doi.org/10.3390/geosciences10120499
Zimmaro P, Ausilio E. Numerical Evaluation of Natural Periods and Mode Shapes of Earth Dams for Probabilistic Seismic Hazard Analysis Applications. Geosciences. 2020; 10(12):499. https://doi.org/10.3390/geosciences10120499
Chicago/Turabian StyleZimmaro, Paolo, and Ernesto Ausilio. 2020. "Numerical Evaluation of Natural Periods and Mode Shapes of Earth Dams for Probabilistic Seismic Hazard Analysis Applications" Geosciences 10, no. 12: 499. https://doi.org/10.3390/geosciences10120499
APA StyleZimmaro, P., & Ausilio, E. (2020). Numerical Evaluation of Natural Periods and Mode Shapes of Earth Dams for Probabilistic Seismic Hazard Analysis Applications. Geosciences, 10(12), 499. https://doi.org/10.3390/geosciences10120499





