Measuring Centimeter-Scale Sand Ripples Using Multibeam Echosounder Backscatter Data from the Brown Bank Area of the Dutch Continental Shelf
Abstract
1. Introduction
2. Study Area, Materials, and Methods
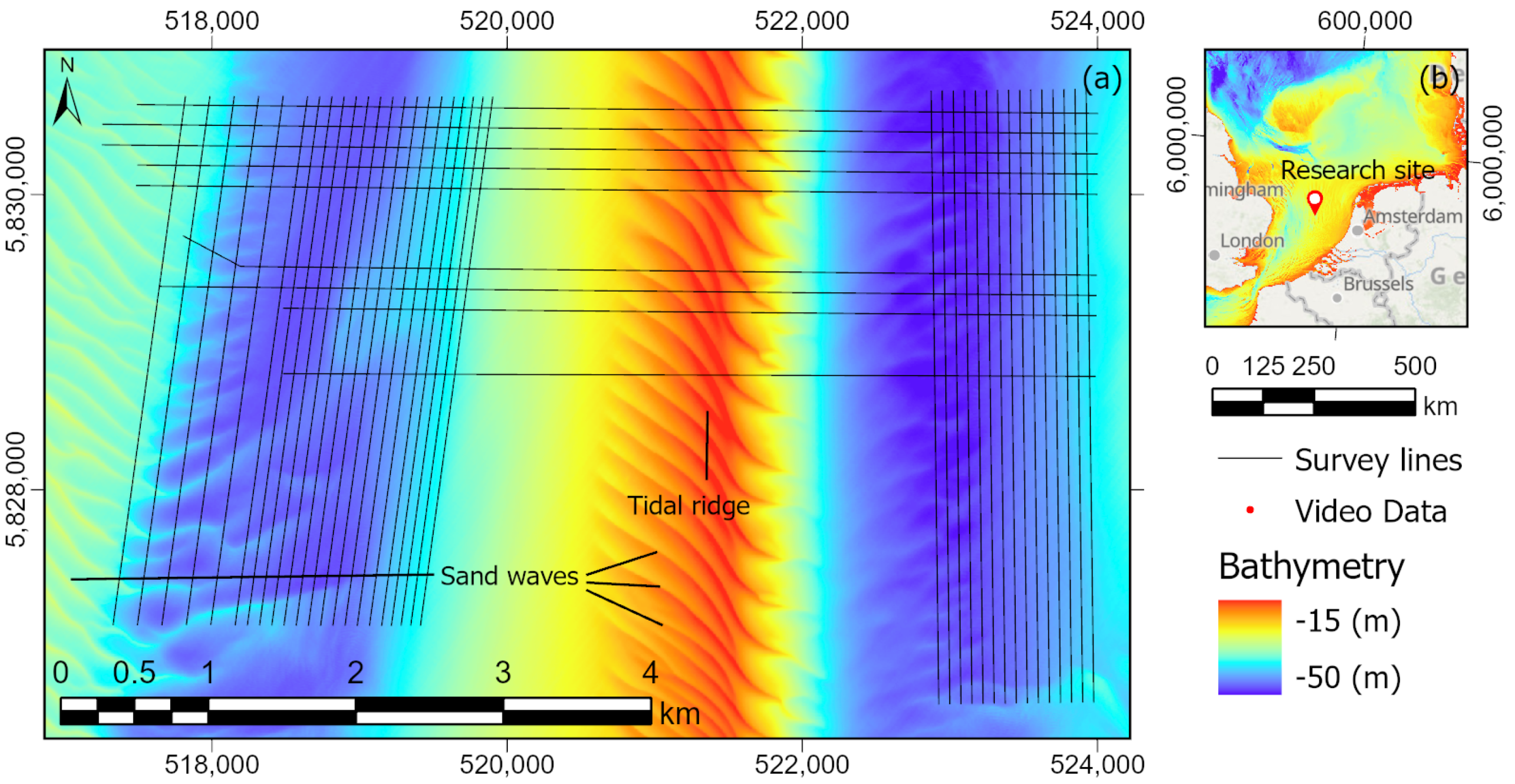
2.1. Study Area
2.2. Multibeam Echosounder Data
2.3. Video Data
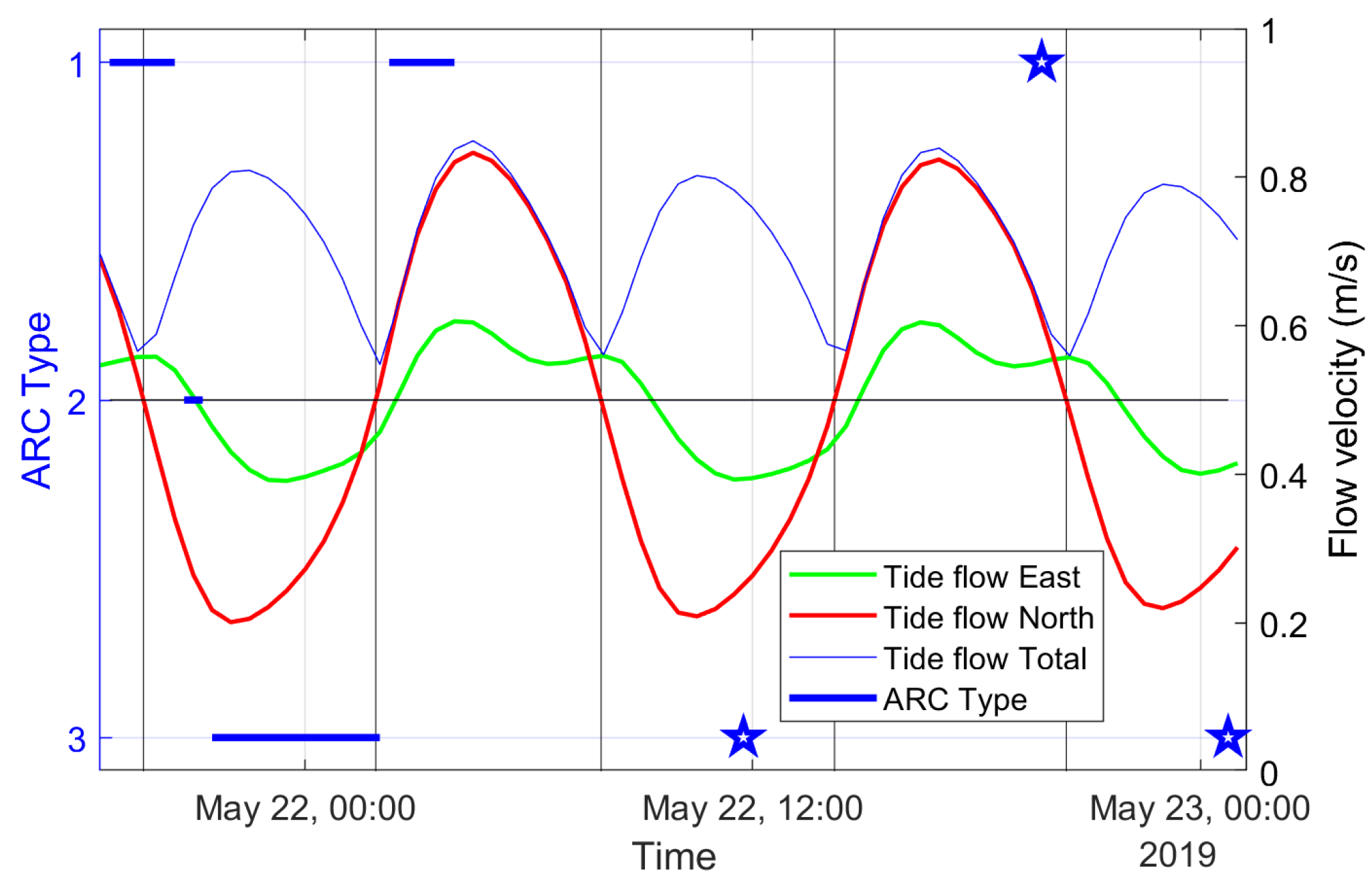
2.4. Tide Model Data
3. Results and Discussion
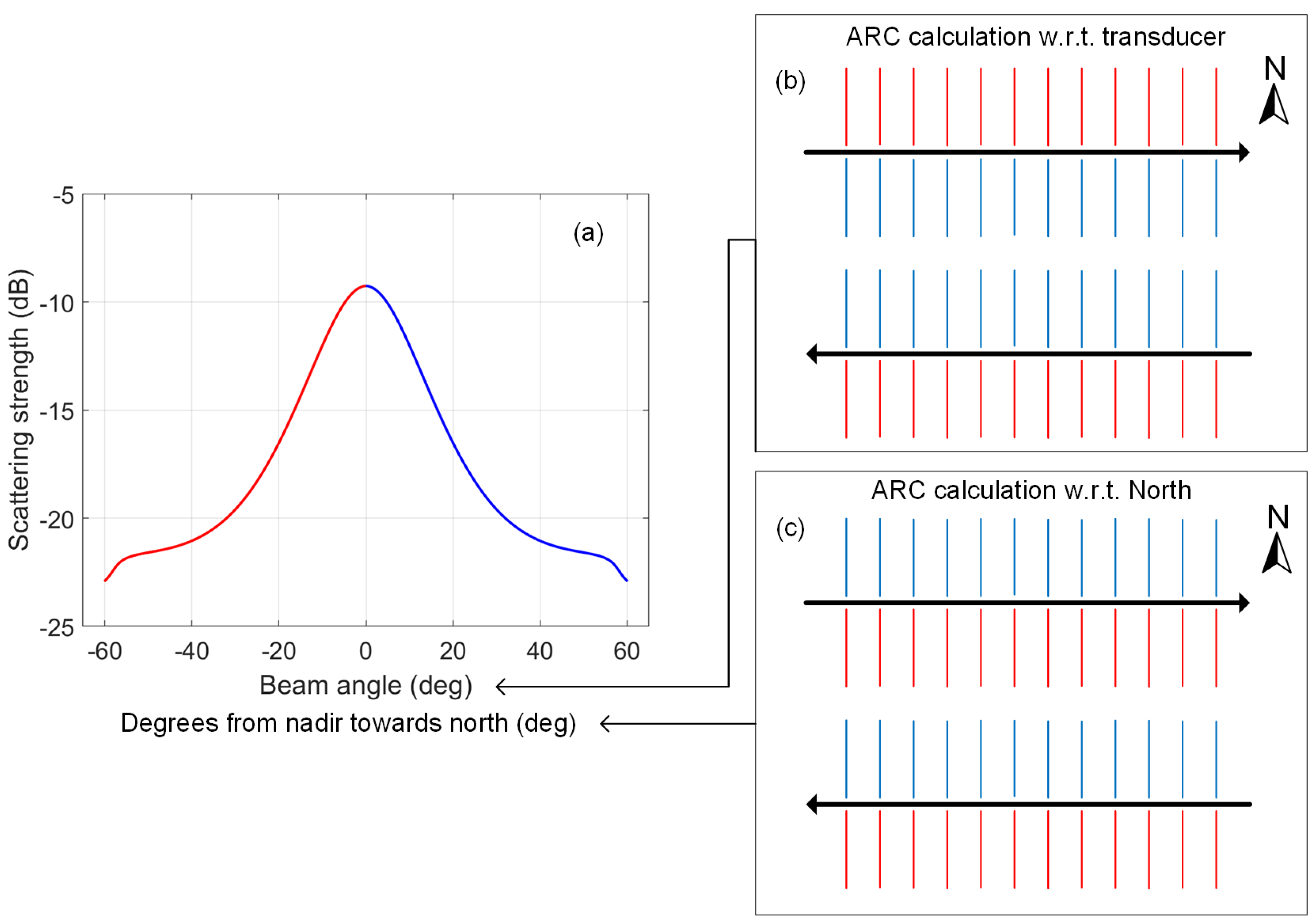
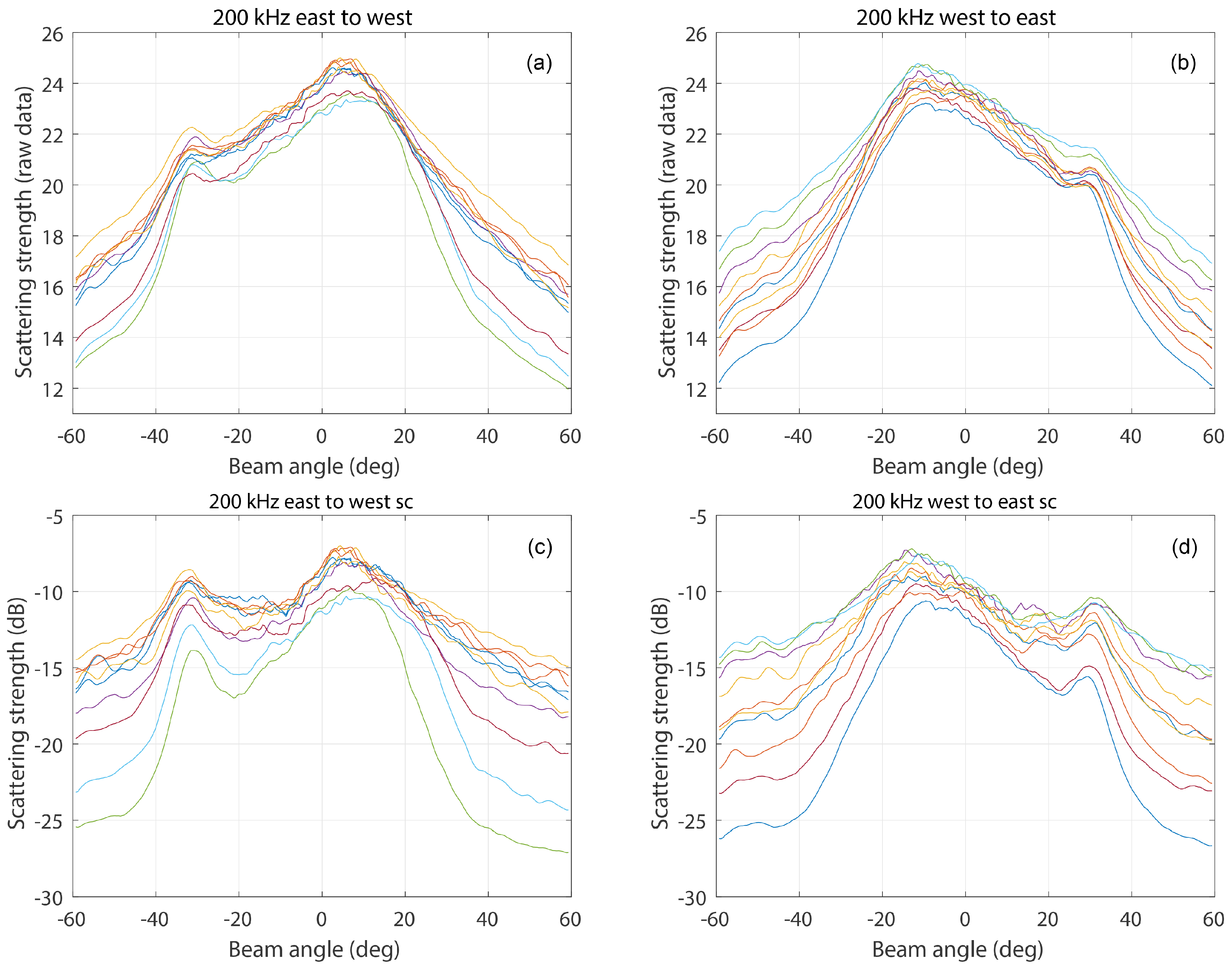
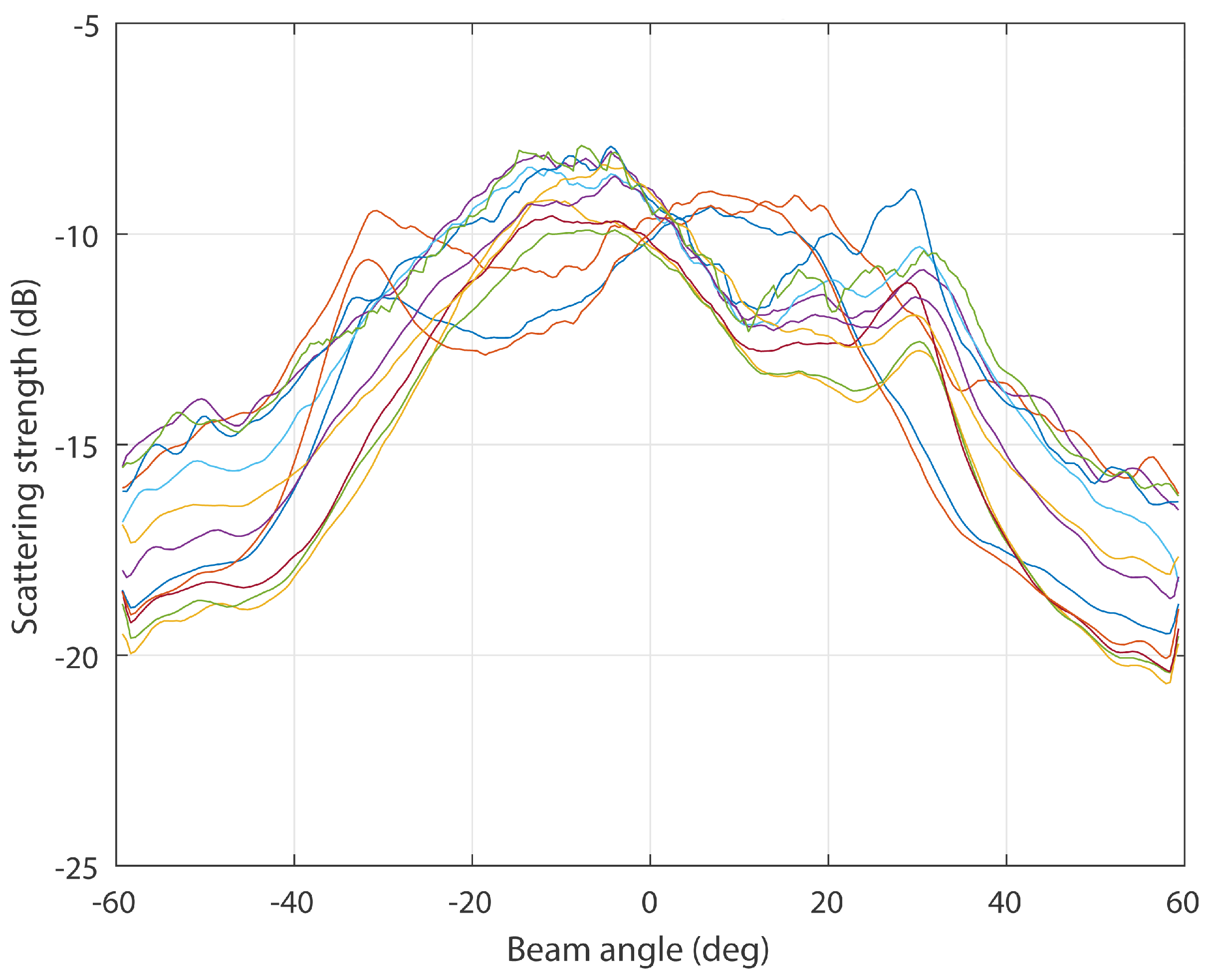
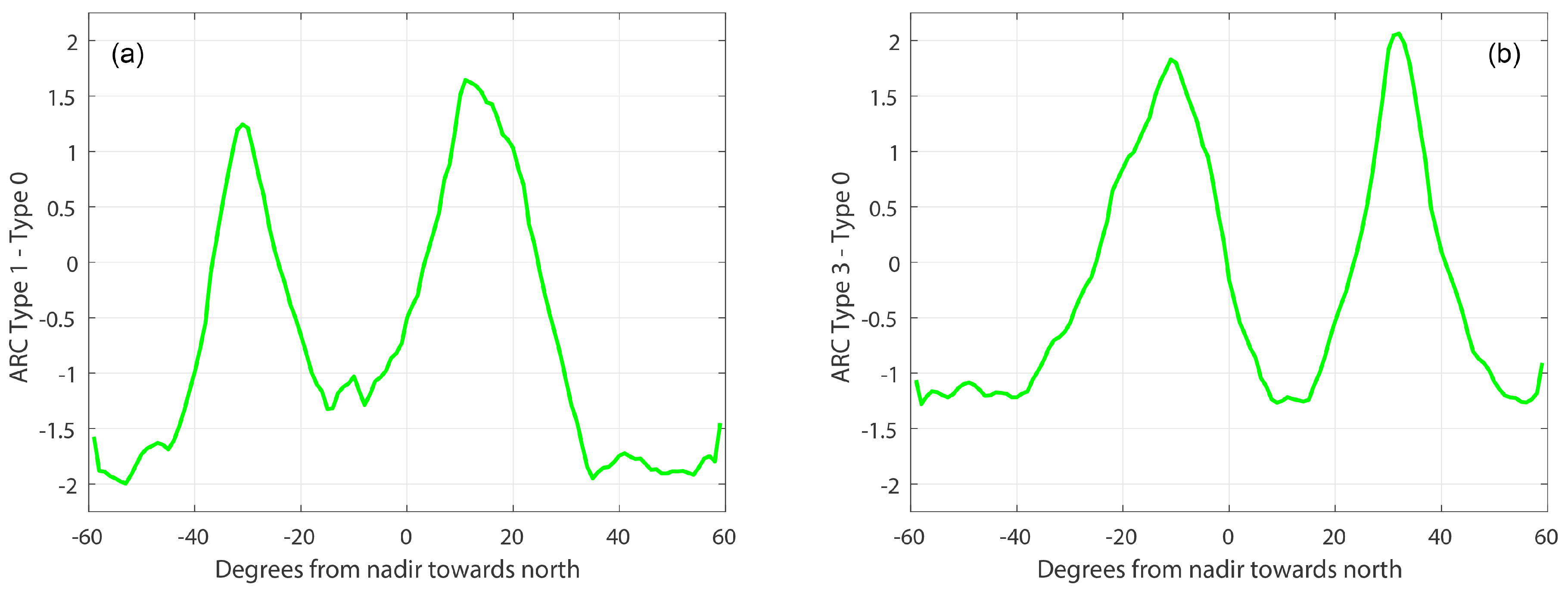
3.1. Angular-Response Curves
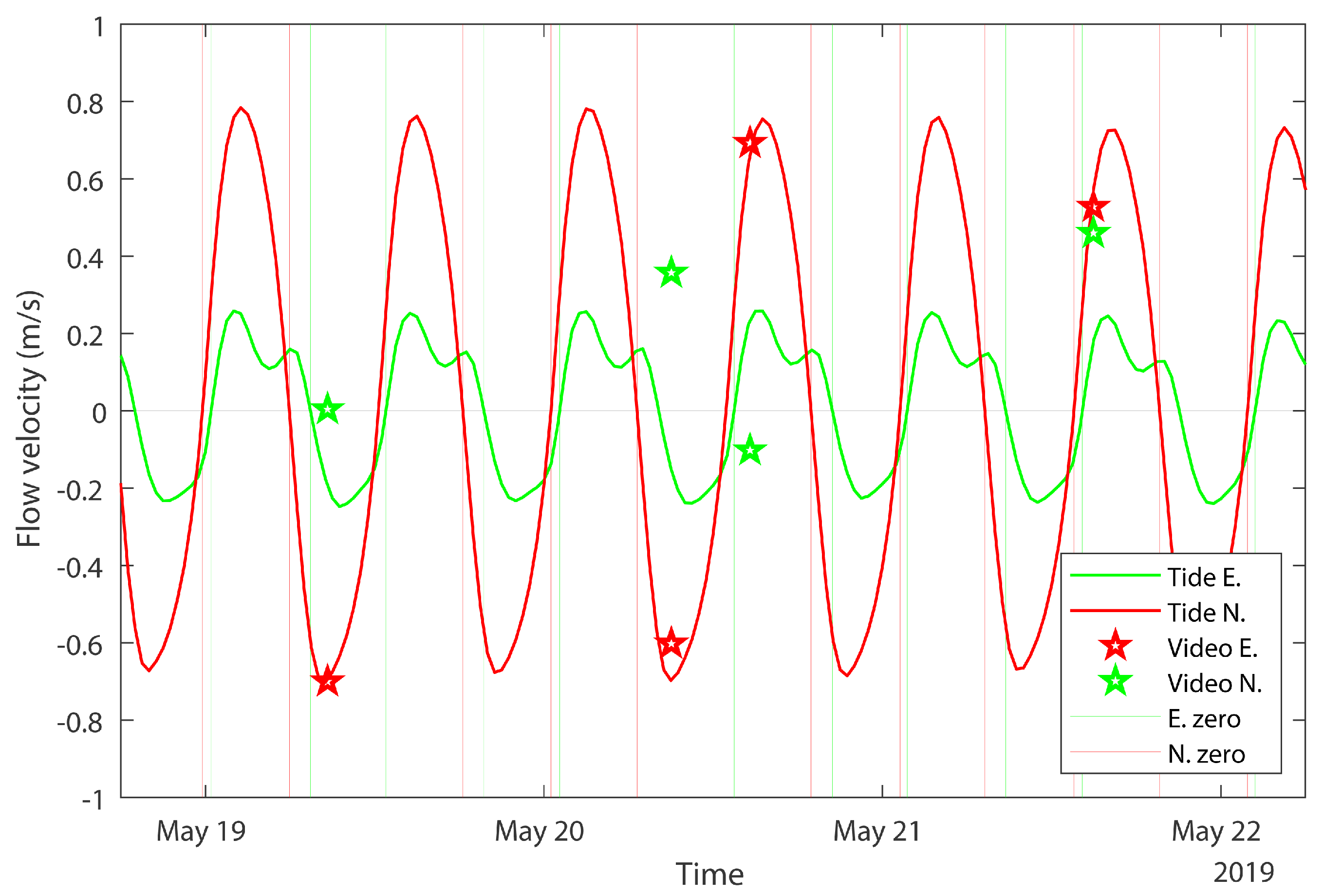
3.2. Video Results
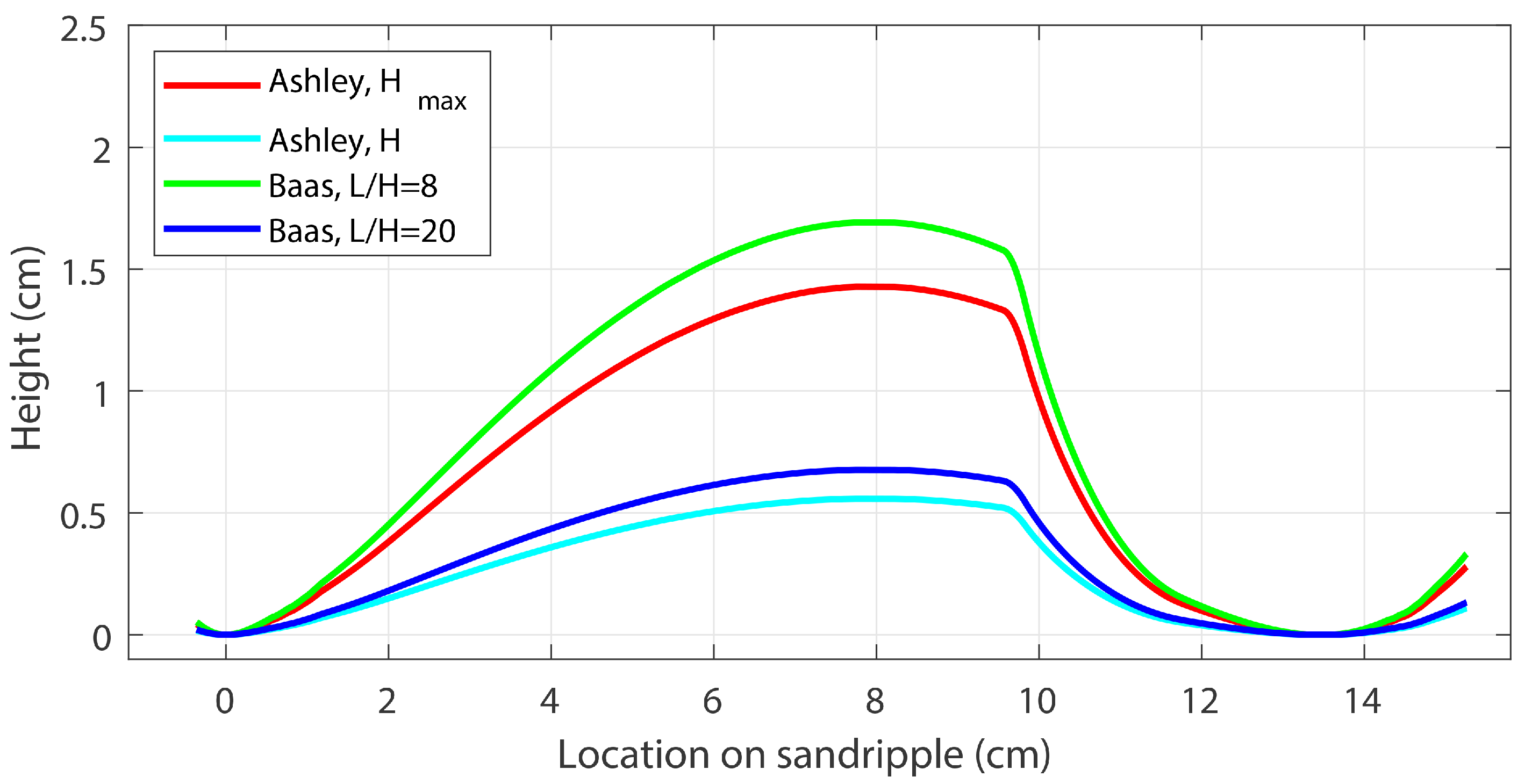
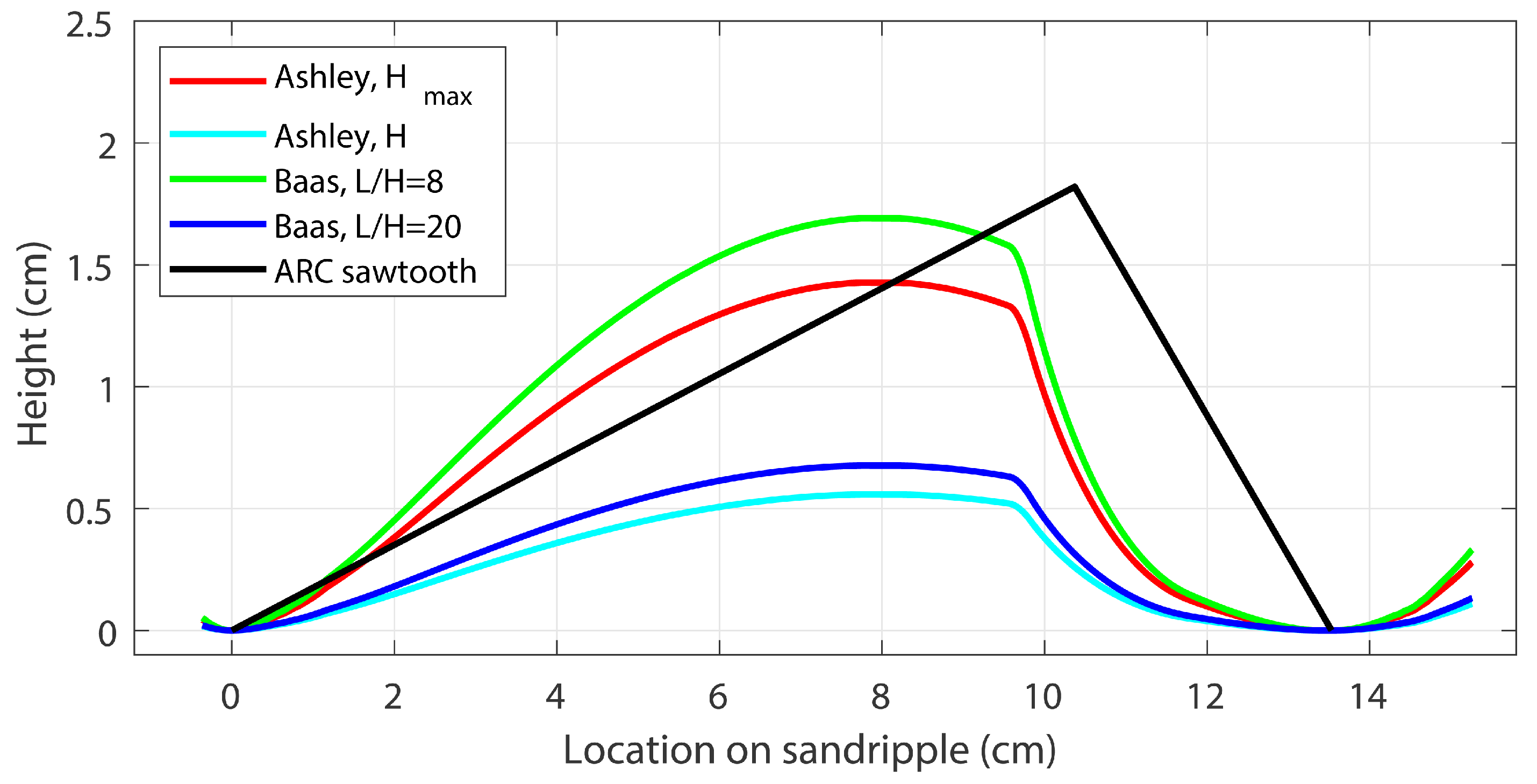
3.3. Quantifying Sand-Ripple Slopes on the Basis of Backscatter Data
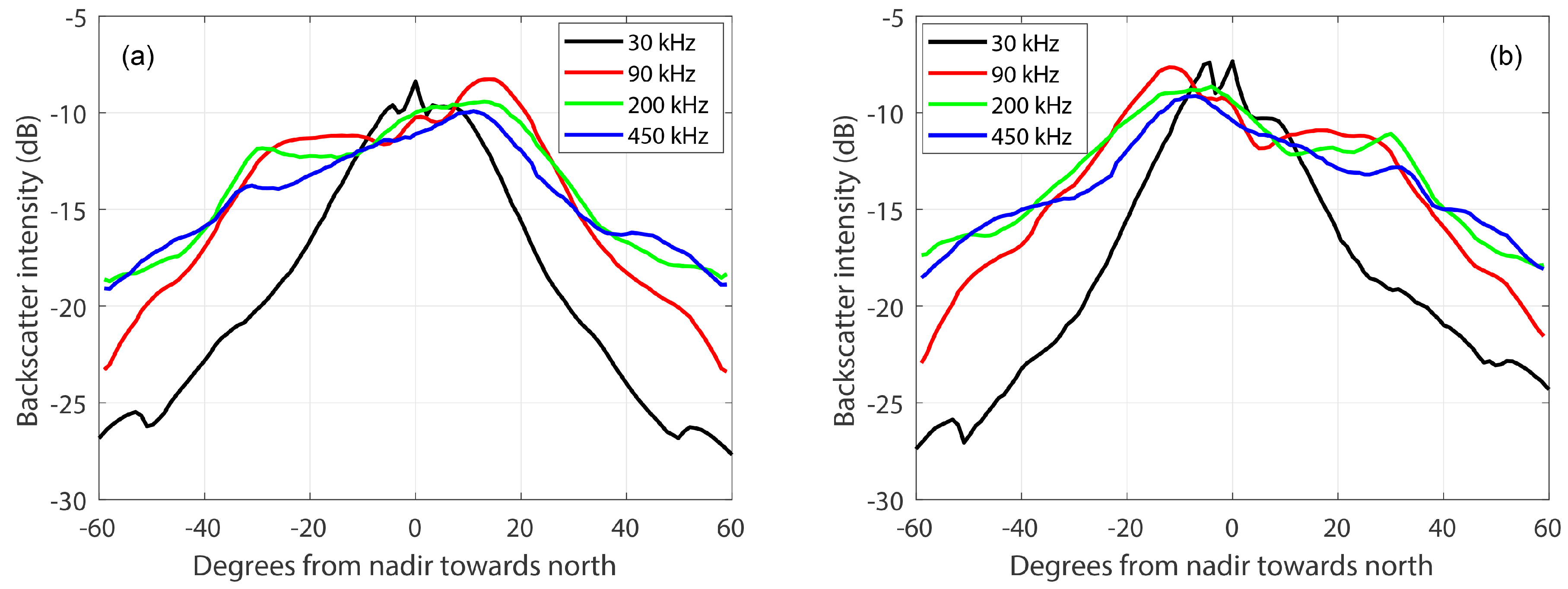
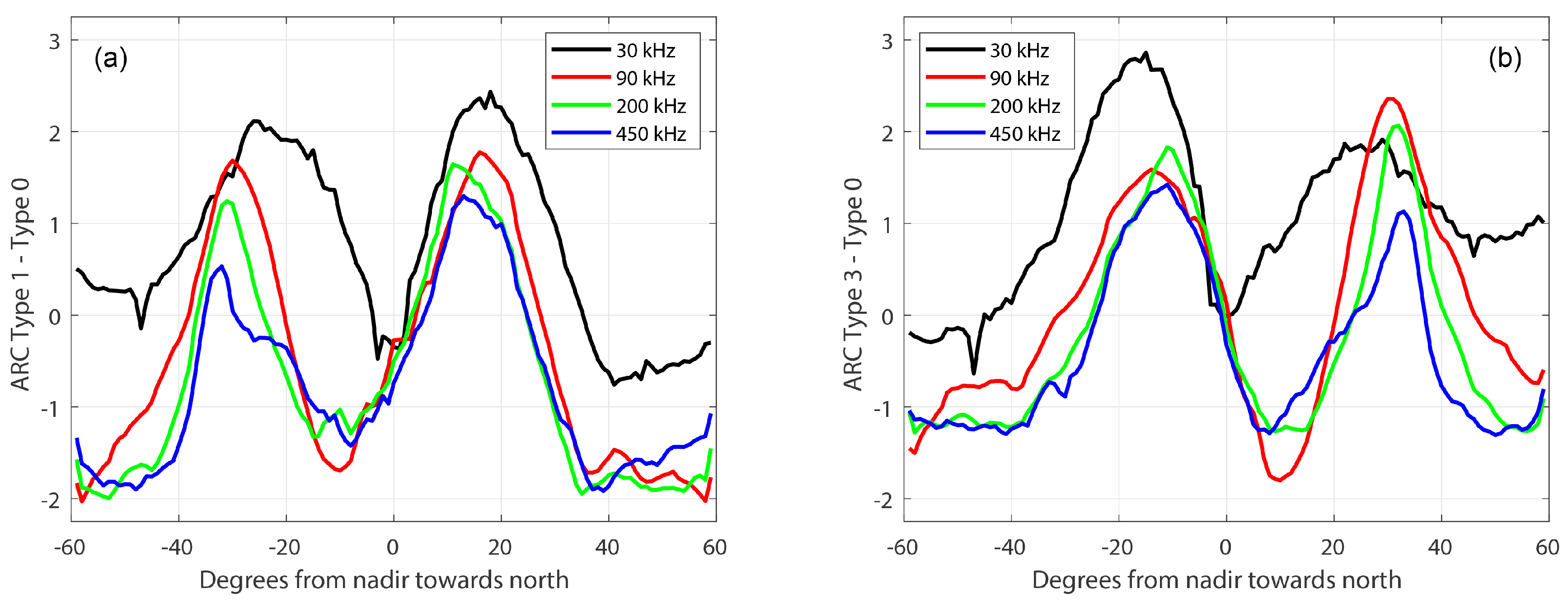
3.4. Sand-Ripple Effects on Different Frequencies
3.5. Implications for Backscatter-Based Sediment Classification
3.6. Sand Ripple Detection over Large Geographical Areas
4. Summary and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| ARC | Angular-response curve |
| BS | Backscatter |
| cm | Centimeter |
| CTD | Conductivity temperature, and pressure |
| dB | Decibel |
| DCS | Dutch continental shelf |
| DTM | Digital terrain model |
| GPS | Global positioning system |
| gsf | Generic sensor format |
| MBES | Multibeam echosounder |
| m | Meter |
| mm | Millimeter |
| MRU | Motion reference unit |
| MSFD | Marine Strategy Framework Directive |
| NIOZ | Royal Netherlands Institute for Sea Research |
| QPS | Quality positioning services |
| ROV | Remotely operated vehicle |
| SIS | Seafloor information system |
| SSS | Side scan sonar |
References
- Halpern, B.S.; Walbridge, S.; Selkoe, K.A.; Kappel, C.V.; Micheli, F.; D’Agrosa, C.; Bruno, J.F.; Casey, K.S.; Ebert, C.; Fox, H.E.; et al. A global map of human impact on marine ecosystems. Science 2008, 319, 948–952. [Google Scholar] [CrossRef] [PubMed]
- Glegg, G.; Jefferson, R.; Fletcher, S. Marine governance in the English Channel (La Manche): Linking science and management. Mar. Pollut. Bull. 2015, 95, 707–718. [Google Scholar] [CrossRef] [PubMed]
- Busiest Shipping Lane. Online, Guinness World Records. 2020. Available online: https://www.guinnessworldrecords.com/world-records/busiest-shipping-lane (accessed on 8 December 2020).
- Amoroso, R.O.; Pitcher, C.R.; Rijnsdorp, A.D.; McConnaughey, R.A.; Parma, A.M.; Suuronen, P.; Eigaard, O.R.; Bastardie, F.; Hintzen, N.T.; Althaus, F.; et al. Bottom trawl fishing footprints on the world’s continental shelves. Proc. Natl. Acad. Sci. USA 2018, 115, E10275–E10282. [Google Scholar] [CrossRef] [PubMed]
- Van der Reijden, K.J.; Hintzen, N.T.; Govers, L.L.; Rijnsdorp, A.D.; Olff, H. North Sea demersal fisheries prefer specific benthic habitats. PLoS ONE 2018, 13, e0208338. [Google Scholar] [CrossRef] [PubMed]
- Rice, J.; Arvanitidis, C.; Borja, A.; Frid, C.; Hiddink, J.G.; Krause, J.; Lorance, P.; Ragnarsson, S.Á.; Sköld, M.; Trabucco, B.; et al. Indicators for sea-floor integrity under the European Marine Strategy Framework Directive. Ecol. Indic. 2012, 12, 174–184. [Google Scholar] [CrossRef]
- Snellen, M.; Gaida, T.C.; Koop, L.; Alevizos, E.; Simons, D.G. Performance of Multibeam Echosounder Backscatter-Based Classification for Monitoring Sediment Distributions Using Multitemporal Large-Scale Ocean Data Sets. IEEE J. Ocean. Eng. 2019, 44, 142–155. [Google Scholar] [CrossRef]
- Glenn, M.F. Introducing an operational multi-beam array sonar. Int. Hydrogr. Rev. 1970. [Google Scholar]
- Lamarche, G.; Lurton, X. Recommendations for improved and coherent acquisition and processing of backscatter data from seafloor-mapping sonars. Mar. Geophys. Res. 2018, 39, 5–22. [Google Scholar] [CrossRef]
- Koop, L.; Amiri-Simkooei, A.; J van der Reijden, K.; O’Flynn, S.; Snellen, M.; G Simons, D. Seafloor Classification in a Sand Wave Environment on the Dutch Continental Shelf Using Multibeam Echosounder Backscatter Data. Geosciences 2019, 9, 142. [Google Scholar] [CrossRef]
- Schimel, A.C.; Beaudoin, J.; Parnum, I.M.; Le Bas, T.; Schmidt, V.; Keith, G.; Ierodiaconou, D. Multibeam sonar backscatter data processing. Mar. Geophys. Res. 2018, 39, 121–137. [Google Scholar] [CrossRef]
- Lurton, X.; Eleftherakis, D.; Augustin, J.M. Analysis of seafloor backscatter strength dependence on the survey azimuth using multibeam echosounder data. Mar. Geophys. Res. 2018, 39, 183–203. [Google Scholar] [CrossRef]
- Simons, D.G.; Snellen, M. A Bayesian approach to seafloor classification using multi-beam echo-sounder backscatter data. Appl. Acoust. 2009, 70, 1258–1268. [Google Scholar] [CrossRef]
- Montereale-Gavazzi, G.; Roche, M.; Degrendele, K.; Lurton, X.; Terseleer, N.; Baeye, M.; Francken, F.; Van Lancker, V. Insights into the short-term tidal variability of multibeam backscatter from field experiments on different seafloor types. Geosciences 2019, 9, 34. [Google Scholar] [CrossRef]
- Elston, G.R.; Bell, J.M. Pseudospectral time-domain modeling of non-Rayleigh reverberation: Synthesis and statistical analysis of a sidescan sonar image of sand ripples. IEEE J. Ocean. Eng. 2004, 29, 317–329. [Google Scholar] [CrossRef]
- Von Rönn, G.A.; Schwarzer, K.; Reimers, H.C.; Winter, C. Limitations of Boulder Detection in Shallow Water Habitats Using High-Resolution Sidescan Sonar Images. Geosciences 2019, 9, 390. [Google Scholar] [CrossRef]
- Hansen, R.E. Mapping the ocean floor in extreme resolution using interferometric synthetic aperture sonar. In Proceedings of the Meetings on Acoustics ICU. Acoustical Society of America, Aachen, Germany, 9–13 September 2019; Volume 38, p. 055003. [Google Scholar]
- Damveld, J.H.; Van Der Reijden, K.; Cheng, C.; Koop, L.; Haaksma, L.; Walsh, C.; Soetaert, K.; Borsje, B.W.; Govers, L.; Roos, P.; et al. Video transects reveal that tidal sand waves affect the spatial distribution of benthic organisms and sand ripples. Geophys. Res. Lett. 2018, 45, 11–837. [Google Scholar] [CrossRef]
- Ferrini, V.L.; Flood, R.D. The effects of fine-scale surface roughness and grain size on 300 kHz multibeam backscatter intensity in sandy marine sedimentary environments. Mar. Geol. 2006, 228, 153–172. [Google Scholar] [CrossRef]
- Van Lancker, V.; Jacobs, P. The dynamical behaviour of shallow-marine dunes. In Proceedings of the International Workshop on Marine Sandwave Dynamics, Lille, France, 23–24 March 2000; pp. 213–220. [Google Scholar]
- Walgreen, M.; De Swart, H.E.; Calvete, D. A model for grain-size sorting over tidal sand ridges. Ocean. Dyn. 2004, 54, 374–384. [Google Scholar] [CrossRef]
- Svenson, C.; Ernstsen, V.B.; Winter, C.; Bartholomä, A.; Hebbeln, D. Tide-driven sediment variations on a large compound dune in the Jade tidal inlet channel, Southeastern North Sea. J. Coast. Res. 2009, 361–365. [Google Scholar]
- Van Dijk, T.A.; van Dalfsen, J.A.; Van Lancker, V.; van Overmeeren, R.A.; van Heteren, S.; Doornenbal, P.J. Benthic habitat variations over tidal ridges, North Sea, The Netherlands. In Seafloor Geomorphology as Benthic Habitat; Elsevier: Amsterdam, The Netherlands, 2012; pp. 241–249. [Google Scholar]
- Knaapen, M.A. Sandbank occurrence on the Dutch continental shelf in the North Sea. Geo-Mar. Lett. 2009, 29, 17–24. [Google Scholar] [CrossRef]
- Van Dijk, T.A.; Lindenbergh, R.C.; Egberts, P.J. Separating bathymetric data representing multiscale rhythmic bed forms: A geostatistical and spectral method compared. J. Geophys. Res. Earth Surf. 2008, 113. [Google Scholar] [CrossRef]
- Van Oyen, T.; Blondeaux, P.; Van den Eynde, D. Sediment sorting along tidal sand waves: A comparison between field observations and theoretical predictions. Cont. Shelf Res. 2013, 63, 23–33. [Google Scholar] [CrossRef]
- Van Der Reijden, K.J.; Koop, L.; O’flynn, S.; Garcia, S.; Bos, O.; Van Sluis, C.; Maaholm, D.J.; Herman, P.M.; Simons, D.G.; Olff, H. Discovery of Sabellaria spinulosa reefs in an intensively fished area of the Dutch Continental Shelf, North Sea. J. Sea Res. 2019, 144, 85–94. [Google Scholar] [CrossRef]
- Biber, M.F.; Duineveld, G.C.; Lavaleye, M.S.; Davies, A.J.; Bergman, M.J.; van den Beld, I.M. Investigating the association of fish abundance and biomass with cold-water corals in the deep Northeast Atlantic Ocean using a generalised linear modelling approach. Deep. Sea Res. Part II Top. Stud. Oceanogr. 2014, 99, 134–145. [Google Scholar] [CrossRef]
- Herman, P.; Beauchard, O.; van Duren, L. De staat van de Noordzee. Noordzeedagen. 2014. Available online: https://www.noordzeedagen.nl/nl/noordzeedagen/Vorige-edities/Noordzeedagen-2014-1/Thema-Leven-met-een-veranderende-Noordzee-Horizon-2050./De-staat-van-de-Noordzee.htm (accessed on 8 December 2020).
- Ashley, G.M. Classification of large-scale subaqueous bedforms; a new look at an old problem. J. Sediment. Res. 1990, 60, 160–172. [Google Scholar]
- Flemming, B. Zur klassifikation subaquatischer, strömungstransversaler Transportkörper. Boch. Geol. Und Geotech. Arb. 1988, 29. [Google Scholar]
- Baas, J.H. Ripple, ripple mark, ripple structure. Sedimentology 1978, 921–925. [Google Scholar]
- Hammerstad, E. EM Technical Note: Backscattering and Seabed Image Reflectivity. In Horten, Norway: Kongsberg Maritime AS. 2000. Available online: https://www.kongsberg.com/globalassets/maritime/km-products/product-documents/em_technical_note_web_backscatteringseabedimagereflectivity.pdf (accessed on 8 December 2020).
- Gaida, T.; Tengku Ali, T.; Snellen, M.; Amiri-Simkooei, A.; van Dijk, T.; Simons, D. A Multispectral Bayesian Classification Method for Increased Acoustic Discrimination of Seabed Sediments Using Multi-Frequency Multibeam Backscatter Data. Geosciences 2018, 8, 455. [Google Scholar] [CrossRef]
- Amiri-Simkooei, A.; Snellen, M.; Simons, D.G. Riverbed sediment classification using multi-beam echo-sounder backscatter data. J. Acoust. Soc. Am. 2009, 126, 1724–1738. [Google Scholar] [CrossRef] [PubMed]
- Applied Physics Laboratory, University of Washington. APL-UW High-Frequency Ocean Environmental Acoustic Models Handbook; Technical Report APL-UW TR9407; Applied Physics Laboratory, University of Washington: Seattle, WA, USA, 1994. [Google Scholar]
- Rijkswaterstaat and Deltares. Dutch Continental Shelf Model Modelbeschrijving. 2009. Available online: https://www.helpdeskwater.nl/publish/pages/131723/dcsm-v5.pdf (accessed on 8 December 2020).
- Tang, D.; Williams, K.L.; Thorsos, E.I. Utilizing high-frequency acoustic backscatter to estimate bottom sand ripple parameters. IEEE J. Ocean. Eng. 2009, 34, 431–443. [Google Scholar] [CrossRef]
- Al-Hashemi, H.M.B.; Al-Amoudi, O.S.B. A review on the angle of repose of granular materials. Powder Technol. 2018, 330, 397–417. [Google Scholar] [CrossRef]
- Yang, F.G.; Liu, X.N.; Yang, K.J.; Cao, S.Y. Study on the angle of repose of nonuniform sediment. J. Hydrodyn. 2009, 21, 685–691. [Google Scholar] [CrossRef]
- Brown, C.J.; Smith, S.J.; Lawton, P.; Anderson, J.T. Benthic habitat mapping: A review of progress towards improved understanding of the spatial ecology of the seafloor using acoustic techniques. Estuarine Coast. Shelf Sci. 2011, 92, 502–520. [Google Scholar] [CrossRef]
- Lamarche, G.; Lurton, X.; Verdier, A.L.; Augustin, J.M. Quantitative characterisation of seafloor substrate and bedforms using advanced processing of multibeam backscatter—Application to Cook Strait, New Zealand. Cont. Shelf Res. 2011, 31, S93–S109. [Google Scholar] [CrossRef]
- Knaapen, M. Sandwave migration predictor based on shape information. J. Geophys. Res. Earth Surf. 2005, 110. [Google Scholar] [CrossRef]
- Nemeth, A. Modelling Offshore Sand Waves. 2003. Available online: https://research.utwente.nl/en/publications/modelling-offshore-sand-waves (accessed on 8 December 2020).
- Idier, D.; Ehrhold, A.; Garlan, T. Morphodynamique d’une dune sous-marine du détroît du pas de Calais. C. R. Geosci. 2002, 334, 1079–1085. [Google Scholar] [CrossRef]
- Lindenbergh, R.C.; van Dijk, T.A.; Egberts, P.J. Separating bedforms of different scales in echo sounding data. In Coastal Dynamics 2005: State of the Practice; ASCE Library: Barcelona, Spain, 2006; pp. 1–14. [Google Scholar]
- James, J.C.; Mackie, A.S.; Rees, E.I.S.; Darbyshire, T. Sand wave field: The OBel Sands, Bristol Channel, UK. In Seafloor Geomorphology as Benthic Habitat; Elsevier: Amsterdam, The Netherlands, 2012; pp. 227–239. [Google Scholar]
- Aird, P. Chapter 4—Deepwater Metocean Environments. In Deepwater Drilling; Aird, P., Ed.; Gulf Professional Publishing: Houston, TX, USA, 2019; pp. 111–164. [Google Scholar] [CrossRef]
- Yincan, Y. Chapter 15—Development Laws of Geological Hazards and Hazard Geology Regionalization of China Seas. In Marine Geo-Hazards in China; Elsevier: Amsterdam, The Netherlands, 2017; pp. 657–687. [Google Scholar] [CrossRef]





| Transect | Date, Time | Orient. (°) | Len. (cm) | SDO (°) | SDL (cm) |
|---|---|---|---|---|---|
| 19-5-19, 08:40 | 179.7 | 10.6 | 32.2 | 2.5 | |
| 20-5-19, 09:00 | 149.3 | 11.0 | 5.9 | 1.9 | |
| 20-5-19, 14:30 | 351.6 | 14.8 | 7.8 | 1.2 | |
| 22-5-19, 15:00 | 41.1 | 17.7 | 10.2 | 3.9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koop, L.; van der Reijden, K.J.; Mestdagh, S.; Ysebaert, T.; Govers, L.L.; Olff, H.; Herman, P.M.J.; Snellen, M.; Simons, D.G. Measuring Centimeter-Scale Sand Ripples Using Multibeam Echosounder Backscatter Data from the Brown Bank Area of the Dutch Continental Shelf. Geosciences 2020, 10, 495. https://doi.org/10.3390/geosciences10120495
Koop L, van der Reijden KJ, Mestdagh S, Ysebaert T, Govers LL, Olff H, Herman PMJ, Snellen M, Simons DG. Measuring Centimeter-Scale Sand Ripples Using Multibeam Echosounder Backscatter Data from the Brown Bank Area of the Dutch Continental Shelf. Geosciences. 2020; 10(12):495. https://doi.org/10.3390/geosciences10120495
Chicago/Turabian StyleKoop, Leo, Karin J. van der Reijden, Sebastiaan Mestdagh, Tom Ysebaert, Laura L. Govers, Han Olff, Peter M. J. Herman, Mirjam Snellen, and Dick G. Simons. 2020. "Measuring Centimeter-Scale Sand Ripples Using Multibeam Echosounder Backscatter Data from the Brown Bank Area of the Dutch Continental Shelf" Geosciences 10, no. 12: 495. https://doi.org/10.3390/geosciences10120495
APA StyleKoop, L., van der Reijden, K. J., Mestdagh, S., Ysebaert, T., Govers, L. L., Olff, H., Herman, P. M. J., Snellen, M., & Simons, D. G. (2020). Measuring Centimeter-Scale Sand Ripples Using Multibeam Echosounder Backscatter Data from the Brown Bank Area of the Dutch Continental Shelf. Geosciences, 10(12), 495. https://doi.org/10.3390/geosciences10120495





