Dreaming of Perfect Data: Characterizing Noise in Archaeo-Geophysical Measurements
Abstract
:1. Introduction
2. What Is Noise?
3. Sources of Noise
3.1. Instruments
3.1.1. Sensors and Electronics
3.1.2. Digitization Noise
3.1.3. Contact Resistance
3.2. Use of Instruments
3.2.1. Spatial Resolution
3.2.2. Orientation of Instrument
3.2.3. Height Variations of Instrument during Survey
3.2.4. Positional Noise
3.3. External Disturbances
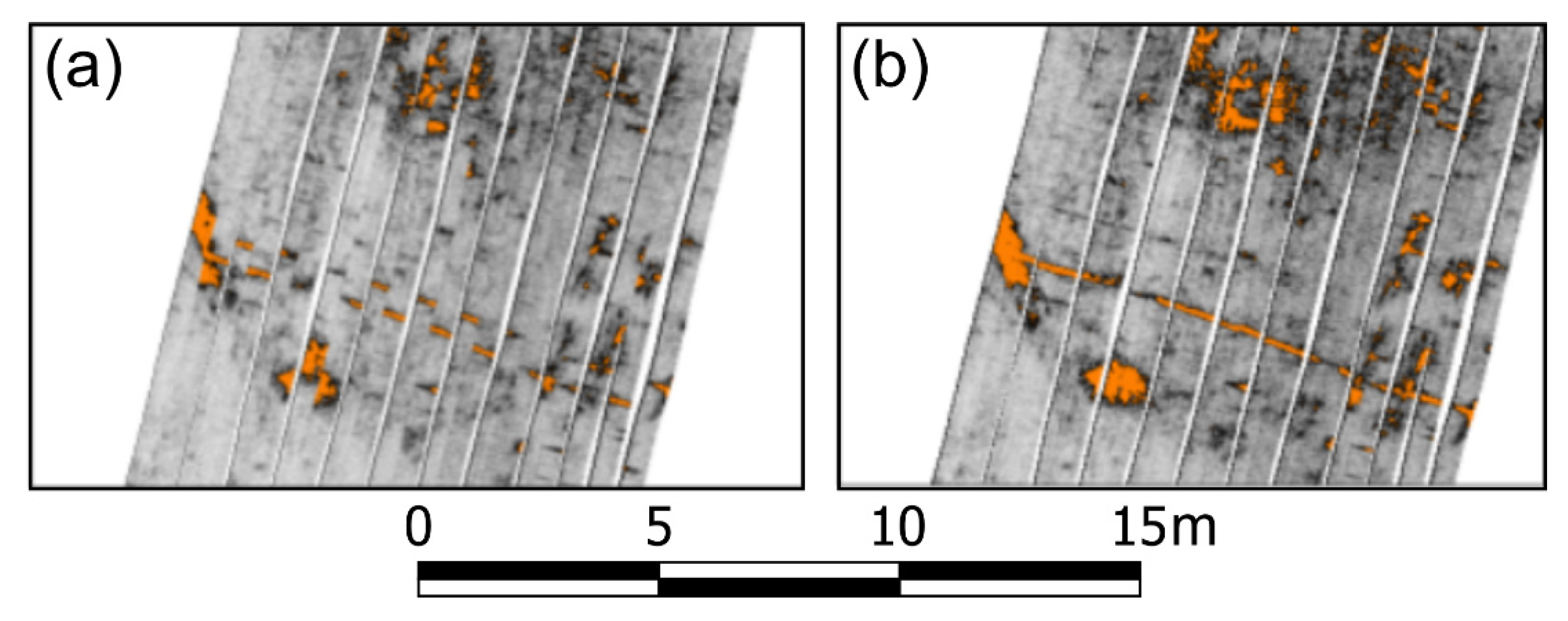
3.3.1. Nonarchaeological Features
3.3.2. External Features Affecting the Data
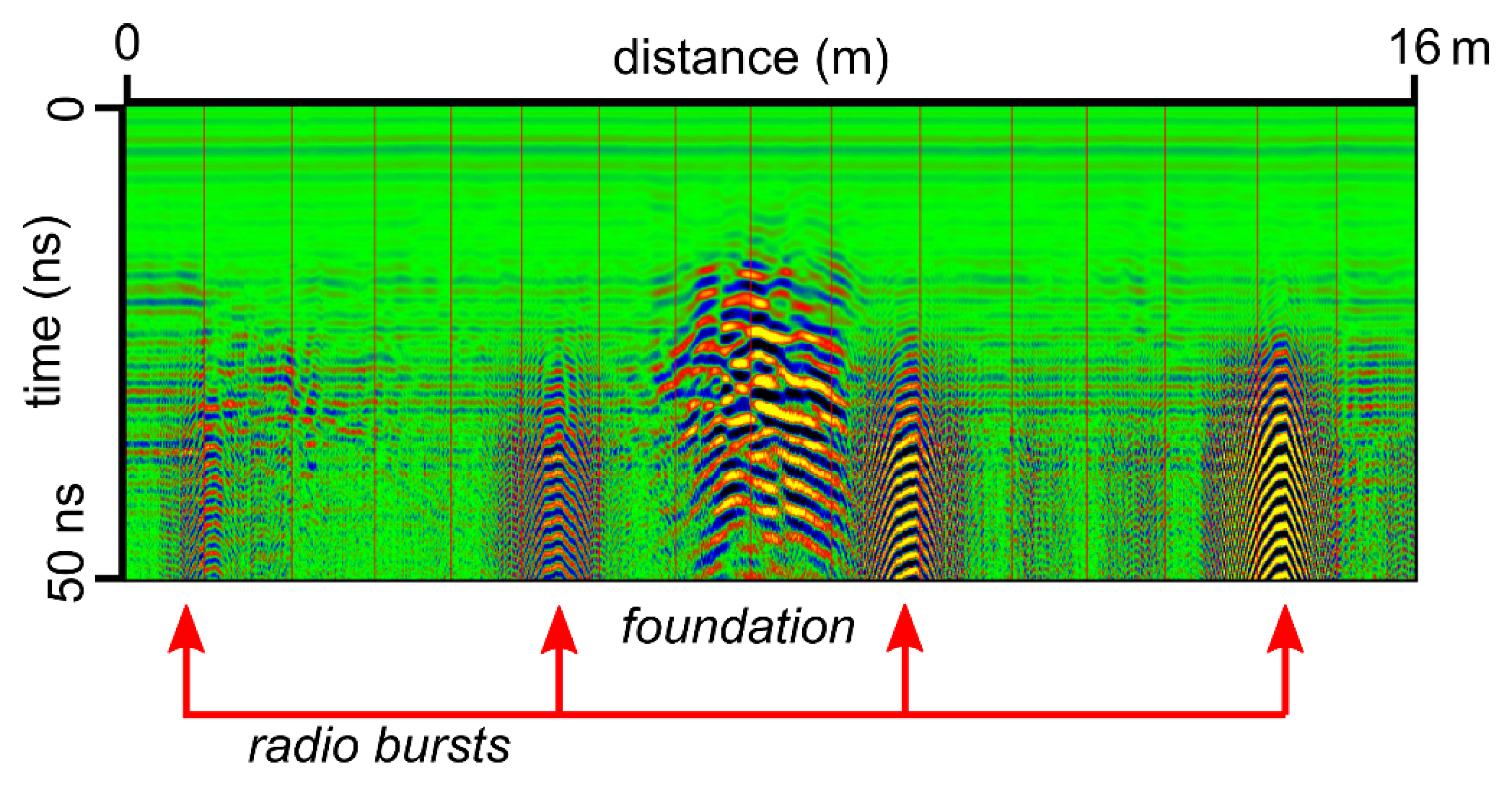
3.3.3. Other External Sources
3.4. Soil Noise
3.4.1. Magnetic Surveys
3.4.2. Contact Resistance
3.4.3. Meter-Scale Topography
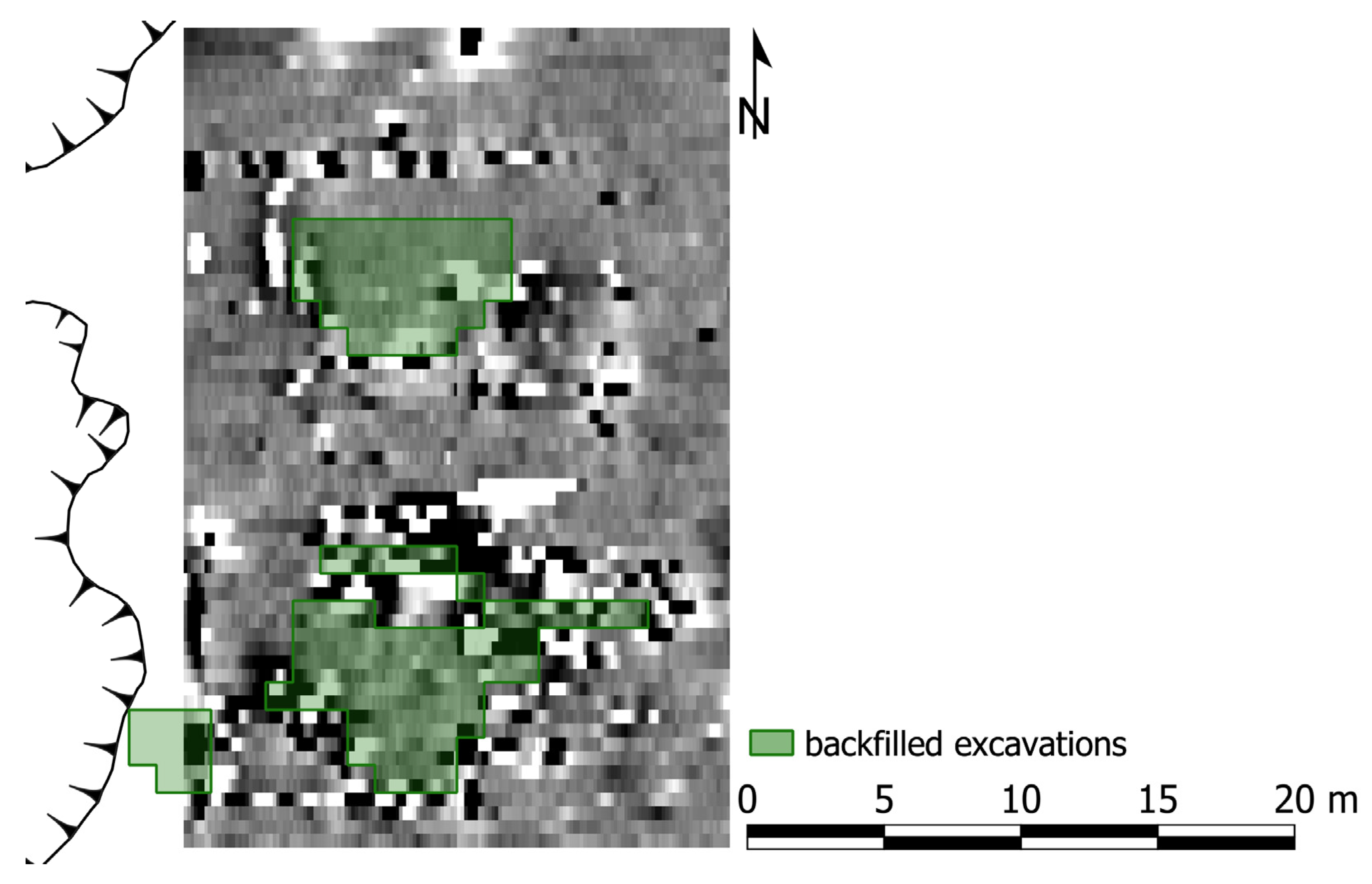
3.4.4. Unwanted Features in the Soil
3.4.5. Time-Varied (Nonstationary) Soil Noise
4. How to Characterize Noise
5. Removal of Noise
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Correction Statement
References
- Lea, D.; Bradbery, J. Oxford Advanced Learners Dictionary, 10th ed.; Oxford University Press: Oxford, UK, 2020. [Google Scholar]
- Scales, J.A.; Snieder, R. What is noise? Geophysics 1998, 63, 1122–1124. [Google Scholar] [CrossRef]
- Graham, I.D.G.; Scollar, I. Limitations on Magnetic Prospection in Archaeology Imposed by Soil Properties. Archaeo Phys. Tech. Nat. Beiträge Feldarchäologie 1976, 6, 1–124. [Google Scholar]
- Ghezzi, A.; Schettino, A.; Tassi, L.; Pierantoni, P.P. Magnetic modelling and error assessment in archaeological geophysics: The case study of Urbs Salvia, central Italy. Ann. Geophys. 2019, 62, GM451. [Google Scholar] [CrossRef]
- Buchsenschutz, O.; Coulon, G.; Gratier, M.; Hesse, A.; Holmgren, J.; Mills, N.; Orssaud, D.; Querrien, A.; Rialland, Y.; Soyer, C.; et al. L’évolution du Canton de Levroux d’après les Prospections et les Sondages Archéologiques—Levroux 1; Fédération pour l’édition de la Revue Archéologique du Centre de la France: Tours, France, 1988. [Google Scholar]
- Linford, N.; Linford, P.; Martin, L.; Payne, A. Recent results from the English Heritage caesium magnetometer system in comparison with recent fluxgate gradiometers. Archaeol. Prospect. 2007, 14, 151–166. [Google Scholar] [CrossRef]
- Schettino, A.; Ghezzi, A.; Pierantoni, P.P. Magnetic field modelling and analysis of uncertainty in archaeological geophysics. Archaeol. Prospect. 2019, 26, 137–153. [Google Scholar] [CrossRef]
- Scollar, I.; Tabbagh, A.; Hesse, A.; Herzog, I. Archaeological Prospecting and Remote Sensing; Cambridge University Press: Cambridge, NY, USA, 1990. [Google Scholar]
- Telford, W.M.; Geldart, L.P.; Sheriff, R.E. Applied Geophysics, 2nd ed.; Cambridge University Press: Cambridge, NY, USA, 1990. [Google Scholar]
- Sheriff, R. Encyclopedic Dictionary of Applied Geophysics; SEG: Tulsa, OK, USA, 2002. [Google Scholar]
- Sheriff, R.E.; Geldart, L.P. Exploration Seismology, 2nd ed.; Cambridge University Press: Cambridge, NY, USA, 1995. [Google Scholar]
- Parzen, E. Modern Probability Theory and Its Applications; John Wiley & Sons, Inc.: New York, NY, USA; London, UK; Sydney, Australia, 1960. [Google Scholar]
- Manoli, S. Fluxgate Magnetometer for Archaeological Prospection: Adaptation, Installation, Set-up and Comparative Measurements with Caesium Magnetometer on Archaeological Sites in Bavaria. Master's Thesis, Department of Earth and Environmental Sciences, Geophysics, Ludwig-Maximilians-Universität München, Munich, Germany, 2014. [Google Scholar]
- Gebbers, R.; Lück, E.; Dabas, M.; Domsch, H. Comparison of instruments for geoelectrical soil mapping at the field scale. Near Surf. Geophys. 2009, 7, 179–190. [Google Scholar] [CrossRef]
- Schmidt, A. Earth Resistance for Archaeologists; AltaMira Press: Lanham, MD, USA, 2013. [Google Scholar]
- Unser, M. Sampling-50 years after Shannon. Proc. IEEE 2000, 88, 569–587. [Google Scholar] [CrossRef]
- Geometrics. Total Field Magnetometer Performance, Published Specifications and What They Mean; Geometrics: San Jose, CA, USA, 2000. [Google Scholar]
- Bartington, G.; Chapman, C.E. A High-Stability Fluxgate Magnetic Gradiometer for Shallow surface Application. Archaeol. Prospect. 2004, 11, 19–34. [Google Scholar] [CrossRef]
- Neubauer, W. Magnetische Prospektion in der Archäologie; Austrian Academy of Sciences: Vienna, Austria, 2001; p. 238. [Google Scholar]
- Dabas, M.; Anest, A.; Thiesson, J.; Tabbagh, A. Slingram EMI Devices for Characterizing Resistive Features Using Apparent Conductivity Measurements: Check of the DualEM-421S Instrument and Field Tests. Archaeol. Prospect. 2016, 23, 165–180. [Google Scholar] [CrossRef]
- Tabbagh, A. What is the best coil orientation in the Slingram electromagnetic prospection method? Archaeometry 1986, 28, 185–196. [Google Scholar] [CrossRef]
- Nobes, D.C.; Wallace, L.R. Geophysical Imaging of an Early Nineteenth Century Colonial Defensive Blockhouse: Applications of EM Directionality and Multi-parameter Imaging. In Archaeogeophysics: State of the Art and Case Studies; El-Qady, G., Metwaly, M., Eds.; Springer International Publishing: Berlin/Heidelberg, Germany, 2019; pp. 219–232. [Google Scholar]
- Thiesson, J.; Tabbagh, A.; Dabas, M.; Chevalier, A. Characterization of buried cables and pipes using electromagnetic induction loop-loop frequency-domain devices. Geophysics 2017, 83, E1–E10. [Google Scholar] [CrossRef]
- Hinterleitner, A.; Trinks, I.; Löcker, K.; Kainz, J.; Totschnig, R.; Kucera, M.; Neubauer, W. Not-so good vibrations: Removing measurement induced noise from motorized multi-sensor magnetometry data. In Proceedings of the 12th International Conference of Archaeological Prospection, Bradford, UK, 16 September 2017; Jennings, B., Gaffney, C., Sparrow, T., Gaffney, S., Eds.; Archaeopress: Oxford, UK, 2017; pp. 110–111. [Google Scholar]
- Verdonck, L. High-Resolution Ground-Penetrating Radar Prospection with a Modular Configuration; Ghent University: Ghent, Belgium, 2012. [Google Scholar]
- Böniger, U.; Tronicke, J. On the Potential of Kinematic GPR Surveying Using a Self-Tracking Total Station: Evaluating System Crosstalk and Latency. IEEE Trans. Geosci. Remote Sens. 2010, 48, 3792–3798. [Google Scholar] [CrossRef]
- Dabas, M. Theory and practice of the new fast electrical imaging system ARP©. In Seeing the Unseen. Geophysics and Landscape Archaeology; Campana, S., Piro, S., Eds.; Taylor & Francis Group: London, UK, 2009; pp. 105–126. [Google Scholar]
- Gerrard, J.; Caldwell, L.; Kennedy, A. Green Waste and Archaeological Geophysics. Archaeol. Prospect. 2015, 22, 139–142. [Google Scholar] [CrossRef]
- Sarris, A.; Papadopoulos, N.; Dederix, S.; Driessen, J.; Dirix, T.; Merkouri, C. The Quest of the Grave of Andreas Vesalius in Zakynthos. In Spreading Excellence in Computer Applications for Archaeology and Cultural Heritage, Proceedings of the 3rd Conference on Computer Applications and Quantitative Methods in Archaeology, Limassol, Cyprus, 18 June 2018; Kyriakidis, P., Agapiou, A., Lysandrou, V., Eds.; Cyprus University of Technology: Limassol, Cyprus, 2019; pp. 11–18. [Google Scholar]
- Sarris, A.; Papadopoulos, N.; Cuenca-Garcia, C.; Alexakis, D.; Manataki, M.; Cantoro, G. Exposing the Urban Plan of the ancient city of Hyettos, Boeotia, Greece. Archaeol. Pol. 2015, 53, 364–367. [Google Scholar]
- Sarris, A.; Bintliff, J. Scourcing the Surface and Peering beneath it at the Ancient City of Hyettos, Boeotia, Greece. In Sensing the Past, Contributions from the ArcLand Conference on Remote Sensing for Archaeology; Posluschny, A., Ed.; Habelt-Verlag: Bonn, Germany, 2015; pp. 70–71. [Google Scholar]
- Doneus, M.; Neubauer, W. 2D combination of prospection data. Archaeol. Prospect. 1998, 5, 29–56. [Google Scholar] [CrossRef]
- Booth, A.D.; Clark, R.A.; Hamilton, K.; Murray, T. Multi-offset ground penetrating radar methods to image buried foundations of a medieval town wall, Great Yarmouth, UK. Archaeol. Prospect. 2010, 17, 103–116. [Google Scholar] [CrossRef]
- Schmidt, A.; Coningham, R.; Acharya, K.P.; Davis, C.; Kunwar, R.B. Seismic safety in Nepal: Authenticity, protection and historic tradition. In Proceedings of Recent Work in Archaeological Geophysics; Archprospection: London, UK, December 2018; pp. 16–18. Available online: http://www.archprospection.org/sites/archprospection.org/files/ArchGeo18_abstracts.pdf (accessed on 18 September 2020).
- Eppelbaum, L.V. Geophysical Observations at Archaeological Sites: Estimating Informational Content. Archaeol. Prospect. 2014, 21, 125–138. [Google Scholar] [CrossRef]
- Macmillan, S.; Reay, S. Should Archaeologists Be Concerned about Naturally Varying Magnetic Fields? In Proceedings of Recent Work in Archaeological Geophysics; Archprospection: London, UK, December 2012; pp. 77–78. [Google Scholar]
- Carrier, B.M.; Pulkkinen, A.; Heinz, M. Recognizing Geomagnetic Storms in Marine Magnetometer Data: Toward Improved Archaeological Resource Identification Practices. STAR Sci. Technol. Archaeol. Res. 2016, 2, 1–14. [Google Scholar] [CrossRef]
- Maus, S. Ocean, Electromagnetic Effects. In Encyclopedia of Geomagnetism and Paleomagnetism; Gubbins, D., Herrero-Bervera, E., Eds.; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2007; pp. 740–742. [Google Scholar]
- Gannon, J.L.; Swidinsky, A.; Xu, Z. Geomagnetically Induced Currents from the Sun to the Power Grid; John Wiley and Sons, Inc.: Hoboken, NJ, USA, 2019. [Google Scholar]
- Aye, M.M.M.; Faize, A.; Alsharahi, G.; Louzazni, M.; Driouach, A. Effect of External Noise on Ground Penetrating Radar Ability to Detect Objects. Int. J. Microw. Opt. Technol. 2019, 14, 124–131. [Google Scholar]
- Olhoeft, G. Applications and Frustrations in Using Ground Penetrating Radar. IEEE AESS Syst. Mag. 2002, 17, 12–20. [Google Scholar] [CrossRef]
- Olhoeft, G. Maximizing the information return from ground penetrating radar. J. Appl. Geophys. 2000, 43, 175–187. [Google Scholar] [CrossRef]
- Conyers, L.B. Ground-Penetrating Radar for Archaeology, 3rd ed.; Altamira Press: Lanham, MD, USA, 2013. [Google Scholar]
- Schmidt, A. What shielding? How to pick up signals with a GPR antenna. In Proceedings of Recent Work in Archaeological Geophysics; Archprospection: London, UK, December 2010; pp. 28–29. [Google Scholar]
- Schmidt, A. Pessinus—Advanced GPR processing 2010–2011. Geophysical survey report. In Pessinus and Its Regional Setting. Volume 2: Work in 2009–2013; Tsetskhladze, G.R., Ed.; Peeters: Leuven, Belgium; Paris, France; Bristol (CT), UK, 2019; pp. 171–222. [Google Scholar]
- Souffaché, B.; Cosenza, P.; Flageul, S.; Pencolé, J.P.; Seladji, S.; Tabbagh, A. Electrostatic multipole for electrical resistivity measurements at the decimetric scale. J. Appl. Geophys. 2010, 71, 6–12. [Google Scholar] [CrossRef]
- Matthews, W.; French, C.A.I.; Lawrence, T.; Cutler, D.F.; Jones, M.K. Microstratigraphic traces of site formation processes and human activities. World Archaeol. 1997, 29, 281–308. [Google Scholar] [CrossRef]
- Mathe, V.; Leveque, F.; Mathe, P.-E.; Chevallier, C.; Pons, Y. Soil anomaly mapping using a caesium magnetometer: Limits in the low magnetic amplitude case. J. Appl. Geophys. 2006, 58, 202–217. [Google Scholar] [CrossRef]
- Scollar, I. A Contribution to Magnetic Prospecting in Archaeology. Archaeo Phys. Tech. Nat. Beiträge Feldarchäologie Beih. Bonn. Jahrbuecher 1965, 15, 21–93. [Google Scholar]
- Tetegan, M.; Pasquier, C.; Besson, A.; Nicoullaud, B.; Bouthier, A.; Bourennane, H.; Desbourdes, C.; King, D.; Cousin, I. Field-Scale Estimation of the Volume Percentage of Rock Fragments in Stony Soils by Electrical Resistivity. CATENA 2012, 92, 67–74. [Google Scholar] [CrossRef]
- Heathcote, C.; Aspinall, A. Some Aspects of the Use of Fluxgate Magnetometers (Gradiometers) in Geophysical Prospection in Archaeology. Revue D’ Archeom. 1981, 5, 61–70. [Google Scholar] [CrossRef]
- Linington, R.E. Topographical and Terrain Effects in Magnetic Prospecting. Prospez. Archeol. 1972, 7–8, 61–84. [Google Scholar]
- Horsley, T.; Schmidt, A.; Linford, P. The use of geophysical methods for the archaeological prospection of medieval kilns. In Archaeological Prospection 2001; Doneus, M., Eder-Hinterleitner, A., Neubauer, W., Eds.; Austrian Academy of Sciences: Vienna, Austria, 2001; pp. 116–117. [Google Scholar]
- Tsourlos, P.I.; Szymanski, J.E.; Tsokas, G.N. The effect of terrain topography on commonly used resistivity arrays. Geophysics 1999, 64, 1357–1363. [Google Scholar] [CrossRef]
- Fox, R.C.; Hohmann, G.W.; Killpack, T.J.; Rijo, L. Topographic effects in resistivity and induce-polarization surveys. Geophysics 1980, 45, 75–93. [Google Scholar] [CrossRef]
- Sutherland, T.L.; Schmidt, A.; Dockrill, S. Resistivity pseudosections and their topographic correction: A report on a case study at Scatness, Shetland. Archaeol. Prospect. 1998, 5, 229–237. [Google Scholar] [CrossRef]
- Tong, L.T.; Yang, C.H. Incorporation of topography into two-dimensional resistivity inversion. Geophysics 1990, 55, 354–361. [Google Scholar] [CrossRef]
- Loke, M.H.; Barker, R.D. Rapid least-squares inversion of apparent resistivity pseudosections by a quasi-Newton method. Geophys. Prospect. 1996, 44, 131–152. [Google Scholar] [CrossRef]
- Giao, P.H.; Weller, A.; Hien, D.H.; Adisornsupawat, K. An approach to construct the weathering profile in a hilly granitic terrain based on electrical imaging. J. Appl. Geophys. 2008, 65, 30–38. [Google Scholar] [CrossRef]
- Loke, M.H. Tutorial: 2-D and 3-D Electrical Imaging Surveys; Geotomo Software, Res2dinv 3.5 Software: Aarhus, Denmark, 2004. [Google Scholar]
- Lehmann, F.; Green, A.G. Topographic migration of georadar data: Implications for acquisition and processing. Geophysics 2000, 65, 836–848. [Google Scholar] [CrossRef]
- Wilken, D.; Wunderlich, T.; Zori, D.; Kalmring, S.; Rabbel, W.; Byock, J. Integrated GPR and archaeological investigations reveal internal structure of man-made Skiphóll mound in Leiruvogur, Iceland. J. Archaeol. Sci. Rep. 2016, 9, 64–72. [Google Scholar] [CrossRef]
- Prokhorenko, V.; Ivashchuk, V.; Korsun, S.; Musiyachenko, S.; Borodavka, V. Topographic correction of GPR profile based on odometer and inclinometer data. In Proceedings of the 14th International Conference on Ground Penetrating Radar (GPR), Shanghai, China, 5–8 June 2012; pp. 425–429. [Google Scholar]
- Leckebusch, J.; Rychener, J. Verification and topographic correction of GPR data in three dimensions. Near Surf. Geophys. 2007, 5, 395–403. [Google Scholar] [CrossRef]
- Feng, X.; Sato, M.; Liu, C.; Takahashi, K.; Zhang, Y. Topographic Correction of Elevated GPR. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 799–804. [Google Scholar] [CrossRef]
- Frei, W.; Chen, C.-C. Fast Boundary Detection: A Generalization and a New Algorithm. IEEE Trans. Comput. 1977, C-26, 988–998. [Google Scholar] [CrossRef]
- Sarris, A.; Papadopoulos, N.; Argyriou, N.; Donati, J.; Manataki, M.; Trapero-Fernandez, P.; Chatzitoulousis, S.; Stefanidis, K.; Parcharidou, M.; Tsioumas, M. Underground Images from the Cultural Landscape of Eidomeni. In Proceedings of Spreading Excellence in Computer Applications for Archaeology and Cultural Heritage, Proceedings of the 3rd Conference on Computer Applications and Quantitative Methods in Archaeology, Limassol, Cyprus, 18 June 2018; Kyriakidis, P., Agapiou, A., Lysandrou, V., Eds.; Cyprus University of Technology: Limassol, Cyprus, 2019; pp. 2–10. [Google Scholar]
- Rakov, V.A.; Uman, M.A. Lightning: Physics and Effects; Cambridge University Press: Cambridge, NY, USA, 2003. [Google Scholar]
- Jones, G.; Maki, D.L. Lightning-induced magnetic anomalies on archaeological sites. Archaeol. Prospect. 2005, 12, 191–197. [Google Scholar] [CrossRef]
- Verrier, V.; Rochette, P. Estimating peak currents at ground lightning impacts using remanent magnetization. Geophys. Res. Lett. 2002, 29, 1867. [Google Scholar] [CrossRef]
- Trinks, I. Lightning-induced remanent magnetisation as plausible explanation for a geophysical anomaly at Gråborg. Fornvännen J. Swed. Antiqu. Res. 2011, 106, 350–354. [Google Scholar]
- Sarris, A.; Papadopoulos, N.; Salvi, M.C.; Seferou, E.; Agapiou, A. Mapping the Archaeological Landscape of Palaepaphos through Remote Sensing Techniques. In A Sense of the Past. Studies in Current Archaeological Applications of Remote Sensing and Non-Invasive Prospection Methods; Kamermans, H., Gojda, M., Posluschny, A.G., Eds.; Archaeopress: Oxford, UK, 2014; pp. 41–46. [Google Scholar]
- Maki, D. Lightning Induced Remanent Magnetization at the Buffalo Slough Burial Mound Complex. Minn. Archaeol. 2015, 74, 30–47. [Google Scholar]
- Bates, R.C.; Bates, M.; Gaffney, C.; Gaffney, V.; Raub, D.T. Geophysical Investigation of the Neolithic Calanais Landscape. Remote Sens. 2019, 11, 2975. [Google Scholar] [CrossRef]
- Campana, S.; Dabas, M. Archaeological Impact Assessment: The BREBEMI Project (Italy). Archaeol. Prospect. 2011, 18, 139–148. [Google Scholar] [CrossRef]
- Dabas, M.; Guyard, L.; Leppert, T. Gisacum revisité: Croisement géophysique et archéologie. Doss. l’Archéologie no Spécial “La Prospection Géophysique” 2005, 308, 52–61. [Google Scholar]
- Dabas, M. Sistemi di mesura della resistivita: Da manuale ad autotrainata (ARPs). In Groma2: In profondita Senza Scavare; Giorgi, E., Ed.; BraDypUS s.a.: Bologna, Italy, 2009; pp. 323–333. [Google Scholar]
- Al Chalabi, M.M.; Rees, A.I. An Experiment on the effect of rainfall on electrical resistivity anomalies in the near surface. Bonn. Jahrbücher 1962, 162, 266–271. [Google Scholar]
- Atkinson, R.J.C. Resistivity Surveying in Archaeology. In The Scientist and Archaeology; Pyddoke, E., Ed.; Phoenix House: London, UK, 1963; pp. 1–30. [Google Scholar]
- Hesse, A. Prospections Géophysiques a Faible Profondeur. Applications a L’archéologie; Dunod: Paris, France, 1966. [Google Scholar]
- Clark, A.J. Archaeological Detection by Resistivity; University of Southampton: Southampton, UK, 1980. [Google Scholar]
- Schmidt, A.; Fry, R.; Parkyn, A.; Bonsall, J.; Gaffney, C. When the Time is Right: The Impact of Weather Variations on the Contrast in Earth Resistance Data. In Proceedings of the 12th International Conference of Archaeological Prospection, Bradford, UK, September 2017; Jennings, B., Gaffney, C., Sparrow, T., Gaffney, S., Eds.; Archaeopress: Oxford, UK, 2017; pp. 218–219. [Google Scholar]
- Hesse, A. The importance of climatic observations in archaeological prospecting. Prospez. Archeol. 1966, 1, 11–13. [Google Scholar]
- Besson, A.; Cousin, I.; Dorigny, A.; Dabas, M.; King, D. The temperature correction for the electrical resistivity measurements in undisturbed soil samples: Analysis of the existing conversion models and proposal of a new model. Soil Sci. 2008, 173, 707–720. [Google Scholar] [CrossRef]
- Fassbinder, J.W.E. Seeing beneath the farmland, steppe and desert soil: Magnetic prospecting and soil magnetism. J. Archaeol. Sci. 2015, 56, 85–95. [Google Scholar] [CrossRef]
- Singer, M.J.; Fine, P. Pedogenic Factors Affecting Magnetic Susceptibility of Northern California Soils. J. Soil Sci. 1989, 53, 1119–1127. [Google Scholar] [CrossRef]
- Kattenberg, A.E.; Aalbersberg, G. Archaeological prospection of the Dutch perimarine landscape by means of magnetic methods. Archaeol. Prospect. 2004, 11, 227–235. [Google Scholar] [CrossRef]
- Matheron, G. Le Krigeage Universel; École Nationale Supérieure des Mines de Paris: Fontainebleau, France, 1969. [Google Scholar]
- Dabas, M. Contribution de la prospection géophysique a large maille et de la geostatistique a l’etude des tracés autoroutiers: Application aux ferriers de la Bussiére sur l’A77. Revue d’Archéométrie 1999, 23, 17–32. [Google Scholar] [CrossRef]
- Schmidt, A.; Linford, P.; Linford, N.; David, A.; Gaffney, C.; Sarris, A.; Fassbinder, J. Guidelines for the Use of Geophysics in Archaeology: Questions to Ask and Points to Consider; Europae Archaeologia Consilium (EAC): Namur, Belgium, 2015. [Google Scholar]
- Schmidt, A. Guidelines for the use of geophysics in archaeology: Should they be prescriptive? In The Use of Geophysical Prospection Methods in Archaeology; Meylemans, E., De Smedt, P., Eds.; Agentschap Onroerend Erfgoed: Brussels, Belgium, 2019; pp. 23–34. [Google Scholar]
- Mares, S. Introduction to Applied Geophysics; D. Reidel Publishing Company: Dordrecht, The Netherlands, 1984. [Google Scholar]
- Spector, A.; Grant, F.S. Statistical models for interpreting aeromagnetic data. Geophysics 1970, 35, 293–302. [Google Scholar] [CrossRef]
- Ciminale, M.; Loddo, M. Aspects of magnetic data processing. Archaeol. Prospect. 2001, 8, 239–246. [Google Scholar] [CrossRef]
- Aspinall, A.; Gaffney, C.F.; Schmidt, A. Magnetometry for Archaeologists; AltaMira Press: Lanham, MD, USA, 2008. [Google Scholar]
- Noviello, M.; Ciminale, M.; Del Gaudio, V.; Amoruso, L. Advances in Reconstructing Archaeological Magnetic Signals; an Algorithm for Filtering Noise due to the Ploughing Effect. Archaeol. Prospect. 2017, 24, 87–99. [Google Scholar] [CrossRef]
- Sarris, A. Processing and analyzing Geophysical Data. In Archaeological Spatial Analysis: A Methodological Guide; Gillings, M., Hacıgüzeller, P., Lock, G., Eds.; Routledge: Abingdon-on-Thames, UK, 2020; pp. 376–407. [Google Scholar]
- Bagheri, M.; Riahi, M.A. Using a Novel Method for Random Noise Reduction of Seismic Records. Iran. J. Oil Gas Sci. Technol. 2018, 7, 65–72. [Google Scholar]
- Yilmaz, Ö. Seismic Data Analysis: Processing, Inversion, and Interpretation of Seismic Data, 2nd ed.; Society of Exploration Geophysicists: Tulsa, OK, USA, 2001. [Google Scholar]
- Liu, Y. Local time-frequency transform and its application to ground-roll noise attenuation. In SEG Technical Program Expanded Abstracts 2010; Bevc, D., Nedorub, O., Eds.; Society of Exploration Geophysicists: Tulsa, OK, USA, 2010; pp. 3711–3716. [Google Scholar]
- Hu, H.; Zheng, Y. Data-driven dispersive surface-wave prediction and mode separation using high-resolution dispersion estimation. J. Appl. Geophys. 2019, 171, 103867. [Google Scholar] [CrossRef]
- Eppelbaum, L. Detecting Buried Archaeological Remains by the Use of Geophysical Data Processing with ‘Diffusion Maps’ Methodology. Geophys. Res. Abstr. 2015, 17, EGU2015-2793. [Google Scholar]
- Tsivouraki, B.; Tsokas, G.N. Wavelet transform in denoising magnetic archaeological prospecting data. Archaeol. Prospect. 2007, 14, 130–141. [Google Scholar] [CrossRef]
- Bi, W.; Zhao, Y.; An, C.; Hu, S. Clutter Elimination and Random-Noise Denoising of GPR Signals Using an SVD Method Based on the Hankel Matrix in the Local Frequency Domain. Sensors 2018, 18, 3422. [Google Scholar] [CrossRef] [PubMed]
- Xue, W.; Luo, Y.; Yang, Y.; Huang, Y. Noise Suppression for GPR Data Based on SVD of Window-Length-Optimized Hankel Matrix. Sensors 2019, 19, 3807. [Google Scholar] [CrossRef]
- Tronicke, J.; Allroggen, N.; Biermann, F.; Fanselow, F.; Guillemoteau, J.; Krauskopf, C.; Lück, E. Rapid multiscale analysis of near-surface geophysical anomaly maps: Application to an archaeogeophysical data set. Geophysics 2020, 85, B109–B118. [Google Scholar] [CrossRef]
- Zhu, J.; Xue, Y.; Zhang, N.; Li, Z.; Tao, Y.; Qiu, D. A noise reduction method for Ground Penetrating Radar signal based on wavelet transform and application in tunnel lining. IOP Conf. Ser. Earth Environ. Sci. 2017, 61, 012088. [Google Scholar] [CrossRef]
- Daniels, D.J. Ground Penetrating Radar, 2nd ed.; Institution of Electrical Engineers: London, UK, 2004. [Google Scholar]
- Vetterli, M.; Kovačević, J.; Goyal, V.K.A. Foundations of Signal Processing; Cambridge University Press: Cambridge, NY, USA, 2014. [Google Scholar]
- Weymouth, J.W.; Lessard, Y.A. Simulation Studies of Diurnal Corrections for Magnetic Prospection. Prospez. Archeol. 1986, 10, 37–47. [Google Scholar]
- Lessard, Y.A. Simulation of Magnetic Surveying Techniques to Study the Effects of Diurnal Variations; University of Nebraska-Lincoln: Lincoln, NE, USA, 1981. [Google Scholar]
- Dobrin, M.B. Introduction to Geophysical Prospecting, 2nd ed.; McGraw-Hill: New York, NY, USA, 1960. [Google Scholar]
- Tabbagh, J. Total field magnetic prospection: Are vertical gradiometer measurements preferable to single sensor survey? Archaeol. Prospect. 2003, 10, 75–81. [Google Scholar] [CrossRef]
- Barnes, H.E. Electrical Subsurface Exploration Simplified. Roads Str. 1954, 97, 81–84. [Google Scholar]
- Weymouth, J.W.; Huggins, R. Geophysical Surveying of Archaeological Sites. In Archaeological Geology; George Rapp, J., Gifford, J.A., Eds.; Yale University Press: New Haven, CT, USA, 1985; pp. 191–235. [Google Scholar]
- Christiansen, A.; Pedersen, J.; Auken, E.; Søe, N.; Holst, M.; Kristiansen, S. Improved Geoarchaeological Mapping with Electromagnetic Induction Instruments from Dedicated Processing and Inversion. Remote Sens. 2016, 8, 1022. [Google Scholar] [CrossRef]
- Trinks, I.; Hinterleitner, A.; Neubauer, W.; Nau, E.; Löcker, K.; Wallner, M.; Gabler, M.; Filzwieser, R.; Wilding, J.; Schiel, H.; et al. Large-area high-resolution ground-penetrating radar measurements for archaeological prospection. Archaeol. Prospect. 2018, 25, 171–195. [Google Scholar] [CrossRef]
- Dabas, M. Prospections archéologiques à grande échelle et géophysique pour les grands projets. Archéologies Numériques 2017, 2, 1–8. [Google Scholar] [CrossRef]
- Bénard, C.; Blin, O.; Dabas, M. Les nouvelles techniques de résistivité électrique employées dans la prospection de grandes surfaces en archéologie: Une expérience pilote en Île-de-France: Le plateau de Saclay. Les Nouvelles L’archéologie 2005, 101, 24–32. [Google Scholar]
- Verdonck, L.; De Smedt, P.; Verhegge, J. Making sense of anomalies: Practices and challenges in the archaeological interpretation of geophysical data. In Innovation in Near-Surface Geophysics; Persico, R., Piro, S., Linford, N., Eds.; Elsevier: Amsterdam, The Netherlands, 2019; pp. 151–194. [Google Scholar]
- Cuenca-Garcia, C.; Armstrong, K.; Aidona, E.; De Smedt, P.; Rosveare, A.; Rosveare, M.; Schneidhofer, P.; Wilson, C.; Faßbinder, J.; Moffat, I.; et al. The Soil Science & Archaeo-Geophysics Alliance (SAGA): Going beyond prospection. Res. Ideas Outcomes 2018, 4, e31648. [Google Scholar] [CrossRef]
- Mullins, C.E. The Magnetic Properties of the Soil and their Application to Archaeological Prospecting. In Technische und Naturwissenschaftliche Beitraege zur Feldarchaeologie; Wilkinson, E.M., Mullins, C.E., Tabbagh, A., Eds.; Rheinland-Verlag GmbH: Köln, Germany, 1974; pp. 143–347. [Google Scholar]
- Tite, M.S.; Mullins, C. Enhancement of the magnetic susceptibility of soils on archaeological sites. Archaeometry 1971, 13, 209–219. [Google Scholar] [CrossRef]















| Instrument/Sensor | RMS (nT) | Range, Peak-to-Peak over 60 s (nT) |
|---|---|---|
| Geoscan FM36 [6] | 0.29 | |
| Bartington Grad 601 [6] | 0.06 | |
| Scintrex SM4s [6] | 0.01 | |
| Ferex CON 650 [13] | 0.21 | |
| Ferex CON 650, specialized acquisition board | 0.16 | 0.60 |
| Bartington Grad-01-1000L, specialized acquisition board | 0.03 | 0.05 |
| Geometrics G-858 | 0.02 | 0.08 |
| Frequency (Hz) | Without Filter (nT) | With Filter (nT) |
|---|---|---|
| 25 | 0.0132 | 0.0094 |
| 80 | 0.0171 | 0.0104 |
| 200 | 0.0181 | 0.0125 |
| 1000 | 0.0324 | 0.0207 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schmidt, A.; Dabas, M.; Sarris, A. Dreaming of Perfect Data: Characterizing Noise in Archaeo-Geophysical Measurements. Geosciences 2020, 10, 382. https://doi.org/10.3390/geosciences10100382
Schmidt A, Dabas M, Sarris A. Dreaming of Perfect Data: Characterizing Noise in Archaeo-Geophysical Measurements. Geosciences. 2020; 10(10):382. https://doi.org/10.3390/geosciences10100382
Chicago/Turabian StyleSchmidt, Armin, Michel Dabas, and Apostolos Sarris. 2020. "Dreaming of Perfect Data: Characterizing Noise in Archaeo-Geophysical Measurements" Geosciences 10, no. 10: 382. https://doi.org/10.3390/geosciences10100382
APA StyleSchmidt, A., Dabas, M., & Sarris, A. (2020). Dreaming of Perfect Data: Characterizing Noise in Archaeo-Geophysical Measurements. Geosciences, 10(10), 382. https://doi.org/10.3390/geosciences10100382






