Determination of Peak Impact Force for Buildings Exposed to Structural Pounding during Earthquakes
Abstract
1. Introduction
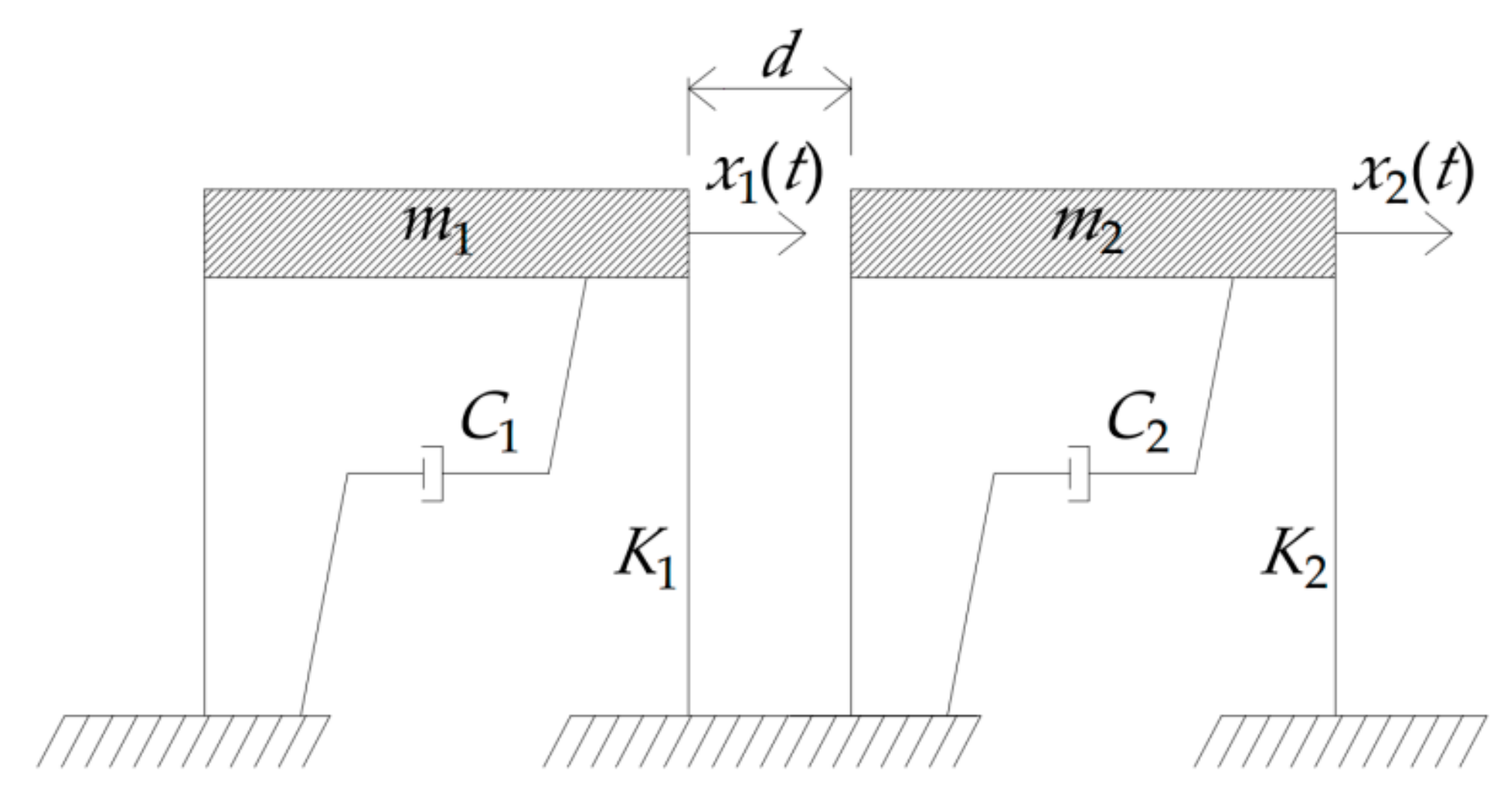
2. Materials and Methods
3. Results of the Analysis for Basic Parameters
4. Results of Parametric Study
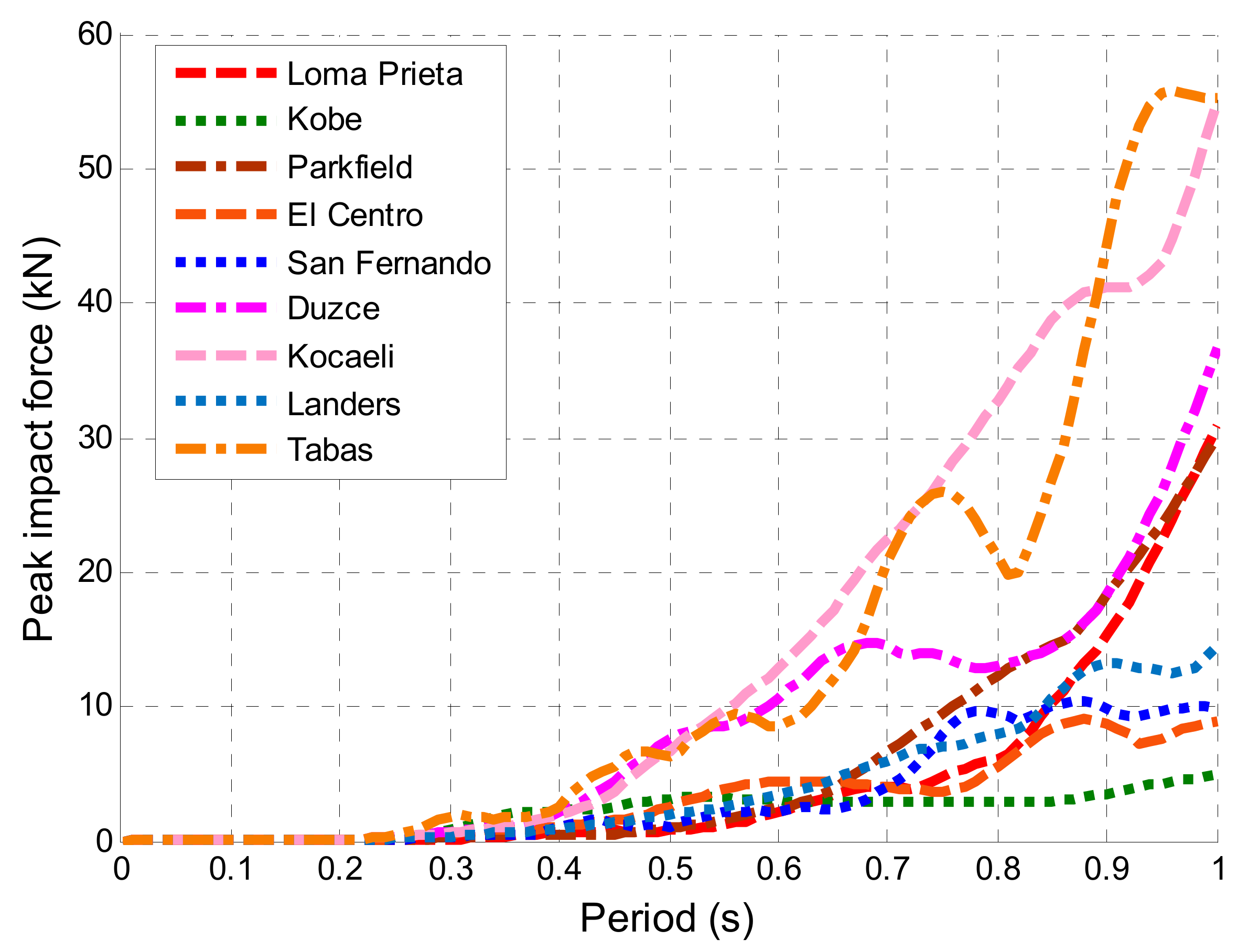
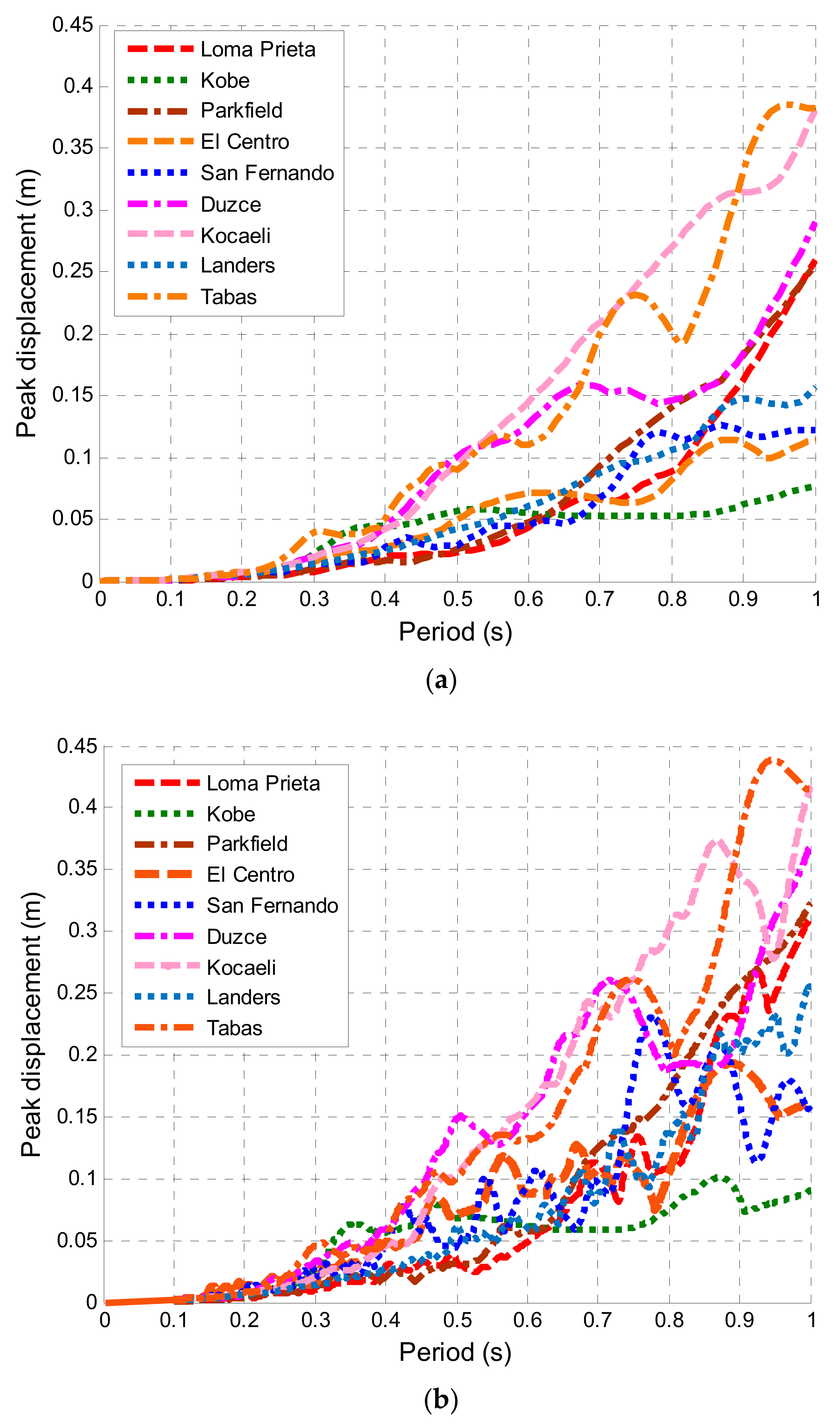
4.1. Effect of Structural Natural Period
4.2. Effect of Structural Damping Ratio
4.3. Effect of Gap Size between Buildings
4.4. Effect of Coefficient of Restitution
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Anagnostopoulos, S.A. Pounding of building in series during earthquakes. Earthq. Eng. Struct. Dyn. 1988, 16, 443–456. [Google Scholar] [CrossRef]
- Sołtysik, B.; Jankowski, R. Non-linear strain rate analysis of earthquake-induced pounding between steel buildings. Int. J. Earth Sci. Eng. 2013, 6, 429–433. [Google Scholar]
- Chouw, N.; Hao, H. Study of SSI and non-uniform ground motion effect on pounding between bridge girders. Soil Dyn. Earthq. Eng. 2005, 25, 717–728. [Google Scholar] [CrossRef]
- Jankowski, R. Pounding between superstructure segments in multi-supported elevated bridge with three-span continuous deck under 3D non-uniform earthquake excitation. J. Earthq. Tsunami 2015, 9, 1550012. [Google Scholar] [CrossRef]
- Kasai, K.; Maison, B.F. Building pounding damage during the 1989 Loma Prieta earthquake. Eng. Struct. 1997, 19, 195–207. [Google Scholar] [CrossRef]
- Northridge Earthquake of January 17, 1994—Reconnaissance Report. In EERI Report 95–03; Earthquake Engineering Research Institute: Oakland, CA, USA, 1995; Volume 1.
- Anagnostopoulos, S.A. Equivalent viscous damping for modeling inelastic impacts in earthquake pounding problems. Earthq. Eng. Struct. Dyn. 2004, 33, 897–902. [Google Scholar] [CrossRef]
- Jankowski, R. Non-linear viscoelastic modelling of earthquake-induced structural pounding. Earthq. Eng. Struct. Dyn. 2005, 34, 595–611. [Google Scholar] [CrossRef]
- Jankowski, R. Analytical expression between the impact damping ratio and the coefficient of restitution in the non-linear viscoelastic model of structural pounding. Earthq. Eng. Struct. Dyn. 2006, 35, 517–524. [Google Scholar] [CrossRef]
- Muthukumar, S.; DesRoches, R.A. Hertz contact model with nonlinear damping for pounding simulation. Earthq. Eng. Struct. Dyn. 2006, 35, 811–828. [Google Scholar] [CrossRef]
- Ye, K.; Li, L.; Zhu, H. A note on the Hertz contact model with nonlinear damping for pounding simulation. Earthq. Eng. Struct. Dyn. 2008, 38, 1135–1142. [Google Scholar] [CrossRef]
- Filiatrault, A.; Wagner, P.; Cherry, S. Analytical prediction of experimental building pounding. Earthq. Eng. Struct. Dyn. 1995, 24, 1131–1154. [Google Scholar] [CrossRef]
- Komodromos, P.; Polycarpou, P.C.; Papaloizou, L.; Phocas, M.C. Response of seismically isolated buildings considering poundings. Earthq. Eng. Struct. Dyn. 2007, 36, 1605–1622. [Google Scholar] [CrossRef]
- Polycarpou, P.C.; Komodromos, P. Earthquake-induced poundings of a seismically isolated building with adjacent structures. Eng. Struct. 2010, 32, 1937–1951. [Google Scholar] [CrossRef]
- Masroor, A.; Mosqueda, G. Experimental simulation of base-isolated buildings pounding against moat wall and effects on superstructure response. Earthq. Eng. Struct. Dyn. 2012, 41, 2093–2109. [Google Scholar] [CrossRef]
- Naderpour, H.; Barros, R.C.; Khatami, S.M.; Jankowski, R. Numerical study on pounding between two adjacent buildings under earthquake excitation. Shock Vib. 2016, 2016, 1504783. [Google Scholar] [CrossRef]
- Naderpour, H.; Barros, R.C.; Khatami, S.M. Suggestion of an equation of motion to calculate damping ratio during earthquake based on cyclic procedure. J. Theor. Appl. Mech. 2016, 54, 963–973. [Google Scholar] [CrossRef][Green Version]
- Naderpour, H.; Khatami, S.M.; Barros, R.C. Prediction of critical distance between two MDOF systems subject to seismic excitation in terms of artificial neural networks. Period. Polytech. Civ. Eng. 2017, 61, 516–529. [Google Scholar]
- Miari, M.; Choong, K.K.; Jankowski, R. Seismic pounding between adjacent buildings: Identification of parameters, soil interaction issues and mitigation measures. Soil Dyn. Earthq. Eng. 2019, 121, 135–150. [Google Scholar] [CrossRef]
- Papadrakakis, M.; Mouzakis, H.; Plevris, N.; Bitzarakis, S. Lagrange multiplier solution method for pounding of buildings during earthquakes. Earthq. Eng. Struct. Dyn. 1991, 20, 981–998. [Google Scholar] [CrossRef]
- Shakya, K.; Wijeyewickrema, A.C. Mid-column pounding of multi-story reinforced concrete buildings considering soil effects. Adv. Struct. Eng. 2019, 12, 71–85. [Google Scholar] [CrossRef]
- Kajita, Y.; Kitahara, T.; Nishimoto, Y.; Otsuka, H. Estimation of maximum impact force on natural rubber during collision of two steel bars. In Proceedings of the First European Conference on Earthquake Engineering and Seismology, Geneva, Switzerland, 3–8 September 2006. Paper No. 488. [Google Scholar]
- Crozet, V.; Politopoulos, I.; Chaudat, T. Shake table tests of structures subject to pounding. Earthq. Eng. Struct. Dyn. 2019, 48, 1156–1173. [Google Scholar] [CrossRef]
- Isteita, M. Studies of Earthquake Pounding Risk and of Above-Code Seismic Design. Ph.D. Thesis, University of Colorado at Boulder, Boulder, CO, USA, 2019. [Google Scholar]
- Isteita, M.; Porter, K. Safe distance between adjacent buildings to avoid pounding in earthquakes. In Proceedings of the 16th World Conference on Earthquake Engineering, Santiago, Chile, 8–13 January 2017. Paper No. 2532. [Google Scholar]
- Elwardany, H.; Seleemah, A.; Jankowski, R. Seismic pounding behavior of multi-story buildings in series considering the effect of infill panels. Eng. Struct. 2017, 144, 139–150. [Google Scholar] [CrossRef]
- Bamer, F.; Markert, B. A nonlinear visco-elastoplastic model for structural pounding. Earthq. Eng. Struct. Dyn. 2018, 47, 2490–2495. [Google Scholar]
- Kun, C.; Yang, Z.; Chouw, N. Seismic response of skewed bridges including pounding effects. Earthq. Struct. 2018, 14, 467–476. [Google Scholar]
- Maniatakis, C.A.; Spyrakos, C.C.; Kiriakopoulos, P.D.; Tsellos, K.P. Seismic response of a historic church considering pounding phenomena. Bull. Earthq. Eng. 2018, 16, 2913–2941. [Google Scholar] [CrossRef]
- Fatahi, B.; Van Nguyen, Q.; Xu, R.; Sun, W.J. Three-dimensional response of neighboring buildings sitting on pile foundations to seismic pounding. Int. J. Geomech. 2018, 18, 04018007. [Google Scholar] [CrossRef]
- Li, C.; Bi, K.; Hao, H. Seismic performances of precast segmental column under bidirectional earthquake motions: Shake table test and numerical evaluation. Eng. Struct. 2019, 187, 314–328. [Google Scholar] [CrossRef]
- Raheem, S.E.A.; Fooly, M.Y.; Shafy, A.G.A.; Taha, A.M.; Abbas, Y.A.; Latif, M.M.A. Numerical simulation of potential seismic pounding among adjacent buildings in series. Bull. Earthq. Eng. 2019, 17, 439–471. [Google Scholar] [CrossRef]
- Jankowski, R.; Mahmoud, S. Linking of adjacent three-storey buildings for mitigation of structural pounding during earthquakes. Bull. Earthq. Eng. 2016, 14, 3075–3097. [Google Scholar] [CrossRef]
- Elassaly, M. Effects of ground motion characteristics on damage of RC buildings: A detailed investigation. Int. J. Civ. Environ. Eng. 2015, 9, 693–701. [Google Scholar]
- Song, R.; Li, Y.; van de Lindt, J.W. Impact of earthquake ground motion characteristics on collapse risk of post-mainshock buildings considering aftershocks. Eng. Struct. 2014, 81, 349–361. [Google Scholar] [CrossRef]
- Khatami, S.M.; Naderpour, H.; Barros, R.C.; Jakubczyk-Gałczyńska, A.; Jankowski, R. Effective formula for impact damping ratio for simulation of earthquake-induced structural pounding. Geosciences 2019, 9, 347. [Google Scholar] [CrossRef]
- Yazdani, A.; Eftekhari, S.N. The effect of structural properties and ground motion variables on the global response of structural systems. Civ. Eng. Environ. Syst. 2015, 32, 216–229. [Google Scholar] [CrossRef]
- Dolsek, M. Incremental dynamic analysis with consideration of modeling uncertainties. Earthq. Eng. Struct. Dyn. 2009, 38, 805–825. [Google Scholar] [CrossRef]
- Jankowski, R.; Walukiewicz, H. Modeling of two-dimensional random fields. Probabilistic Eng. Mech. 1997, 12, 115–121. [Google Scholar] [CrossRef]
- Baker, J.W.; Cornell, C.A. Uncertainty propagation in probabilistic seismic loss estimation. Struct. Saf. 2008, 30, 236–252. [Google Scholar] [CrossRef]
- Boore, D.M. Simulation of ground motion using the stochastic method. Pure Appl. Geophys. 2003, 160, 635–676. [Google Scholar] [CrossRef]
- Jankowski, R.; Wilde, K. A simple method of conditional random field simulation of ground motions for long structures. Eng. Struct. 2000, 22, 552–561. [Google Scholar] [CrossRef]
- Chopra, A.K. Dynamics of Structures: Theory and Applications to Earthquake Engineering; Prentice Hall: Upper Saddle River, NJ, USA, 1995. [Google Scholar]
- Polycarpou, P.C.; Komodromos, P.; Polycarpou, A.C. A nonlinear impact model for simulating the use of rubber shock absorbers for mitigating the effects of structural pounding during earthquakes. Earthq. Eng. Struct. Dyn. 2013, 42, 81–100. [Google Scholar] [CrossRef]
- Sołtysik, B.; Falborski, T.; Jankowski, R. Preventing of earthquake-induced pounding between steel structures by using polymer elements—Experimental study. Procedia Eng. 2017, 199, 278–283. [Google Scholar] [CrossRef]
- Falborski, T.; Jankowski, R.; Kwiecień, A. Experimental study on polymer mass used to repair damaged structures. Key Eng. Mater. 2012, 488–489, 347–350. [Google Scholar] [CrossRef]
- Anagnostopoulos, S.A.; Karamaneas, C.E. Use of collision shear walls to minimize seismic separation and to protect adjacent buildings from collapse due to earthquake-induced pounding. Earthq. Eng. Struct. Dyn. 2008, 37, 1371–1388. [Google Scholar] [CrossRef]
- Divyashree, M.; Bhavyashree, B.N.; Siddappa, G. Comparison of bracing and shear walls as seismic strengthening methods to buildings with plan irregularities. Int. J. Res. Eng. Technol. 2014, 3, 205–210. [Google Scholar]
- Patel, C.C.; Jangid, R.S. Seismic response of dynamically similar adjacent structures connected with viscous dampers. IES J. Part A Civ. Struct. Eng. 2010, 3, 1–13. [Google Scholar] [CrossRef]
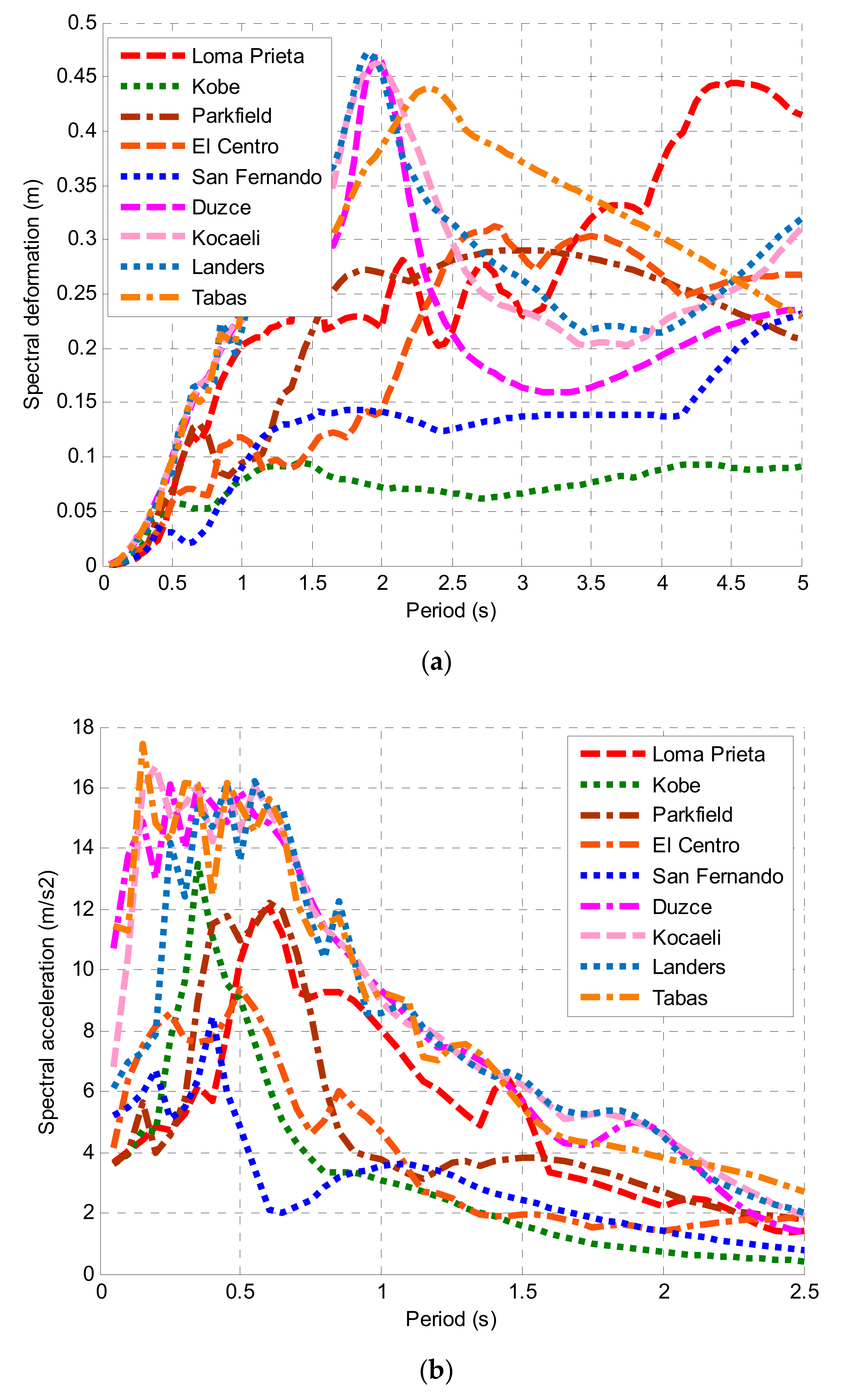

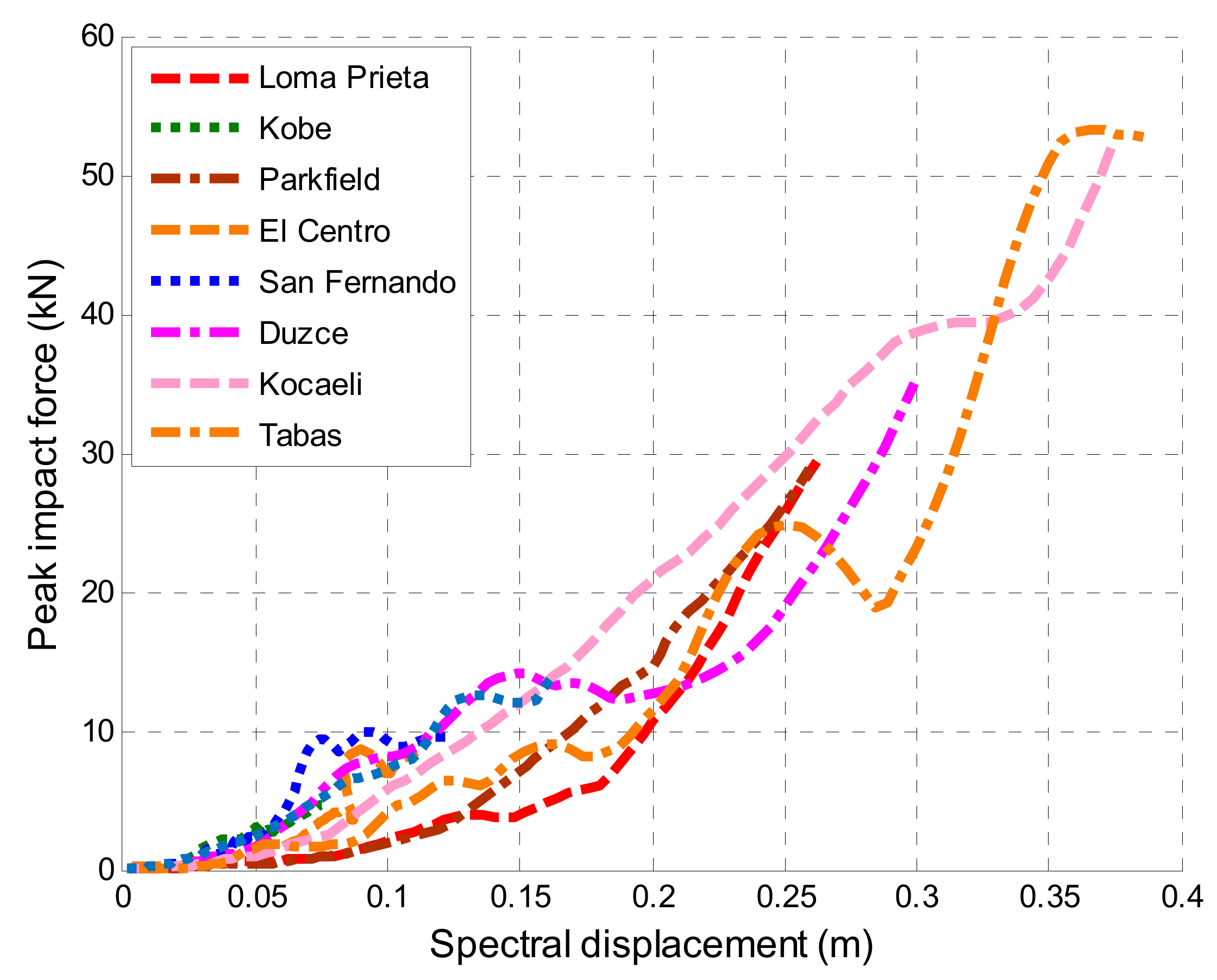
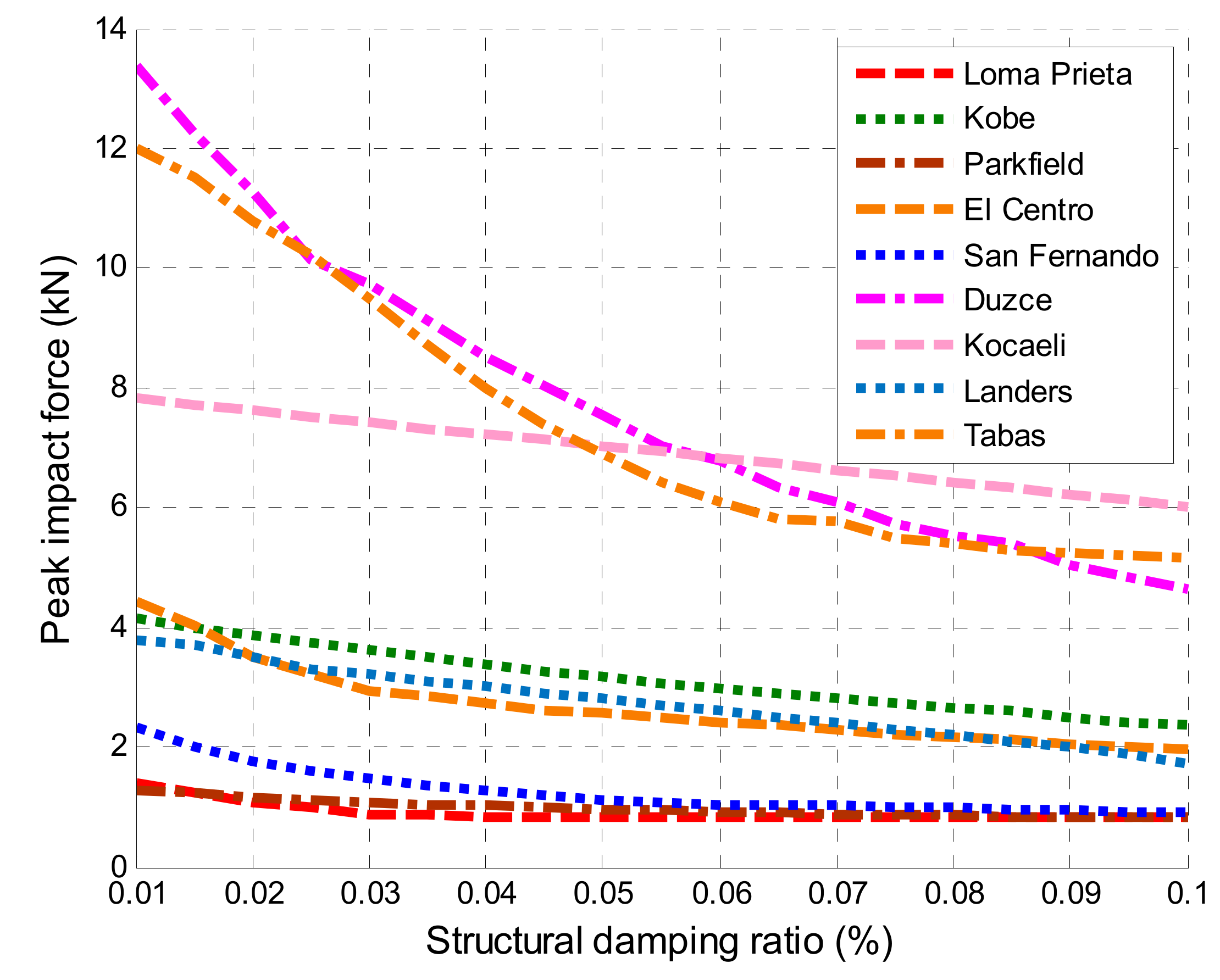
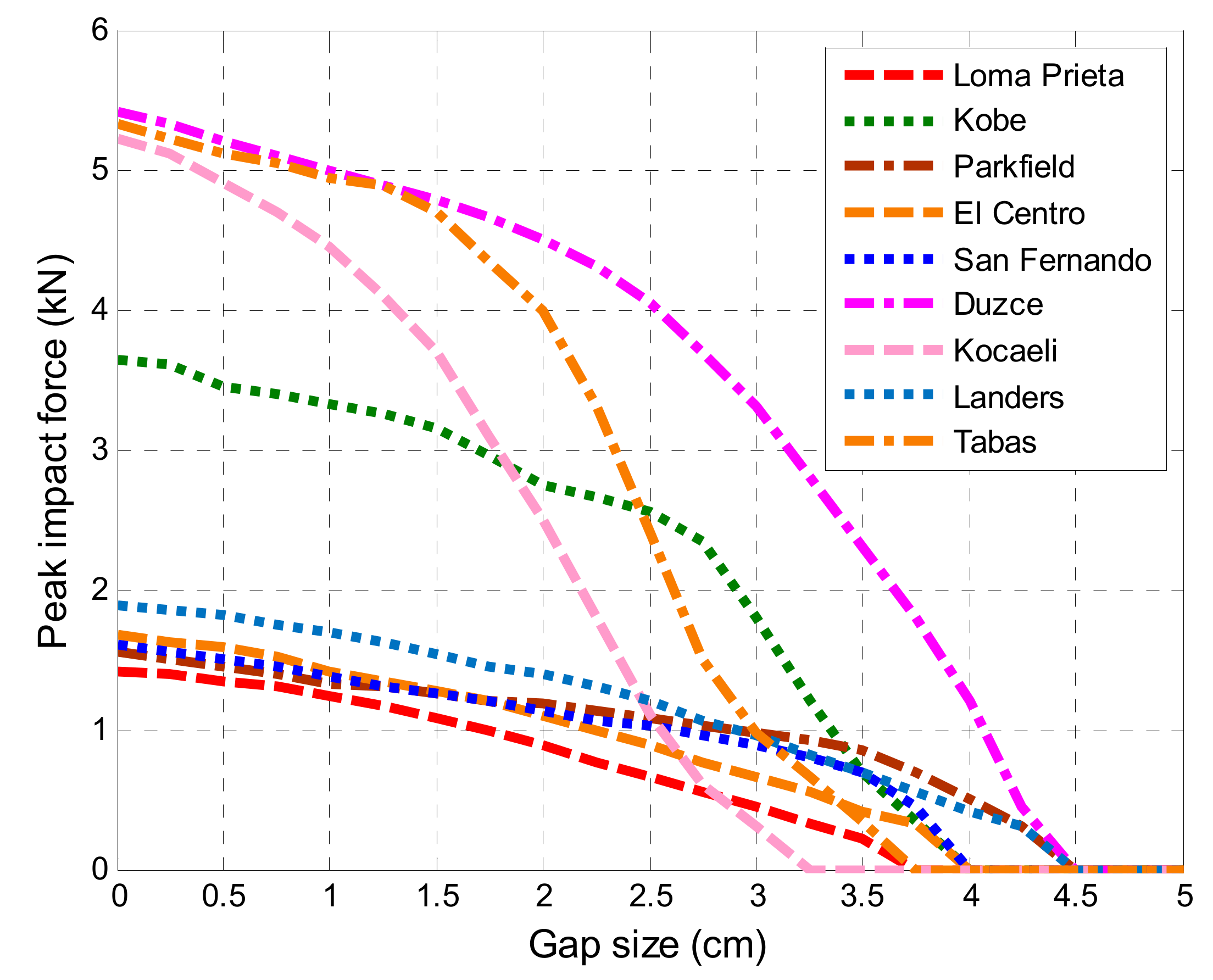

| Earthquake | Date | Magnitude | Station | Component | PGA (cm/s2) |
|---|---|---|---|---|---|
| Loma Prieta | 17.10.1989 | 6.9 | Corralitos | NS | 631.51 |
| Kobe | 17.01.1995 | 7.2 | JMA | NS | 817.82 |
| Parkfield | 28.06.1966 | 6.2 | Jennings (CGS) | NS | 462.00 |
| El Centro | 18.05.1940 | 6.9 | El Centro | NS | 307.00 |
| San Fernando | 09.02.1971 | 6.6 | Pacoima Dam | N16°W | 1202.62 |
| Duzce | 12.11.1999 | 7.2 | Izmit | NS | 754.23 |
| Kocaeli | 17.08.1999 | 7.6 | Izmit | NS | 695.24 |
| Landers | 28.06.1992 | 7.3 | Baker | NS | 853.00 |
| Tabas | 16.09.1978 | 7.4 | Tabas | NS | 784.81 |
| Earthquake | Largest Peak Impact Force (kN) |
|---|---|
| Loma Prieta | 30.0 |
| Kobe | 5.9 |
| Parkfield | 30.0 |
| El Centro | 9.3 |
| San Fernando | 9.9 |
| Duzce | 38.0 |
| Kocaeli | 57.0 |
| Landers | 12.0 |
| Tabas | 57.0 |
| Earthquake | Peak Impact Force (kN) |
|---|---|
| Loma Prieta | 1.5 |
| Kobe | 3.6 |
| Parkfield | 1.5 |
| El Centro | 2.3 |
| San Fernando | 1.7 |
| Duzce | 7.8 |
| Kocaeli | 7.1 |
| Landers | 2.0 |
| Tabas | 6.2 |
| Earthquake | Largest Peak Impact Force (kN) | Minimum Gap Size Preventing Pounding (cm) |
|---|---|---|
| Loma Prieta | 1.6 | 3.7 |
| Kobe | 3.8 | 4.0 |
| Parkfield | 1.6 | 4.5 |
| El Centro | 1.7 | 4.0 |
| San Fernando | 1.7 | 4.0 |
| Duzce | 5.7 | 4.5 |
| Kocaeli | 5.5 | 3.2 |
| Landers | 2.0 | 4.5 |
| Tabas | 5.6 | 3.7 |
| Earthquake | Peak Impact Force (kN) | |
|---|---|---|
| CR ~ 0 | CR = 1 | |
| Loma Prieta | 1.9 | 0.83 |
| Kobe | 8.4 | 3.2 |
| Parkfield | 2.5 | 1.0 |
| El Centro | 6.2 | 2.6 |
| San Fernando | 3.7 | 1.1 |
| Duzce | 16.0 | 7.5 |
| Kocaeli | 13.0 | 6.7 |
| Landers | 2.7 | 2.0 |
| Tabas | 15.0 | 6.4 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khatami, S.M.; Naderpour, H.; Barros, R.C.; Jakubczyk-Gałczyńska, A.; Jankowski, R. Determination of Peak Impact Force for Buildings Exposed to Structural Pounding during Earthquakes. Geosciences 2020, 10, 18. https://doi.org/10.3390/geosciences10010018
Khatami SM, Naderpour H, Barros RC, Jakubczyk-Gałczyńska A, Jankowski R. Determination of Peak Impact Force for Buildings Exposed to Structural Pounding during Earthquakes. Geosciences. 2020; 10(1):18. https://doi.org/10.3390/geosciences10010018
Chicago/Turabian StyleKhatami, Seyed Mohammad, Hosein Naderpour, Rui Carneiro Barros, Anna Jakubczyk-Gałczyńska, and Robert Jankowski. 2020. "Determination of Peak Impact Force for Buildings Exposed to Structural Pounding during Earthquakes" Geosciences 10, no. 1: 18. https://doi.org/10.3390/geosciences10010018
APA StyleKhatami, S. M., Naderpour, H., Barros, R. C., Jakubczyk-Gałczyńska, A., & Jankowski, R. (2020). Determination of Peak Impact Force for Buildings Exposed to Structural Pounding during Earthquakes. Geosciences, 10(1), 18. https://doi.org/10.3390/geosciences10010018






