ExAutoGP: Enhancing Genomic Prediction Stability and Interpretability with Automated Machine Learning and SHAP
Simple Summary
Abstract
1. Introduction
2. Materials and Methods
2.1. Datasets
2.1.1. Simulation Dataset
2.1.2. German Holstein Cattle
2.1.3. Chicken Dataset
2.2. Genomic Prediction Models
2.2.1. GBLUP
2.2.2. BayesB
2.2.3. SVR
2.2.4. KRR
2.2.5. RF
2.2.6. TPOT: ExAutoGP Framework
2.3. Evaluation
2.4. SHAP: Modelling Interpretation
3. Results
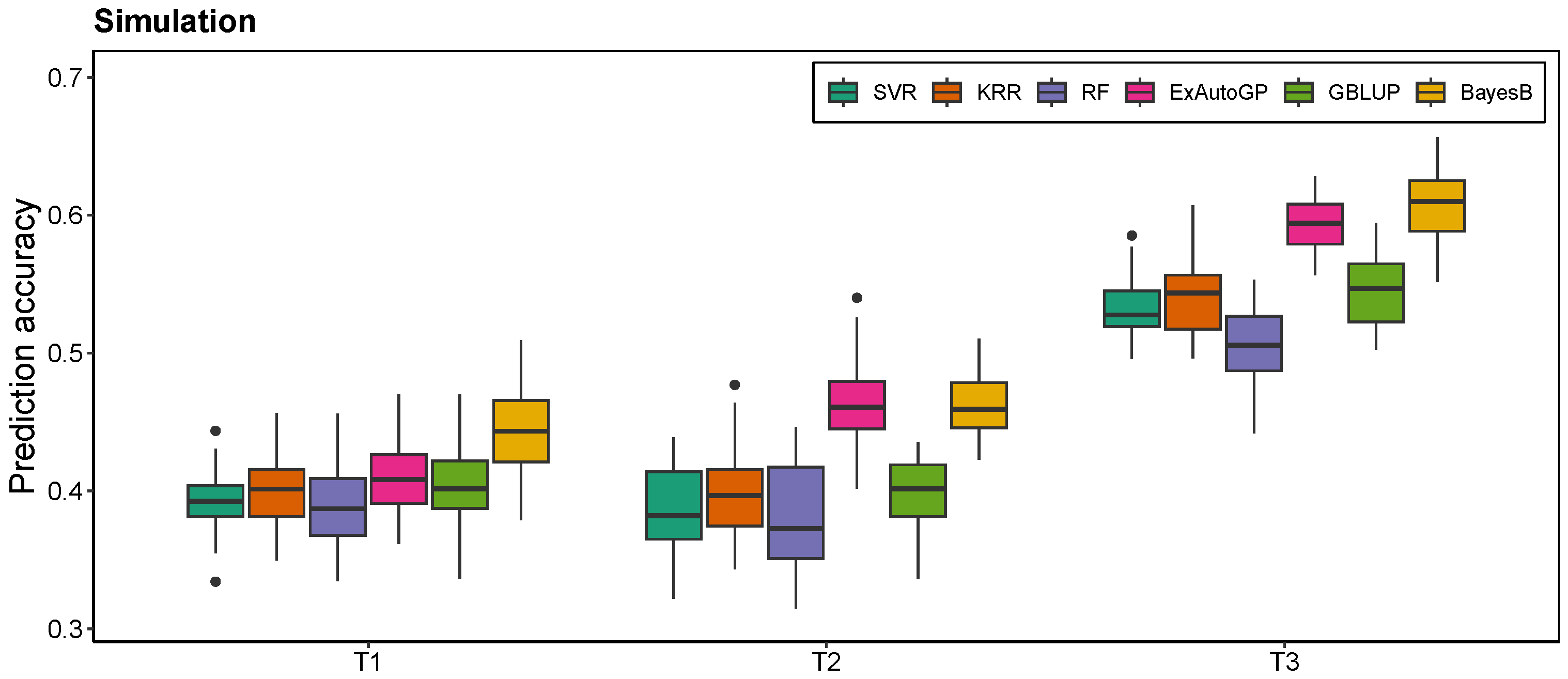
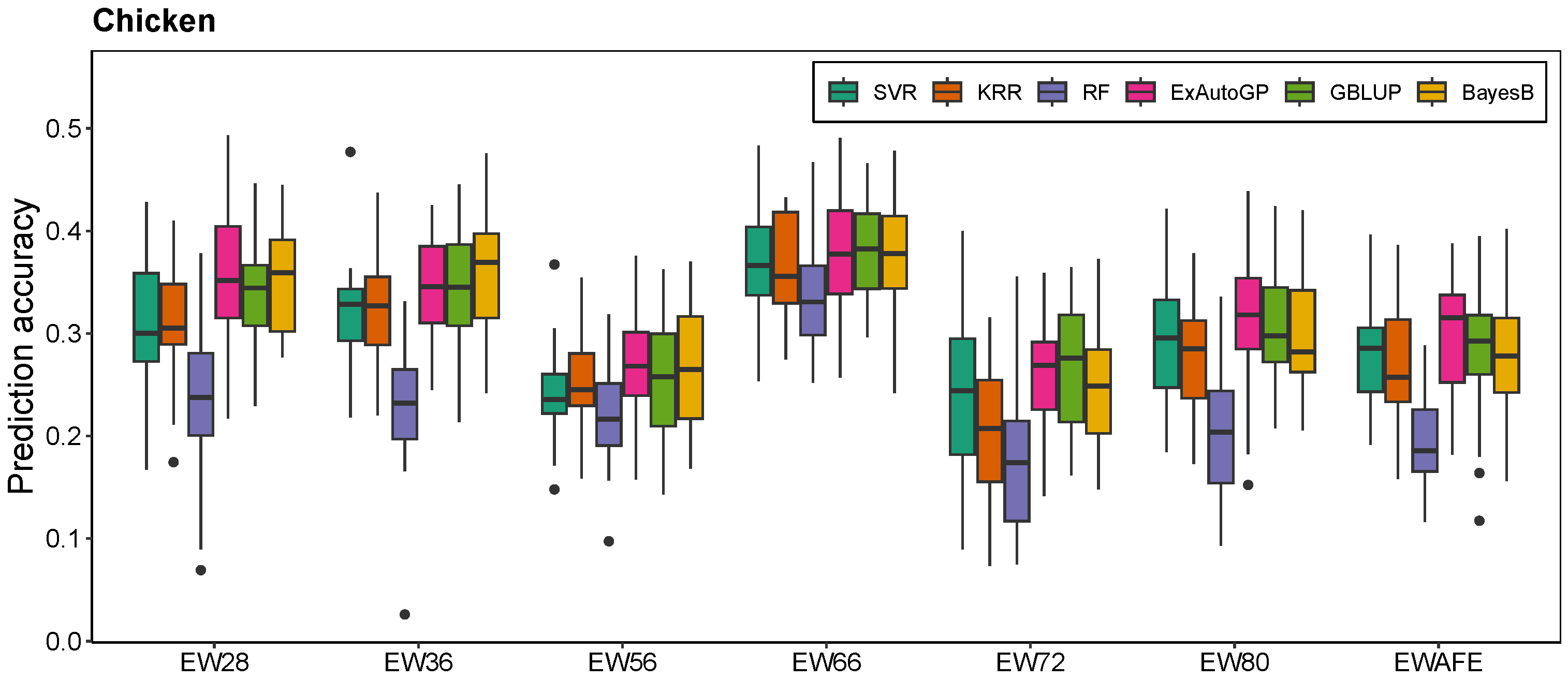
3.1. Comparison of ExAutoGP with GBLUP and BayesB in Genomic Prediction Accuracy
3.2. Comparison of ExAutoGP and Traditional Machine Learning Methods in Genomic Prediction Accuracy
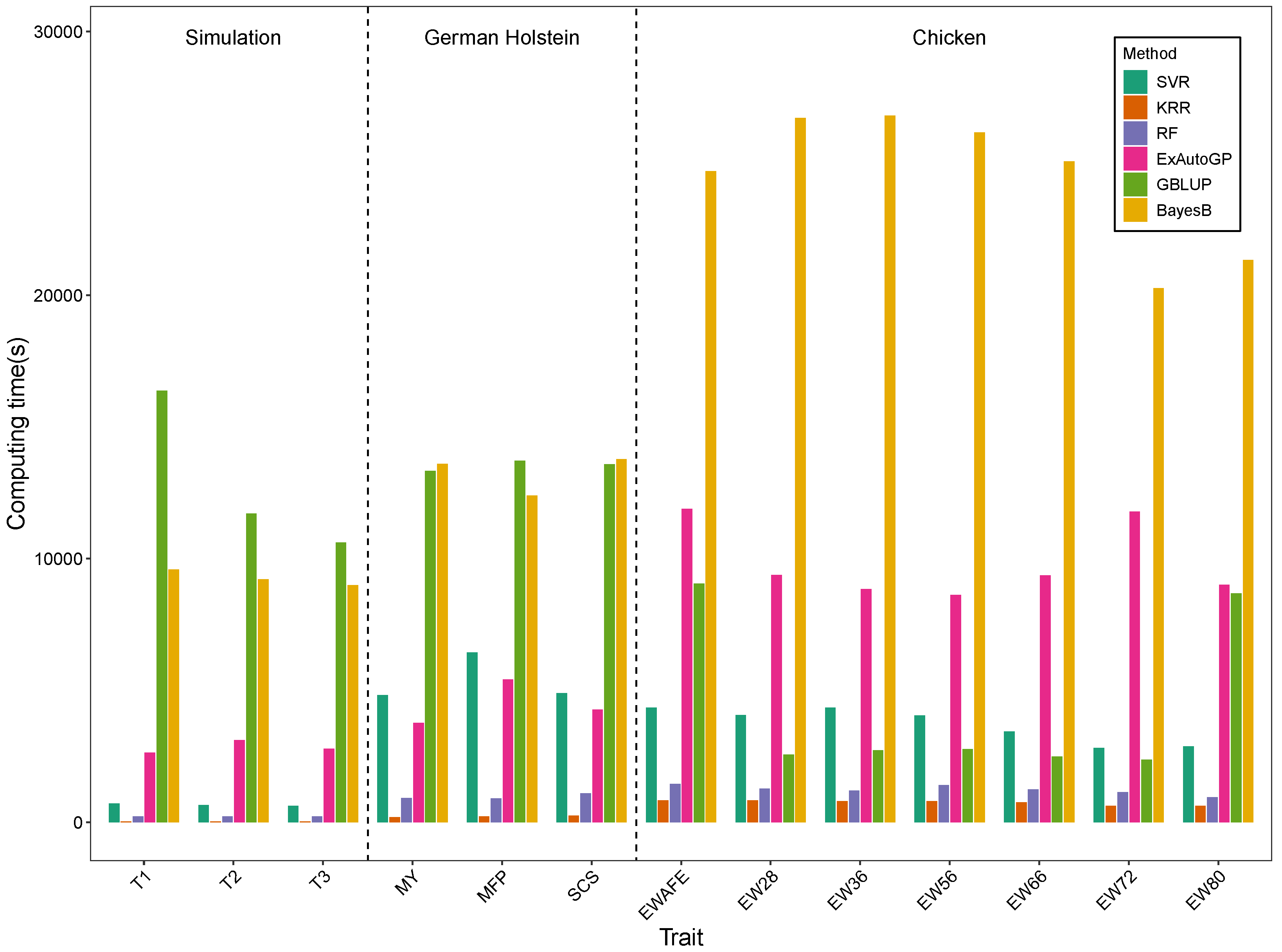
3.3. Comparison of Computation Time
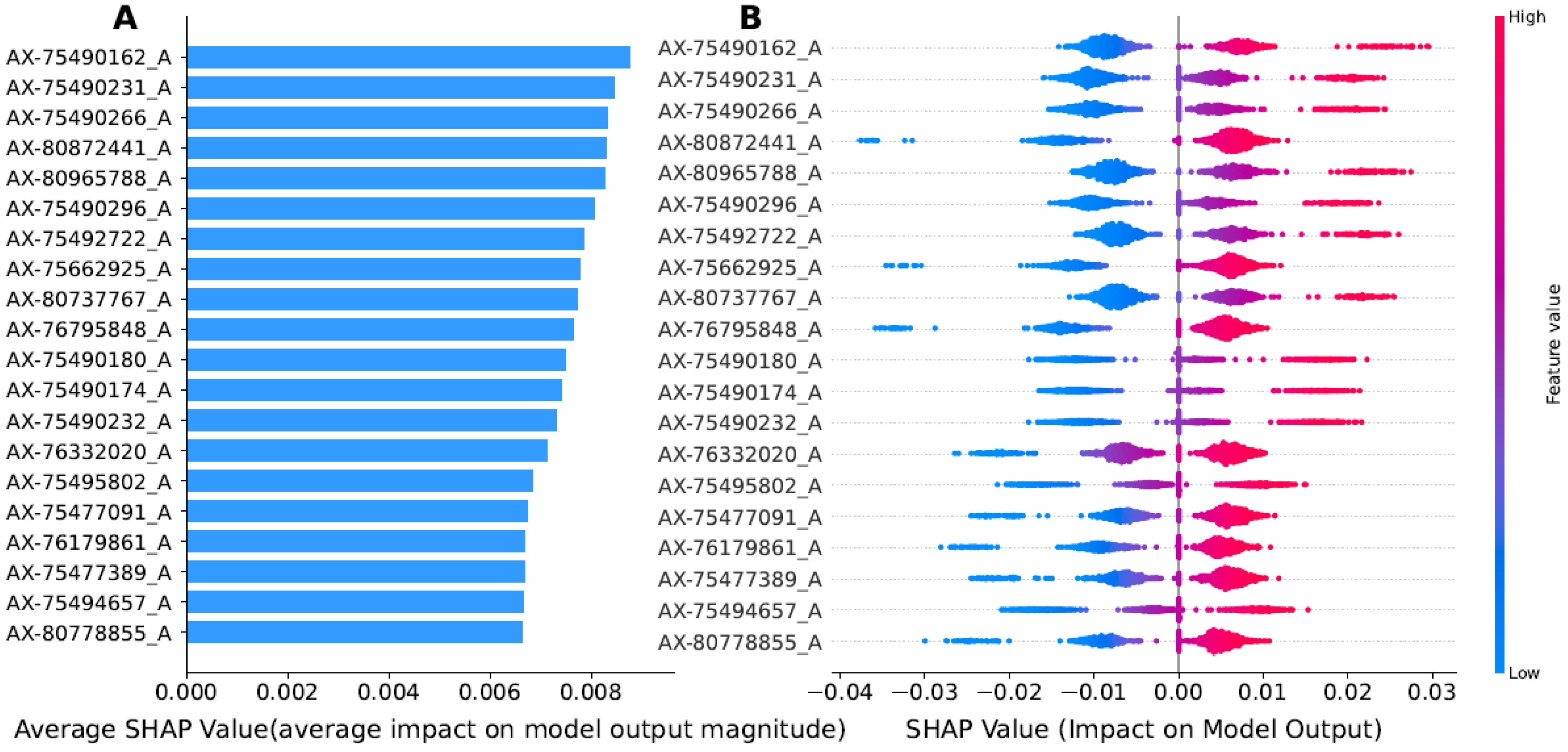
3.4. Interpreting ExAutoGP Model Using the SHAP Method
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ML | Machine learning |
| SHAP | SHapley Additive exPlanations |
| AutoML | Automated machine learning |
| SNP | Single nucleotide polymorphism |
| GEBV | Genomic estimated breeding value |
| QTL | Quantitative trait locus |
| GBLUP | Genomic best linear unbiased prediction |
| SVR | Support vector regression |
| KRR | Kernel ridge regression |
| RF | Random forest |
| TPOT | Tree-based pipeline optimization tool |
| MY | Milk yield |
| MFP | Milk fat percentage |
| SCS | Somatic cell score |
| EW | Egg weight |
| EWAFE | First egg weight |
| EW28 | Egg weight at 28 weeks of age |
| EW36 | Egg weight at 36 weeks of age |
| EW56 | Egg weight at 56 weeks of age |
| EW66 | Egg weight at 66 weeks of age |
| EW72 | Egg weight at 72 weeks of age |
| EW80 | Egg weight at 80 weeks of age |
References
- Meuwissen, T.H.; Hayes, B.J.; Goddard, M. Prediction of total genetic value using genome-wide dense marker maps. Genetics 2001, 157, 1819–1829. [Google Scholar] [CrossRef]
- De Roos, A.; Schrooten, C.; Veerkamp, R.; Van Arendonk, J. Effects of genomic selection on genetic improvement, inbreeding, and merit of young versus proven bulls. J. Dairy Sci. 2011, 94, 1559–1567. [Google Scholar] [CrossRef]
- Heffner, E.L.; Jannink, J.L.; Sorrells, M.E. Genomic selection accuracy using multifamily prediction models in a wheat breeding program. Plant Genome 2011, 4, 65. [Google Scholar] [CrossRef]
- Hayes, B.J.; Bowman, P.J.; Chamberlain, A.J.; Goddard, M.E. Invited review: Genomic selection in dairy cattle: Progress and challenges. J. Dairy Sci. 2009, 92, 433–443. [Google Scholar] [CrossRef] [PubMed]
- Schaeffer, L. Strategy for applying genome-wide selection in dairy cattle. J. Anim. Breed. Genet. 2006, 123, 218–223. [Google Scholar] [CrossRef] [PubMed]
- García-Ruiz, A.; Cole, J.B.; VanRaden, P.M.; Wiggans, G.R.; Ruiz-López, F.J.; Van Tassell, C.P. Changes in genetic selection differentials and generation intervals in US Holstein dairy cattle as a result of genomic selection. Proc. Natl. Acad. Sci. USA 2016, 113, E3995–E4004. [Google Scholar] [CrossRef] [PubMed]
- Voss-Fels, K.P.; Cooper, M.; Hayes, B.J. Accelerating crop genetic gains with genomic selection. Theor. Appl. Genet. 2019, 132, 669–686. [Google Scholar] [CrossRef]
- Sandhu, K.; Patil, S.S.; Pumphrey, M.; Carter, A. Multitrait machine-and deep-learning models for genomic selection using spectral information in a wheat breeding program. Plant Genome 2021, 14, e20119. [Google Scholar] [CrossRef]
- Crossa, J.; Pérez-Rodríguez, P.; Cuevas, J.; Montesinos-López, O.; Jarquín, D.; De Los Campos, G.; Burgueño, J.; González-Camacho, J.M.; Pérez-Elizalde, S.; Beyene, Y.; et al. Genomic selection in plant breeding: Methods, models, and perspectives. Trends Plant Sci. 2017, 22, 961–975. [Google Scholar] [CrossRef]
- VanRaden, P.M. Efficient methods to compute genomic predictions. J. Dairy Sci. 2008, 91, 4414–4423. [Google Scholar] [CrossRef]
- Misztal, I.; Legarra, A.; Aguilar, I. Computing procedures for genetic evaluation including phenotypic, full pedigree, and genomic information. J. Dairy Sci. 2009, 92, 4648–4655. [Google Scholar] [CrossRef] [PubMed]
- Daneshvar, A.; Mousa, G. Regression shrinkage and selection via least quantile shrinkage and selection operator. PLoS ONE 2023, 18, e0266267. [Google Scholar] [CrossRef]
- González-Recio, O.; Forni, S. Genome-wide prediction of discrete traits using Bayesian regressions and machine learning. Genet. Sel. Evol. 2011, 43, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Yi, N.; Xu, S. Bayesian LASSO for quantitative trait loci mapping. Genetics 2008, 179, 1045–1055. [Google Scholar] [CrossRef] [PubMed]
- Meuwissen, T.; Hayes, B.; Goddard, M. Genomic selection: A paradigm shift in animal breeding. Anim. Front. 2016, 6, 6–14. [Google Scholar] [CrossRef]
- Pérez, P.; de Los Campos, G. Genome-wide regression and prediction with the BGLR statistical package. Genetics 2014, 198, 483–495. [Google Scholar] [CrossRef]
- Ge, X.J.; Hwang, C.C.; Liu, Z.H.; Huang, C.C.; Huang, W.H.; Hung, K.H.; Wang, W.K.; Chiang, T.Y. Conservation genetics and phylogeography of endangered and endemic shrub Tetraena mongolica (Zygophyllaceae) in Inner Mongolia, China. BMC Genet. 2011, 12, 1–12. [Google Scholar] [CrossRef]
- Montesinos López, O.A.; Montesinos López, A.; Crossa, J. Multivariate Statistical Machine Learning Methods for Genomic Prediction; Springer Nature: Berlin/Heidelberg, Germany, 2022. [Google Scholar]
- Weigel, K.; VanRaden, P.; Norman, H.; Grosu, H. A 100-Year Review: Methods and impact of genetic selection in dairy cattle—From daughter–dam comparisons to deep learning algorithms. J. Dairy Sci. 2017, 100, 10234–10250. [Google Scholar] [CrossRef]
- Shahinfar, S.; Mehrabani-Yeganeh, H.; Lucas, C.; Kalhor, A.; Kazemian, M.; Weigel, K.A. Prediction of Breeding Values for Dairy Cattle Using Artificial Neural Networks and Neuro-Fuzzy Systems. Comput. Math. Methods Med. 2012, 2012, 127130. [Google Scholar] [CrossRef]
- Baratchi, M.; Wang, C.; Limmer, S.; van Rijn, J.N.; Hoos, H.; Bäck, T.; Olhofer, M. Automated machine learning: Past, present and future. Artif. Intell. Rev. 2024, 57, 122. [Google Scholar] [CrossRef]
- Olson, R.S.; Moore, J.H. TPOT: A tree-based pipeline optimization tool for automating machine learning. In Proceedings of the Workshop on Automatic Machine Learning, PMLR, New York, NY, USA, 24 June 2016; pp. 66–74. [Google Scholar]
- Castagno, S.; Birch, M.; van der Schaar, M.; McCaskie, A. Predicting rapid progression in knee osteoarthritis: A novel and interpretable automated machine learning approach, with specific focus on young patients and early disease. Ann. Rheum. Dis. 2025, 84, 124–135. [Google Scholar] [CrossRef] [PubMed]
- SenthilKumar, G.; Madhusudhana, S.; Flitcroft, M.; Sheriff, S.; Thalji, S.; Merrill, J.; Clarke, C.N.; Maduekwe, U.N.; Tsai, S.; Christians, K.K.; et al. Automated machine learning (AutoML) can predict 90-day mortality after gastrectomy for cancer. Sci. Rep. 2023, 13, 11051. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Ma, J. CascadeDumpNet: Enhancing open dumpsite detection through deep learning and AutoML integrated dual-stage approach using high-resolution satellite imagery. Remote Sens. Environ. 2024, 313, 114349. [Google Scholar] [CrossRef]
- Azodi, C.B.; Tang, J.; Shiu, S.H. Opening the black box: Interpretable machine learning for geneticists. Trends Genet. 2020, 36, 442–455. [Google Scholar] [CrossRef]
- Usai, M.G.; Gaspa, G.; Macciotta, N.P.; Carta, A.; Casu, S. XVI th QTLMAS: Simulated dataset and comparative analysis of submitted results for QTL mapping and genomic evaluation. BMC Proc. 2014, 8, 1–9. [Google Scholar] [CrossRef]
- Zhang, Z.; Erbe, M.; He, J.; Ober, U.; Gao, N.; Zhang, H.; Simianer, H.; Li, J. Accuracy of whole-genome prediction using a genetic architecture-enhanced variance-covariance matrix. G3: Genes, Genomes, Genet. 2015, 5, 615–627. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Su, G.; Jiang, L.; Bao, Z. An efficient unified model for genome-wide association studies and genomic selection. Genet. Sel. Evol. 2017, 49, 1–8. [Google Scholar] [CrossRef]
- Hu, Z.L.; Park, C.A.; Wu, X.L.; Reecy, J.M. Animal QTLdb: An improved database tool for livestock animal QTL/association data dissemination in the post-genome era. Nucleic Acids Res. 2013, 41, D871–D879. [Google Scholar] [CrossRef]
- Zhang, Z.; Ober, U.; Erbe, M.; Zhang, H.; Gao, N.; He, J.; Li, J.; Simianer, H. Improving the accuracy of whole genome prediction for complex traits using the results of genome wide association studies. PLoS ONE 2014, 9, e93017. [Google Scholar] [CrossRef]
- Liu, Z.; Sun, C.; Yan, Y.; Li, G.; Wu, G.; Liu, A.; Yang, N. Genome-wide association analysis of age-dependent egg weights in chickens. Front. Genet. 2018, 9, 128. [Google Scholar] [CrossRef]
- Habier, D.; Fernando, R.L.; Dekkers, J. The impact of genetic relationship information on genome-assisted breeding values. Genetics 2007, 177, 2389–2397. [Google Scholar] [CrossRef] [PubMed]
- Gelman, A. Prior distributions for variance parameters in hierarchical models (comment on article by Browne and Draper). Bayesian Anal. 2006, 1, 515–534. [Google Scholar] [CrossRef]
- Maenhout, S.; De Baets, B.; Haesaert, G.; Van Bockstaele, E. Support vector machine regression for the prediction of maize hybrid performance. Theor. Appl. Genet. 2007, 115, 1003–1013. [Google Scholar] [CrossRef] [PubMed]
- Müller, A.C.; Guido, S. Introduction to Machine Learning with Python: A Guide for Data Scientists; O’Reilly Media, Inc.: Sebastopol, CA, USA, 2016. [Google Scholar]
- Christmann, A.; Xiang, D.; Zhou, D.X. Total stability of kernel methods. Neurocomputing 2018, 289, 101–118. [Google Scholar] [CrossRef]
- He, J.; Ding, L.; Jiang, L.; Ma, L. Kernel ridge regression classification. In Proceedings of the 2014 International Joint Conference on Neural Networks (IJCNN), Beijing, China, 6–11 July 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 2263–2267. [Google Scholar]
- Chen, B.W.; Abdullah, N.N.B.; Park, S.; Gu, Y. Efficient multiple incremental computation for Kernel Ridge Regression with Bayesian uncertainty modeling. Future Gener. Comput. Syst. 2018, 82, 679–688. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Classification and regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Zhang, P.; Liu, C.; Lao, D.; Nguyen, X.C.; Paramasivan, B.; Qian, X.; Inyinbor, A.A.; Hu, X.; You, Y.; Li, F. Unveiling the drives behind tetracycline adsorption capacity with biochar through machine learning. Sci. Rep. 2023, 13, 11512. [Google Scholar] [CrossRef]
- Xiang, T.; Li, T.; Li, J.; Li, X.; Wang, J. Using machine learning to realize genetic site screening and genomic prediction of productive traits in pigs. FASEB J. 2023, 37, e22961. [Google Scholar] [CrossRef]
- Elshawi, R.; Maher, M.; Sakr, S. Automated machine learning: State-of-the-art and open challenges. arXiv 2019, arXiv:1906.02287. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Radzi, S.F.M.; Karim, M.K.A.; Saripan, M.I.; Rahman, M.A.A.; Isa, I.N.C.; Ibahim, M.J. Hyperparameter tuning and pipeline optimization via grid search method and tree-based autoML in breast cancer prediction. J. Pers. Med. 2021, 11, 978. [Google Scholar] [CrossRef] [PubMed]
- Kiala, Z.; Odindi, J.; Mutanga, O. Determining the capability of the tree-based pipeline optimization tool (tpot) in mapping parthenium weed using multi-date sentinel-2 image data. Remote Sens. 2022, 14, 1687. [Google Scholar] [CrossRef]
- Mosca, E.; Szigeti, F.; Tragianni, S.; Gallagher, D.; Groh, G. SHAP-based explanation methods: A review for NLP interpretability. In Proceedings of the 29th International Conference on Computational Linguistics, Gyeongju, Republic of Korea, 12–17 October 2022; pp. 4593–4603. [Google Scholar]
- Liang, M.; An, B.; Li, K.; Du, L.; Deng, T.; Cao, S.; Du, Y.; Xu, L.; Gao, X.; Zhang, L.; et al. Improving genomic prediction with machine learning incorporating TPE for hyperparameters optimization. Biology 2022, 11, 1647. [Google Scholar] [CrossRef]
- Li, M.; Hall, T.; MacHugh, D.E.; Chen, L.; Garrick, D.; Wang, L.; Zhao, F. KPRR: A novel machine learning approach for effectively capturing nonadditive effects in genomic prediction. Briefings Bioinform. 2025, 26, bbae683. [Google Scholar] [CrossRef] [PubMed]
- An, B.; Liang, M.; Chang, T.; Duan, X.; Du, L.; Xu, L.; Zhang, L.; Gao, X.; Li, J.; Gao, H. KCRR: A nonlinear machine learning with a modified genomic similarity matrix improved the genomic prediction efficiency. Briefings Bioinform. 2021, 22, bbab132. [Google Scholar] [CrossRef]
- Zingaretti, L.M.; Gezan, S.A.; Ferrão, L.F.V.; Osorio, L.F.; Monfort, A.; Muñoz, P.R.; Whitaker, V.M.; Pérez-Enciso, M. Exploring deep learning for complex trait genomic prediction in polyploid outcrossing species. Front. Plant Sci. 2020, 11, 25. [Google Scholar] [CrossRef]
- Yin, L.; Zhang, H.; Zhou, X.; Yuan, X.; Zhao, S.; Li, X.; Liu, X. KAML: Improving genomic prediction accuracy of complex traits using machine learning determined parameters. Genome Biol. 2020, 21, 1–22. [Google Scholar] [CrossRef]
- Wang, X.; Shi, S.; Wang, G.; Luo, W.; Wei, X.; Qiu, A.; Luo, F.; Ding, X. Using machine learning to improve the accuracy of genomic prediction of reproduction traits in pigs. J. Anim. Sci. Biotechnol. 2022, 13, 60. [Google Scholar] [CrossRef]
- Chafai, N.; Hayah, I.; Houaga, I.; Badaoui, B. A review of machine learning models applied to genomic prediction in animal breeding. Front. Genet. 2023, 14, 1150596. [Google Scholar] [CrossRef]
- Liu, B.; Liu, H.; Tu, J.; Xiao, J.; Yang, J.; He, X.; Zhang, H. An investigation of machine learning methods applied to genomic prediction in yellow-feathered broilers. Poult. Sci. 2025, 104, 104489. [Google Scholar] [CrossRef] [PubMed]
- Meyer, P.G.; Cherstvy, A.G.; Seckler, H.; Hering, R.; Blaum, N.; Jeltsch, F.; Metzler, R. Directedeness, correlations, and daily cycles in springbok motion: From data via stochastic models to movement prediction. Phys. Rev. Res. 2023, 5, 043129. [Google Scholar] [CrossRef]
- Long, N.; Gianola, D.; Rosa, G.J.; Weigel, K.A. Application of support vector regression to genome-assisted prediction of quantitative traits. Theor. Appl. Genet. 2011, 123, 1065–1074. [Google Scholar] [CrossRef]
- Millet, E.J.; Kruijer, W.; Coupel-Ledru, A.; Alvarez Prado, S.; Cabrera-Bosquet, L.; Lacube, S.; Charcosset, A.; Welcker, C.; van Eeuwijk, F.; Tardieu, F. Genomic prediction of maize yield across European environmental conditions. Nat. Genet. 2019, 51, 952–956. [Google Scholar] [CrossRef] [PubMed]


| Dataset | Trait | N | SNPs | Mean | SD | |
|---|---|---|---|---|---|---|
| Simulation | T1 | 3000 | 10,000 | 0.36 | 0.00 | 176.52 |
| T2 | 3000 | 10,000 | 0.35 | 0.00 | 9.51 | |
| T3 | 3000 | 10,000 | 0.52 | 0.00 | 0.02 | |
| German Holstein | MY | 5024 | 42,551 | 0.95 | 370.79 | 641.60 |
| MFP | 5024 | 42,551 | 0.94 | −0.06 | 0.28 | |
| SCS | 5024 | 42,551 | 0.88 | 102.32 | 11.73 | |
| Chicken | EWAFE | 1052 | 294,705 | 0.10 | 0.00 | 3.27 |
| EW28 | 1063 | 294,705 | 0.50 | 57.19 | 3.47 | |
| EW36 | 1063 | 294,705 | 0.50 | 59.15 | 3.28 | |
| EW56 | 1027 | 294,705 | 0.51 | 65.83 | 4.25 | |
| EW66 | 960 | 294,705 | 0.51 | 80.85 | 4.34 | |
| EW72 | 847 | 294,705 | 0.54 | 60.97 | 3.53 | |
| EW80 | 852 | 294,705 | 0.29 | 62.33 | 5.07 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rao, Y.; Zhang, L.; Gao, L.; Wang, S.; Yang, L. ExAutoGP: Enhancing Genomic Prediction Stability and Interpretability with Automated Machine Learning and SHAP. Animals 2025, 15, 1172. https://doi.org/10.3390/ani15081172
Rao Y, Zhang L, Gao L, Wang S, Yang L. ExAutoGP: Enhancing Genomic Prediction Stability and Interpretability with Automated Machine Learning and SHAP. Animals. 2025; 15(8):1172. https://doi.org/10.3390/ani15081172
Chicago/Turabian StyleRao, Yao, Lilian Zhang, Lutao Gao, Shuran Wang, and Linnan Yang. 2025. "ExAutoGP: Enhancing Genomic Prediction Stability and Interpretability with Automated Machine Learning and SHAP" Animals 15, no. 8: 1172. https://doi.org/10.3390/ani15081172
APA StyleRao, Y., Zhang, L., Gao, L., Wang, S., & Yang, L. (2025). ExAutoGP: Enhancing Genomic Prediction Stability and Interpretability with Automated Machine Learning and SHAP. Animals, 15(8), 1172. https://doi.org/10.3390/ani15081172






