Weighted GBLUP in Simulated Beef Cattle Populations: Impact of Reference Population, Marker Density, and Heritability
Simple Summary
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Simulation
2.2. Model and Analysis
2.2.1. Pedigree-Based Best Linear Unbiased Prediction (PBLUP)
2.2.2. Genomic-Based Best Linear Unbiased Prediction (GBLUP)
2.2.3. Weighted Genomic-Based Best Linear Unbiased Prediction (wGBLUP)
2.3. Accuracy of Genomic Prediction
3. Results
3.1. Genomic Prediction Accuracy Across All Scenarios Based on Pedigree Information
3.2. Genomic Prediction Accuracy Across All Scenarios Based on Genomic Information
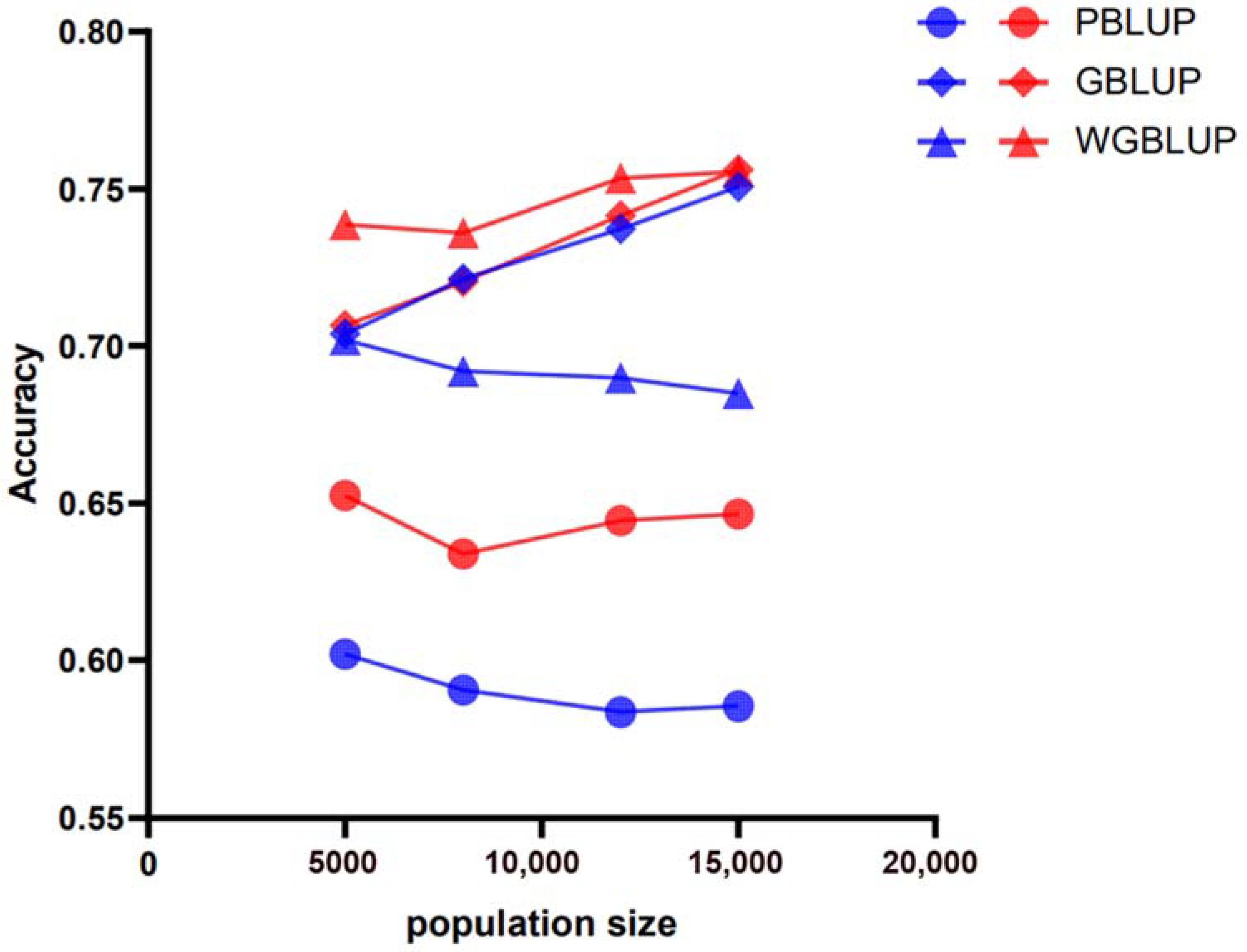
3.3. Genomic Prediction Accuracy Across All Scenarios Based on SNP Weighting
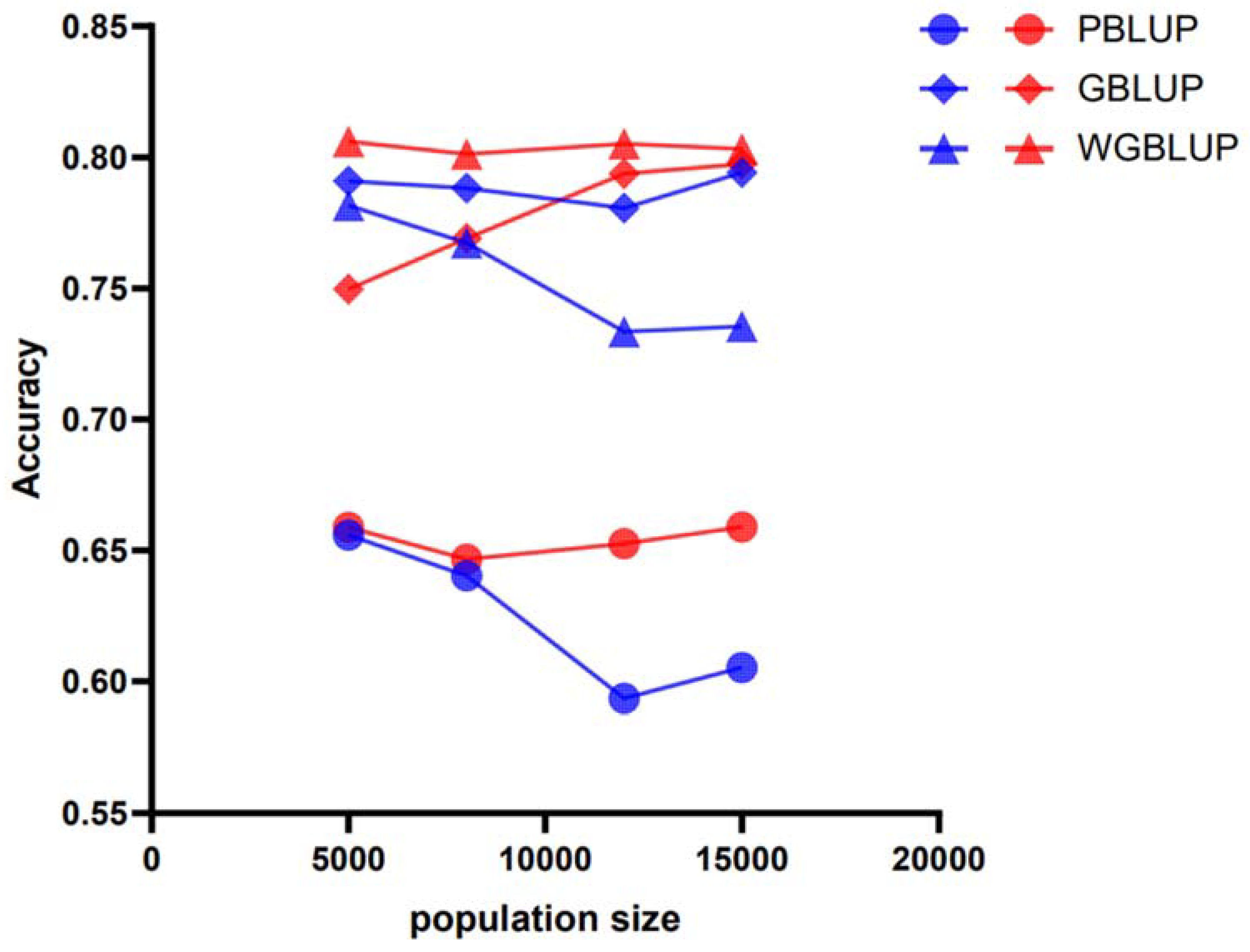
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| GS | Genomic selection |
| TBV | True breeding values |
| EBV | Estimation of breeding values |
| BLUP | Best linear unbiased prediction |
| GEBV | Genomic estimated breeding value |
| SNP | Single-nucleotide polymorphisms |
| MAF | Minor allele frequency |
| LD | Linkage disequilibrium |
| QTL | Quantitative trait loci |
| PBLUP | Traditional pedigree-based best linear unbiased prediction |
| GBLUP | Genomic best linear unbiased prediction |
| wGBLUP | Weighted best linear unbiased prediction |
| GRM | Genomic relationship matrix |
References
- Mehrban, H.; Lee, D.H.; Naserkheil, M.; Moradi, M.H.; Ibáñez-Escriche, N. Comparison of conventional BLUP and single-step genomic BLUP evaluations for yearling weight and carcass traits in Hanwoo beef cattle using single trait and multi-trait models. PLoS ONE 2019, 14, e0223352. [Google Scholar] [CrossRef] [PubMed]
- Henderson, C.R. Theoretical Basis and Computational Methods for a Number of Different Animal Models. J. Dairy Sci. 1988, 71, 1–16. [Google Scholar] [CrossRef]
- Hayes, B.J.; Visscher, P.M.; Goddard, M.E. Increased accuracy of artificial selection by using the realized relationship matrix. Genet. Res. 2009, 91, 47–60. [Google Scholar] [CrossRef] [PubMed]
- Goddard, M.E.; Hayes, B.J.; Meuwissen, T.H. Using the genomic relationship matrix to predict the accuracy of genomic selection. J. Anim. Breed. Genet. 2011, 128, 409–421. [Google Scholar] [CrossRef]
- Sullivan, P.G. Mendelian Sampling variance tests with genomic preselection. In Proceedings of the 2018 Interbull Technical Workshop, Dubrovnik, Croatia, 25–26 August 2018. [Google Scholar]
- Henderson, C.R. Best Linear Unbiased Estimation and Prediction under a Selection Model. Biometrics 1975, 31, 423. [Google Scholar] [CrossRef]
- Meuwissen, T.H.; Hayes, B.J.; Goddard, M.E. Prediction of total genetic value using genome-wide dense marker maps. Genetics 2001, 157, 1819–1829. [Google Scholar] [CrossRef] [PubMed]
- Misztal, I.; Lourenco, D.; Legarra, A. Current status of genomic evaluation. J. Anim. Sci. 2020, 98, skaa101. [Google Scholar] [CrossRef]
- Nwogwugwu, C.P.; Kim, Y.; Chung, Y.J.; Jang, S.B.; Roh, S.H.; Kim, S.; Lee, J.H.; Choi, T.J.; Lee, S.H. Effect of errors in pedigree on the accuracy of estimated breeding value for carcass traits in Korean Hanwoo cattle. Asian-Australas. J. Anim. Sci. 2020, 33, 1057–1067. [Google Scholar] [CrossRef]
- Gao, H.; Christensen, O.F.; Madsen, P.; Nielsen, U.S.; Zhang, Y.; Lund, M.S.; Su, G. Comparison on genomic predictions using three GBLUP methods and two single-step blending methods in the Nordic Holstein population. Genet. Sel. Evol. 2012, 44, 8. [Google Scholar] [CrossRef]
- Mehrban, H.; Lee, D.H.; Moradi, M.H.; IlCho, C.; Naserkheil, M.; Ibáñez-Escriche, N. Predictive performance of genomic selection methods for carcass traits in Hanwoo beef cattle: Impacts of the genetic architecture. Genet. Sel. Evol. 2017, 49, 1. [Google Scholar] [CrossRef]
- Lourenco, D.A.; Misztal, I.; Tsuruta, S.; Aguilar, I.; Ezra, E.; Ron, M.; Shirak, A.; Weller, J.I. Methods for genomic evaluation of a relatively small genotyped dairy population and effect of genotyped cow information in multiparity analyses. J. Dairy Sci. 2014, 97, 1742–1752. [Google Scholar] [CrossRef]
- van den Berg, I.; Meuwissen, T.H.E.; MacLeod, I.M.; Goddard, M.E. Predicting the effect of reference population on the accuracy of within, across, and multibreed genomic prediction. J. Dairy Sci. 2019, 102, 3155–3174. [Google Scholar] [CrossRef]
- Ren, D.; Cai, X.; Lin, Q.; Ye, H.; Teng, J.; Li, J.; Ding, X.; Zhang, Z. Impact of linkage disequilibrium heterogeneity along the genome on genomic prediction and heritability estimation. Genet. Sel. Evol. 2022, 54, 47. [Google Scholar] [CrossRef] [PubMed]
- Grotzinger, A.D.; Rhemtulla, M.; de Vlaming, R.; Ritchie, S.J.; Mallard, T.T.; Hill, W.D.; Ip, H.F.; Marioni, R.E.; McIntosh, A.M.; Deary, I.J.; et al. Genomic structural equation modelling provides insights into the multivariate genetic architecture of complex traits. Nat. Hum. Behav. 2019, 3, 513–525. [Google Scholar] [CrossRef]
- Solberg, T.R.; Sonesson, A.K.; Woolliams, J.A.; Meuwissen, T.H. Genomic selection using different marker types and densities. J. Anim. Sci. 2008, 86, 2447–2454. [Google Scholar] [CrossRef] [PubMed]
- de Las Heras-Saldana, S.; Lopez, B.I.; Moghaddar, N.; Park, W.; Park, J.E.; Chung, K.Y.; Lim, D.; Lee, S.H.; Shin, D.; van der Werf, J.H.J. Use of gene expression and whole-genome sequence information to improve the accuracy of genomic prediction for carcass traits in Hanwoo cattle. Genet. Sel. Evol. 2020, 52, 54. [Google Scholar] [CrossRef]
- Zhao, W.; Zhang, Z.; Ma, P.; Wang, Z.; Wang, Q.; Zhang, Z.; Pan, Y. The effect of high-density genotypic data and different methods on joint genomic prediction: A case study in large white pigs. Anim. Genet. 2023, 54, 45–54. [Google Scholar] [CrossRef] [PubMed]
- Romé, H.; Chu, T.T.; Marois, D.; Huang, C.H.; Madsen, P.; Jensen, J. Accounting for genetic architecture for body weight improves accuracy of predicting breeding values in a commercial line of broilers. J. Anim. Breed. Genet. 2021, 138, 528–540. [Google Scholar] [CrossRef]
- Song, H.; Hu, H. Strategies to improve the accuracy and reduce costs of genomic prediction in aquaculture species. Evol. Appl. 2021, 15, 578–590. [Google Scholar] [CrossRef]
- Lund, M.S.; Su, G.; Janss, L. Genomic evaluation of cattle in a multi-breed context. Livest. Sci. 2014, 166, 101–110. [Google Scholar] [CrossRef]
- Cole, J.B.; Silva, M.V.G.B.D. Genomic selection in multi-breed dairy cattle populations. Rev. Bras. Zootec. 2016, 45, 195–202. [Google Scholar] [CrossRef]
- Barani, S.; Miraie Ashtiani, S.R.; Nejati Javaremi, A.; Khansefid, M.; Esfandyari, H. Optimizing purebred selection to improve crossbred performance. Front. Genet. 2024, 15, 1384973. [Google Scholar] [CrossRef]
- Sargolzaei, M.; Schenkel, F.S. QMSim: A large-scale genome simulator for livestock. Bioinformatics 2009, 25, 680–681. [Google Scholar] [CrossRef] [PubMed]
- Henderson, C.R. Inverse of a Matrix of Relationships Due to Sires and Maternal Grandsires. J. Dairy Sci. 1975, 58, 1917–1921. [Google Scholar] [CrossRef]
- Purcell, S.; Neale, B.; Todd-Brown, K.; Thomas, L.; Ferreira, M.A.; Bender, D.; Maller, J.; Sklar, P.; de Bakker, P.I.; Daly, M.J.; et al. PLINK: A tool set for whole-genome association and population-based linkage analyses. Am. J. Hum. Genet. 2007, 81, 559–575. [Google Scholar] [CrossRef]
- Lee, H.S.; Kim, Y.; Lee, D.H.; Seo, D.; Lee, D.J.; Do, C.H.; Dinh, P.T.N.; Ekanayake, W.; Lee, K.H.; Yoon, D.; et al. Comparison of accuracy of breeding value for cow from three methods in Hanwoo (Korean cattle) population. J. Anim. Sci. Technol. 2023, 65, 720–734. [Google Scholar] [CrossRef]
- Yin, L.; Zhang, H.; Tang, Z.; Yin, D.; Fu, Y.; Yuan, X.; Li, X.; Liu, X.; Zhao, S. HIBLUP: An integration of statistical models on the BLUP framework for efficient genetic evaluation using big genomic data. Nucleic Acids Res. 2023, 51, 3501–3512. [Google Scholar] [CrossRef]
- Clark, S.A.; van der Werf, J. Genomic best linear unbiased prediction (gBLUP) for the estimation of genomic breeding values. Methods Mol. Biol. 2013, 1019, 321–330. [Google Scholar] [CrossRef]
- Kim, E.H.; Kang, H.C.; Sun, D.W.; Myung, C.H.; Kim, J.Y.; Lee, D.H.; Lee, S.H.; Lim, H.T. Estimation of breeding value and accuracy using pedigree and genotype of Hanwoo cows (Korean cattle). J. Anim. Breed. Genet. 2022, 139, 281–291. [Google Scholar] [CrossRef]
- Ma, H.; Li, H.; Ge, F.; Zhao, H.; Zhu, B.; Zhang, L.; Gao, H.; Xu, L.; Li, J.; Wang, Z. Improving Genomic Predictions in Multi-Breed Cattle Populations: A Comparative Analysis of BayesR and GBLUP Models. Genes 2024, 15, 253. [Google Scholar] [CrossRef]
- Cheng, J.; Maltecca, C.; VanRaden, P.M.; O’Connell, J.R.; Ma, L.; Jiang, J. SLEMM: Million-scale genomic predictions with window-based SNP weighting. Bioinformatics 2023, 39, btad127. [Google Scholar] [CrossRef]
- Porto-Neto, L.R.; Kijas, J.W.; Reverter, A. The extent of linkage disequilibrium in beef cattle breeds using high-density SNP genotypes. Genet. Sel. Evol. 2014, 46, 22. [Google Scholar] [CrossRef]
- Border, R.; Becker, S. Stochastic Lanczos estimation of genomic variance components for linear mixed-effects models. BMC Bioinformatics 2019, 20, 411. [Google Scholar] [CrossRef]
- Zhang, X.; Lourenco, D.; Aguilar, I.; Legarra, A.; Misztal, I. Weighting Strategies for Single-Step Genomic BLUP: An Iterative Approach for Accurate Calculation of GEBV and GWAS. Front. Genet. 2016, 7, 151. [Google Scholar] [CrossRef]
- Brito, L.F.; Clarke, S.M.; McEwan, J.C.; Miller, S.P.; Pickering, N.K.; Bain, W.E.; Dodds, K.G.; Sargolzaei, M.; Schenkel, F.S. Prediction of genomic breeding values for growth, carcass and meat quality traits in a multi-breed sheep population using a HD SNP chip. BMC Genet. 2017, 18, 7. [Google Scholar] [CrossRef] [PubMed]
- de Rezende Neves, H.H.; Carvalheiro, R.; de Queiroz, S.A. Trait-specific long-term consequences of genomic selection in beef cattle. Genetica 2018, 146, 85–99. [Google Scholar] [CrossRef] [PubMed]
- Erbe, M.; Gredler, B.; Seefried, F.R.; Bapst, B.; Simianer, H. A function accounting for training set size and marker density to model the average accuracy of genomic prediction. PLoS ONE 2013, 8, e81046. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Seefried, F.R.; Reinhardt, F.; Rensing, S.; Thaller, G.; Reents, R. Impacts of both reference population size and inclusion of a residual polygenic effect on the accuracy of genomic prediction. Genet. Sel. Evol. 2011, 43, 19. [Google Scholar] [CrossRef]
- Moser, G.; Khatkar, M.S.; Hayes, B.J.; Raadsma, H.W. Accuracy of direct genomic values in Holstein bulls and cows using subsets of SNP markers. Genet. Sel. Evol. 2010, 42, 37. [Google Scholar] [CrossRef]
- Carillier, C. Evaluation of a Reference Population in Dairy Goats for Genomic Selection. Master’s Thesis, AgroParisTech, Paris France, 2012. [Google Scholar]
- Takeda, M.; Inoue, K.; Oyama, H.; Uchiyama, K.; Yoshinari, K.; Sasago, N.; Kojima, T.; Kashima, M.; Suzuki, H.; Kamata, T.; et al. Exploring the size of reference population for expected accuracy of genomic prediction using simulated and real data in Japanese Black cattle. BMC Genom. 2021, 22, 799. [Google Scholar] [CrossRef]
- Wang, H.; Misztal, I.; Aguilar, I.; Legarra, A.; Muir, W.M. Genome-wide association mapping including phenotypes from relatives without genotypes. Genet. Res. 2012, 94, 73–83. [Google Scholar] [CrossRef]
- Uemoto, Y.; Sasaki, S.; Kojima, T.; Sugimoto, Y.; Watanabe, T. Impact of QTL minor allele frequency on genomic evaluation using real genotype data and simulated phenotypes in Japanese Black cattle. BMC Genet. 2015, 16, 134. [Google Scholar] [CrossRef]
- Kolbehdari, D.; Schaeffer, L.R.; Robinson, J.A. Estimation of genome-wide haplotype effects in half-sib designs. J. Anim. Breed. Genet. 2007, 124, 356–361. [Google Scholar] [CrossRef] [PubMed]
- Zhang, M.; Luo, H.; Xu, L.; Shi, Y.; Zhou, J.; Wang, D.; Zhang, X.; Huang, X.; Wang, Y. Genomic Selection for Milk Production Traits in Xinjiang Brown Cattle. Animals 2022, 12, 136. [Google Scholar] [CrossRef]
- Luan, T.; Woolliams, J.A.; Lien, S.; Kent, M.; Svendsen, M.; Meuwissen, T.H. The accuracy of Genomic Selection in Norwegian red cattle assessed by cross-validation. Genetics 2009, 183, 1119–1126. [Google Scholar] [CrossRef] [PubMed]
- Gualdrón Duarte, J.L.; Gori, A.S.; Hubin, X.; Lourenco, D.; Charlier, C.; Misztal, I.; Druet, T. Performances of Adaptive MultiBLUP, Bayesian regressions, and weighted-GBLUP approaches for genomic predictions in Belgian Blue beef cattle. BMC Genom. 2020, 21, 545. [Google Scholar] [CrossRef] [PubMed]
- Zhu, S.; Guo, T.; Yuan, C.; Liu, J.; Li, J.; Han, M.; Zhao, H.; Wu, Y.; Sun, W.; Wang, X.; et al. Evaluation of Bayesian alphabet and GBLUP based on different marker density for genomic prediction in Alpine Merino sheep. G3 2021, 11, jkab206. [Google Scholar] [CrossRef]
- Zhu, B. Effects of marker density and minor allele frequency on genomic prediction for growth traits in Chinese Simmental beef cattle. J. Integr. Agric. 2017, 16, 911–920. [Google Scholar] [CrossRef]
- Brito, F.V.; Neto, J.B.; Sargolzaei, M.; Cobuci, J.A.; Schenkel, F.S. Accuracy of genomic selection in simulated populations mimicking the extent of linkage disequilibrium in beef cattle. BMC Genet. 2011, 12, 80. [Google Scholar] [CrossRef]
- Rabier, C.E.; Barre, P.; Asp, T.; Charmet, G.; Mangin, B. On the Accuracy of Genomic Selection. PLoS ONE 2016, 11, e0156086. [Google Scholar] [CrossRef]
- Su, G.; Brøndum, R.F.; Ma, P.; Guldbrandtsen, B.; Aamand, G.P.; Lund, M.S. Comparison of genomic predictions using medium-density (~54,000) and high-density (~777,000) single nucleotide polymorphism marker panels in Nordic Holstein and Red Dairy Cattle populations. J. Dairy Sci. 2012, 95, 4657–4665. [Google Scholar] [CrossRef]
- Toosi, A.; Fernando, R.L.; Dekkers, J.C. Genomic selection in admixed and crossbred populations. J. Anim. Sci. 2010, 88, 32–46. [Google Scholar] [CrossRef] [PubMed]
- Ogawa, S.; Matsuda, H.; Taniguchi, Y.; Watanabe, T.; Nishimura, S.; Sugimoto, Y.; Iwaisaki, H. Effects of single nucleotide polymorphism marker density on degree of genetic variance explained and genomic evaluation for carcass traits in Japanese Black beef cattle. BMC Genet. 2014, 15, 15. [Google Scholar] [CrossRef] [PubMed]
- Calus, M.P.; Meuwissen, T.H.; de Roos, A.P.; Veerkamp, R.F. Accuracy of genomic selection using different methods to define haplotypes. Genetics 2008, 178, 553–561. [Google Scholar] [CrossRef] [PubMed]
- Muir, W.M. Comparison of genomic and traditional BLUP-estimated breeding value accuracy and selection response under alternative trait and genomic parameters. J. Anim. Breed. Genet. 2007, 124, 342–355. [Google Scholar] [CrossRef]
- Misztal, I.; Aggrey, S.E.; Muir, W.M. Experiences with a single-step genome evaluation. Poult. Sci. 2013, 92, 2530–2534. [Google Scholar] [CrossRef]
- Silva, R.M.; Fragomeni, B.O.; Lourenco, D.A.; Magalhães, A.F.; Irano, N.; Carvalheiro, R.; Canesin, R.C.; Mercadante, M.E.; Boligon, A.A.; Baldi, F.S.; et al. Accuracies of genomic prediction of feed efficiency traits using different prediction and validation methods in an experimental Nelore cattle population. J. Anim. Sci. 2016, 94, 3613–3623. [Google Scholar] [CrossRef]
- Naserkheil, M.; Mehrban, H.; Lee, D.; Park, M.N. Evaluation of Genome-Enabled Prediction for Carcass Primal Cut Yields Using Single-Step Genomic Best Linear Unbiased Prediction in Hanwoo Cattle. Genes 2021, 12, 1886. [Google Scholar] [CrossRef]
- Lourenco, D.A.; Tsuruta, S.; Fragomeni, B.O.; Masuda, Y.; Aguilar, I.; Legarra, A.; Bertrand, J.K.; Amen, T.S.; Wang, L.; Moser, D.W.; et al. Genetic evaluation using single-step genomic best linear unbiased predictor in American Angus. J. Anim. Sci. 2015, 93, 2653–2662. [Google Scholar] [CrossRef]
- Putz, A.M.; Tiezzi, F.; Maltecca, C.; Gray, K.A.; Knauer, M.T. A comparison of accuracy validation methods for genomic and pedigree-based predictions of swine litter size traits using Large White and simulated data. J. Anim. Breed. Genet. 2018, 135, 5–13. [Google Scholar] [CrossRef]
- Karimi, K.; Sargolzaei, M.; Plastow, G.S.; Wang, Z.; Miar, Y. Opportunities for genomic selection in American mink: A simulation study. PLoS ONE 2019, 14, e0213873. [Google Scholar] [CrossRef] [PubMed]
- Nwogwugwu, C.P.; Kim, Y.; Choi, H.; Lee, J.H.; Lee, S.H. Assessment of genomic prediction accuracy using different selection and evaluation approaches in a simulated Korean beef cattle population. Asian-Australas. J. Anim. Sci. 2020, 33, 1912–1921. [Google Scholar] [CrossRef] [PubMed]
- Haque, M.A.; Iqbal, A.; Alam, M.Z.; Lee, Y.M.; Ha, J.J.; Kim, J.J. Estimation of genetic correlations and genomic prediction accuracy for reproductive and carcass traits in Hanwoo cows. J. Anim. Sci. Technol. 2024, 66, 682–701. [Google Scholar] [CrossRef]
- Karaman, E.; Lund, M.S.; Anche, M.T.; Janss, L.; Su, G. Genomic Prediction Using Multi-trait Weighted GBLUP Accounting for Heterogeneous Variances and Covariances Across the Genome. G3 2018, 8, 3549–3558. [Google Scholar] [CrossRef] [PubMed]
- Lopez, B.I.; Lee, S.H.; Park, J.E.; Shin, D.H.; Oh, J.D.; de Las Heras-Saldana, S.; van der Werf, J.; Chai, H.H.; Park, W.; Lim, D. Weighted Genomic Best Linear Unbiased Prediction for Carcass Traits in Hanwoo Cattle. Genes 2019, 10, 1019, Erratum in Genes 2020, 11, E1013. [Google Scholar] [CrossRef]
- Nishio, M.; Arakawa, A.; Inoue, K.; Ichinoseki, K.; Kobayashi, E.; Okamura, T.; Fukuzawa, Y.; Ogawa, S.; Taniguchi, M.; Oe, M.; et al. Evaluating the performance of genomic prediction accounting for effects of single nucleotide polymorphism markers in reproductive traits of Japanese Black cattle. Anim. Sci. J. 2023, 94, e13850. [Google Scholar] [CrossRef]
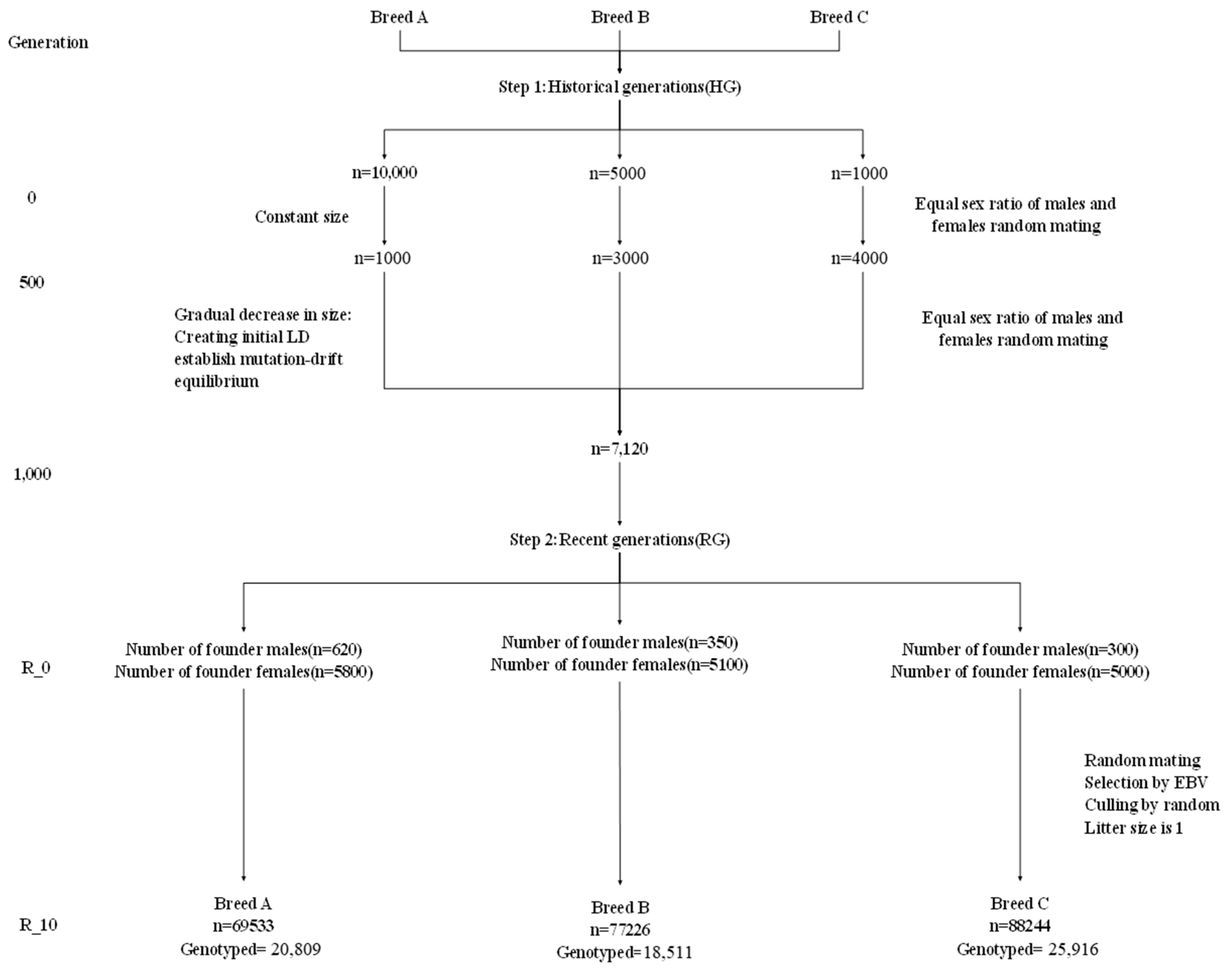

| Population Structure | A | B | C |
|---|---|---|---|
| Step 1: Historical generations (HG) | |||
| Number of generations phase 1 (size) | 0 (10,000) | 0 (5000) | 0 (1000) |
| Number of generations phase 2 (size) | 500 (1000) | 500 (3000) | 500 (4000) |
| Number of generations phase 3 (size) | 1000 (7120) | ||
| Step 2: Expanded generations (EG) | |||
| Number of founder males from HG | 620 | 350 | 300 |
| Number of founder females from HG | 5800 | 5100 | 5000 |
| Number of generations | 10 | ||
| Number of offspring per dam | 1 | ||
| Selection and mating | ebv/h | ||
| Sire replacement and growth rate | 0.5065 0.072 | 0.1851 0.1038 | 0.063 0.123 |
| Dam replacement and growth rate | 0.30 0.098 | 0.3015 0.1629 | 0.105 0.355 |
| Mating system | Random | ||
| Culling design | Random | ||
| Genome | |||
| Number of chromosomes | 29 (no X Chr) | ||
| Genome length | 2486cM | ||
| Number of markers | 58,990 (50 k)/777,962 (770 k) | ||
| Marker/QTL positions | Random | ||
| Number of marker/QTL alleles | 2/2 3 4 | ||
| Marker of allele frequencies | Equal | ||
| QTL allele effects | Equal | ||
| Mutation rate | 2.5 × 105 | ||
| Population Size | h2 | 50 k | 770 k | ||||
|---|---|---|---|---|---|---|---|
| PBLUP | GBLUP | wGBLUP | PBLUP | GBLUP | wGBLUP | ||
| 5000 | 0.3 | 0.5609333 | 0.6085367 | 0.6289896 | 0.5793174 | 0.6243117 | 0.6543064 |
| 0.5 | 0.6018924 | 0.703766 | 0.7018991 | 0.6524662 | 0.7065225 | 0.7386434 | |
| 0.7 | 0.6658209 | 0.7908608 | 0.781666 | 0.6588115 | 0.7497605 | 0.8060416 | |
| 8000 | 0.3 | 0.5639306 | 0.6323918 | 0.6272176 | 0.5843689 | 0.6368854 | 0.6608198 |
| 0.5 | 0.590504 | 0.7213553 | 0.6919124 | 0.6338298 | 0.7204071 | 0.7359905 | |
| 0.7 | 0.6403381 | 0.7882723 | 0.7673341 | 0.646572 | 0.7690514 | 0.8011734 | |
| 12,000 | 0.3 | 0.5797459 | 0.6691037 | 0.6550116 | 0.6209803 | 0.6783403 | 0.6995511 |
| 0.5 | 0.5835927 | 0.7372556 | 0.6898773 | 0.6443724 | 0.7414165 | 0.7533543 | |
| 0.7 | 0.5935911 | 0.7806763 | 0.733462 | 0.652524 | 0.7937998 | 0.8052261 | |
| 15,000 | 0.3 | 0.5963547 | 0.7011606 | 0.6717033 | 0.6431027 | 0.7049134 | 0.7192473 |
| 0.5 | 0.5854196 | 0.750636 | 0.684855 | 0.6465078 | 0.7560124 | 0.7554457 | |
| 0.7 | 0.6052722 | 0.7941701 | 0.7355052 | 0.6588932 | 0.7974239 | 0.803195 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, L.; Zhu, L.; Chang, C.; Ma, F.; Liu, Z.; Gu, M.; Na, R.; Zhang, W. Weighted GBLUP in Simulated Beef Cattle Populations: Impact of Reference Population, Marker Density, and Heritability. Animals 2025, 15, 1118. https://doi.org/10.3390/ani15081118
Zhou L, Zhu L, Chang C, Ma F, Liu Z, Gu M, Na R, Zhang W. Weighted GBLUP in Simulated Beef Cattle Populations: Impact of Reference Population, Marker Density, and Heritability. Animals. 2025; 15(8):1118. https://doi.org/10.3390/ani15081118
Chicago/Turabian StyleZhou, Le, Lin Zhu, Chencheng Chang, Fengying Ma, Zaixia Liu, Mingjuan Gu, Risu Na, and Wenguang Zhang. 2025. "Weighted GBLUP in Simulated Beef Cattle Populations: Impact of Reference Population, Marker Density, and Heritability" Animals 15, no. 8: 1118. https://doi.org/10.3390/ani15081118
APA StyleZhou, L., Zhu, L., Chang, C., Ma, F., Liu, Z., Gu, M., Na, R., & Zhang, W. (2025). Weighted GBLUP in Simulated Beef Cattle Populations: Impact of Reference Population, Marker Density, and Heritability. Animals, 15(8), 1118. https://doi.org/10.3390/ani15081118





