Optimization of Genomic Breeding Value Estimation Model for Abdominal Fat Traits Based on Machine Learning
Simple Summary
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.1.1. Phenotypic Data
2.1.2. Genotypic Data
2.2. Methods
2.2.1. Genome-Wide Association Analysis and ML Prediction Models
2.2.2. Feature Selection
2.2.3. Dynamic Adaptive Weighted Stacking Ensemble Learning Framework
2.3. Cross-Validation and Evaluation Metrics
3. Results
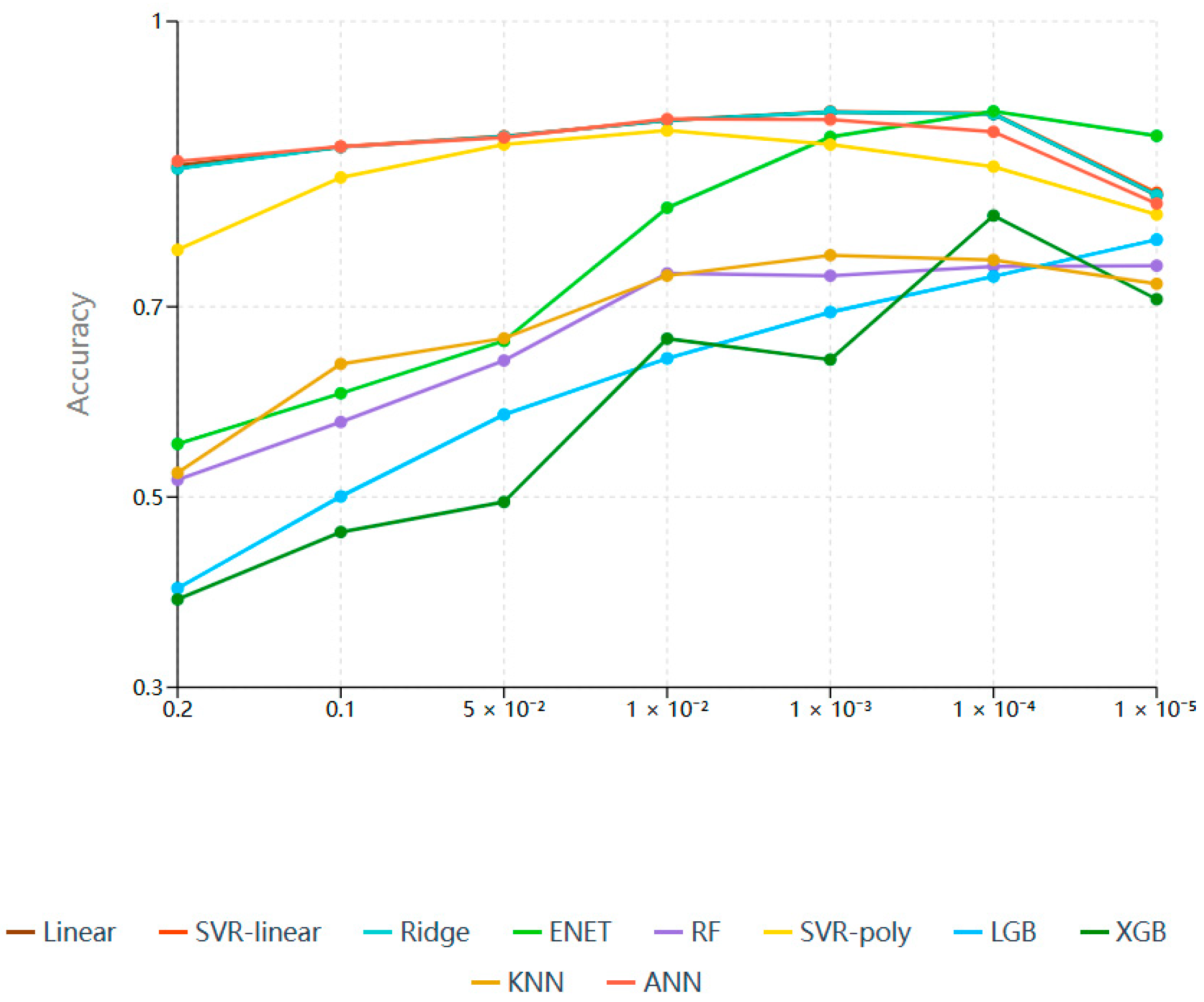
3.1. Initial SNP Screening Based on GWAS and LD Methods
3.1.1. Genome-Wide Association Analysis
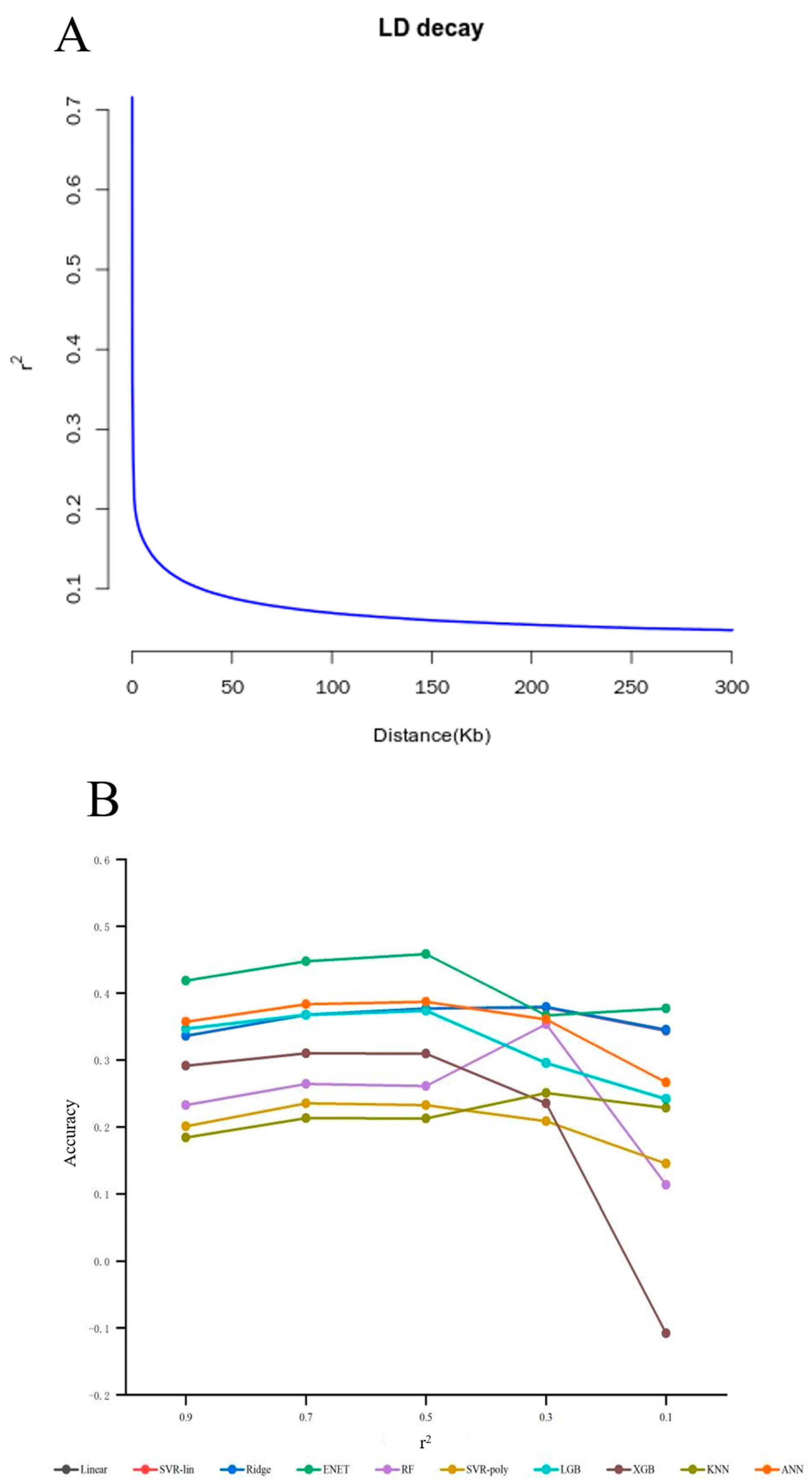
3.1.2. Linkage Disequilibrium
3.1.3. GWAS + LD
3.2. Fine SNP Selection Based on Multiple Machine Learning Feature Selection Algorithms
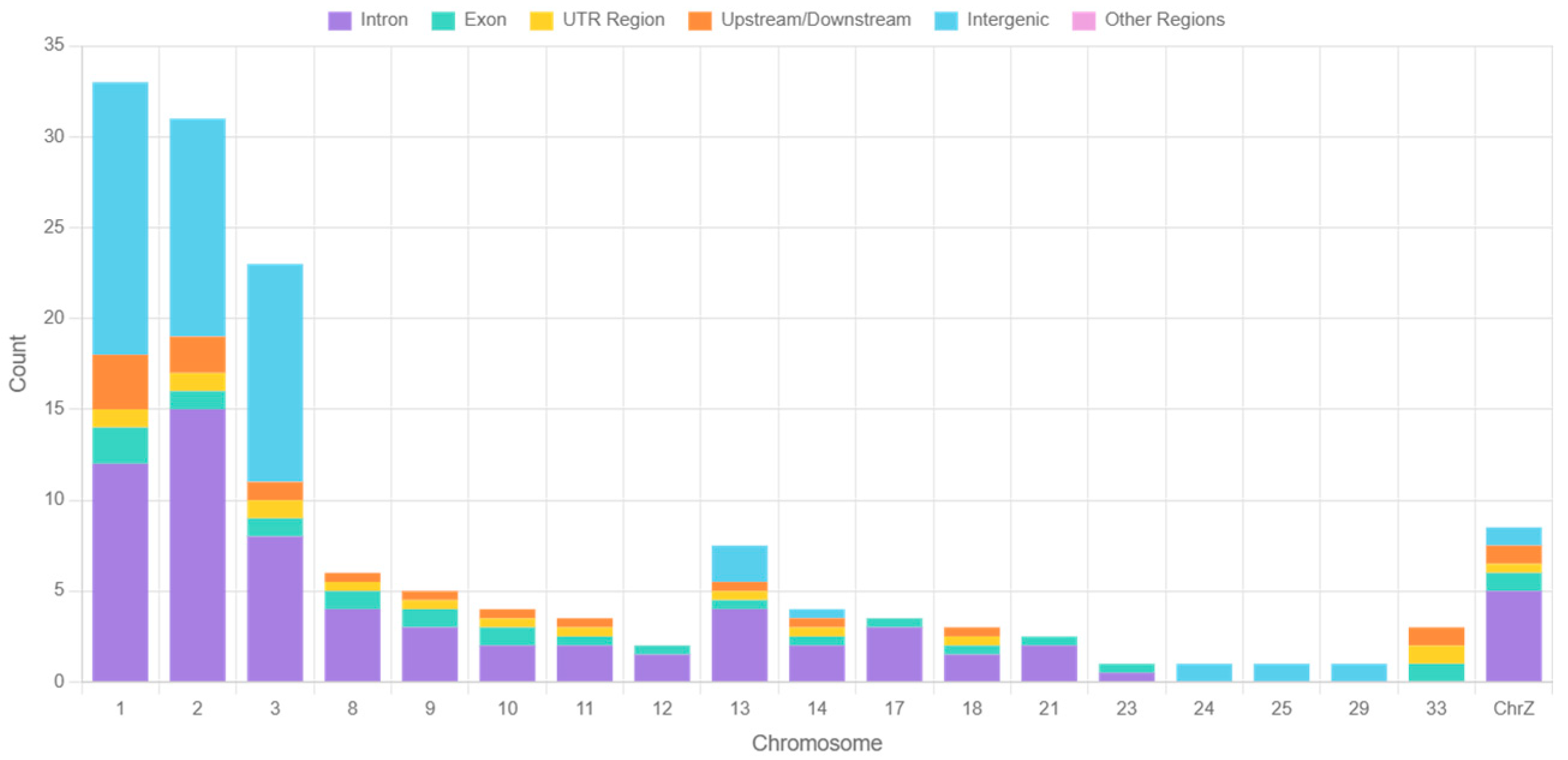
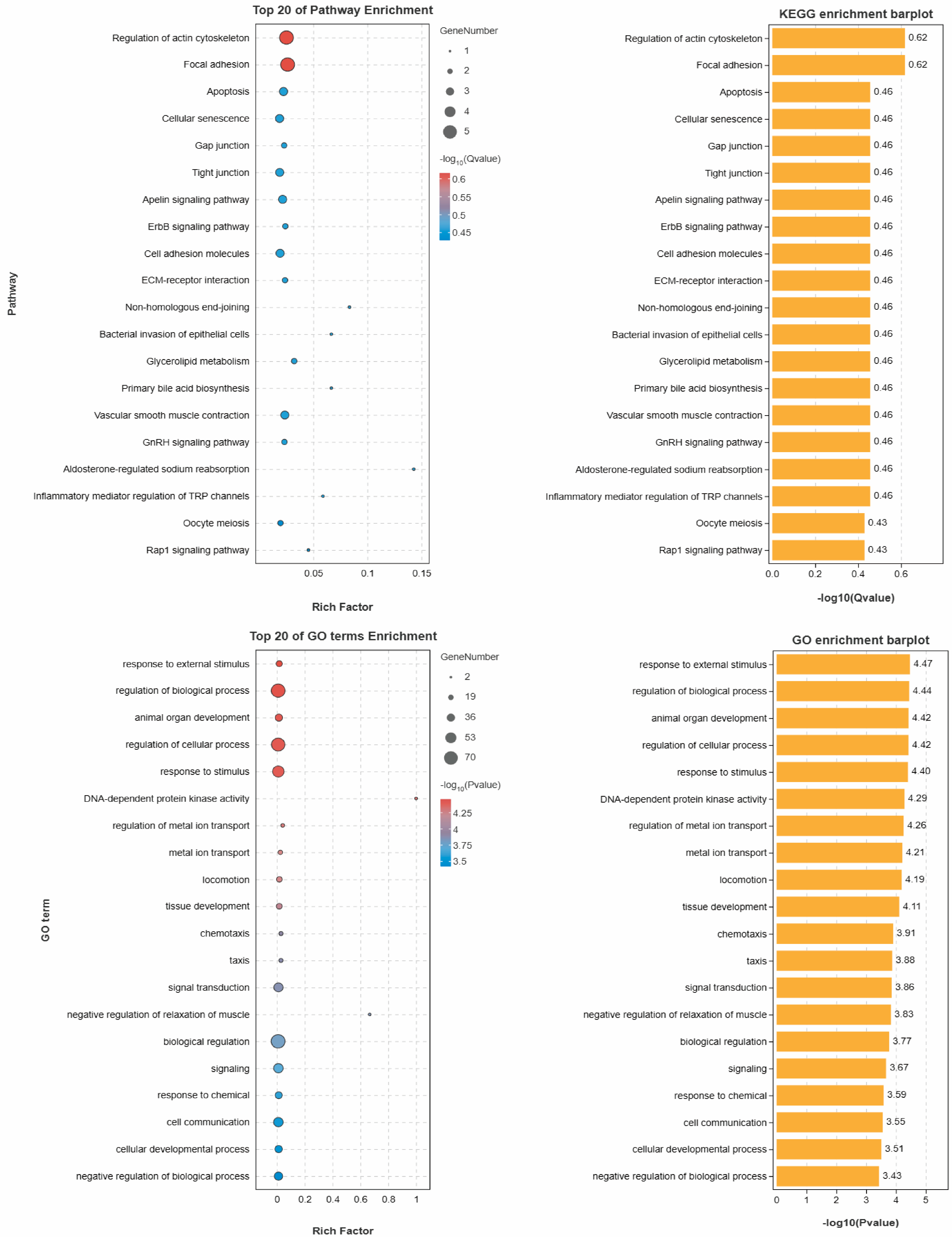
3.3. Gene Annotation Results
3.4. Comparison of Prediction Performance Between DAWSELF, Base Models, and Conventional Stacking Frameworks
3.5. Model Evaluation in Validation Populations
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Smith, K.; Watson, A.W.; Lonnie, M.; Peeters, W.M.; Oonincx, D.; Tsoutsoura, N.; Simon-Miquel, G.; Szepe, K.; Cochetel, N.; Pearson, A.G.; et al. Meeting the Global Protein Supply Requirements of a Growing and Ageing Population. Eur. J. Nutr. 2024, 63, 1425–1433. [Google Scholar] [CrossRef]
- Saxena, V.K.; Kolluri, G.; Saxena, V.K.; Kolluri, G. Selection Methods in Poultry Breeding: From Genetics to Genomics. In Application of Genetics and Genomics in Poultry Science; IntechOpen: Rijeka, Croatia, 2018; ISBN 978-1-78923-631-6. [Google Scholar]
- Meuwissen, T.H.; Hayes, B.J.; Goddard, M.E. Prediction of Total Genetic Value Using Genome-Wide Dense Marker Maps. Genetics 2001, 157, 1819–1829. [Google Scholar] [CrossRef]
- Daetwyler, H.D.; Pong-Wong, R.; Villanueva, B.; Woolliams, J.A. The Impact of Genetic Architecture on Genome-Wide Evaluation Methods. Genetics 2010, 185, 1021–1031. [Google Scholar] [CrossRef]
- Habier, D.; Fernando, R.L.; Dekkers, J.C.M. The Impact of Genetic Relationship Information on Genome-Assisted Breeding Values. Genetics 2007, 177, 2389–2397. [Google Scholar] [CrossRef]
- Endelman, J.B. Ridge Regression and Other Kernels for Genomic Selection with R Package rrBLUP. Plant Genome 2011, 4, 255–258. [Google Scholar] [CrossRef]
- Habier, D.; Fernando, R.L.; Kizilkaya, K.; Garrick, D.J. Extension of the Bayesian Alphabet for Genomic Selection. BMC Bioinf. 2011, 12, 186. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-Vector Networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Xiang, T.; Li, T.; Li, J.; Li, X.; Wang, J. Using Machine Learning to Realize Genetic Site Screening and Genomic Prediction of Productive Traits in Pigs. FASEB J. Off. Publ. Fed. Am. Soc. Exp. Biol. 2023, 37, e22961. [Google Scholar] [CrossRef]
- Mota, L.F.M.; Arikawa, L.M.; Santos, S.W.B.; Fernandes Júnior, G.A.; Alves, A.A.C.; Rosa, G.J.M.; Mercadante, M.E.Z.; Cyrillo, J.N.S.G.; Carvalheiro, R.; Albuquerque, L.G. Benchmarking Machine Learning and Parametric Methods for Genomic Prediction of Feed Efficiency-Related Traits in Nellore Cattle. Sci. Rep. 2024, 14, 6404. [Google Scholar] [CrossRef]
- Faridi, A.; Sakomura, N.K.; Golian, A.; Marcato, S.M. Predicting Body and Carcass Characteristics of 2 Broiler Chicken Strains Using Support Vector Regression and Neural Network Models. Poult. Sci. 2012, 91, 3286–3294. [Google Scholar] [CrossRef] [PubMed]
- Liang, M.; Chang, T.; An, B.; Duan, X.; Du, L.; Wang, X.; Miao, J.; Xu, L.; Gao, X.; Zhang, L.; et al. A Stacking Ensemble Learning Framework for Genomic Prediction. Front. Genet. 2021, 12, 600040. [Google Scholar] [CrossRef]
- Guo, L.; Sun, B.; Shang, Z.; Leng, L.; Wang, Y.; Wang, N.; Li, H. Comparison of Adipose Tissue Cellularity in Chicken Lines Divergently Selected for Fatness. Poult. Sci. 2011, 90, 2024–2034. [Google Scholar] [CrossRef]
- Gilmour, A.R. ASReml User Guide Release 4.1 Structural Specification; VSN International Ltd.: Hemel Hempstead, UK, 2015. [Google Scholar]
- Swami, A.; Jain, R. Scikit-Learn: Machine Learning in Python. J. Mach. Learn. Res. 2013, 12, 2825–2830. [Google Scholar] [CrossRef]
- Danecek, P.; Auton, A.; Abecasis, G.; Albers, C.A.; Banks, E.; DePristo, M.A.; Handsaker, R.E.; Lunter, G.; Marth, G.T.; Sherry, S.T.; et al. The Variant Call Format and VCFtools. Bioinformatics 2011, 27, 2156–2158. [Google Scholar] [CrossRef] [PubMed]
- Chang, C.C.; Chow, C.C.; Tellier, L.C.; Vattikuti, S.; Purcell, S.M.; Lee, J.J. Second-Generation PLINK: Rising to the Challenge of Larger and Richer Datasets. GigaScience 2015, 4, 7. [Google Scholar] [CrossRef]
- Browning, B.L.; Tian, X.; Zhou, Y.; Browning, S.R. Fast Two-Stage Phasing of Large-Scale Sequence Data. Am. J. Hum. Genet. 2021, 108, 1880–1890. [Google Scholar] [CrossRef]
- Muthukrishnan, R.; Rohini, R. LASSO: A Feature Selection Technique in Predictive Modeling for Machine Learning. In Proceedings of the 2016 IEEE International Conference on Advances in Computer Applications (ICACA), Coimbatore, India, 24 October 2016. [Google Scholar]
- Tibshirani, R. Regression Shrinkage and Selection via the Lasso. J. R. Stat. Soc. B 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Luts, J.; Ojeda, F.; Van de Plas, R.; De Moor, B.; Van Huffel, S.; Suykens, J.A.K. A Tutorial on Support Vector Machine-Based Methods for Classification Problems in Chemometrics. Anal. Chim. Acta 2010, 665, 129–145. [Google Scholar] [CrossRef]
- Zou, H.; Hastie, T. Regularization and Variable Selection via the Elastic Net. J. R. Stat. Soc. B 2005, 67, 301–320. [Google Scholar] [CrossRef]
- Geva, S.; Sitte, J. Adaptive Nearest Neighbor Pattern Classification. IEEE Trans. Neural Netw. 1991, 2, 318–322. [Google Scholar] [CrossRef] [PubMed]
- Schmidhuber, J. Deep Learning in Neural Networks: An Overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef] [PubMed]
- Biau, G.; Scornet, E. A Random Forest Guided Tour. Test 2016, 25, 197–227. [Google Scholar] [CrossRef]
- Schapire, R.E. The Boosting Approach to Machine Learning: An Overview. In Nonlinear Estimation and Classification; Denison, D.D., Hansen, M.H., Holmes, C.C., Mallick, B., Yu, B., Eds.; Springer: New York, NY, USA, 2003; pp. 149–171. ISBN 978-0-387-21579-2. [Google Scholar]
- Friedman, J.H. Greedy Function Approximation: A Gradient Boosting Machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13 August 2016; pp. 785–794. [Google Scholar]
- Weinberger, K.Q.; Blitzer, J.; Saul, L.K. Distance Metric Learning for Large Margin Nearest Neighbor Classification. In Proceedings of the 19th International Conference on Neural Information Processing Systems, Doha, Qatar, 12–15 November 2012; MIT Press: Cambridge, MA, USA, 2005; pp. 1473–1480. [Google Scholar]
- Isabelle, G.; André, E. An Introduction to Variable and Feature Selection. J. Mach. Learn. Res. 2003, 3, 1157–1182. [Google Scholar] [CrossRef]
- Lal, T.N.; Chapelle, O.; Weston, J.; Elisseeff, A. Embedded Methods. In Feature Extraction: Foundations and Applications; Guyon, I., Nikravesh, M., Gunn, S., Zadeh, L.A., Eds.; Springer: Berlin/Heidelberg, Germany, 2006; pp. 137–165. ISBN 978-3-540-35488-8. [Google Scholar]
- Kohavi, R.; John, G.H. Wrappers for Feature Subset Selection. Artif. Intell. 1997, 97, 273–324. [Google Scholar] [CrossRef]
- Hinton, G.E.; Salakhutdinov, R.R. Reducing the Dimensionality of Data with Neural Networks. Science 2006, 313, 504–507. [Google Scholar] [CrossRef]
- Zhou, X.; Stephens, M. Genome-Wide Efficient Mixed Model Analysis for Association Studies. Nat. Genet. 2012, 44, 821–824. [Google Scholar] [CrossRef]
- Zhang, C.; Dong, S.-S.; Xu, J.-Y.; He, W.-M.; Yang, T.-L. PopLDdecay: A Fast and Effective Tool for Linkage Disequilibrium Decay Analysis Based on Variant Call Format Files. Bioinformatics 2019, 35, 1786–1788. [Google Scholar] [CrossRef]
- Song, H.; Wang, W.; Dong, T.; Yan, X.; Geng, C.; Bai, S.; Hu, H. Prioritized SNP Selection from Whole-Genome Sequencing Improves Genomic Prediction Accuracy in Sturgeons Using Linear and Machine Learning Models. Int. J. Mol. Sci. 2025, 26, 7007. [Google Scholar] [CrossRef]
- Lopez-Cruz, M.; de Los Campos, G. Optimal Breeding-Value Prediction Using a Sparse Selection Index. Genetics 2021, 218, iyab030. [Google Scholar] [CrossRef]
- Stranger, B.E.; Stahl, E.A.; Raj, T. Progress and Promise of Genome-Wide Association Studies for Human Complex Trait Genetics. Genetics 2011, 187, 367–383. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Zhang, M.; Ye, J.; Xu, Q.; Feng, Y.; Xu, S.; Hu, D.; Wei, X.; Hu, P.; Yang, Y. Integrating Genome-Wide Association Study into Genomic Selection for the Prediction of Agronomic Traits in Rice (Oryza sativa L.). Mol. Breed. 2023, 43, 81. [Google Scholar] [CrossRef]
- Domingues, V. Replication–Transcription Conflict Promotes Gene Evolution. Nat. Rev. Genet. 2013, 14, 302–303. [Google Scholar] [CrossRef] [PubMed]
- Kang, H.M.; Zaitlen, N.A.; Wade, C.M.; Kirby, A.; Heckerman, D.; Daly, M.J.; Eskin, E. Efficient Control of Population Structure in Model Organism Association Mapping. Genetics 2008, 178, 1709–1723. [Google Scholar] [CrossRef]
- Vovk, V.; Shafer, G. Good Randomized Sequential Probability Forecasting Is Always Possible. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 2005, 67, 747–763. [Google Scholar] [CrossRef]
- Gomede, E. Recursive Feature Elimination: A Powerful Technique for Feature Selection in Machine Learning. Medium, 2 September 2023. Available online: https://medium.com/the-modern-scientist/recursive-feature-elimination-a-powerful-technique-for-feature-selection-in-machine-learning-89b3c2f3c26a (accessed on 3 July 2025).
- Varma, S.; Simon, R. Bias in Error Estimation When Using Cross-Validation for Model Selection. BMC Bioinf. 2006, 7, 91. [Google Scholar] [CrossRef]
- Chang, C.-C.; Lin, C.-J. LIBSVM: A Library for Support Vector Machines. ACM Trans. Intell. Syst. Technol. 2011, 2, 27. [Google Scholar] [CrossRef]
- Hoerl, A.E.; Kennard, R.W. Ridge Regression: Biased Estimation for Nonorthogonal Problems. Technometrics 1970, 12, 55–67. [Google Scholar] [CrossRef]
- Li, B.; Zhang, N.; Wang, Y.-G.; George, A.W.; Reverter, A.; Li, Y. Genomic Prediction of Breeding Values Using a Subset of SNPs Identified by Three Machine Learning Methods. Front. Genet. 2018, 9, 237. [Google Scholar] [CrossRef] [PubMed]
- Ahn, E.; Oh, S.; Botkin, J.; Bhatt, J.; Lee, D.; Magill, C. Machine Learning Reveals Signatures of Transposable Element Activity Driving Agronomic and Phenolic Traits in Mutagenized Sorghum. Discov. Plants 2025, 2, 265. [Google Scholar] [CrossRef]

| Population | Sample Size | Covariates | Heritability (h2) |
|---|---|---|---|
| G19 | 330 | Line, Weight | 0.74 |
| G23 | 439 | Line, Sex, Weight | 0.69 |
| G27 | 446 | Line, Weight | 0.72 |
| AA | 400 | Line, Sex, Weight | 0.55 |
| GWAS(p) | LD(r2) | SNP Count | Linear | SVR-Lin | Ridge | ENET | RF | SVR-Poly | LGB | XGB | KNN | ANN | Mean |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.2 | - | 1,885,605 | 0.8485 | 0.8457 | 0.8454 | 0.5558 | 0.5181 | 0.7598 | 0.4041 | 0.3924 | 0.5254 | 0.8530 | 0.6548 |
| 0.9 | 1,648,819 | 0.8496 | 0.8498 | 0.8496 | 0.5495 | 0.5187 | 0.7553 | 0.3934 | 0.4062 | 0.5284 | 0.8563 | 0.6557 | |
| 0.7 | 1,209,506 | 0.8556 | 0.8558 | 0.8557 | 0.5447 | 0.5163 | 0.7285 | 0.3800 | 0.4097 | 0.5293 | 0.8644 | 0.6540 | |
| 0.5 | 560,572 | 0.8600 | 0.8601 | 0.8601 | 0.5395 | 0.5271 | 0.7177 | 0.4089 | 0.4015 | 0.5091 | 0.8693 | 0.6553 | |
| 0.3 | 220,282 | 0.8545 | 0.8538 | 0.8543 | 0.5536 | 0.4806 | 0.6874 | 0.4152 | 0.4111 | 0.5030 | 0.8507 | 0.6464 | |
| 0.1 | 64,779 | 0.8507 | 0.8489 | 0.8492 | 0.5640 | 0.4346 | 0.6710 | 0.4440 | 0.3761 | 0.4985 | 0.8386 | 0.6376 | |
| 0.1 | - | 1,019,085 | 0.8680 | 0.8683 | 0.8680 | 0.6090 | 0.5788 | 0.8359 | 0.5006 | 0.4632 | 0.6399 | 0.8684 | 0.7100 |
| 0.9 | 891,723 | 0.8698 | 0.8699 | 0.8698 | 0.6098 | 0.5672 | 0.8333 | 0.4321 | 0.4726 | 0.6386 | 0.8625 | 0.7026 | |
| 0.7 | 651,664 | 0.8722 | 0.8724 | 0.8722 | 0.6101 | 0.5596 | 0.8286 | 0.3918 | 0.4619 | 0.6464 | 0.8793 | 0.6995 | |
| 0.5 | 314,163 | 0.8772 | 0.8779 | 0.8778 | 0.6108 | 0.5504 | 0.8206 | 0.3833 | 0.4524 | 0.6372 | 0.8847 | 0.6972 | |
| 0.3 | 134,124 | 0.8648 | 0.8650 | 0.8649 | 0.6421 | 0.5841 | 0.7976 | 0.4672 | 0.4013 | 0.5947 | 0.8740 | 0.6956 | |
| 0.1 | 42,253 | 0.8591 | 0.8590 | 0.8591 | 0.6945 | 0.5448 | 0.7737 | 0.5574 | 0.3495 | 0.5509 | 0.8565 | 0.6905 | |
| 0.05 | - | 57,0318 | 0.8788 | 0.8792 | 0.8788 | 0.6641 | 0.6435 | 0.8706 | 0.5867 | 0.4948 | 0.6668 | 0.8779 | 0.7441 |
| 0.9 | 499,542 | 0.8791 | 0.8795 | 0.8791 | 0.6774 | 0.6396 | 0.8689 | 0.5788 | 0.5671 | 0.6677 | 0.8767 | 0.7514 | |
| 0.7 | 362,390 | 0.8808 | 0.8810 | 0.8808 | 0.6728 | 0.6217 | 0.8638 | 0.5701 | 0.5384 | 0.7380 | 0.8736 | 0.7521 | |
| 0.5 | 181,130 | 0.8847 | 0.8848 | 0.8847 | 0.6834 | 0.5982 | 0.8641 | 0.4294 | 0.5776 | 0.6880 | 0.8852 | 0.7380 | |
| 0.3 | 85,012 | 0.8821 | 0.8820 | 0.8821 | 0.7184 | 0.6147 | 0.8544 | 0.4386 | 0.5028 | 0.7154 | 0.8781 | 0.7369 | |
| 0.1 | 31,104 | 0.8664 | 0.8667 | 0.8668 | 0.7669 | 0.5549 | 0.8395 | 0.4982 | 0.4245 | 0.7190 | 0.8666 | 0.7270 | |
| 0.01 | - | 162,799 | 0.8960 | 0.8960 | 0.8958 | 0.8040 | 0.7351 | 0.8852 | 0.6457 | 0.6664 | 0.7327 | 0.8973 | 0.8054 |
| 0.9 | 143,569 | 0.8966 | 0.8968 | 0.8968 | 0.8096 | 0.7302 | 0.8911 | 0.6368 | 0.6685 | 0.7364 | 0.8926 | 0.8055 | |
| 0.7 | 103,125 | 0.8983 | 0.8984 | 0.8983 | 0.8088 | 0.7146 | 0.8942 | 0.6176 | 0.6798 | 0.7641 | 0.8900 | 0.8064 | |
| 0.5 | 57,943 | 0.9006 | 0.9007 | 0.9007 | 0.8143 | 0.6994 | 0.8986 | 0.6006 | 0.6706 | 0.7823 | 0.8971 | 0.8065 | |
| 0.3 | 35,967 | 0.9034 | 0.9038 | 0.9038 | 0.8199 | 0.7035 | 0.8951 | 0.5849 | 0.6637 | 0.7838 | 0.8939 | 0.8056 | |
| 0.1 | 22,614 | 0.8924 | 0.8923 | 0.8924 | 0.8279 | 0.7704 | 0.8925 | 0.5473 | 0.6524 | 0.7855 | 0.8899 | 0.8043 | |
| 1 × 10−3 | - | 33,738 | 0.9048 | 0.9051 | 0.9048 | 0.8785 | 0.7326 | 0.8705 | 0.6943 | 0.6445 | 0.7542 | 0.8968 | 0.8186 |
| 0.9 | 30,336 | 0.9073 | 0.9074 | 0.9073 | 0.8813 | 0.7375 | 0.8738 | 0.6816 | 0.6497 | 0.7679 | 0.8961 | 0.8210 | |
| 0.7 | 21,777 | 0.9104 | 0.9105 | 0.9104 | 0.8847 | 0.7412 | 0.8866 | 0.6537 | 0.6515 | 0.8010 | 0.8957 | 0.8246 | |
| 0.5 | 14,594 | 0.9157 | 0.9158 | 0.9157 | 0.8880 | 0.7445 | 0.9046 | 0.6252 | 0.6564 | 0.8205 | 0.8955 | 0.8282 | |
| 0.3 | 11,871 | 0.9178 | 0.9180 | 0.9179 | 0.8884 | 0.7564 | 0.9065 | 0.5949 | 0.6748 | 0.8213 | 0.9029 | 0.8299 | |
| 0.1 | 10,400 | 0.9189 | 0.9191 | 0.9189 | 0.8879 | 0.7607 | 0.9075 | 0.5706 | 0.6845 | 0.8216 | 0.9096 | 0.8299 | |
| 1 × 10−4 | - | 8345 | 0.9027 | 0.9031 | 0.9027 | 0.9055 | 0.7425 | 0.8473 | 0.7319 | 0.7958 | 0.7492 | 0.8839 | 0.8365 |
| 0.9 | 7613 | 0.9060 | 0.9065 | 0.9060 | 0.9070 | 0.7636 | 0.8600 | 0.7344 | 0.7641 | 0.7716 | 0.8870 | 0.8406 | |
| 0.7 | 5505 | 0.9092 | 0.9096 | 0.9092 | 0.9081 | 0.7904 | 0.8871 | 0.7285 | 0.7524 | 0.8388 | 0.8878 | 0.8521 | |
| 0.5 | 4151 | 0.9161 | 0.9169 | 0.9161 | 0.9110 | 0.8003 | 0.9062 | 0.7207 | 0.7452 | 0.8623 | 0.8888 | 0.8584 | |
| 0.3 | 3731 | 0.9188 | 0.9194 | 0.9188 | 0.9139 | 0.8008 | 0.9100 | 0.7310 | 0.7749 | 0.8349 | 0.8965 | 0.8619 | |
| 0.1 | 3549 | 0.9209 | 0.9216 | 0.9209 | 0.9169 | 0.8024 | 0.9162 | 0.7315 | 0.8030 | 0.8322 | 0.9007 | 0.8666 | |
| 1 × 10−5 | - | 2252 | 0.8172 | 0.8198 | 0.8173 | 0.8796 | 0.7432 | 0.7969 | 0.7705 | 0.7079 | 0.7241 | 0.8085 | 0.7885 |
| 0.9 | 2066 | 0.8170 | 0.8191 | 0.8171 | 0.8845 | 0.7490 | 0.8025 | 0.7768 | 0.7146 | 0.7418 | 0.8015 | 0.7924 | |
| 0.7 | 1534 | 0.8243 | 0.8263 | 0.8244 | 0.8889 | 0.7624 | 0.8269 | 0.7857 | 0.7297 | 0.7618 | 0.7819 | 0.8012 | |
| 0.5 | 1268 | 0.8308 | 0.8332 | 0.8310 | 0.8882 | 0.7733 | 0.8574 | 0.7888 | 0.7350 | 0.8096 | 0.7664 | 0.8114 | |
| 0.3 | 1197 | 0.8206 | 0.8231 | 0.8208 | 0.8878 | 0.7722 | 0.8588 | 0.7926 | 0.7410 | 0.8110 | 0.8529 | 0.8181 | |
| 0.1 | 1168 | 0.8163 | 0.8195 | 0.8168 | 0.8875 | 0.7718 | 0.8653 | 0.8031 | 0.7430 | 0.7769 | 0.9195 | 0.8220 |
| Feature Selection Method | SNP Count | Linear | SVR-Lin | Ridge | ENET | RF | SVR-Poly | LGB | XGB | KNN | ANN | Mean |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| p < 1 × 10−4 + r2 < 0.1 | 3549 | 0.9209 | 0.9216 | 0.9209 | 0.9169 | 0.8024 | 0.9162 | 0.7315 | 0.8030 | 0.8322 | 0.9007 | 0.8666 |
| Lasso | 355 | 0.9818 | 0.9825 | 0.9821 | 0.9714 | 0.8471 | 0.9418 | 0.8540 | 0.7880 | 0.8882 | 0.9613 | 0.9198 |
| ENET | 1577 | 0.9696 | 0.9699 | 0.9696 | 0.9310 | 0.8210 | 0.9364 | 0.7851 | 0.8231 | 0.8798 | 0.9497 | 0.9035 |
| GBDT | 445 | 0.8699 | 0.8763 | 0.8704 | 0.9249 | 0.8493 | 0.9177 | 0.8218 | 0.8473 | 0.8924 | 0.8293 | 0.8699 |
| RF | 2833 | 0.9256 | 0.9261 | 0.9256 | 0.9225 | 0.8014 | 0.9196 | 0.7491 | 0.8123 | 0.8684 | 0.8987 | 0.8749 |
| RFE | 1769 | 0.9660 | 0.9664 | 0.9660 | 0.9280 | 0.8189 | 0.9326 | 0.7558 | 0.8087 | 0.8802 | 0.9366 | 0.8959 |
| AE | 10 | 0.9222 | 0.9199 | 0.9222 | 0.9237 | 0.8981 | 0.8832 | 0.8529 | 0.8510 | 0.8757 | 0.7661 | 0.8815 |
| Feature Selection Method | SNP Count | Linear | SVR-Lin | Ridge | ENET | RF | SVR-Poly | LGB | XGB | KNN | ANN | Mean |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Lasso | 355 | 0.9818 | 0.9825 | 0.9821 | 0.9714 | 0.8471 | 0.9418 | 0.8540 | 0.7880 | 0.8882 | 0.9613 | 0.9198 |
| Lasso + RFE | 177 | 0.9936 | 0.9956 | 0.9937 | 0.9830 | 0.8655 | 0.9404 | 0.8746 | 0.8551 | 0.8721 | 0.9296 | 0.9303 |
| Models | Base Models | Meta Model | Accuracy |
|---|---|---|---|
| Conventional stacking | Linear, ENET, SVR-poly, ANN | Ridge | 0.9958 |
| DAWSELF | The first layer is the same as conventional stacking, with each subsequent layer independently selecting base models. | Ridge | 0.9965 |
| Validation Population | SNP Selection Stage | SNP Count | Linear | SVR-Lin | Ridge | ENET | RF | SVR-Poly | LGB | XGB | KNN | ANN | Means | Conventional Stacking | DAWSELF |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| G23 | GWAS + LD | 8998 | 0.9107 | 0.9111 | 0.9107 | 0.8767 | 0.6458 | 0.8204 | 0.5784 | 0.5569 | 0.4755 | 0.9076 | 0.7594 | ||
| Lasso | 864 | 0.9696 | 0.9695 | 0.9696 | 0.9409 | 0.7029 | 0.8848 | 0.6416 | 0.6215 | 0.5547 | 0.9541 | 0.8209 | |||
| Lasso + RFE | 780 | 0.9757 | 0.9756 | 0.9757 | 0.9478 | 0.7290 | 0.8950 | 0.6629 | 0.5057 | 0.5464 | 0.9725 | 0.8186 | 0.9770 | 0.9797 | |
| G27 | GWAS + LD | 6298 | 0.9124 | 0.9127 | 0.9124 | 0.8541 | 0.6454 | 0.8239 | 0.5717 | 0.5954 | 0.6000 | 0.9227 | 0.7751 | ||
| Lasso | 965 | 0.9703 | 0.9703 | 0.9703 | 0.9502 | 0.7005 | 0.9114 | 0.7079 | 0.6689 | 0.6255 | 0.9639 | 0.8439 | |||
| Lasso + RFE | 799 | 0.9816 | 0.9818 | 0.9816 | 0.9634 | 0.6926 | 0.9214 | 0.7385 | 0.6748 | 0.6973 | 0.9751 | 0.8608 | 0.9828 | 0.9842 | |
| AA | GWAS + LD | 6649 | 0.9742 | 0.9743 | 0.9743 | 0.8973 | 0.8565 | 0.9517 | 0.7820 | 0.6416 | 0.8354 | 0.9693 | 0.8857 | ||
| Lasso | 891 | 0.9878 | 0.9880 | 0.9878 | 0.9723 | 0.8492 | 0.9875 | 0.7761 | 0.7223 | 0.8736 | 0.9857 | 0.9130 | |||
| Lasso + RFE | 878 | 0.9881 | 0.9882 | 0.9881 | 0.9729 | 0.8596 | 0.9878 | 0.7865 | 0.7246 | 0.8709 | 0.9873 | 0.9154 | 0.9871 | 0.9882 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, H.; Dou, D.; Lu, M.; Liu, X.; Chang, C.; Zhang, F.; Yang, S.; Cao, Z.; Luan, P.; Li, Y.; et al. Optimization of Genomic Breeding Value Estimation Model for Abdominal Fat Traits Based on Machine Learning. Animals 2025, 15, 2843. https://doi.org/10.3390/ani15192843
Chen H, Dou D, Lu M, Liu X, Chang C, Zhang F, Yang S, Cao Z, Luan P, Li Y, et al. Optimization of Genomic Breeding Value Estimation Model for Abdominal Fat Traits Based on Machine Learning. Animals. 2025; 15(19):2843. https://doi.org/10.3390/ani15192843
Chicago/Turabian StyleChen, Hengcong, Dachang Dou, Min Lu, Xintong Liu, Cheng Chang, Fuyang Zhang, Shengwei Yang, Zhiping Cao, Peng Luan, Yumao Li, and et al. 2025. "Optimization of Genomic Breeding Value Estimation Model for Abdominal Fat Traits Based on Machine Learning" Animals 15, no. 19: 2843. https://doi.org/10.3390/ani15192843
APA StyleChen, H., Dou, D., Lu, M., Liu, X., Chang, C., Zhang, F., Yang, S., Cao, Z., Luan, P., Li, Y., & Zhang, H. (2025). Optimization of Genomic Breeding Value Estimation Model for Abdominal Fat Traits Based on Machine Learning. Animals, 15(19), 2843. https://doi.org/10.3390/ani15192843





