A Novel Combined Model for Predicting Humidity in Sheep Housing Facilities
Abstract
Simple Summary
Abstract
1. Introduction
2. Materials and Methods
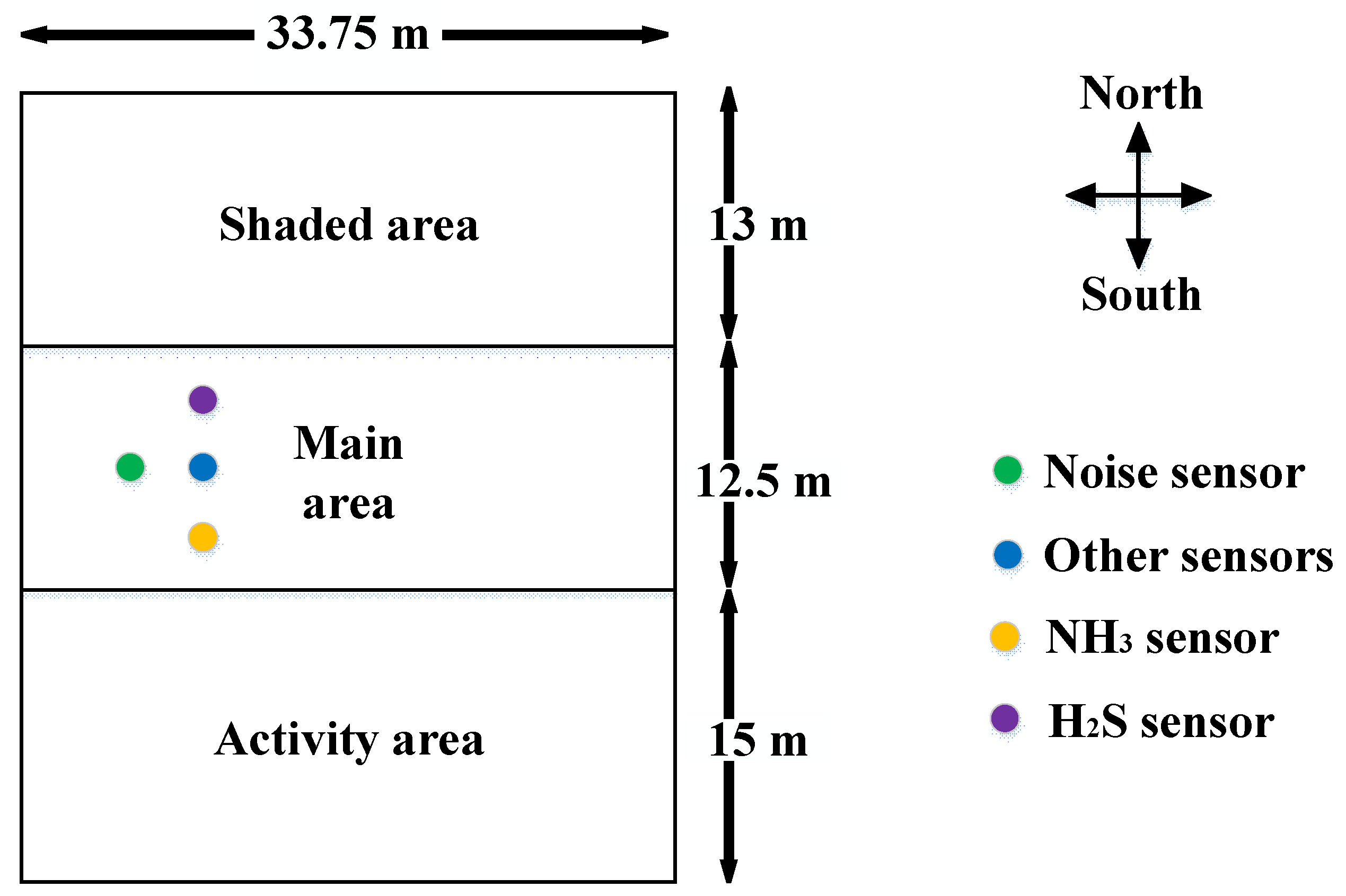
2.1. Data Sources
2.2. Experimental Data Acquisition
2.3. Experimental Data Preprocessing
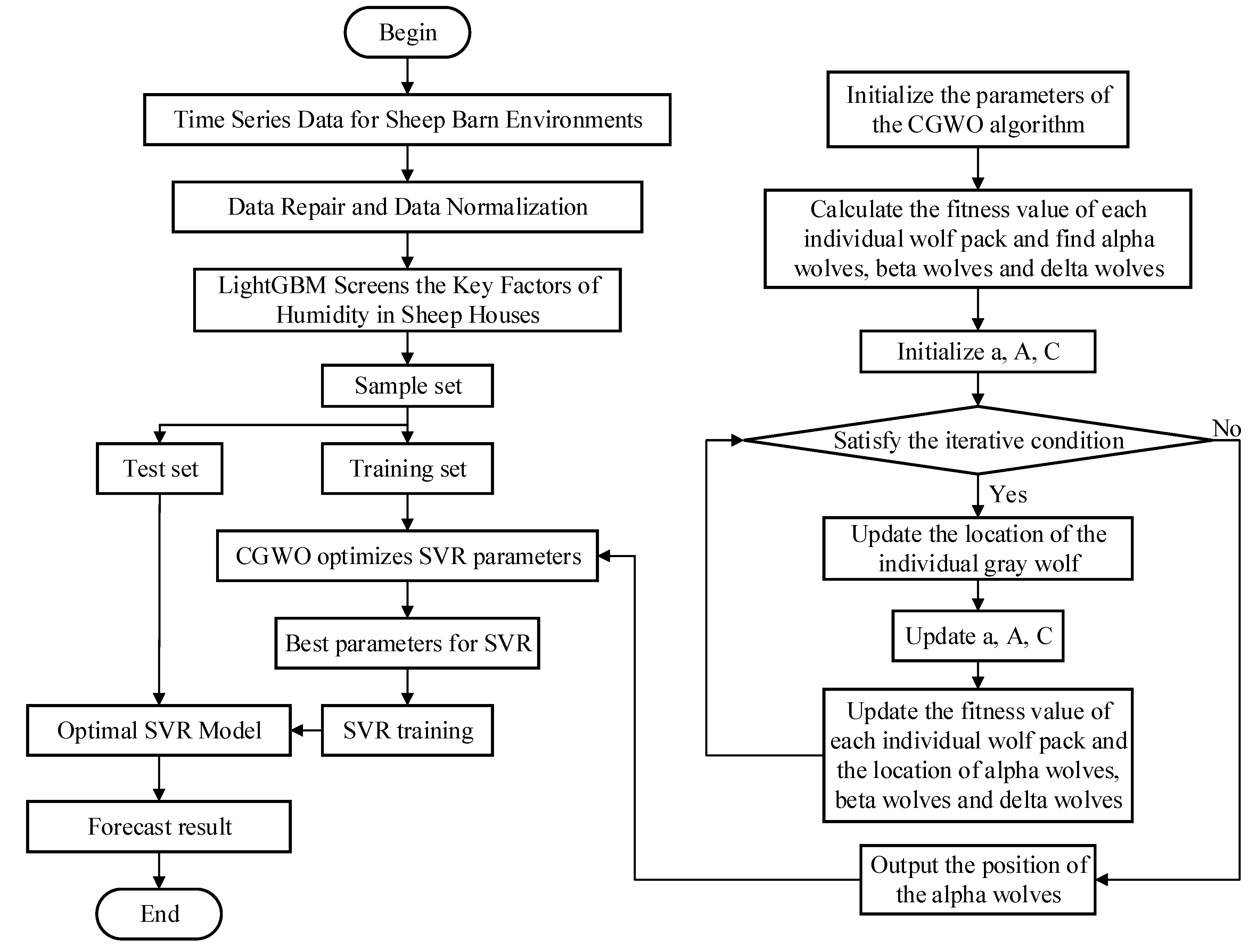
2.4. Construction of the Combined Forecasting Model for Sheep Barn Humidity
2.4.1. LightGBM for Feature Selection
- Step 1:
- Sort the sample points in descending order according to the absolute values of their gradients.
- Step 2:
- Select the top samples of the sorted results to generate a subset of the large gradient samples .
- Step 3:
- Randomly select samples from the remaining samples and generate them as a small gradient sample subset .
- Step 4:
- Combine the large and small gradient samples () to learn a new decision tree; to calculate the information gain (IG), the small gradient samples are multiplied by a weight factor , and the information gain of the split feature for the split point is calculated as:Of which:
- Step 5:
- Repeat Steps 1–4 for a specified number of iterations or until convergence is reached. After traversing the entire model, the sum of IG of all split nodes for a feature is considered an important weight.
2.4.2. GWO Algorithm
- (1)
- Population structure
- (2)
- Surrounding the prey
- (3)
- Hunting process
2.4.3. Improvement of GWO Based on Chaotic Operators
- (1)
- Improvements of update mechanism based on random coefficient vectors
- (2)
- Algorithm implementation of CGWO
- Step 1:
- Initialize the algorithm parameters of the GW population size , with a maximum number of iterations .
- Step 2:
- Population initialization. Randomly generate individual GWs , iterate through all the individual wolves, calculate the fitness values of these individual GWs , and identify , , and wolves: . Initialize the nonlinear decreasing factor and random exploration vectors and .
- Step 3:
- Set (current number of iterations).
- Step 4:
- If (or when the iteration condition is satisfied).
- Step 5:
- Update the distances and directions of the movement of individual GWs in the current pack from the , , and wolves using Equations (9)–(11), respectively, and update the location of each individual GW using Equations (4) and (5).
- Step 6:
- Update the random exploration vectors , , and the convergence factor using Equations (6)–(8).
- Step 7:
- Calculate the fitness of each individual GW for the current iteration , and compare it with the fitness of the last iteration. If the new fitness is higher than the current fitness, the new fitness replaces the current fitness as the global optimal fitness and updates the wolf’s position. If the new fitness value is not higher than the current fitness, it remains unchanged.
- Step 8:
- Update , , and wolves: .
- Step 9:
- , return to Step 4 when the iteration condition is satisfied, exit the loop when the maximum number of iterations () is reached, obtain the position of the wolf, which is the best value for the SVR parameters , , and , and the algorithm ends.
2.4.4. SVR
2.4.5. Humidity Prediction Model of Sheep Barns Based on LightGBM-CGWO-SVR
- Step 1:
- Perform data repair on the collected data.
- Step 2:
- Use LightGBM to calculate the IG for the sheep barn environmental data after the data have been restored, and each parameter factor has been ranked in terms of feature importance, selecting strongly correlated features.
- Step 3:
- Normalize the data after dimensionality reduction, based on LightGBM, and divide the training and test sets in a ratio of 7:3.
- Step 4:
- Based on the training set, optimize , , and for the SVR model using the CGWO algorithm described in Section 2.4.3.
- Step 5:
- Apply the best hyperparameters obtained using CGWO, that is, , , and , to the SVR model to obtain the combined LightGBM–CGWO–SVR prediction model.
3. Results and Discussion
3.1. Experimental Setup and Parameter Determination
3.2. Performance Criteria
- (1)
- R2 shown in Equation (1) was used to assess the fit between the predicted and actual humidity, and considered a value in the range of (0, 1), a value closer to 1 represented a better fit between the predicted and actual humidity values.
- (2)
- MAE was the average distance between the individual and predicted humidity data; a smaller MAE implied that the predicted value was closer to the actual humidity data (Equation (23)).
- (3)
- MSE represented the mean of the square of the difference between individual humidity data and the predicted humidity data. RMSE was the root mean square result of the MSE, which could be intuitive, in terms of the order of magnitude performance; normalized RMSE converted the RMSE value within (0, 1). The smaller the MSE, RMSE, and NRMSE, the smaller the error between the predicted and true values, and the more accurate the model. They were expressed as:
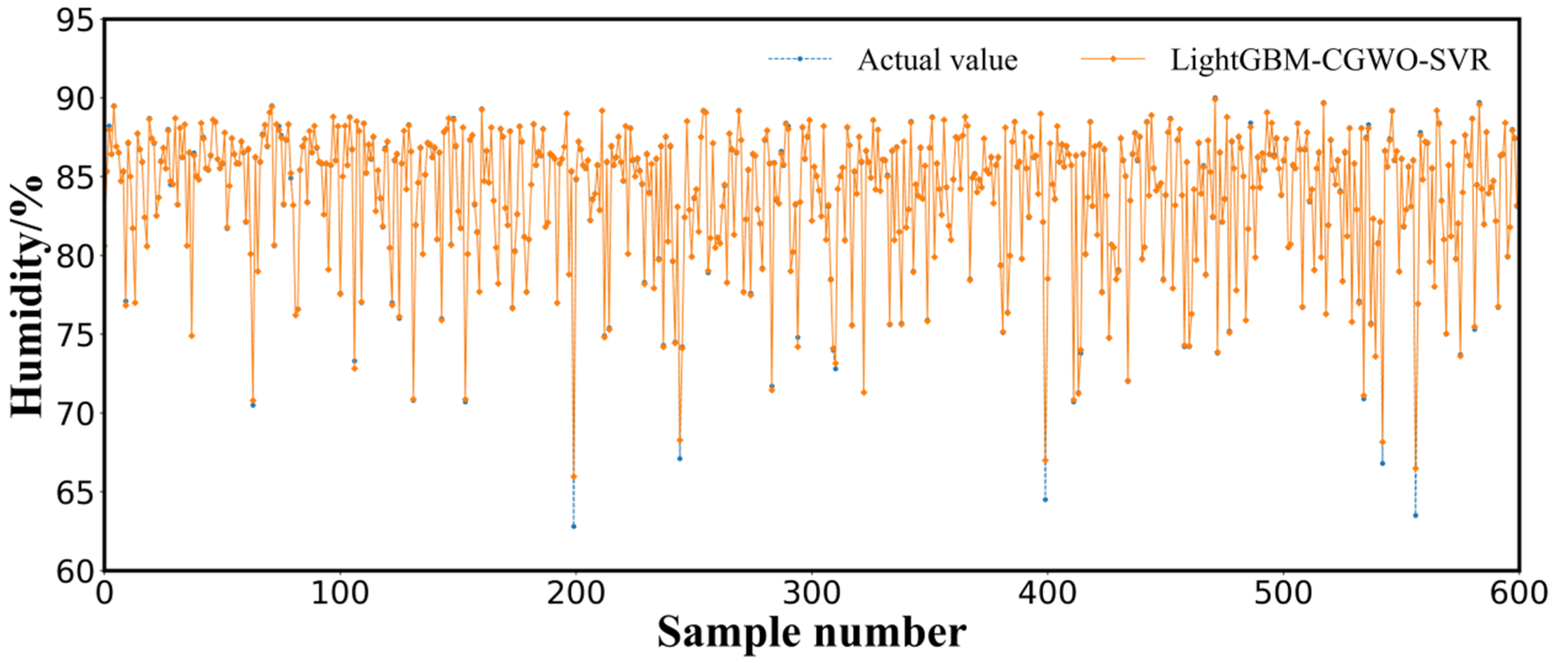
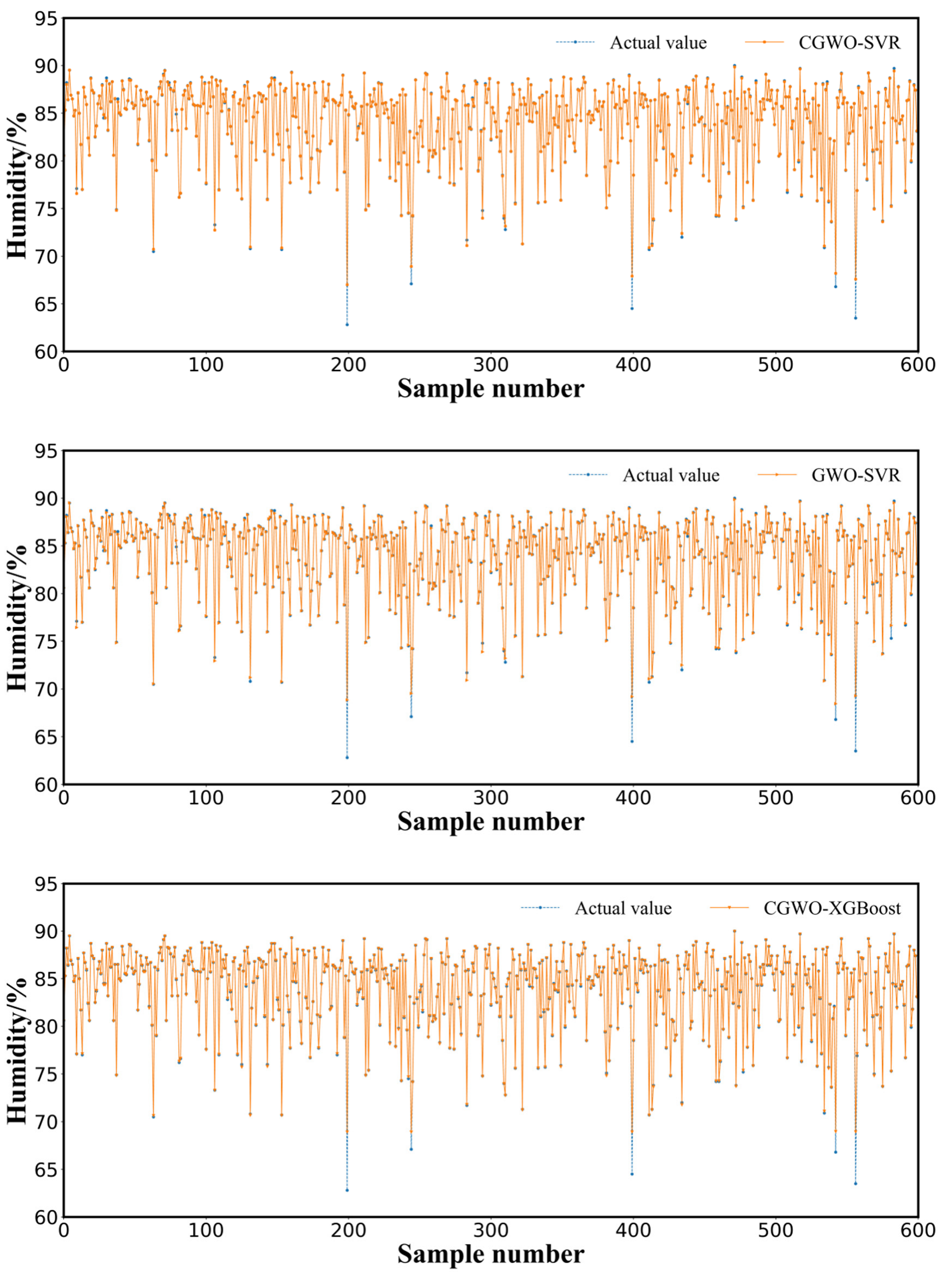
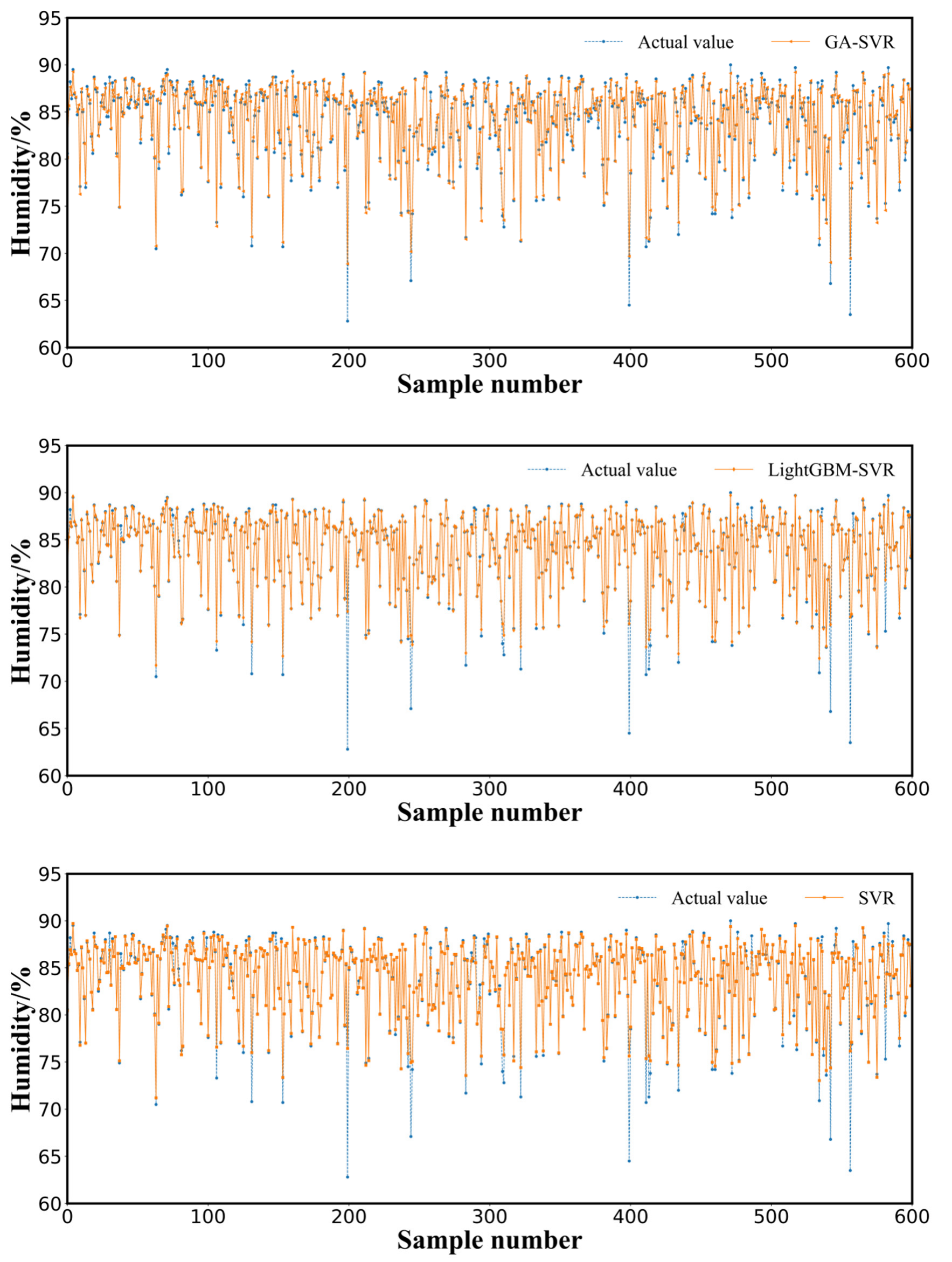
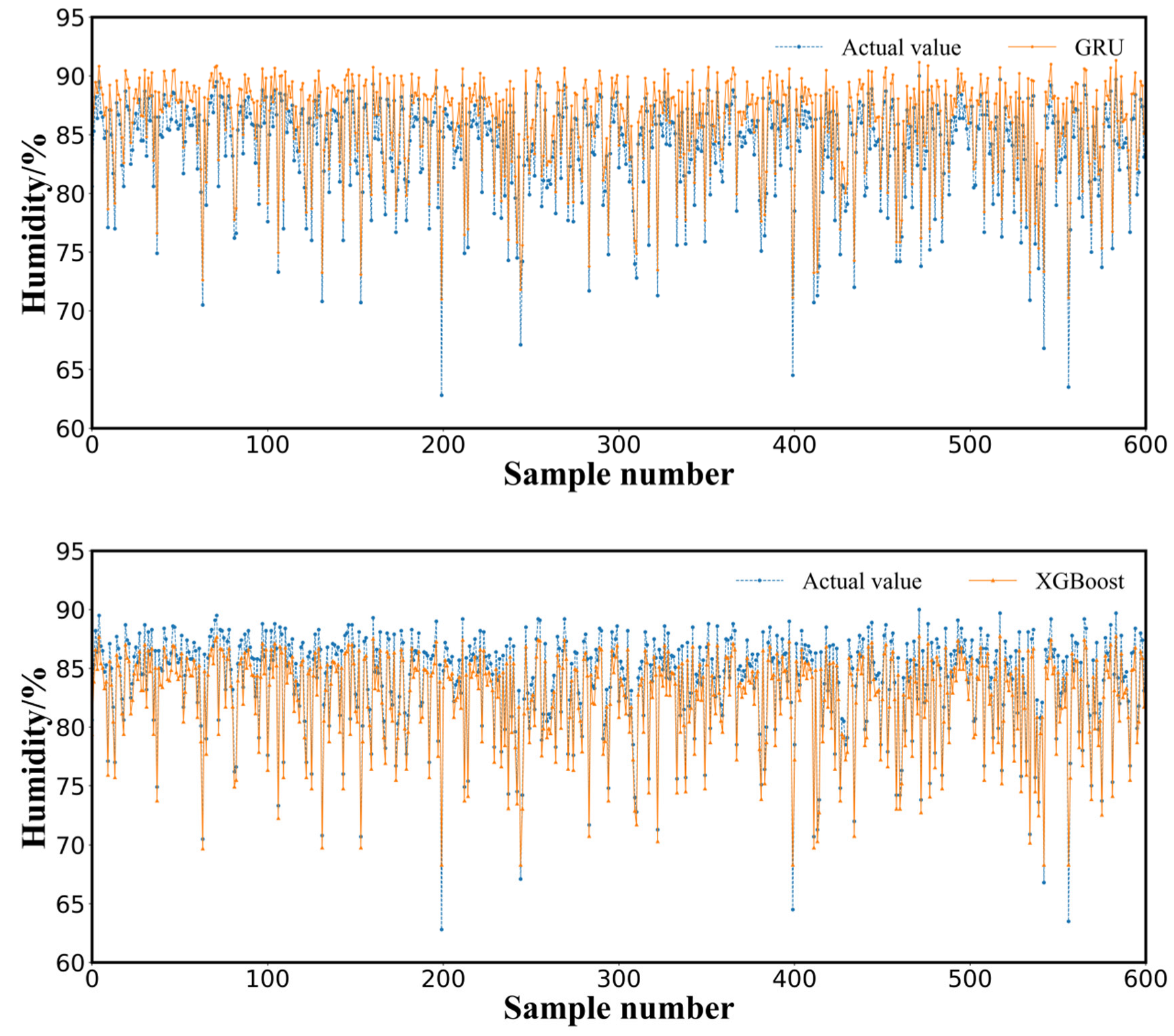
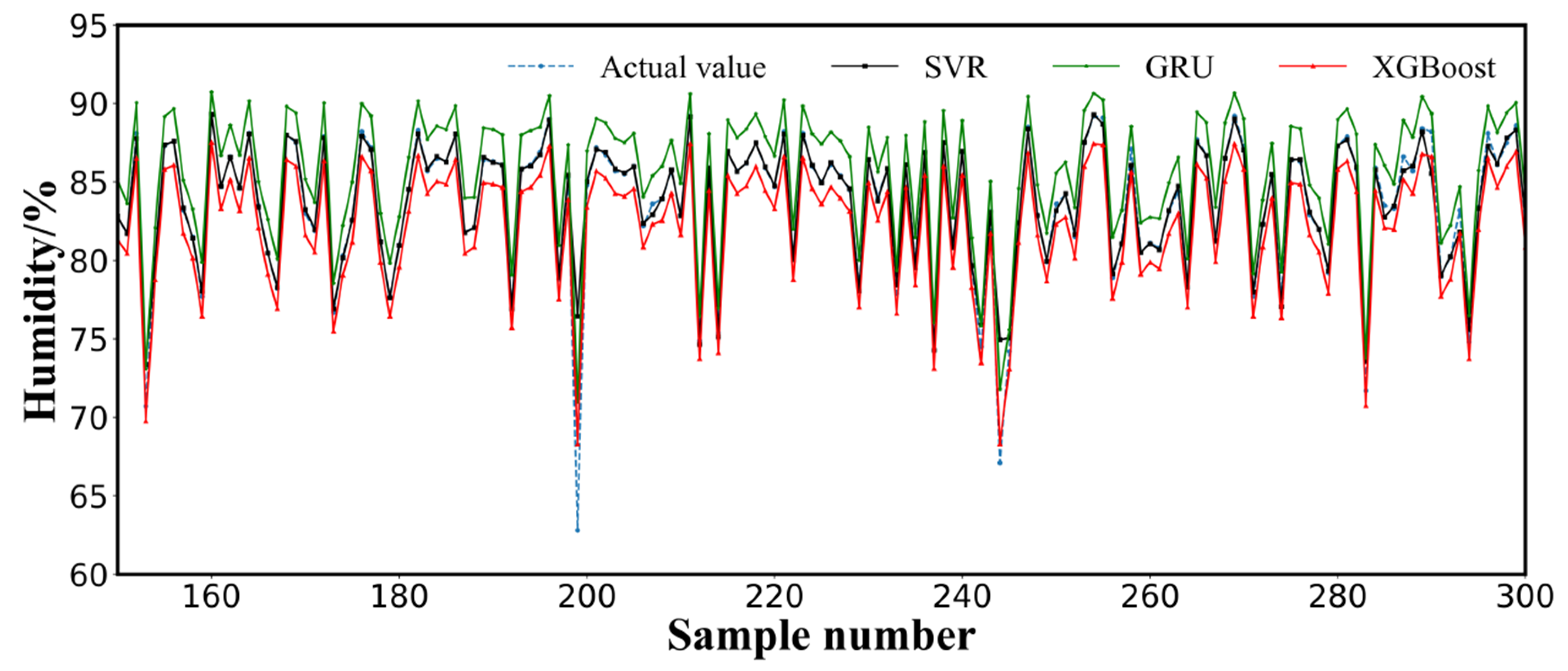
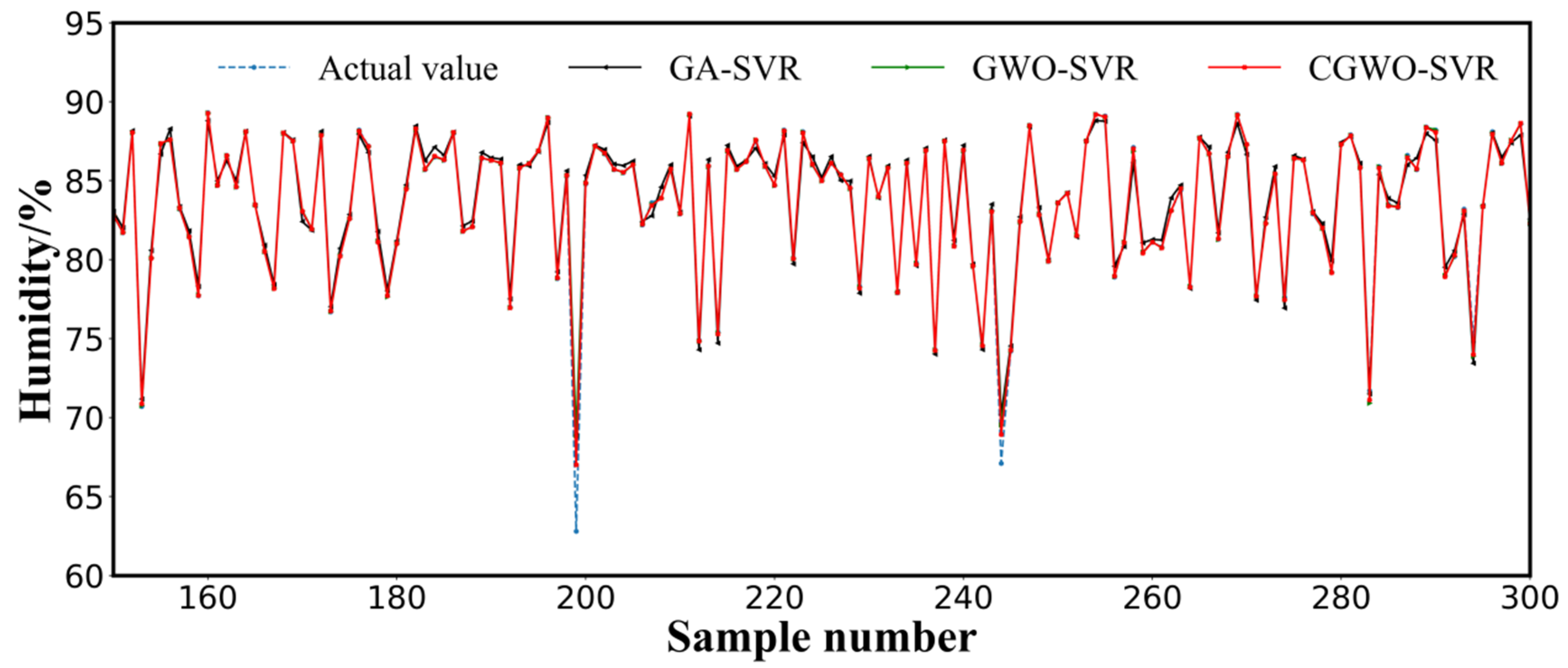
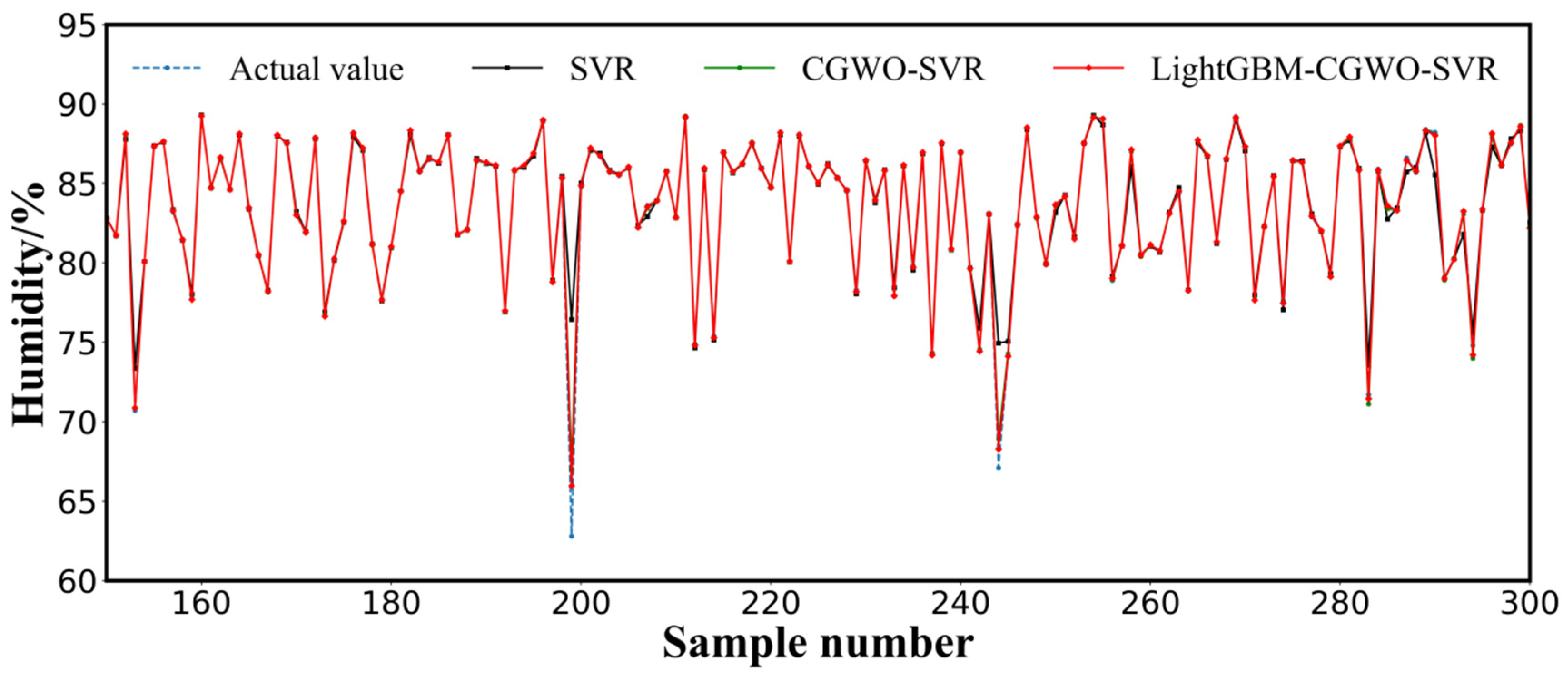
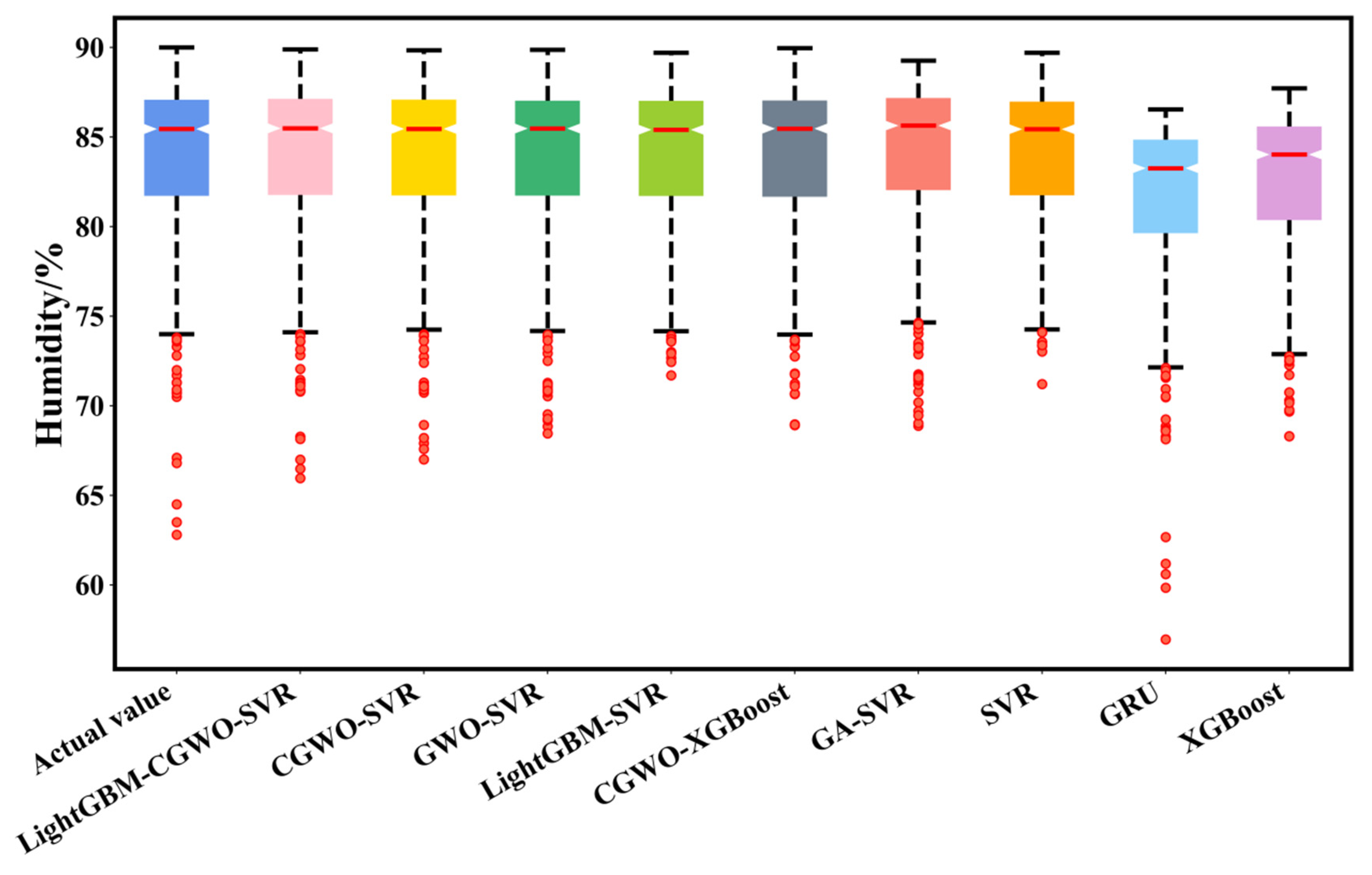
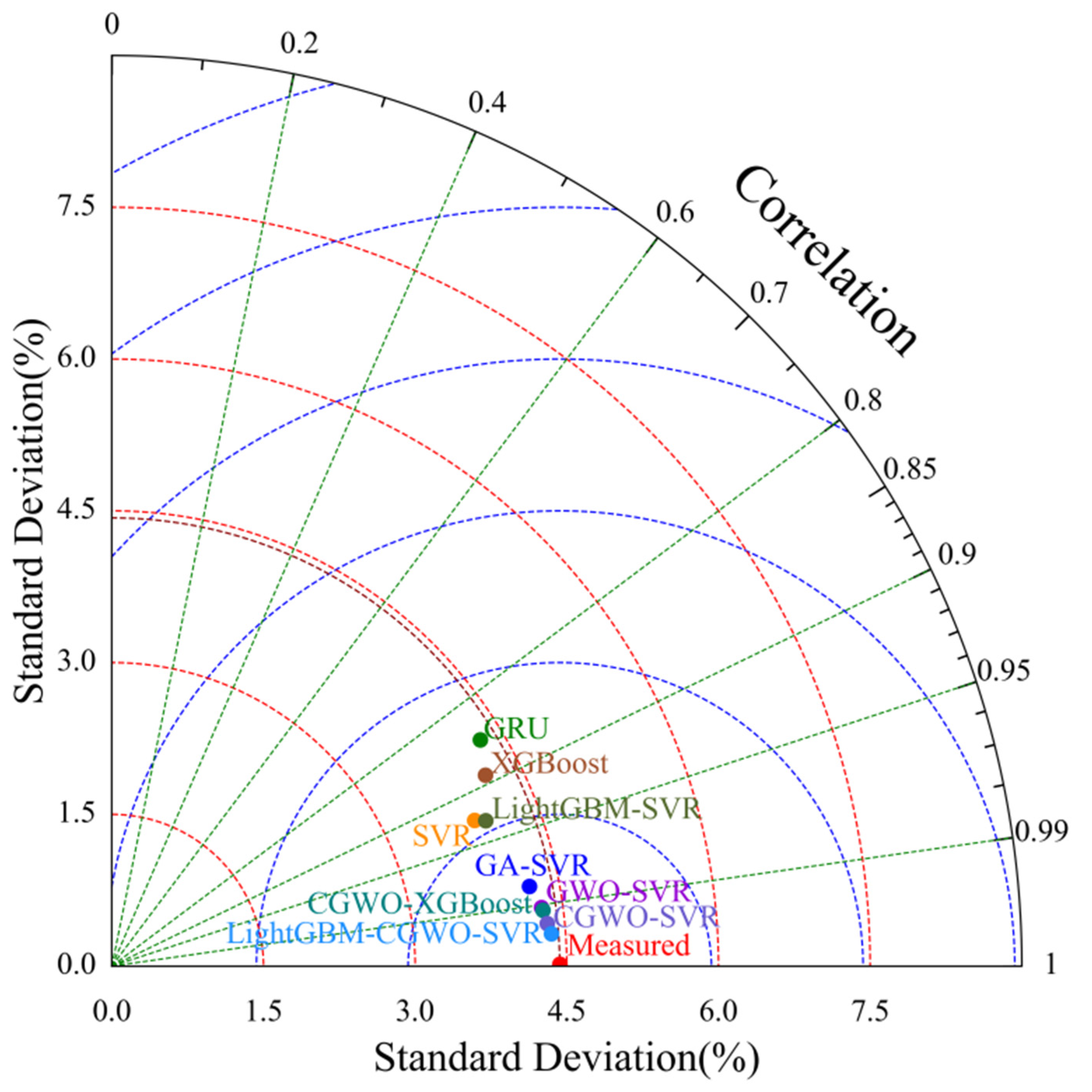
3.3. Results and Analysis
3.4. Discussion
4. Conclusions
- (1)
- The characteristics of the environmental factors of the sheep barn were screened using LightGBM without considering environmental variables with small effects on humidity. The key influencing factors of CO2 concentration, light intensity, air temperature, and PM2.5 were finally screened from the nine variables, including air humidity, CO2 concentration, PM2.5, PM10, light intensity, noise, TSP, NH3 concentration, and H2S concentration, and used for modeling, which effectively improved the computational efficiency of the model and its accuracy.
- (2)
- The CGWO algorithm obtained by introducing chaotic operators in this study retained the advantages of a simple structure, few control parameters, and straightforward implementation of the GWO algorithm, while improving the global search capability of the traditional GWO algorithm and solving the problem of randomness and empiricality in the selection of SVR parameters. The optimized SVR algorithm exhibited higher prediction accuracy and better generalization ability than an SVR algorithm optimized using GA and GWO.
- (3)
- The performance of the proposed LightGBM–CGWO–SVR model in predicting the humidity for 10 min in a sheep barn facility exceeded that of the GRU, SVR, XGBoost, GA–SVR, GWO–SVR, CGWO–XGBoost, CGWO-SVR, and LightGBM–SVR models. The minimum values of the MAE, RMSE, MSE, and NRMSE indices were 0.0662, 0.2284, 0.0521, and 0.0083, respectively, and R2 achieved the highest value of 0.9973. The results indicated that the proposed model can provide an effective guide for the accurate prediction of humidity in sheep barns in for Suffolk sheep, in Xinjiang, and could provide a reference for future research on the prediction of other environmental factors, such as NH3 and H2S concentration.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Shi, J.; Li, X.; Lu, F.; Zhuge, H.; Dong, S. Variation in group sizes of sympatric Wild yak, Tibetan wild ass and Tibetan antelope in Arjin Shan National Nature Reserve of Xinjiang Province, China. Glob. Ecol. Conserv. 2019, 20, e00749. [Google Scholar] [CrossRef]
- Qiao, Y.; Huang, Z.; Li, Q.; Liu, Z.; Hao, C.; Shi, G.; Dai, R.; Xie, Z. Developmental Changes of the FAS and HSL mRNA Expression and Their Effects on the Content of Intramuscular Fat in Kazak and Xinjiang Sheep. J. Genet. Genom. 2007, 34, 909–917. [Google Scholar] [CrossRef]
- Huang, J.; Liu, S.; Hassan, S.G.; Xu, L.; Huang, C. A hybrid model for short-term dissolved oxygen content prediction. Comput. Electron. Agric. 2021, 186, 106216. [Google Scholar] [CrossRef]
- Sanikhani, H.; Deo, R.C.; Samui, P.; Kisi, O.; Mert, C.; Mirabbasi, R.; Gavili, S.; Yaseen, Z.M. Survey of different data-intelligent modeling strategies for forecasting air temperature using geographic information as model predictors. Comput. Electron. Agric. 2018, 152, 242–260. [Google Scholar] [CrossRef]
- Tong, X.; Zhao, L.; Heber, A.J.; Ni, J.-Q. Development of a farm-scale, quasi-mechanistic model to estimate ammonia emissions from commercial manure-belt layer houses. Biosyst. Eng. 2020, 196, 67–87. [Google Scholar] [CrossRef]
- Banhazi, T.; Rutley, D.; Pitchford, W. Validation and fine-tuning of a predictive model for air quality in livestock buildings. Biosyst. Eng. 2010, 105, 395–401. [Google Scholar] [CrossRef]
- Banhazi, T.M.; Seedorf, J.; Rutley, D.L.; Pitchford, W.S. Identification of risk factors for sub-optimal housing conditions in Australian piggeries: Part 1. Study justification and design. J. Agric. Saf. Health 2008, 14, 5–20. [Google Scholar] [CrossRef] [PubMed]
- Daskalov, P. Prediction of Temperature and Humidity in a Naturally Ventilated Pig Building. J. Agric. Eng. Res. 1997, 68, 329–339. [Google Scholar] [CrossRef]
- Yang, Z.-C. Hourly ambient air humidity fluctuation evaluation and forecasting based on the least-squares Fourier-model. Measurement 2019, 133, 112–123. [Google Scholar] [CrossRef]
- Qadeer, K.; Ahmad, A.; Qyyum, M.A.; Nizami, A.-S.; Lee, M. Developing machine learning models for relative humidity prediction in air-based energy systems and environmental management applications. J. Environ. Manag. 2021, 292, 112736. [Google Scholar] [CrossRef]
- Hongkang, W.; Li, L.; Yong, W.; Fanjia, M.; Haihua, W.; Sigrimis, N. Recurrent Neural Network Model for Prediction of Microclimate in Solar Greenhouse. IFAC-PapersOnLine 2018, 51, 790–795. [Google Scholar] [CrossRef]
- Zou, W.; Yao, F.; Zhang, B.; He, C.; Guan, Z. Verification and predicting temperature and humidity in a solar greenhouse based on convex bidirectional extreme learning machine algorithm. Neurocomputing 2017, 249, 72–85. [Google Scholar] [CrossRef]
- Jung, D.-H.; Kim, H.S.; Jhin, C.; Kim, H.-J.; Park, S.H. Time-serial analysis of deep neural network models for prediction of climatic conditions inside a greenhouse. Comput. Electron. Agric. 2020, 173, 105402. [Google Scholar] [CrossRef]
- Besteiro, R.; Arango, T.; Ortega, J.A.; Rodríguez, M.R.; Fernández, M.D.; Velo, R. Prediction of carbon dioxide concentration in weaned piglet buildings by wavelet neural network models. Comput. Electron. Agric. 2017, 143, 201–207. [Google Scholar] [CrossRef]
- He, F.; Ma, C. Modeling greenhouse air humidity by means of artificial neural network and principal component analysis. Comput. Electron. Agric. 2010, 71, S19–S23. [Google Scholar] [CrossRef]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.-Y. LightGBM: A Highly Efficient Gradient Boosting Decision Tree. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 3149–3157. [Google Scholar]
- Hao, X.; Zhang, Z.; Xu, Q.; Huang, G.; Wang, K. Prediction of f-CaO content in cement clinker: A novel prediction method based on LightGBM and Bayesian optimization. Chemom. Intell. Lab. Syst. 2022, 220, 104461. [Google Scholar] [CrossRef]
- Li, Y.; Yang, C.; Zhang, H.; Jia, C. A Model Combining Seq2Seq Network and LightGBM Algorithm for Industrial Soft Sensor. IFAC-PapersOnLine 2020, 53, 12068–12073. [Google Scholar] [CrossRef]
- Candido, C.; Blanco, A.; Medina, J.; Gubatanga, E.; Santos, A.; Ana, R.S.; Reyes, R. Improving the consistency of multi-temporal land cover mapping of Laguna lake watershed using light gradient boosting machine (LightGBM) approach, change detection analysis, and Markov chain. Remote Sens. Appl. Soc. Environ. 2021, 23, 100565. [Google Scholar] [CrossRef]
- Guyon, I.; Elisseeff, A. An introduction to variable and feature selection. J. Mach. Learn. Res. 2003, 3, 1157–1182. [Google Scholar] [CrossRef][Green Version]
- Zhang, Y.; Jiang, Z.; Chen, C.; Wei, Q.; Gu, H.; Yu, B. DeepStack-DTIs: Predicting Drug–Target Interactions Using LightGBM Feature Selection and Deep-Stacked Ensemble Classifier. Interdiscip. Sci. Comput. Life Sci. 2022, 14, 311–330. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, R.; Ma, Q.; Wang, Y.; Wang, Q.; Huang, Z.; Huang, L. A feature selection and multi-model fusion-based approach of predicting air quality. ISA Trans. 2020, 100, 210–220. [Google Scholar] [CrossRef]
- Smola, A.J.; Schölkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef]
- Gu, Y.; Yoo, S.; Park, C.; Kim, Y.; Park, S.; Kim, J.; Lim, J. BLITE-SVR: New forecasting model for late blight on potato using support-vector regression. Comput. Electron. Agric. 2016, 130, 169–176. [Google Scholar] [CrossRef]
- Esfandiarpour-Boroujeni, I.; Karimi, E.; Shirani, H.; Esmaeilizadeh, M.; Mosleh, Z. Yield prediction of apricot using a hybrid particle swarm optimization-imperialist competitive algorithm- support vector regression (PSO-ICA-SVR) method. Sci. Hortic. 2019, 257, 108756. [Google Scholar] [CrossRef]
- Ghimire, S.; Deo, R.C.; Raj, N.; Mi, J. Wavelet-based 3-phase hybrid SVR model trained with satellite-derived predictors, particle swarm optimization and maximum overlap discrete wavelet transform for solar radiation prediction. Renew. Sustain. Energy Rev. 2019, 113, 109247. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Niu, M.; Wang, Y.; Sun, S.; Li, Y. A novel hybrid decomposition-and-ensemble model based on CEEMD and GWO for short-term PM2.5 concentration forecasting. Atmos. Environ. 2016, 134, 168–180. [Google Scholar] [CrossRef]
- Tikhamarine, Y.; Souag-Gamane, D.; Ahmed, A.N.; Kisi, O.; El-Shafie, A. Improving artificial intelligence models accuracy for monthly streamflow forecasting using grey Wolf optimization (GWO) algorithm. J. Hydrol. 2020, 582, 124435. [Google Scholar] [CrossRef]
- Tian, Y.; Yu, J.; Zhao, A. Predictive model of energy consumption for office building by using improved GWO-BP. Energy Rep. 2020, 6, 620–627. [Google Scholar] [CrossRef]
- Emary, E.; Zawbaa, H.M.; Grosan, C.; Hassenian, A.E. Feature Subset Selection Approach by Gray-Wolf Optimization. In Proceedings of the Afro-European Conference for Industrial Advancement, Addis Ababa, Ethiopia, 17–19 November 2014; Springer: Cham, Switzerland, 2015; pp. 1–13. [Google Scholar]
- Lu, C.; Gao, L.; Yi, J. Grey wolf optimizer with cellular topological structure. Expert Syst. Appl. 2018, 107, 89–114. [Google Scholar] [CrossRef]
- Song, D.; Liu, J.; Yang, Y.; Yang, J.; Su, M.; Wang, Y.; Gui, N.; Yang, X.; Huang, L.; Joo, Y.H. Maximum wind energy extraction of large-scale wind turbines using nonlinear model predictive control via Yin-Yang grey wolf optimization algorithm. Energy 2021, 221, 119866. [Google Scholar] [CrossRef]
- Zhang, Z.; Hong, W.-C. Application of variational mode decomposition and chaotic grey wolf optimizer with support vector regression for forecasting electric loads. Knowl. -Based Syst. 2021, 228, 107297. [Google Scholar] [CrossRef]
- Zhao, X.; Lv, H.; Lv, S.; Sang, Y.; Wei, Y.; Zhu, X. Enhancing robustness of monthly streamflow forecasting model using gated recurrent unit based on improved grey wolf optimizer. J. Hydrol. 2021, 601, 126607. [Google Scholar] [CrossRef]
- Liu, D.; Li, M.; Ji, Y.; Fu, Q.; Li, M.; Faiz, M.A.; Ali, S.; Li, T.; Cui, S.; Khan, M.I. Spatial-temporal characteristics analysis of water resource system resilience in irrigation areas based on a support vector machine model optimized by the modified gray wolf algorithm. J. Hydrol. 2021, 597, 125758. [Google Scholar] [CrossRef]
- Yu, C.; Li, Z.; Yang, Z.; Chen, X.; Su, M. A feedforward neural network based on normalization and error correction for predicting water resources carrying capacity of a city. Ecol. Indic. 2020, 118, 106724. [Google Scholar] [CrossRef]

| Time | Air Temperature /°C | Air Humidity /% | CO2 /(mL/m3) | PM2.5 /(μg/m3) | PM10 /(μg/m3) | Light Intensity /lx | Noise /dB | TSP /(μg/m3) | NH3 /(mL/m3) | H2S /(mL/m3) |
|---|---|---|---|---|---|---|---|---|---|---|
| 2021/2/8 17:11:56 | 4.2 | 78 | 1355 | 16.3 | 81.3 | 146 | 31.1 | 120.7 | 0 | 5.2 |
| 2021/2/8 17:21:35 | 3.9 | 78.4 | 1330 | 26.5 | 107.1 | 97 | 72.7 | 165.3 | 0 | 5.2 |
| ...... | ...... | ...... | ...... | ...... | ...... | ...... | ...... | ...... | ...... | ...... |
| 2021/2/22 17:12:15 | 6.6 | 81.2 | 855 | 12.5 | 24 | 97 | 40.2 | 45.3 | 0 | 5.2 |
| 2021/2/22 17:22:15 | 6.4 | 81.4 | 780 | 9.3 | 24.6 | 183 | 34.1 | 42 | 0 | 5 |
| 2021/2/22 17:32:16 | 6.3 | 81.4 | 770 | 12.2 | 34.8 | 159 | 31.8 | 58.2 | 0 | 1.4 |
| Parameter | Feature Weights |
|---|---|
| CO2 | 29.741152 |
| Light intensity | 13.195553 |
| Air temperature | 13.092886 |
| PM2.5 | 6.540839 |
| H2S | 5.084741 |
| PM10 | 3.862321 |
| Noise | 3.290505 |
| TSP | 1.477563 |
| NH3 | 0.000000 |
| Prediction Model | C | g | ε |
|---|---|---|---|
| SVR | 1.000 | 0.100 | 0.100 |
| GA–SVR | 6.564 | 0.831 | 0.011 |
| GWO–SVR | 8.958 | 0.023 | 0.016 |
| CGWO–SVR | 9.346 | 0.011 | 0.040 |
| LightGBM–SVR | 1.000 | 0.100 | 0.100 |
| LightGBM–CGWO–SVR | 9.849 | 0.010 | 0.059 |
| Prediction Model | Error Type | ||||
|---|---|---|---|---|---|
| MAE | RMSE | MSE | NRMSE | ||
| GRU 1 | 1.4307 | 1.7019 | 2.8964 | 0.0625 | 0.8522 |
| SVR | 0.3451 | 1.1878 | 1.4110 | 0.0436 | 0.9280 |
| XGBoost 2 | 1.4372 | 1.4645 | 2.1450 | 0.0538 | 0.8906 |
| GA–SVR | 0.3732 | 0.5897 | 0.3477 | 0.0216 | 0.9822 |
| GWO–SVR | 0.0763 | 0.4230 | 0.1789 | 0.0155 | 0.9908 |
| CGWO–XGBoost 3 | 0.0772 | 0.4025 | 0.1620 | 0.0147 | 0.9917 |
| CGWO–SVR | 0.0731 | 0.3048 | 0.0929 | 0.0112 | 0.9952 |
| LightGBM–SVR | 0.2596 | 1.1545 | 1.3328 | 0.0424 | 0.9320 |
| LightGBM–CGWO–SVR | 0.0662 | 0.2284 | 0.0521 | 0.0083 | 0.9973 |
| MAE | RMSE | MSE | NRMSE | R2 | |
|---|---|---|---|---|---|
| 10 min | 0.0597 | 0.1950 | 0.0380 | 0.0073 | 0.9979 |
| 30 min | 0.0674 | 0.2494 | 0.0622 | 0.0092 | 0.9972 |
| 60 min | 0.2181 | 0.2786 | 0.0776 | 0.0149 | 0.9956 |
| 90 min | 0.2254 | 0.3298 | 0.1087 | 0.0179 | 0.9940 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, D.; Zhou, B.; Han, Q.; Xu, L.; Guo, J.; Cao, L.; Zhuang, L.; Liu, S.; Liu, T. A Novel Combined Model for Predicting Humidity in Sheep Housing Facilities. Animals 2022, 12, 3300. https://doi.org/10.3390/ani12233300
Feng D, Zhou B, Han Q, Xu L, Guo J, Cao L, Zhuang L, Liu S, Liu T. A Novel Combined Model for Predicting Humidity in Sheep Housing Facilities. Animals. 2022; 12(23):3300. https://doi.org/10.3390/ani12233300
Chicago/Turabian StyleFeng, Dachun, Bing Zhou, Qianyu Han, Longqin Xu, Jianjun Guo, Liang Cao, Lvhan Zhuang, Shuangyin Liu, and Tonglai Liu. 2022. "A Novel Combined Model for Predicting Humidity in Sheep Housing Facilities" Animals 12, no. 23: 3300. https://doi.org/10.3390/ani12233300
APA StyleFeng, D., Zhou, B., Han, Q., Xu, L., Guo, J., Cao, L., Zhuang, L., Liu, S., & Liu, T. (2022). A Novel Combined Model for Predicting Humidity in Sheep Housing Facilities. Animals, 12(23), 3300. https://doi.org/10.3390/ani12233300







