An Approach for Autonomous Feeding Robot Path Planning in Poultry Smart Farm
Abstract
Simple Summary
Abstract
1. Introduction
2. Materials and Methods
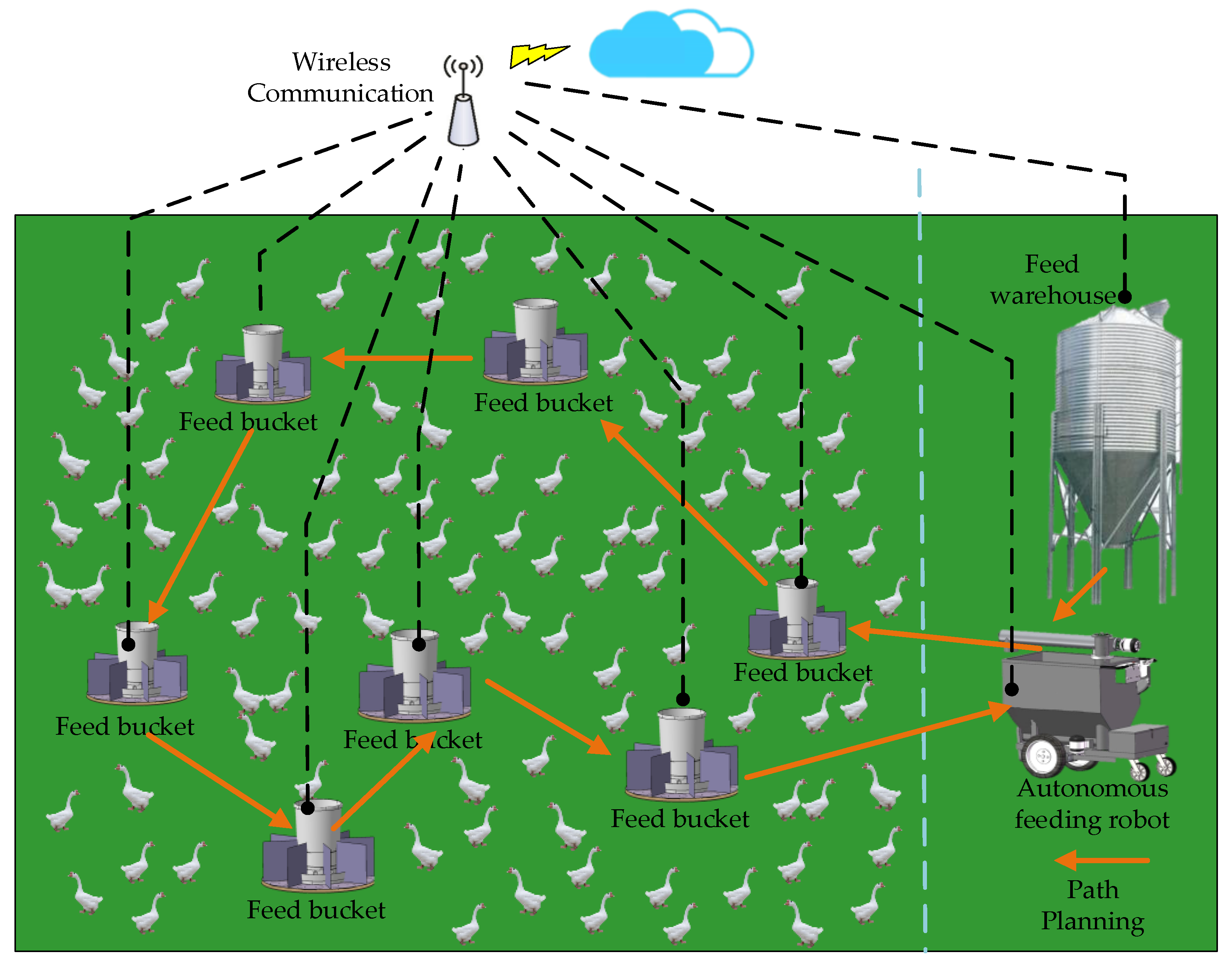
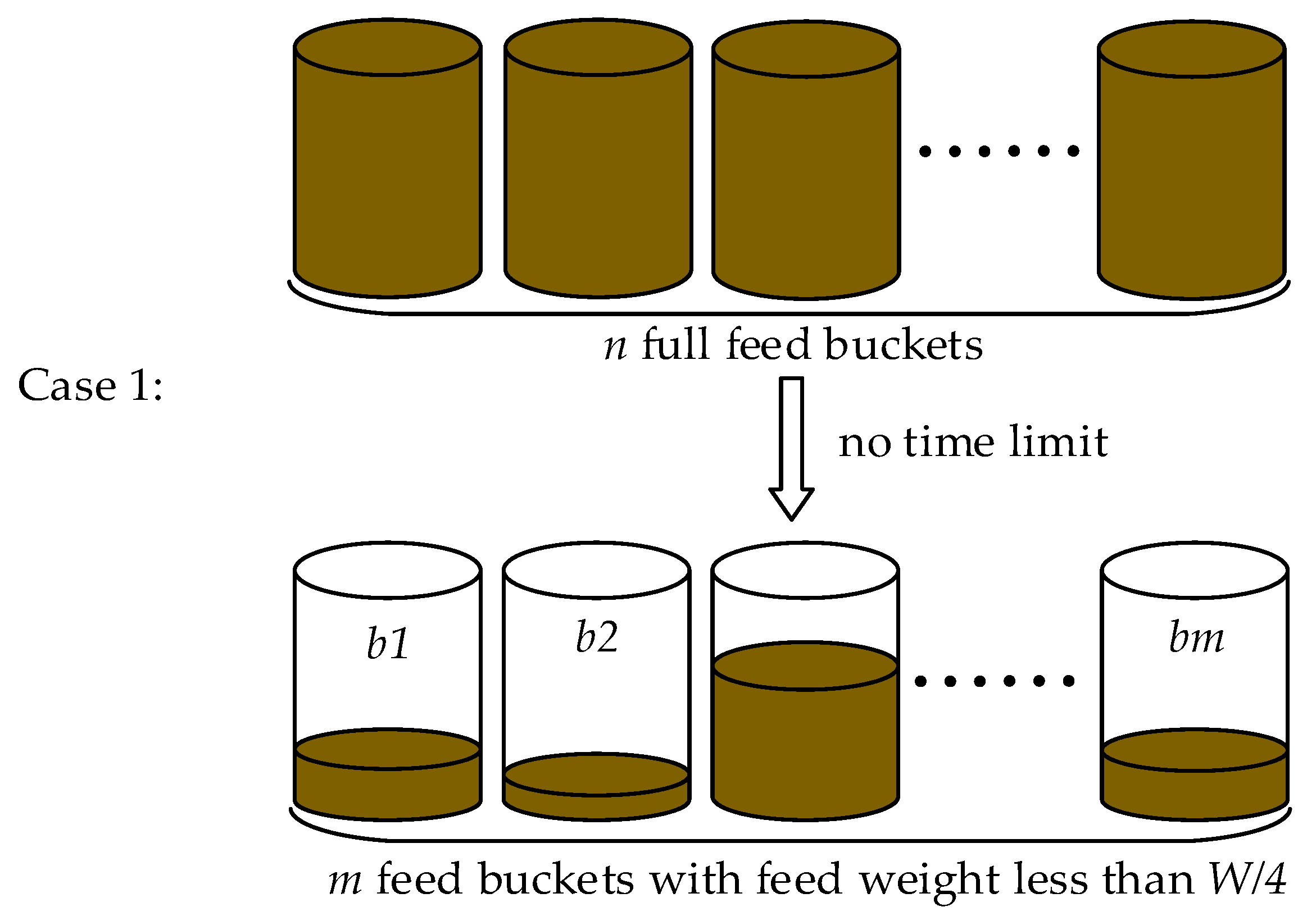
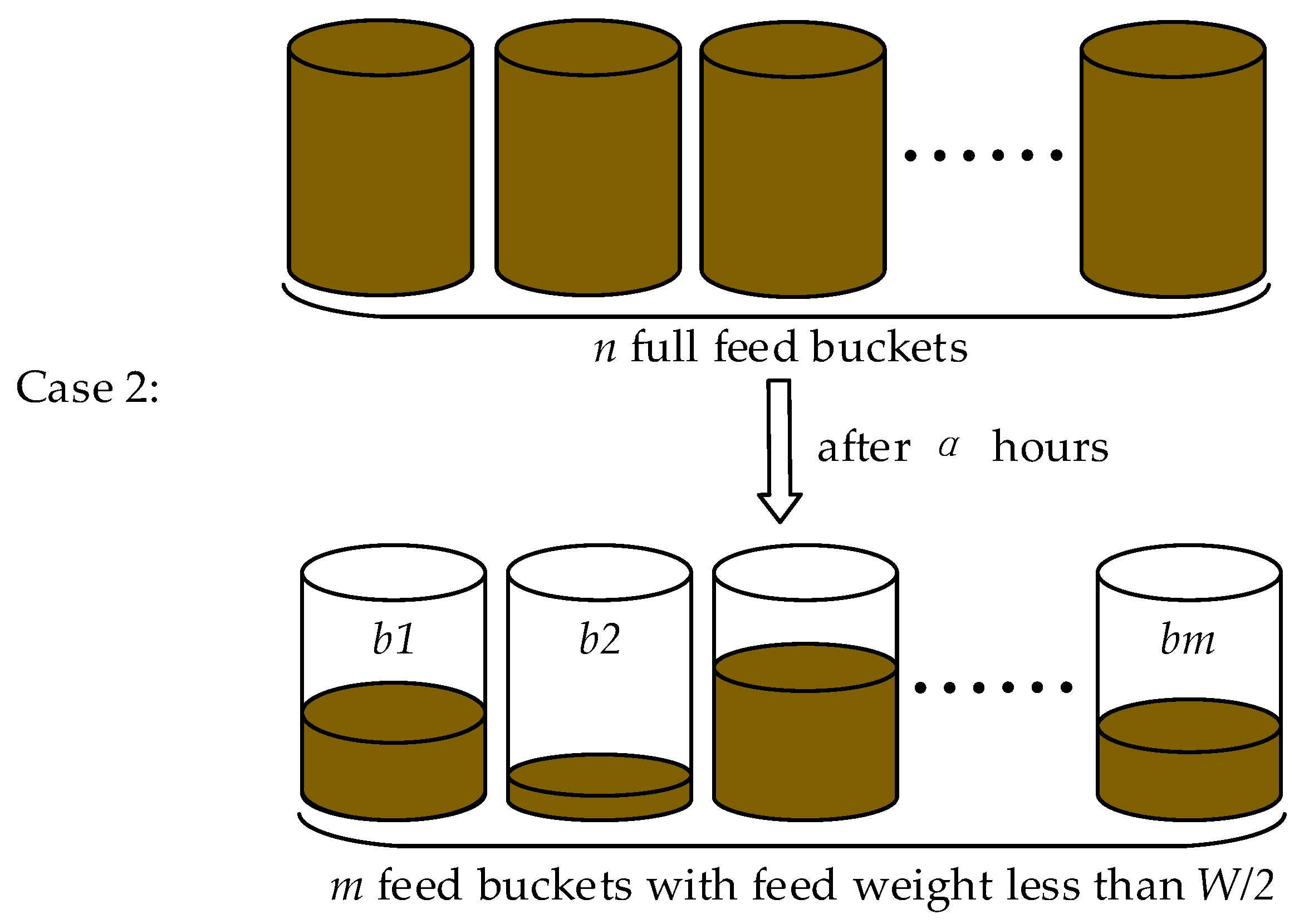
2.1. Problem Description and Analysis
2.2. Path Planning for Small-Scale Feeding Point
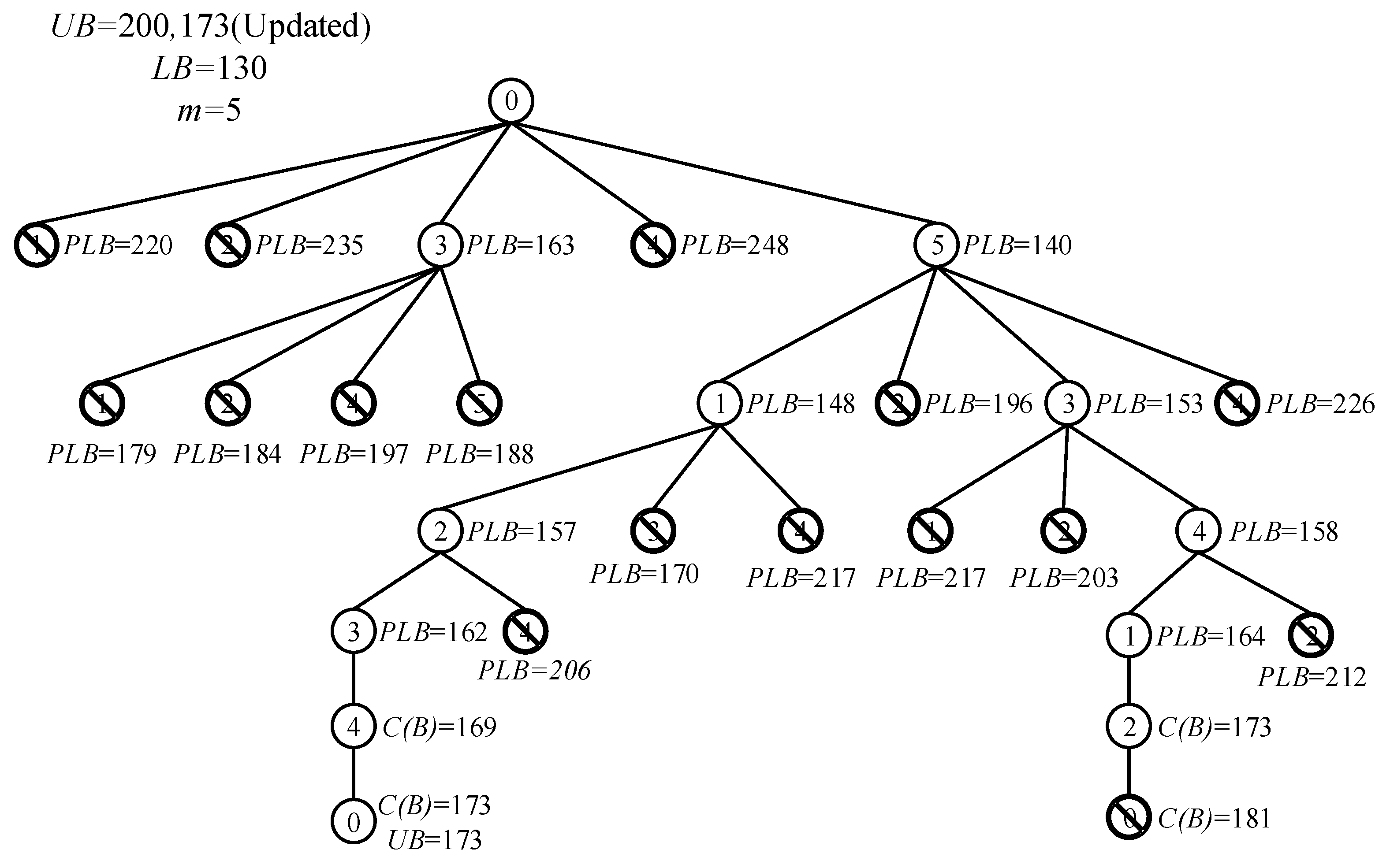
2.2.1. Theory of the Branch and Bound Algorithm
2.2.2. Boundary Constraints of Branch and Bound Algorithms
2.2.3. Solution of the Global Lower Bound
2.2.4. Solution of the Partial Lower Bound for the Energy Consumption
2.2.5. Solution of the Upper Bound of Energy Consumption
2.3. Large Scale Feeding Point Path Planning
2.3.1. Determination of the Fitness Function
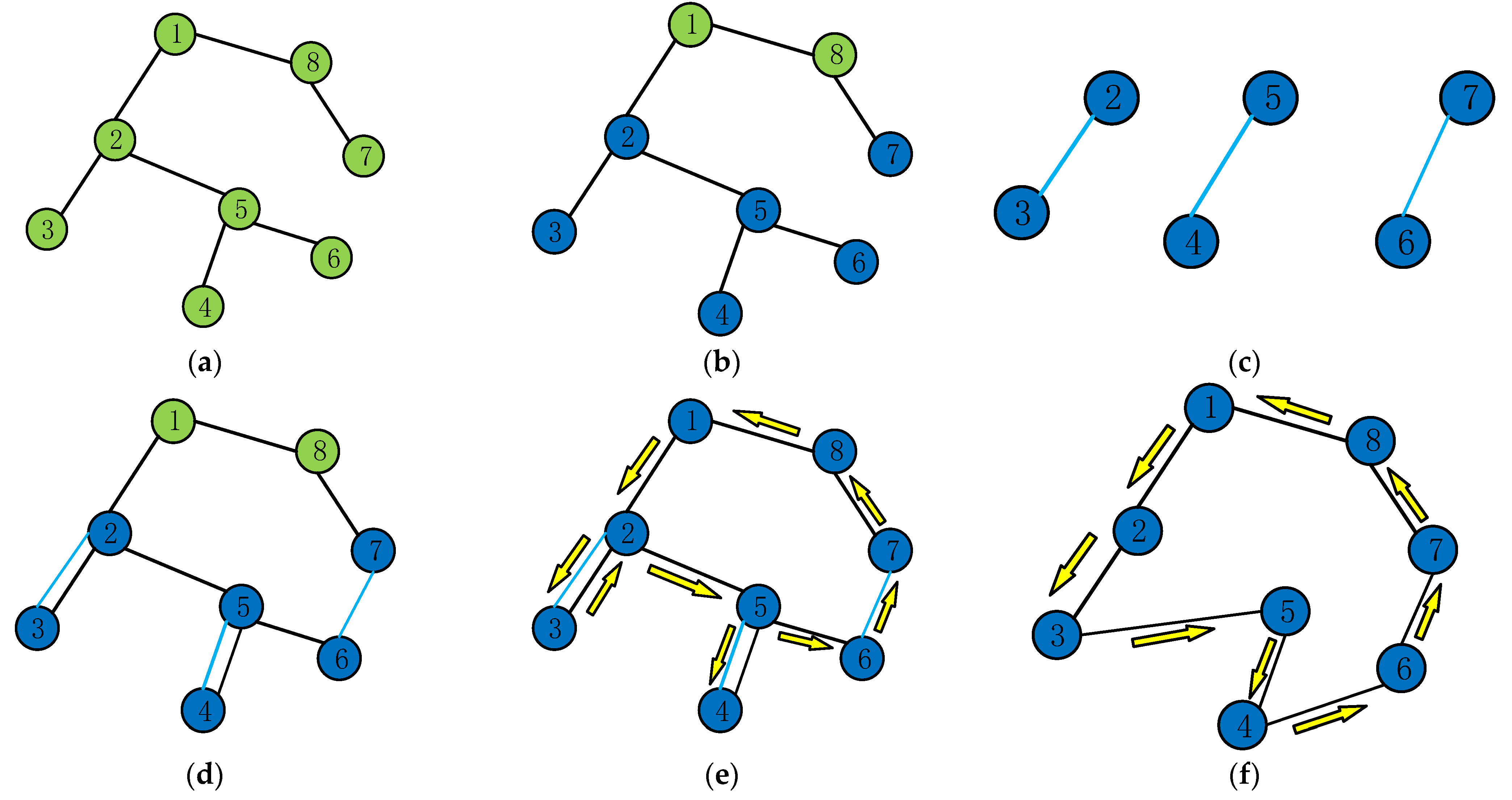
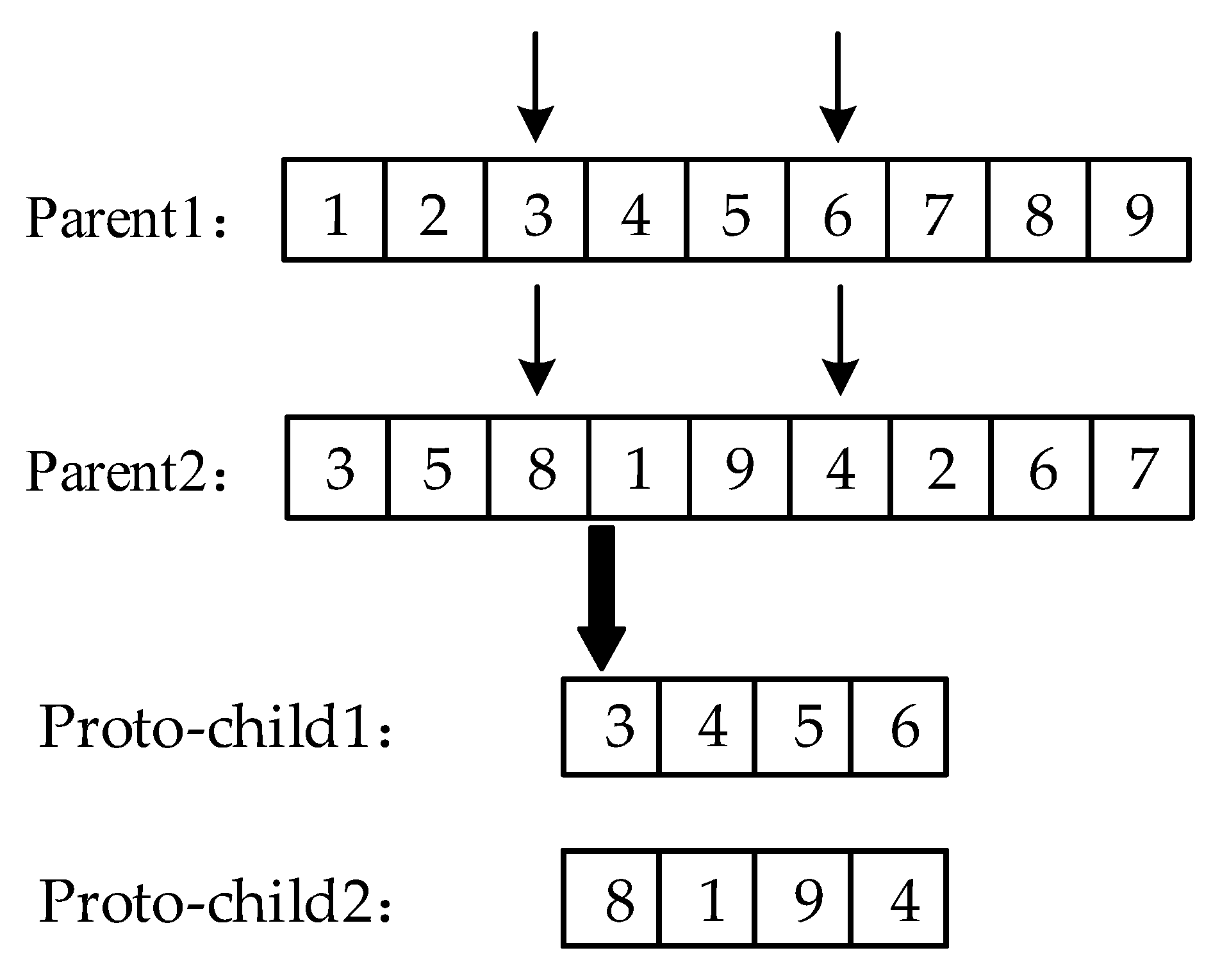
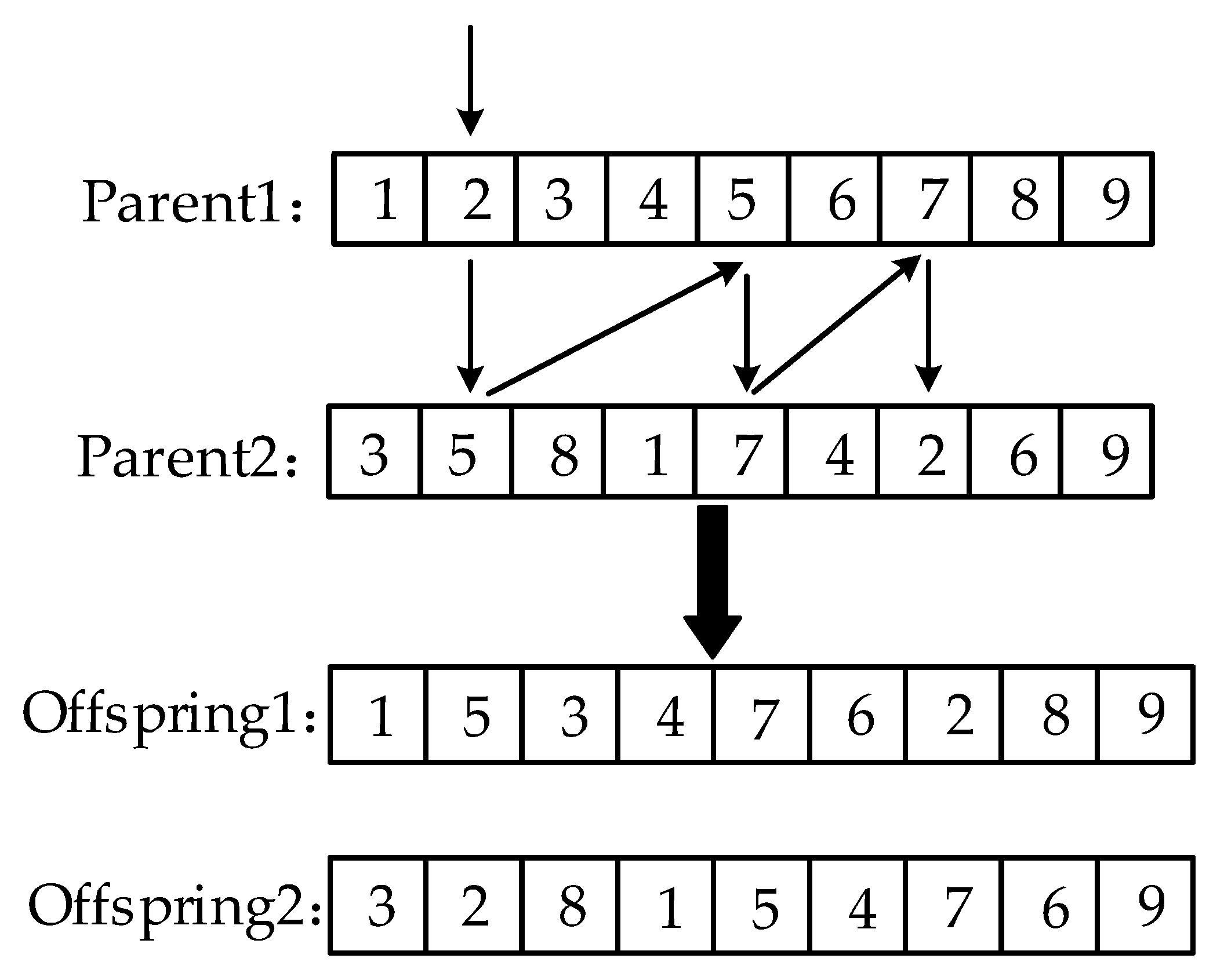
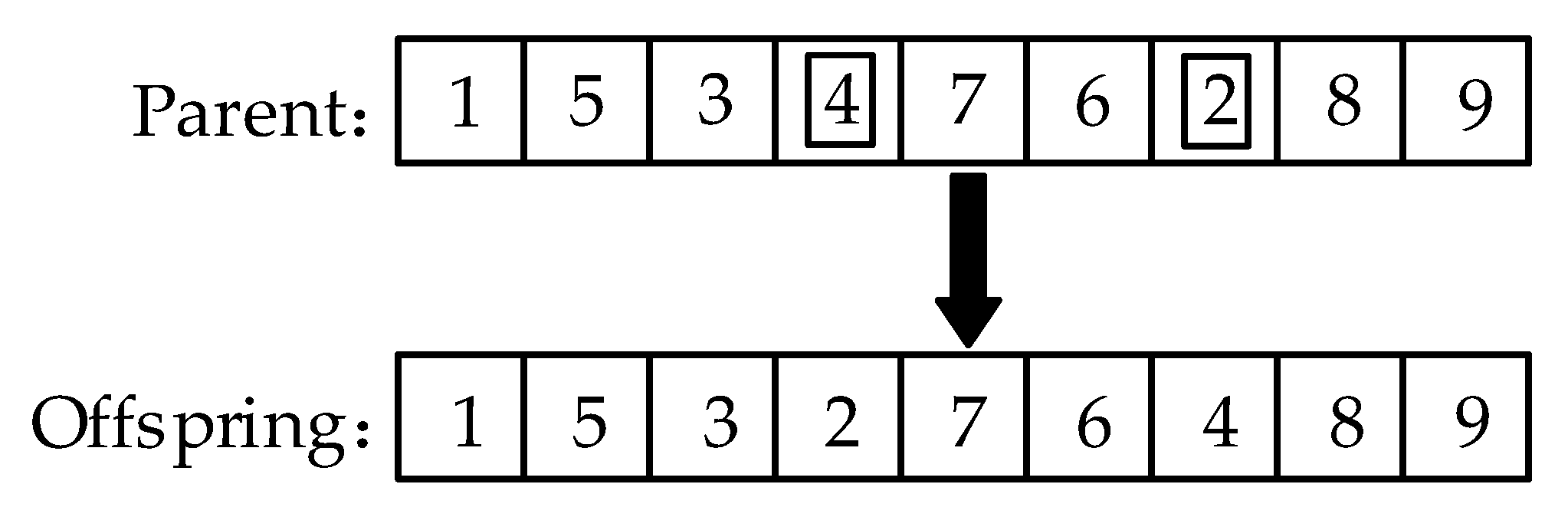
2.3.2. Double Choice Operator
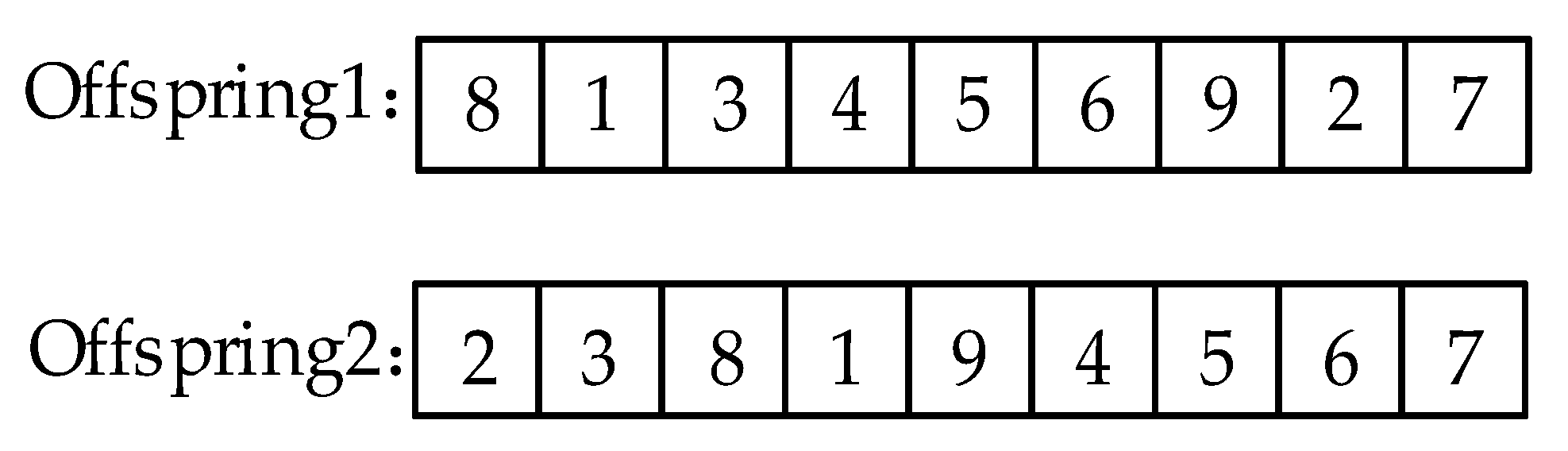
2.3.3. Double Cross Operator Based on Upper Bound on Energy Consumption
2.3.4. Based on the Energy Consumption Upper Bound Mutation Operator
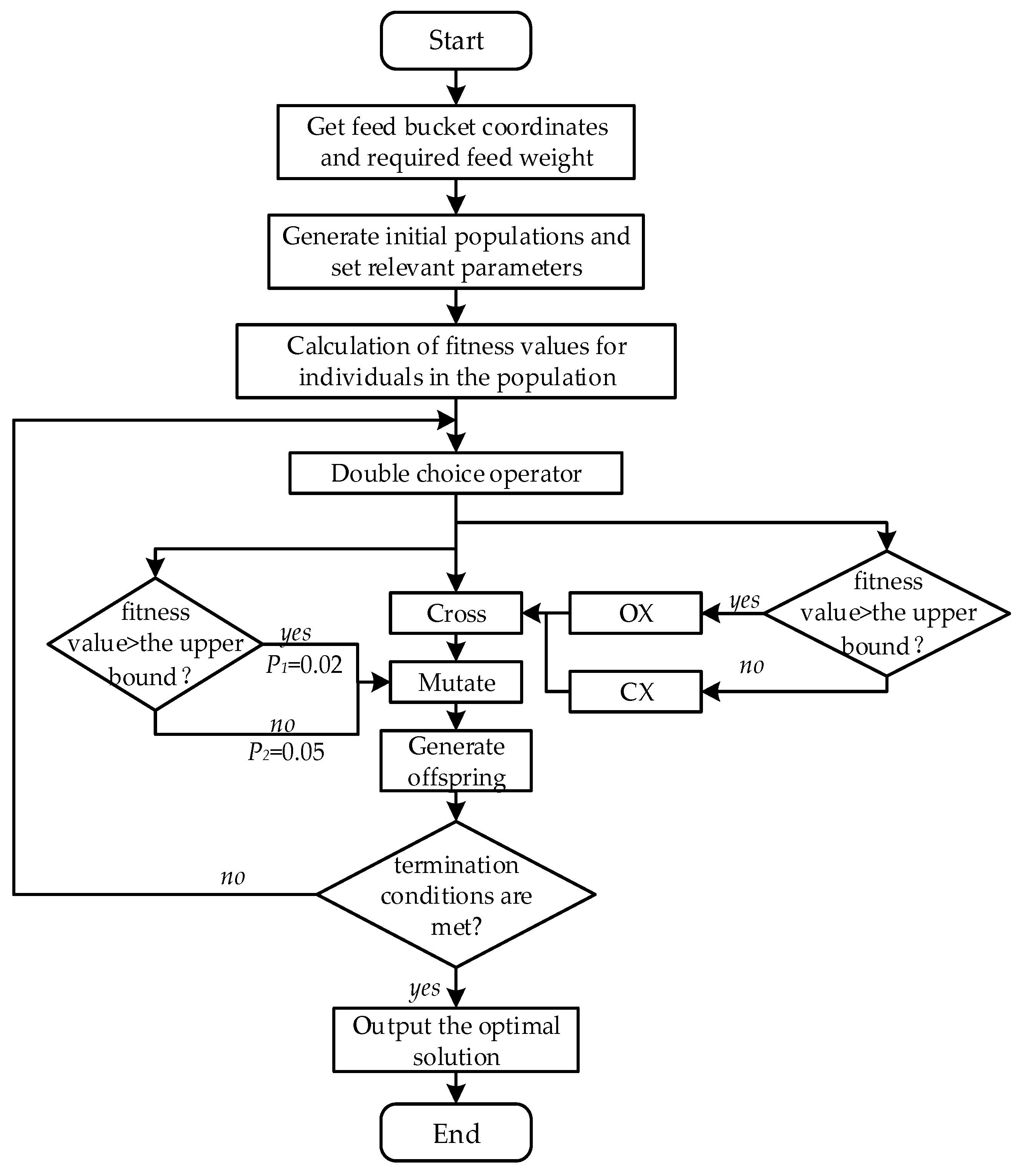
2.3.5. Flow of the Large Scale Feeding Point Path Planning Approach
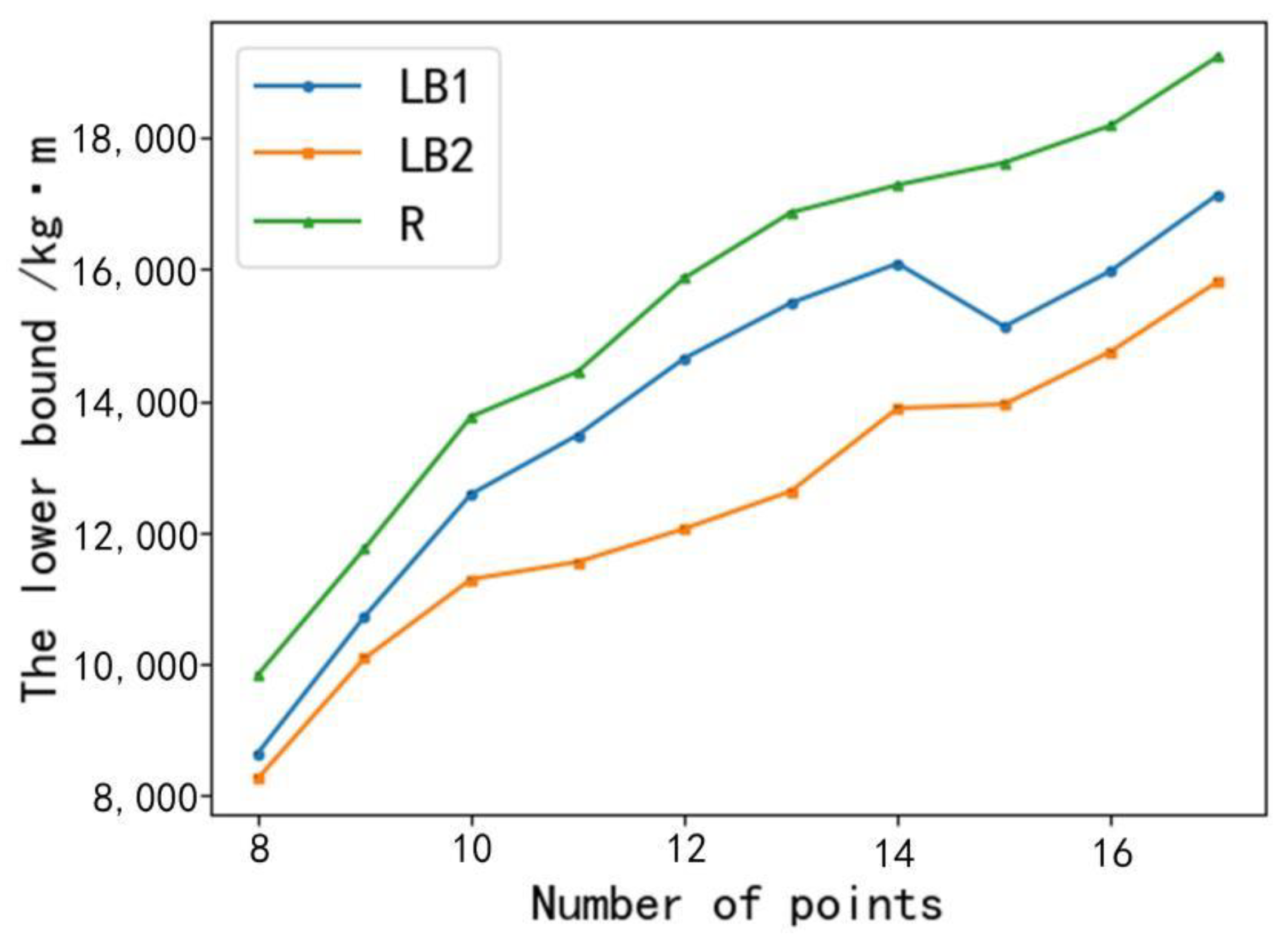
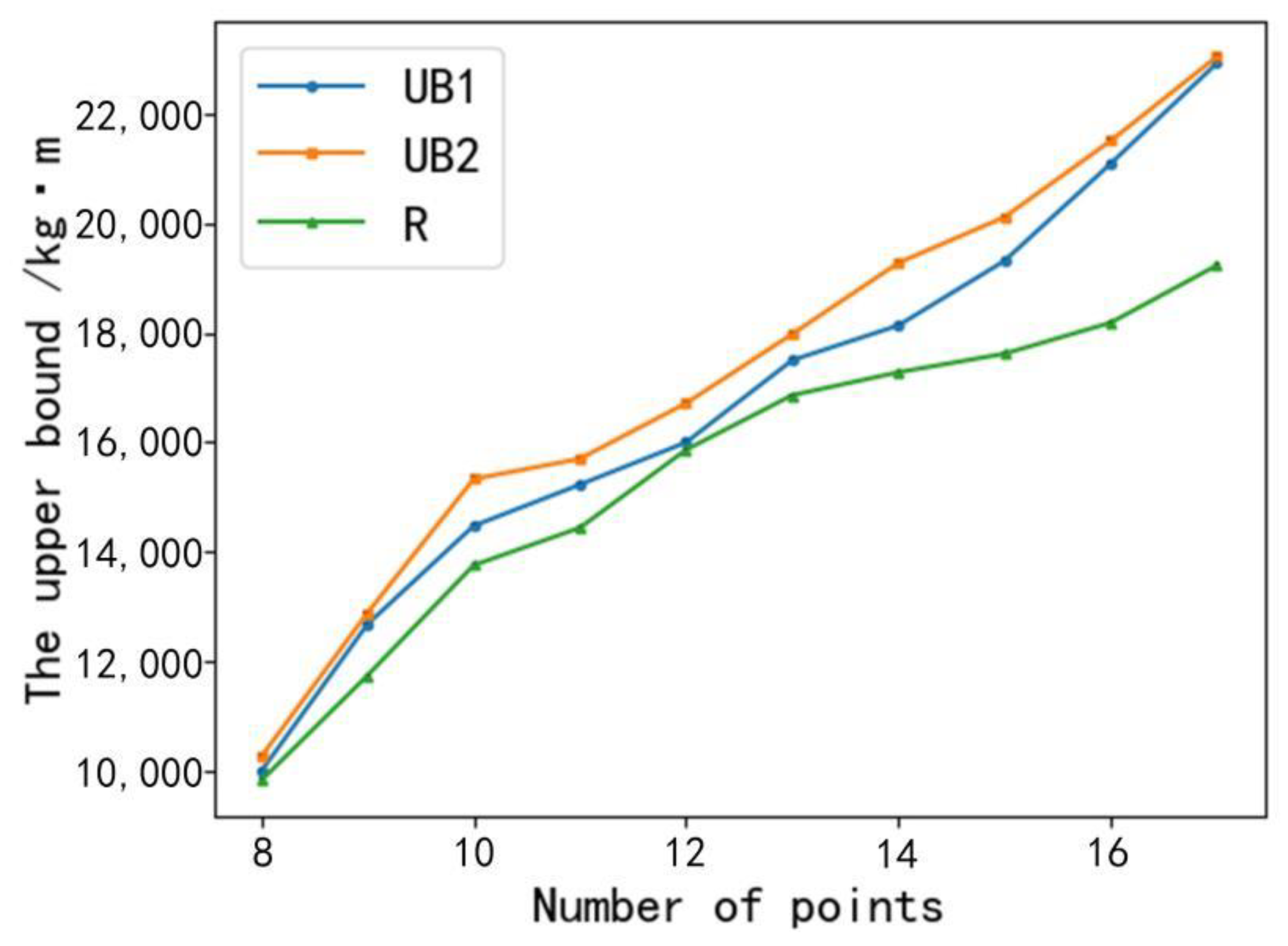
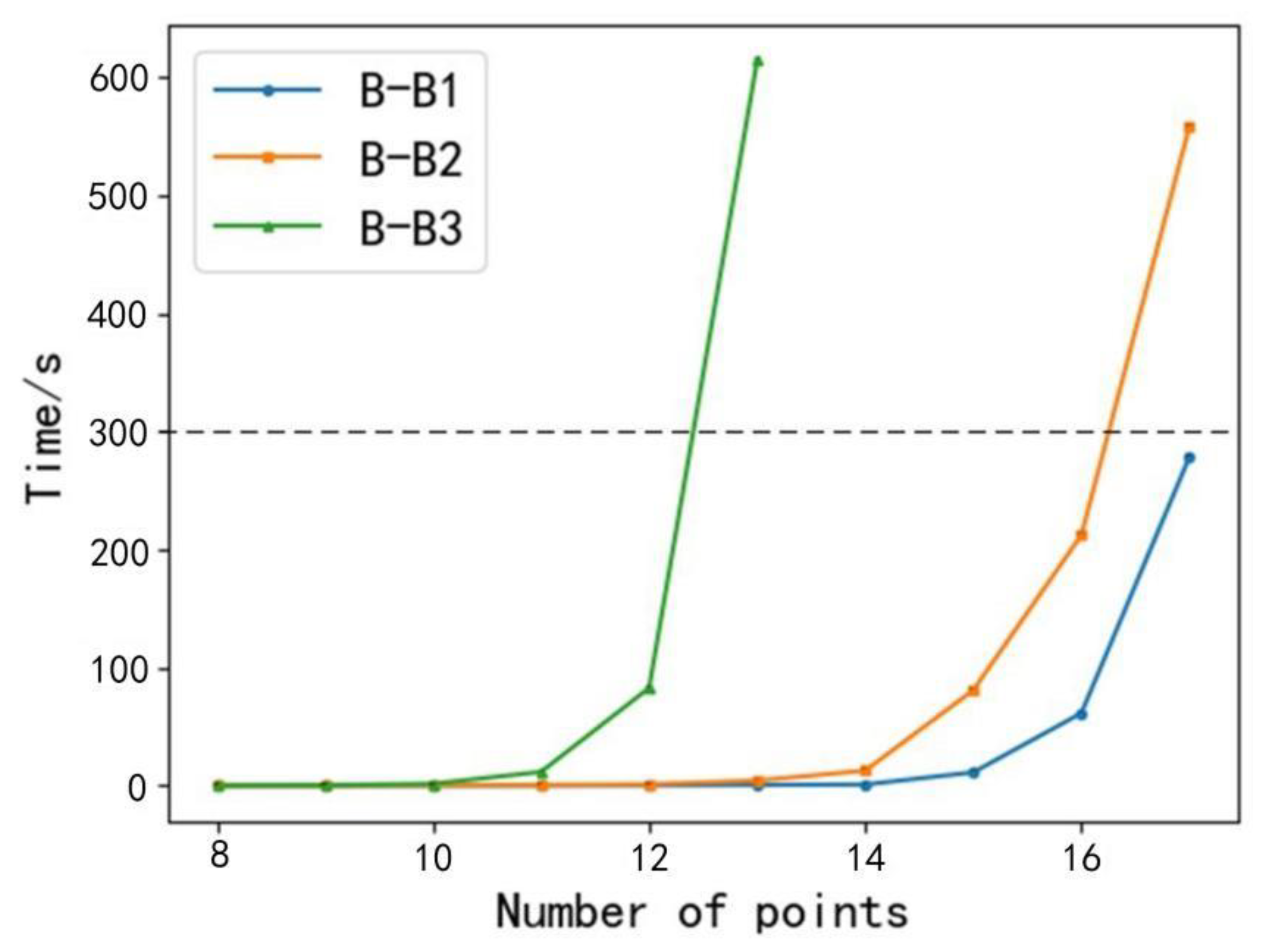
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| G | a complete graph representing the smart farm |
| V | the set of feed buckets in the farm |
| E | the set of edges of the complete graph G |
| LB | the lower bound |
| UB | the upper bound |
| Gm | a complete graph representing the smart farm with feed buckets lacking feed |
| Vm | the set of feed buckets lacking feed in the farm, include the starting and the final return point of the feeding robot |
| V1 | the set of feed buckets in the farm |
| Em | the set of edges of the complete graph Gm |
| B | a complete path of the feeding robot |
| PLB | partial lower bound |
| LBm−k | lower bound of energy consumption of non driving path points |
| C(Bk) | energy consumption of the determined path |
| Vk | the determined path that feeding robot has traveled |
| Bk | the undetermined path that feeding robot has not traveled |
| OX | order crossover operator |
| CX | cycle crossover operator |
| LB1 | the lower bound obtained by using the approach proposed in this study |
| LB2 | the lower bound of energy consumption obtained by the minimum spanning tree algorithm |
| R | the exact result of energy consumption |
| UB1 | the upper bound of energy consumption obtained by the Christofides’s Heuristic algorithm |
| UB2 | the upper bound of energy consumption obtained by greedy algorithm |
| B-B1 | the branch and bound algorithm proposed in this study |
| B-B2 | change the calculation method of obtaining the upper bound of B-B1 to the greedy algorithm, and the rest is same as B-B2 |
| B-B3 | change the calculation method of obtaining the lower bound of B-B1 to the minimum spanning tree method, and the rest is same as B-B2 |
| GA-1 | the double-crossing operator genetic algorithm based on the upper bound of energy consumption described in this study |
| GA-2 | genetic algorithm with only use order crossover operator as its crossover operator |
References
- Uehleke, R.; Seifert, S.; Hüttel, S. Do animal welfare schemes promote better animal health? An empirical investigation of german pork production. Livest. Sci. 2021, 247, 104481. [Google Scholar] [CrossRef]
- Iannetti, L.; Neri, D.; Santarelli, G.A.; Cotturone, G.; Vulpiani, M.P.; Salini, R.; Antoci, S.; Di Serafino, G.; Di Giannatale, E.; Pomilio, F.; et al. Animal welfare and microbiological safety of poultry meat: Impact of different at-farm animal welfare levels on at-slaughterhouse Campylobacter and Salmonella contamination. Food Control 2020, 109, 106921. [Google Scholar] [CrossRef]
- Temple, D.; Manteca, X.; Velarde, A.; Dalmau, A. Assessment of animal welfare through behavioural parameters in Iberian pigs in intensive and extensive conditions. Appl. Anim. Behav. Sci. 2011, 131, 29–39. [Google Scholar] [CrossRef]
- Wang, T.; Xu, X.; Wang, C.; Li, Z.; Li, D. From smart farming towards unmanned farms: A new mode of agricultural production. Agriculture 2021, 11, 145. [Google Scholar] [CrossRef]
- Wicaksono, M.G.S.; Suryani, E.; Hendrawan, R.A. Increasing productivity of rice plants based on IoT (Internet Of Things) to realize Smart Agriculture using System Thinking approach. Procedia Comput. Sci. 2022, 197, 607–616. [Google Scholar] [CrossRef]
- Tao, W.; Zhao, L.; Wang, G.; Liang, R. Review of the internet of things communication technologies in smart agriculture and challenges. Comput. Electron. Agric. 2021, 189, 106352. [Google Scholar] [CrossRef]
- Osinga, S.A.; Paudel, D.; Mouzakitis, S.A.; Athanasiadis, I.N. Big data in agriculture: Between opportunity and solution. Agric. Syst. 2022, 195, 103298. [Google Scholar] [CrossRef]
- Torky, M.; Hassanein, A.E. Integrating blockchain and the internet of things in precision agriculture: Analysis, opportunities, and challenges. Comput. Electron. Agric. 2020, 178, 105476. [Google Scholar] [CrossRef]
- Eli-Chukwu, N.C. Applications of artificial intelligence in agriculture: A review. Eng. Technol. Appl. Sci. Res. 2019, 9, 4377–4383. [Google Scholar] [CrossRef]
- da Silveira, F.; Lermen, F.H.; Amaral, F.G. An overview of agriculture 4.0 development: Systematic review of descriptions, technologies, barriers, advantages, and disadvantages. Comput. Electron. Agric. 2021, 189, 106405. [Google Scholar] [CrossRef]
- Wan, J.; Li, J.; Hua, Q.; Celesti, A.; Wang, Z. Intelligent equipment design assisted by Cognitive Internet of Things and industrial big data. Neural Comput. Appl. 2020, 32, 4463–4472. [Google Scholar] [CrossRef]
- Shi, Y.L. Application of artificial intelligence technology in modern agricultural production. S. Agric. Mach. 2019, 50, 14–73. [Google Scholar]
- Aquilani, C.; Confessore, A.; Bozzi, R.; Sirtori, F.; Pugliese, C. Precision Livestock Farming technologies in pasture-based livestock systems. Animal 2022, 16, 100429. [Google Scholar] [CrossRef] [PubMed]
- Vaintrub, M.O.; Levit, H.; Chincarini, M.; Fusaro, I.; Giammarco, M.; Vignola, G. Precision livestock farming, automats and new technologies: Possible applications in extensive dairy sheep farming. Animal 2021, 15, 100143. [Google Scholar] [CrossRef] [PubMed]
- Ren, G.; Lin, T.; Ying, Y.; Chowdhary, G.; Ting, K.C. Agricultural robotics research applicable to poultry production: A review. Comput. Electron. Agric. 2020, 169, 105216. [Google Scholar] [CrossRef]
- Wang, Z.; Zeng, Q. A branch-and-bound approach for AGV dispatching and routing problems in automated container terminals. Comput. Ind. Eng. 2022, 166, 107968. [Google Scholar] [CrossRef]
- Meneguzzi, C.C.; da Silva, G.F.; Mauri, G.R.; de Mendonça, A.R.; de Barros Junior, A.A. Routing model applied to forest inventory vehicles planning. Comput. Electron. Agric. 2020, 175, 105544. [Google Scholar] [CrossRef]
- Thakar, S.; Malhan, R.K.; Bhatt, P.M.; Gupta, S.K. Area-coverage planning for spray-based surface disinfection with a mobile manipulator. Robot. Auton. Syst. 2021, 147, 103920. [Google Scholar] [CrossRef]
- Xie, X.; Tang, Z.; Cai, J. The multi-objective inspection path-planning in radioactive environment based on an improved ant colony optimization algorithm. Prog. Nucl. Energy 2021, 144, 104076. [Google Scholar] [CrossRef]
- Mahmud, M.S.A.; Abidin, M.S.Z.; Mohamed, Z.; Abd Rahman, M.K.I.; Iida, M. Multi-objective path planner for an agricultural mobile robot in a virtual greenhouse environment. Comput. Electron. Agric. 2019, 157, 488–499. [Google Scholar] [CrossRef]
- Zacharia, P.T.; Aspragathos, N.A. Optimal robot task scheduling based on genetic algorithms. Robot. Comput. Integr. Manuf. 2005, 21, 67–79. [Google Scholar] [CrossRef]
- Zajac, S.; Huber, S. Objectives and approachs in multi-objective routing problems: A survey and classification scheme. Eur. J. Oper. Res. 2021, 290, 1–25. [Google Scholar] [CrossRef]
- Laporte, G. The vehicle routing problem: An overview of exact and approximate algorithms. Eur. J. Oper. Res. 1992, 59, 345–358. [Google Scholar] [CrossRef]
- Bukata, L.; Šůcha, P.; Hanzálek, Z. Optimizing energy consumption of robotic cells by a Branch & Bound algorithm. Comput. Oper. Res. 2019, 102, 52–66. [Google Scholar]
- Hardy, G.H.; Littlewood, J.E.; Pólya, G.; Pólya, G. Inequalities; Cambridge University Press: Cambridge, UK, 1952. [Google Scholar]
- Cook, W.; Lovász, L.; Seymour, P.D. (Eds.) Combinatorial Optimization: Papers from the DIMACS Special Year; American Mathematical Society: Providence, RI, USA, 1995; Volume 20. [Google Scholar]
- Qu, L.; Sun, R. A synergetic approach to genetic algorithms for solving traveling salesman problem. Inf. Sci. 1999, 117, 267–283. [Google Scholar] [CrossRef]
- Xue, Y.; Zhu, H.; Liang, J.; Słowik, A. Adaptive crossover operator based multi-objective binary genetic algorithm for feature selection in classification. Knowl.-Based Syst. 2021, 227, 107218. [Google Scholar] [CrossRef]
- Kaya, M. The effects of two new crossover operators on genetic algorithm performance. Appl. Soft Comput. 2011, 11, 881–890. [Google Scholar] [CrossRef]
- Kumar, N.; Karambir, R.K. A comparative analysis of pmx, cx and ox crossover operators for solving traveling salesman problem. Int. J. Latest Res. Sci. Technol. 2012, 1, 98–101. [Google Scholar]
- Herrera, F.; Lozano, M. Gradual distributed real-coded genetic algorithms. IEEE Trans. Evol. Comput. 2000, 4, 43–63. [Google Scholar] [CrossRef]
- Morais, V.; da Cunha, A.S.; Mahey, P. A Branch-and-cut-and-price algorithm for the Stackelberg Minimum Spanning Tree Game. Electron. Notes Discret. Math. 2016, 52, 309–316. [Google Scholar] [CrossRef][Green Version]
- Karabulut, K.; Tasgetiren, M.F. A variable iterated greedy algorithm for the traveling salesman problem with time windows. Inf. Sci. 2014, 279, 383–395. [Google Scholar] [CrossRef]
- Sandamurthy, K.; Ramanujam, K. A hybrid weed optimized coverage path planning technique for autonomous harvesting in cashew orchards. Inf. Process. Agric. 2020, 7, 152–164. [Google Scholar] [CrossRef]
- Dell’Amico, M.; Montemanni, R.; Novellani, S. Algorithms based on branch and bound for the flying sidekick traveling salesman problem. Omega 2021, 104, 102493. [Google Scholar] [CrossRef]
- Ha, Q.M.; Deville, Y.; Pham, Q.D.; Hà, M.H. On the min-cost traveling salesman problem with drone. Transp. Res. Part C Emerg. Technol. 2018, 86, 597–621. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Sun, W.; Yang, J.; Wu, W.; Miao, H.; Zhang, S. An Approach for Autonomous Feeding Robot Path Planning in Poultry Smart Farm. Animals 2022, 12, 3089. https://doi.org/10.3390/ani12223089
Zhang Y, Sun W, Yang J, Wu W, Miao H, Zhang S. An Approach for Autonomous Feeding Robot Path Planning in Poultry Smart Farm. Animals. 2022; 12(22):3089. https://doi.org/10.3390/ani12223089
Chicago/Turabian StyleZhang, Yanjun, Weiming Sun, Jian Yang, Weiwei Wu, Hong Miao, and Shanwen Zhang. 2022. "An Approach for Autonomous Feeding Robot Path Planning in Poultry Smart Farm" Animals 12, no. 22: 3089. https://doi.org/10.3390/ani12223089
APA StyleZhang, Y., Sun, W., Yang, J., Wu, W., Miao, H., & Zhang, S. (2022). An Approach for Autonomous Feeding Robot Path Planning in Poultry Smart Farm. Animals, 12(22), 3089. https://doi.org/10.3390/ani12223089





