Breeding Strategies to Optimize Effective Population Size in Low Census Captive Populations: The Case of Gazella cuvieri
Abstract
Simple Summary
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Species
2.2. Strategies to Minimize the Parents’ Coancestry
- For minimum coancestry (F), , where Cjk is the coancestry between male j and female k. In this strategy, all the females were involved in the solution. Two alternatives were checked:
- Strategy F0, i.e., not all males were expected to contribute offspring to the next generation;
- Strategy F1, i.e., all males were expected to contribute offspring to the next generation.
- For minimum increase in coancestry (ΔF), where [15], with gj and gk, being the equivalent discrete generations known for individuals j and k [29,30]. Since coancestry accumulates per generation, under this strategy increases in coancestry were corrected for individual differences in pedigree depth. Again, there were two alternatives:
- Strategy ΔF0, i.e., not all males were expected to contribute offspring to the next generation;
- Strategy ΔF1, i.e., all the males were expected to contribute offspring to the next generation.
- The strategy for minimum coancestry free (Ff) was similar to Strategy F1, but, in this case, not all the females were expected to contribute offspring to the next generation, while other females had a higher number of descendants.
- For minimum weighted coancestry (mFm), , where mj (mk) is the mean coancestries between the individual j (k) and all the other animals in the mating group. This strategy is employed to account for the current representation of each individual in the group and penalizes those already highly represented. Two alternatives were checked:
- Strategy mFm0, i.e., not all males were expected to contribute offspring to the next generation;
- Strategy mFm1, i.e., all the males were expected to contribute offspring to the next generation.
- For minimum weighted increase in coancestry (ΔmΔFΔm), , where Δmj and Δmk are the mean of the increase in coancestries [19] between the corresponding individuals and all the other animals involved in the mating plan. This strategy simultaneously accounts for the possible differences in pedigree among the animals, and their current representation, again with two options:
- Strategy ΔmΔFΔm0, i.e., not all males were expected to contribute offspring to the next generation;
- Strategy ΔmΔFΔm1, i.e., all the males were expected to contribute offspring to the next generation.
2.3. Strategies to Minimize the Offspring Coancestry
- 6.
- For minimum offspring coancestry (C), , where Clm is the coancestry between two offsprings l and m of the mating design. Each mating was assumed to provide exactly one offspring for the next generation and two alternatives were also checked:
- Strategy C0, i.e., not all males were expected to contribute offspring to the next generation;
- Strategy C1, i.e., all the males were expected to contribute offspring to the next generations.
- 7.
- For minimum offspring increase in coancestry (ΔC), , where ΔClm is the increase in the coancestry [15] between two offspring l and m of the mating design. Each mating only provides exactly one offspring, and also with two alternatives:
- Strategy ΔC0, i.e., not all males were expected to contribute offspring to the next generation;
- Strategy ΔC1, i.e., all the males were expected to contribute offspring to the next generations.
- 8.
- The strategy for minimum offspring coancestry free (Cf) was similar to Strategy 6 (C), but, in this case, not all the females were expected to contribute offspring to the next generation, while other females had a higher number of descendants.
- 9.
- The strategy for minimum offspring increases in coancestry free (ΔCf) was similar to Strategy 7 (ΔC) but, in this case, not all the females participated with offspring for the next generation.
2.4. Mixed Strategies
- 10.
- The strategy for mixing information from two generations (mix) was a combination of Strategies 1 and 6, i.e., . All terms in the expression are already given above, being p1 a value between 0 and 1 indicating the weighting to be given in the coancestry in the previous generation. These values were tested, and all females were expected to contribute at least one offspring to the next generation, but not all males. The following values were tested for p1: 0.01 (mix 1–99), 0.05 (mix 5–95), 0.50 (mix 50–50), and 0.95 (mix 95–5).
- 11.
- The strategy for mixing information from two generations free (mixf) was similar to Strategy 10 (mix) but, in this case, not all males and all females were expected to have an offspring for the next generation, while other females had a higher number of descendants. These scenarios were called mixf 1–99, mixf 5–95, mixf 50–50, and mixf 95–5.
2.5. Computations Performed
3. Results
3.1. Almería Population
3.2. La Lajita Population
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gicquel, E.; Boettcher, P.; Besbes, B.; Furre, S.; Fernández, J.; Danchin-Burge, C.; Berger, B.; Baumung, R.; Feijóo, J.R.J.; Leroy, G. Impact of conservation measures on demography and genetic variability of livestock breeds. Animal 2020, 14, 670–680. [Google Scholar] [CrossRef]
- Álvarez, I.; Royo, L.J.; Gutiérrez, J.P.; Fernández, I.; Arranz, J.J.; Goyache, F. Relationship between genealogical and microsatellite information characterizing losses of genetic variability: Empirical evidence from the rare Xalda sheep breed. Livest. Sci. 2008, 115, 80–88. [Google Scholar] [CrossRef]
- Cervantes, I.; Gutiérrez, J.P.; Meuwissen, T.H. Response to selection while maximizing genetic variance in small populations. Genet. Sel. Evol. 2016, 48, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Granleese, T.; Clark, S.A.; Swan, A.A.; Van der Werf, J.H. Increased genetic gains in sheep, beef and dairy breeding programs from using female reproductive technologies combined with optimal contribution selection and genomic breeding values. Genet. Sel. Evol. 2015, 14, 47–70. [Google Scholar] [CrossRef] [PubMed]
- Collen, B.; Ram, M.; Dewhurst, N.; Clausnitzer, V.; Kalkman, V.; Cumberlidge, N.; Baillie, J.E.M. Broadening the Coverage of Biodiversity Assessments. In 2008 Rev IUCN Red List Threat Species; IUCN: Gland, Switzerland, 2008; pp. 1–12. [Google Scholar]
- Frankham, R.; Ballou, J.D.; Briscoe, D.A.; McInnes, K.H. Introduction to Conservation Genetics, 1st ed.; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Caballero, A.; Toro, M.A. Interrelations between effective population size and other pedigree tools for the management of conserved populations. Genet. Res. 2000, 75, 331–343. [Google Scholar] [CrossRef] [PubMed]
- Ballou, J.D.; Lacy, R.C. Identifying Genetically Important Individuals for Management of Genetic Diversity in Pedigreed Populations. In Population Management for Survival and Recovery: Analytical Methods and Strategies in Small Population Conservation, 2nd ed.; Ballou, J.D., Gilpin, M., Foose, T.J., Eds.; Columbia Press: New York, NY, USA, 1995; pp. 76–111. [Google Scholar]
- Caballero, A.; Fernández, J. A comparison of management strategies for conservation with regard to population fitness. Conserv. Genet. 2001, 2, 121–131. [Google Scholar]
- Fernández, J.; Toro, M.A.; Caballero, A. Fixed Contributions Designs vs. Minimization of Global Coancestry to Control Inbreeding in Small Populations. Genetics 2003, 165, 885–894. [Google Scholar] [CrossRef]
- Notter, D.R. The importance of genetic diversity in livestock populations of the future. J. Anim. Sci. 1999, 7, 61–69. [Google Scholar] [CrossRef]
- Groeneveld, L.F.; Lenstra, J.A.; Eding, H.; Toro, M.A.; Scherf, B.; Pilling, D.; Negrini, R.; Finlay, E.K.; Jianlin, H.; Groeneveld, E.; et al. The GLOBALDIV Consortium. “Genetic diversity in farm animals—A review. Anim. Genet. 2010, 21, 6–31. [Google Scholar] [CrossRef]
- Wang, J. More efficient breeding systems for controlling inbreeding and effective size in animal populations. Heredity 1997, 79, 591–599. [Google Scholar] [CrossRef]
- Falconer, D.S.; Mackay, T.F. Introduction to Quantitative Genetics, 4th ed.; Longman House: Harlow, UK, 1996. [Google Scholar]
- Ivy, J.A.; Lacy, R.C. A comparison of strategies for selecting breeding pairs to maximize genetic diversity retention in managed populations. J. Hered. 2001, 103, 186–196. [Google Scholar] [CrossRef]
- Caballero, A.; Toro, M.A. Analysis of genetic diversity for the management of conserved subdivided populations. Conserv. Genet. 2002, 3, 289–299. [Google Scholar] [CrossRef]
- Cervantes, I.; Goyache, F.; Molina, A.; Valera, M.; Gutiérrez, J.P. Application of individual increase in inbreeding to estimate realized effective sizes from real pedigrees. J. Anim. Breed. Genet. 2008, 125, 301–310. [Google Scholar] [CrossRef] [PubMed]
- Gutiérrez, J.P.; Cervantes, I.; Goyache, F. Improving the estimation of realized effective population sizes in farm animals. J. Anim. Breed. Genet. 2009, 126, 327–332. [Google Scholar] [CrossRef]
- Cervantes, I.; Goyache, F.; Molina, A.; Valera, M.; Gutiérrez, J.P. Estimation of effective population size from the rate of coancestry in pedigreed populations. J. Anim. Breed. Genet. 2011, 128, 56–63. [Google Scholar] [CrossRef] [PubMed]
- Leroy, G.; Mary-Huard, T.; Verrier, E.; Danvy, S.; Charvolin, E.; Danchin-Burge, C. Methods to estimate effective population size using pedigree data: Examples in dog, sheep, cattle and horse. Genet. Sel. Evol. 2013, 45, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Moreno, E.; Espeso, G. Cuvier’s gazelle International Studbook. In Managing and Husbandry Guidelines; Ayuntamiento de Roquetas de Mar: Almería, Spain, 2008. [Google Scholar]
- Ibáñez, B.; Cervantes, I.; Gutiérrez, J.P.; Goyache, F.; Moreno, E. Estimates of direct and indirect effects for early juvenile survival in captive populations maintained for conservation purposes: The case of Cuvier’s gazelle. Ecol. Evol. 2014, 4, 4117–4129. [Google Scholar] [CrossRef] [PubMed]
- Beudels, R.C.; Devillers, P.; Lafontaine, R.M.; Devillers-Terschuren, J.; Beudels, M.O. Sahelo-Saharan Antelopes. In Status and Perspectives; UNEP/CMS Secretariat: Bonn, Germany, 2005; pp. 57–70. [Google Scholar]
- IUCN. Conservation Strategy and Action Plan for Cuvier’s Gazelle (Gazella Cuvieri) in North Africa 2017–2026; IUCN: Gland, Switzerland; Malaga, Spain, 2018. [Google Scholar]
- Cuzin, F. Les Grands Mammifères du Marocméridional (Haut Atlas, Anti-Atlas, Sahara). Distribution, Écologie et Conservation. Ph.D. Thesis, EPHE, Montpellier II, Montpellier, France, 2003. [Google Scholar]
- Gil-Sánchez, J.M.; Herrera-Sánchez, F.J.; Álvarez, B.; Arredondo, A.; Bautista, J.; Cancio, I.; Castillo, S.; Díaz-Portero, M.A.; de Lucas, J.; McCain, E.; et al. Evaluating methods for surveying the Endangered Cuvier’s gazelle Gazella cuvieri in arid landscapes. Oryx 2017, 51, 648–655. [Google Scholar] [CrossRef][Green Version]
- Gutiérrez, J.P.; Goyache, F. A note on ENDOG: A computer program for analysing pedigree information. J. Anim. Breed. Genet. 2005, 122, 172–176. [Google Scholar] [CrossRef]
- Meuwissen, T.H.E.; Luo, Z. Computing inbreeding coefficients in large populations. Genet. Sel. Evol. 1992, 24, 305–313. [Google Scholar] [CrossRef]
- Maignel, L.; Boichard, D.; Verrier, E. Genetic variability of French dairy breeds estimated from pedigree information. Interbull Bull. 1996, 14, 49–54. [Google Scholar]
- Boichard, D.; Maignel, L.; Verrier, É. The value of using probabilities of gene origin to measure genetic variability in a population. Genet. Sel. Evol. 1997, 29, 5–23. [Google Scholar] [CrossRef]
- Sonesson, A.K.; Meuwissen, T.H. Mating schemes for optimum contribution selection with constrained rates of inbreeding. Genet. Sel. Evol. 2009, 32, 231–248. [Google Scholar] [CrossRef] [PubMed]
- Royo, L.J.; Álvarez, I.; Gutiérrez, J.P.; Fernández, I.; Goyache, F. Genetic variability in the endangered Asturcón pony assessed using genealogical and molecular information. Livest. Sci. 2007, 107, 162–169. [Google Scholar] [CrossRef]
- Gómez, M.D.; Sánchez, M.J.; Bartolomé, E.; Cervantes, I.; Poyato-Bonilla, J.; Demyda-Peyrás, S.; Valera, M. Phenotypic and genetic analysis of reproductive traits in horse populations with different breeding purposes. Animal 2020, 14, 1351–1361. [Google Scholar] [CrossRef] [PubMed]
- De La Rosa, A.J.M.; Cervantes, I.; Gutiérrez, J.P. Equivalent effective population size mating as a useful tool in the genetic management of the Ibicenco rabbit breed (Conill Pages d’Eivissa). Czech J. Anim. Sci. 2016, 6, 108–116. [Google Scholar] [CrossRef]
- Li, C.; Jiang, Z.; Li, L.; Li, Z.; Fang, H.; Li, C.; Beauchamp, G. Effects of reproductive status, social rank, sex and group size on vigilance patterns in Przewalski’s gazelle. PLoS ONE 2012, 7, e32607. [Google Scholar] [CrossRef] [PubMed]
- Carson, H.L. Mate choice theory and the mode of selection in sexual populations. Proc. Natl. Acad. Sci. USA 2003, 100, 6584–6587. [Google Scholar] [CrossRef] [PubMed]
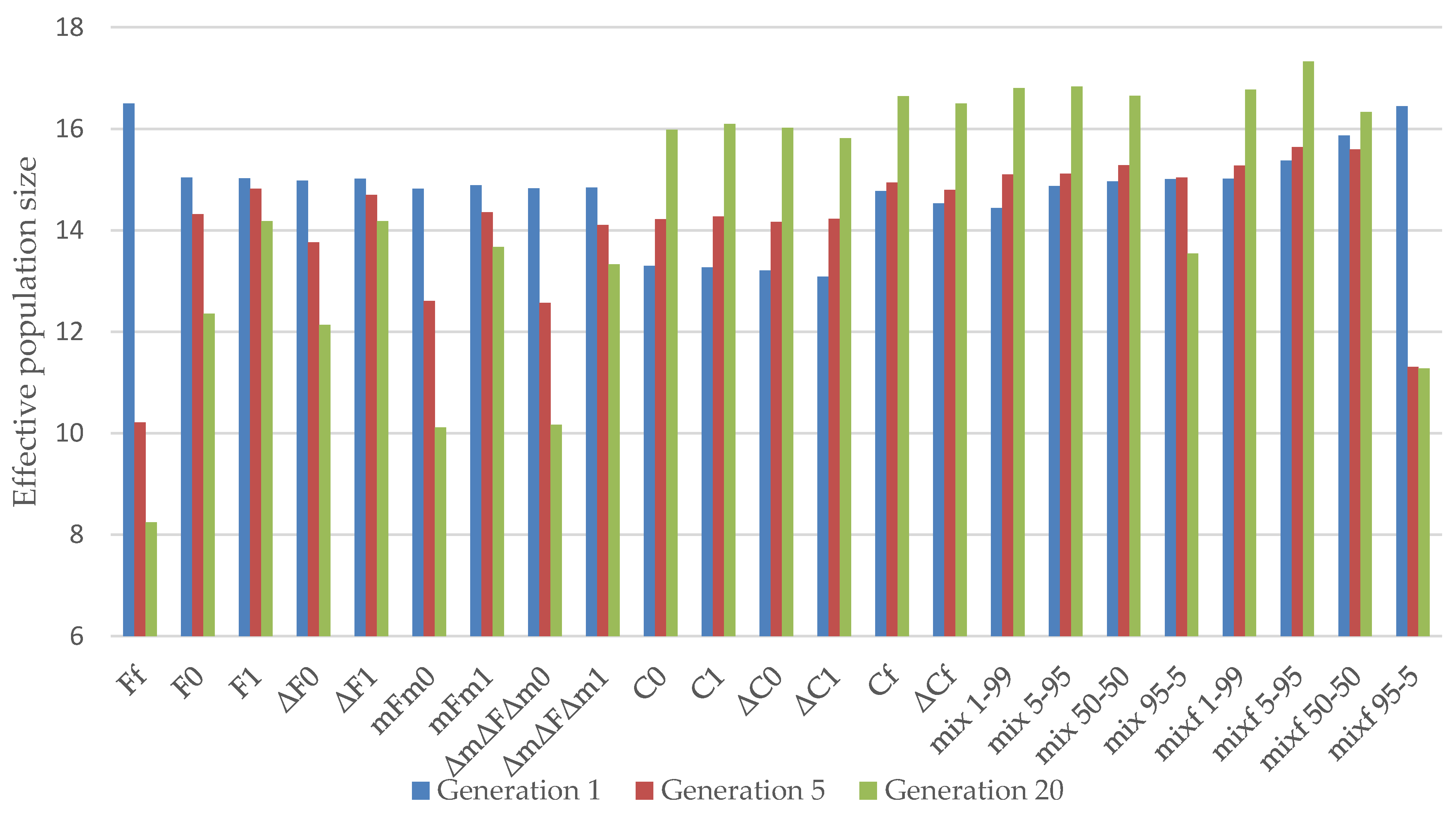
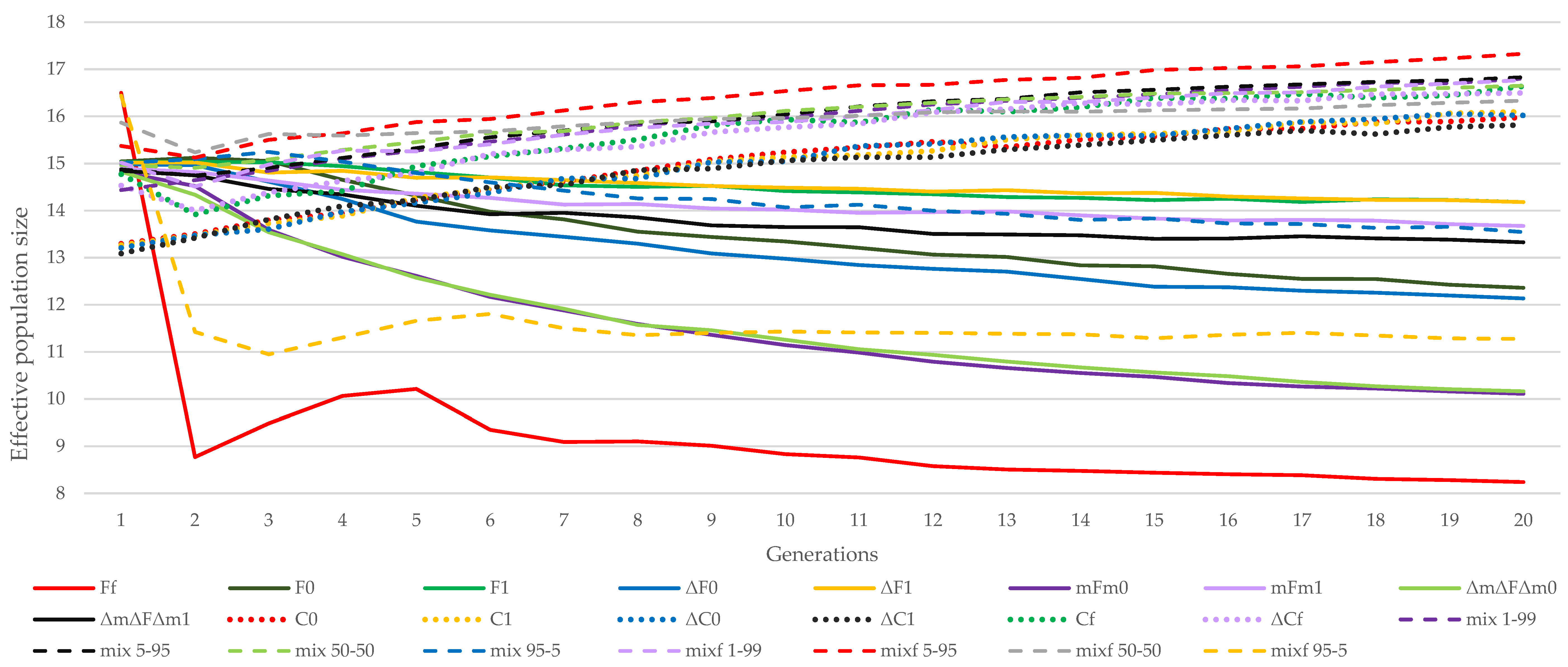


| Population of Almería | Population of La Lajita | |
|---|---|---|
| Males | 6 | 8 |
| Females | 16 | 11 |
| Ratio females/males | 1.80 | 1.30 |
| EG | 8.78 | 9.01 |
| Standard deviation of EG | 0.64 | 1.04 |
| Inbreeding | 0.26 | 0.37 |
| Inbreeding of males | 0.27 | 0.37 |
| Inbreeding of females | 0.24 | 0.37 |
| NeF | 13.27 | 8.91 |
| NeC | 12.90 | 8.14 |
| NeC/NeF | 0.97 | 0.91 |
| Generation interval | 6.36 | 4.88 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ojeda-Marín, C.; Cervantes, I.; Moreno, E.; Goyache, F.; Gutiérrez, J.P. Breeding Strategies to Optimize Effective Population Size in Low Census Captive Populations: The Case of Gazella cuvieri. Animals 2021, 11, 1559. https://doi.org/10.3390/ani11061559
Ojeda-Marín C, Cervantes I, Moreno E, Goyache F, Gutiérrez JP. Breeding Strategies to Optimize Effective Population Size in Low Census Captive Populations: The Case of Gazella cuvieri. Animals. 2021; 11(6):1559. https://doi.org/10.3390/ani11061559
Chicago/Turabian StyleOjeda-Marín, Candela, Isabel Cervantes, Eulalia Moreno, Félix Goyache, and Juan Pablo Gutiérrez. 2021. "Breeding Strategies to Optimize Effective Population Size in Low Census Captive Populations: The Case of Gazella cuvieri" Animals 11, no. 6: 1559. https://doi.org/10.3390/ani11061559
APA StyleOjeda-Marín, C., Cervantes, I., Moreno, E., Goyache, F., & Gutiérrez, J. P. (2021). Breeding Strategies to Optimize Effective Population Size in Low Census Captive Populations: The Case of Gazella cuvieri. Animals, 11(6), 1559. https://doi.org/10.3390/ani11061559








