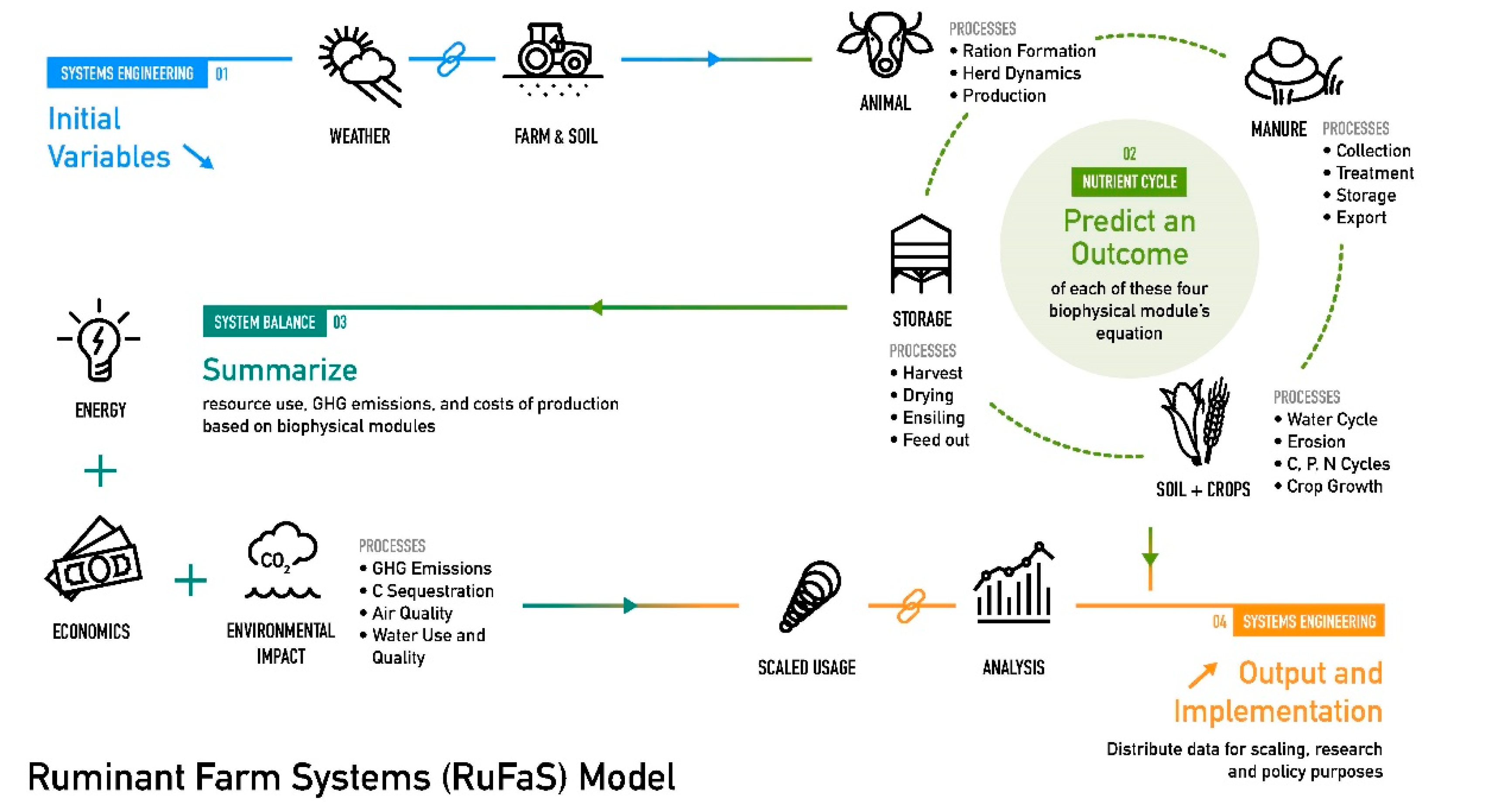
The Ruminant Farm Systems Animal Module: A Biophysical Description of Animal Management
Abstract
Simple Summary
Abstract
1. Introduction
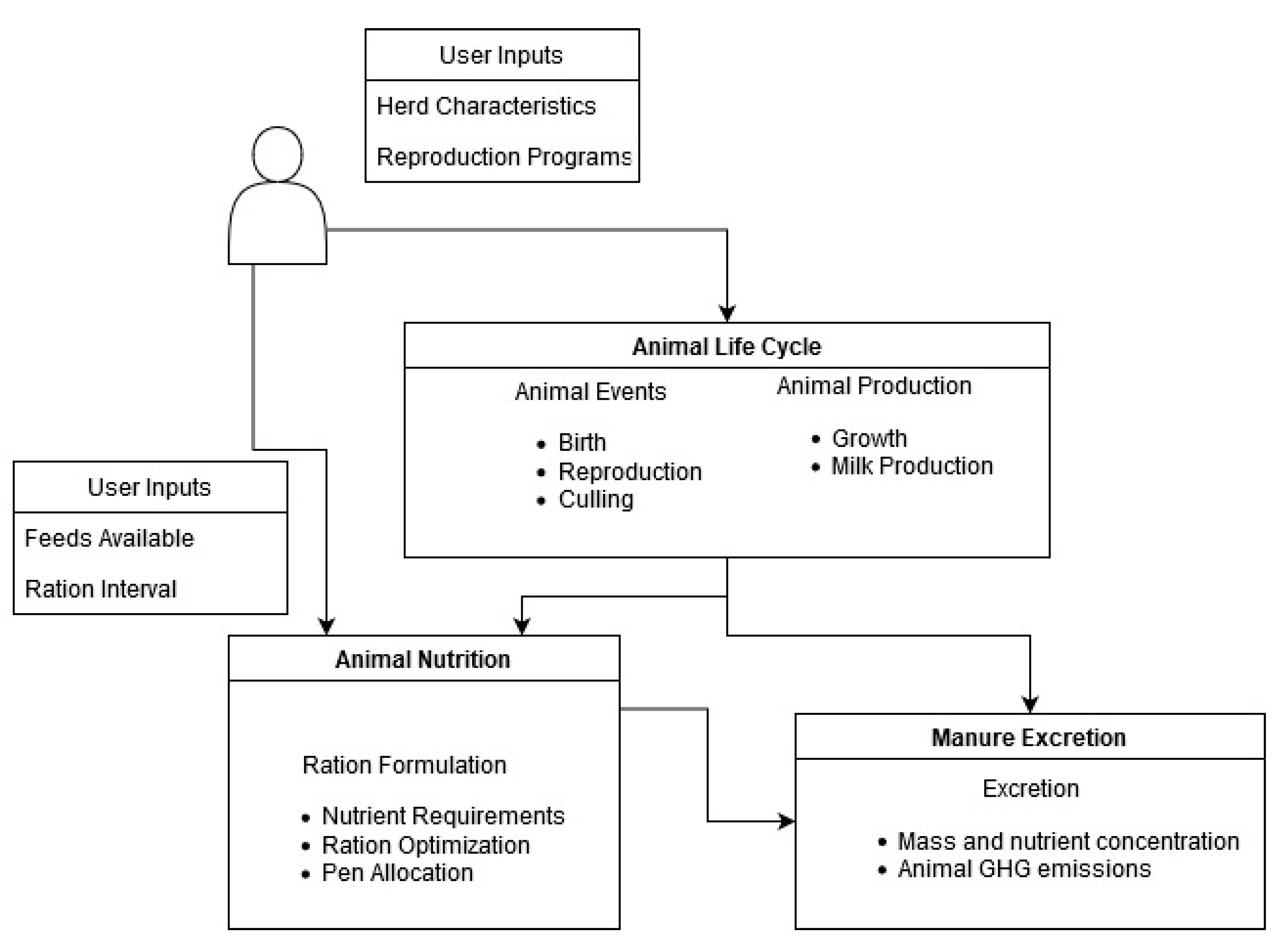
2. Materials and Methods
−20/65 × exp(1-days in milk/65) + 20/(65^2) × days in milk × exp(1-days in milk/65) if parity = 1
Or −40/70 × exp(1-days in milk/70) + 40/(70^2) × days in milk × exp(1-days in milk/70) if parity > 1
−0.24783 + 0.0049567 × body weight if body weight ≤ 69.365
Or −6.2263 + 0.091145 × body weight if body weight > 69.365,
2.1. Running the Simulation
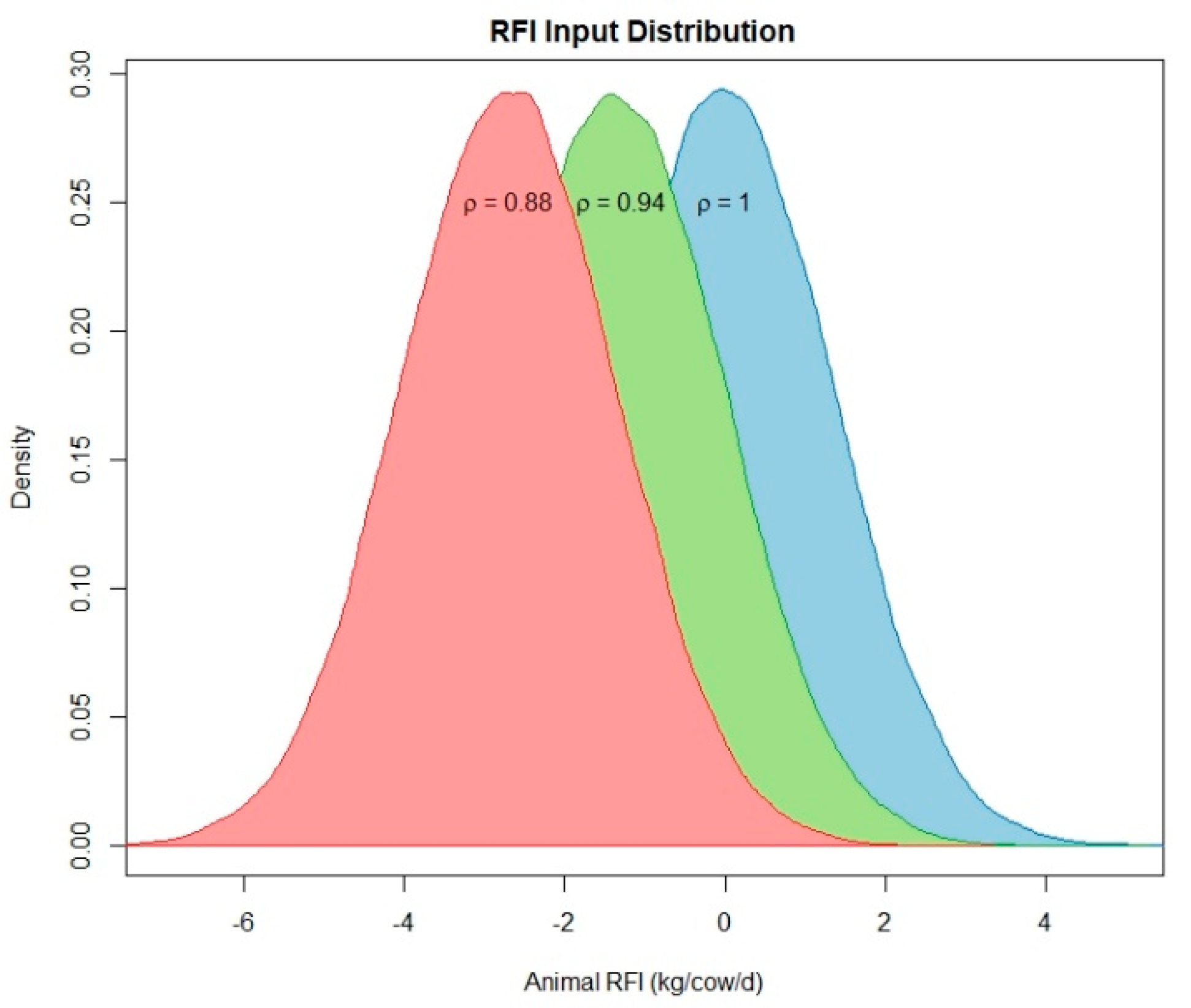
2.2. Feed Efficiency Case Study
3. Results
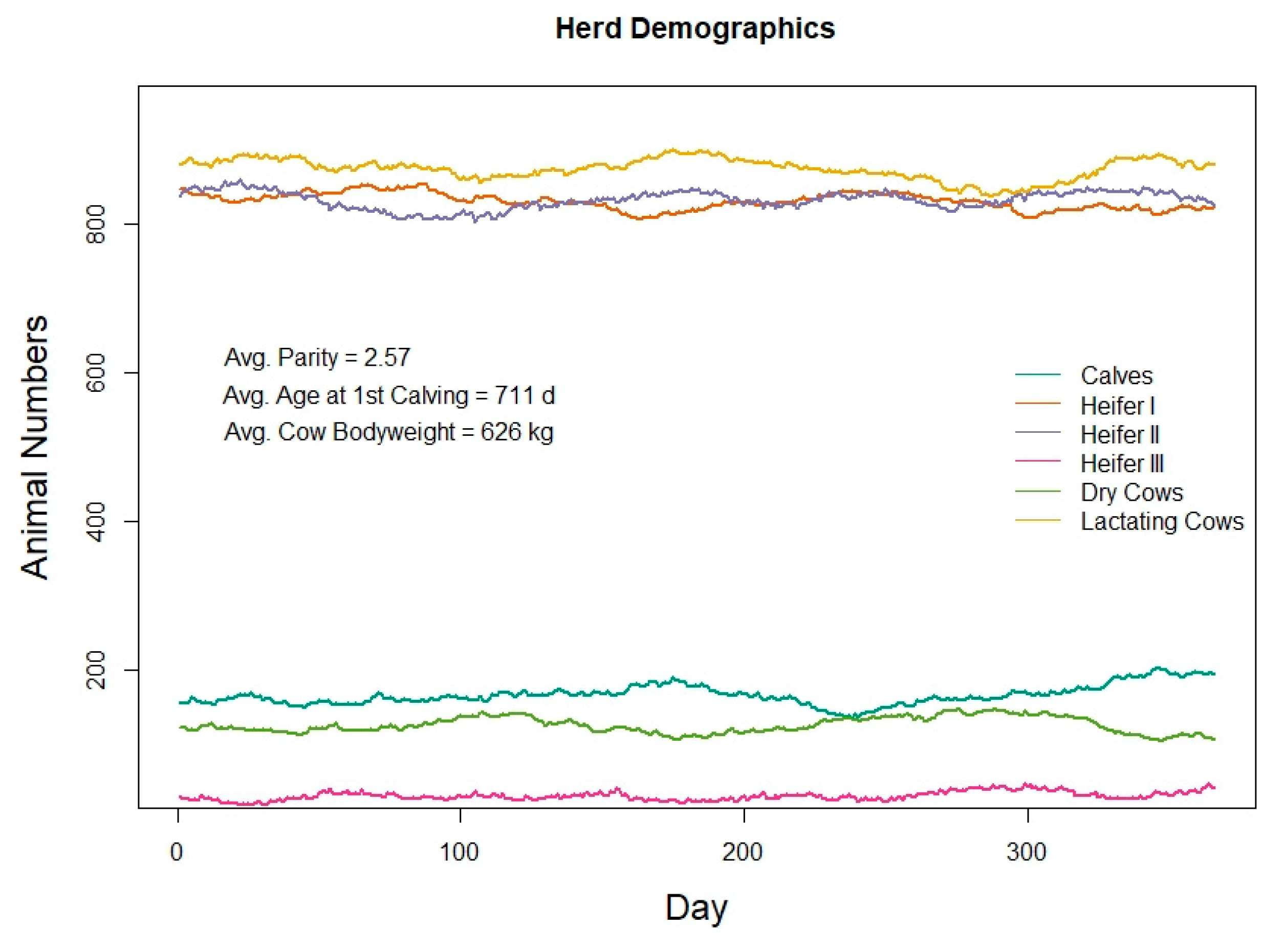
3.1. Herd Demographics
3.2. Feed Efficiency Case Study
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. User Inputs for the Animal Module of the Ruminant Farm System
| Item | Type | Value | Description |
|---|---|---|---|
| Herd Information | |||
| Calf No. | Integer | 75 | Number of calves randomly selected from initialization herd |
| Heifer I No. | Integer | 150 | Number of heifers between weaning and first breeding randomly selected from the initialization herd |
| Heifer II No. | Integer | 150 | Number of heifers between first breeding and close to parturition randomly selected from the initialization herd |
| Heifer III No. | Integer | 40 | Number of heifers close to parturition randomly selected from the initialization herd |
| Cow No. | Integer | 1000 | Number of cows randomly selected from the initialization herd |
| Replace No. | Integer | 5000 | Number of |
| Herd No. | Integer | 1000 | Goal for number of cows in the herd |
| Herd init | Boolean | False | When herd init is true, simulate a replacement herd database to populate the farm simulation |
| Breed | “HO” or “JE” | “HO” | The breed of cattle in the simulation. Input “HO” for Holsteins and “JE” for Jerseys. |
| Animal Life Cycle Inputs | |||
| Breeding start day | Integer | 420 | Target start days born of reproduction protocols |
| Heifer repro method | “TAI” other protocols | “TAI” | Reproductive protocol for heifers |
| Cow repro method | protocol | “TAI” | Reproductive protocol for cows |
| Semen type | “conventional” or “sexed” | “conventional” | Type of semen used in reproduction protocols |
| Days in preg when dry | integer | 218 | Days when the cow is dried off after parturition |
| Lactation curve | “wood” or “milkbot” | “wood” | Model selection for milk production |
| Heifer repro cull time | Integer | 650 | Days old when a heifer would be culled if unsuccessful in breeding |
| Repro cull time | Integer | 300 | Threshold of heifer culling age: when the heifer is not pregnant at this age, she will be culled for repro failure |
| Do not breed time | Integer | 300 | Days in pregnancy when reproduction protocols are stopped: when the cow is not pregnant at this DIM, it will not be bred anymore and will be culled when her milk production drops below the production culling line. |
| Cull milk production | Number | 22 | Minimum milk production before animal is culled |
| Milkings per day | Integer | 1 | Number of times per day cows are milked |
| Item | Type | Value | Description |
|---|---|---|---|
| Male calf rate sexed semen | Decimal | 0.1 | Probability of male calf if sexed semen used |
| Male calf rate conventional semen | Decimal | 0.53 | Probability of male calf if sexed semen used |
| Birth weight average ho | Number | 43.9 | Average birth weight of Holstein cattle |
| Birth weight std ho | Number | 1.0 | Standard deviation of birth weight of Holstein cattle |
| Birth weight average je | Number | 35.2 | Average birth weight of Jersey cattle |
| Birth weight std je | Number | 1 | Standard deviation of birth weight of Jersey cattle |
| Keep female calf rate | Number | 1 | The rate female calves are kept and raised on-farm |
| Wean day | Integer | 60 | Day the calf is fully weaned from milk or milk replacer |
| Wean length | Integer | 7 | Number of days that the cow is stepped down from milk or milk replacer |
| Milk type | “whole” or “replacer” | ‘whole’ | Type of milk fed to calves |
| Grow end day | Integer | 780 | Days when animal will cease growing to reach target mature body weight |
| Mature body weight, left | Number | 730 | The minimum, mode, and maximum values defining the triangular distribution of Mature Body Weight |
| Mature body weight, mode | Number | 750 | |
| Mature body weight, right | Number | 770 |
| Item | Type | Value | Description |
|---|---|---|---|
| Methane model | “IPCC”, “Mills”, “Niu” | “IPCC” | Methane model for lactating cows |
| RationFormulation interval | Integer | 3 | Number of days between reformulating animal rations |
| Pen Characteristics | |||
| Id | Integer | - | Pen identification number |
| Vertical dist to milking parlor | Number | 0.2 | Change in elevation between the pen and milking parlor |
| Horizontal dist to milking parlor | Number | 1.6 | Flat distance between the pen and milking parlor |
| Number of stalls | Integer | 1000 | Number of stalls in barn. The number of animals in the pen can be 120% of the number of stalls. |
| Bedding type | “sand” “manure solids” “organics” | “sand” | Type of bedding used in the barn |
| Pen type | “tiestall” or “freestall” | “freestall” | Type of pen |
| Manure management | “default”: “manual scraping” “flush system” “anaerobic lagoon” | “flush” | Options for manure management with handling, separation, treatment, and storage options specified in the manure management inputs. |
References
- FAO. The Future of food and Agriculture—Trends and Challenges; Food and Agriculture Organization of the United Nations: Rome, Italy, 2017. [Google Scholar]
- Keyzer, M.A.; Merbis, M.; Pavel, I.; Van Wesenbeeck, C. Diet shifts towards meat and the effects on cereal use: Can we feed the animals in 2030? Ecol. Econ. 2005, 55, 187–202. [Google Scholar] [CrossRef]
- White, R.R.; Hall, M.B. Nutritional and greenhouse gas impacts of removing animals from US agriculture. Proc. Natl. Acad. Sci. USA 2017, 114, E10301–E10308. [Google Scholar] [CrossRef]
- Marti, D.; Johnson, R.J.; Mathews, K.H. Where’s the (Not) Meat?: Byproducts from Beef and Pork Production; US Department of Agriculture: Washington DC, USA, 2011. [Google Scholar]
- Garnett, T. Food sustainability: Problems, perspectives and solutions. Proc. Nutr. Soc. 2013, 72, 29–39. [Google Scholar] [CrossRef]
- Beede, D. 18 Animal Agriculture: How Can It Be Sustainable in the Future? Sustain. Anim. Agric. 2013, 284. [Google Scholar] [CrossRef]
- Rotz, C.; Isenberg, B.; Stackhouse-Lawson, K.; Pollak, E. A simulation-based approach for evaluating and comparing the environmental footprints of beef production systems. J. Anim. Sci. 2013, 91, 5427–5437. [Google Scholar] [CrossRef]
- Johnson, I.; Chapman, D.; Snow, V.; Eckard, R.; Parsons, A.; Lambert, M.; Cullen, B. DairyMod and EcoMod: Biophysical pasture-simulation models for Australia and New Zealand. Aust. J. Exp. Agric. 2008, 48, 621–631. [Google Scholar] [CrossRef]
- Cabrera, V.E.; Hildebrand, P.E.; Jones, J.W.; Letson, D.; De Vries, A. An integrated North Florida dairy farm model to reduce environmental impacts under seasonal climate variability. Agric. Ecosyst. Environ. 2006, 113, 82–97. [Google Scholar] [CrossRef]
- Del Prado, A.; Misselbrook, T.; Chadwick, D.; Hopkins, A.; Dewhurst, R.; Davison, P.; Butler, A.; Schröder, J.; Scholefield, D. SIMSDAIRY: A modelling framework to identify sustainable dairy farms in the UK. Framework description and test for organic systems and N fertiliser optimisation. Sci. Total Environ. 2011, 409, 3993–4009. [Google Scholar] [CrossRef] [PubMed]
- Kebreab, E.; Reed, K.F.; Cabrera, V.E.; Vadas, P.A.; Thoma, G.; Tricarico, J.M. A new modeling environment for integrated dairy system management. Anim. Front. 2019, 9, 25–32. [Google Scholar] [CrossRef]
- Jones, J.W.; Antle, J.M.; Basso, B.; Boote, K.J.; Conant, R.T.; Foster, I.; Godfray, H.C.J.; Herrero, M.; Howitt, R.E.; Janssen, S.; et al. Brief history of agricultural systems modeling. Agric. Syst. 2017, 155, 240–254. [Google Scholar] [CrossRef]
- Thoma, G.; Popp, J.; Nutter, D.; Shonnard, D.; Ulrich, R.; Matlock, M.; Kim, D.S.; Neiderman, Z.; Kemper, N.; East, C.; et al. Greenhouse gas emissions from milk production and consumption in the United States: A cradle to grave life cycle assessment circa 2008. Int. Dairy J. 2013, 31, S3–S14. [Google Scholar] [CrossRef]
- Capper, J.L.; Cady, R.A. The effects of improved performance in the U.S. dairy cattle industry on environmental impacts between 2007 and 2017. J. Anim. Sci. 2020, 98. [Google Scholar] [CrossRef] [PubMed]
- Capper, J.L.; Cady, R.A.; Bauman, D.E. The environmental impact of dairy production: 1944 compared with 2007. J. Anim. Sci. 2009, 87, 2160–2167. [Google Scholar] [CrossRef]
- Capper, J.L.; Bauman, D.E. The role of productivity in improving the environmental sustainabiliyt of ruminant production systems. Annu. Rev. Anim. Biosci. 2013, 1, 469–489. [Google Scholar] [CrossRef]
- Herd, R.M.; Oddy, V.H.; Richardson, E.C. Biological basis for variation in residual feed intake in beef cattle. 1. Review of potential mechanisms. Aust. J. Exp. Agric. 2004, 44, 423–430. [Google Scholar] [CrossRef]
- Hoque, M.A.; Susuki, K. Genetics of residual feed intake in cattle and pigs: A Review. Asian-Australas. J. Anim. Sci. 2009, 22, 747–755. [Google Scholar] [CrossRef]
- VandeHaar, M.J.; Armentano, L.E.; Weigel, K.; Spurlock, D.M.; Tempelman, R.J.; Veerkamp, R. Harnessing the genetics of the modern dairy cow to continue improvements in feed efficiency. J. Dairy Sci. 2016, 99, 4941–4954. [Google Scholar] [CrossRef]
- Li, B.; VanRaden, P.M.; Guduk, E.; O’Connell, J.R.; Null, D.J.; Connor, E.E.; VandeHaar, M.J.; Tempelman, R.J.; Weigel, K.A.; Cole, J.B. Genomic prediction of residual feed intake in US Holstein dairy cattle. J. Dairy Sci. 2020, 103, 2477–2486. [Google Scholar] [CrossRef]
- Rubenstein, R.Y.; Kroese, D.P. Simulation of Discrete-Event Systems. In Simulation and the Monte Carlo Method; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2016; pp. 91–106. [Google Scholar] [CrossRef]
- NRC. Nutrient Requirements of Dairy Cattle Seventh Revised Edition; The National Academies Press: Washington, DC, USA, 2001. [Google Scholar]
- DCRC. Dairy Reproduction Protocols. Dairy Cattle Reproduction Council. 2018. Available online: https://www.dcrcouncil.org/protocols/ (accessed on 12 November 2020).
- Wood, P. Factors affecting the shape of the lactation curve in cattle. Anim. Sci. 1969, 11, 307–316. [Google Scholar] [CrossRef]
- Wood, P. Algebraic models of the lactation curves for milk, fat and protein production, with estimates of seasonal variation. Anim. Sci. 1976, 22, 35–40. [Google Scholar] [CrossRef]
- Miller-Cushion, E. (University of Florida, Gainesville, FL, USA). Personal communication, 2019. [Google Scholar]
- Khan, M.A.; Weary, D.M.; von Keyserlingk, M.A. Invited review: Effects of milk ration on solid feed intake, weaning, and performance in dairy heifers. J. Dairy Sci. 2011, 94, 1071–1081. [Google Scholar] [CrossRef]
- Rotz, C.A.; Corson, M.S.; Chianese, D.S.; Montes, F.; Hafner, S.D.; Coiner, C.U. Integrated Farm System Model: Reference Manual; USDA Agricultural Research Service: University Park, PA, USA, 2013. [Google Scholar]
- Qu, J.; Hsiao, T.; DePeters, E.; Zaccaria, D.; Snyder, R.; Fadel, J. A goal programming approach for balancing diet costs and feed water use under different environmental conditions. J. Dairy Sci. 2019, 102, 11504–11522. [Google Scholar] [CrossRef]
- Boggs, P.T.; Tolle, J.W. Sequential Quadratic Programming. Acta Numer. 1995, 4, 1–51. [Google Scholar] [CrossRef]
- Moraes, L.E.; Wilen, J.E.; Robinson, P.H.; Fadel, J.G. A linear programming model to optimize diets in environmental policy scenarios. J. Dairy Sci. 2012, 95, 1267–1282. [Google Scholar] [CrossRef]
- ASABE. Manure Production and Characteristics; ASABE: St. Joseph, MN, USA, 2005; pp. 1–32. [Google Scholar]
- Pattanaik, A.K.; Sastry, V.R.B.; Katiyar, R.C.; Lal, M. Influence of Grain Processing and Dietary Protein Degradability on Nitrogen Metabolism, Energy Balance and Methane Production in Young Calves. Asian-Australas. J. Anim. Sci. 2003, 16, 1443–1450. [Google Scholar] [CrossRef]
- Boadi, D.; Wittenberg, K. Methane production from dairy and beef heifers fed forages differing in nutrient density using the sulphur hexafluoride (SF6) tracer gas technique. Can. J. Anim. Sci. 2002, 82, 201–206. [Google Scholar] [CrossRef]
- Appuhamy, J.A.D.R.N.; Moraes, L.E.; Wagner-Riddle, C.; Casper, D.P.; France, J.; Kebreab, E. Development of mathematical models to predict volume and nutrient composition of fresh manure from lactating Holstein cows. Anim. Prod. Sci. 2014, 54. [Google Scholar] [CrossRef]
- Niu, M.; Kebreab, E.; Hristov, A.N.; Oh, J.; Arndt, C.; Bannink, A.; Bayat, A.R.; Brito, A.F.; Boland, T.; Casper, D.; et al. Prediction of enteric methane production, yield, and intensity in dairy cattle using an intercontinental database. Glob. Chang. Biol. 2018, 24, 3368–3389. [Google Scholar] [CrossRef]
- Mills, J.A.; Kebreab, E.; Yates, C.M.; Crompton, L.A.; Cammell, S.B.; Dhanoa, M.S.; Agnew, R.E.; France, J. Alternative approaches to predicting methane emissions from dairy cows. J. Anim. Sci. 2003, 81, 3141–3150. [Google Scholar] [CrossRef]
- IPCC. IPCC Guidelines for National Greenhouse Gas Inventories. 2006. Available online: https://www.ipcc.ch/report/2006-ipcc-guidelines-for-national-greenhouse-gas-inventories/ (accessed on 1 August 2019).
- Van Amburgh, M.; Collao-Saenz, E.; Higgs, R.; Ross, D.; Recktenwald, E.; Raffrenato, E.; Chase, L.; Overton, T.; Mills, J.; Foskolos, A. The Cornell Net Carbohydrate and Protein System: Updates to the model and evaluation of version 6.5. J. Dairy Sci. 2015, 98, 6361–6380. [Google Scholar] [CrossRef]
- Connor, E.E.; Hutchison, J.L.; Van Tassell, C.P.; Cole, J.B. Defining the optimal period length and stage of growth or lactation to estimate residual feed intake in dairy cows. J. Dairy Sci. 2019, 102, 6131–6143. [Google Scholar] [CrossRef] [PubMed]
- IPCC. Climate Change and Land: An IPCC Special Report on Climate Change, Desertification, Land Degradation, Sustainable Land Management, Food Security, and Greenhouse Gas Fluxes in Terrestrial Ecosystems; 2019. Available online: https://www.ipcc.ch/srccl/ (accessed on 1 March 2020).
- Liu, E.; VandeHaar, M.J. Relationship of residual feed intake and protein efficiency in lactating cows fed high- or low-protein diets. J. Dairy Sci. 2020, 103, 3177–3190. [Google Scholar] [CrossRef] [PubMed]
- EcoFeed by STI Genetics. Available online: https://stgen.com/article/article.aspx?code=4247&language=english&pego=consulta (accessed on 30 March 2021).
- Holstein Association USA, I. TPI Formula—April 2021. Available online: https://www.holsteinusa.com/genetic_evaluations/ss_tpi_formula.html# (accessed on 30 March 2021).
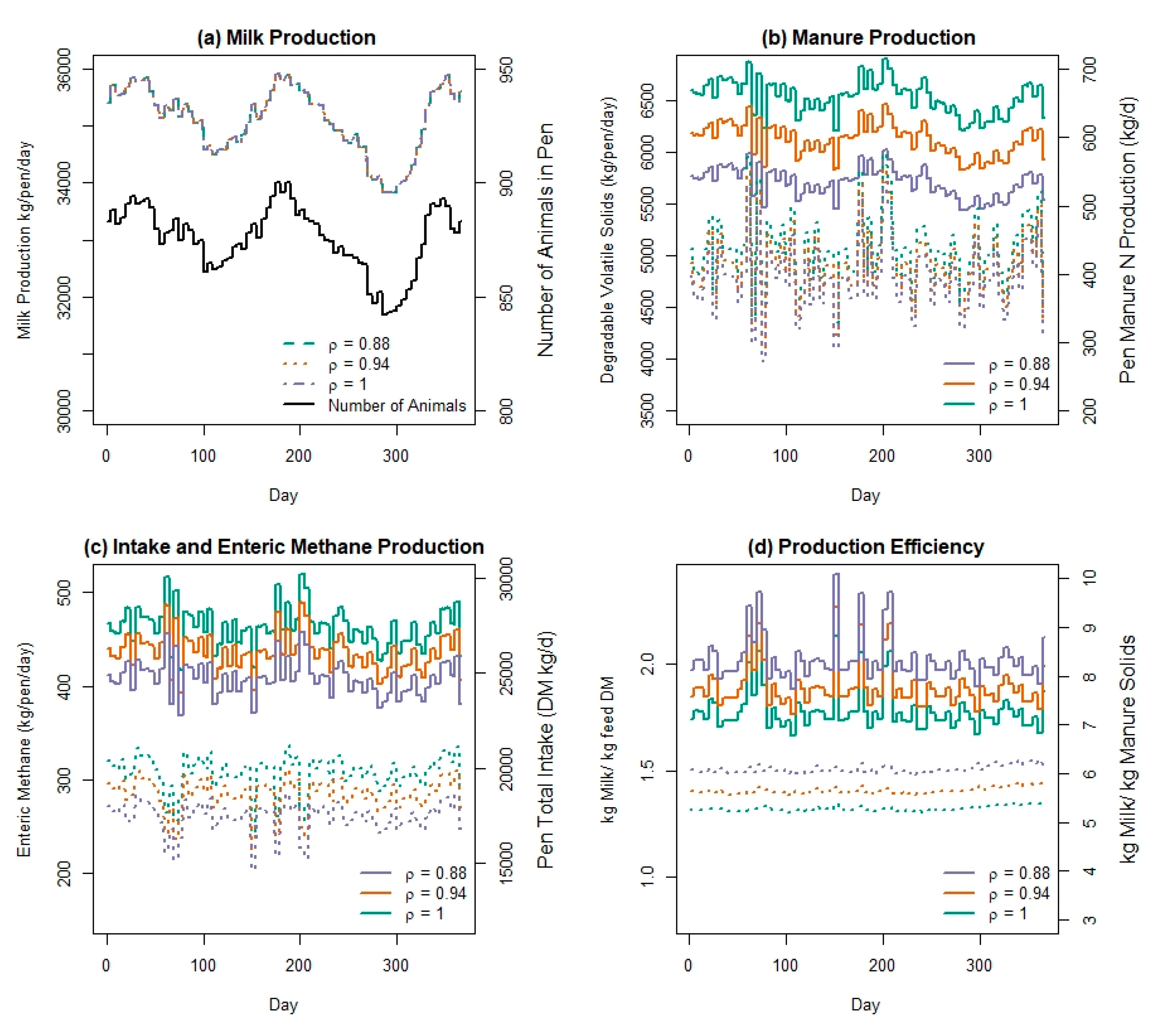
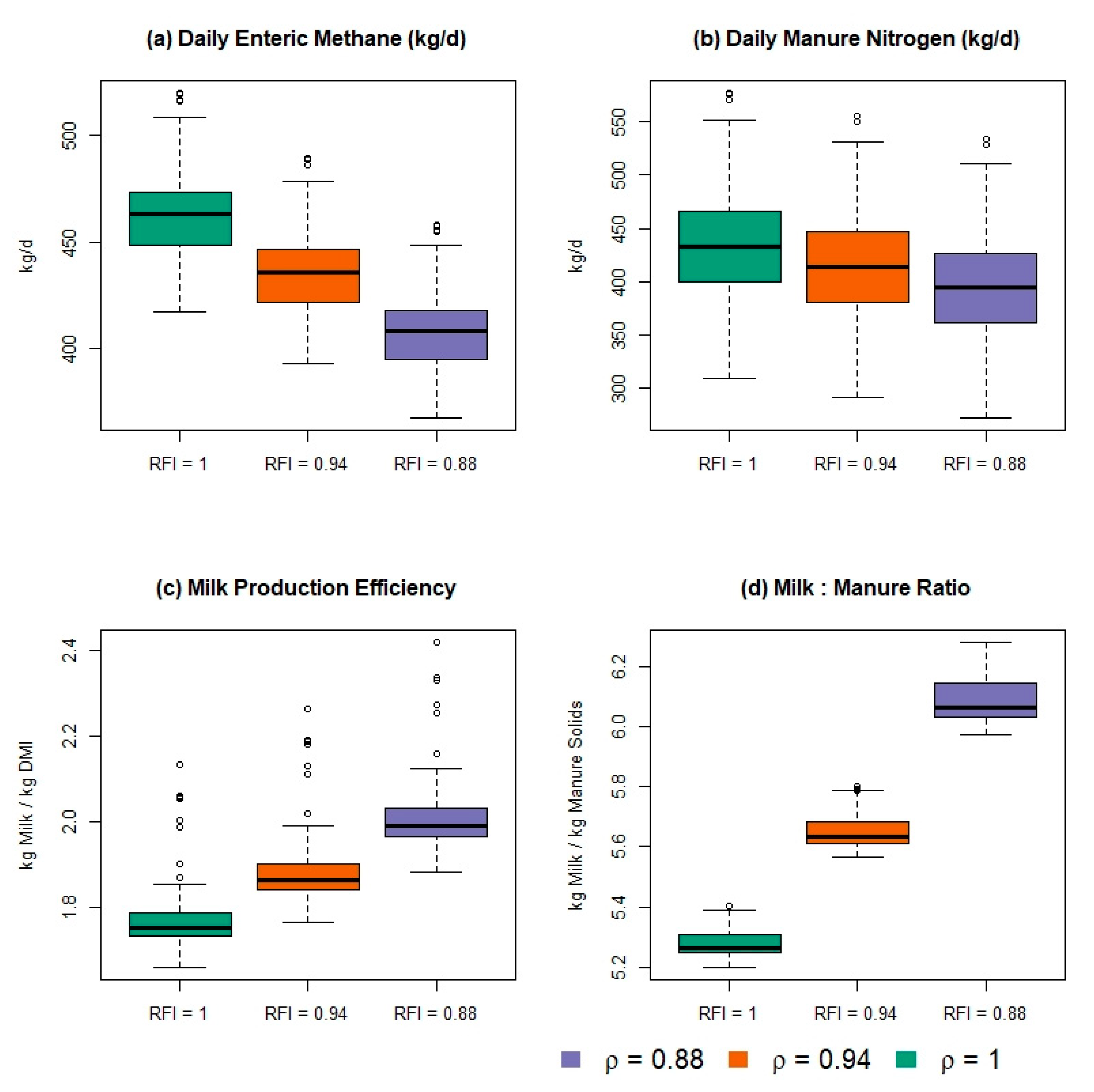
| Animal Class | Number of Animals | Mean Age (Days) | Days in Milk |
|---|---|---|---|
| Calves | 1323 | 29 | - |
| Heifer I | 6425 | 208 | - |
| Heifer II | 5825 | 509 | - |
| Heifer III | 587 | 667 | - |
| Cows | 16465 | 1289 | 182 |
| Replacement Market Number | 30426 | 683 | - |
| Culling Reason | Low Production | Lameness | Injury | Mastitis | Udder Deformity | Unknown |
|---|---|---|---|---|---|---|
| Number of Animals | 69 | 52 | 85 | 62 | 20 | 44 |
| Model Output 1 | Baseline (ρ = 1) | High Efficiency (−1 SD RFI, ρ = 0.94) | Very High Efficiency (−2 SD RFI, ρ = 0.88) |
|---|---|---|---|
| RFI, kg | 0.022 | 1.4 | 2.71 |
| SDRFI, kg | 0.022 | 0.64 | 0.127 |
| Ρsim | 0.00 | 0.940 | 0.880 |
| SDΡsim | 0.0093 | 0.0094 | 0.0096 |
| Feed | Ration Composition | Simulated Intake (Tons/Yr) | ||
|---|---|---|---|---|
| % DM | (ρ = 1) | (ρ = 0.94) | (ρ = 0.88) | |
| Corn Silage | 68.9 (9.79) | 4,998 | 4,703 | 4403 |
| Soybean Meal | 27.2 (5.37) | 1,973 | 1,857 | 1738 |
| Brewers Grain | 3.1 (7.26) | 210.7 | 198.3 | 185.6 |
| Dicalcium phosphate | 0.01 (0.029) | 0.708 | 0.666 | 0.624 |
| Limestone | 0.47 (0.030) | 3.41 | 3.21 | 3.01 |
| Feed Efficiency | Milk (Ton/Yr) | Enteric Methane (Ton/Yr) | Manure Volatile Solids (Ton/Yr) | Manure N (Ton/Yr) | Direct N2O from Manure (Ton/Yr) | ||||
|---|---|---|---|---|---|---|---|---|---|
| - | - | CH4 | CO2-eq | mass | CH4 | CO2-eq | - | N2O | CO2-eq |
| Baseline | 12,874 | 169.5 | 5085 | 2390 | 270.0 | 8099 | 159.2 | 0.500 | 155,110 |
| High Efficiency | 12,874 | 159.6 | 4787 | 2240 | 253.4 | 7592 | 152.1 | 0.478 | 148,190 |
| Very High Efficiency | 12,874 | 149.4 | 4482 | 2088 | 235.9 | 7077 | 144.9 | 0.455 | 141,140 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hansen, T.L.; Li, M.; Li, J.; Vankerhove, C.J.; Sotirova, M.A.; Tricarico, J.M.; Cabrera, V.E.; Kebreab, E.; Reed, K.F. The Ruminant Farm Systems Animal Module: A Biophysical Description of Animal Management. Animals 2021, 11, 1373. https://doi.org/10.3390/ani11051373
Hansen TL, Li M, Li J, Vankerhove CJ, Sotirova MA, Tricarico JM, Cabrera VE, Kebreab E, Reed KF. The Ruminant Farm Systems Animal Module: A Biophysical Description of Animal Management. Animals. 2021; 11(5):1373. https://doi.org/10.3390/ani11051373
Chicago/Turabian StyleHansen, Tayler L., Manfei Li, Jinghui Li, Chris J. Vankerhove, Militsa A. Sotirova, Juan M. Tricarico, Victor E. Cabrera, Ermias Kebreab, and Kristan F. Reed. 2021. "The Ruminant Farm Systems Animal Module: A Biophysical Description of Animal Management" Animals 11, no. 5: 1373. https://doi.org/10.3390/ani11051373
APA StyleHansen, T. L., Li, M., Li, J., Vankerhove, C. J., Sotirova, M. A., Tricarico, J. M., Cabrera, V. E., Kebreab, E., & Reed, K. F. (2021). The Ruminant Farm Systems Animal Module: A Biophysical Description of Animal Management. Animals, 11(5), 1373. https://doi.org/10.3390/ani11051373







