The Expanding Computational Toolbox for Engineering Microbial Phenotypes at the Genome Scale
Abstract
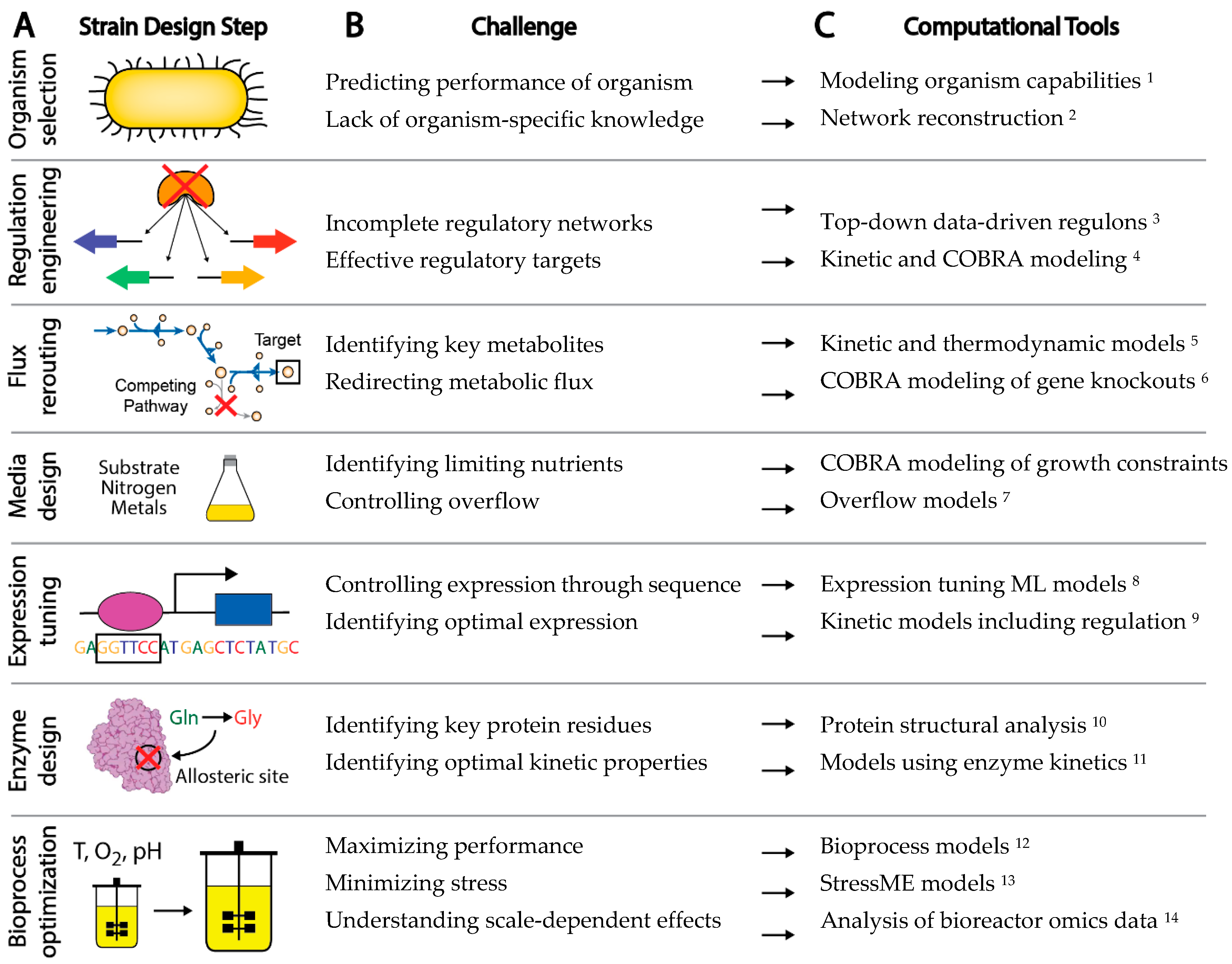
1. Introduction
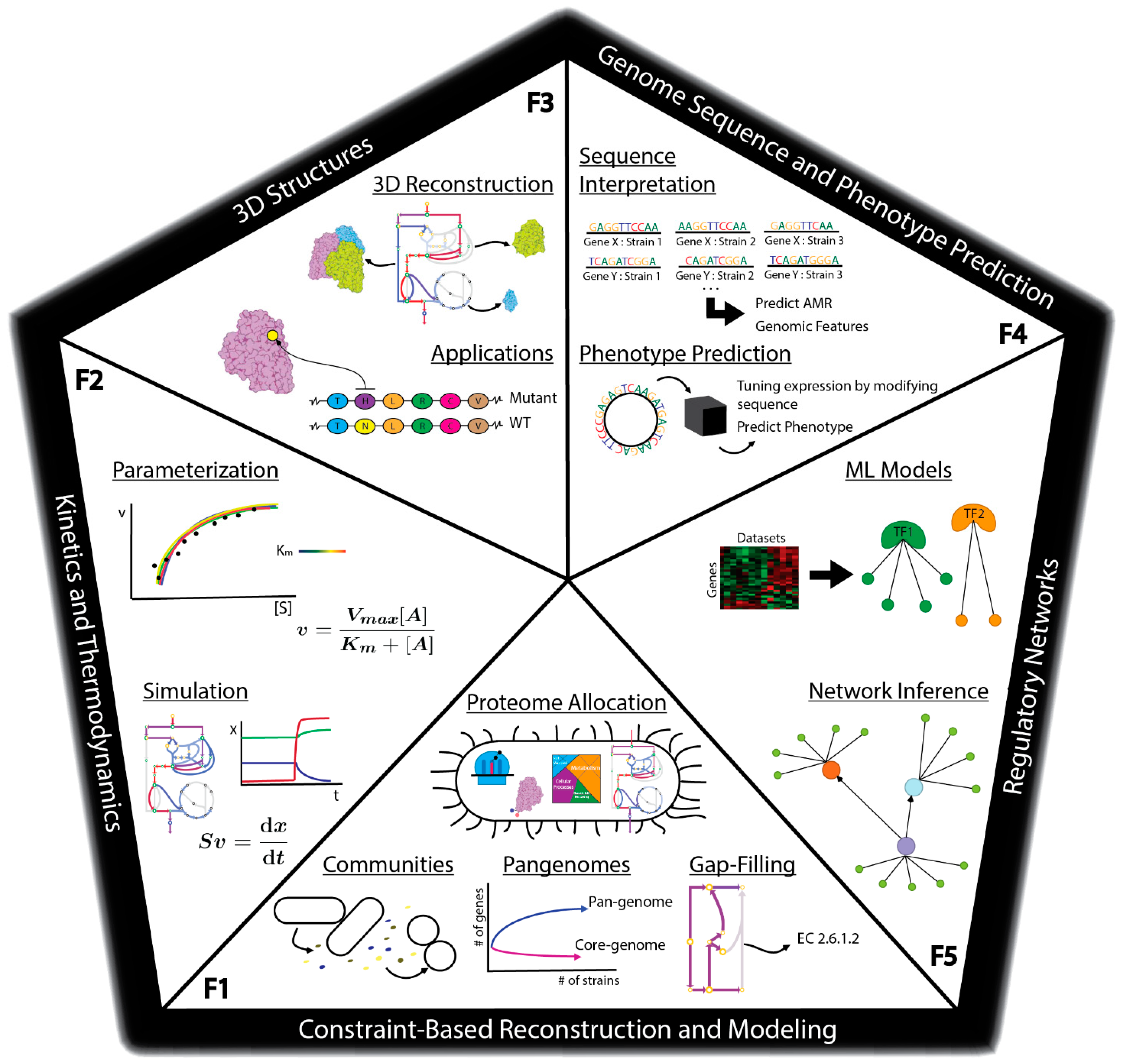
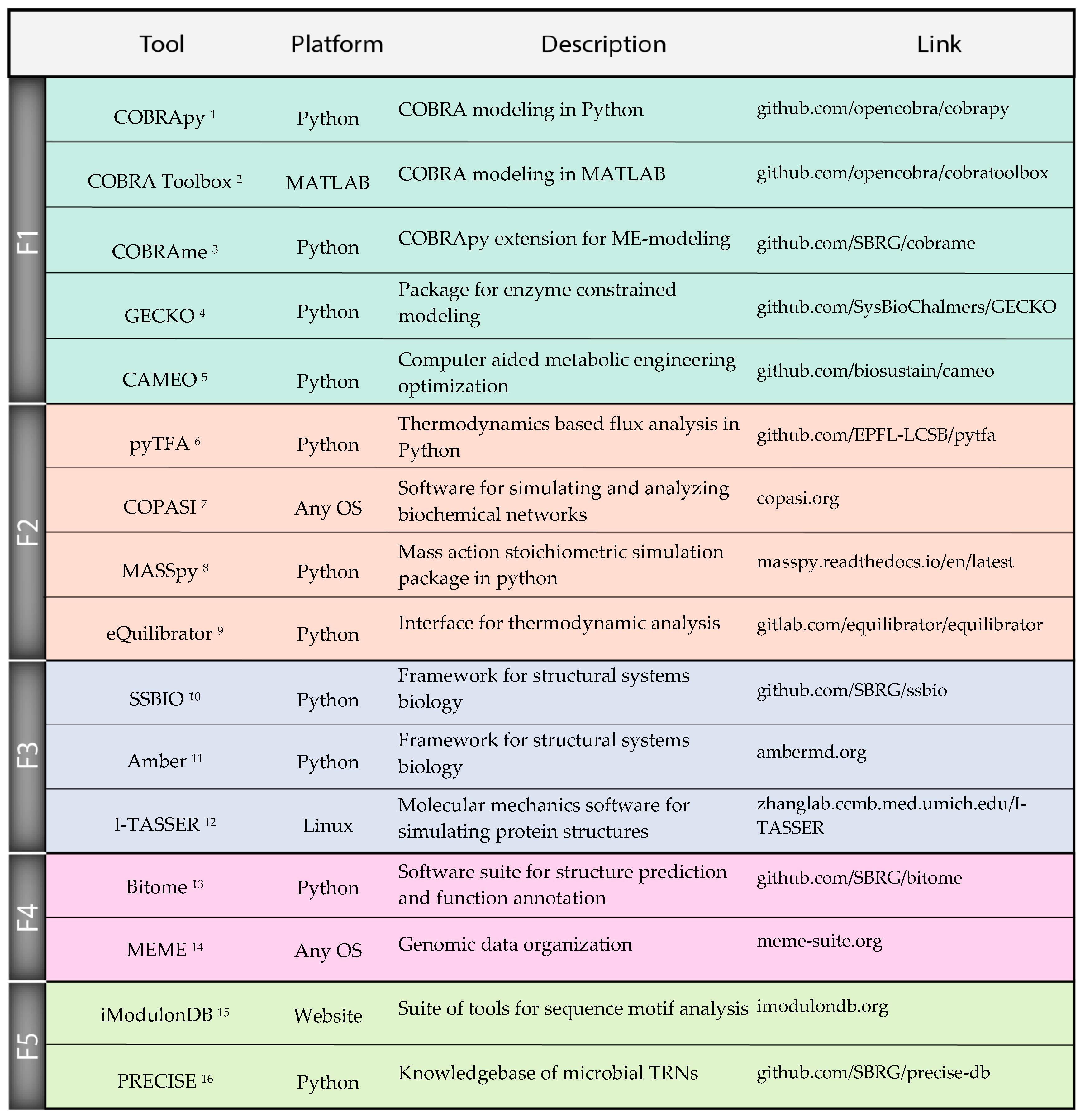
2. Frontier 1: Constraint-Based Reconstruction and Modeling
2.1. Proteome Allocation Models
2.2. Communities
2.3. Pangenomes and Multistrain Models
2.4. Gap filling, Discovery, and Annotation
3. Frontier 2: Kinetics and Thermodynamics
3.1. Parameterization
3.2. Simulation
4. Frontier 3: 3D Structures
4.1. 3D Reconstruction
4.2. Applications
5. Frontier 4: Genome Sequence and Phenotype Prediction
5.1. Sequence Interpretation
5.2. Phenotype Prediction
6. Frontier 5: Regulatory Networks
6.1. Regulatory Network Machine Learning Models
6.2. Network Inference
7. Drivers of Advances in Computational Tools for Strain Design
8. Outlook for Synthetic Genome Design
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Liao, J.C.; Mi, L.; Pontrelli, S.; Luo, S. Fuelling the Future: Microbial Engineering for the Production of Sustainable Biofuels. Nat. Rev. Microbiol. 2016, 14, 288–304. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.Y.; Kim, H.U.; Chae, T.U.; Cho, J.S.; Kim, J.W.; Shin, J.H.; Kim, D.I.; Ko, Y.-S.; Jang, W.D.; Jang, Y.-S. A Comprehensive Metabolic Map for Production of Bio-Based Chemicals. Nat. Catal. 2019, 2, 18–33. [Google Scholar] [CrossRef]
- Kalia, V.C.; Saini, A.K. (Eds.) Metabolic Engineering for Bioactive Compounds: Strategies and Processes; Springer: Singapore, 2017. [Google Scholar]
- Matassa, S.; Boon, N.; Pikaar, I.; Verstraete, W. Microbial Protein: Future Sustainable Food Supply Route with Low Environmental Footprint. Microb. Biotechnol. 2016, 9, 568–575. [Google Scholar] [CrossRef] [PubMed]
- Das, S.; Dash, H.R. 1—Microbial Bioremediation: A Potential Tool for Restoration of Contaminated Areas. In Microbial Biodegradation and Bioremediation; Das, S., Ed.; Elsevier: Oxford, UK, 2014; pp. 1–21. [Google Scholar]
- Bereza-Malcolm, L.T.; Mann, G.; Franks, A.E. Environmental Sensing of Heavy Metals Through Whole Cell Microbial Biosensors: A Synthetic Biology Approach. ACS Synth. Biol. 2015, 4, 535–546. [Google Scholar] [CrossRef] [PubMed]
- Danino, T.; Mondragón-Palomino, O.; Tsimring, L.; Hasty, J. A Synchronized Quorum of Genetic Clocks. Nature 2010, 463, 326–330. [Google Scholar] [CrossRef] [PubMed]
- Din, M.O.; Danino, T.; Prindle, A.; Skalak, M.; Selimkhanov, J.; Allen, K.; Julio, E.; Atolia, E.; Tsimring, L.S.; Bhatia, S.N.; et al. Synchronized Cycles of Bacterial Lysis for in Vivo Delivery. Nature 2016, 536, 81–85. [Google Scholar] [CrossRef]
- Yadav, R.; Singh, P.K.; Shukla, P. Metabolic Engineering for Probiotics and Their Genome-Wide Expression Profiling. Curr. Protein Pept. Sci. 2018, 19, 68–74. [Google Scholar] [CrossRef]
- Lee, S.Y.; Kim, H.U. Systems Strategies for Developing Industrial Microbial Strains. Nat. Biotechnol. 2015, 33, 1061–1072. [Google Scholar] [CrossRef]
- St. John, P.C.; Bomble, Y.J. Approaches to Computational Strain Design in the Multiomics Era. Front. Microbiol. 2019, 10. [Google Scholar] [CrossRef]
- Brophy, J.A.N.; Voigt, C.A. Principles of Genetic Circuit Design. Nat. Methods 2014, 11, 508–520. [Google Scholar] [CrossRef]
- Nielsen, A.A.K.; Der, B.S.; Shin, J.; Vaidyanathan, P.; Paralanov, V.; Strychalski, E.A.; Ross, D.; Densmore, D.; Voigt, C.A. Genetic Circuit Design Automation. Science 2016, 352, aac7341. [Google Scholar] [CrossRef] [PubMed]
- Sedlmayer, F.; Aubel, D.; Fussenegger, M. Synthetic Gene Circuits for the Detection, Elimination and Prevention of Disease. Nat. Biomed. Eng. 2018, 2, 399–415. [Google Scholar] [CrossRef] [PubMed]
- Khalil, A.S.; Collins, J.J. Synthetic Biology: Applications Come of Age. Nat. Rev. Genet. 2010, 11, 367–379. [Google Scholar] [CrossRef] [PubMed]
- Kim, W.J.; Kim, H.U.; Lee, S.Y. Current State and Applications of Microbial Genome-Scale Metabolic Models. Curr. Opin. Syst. Biol. 2017, 2, 10–18. [Google Scholar] [CrossRef]
- Heirendt, L.; Arreckx, S.; Pfau, T.; Mendoza, S.N.; Richelle, A.; Heinken, A.; Haraldsdóttir, H.S.; Wachowiak, J.; Keating, S.M.; Vlasov, V.; et al. Creation and Analysis of Biochemical Constraint-Based Models Using the COBRA Toolbox v.3.0. Nat. Protoc. 2019, 14, 639–702. [Google Scholar] [CrossRef]
- Mendoza, S.N.; Olivier, B.G.; Molenaar, D.; Teusink, B. A Systematic Assessment of Current Genome-Scale Metabolic Reconstruction Tools. Genome Biol. 2019, 20, 158. [Google Scholar] [CrossRef]
- Lieven, C.; Beber, M.E.; Olivier, B.G.; Bergmann, F.T.; Ataman, M.; Babaei, P.; Bartell, J.A.; Blank, L.M.; Chauhan, S.; Correia, K.; et al. MEMOTE for Standardized Genome-Scale Metabolic Model Testing. Nat. Biotechnol. 2020, 38, 272–276. [Google Scholar] [CrossRef]
- Lloyd, C.J.; Ebrahim, A.; Yang, L.; King, Z.A.; Catoiu, E.; O’Brien, E.J.; Liu, J.K.; Palsson, B.O. COBRAme: A Computational Framework for Genome-Scale Models of Metabolism and Gene Expression. PLoS Comput. Biol. 2018, 14, e1006302. [Google Scholar] [CrossRef]
- O’Brien, E.J.; Monk, J.M.; Palsson, B.O. Using Genome-Scale Models to Predict Biological Capabilities. Cell 2015, 161, 971–987. [Google Scholar] [CrossRef]
- O’Brien, E.J.; Lerman, J.A.; Chang, R.L.; Hyduke, D.R.; Palsson, B.Ø. Genome-Scale Models of Metabolism and Gene Expression Extend and Refine Growth Phenotype Prediction. Mol. Syst. Biol. 2013, 9, 693. [Google Scholar] [CrossRef]
- Karr, J.R.; Sanghvi, J.C.; Macklin, D.N.; Gutschow, M.V.; Jacobs, J.M.; Bolival, B., Jr.; Assad-Garcia, N.; Glass, J.I.; Covert, M.W. A Whole-Cell Computational Model Predicts Phenotype from Genotype. Cell 2012, 150, 389–401. [Google Scholar] [CrossRef] [PubMed]
- McCloskey, D.; Palsson, B.Ø.; Feist, A.M. Basic and Applied Uses of Genome-Scale Metabolic Network Reconstructions of Escherichia Coli. Mol. Syst. Biol. 2013, 9, 661. [Google Scholar] [CrossRef] [PubMed]
- Richelle, A.; David, B.; Demaegd, D.; Dewerchin, M.; Kinet, R.; Morreale, A.; Portela, R.; Zune, Q.; von Stosch, M. Towards a Widespread Adoption of Metabolic Modeling Tools in Biopharmaceutical Industry: A Process Systems Biology Engineering Perspective. NPJ Syst. Biol. Appl. 2020, 6, 6. [Google Scholar] [CrossRef] [PubMed]
- Andreozzi, S.; Chakrabarti, A.; Soh, K.C.; Burgard, A.; Yang, T.H.; Van Dien, S.; Miskovic, L.; Hatzimanikatis, V. Identification of Metabolic Engineering Targets for the Enhancement of 1,4-Butanediol Production in Recombinant E. Coli Using Large-Scale Kinetic Models. Metab. Eng. 2016, 35, 148–159. [Google Scholar] [CrossRef] [PubMed]
- Monk, J.M.; Koza, A.; Campodonico, M.A.; Machado, D.; Seoane, J.M.; Palsson, B.O.; Herrgård, M.J.; Feist, A.M. Multi-Omics Quantification of Species Variation of Escherichia Coli Links Molecular Features with Strain Phenotypes. Cell Syst. 2016, 3, 238–251.e12. [Google Scholar] [CrossRef]
- Sastry, A.V.; Gao, Y.; Szubin, R.; Hefner, Y.; Xu, S.; Kim, D.; Choudhary, K.S.; Yang, L.; King, Z.A.; Palsson, B.O. The Escherichia Coli Transcriptome Mostly Consists of Independently Regulated Modules. Nat. Commun. 2019, 10, 5536. [Google Scholar] [CrossRef]
- Kümmel, A.; Panke, S.; Heinemann, M. Putative Regulatory Sites Unraveled by Network-Embedded Thermodynamic Analysis of Metabolome Data. Mol. Syst. Biol. 2006, 2, 2006.0034. [Google Scholar] [CrossRef]
- Burgard, A.P.; Pharkya, P.; Maranas, C.D. Optknock: A Bilevel Programming Framework for Identifying Gene Knockout Strategies for Microbial Strain Optimization. Biotechnol. Bioeng. 2003, 84, 647–657. [Google Scholar] [CrossRef]
- De Groot, D.H.; Lischke, J.; Muolo, R.; Planqué, R.; Bruggeman, F.J.; Teusink, B. The Common Message of Constraint-Based Optimization Approaches: Overflow Metabolism Is Caused by Two Growth-Limiting Constraints. Cell. Mol. Life Sci. 2020, 77, 441–453. [Google Scholar] [CrossRef]
- Zrimec, J.; Börlin, C.S.; Buric, F.; Muhammad, A.S.; Chen, R.; Siewers, V.; Verendel, V.; Nielsen, J.; Töpel, M.; Zelezniak, A. Deep Learning Suggests That Gene Expression Is Encoded in All Parts of a Co-Evolving Interacting Gene Regulatory Structure. Nat. Commun. 2020, 11, 6141. [Google Scholar] [CrossRef]
- Kotte, O.; Zaugg, J.B.; Heinemann, M. Bacterial Adaptation through Distributed Sensing of Metabolic Fluxes. Mol. Syst. Biol. 2010, 6, 355. [Google Scholar] [CrossRef] [PubMed]
- Brunk, E.; Mih, N.; Monk, J.; Zhang, Z.; O’Brien, E.J.; Bliven, S.E.; Chen, K.; Chang, R.L.; Bourne, P.E.; Palsson, B.O. Systems Biology of the Structural Proteome. BMC Syst. Biol. 2016, 10, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Kim, O.D.; Rocha, M.; Maia, P. A Review of Dynamic Modeling Approaches and Their Application in Computational Strain Optimization for Metabolic Engineering. Front. Microbiol. 2018, 9, 1690. [Google Scholar] [CrossRef] [PubMed]
- Jabarivelisdeh, B.; Waldherr, S. Optimization of Bioprocess Productivity Based on Metabolic-Genetic Network Models with Bilevel Dynamic Programming. Biotechnol. Bioeng. 2018, 115, 1829–1841. [Google Scholar] [CrossRef]
- Chen, K.; Gao, Y.; Mih, N.; O’Brien, E.J.; Yang, L.; Palsson, B.O. Thermosensitivity of Growth Is Determined by Chaperone-Mediated Proteome Reallocation. Proc. Natl. Acad. Sci. USA 2017, 114, 11548–11553. [Google Scholar] [CrossRef]
- Du, B.; Yang, L.; Lloyd, C.J.; Fang, X.; Palsson, B.O. Genome-Scale Model of Metabolism and Gene Expression Provides a Multi-Scale Description of Acid Stress Responses in Escherichia Coli. PLoS Comput. Biol. 2019, 15, e1007525. [Google Scholar] [CrossRef]
- Yang, L.; Mih, N.; Anand, A.; Park, J.H.; Tan, J.; Yurkovich, J.T.; Monk, J.M.; Lloyd, C.J.; Sandberg, T.E.; Seo, S.W.; et al. Cellular Responses to Reactive Oxygen Species Are Predicted from Molecular Mechanisms. Proc. Natl. Acad. Sci. USA 2019, 116, 14368–14373. [Google Scholar] [CrossRef]
- Wang, G.; Haringa, C.; Tang, W.; Noorman, H.; Chu, J.; Zhuang, Y.; Zhang, S. Coupled Metabolic-Hydrodynamic Modeling Enabling Rational Scale-up of Industrial Bioprocesses. Biotechnol. Bioeng. 2020, 117, 844–867. [Google Scholar] [CrossRef]
- Monk, J.; Nogales, J.; Palsson, B.O. Optimizing Genome-Scale Network Reconstructions. Nat. Biotechnol. 2014, 32, 447–452. [Google Scholar] [CrossRef]
- Ebrahim, A.; Lerman, J.A.; Palsson, B.O.; Hyduke, D.R. COBRApy: COnstraints-Based Reconstruction and Analysis for Python. BMC Syst. Biol. 2013, 7, 74. [Google Scholar] [CrossRef]
- Cardoso, J.G.R.; Jensen, K.; Lieven, C.; Lærke Hansen, A.S.; Galkina, S.; Beber, M.; Özdemir, E.; Herrgård, M.J.; Redestig, H.; Sonnenschein, N. Cameo: A Python Library for Computer Aided Metabolic Engineering and Optimization of Cell Factories. ACS Synth. Biol. 2018, 7, 1163–1166. [Google Scholar] [CrossRef] [PubMed]
- Bordbar, A.; Monk, J.M.; King, Z.A.; Palsson, B.O. Constraint-Based Models Predict Metabolic and Associated Cellular Functions. Nat. Rev. Genet. 2014, 15, 107–120. [Google Scholar] [CrossRef]
- Lerman, J.A.; Hyduke, D.R.; Latif, H.; Portnoy, V.A.; Lewis, N.E.; Orth, J.D.; Schrimpe-Rutledge, A.C.; Smith, R.D.; Adkins, J.N.; Zengler, K.; et al. In Silico Method for Modelling Metabolism and Gene Product Expression at Genome Scale. Nat. Commun. 2012, 3, 1–10. [Google Scholar] [CrossRef]
- Liu, J.K.; Lloyd, C.; Al-Bassam, M.M.; Ebrahim, A.; Kim, J.-N.; Olson, C.; Aksenov, A.; Dorrestein, P.; Zengler, K. Predicting Proteome Allocation, Overflow Metabolism, and Metal Requirements in a Model Acetogen. PLoS Comput. Biol. 2019, 15, e1006848. [Google Scholar] [CrossRef] [PubMed]
- Dinh, H.V.; King, Z.A.; Palsson, B.O.; Feist, A.M. Identification of Growth-Coupled Production Strains Considering Protein Costs and Kinetic Variability. Metab. Eng. Commun. 2018, 7, e00080. [Google Scholar] [CrossRef] [PubMed]
- King, Z.A.; O’Brien, E.J.; Feist, A.M.; Palsson, B.O. Literature Mining Supports a next-Generation Modeling Approach to Predict Cellular Byproduct Secretion. Metab. Eng. 2017, 39, 220–227. [Google Scholar] [CrossRef] [PubMed]
- Yang, L.; Ebrahim, A.; Lloyd, C.J.; Saunders, M.A.; Palsson, B.O. DynamicME: Dynamic Simulation and Refinement of Integrated Models of Metabolism and Protein Expression. BMC Syst. Biol. 2019, 13, 2. [Google Scholar] [CrossRef]
- Adadi, R.; Volkmer, B.; Milo, R.; Heinemann, M.; Shlomi, T. Prediction of Microbial Growth Rate versus Biomass Yield by a Metabolic Network with Kinetic Parameters. PLoS Comput. Biol. 2012, 8, e1002575. [Google Scholar] [CrossRef]
- Massaiu, I.; Pasotti, L.; Sonnenschein, N.; Rama, E.; Cavaletti, M.; Magni, P.; Calvio, C.; Herrgård, M.J. Integration of Enzymatic Data in Bacillus Subtilis Genome-Scale Metabolic Model Improves Phenotype Predictions and Enables in Silico Design of Poly-γ-Glutamic Acid Production Strains. Microb. Cell Fact. 2019, 18, 3. [Google Scholar] [CrossRef]
- Sánchez, B.J.; Zhang, C.; Nilsson, A.; Lahtvee, P.-J.; Kerkhoven, E.J.; Nielsen, J. Improving the Phenotype Predictions of a Yeast Genome-Scale Metabolic Model by Incorporating Enzymatic Constraints. Mol. Syst. Biol. 2017, 13, 935. [Google Scholar] [CrossRef]
- Bekiaris, P.S.; Klamt, S. Automatic Construction of Metabolic Models with Enzyme Constraints. BMC Bioinformatics 2020, 21, 19. [Google Scholar] [CrossRef] [PubMed]
- Zuñiga, C.; Li, T.; Guarnieri, M.T.; Jenkins, J.P.; Li, C.-T.; Bingol, K.; Kim, Y.-M.; Betenbaugh, M.J.; Zengler, K. Synthetic Microbial Communities of Heterotrophs and Phototrophs Facilitate Sustainable Growth. Nat. Commun. 2020, 11, 3803. [Google Scholar] [CrossRef] [PubMed]
- Özcan, E.; Seven, M.; Şirin, B.; Çakır, T.; Nikerel, E.; Teusink, B.; Toksoy Öner, E. Dynamic Co-Culture Metabolic Models Reveal the Fermentation Dynamics, Metabolic Capacities and Interplays of Cheese Starter Cultures. Biotechnol. Bioeng. 2020. [Google Scholar] [CrossRef] [PubMed]
- Zhou, K.; Qiao, K.; Edgar, S.; Stephanopoulos, G. Distributing a Metabolic Pathway among a Microbial Consortium Enhances Production of Natural Products. Nat. Biotechnol. 2015, 33, 377–383. [Google Scholar] [CrossRef] [PubMed]
- Lloyd, C.J.; King, Z.; Sandberg, T.; Hefner, Y.; Feist, A. Model-Driven Design and Evolution of Non-Trivial Synthetic Syntrophic Pairs. BioRxiv 2018. [Google Scholar] [CrossRef]
- Monk, J.M.; Charusanti, P.; Aziz, R.K.; Lerman, J.A.; Premyodhin, N.; Orth, J.D.; Feist, A.M.; Palsson, B.Ø. Genome-Scale Metabolic Reconstructions of Multiple Escherichia Coli Strains Highlight Strain-Specific Adaptations to Nutritional Environments. Proc. Natl. Acad. Sci. USA 2013, 110, 20338–20343. [Google Scholar] [CrossRef]
- Poudel, S.; Tsunemoto, H.; Seif, Y.; Sastry, A.V.; Szubin, R.; Xu, S.; Machado, H.; Olson, C.A.; Anand, A.; Pogliano, J.; et al. Revealing 29 Sets of Independently Modulated Genes in Staphylococcus Aureus, Their Regulators, and Role in Key Physiological Response. Proc. Natl. Acad. Sci. USA 2020, 117, 17228–17239. [Google Scholar] [CrossRef]
- Norsigian, C.J.; Attia, H.; Szubin, R.; Yassin, A.S.; Palsson, B.Ø.; Aziz, R.K.; Monk, J.M. Comparative Genome-Scale Metabolic Modeling of Metallo-Beta-Lactamase-Producing Multidrug-Resistant Klebsiella Pneumoniae Clinical Isolates. Front. Cell. Infect. Microbiol. 2019, 9. [Google Scholar] [CrossRef]
- Seif, Y.; Kavvas, E.; Lachance, J.-C.; Yurkovich, J.T.; Nuccio, S.-P.; Fang, X.; Catoiu, E.; Raffatellu, M.; Palsson, B.O.; Monk, J.M. Genome-Scale Metabolic Reconstructions of Multiple Salmonella Strains Reveal Serovar-Specific Metabolic Traits. Nat. Commun. 2018, 9, 3771. [Google Scholar] [CrossRef]
- Prigent, S.; Nielsen, J.C.; Frisvad, J.C.; Nielsen, J. Reconstruction of 24 Penicillium Genome-Scale Metabolic Models Shows Diversity Based on Their Secondary Metabolism. Biotechnol. Bioeng. 2018, 115, 2604–2612. [Google Scholar] [CrossRef]
- Fouts, D.E.; Matthias, M.A.; Adhikarla, H.; Adler, B.; Amorim-Santos, L.; Berg, D.E.; Bulach, D.; Buschiazzo, A.; Chang, Y.-F.; Galloway, R.L.; et al. What Makes a Bacterial Species Pathogenic?: Comparative Genomic Analysis of the Genus Leptospira. PLoS Negl. Trop. Dis. 2016, 10, e0004403. [Google Scholar] [CrossRef] [PubMed]
- Ghatak, S.; King, Z.A.; Sastry, A.; Palsson, B.O. The Y-Ome Defines the 35% of Escherichia Coli Genes That Lack Experimental Evidence of Function. Nucleic Acids Res. 2019, 47, 2446–2454. [Google Scholar] [CrossRef] [PubMed]
- Xie, Z.; Tang, H. ISEScan: Automated Identification of Insertion Sequence Elements in Prokaryotic Genomes. Bioinformatics 2017, 33, 3340–3347. [Google Scholar] [CrossRef] [PubMed]
- Tarailo-Graovac, M.; Chen, N. Using RepeatMasker to Identify Repetitive Elements in Genomic Sequences. Curr. Protoc. Bioinform. 2009, 25, 1–4. [Google Scholar] [CrossRef] [PubMed]
- Ryu, J.Y.; Kim, H.U.; Lee, S.Y. Deep Learning Enables High-Quality and High-Throughput Prediction of Enzyme Commission Numbers. Proc. Natl. Acad. Sci. USA 2019, 116, 13996–14001. [Google Scholar] [CrossRef]
- Hadadi, N.; MohammadiPeyhani, H.; Miskovic, L.; Seijo, M.; Hatzimanikatis, V. Enzyme Annotation for Orphan and Novel Reactions Using Knowledge of Substrate Reactive Sites. Proc. Natl. Acad. Sci. USA 2019, 116, 7298–7307. [Google Scholar] [CrossRef]
- Oberhardt, M.A.; Zarecki, R.; Reshef, L.; Xia, F.; Duran-Frigola, M.; Schreiber, R.; Henry, C.S.; Ben-Tal, N.; Dwyer, D.J.; Gophna, U.; et al. Systems-Wide Prediction of Enzyme Promiscuity Reveals a New Underground Alternative Route for Pyridoxal 5’-Phosphate Production in E. Coli. PLoS Comput. Biol. 2016, 12, e1004705. [Google Scholar] [CrossRef]
- Moreno-Sánchez, R.; Saavedra, E.; Rodríguez-Enríquez, S.; Olín-Sandoval, V. Metabolic Control Analysis: A Tool for Designing Strategies to Manipulate Metabolic Pathways. J. Biomed. Biotechnol. 2008, 2008. [Google Scholar] [CrossRef]
- Noor, E.; Flamholz, A.; Liebermeister, W.; Bar-Even, A.; Milo, R. A Note on the Kinetics of Enzyme Action: A Decomposition That Highlights Thermodynamic Effects. FEBS Lett. 2013, 587, 2772–2777. [Google Scholar] [CrossRef]
- Henry, C.S.; Broadbelt, L.J.; Hatzimanikatis, V. Thermodynamics-Based Metabolic Flux Analysis. Biophys. J. 2007, 92, 1792–1805. [Google Scholar] [CrossRef]
- Hamilton, J.J.; Dwivedi, V.; Reed, J.L. Quantitative Assessment of Thermodynamic Constraints on the Solution Space of Genome-Scale Metabolic Models. Biophys. J. 2013, 105, 512–522. [Google Scholar] [CrossRef] [PubMed]
- Du, B.; Zielinski, D.C.; Monk, J.M.; Palsson, B.O. Thermodynamic Favorability and Pathway Yield as Evolutionary Tradeoffs in Biosynthetic Pathway Choice. Proc. Natl. Acad. Sci. USA 2018, 115, 11339–11344. [Google Scholar] [CrossRef] [PubMed]
- Salvy, P.; Hatzimanikatis, V. ETFL: A Formulation for Flux Balance Models Accounting for Expression, Thermodynamics, and Resource Allocation Constraints. bioRxiv 2019. [Google Scholar] [CrossRef]
- Salvy, P.; Hatzimanikatis, V. Emergence of Diauxie as an Optimal Growth Strategy under Resource Allocation Constraints in Cellular Metabolism. bioRxiv 2020. [Google Scholar] [CrossRef]
- Pandey, V.; Hadadi, N.; Hatzimanikatis, V. Enhanced Flux Prediction by Integrating Relative Expression and Relative Metabolite Abundance into Thermodynamically Consistent Metabolic Models. PLoS Comput. Biol. 2019, 15, e1007036. [Google Scholar] [CrossRef]
- Saa, P.A.; Nielsen, L.K. Formulation, Construction and Analysis of Kinetic Models of Metabolism: A Review of Modelling Frameworks. Biotechnol. Adv. 2017, 35, 981–1003. [Google Scholar] [CrossRef]
- Gopalakrishnan, S.; Dash, S.; Maranas, C. K-FIT: An Accelerated Kinetic Parameterization Algorithm Using Steady-State Fluxomic Data. Metab. Eng. 2020, 61, 197–205. [Google Scholar] [CrossRef]
- Saa, P.A.; Nielsen, L.K. Construction of Feasible and Accurate Kinetic Models of Metabolism: A Bayesian Approach. Sci. Rep. 2016, 6, 1–13. [Google Scholar] [CrossRef]
- Davidi, D.; Noor, E.; Liebermeister, W.; Bar-Even, A.; Flamholz, A.; Tummler, K.; Barenholz, U.; Goldenfeld, M.; Shlomi, T.; Milo, R. Global Characterization of in Vivo Enzyme Catalytic Rates and Their Correspondence to in Vitro Kcat Measurements. Proc. Natl. Acad. Sci. USA 2016, 113, 3401–3406. [Google Scholar] [CrossRef]
- Heckmann, D.; Campeau, A.; Lloyd, C.J.; Phaneuf, P.V.; Hefner, Y.; Carrillo-Terrazas, M.; Feist, A.M.; Gonzalez, D.J.; Palsson, B.O. Kinetic Profiling of Metabolic Specialists Demonstrates Stability and Consistency of in Vivo Enzyme Turnover Numbers. Proc. Natl. Acad. Sci. USA 2020. [Google Scholar] [CrossRef]
- Heckmann, D.; Lloyd, C.J.; Mih, N.; Ha, Y.; Zielinski, D.C.; Haiman, Z.B.; Desouki, A.A.; Lercher, M.J.; Palsson, B.O. Machine Learning Applied to Enzyme Turnover Numbers Reveals Protein Structural Correlates and Improves Metabolic Models. Nat. Commun. 2018, 9, 5252. [Google Scholar] [CrossRef] [PubMed]
- Beard, D.A.; Vinnakota, K.C.; Wu, F. Detailed Enzyme Kinetics in Terms of Biochemical Species: Study of Citrate Synthase. PLoS ONE 2008, 3, e1825. [Google Scholar] [CrossRef]
- Andreozzi, S.; Miskovic, L.; Hatzimanikatis, V. iSCHRUNK—In Silico Approach to Characterization and Reduction of Uncertainty in the Kinetic Models of Genome-Scale Metabolic Networks. Metab. Eng. 2016, 33, 158–168. [Google Scholar] [CrossRef] [PubMed]
- Nilsson, A.; Nielsen, J.; Palsson, B.O. Metabolic Models of Protein Allocation Call for the Kinetome. Cell Syst. 2017, 5, 538–541. [Google Scholar] [CrossRef] [PubMed]
- Jankowski, M.D.; Henry, C.S.; Broadbelt, L.J.; Hatzimanikatis, V. Group Contribution Method for Thermodynamic Analysis of Complex Metabolic Networks. Biophys. J. 2008, 95, 1487–1499. [Google Scholar] [CrossRef] [PubMed]
- Noor, E.; Haraldsdóttir, H.S.; Milo, R.; Fleming, R.M.T. Consistent Estimation of Gibbs Energy Using Component Contributions. PLoS Comput. Biol. 2013, 9, e1003098. [Google Scholar] [CrossRef]
- Flamholz, A.; Noor, E.; Bar-Even, A.; Milo, R. eQuilibrator—the Biochemical Thermodynamics Calculator. Nucleic Acids Res. 2012, 40, D770–D775. [Google Scholar] [CrossRef]
- Noor, E.; Bar-Even, A.; Flamholz, A.; Lubling, Y.; Davidi, D.; Milo, R. An Integrated Open Framework for Thermodynamics of Reactions That Combines Accuracy and Coverage. Bioinformatics 2012, 28, 2037–2044. [Google Scholar] [CrossRef]
- Du, B.; Zhang, Z.; Grubner, S.; Yurkovich, J.T.; Palsson, B.O.; Zielinski, D.C. Temperature-Dependent Estimation of Gibbs Energies Using an Updated Group-Contribution Method. Biophys. J. 2018, 114, 2691–2702. [Google Scholar] [CrossRef]
- Du, B.; Zielinski, D.C.; Palsson, B.O. Estimating Metabolic Equilibrium Constants: Progress and Future Challenges. Trends Biochem. Sci. 2018, 43, 960–969. [Google Scholar] [CrossRef]
- Jinich, A.; Rappoport, D.; Dunn, I.; Sanchez-Lengeling, B.; Olivares-Amaya, R.; Noor, E.; Even, A.B.; Aspuru-Guzik, A. Quantum Chemical Approach to Estimating the Thermodynamics of Metabolic Reactions. Sci. Rep. 2014, 4, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Haiman, Z.B.; Zielinski, D.C.; Koike, Y.; Yurkovich, J.T.; Palsson, B.O. MASSpy: Building, Simulating, and Visualizing Dynamic Biological Models in Python Using Mass Action Kinetics. bioRxiv 2020. [Google Scholar] [CrossRef]
- Salvy, P.; Fengos, G.; Ataman, M.; Pathier, T.; Soh, K.C.; Hatzimanikatis, V. pyTFA and matTFA: A Python Package and a Matlab Toolbox for Thermodynamics-Based Flux Analysis. Bioinformatics 2019, 35, 167–169. [Google Scholar] [CrossRef] [PubMed]
- Hoops, S.; Sahle, S.; Gauges, R.; Lee, C.; Pahle, J.; Simus, N.; Singhal, M.; Xu, L.; Mendes, P.; Kummer, U. COPASI—A COmplex PAthway SImulator. Bioinformatics 2006, 22, 3067–3074. [Google Scholar] [CrossRef]
- Khodayari, A.; Zomorrodi, A.R.; Liao, J.C.; Maranas, C.D. A Kinetic Model of Escherichia Coli Core Metabolism Satisfying Multiple Sets of Mutant Flux Data. Metab. Eng. 2014, 25, 50–62. [Google Scholar] [CrossRef]
- Tokic, M.; Hatzimanikatis, V.; Miskovic, L. Large-Scale Kinetic Metabolic Models of Pseudomonas Putida KT2440 for Consistent Design of Metabolic Engineering Strategies. Biotechnol. Biofuels 2020, 13, 1–9. [Google Scholar] [CrossRef]
- Soh, K.C.; Hatzimanikatis, V. Constraining the Flux Space Using Thermodynamics and Integration of Metabolomics Data. Methods Mol. Biol. 2014, 1191, 49–63. [Google Scholar]
- Akbari, A.; Palsson, B.O. Scalable Computation of Intracellular Metabolite Concentrations. arXiv 2020. [Google Scholar] [CrossRef]
- Chowdhury, R.; Ren, T.; Shankla, M.; Decker, K.; Grisewood, M.; Prabhakar, J.; Baker, C.; Golbeck, J.H.; Aksimentiev, A.; Kumar, M.; et al. PoreDesigner for Tuning Solute Selectivity in a Robust and Highly Permeable Outer Membrane Pore. Nat. Commun. 2018, 9, 3661. [Google Scholar] [CrossRef]
- Huang, P.-S.; Boyken, S.E.; Baker, D. The Coming of Age of de Novo Protein Design. Nature 2016, 537, 320–327. [Google Scholar] [CrossRef]
- Arnold, F.H. Directed Evolution: Bringing New Chemistry to Life. Angew. Chem. Int. Ed. Engl. 2018, 57, 4143–4148. [Google Scholar] [CrossRef] [PubMed]
- Pantazes, R.J.; Grisewood, M.J.; Li, T.; Gifford, N.P.; Maranas, C.D. The Iterative Protein Redesign and Optimization (IPRO) Suite of Programs. J. Comput. Chem. 2015, 36, 251–263. [Google Scholar] [CrossRef] [PubMed]
- Monk, J.M.; Lloyd, C.J.; Brunk, E.; Mih, N.; Sastry, A.; King, Z.; Takeuchi, R.; Nomura, W.; Zhang, Z.; Mori, H.; et al. iML1515, a Knowledgebase That Computes Escherichia Coli Traits. Nat. Biotechnol. 2017, 35, 904–908. [Google Scholar] [CrossRef]
- Mih, N.; Brunk, E.; Chen, K.; Catoiu, E.; Sastry, A.; Kavvas, E.; Monk, J.M.; Zhang, Z.; Palsson, B.O. Ssbio: A Python Framework for Structural Systems Biology. Bioinformatics 2018, 34, 2155–2157. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Yan, R.; Roy, A.; Xu, D.; Poisson, J.; Zhang, Y. The I-TASSER Suite: Protein Structure and Function Prediction. Nat. Methods 2015, 12, 7–8. [Google Scholar] [CrossRef] [PubMed]
- Senior, A.W.; Evans, R.; Jumper, J.; Kirkpatrick, J.; Sifre, L.; Green, T.; Qin, C.; Žídek, A.; Nelson, A.W.R.; Bridgland, A.; et al. Improved Protein Structure Prediction Using Potentials from Deep Learning. Nature 2020, 577, 706–710. [Google Scholar] [CrossRef] [PubMed]
- Kavvas, E.S.; Catoiu, E.; Mih, N.; Yurkovich, J.T.; Seif, Y.; Dillon, N.; Heckmann, D.; Anand, A.; Yang, L.; Nizet, V.; et al. Machine Learning and Structural Analysis of Mycobacterium Tuberculosis Pan-Genome Identifies Genetic Signatures of Antibiotic Resistance. Nat. Commun. 2018, 9, 4306. [Google Scholar] [CrossRef]
- Brunk, E.; Chang, R.L.; Xia, J.; Hefzi, H.; Yurkovich, J.T.; Kim, D.; Buckmiller, E.; Wang, H.H.; Cho, B.-K.; Yang, C.; et al. Characterizing Posttranslational Modifications in Prokaryotic Metabolism Using a Multiscale Workflow. Proc. Natl. Acad. Sci. USA 2018, 115, 11096–11101. [Google Scholar] [CrossRef]
- Case, D.A.; Belfon, K.; Ben-Shalom, I.Y.; Brozell, S.R.; Cerutti, D.S.; Cheatham, T.E., III; Cruzeiro, V.W.D.; Darden, T.A.; Duke, R.E.; Giambasu, G.; et al. AMBER 2020; University of California: San Francisco, CA, USA, 2020. [Google Scholar]
- Salomon-Ferrer, R.; Case, D.A.; Walker, R.C. An Overview of the Amber Biomolecular Simulation Package. WIREs Comput. Mol. Sci. 2013, 3, 198–210. [Google Scholar] [CrossRef]
- Kavvas, E.S.; Yang, L.; Monk, J.M.; Heckmann, D.; Palsson, B.O. A Biochemically-Interpretable Machine Learning Classifier for Microbial GWAS. Nat. Commun. 2020, 11, 2580. [Google Scholar] [CrossRef]
- Davis, J.J.; Boisvert, S.; Brettin, T.; Kenyon, R.W.; Mao, C.; Olson, R.; Overbeek, R.; Santerre, J.; Shukla, M.; Wattam, A.R.; et al. Antimicrobial Resistance Prediction in PATRIC and RAST. Sci. Rep. 2016, 6. [Google Scholar] [CrossRef] [PubMed]
- Arango-Argoty, G.; Garner, E.; Pruden, A.; Heath, L.S.; Vikesland, P.; Zhang, L. DeepARG: A Deep Learning Approach for Predicting Antibiotic Resistance Genes from Metagenomic Data. Microbiome 2018, 6, 23. [Google Scholar] [CrossRef] [PubMed]
- Haugen, S.P.; Ross, W.; Gourse, R.L. Advances in Bacterial Promoter Recognition and Its Control by Factors That Do Not Bind DNA. Nat. Rev. Microbiol. 2008, 6, 507–519. [Google Scholar] [CrossRef] [PubMed]
- Bailey, T.L.; Boden, M.; Buske, F.A.; Frith, M.; Grant, C.E.; Clementi, L.; Ren, J.; Li, W.W.; Noble, W.S. MEME SUITE: Tools for Motif Discovery and Searching. Nucleic Acids Res. 2009, 37, W202–W208. [Google Scholar] [CrossRef] [PubMed]
- Phaneuf, P.V.; Gosting, D.; Palsson, B.O.; Feist, A.M. ALEdb 1.0: A Database of Mutations from Adaptive Laboratory Evolution Experimentation. Nucleic Acids Res. 2019, 47, D1164–D1171. [Google Scholar] [CrossRef] [PubMed]
- Phaneuf, P.V.; Yurkovich, J.T.; Heckmann, D.; Wu, M.; Sandberg, T.E.; King, Z.A.; Tan, J.; Palsson, B.O.; Feist, A.M. Causal Mutations from Adaptive Laboratory Evolution Are Outlined by Multiple Scales of Genome Annotations and Condition-Specificity. BMC Genom. 2020, 21, 514. [Google Scholar] [CrossRef]
- Lamoureux, C.R.; Choudhary, K.S.; King, Z.A.; Sandberg, T.E.; Gao, Y.; Sastry, A.V.; Phaneuf, P.V.; Choe, D.; Cho, B.-K.; Palsson, B.O. The Bitome: Digitized Genomic Features Reveal Fundamental Genome Organization. Nucleic Acids Res. 2020, 48, 10157–10163. [Google Scholar] [CrossRef]
- Einav, T.; Phillips, R. How the Avidity of Polymerase Binding to the –35/–10 Promoter Sites Affects Gene Expression. Proc. Natl. Acad. Sci. USA 2019, 116, 13340–13345. [Google Scholar] [CrossRef]
- Tuller, T.; Waldman, Y.Y.; Kupiec, M.; Ruppin, E. Translation Efficiency Is Determined by Both Codon Bias and Folding Energy. Proc. Natl. Acad. Sci. USA 2010, 107, 3645–3650. [Google Scholar] [CrossRef]
- Bonde, M.T.; Pedersen, M.; Klausen, M.S.; Jensen, S.I.; Wulff, T.; Harrison, S.; Nielsen, A.T.; Herrgård, M.J.; Sommer, M.O.A. Predictable Tuning of Protein Expression in Bacteria. Nat. Methods 2016, 13, 233–236. [Google Scholar] [CrossRef]
- Rychel, K.; Sastry, A.V.; Palsson, B.O. Machine Learning Uncovers Independently Regulated Modules in the Bacillus Subtilis Transcriptome. bioRxiv 2020. [Google Scholar] [CrossRef]
- Rychel, K.; Decker, K.; Sastry, A.V.; Phaneuf, P.V.; Poudel, S.; Palsson, B.O. iModulonDB: A Knowledgebase of Microbial Transcriptional Regulation Derived from Machine Learning. Nucleic Acids Res. 2020. [Google Scholar] [CrossRef] [PubMed]
- Ament, S.; Shannon, P.; Richards, M. TReNa: Fit. Transcriptional Regulatory Networks Using Gene Expression, Priors, Machine Learning; Bioconductor: Washington, DC, USA, 2017. [Google Scholar] [CrossRef]
- Fang, X.; Sastry, A.; Mih, N.; Kim, D.; Tan, J.; Yurkovich, J.T.; Lloyd, C.J.; Gao, Y.; Yang, L.; Palsson, B.O. Global Transcriptional Regulatory Network for Escherichia Coli Robustly Connects Gene Expression to Transcription Factor Activities. Proc. Natl. Acad. Sci. USA 2017, 114, 10286–10291. [Google Scholar] [CrossRef] [PubMed]
- Chandrasekaran, S.; Price, N.D. Probabilistic Integrative Modeling of Genome-Scale Metabolic and Regulatory Networks in Escherichia Coli and Mycobacterium Tuberculosis. Proc. Natl. Acad. Sci. USA 2010, 107, 17845–17850. [Google Scholar] [CrossRef]
- Rustad, T.R.; Minch, K.J.; Ma, S.; Winkler, J.K.; Hobbs, S.; Hickey, M.; Brabant, W.; Turkarslan, S.; Price, N.D.; Baliga, N.S.; et al. Mapping and Manipulating the Mycobacterium Tuberculosis Transcriptome Using a Transcription Factor Overexpression-Derived Regulatory Network. Genom. Biol. 2014, 15, 502. [Google Scholar] [CrossRef]
- Kochanowski, K.; Gerosa, L.; Brunner, S.F.; Christodoulou, D.; Nikolaev, Y.V.; Sauer, U. Few Regulatory Metabolites Coordinate Expression of Central Metabolic Genes in Escherichia Coli. Mol. Syst. Biol. 2017, 13, 903. [Google Scholar] [CrossRef]
- Santos-Zavaleta, A.; Salgado, H.; Gama-Castro, S.; Sánchez-Pérez, M.; Gómez-Romero, L.; Ledezma-Tejeida, D.; García-Sotelo, J.S.; Alquicira-Hernández, K.; Muñiz-Rascado, L.J.; Peña-Loredo, P.; et al. RegulonDB v 10.5: Tackling Challenges to Unify Classic and High Throughput Knowledge of Gene Regulation in E. Coli K-12. Nucleic Acids Res. 2019, 47, D212–D220. [Google Scholar] [CrossRef]
- Keseler, I.M.; Mackie, A.; Santos-Zavaleta, A.; Billington, R.; Bonavides-Martínez, C.; Caspi, R.; Fulcher, C.; Gama-Castro, S.; Kothari, A.; Krummenacker, M.; et al. The EcoCyc Database: Reflecting New Knowledge about Escherichia Coli K-12. Nucleic Acids Res. 2017, 45, D543–D550. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zielinski, D.C.; Patel, A.; Palsson, B.O. The Expanding Computational Toolbox for Engineering Microbial Phenotypes at the Genome Scale. Microorganisms 2020, 8, 2050. https://doi.org/10.3390/microorganisms8122050
Zielinski DC, Patel A, Palsson BO. The Expanding Computational Toolbox for Engineering Microbial Phenotypes at the Genome Scale. Microorganisms. 2020; 8(12):2050. https://doi.org/10.3390/microorganisms8122050
Chicago/Turabian StyleZielinski, Daniel Craig, Arjun Patel, and Bernhard O. Palsson. 2020. "The Expanding Computational Toolbox for Engineering Microbial Phenotypes at the Genome Scale" Microorganisms 8, no. 12: 2050. https://doi.org/10.3390/microorganisms8122050
APA StyleZielinski, D. C., Patel, A., & Palsson, B. O. (2020). The Expanding Computational Toolbox for Engineering Microbial Phenotypes at the Genome Scale. Microorganisms, 8(12), 2050. https://doi.org/10.3390/microorganisms8122050




