Sex-Specific Asymmetrical Attack Rates in Combined Sexual-Vectorial Transmission Epidemics
Abstract
1. Introduction
2. Methods
2.1. Attack Rates by Sex
2.2. Sexual Force of Infection
2.3. Epidemic Threshold and
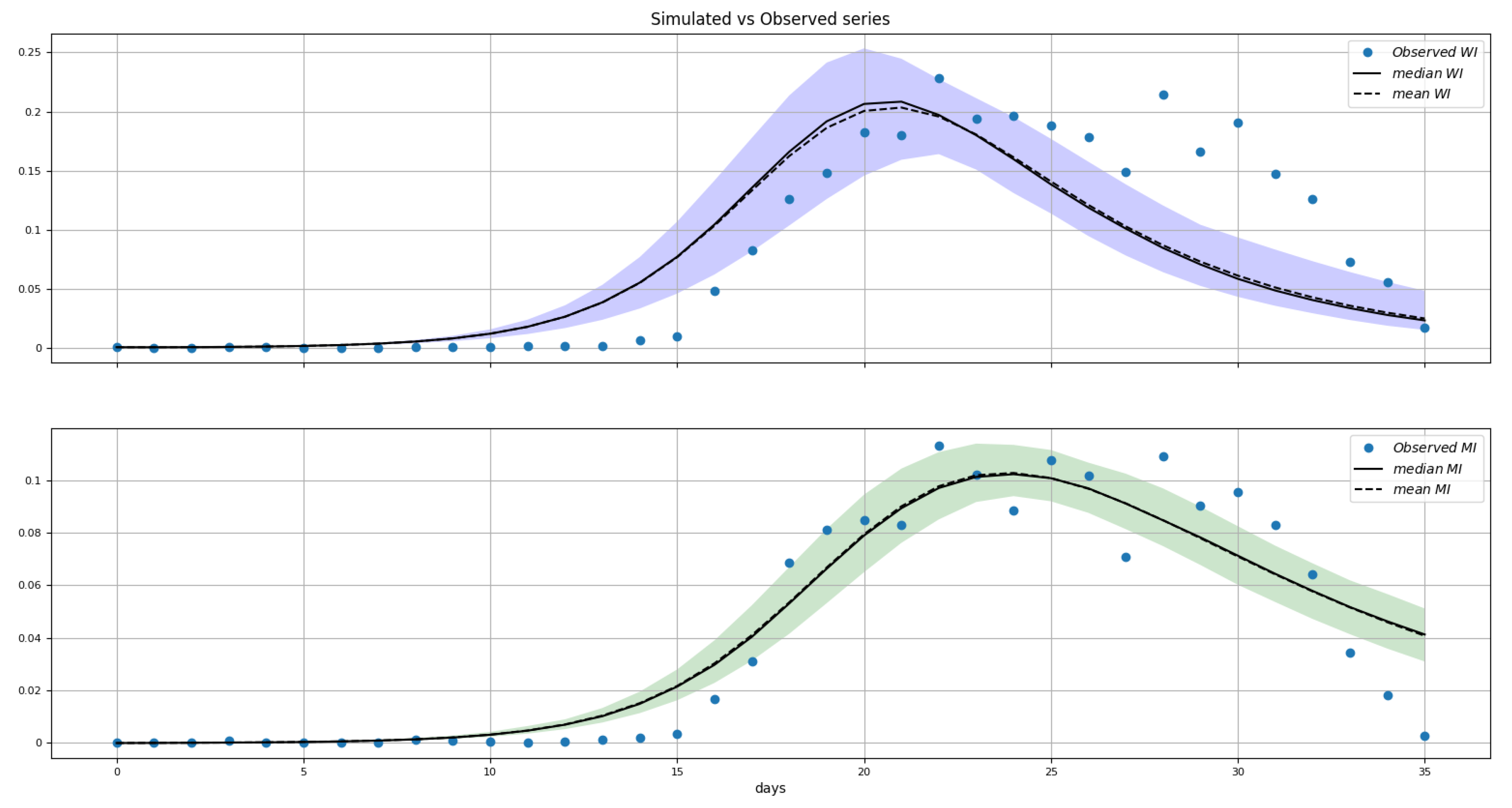
2.4. Fitting the Model to Data
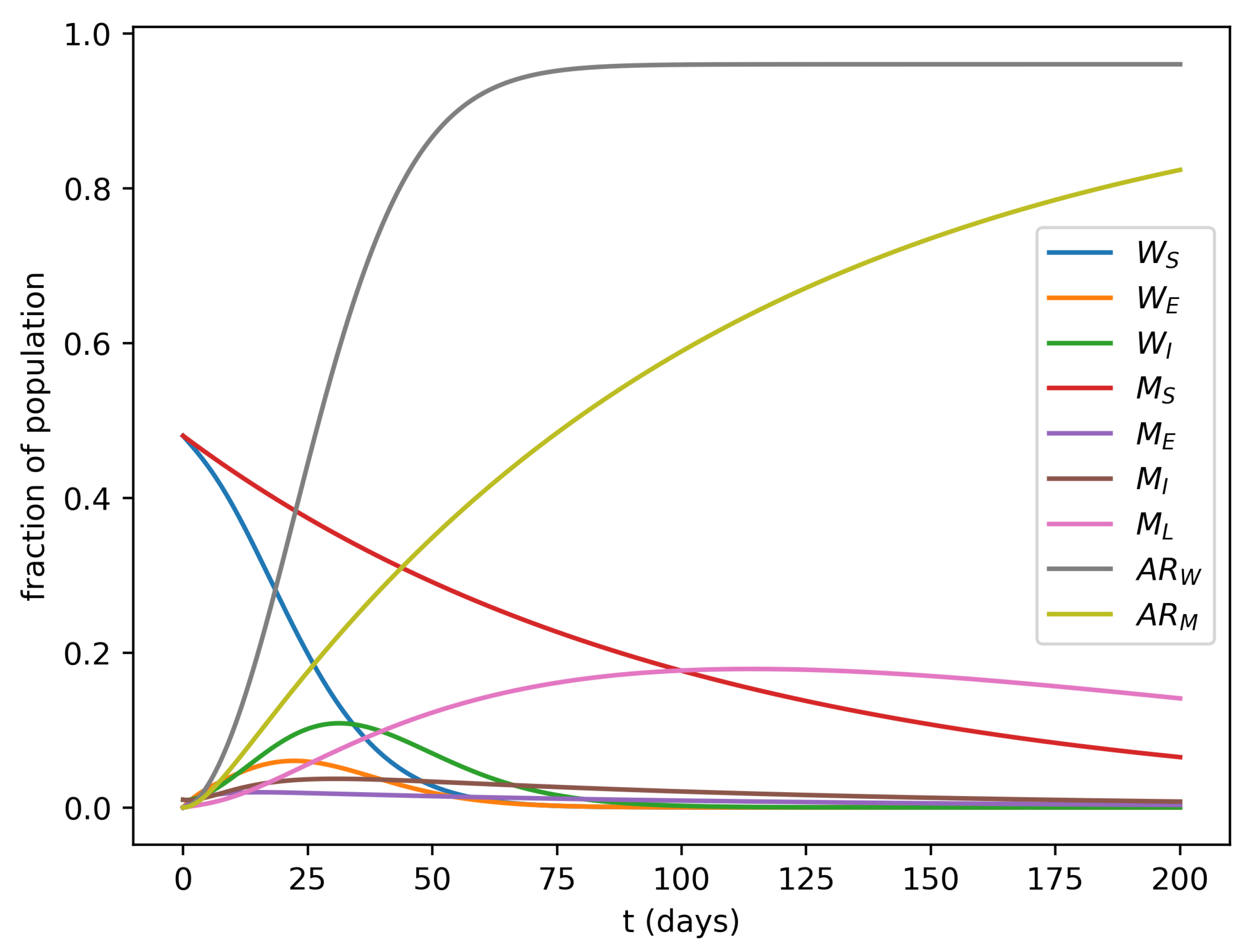
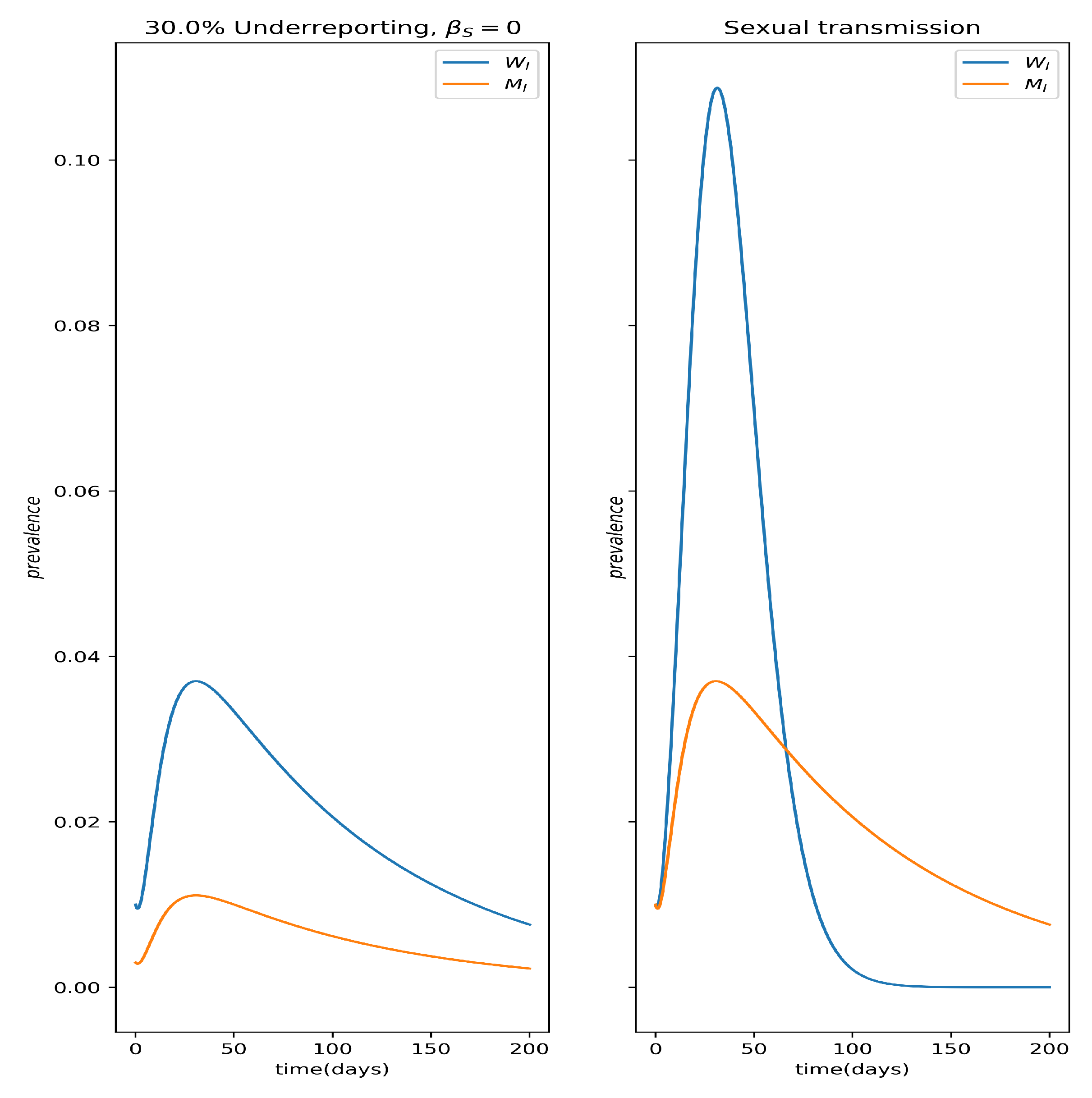
3. Results
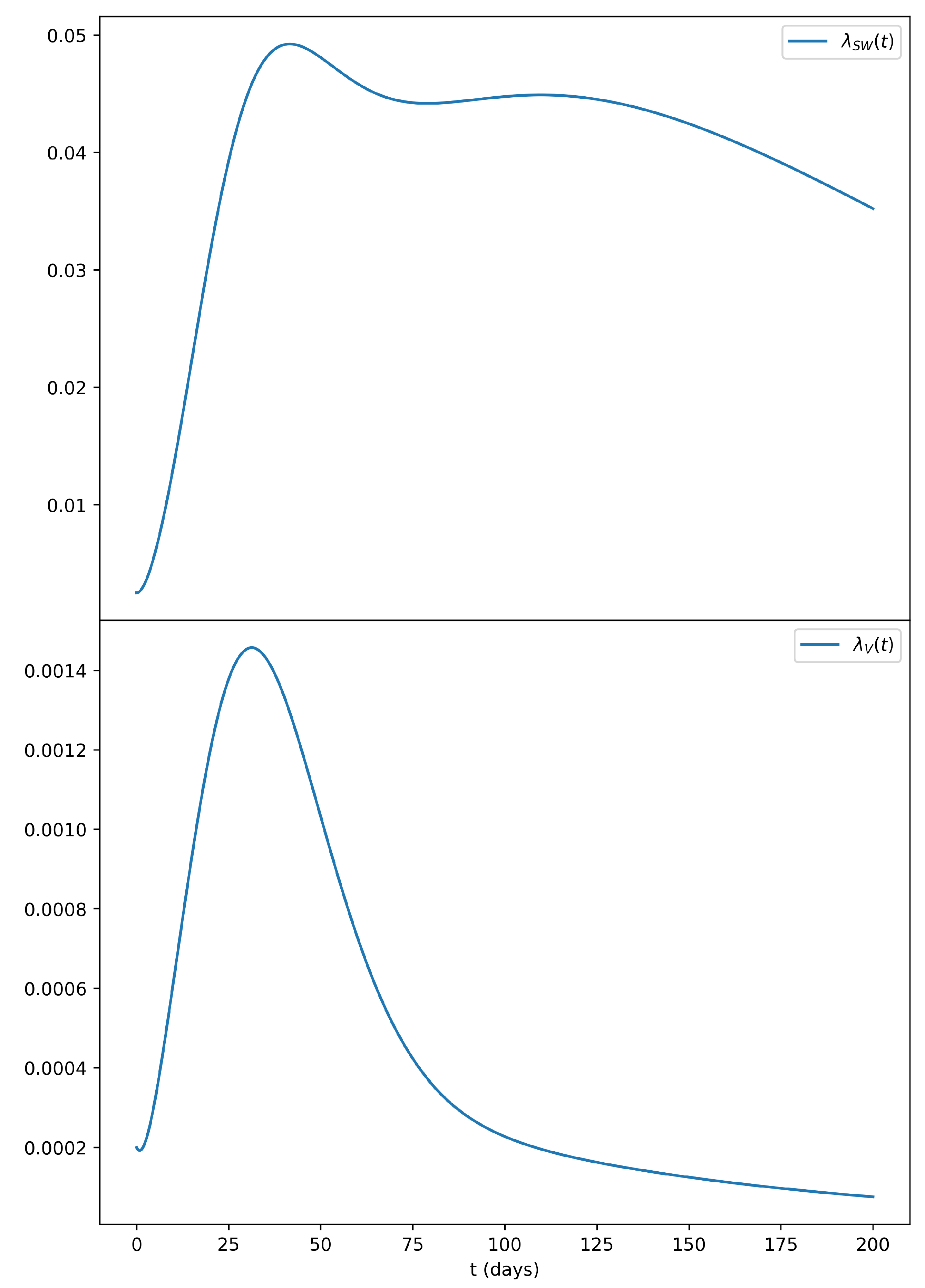
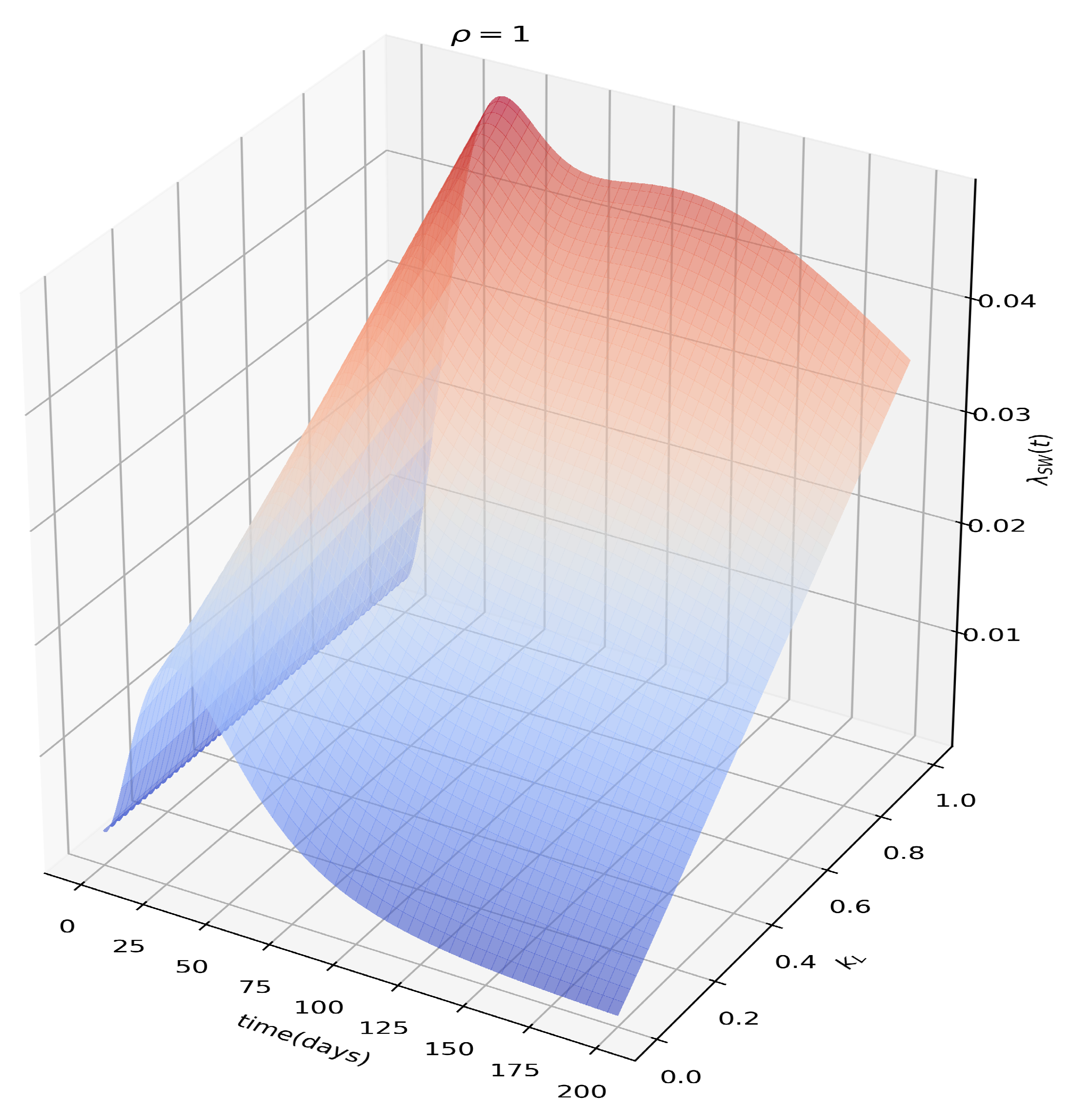
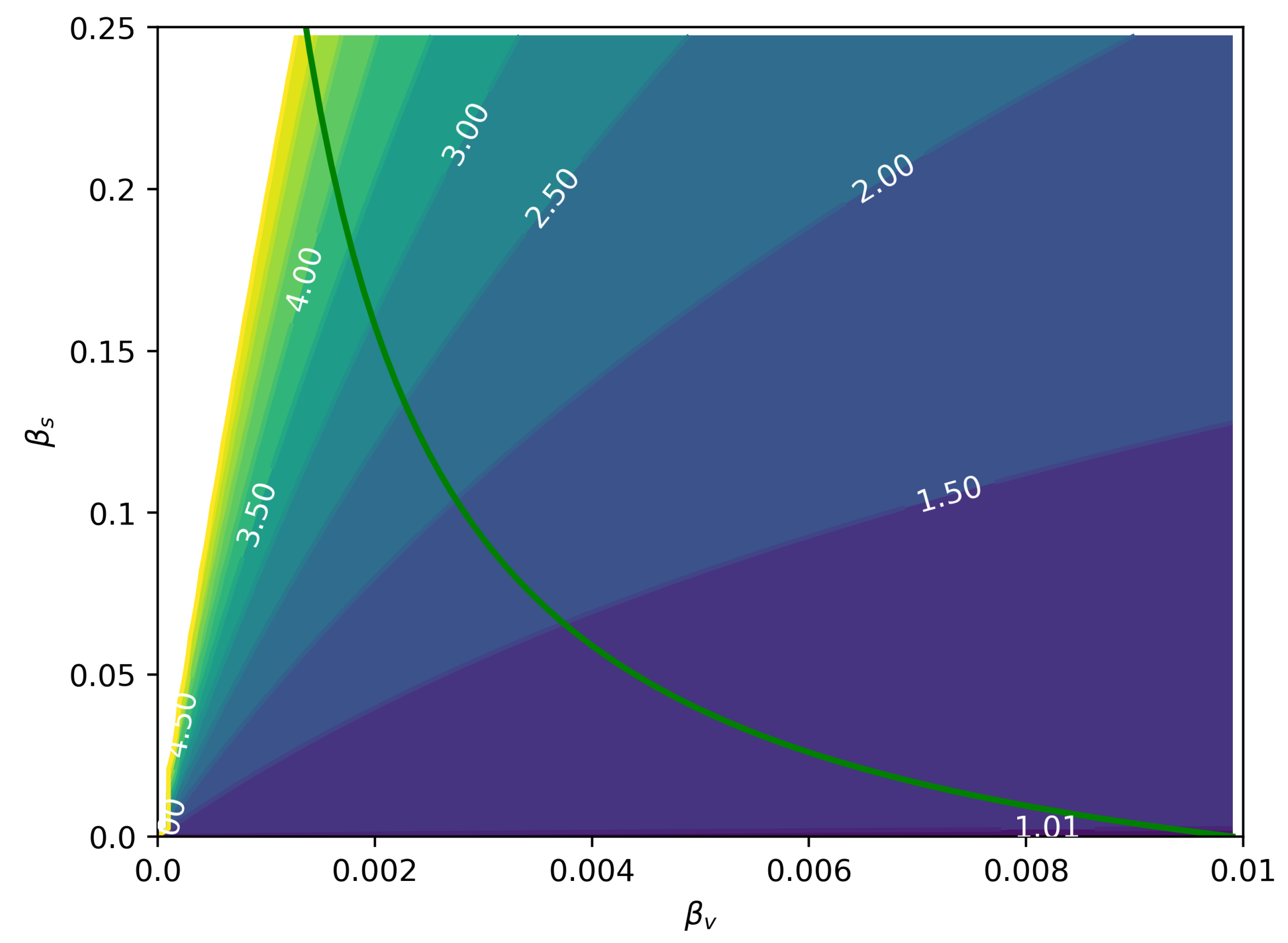
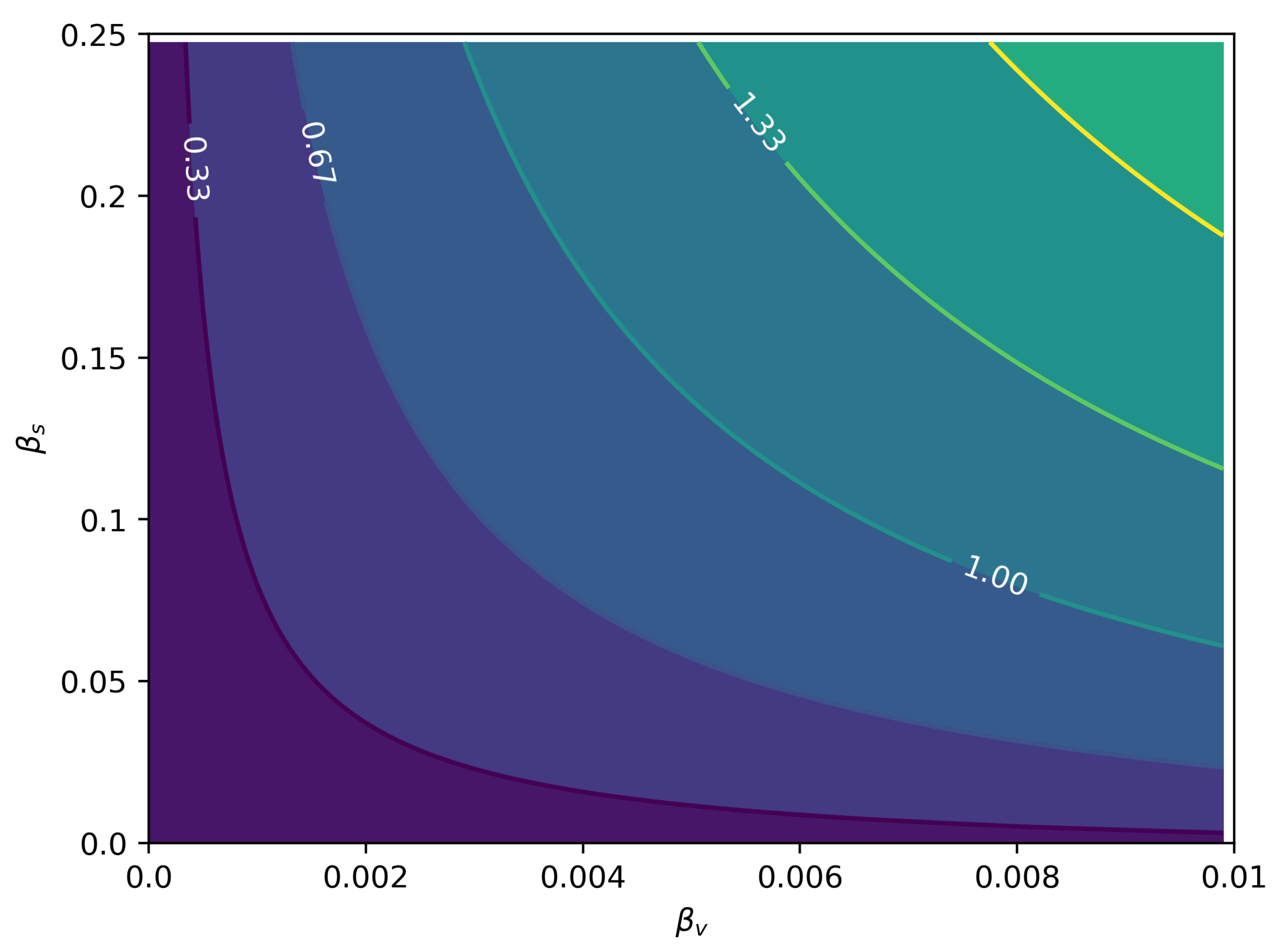
3.1. Sexual Force of Infection
3.2. The Basic Reproduction Number:
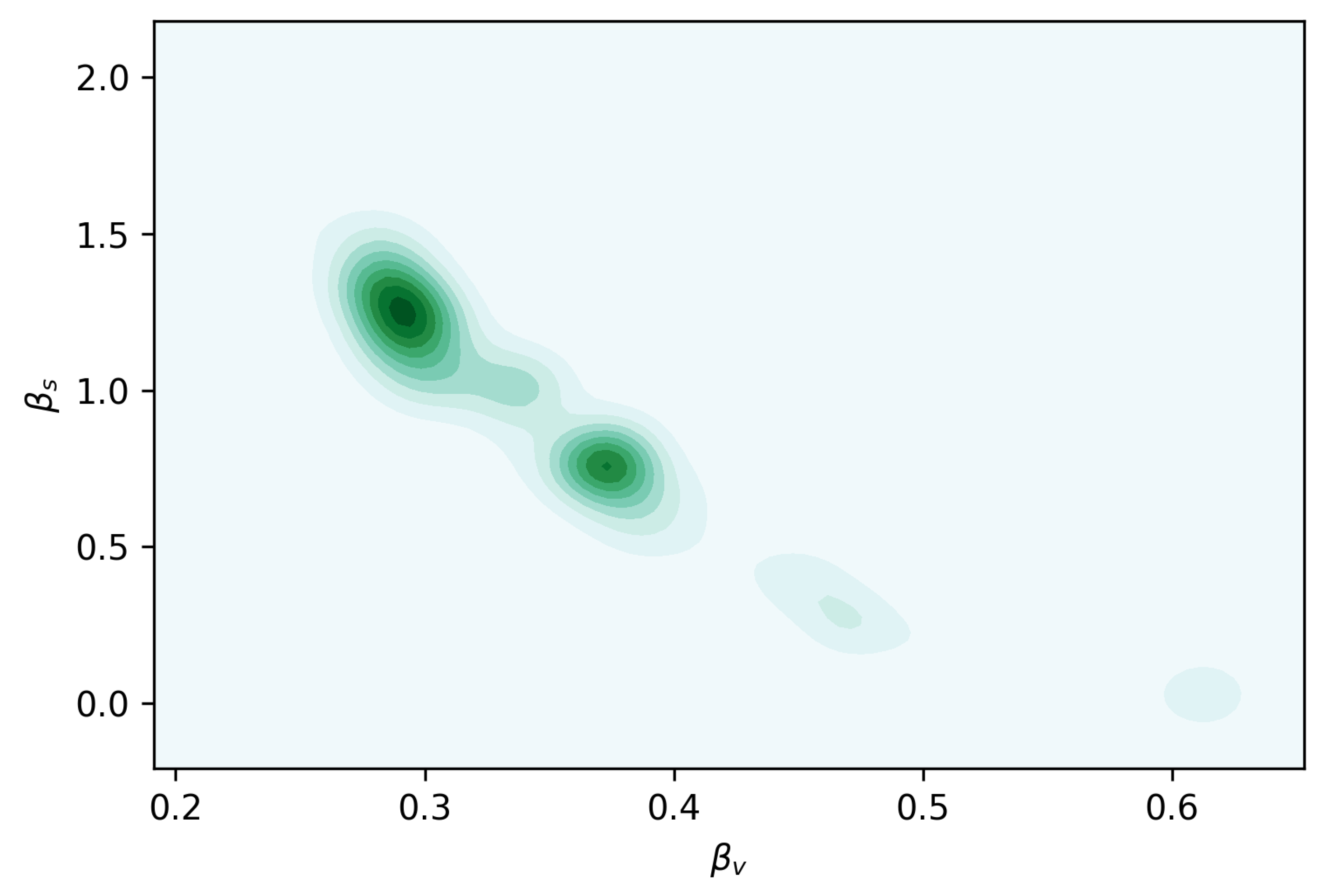
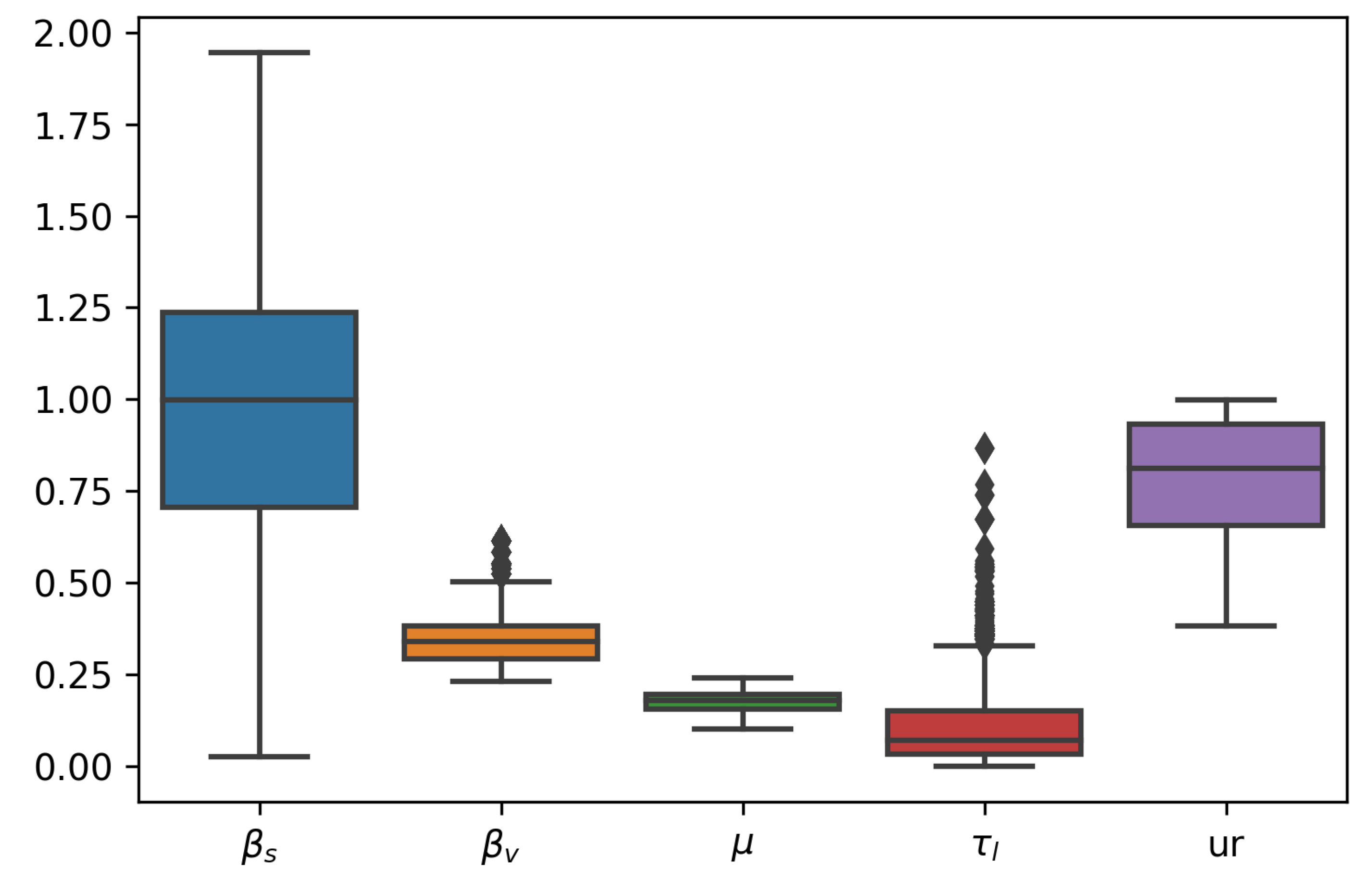
3.3. Fitting the Model to Data
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Reiner, R.C., Jr.; Perkins, T.A.; Barker, C.M.; Niu, T.; Chaves, L.F.; Ellis, A.M.; George, D.B.; Le Menach, A.; Pulliam, J.R.; Bisanzio, D.; et al. A systematic review of mathematical models of mosquito-borne pathogen transmission: 1970–2010. J. R. Soc. Interface 2013, 10, 20120921. [Google Scholar] [CrossRef] [PubMed]
- Anderson, R.M.; Garnett, G.P. Mathematical models of the transmission and control of sexually transmitted diseases. Sex. Transmitted Dis. 2000, 27, 636–643. [Google Scholar] [CrossRef]
- Smith, D.L.; Perkins, T.A.; Reiner, R.C., Jr.; Barker, C.M.; Niu, T.; Chaves, L.F.; Ellis, A.M.; George, D.B.; Le Menach, A.; Pulliam, J.R.; et al. Recasting the theory of mosquito-borne pathogen transmission dynamics and control. Trans. R. Soc. Trop. Med. Hyg. 2014, 108, 185–197. [Google Scholar] [CrossRef]
- Garnett, G.P. An introduction to mathematical models in sexually transmitted disease epidemiology. Sex. Transmitted Infect. 2002, 78, 7–12. [Google Scholar] [CrossRef]
- Lucey, D.R.; Gostin, L.O. The Emerging Zika Pandemic. JAMA 2016, 315, 865. [Google Scholar] [CrossRef]
- Nunes, M.L.; Carlini, C.R.; Marinowic, D.; Neto, F.K.; Fiori, H.H.; Scotta, M.C.; Zanella, P.L.Á.; Soder, R.B.; da Costa, J.C. Microcephaly and Zika virus: A clinical and epidemiological analysis of the current outbreak in Brazil. J. Pediatr. (Versão em Português) 2016, 92, 230–240. [Google Scholar] [CrossRef]
- Wikan, N.; Smith, D.R. Zika virus: History of a newly emerging arbovirus. Lancet Infect. Dis. 2016, 16, e119–e126. [Google Scholar] [CrossRef]
- Abushouk, A.I.; Negida, A.; Ahmed, H. An updated review of Zika virus. J. Clin. Virol. 2016, 84, 53–58. [Google Scholar] [CrossRef] [PubMed]
- Zanluca, C.; de Melo, V.C.A.; Mosimann, A.L.P.; dos Santos, G.I.V.; dos Santos, C.N.D.; Luz, K. First report of autochthonous transmission of Zika virus in Brazil. Memórias do Instituto Oswaldo Cruz 2015, 110, 569–572. [Google Scholar] [CrossRef] [PubMed]
- Heukelbach, J.; Alencar, C.H.; Kelvin, A.A.; De Oliveira, W.K.; Pamplona de Góes Cavalcanti, L. Zika virus outbreak in Brazil. J. Infect. Dev. Ctries. 2016, 10, 116–120. [Google Scholar] [CrossRef]
- Paixão, E.S.; Barreto, F.; da Glória Teixeira, M.; da Conceição, N.; Costa, M.; Rodrigues, L.C. History, Epidemiology, and Clinical Manifestations of Zika: A Systematic Review. Am. J. Public Health 2016, 106, 606–612. [Google Scholar] [CrossRef]
- Atkinson, B.; Hearn, P.; Afrough, B.; Lumley, S.; Carter, D.; Aarons, E.J.; Simpson, A.J.; Brooks, T.J.; Hewson, R. Detection of zika virus in semen. Emerg. Infect. Dis. 2016, 22, 940. [Google Scholar] [CrossRef] [PubMed]
- Mansuy, J.M.; Dutertre, M.; Mengelle, C.; Fourcade, C.; Marchou, B.; Delobel, P.; Izopet, J.; Martin-Blondel, G. Zika virus: High infectious viral load in semen, a new sexually transmitted pathogen? Lancet Infect. Dis. 2016, 16, 405. [Google Scholar] [CrossRef]
- Coelho, F.C.; Durovni, B.; Saraceni, V.; Lemos, C.; Codeço, C.T.; Camargo, S.; De Carvalho, L.M.; Bastos, L.; Arduini, D.; Villela, D.A.; et al. Higher incidence of Zika in adult women than adult men in Rio de Janeiro suggests a significant contribution of sexual transmission from men to women. Int. J. Infect. Dis. 2016, 51, 128–132. [Google Scholar] [CrossRef] [PubMed]
- Davidson, A.; Slavinski, S.; Komoto, K.; Rakeman, J.; Weiss, D. Suspected Female-to-Male Sexual Transmission of Zika Virus—New York City, 2016. MMWR Morb. Mortal. Wkly. Rep. 2016, 65, 716–717. [Google Scholar] [CrossRef] [PubMed]
- Deckard, D.T.; Chung, W.M.; Brooks, J.T.; Smith, J.C.; Woldai, S.; Hennessey, M.; Kwit, N.; Mead, P. Male-to-Male Sexual Transmission of Zika Virus—Texas, January 2016. MMWR Morb. Mortal. Wkly. Rep. 2016, 65, 372–374. [Google Scholar] [CrossRef] [PubMed]
- Towers, S.; Brauer, F.; Castillo-Chavez, C.; Falconar, A.K.; Mubayi, A.; Romero-Vivas, C.M. Estimate of the reproduction number of the 2015 Zika virus outbreak in Barranquilla, Colombia, and estimation of the relative role of sexual transmission. Epidemics 2016, 17, 50–55. [Google Scholar] [CrossRef]
- Gao, D.; Lou, Y.; He, D.; Porco, T.C.; Kuang, Y.; Chowell, G.; Ruan, S. Prevention and control of Zika fever as a mosquito-borne and sexually transmitted disease: A Mathematical Modeling Analysis. Sci. Rep. 2016, 6, 28070. [Google Scholar] [CrossRef] [PubMed]
- Baca-Carrasco, D.; Velasco-Hernández, J.X. Sex, Mosquitoes and Epidemics: An Evaluation of Zika Disease Dynamics. Bull. Math. Biol. 2016, 78, 2228–2242. [Google Scholar] [CrossRef]
- Isea, R.; Lonngren, K.E. A Preliminary Mathematical Model for the Dynamic Transmission of Dengue, Chikungunya and Zika. Am. J. Mod. Phys. Appl. 2016, 3, 11–15. [Google Scholar]
- Bastos, M.M.; Coelho, F.C. Estimating under-observation and the full size of the 2016 Zika epidemic in Rio de Janeiro. PLoS ONE 2018, 13, e0205001. [Google Scholar] [CrossRef] [PubMed]
- Coelho, F.C.; Codeço, C.T.; Gomes, M.G.M. A bayesian framework for parameter estimation in dynamical models. PLoS ONE 2011, 6, e19616. [Google Scholar] [CrossRef] [PubMed]
- Villela, D.; Bastos, L.; De Carvalho, L.; Cruz, O.; Gomes, M.; Durovni, B.; Lemos, M.; Saraceni, V.; Coelho, F.; Codeço, C. Zika in Rio de Janeiro: Assessment of basic reproduction number and comparison with dengue outbreaks. Epidemiol. Infect. 2017, 145, 1649–1657. [Google Scholar] [CrossRef] [PubMed]
- Van den Driessche, P.; Watmough, J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002, 180, 29–48. [Google Scholar] [CrossRef]
- Anderson, R.M.; May, R.M. Infectious Diseases of Humans: Dynamics and Control; Oxford University Press: Oxford, UK, 1992. [Google Scholar]
- Santos, B.M.C.d.; Coelho, F.C.; Armstrong, M.; Saraceni, V.; Lemos, C. Zika: An ongoing threat to women and infants. Cad. Saude Publica 2018, 34, e00038218. [Google Scholar] [CrossRef] [PubMed]
- Pacheco, O.; Beltrán, M.; Nelson, C.A.; Valencia, D.; Tolosa, N.; Farr, S.L.; Padilla, A.V.; Tong, V.T.; Cuevas, E.L.; Espinosa-Bode, A.; et al. Zika virus disease in Colombia—Preliminary report. N. Engl. J. Med. 2016. [Google Scholar] [CrossRef]
- Hess, K.L.; Crepaz, N.; Rose, C.; Purcell, D.; Paz-Bailey, G. Trends in sexual behavior among men who have sex with men (MSM) in high-income countries, 1990–2013: A systematic review. AIDS Behav. 2017, 21, 2811–2834. [Google Scholar] [CrossRef] [PubMed]
- Atkinson, B.; Thorburn, F.; Petridou, C.; Bailey, D.; Hewson, R.; Simpson, A.J.; Brooks, T.J.; Aarons, E.J. Presence and persistence of Zika virus RNA in semen, United Kingdom, 2016. Emerg. Infect. Dis. 2017, 23, 611. [Google Scholar] [CrossRef] [PubMed]
- Kim, C.R.; Counotte, M.; Bernstein, K.; Deal, C.; Mayaud, P.; Low, N.; Broutet, N. Investigating the sexual transmission of Zika virus. Lancet Glob. Health 2018, 6, e24–e25. [Google Scholar] [CrossRef]
- Folkers, K.M.; Caplan, A.L.; Igel, L.H. Zika, sexual transmission and prudent public health policy. Public Health 2017, 148, 66–68. [Google Scholar] [CrossRef]
| Symbols | Description | Value Range |
|---|---|---|
| Susceptible women | * | |
| Exposed women | * | |
| Infectious women | * | |
| Susceptible men | * | |
| Exposed men | * | |
| Infectious men | * | |
| Latent men | * | |
| Recovery rate (day) | [18] | |
| Vector transmission rate (day) | [18] | |
| Sexual transmission rate ((people × day)) | ||
| Women-to-women transmissibility modifier | ||
| Women-to-men transmissibility modifier | ||
| Men-to-men transmissibility modifier | ||
| Latent period transmissibility modifier | ||
| e | Incubation rate (day) | [18] |
| Fraction of men becoming latent | ||
| Latent recovery rate (day) | [12] |
| Parameter | Prior | Posterior |
|---|---|---|
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
de Barros, A.C.W.G.; Santos, K.G.; Massad, E.; Coelho, F.C. Sex-Specific Asymmetrical Attack Rates in Combined Sexual-Vectorial Transmission Epidemics. Microorganisms 2019, 7, 112. https://doi.org/10.3390/microorganisms7040112
de Barros ACWG, Santos KG, Massad E, Coelho FC. Sex-Specific Asymmetrical Attack Rates in Combined Sexual-Vectorial Transmission Epidemics. Microorganisms. 2019; 7(4):112. https://doi.org/10.3390/microorganisms7040112
Chicago/Turabian Stylede Barros, Ana Carolina W. G., Kaline G. Santos, Eduardo Massad, and Flávio Codeço Coelho. 2019. "Sex-Specific Asymmetrical Attack Rates in Combined Sexual-Vectorial Transmission Epidemics" Microorganisms 7, no. 4: 112. https://doi.org/10.3390/microorganisms7040112
APA Stylede Barros, A. C. W. G., Santos, K. G., Massad, E., & Coelho, F. C. (2019). Sex-Specific Asymmetrical Attack Rates in Combined Sexual-Vectorial Transmission Epidemics. Microorganisms, 7(4), 112. https://doi.org/10.3390/microorganisms7040112





