Reproduction of Large-Scale Bioreactor Conditions on Microfluidic Chips
Abstract
1. Introduction
1.1. Large-Scale Bioreactor Conditions
1.2. Microfluidic Single-Cell Analysis
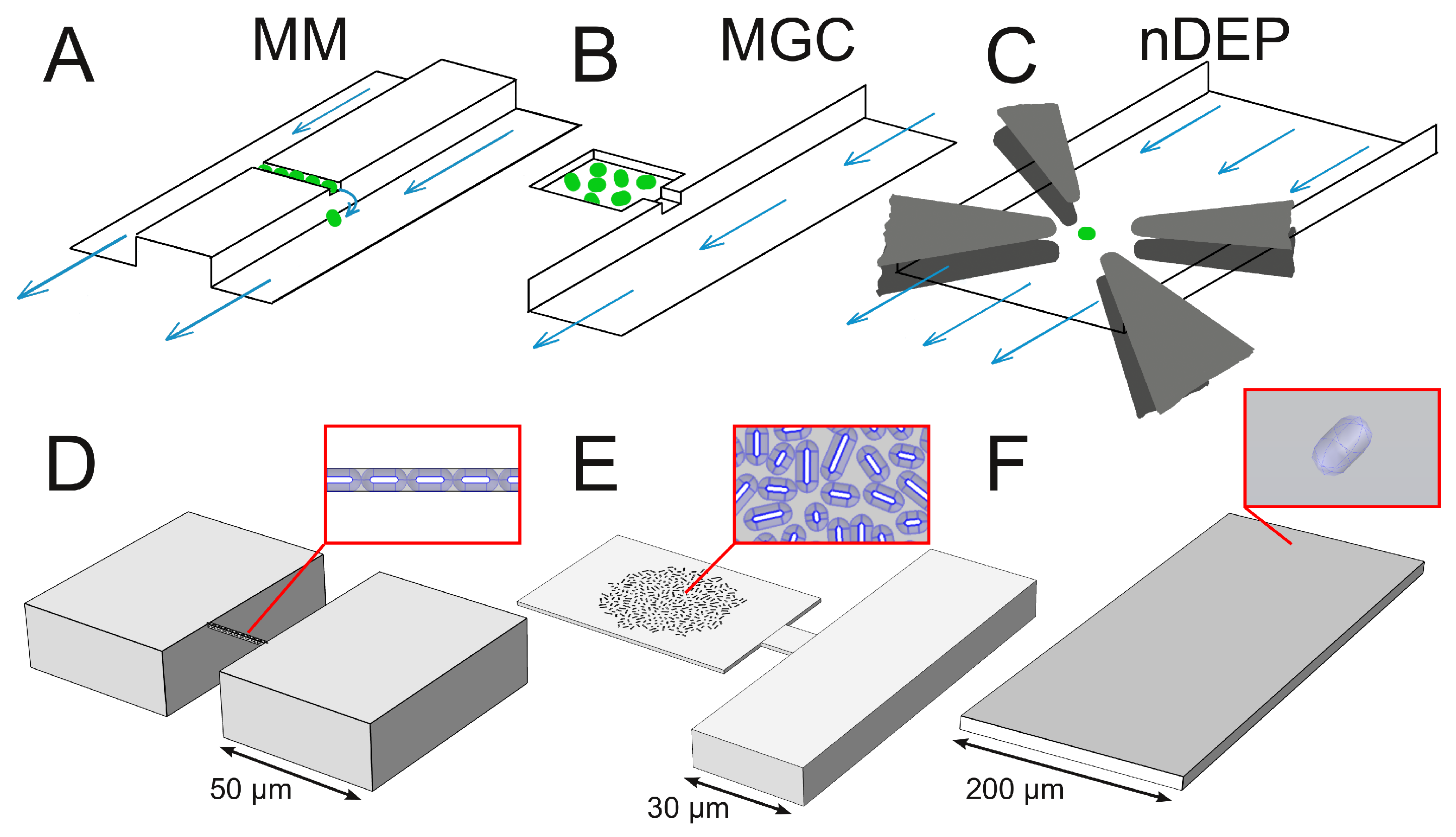
1.2.1. Mother Machine
1.2.2. Monolayer Growth Chamber
1.2.3. Negative Dielectrophoresis
1.3. Scope
2. Materials and Methods
2.1. Computational
2.1.1. Fluid Dynamics
2.1.2. Mass Transport
2.1.3. Inlet Signals
2.1.4. Signal Analysis
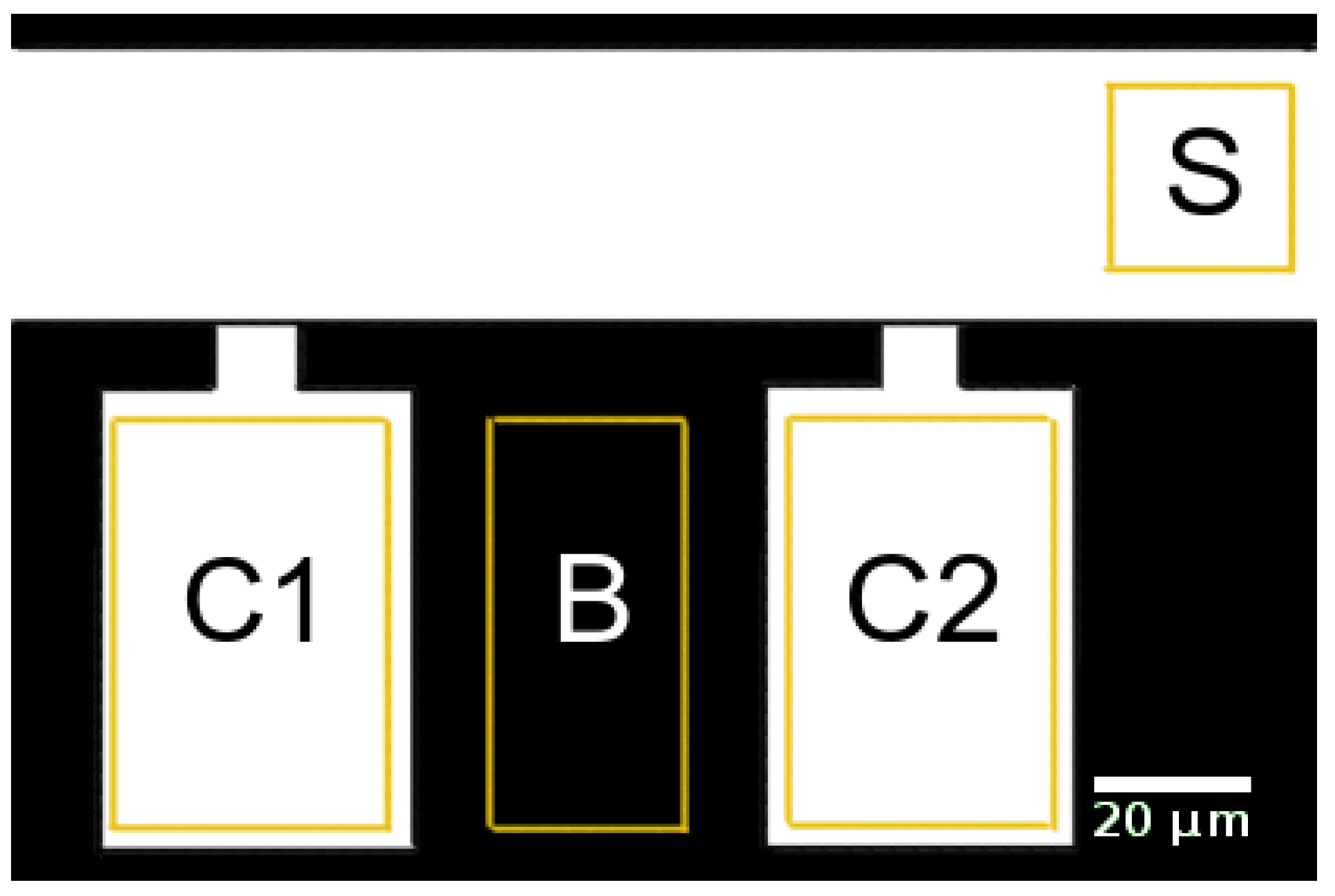
2.1.5. Computational Geometry
2.2. Experimental
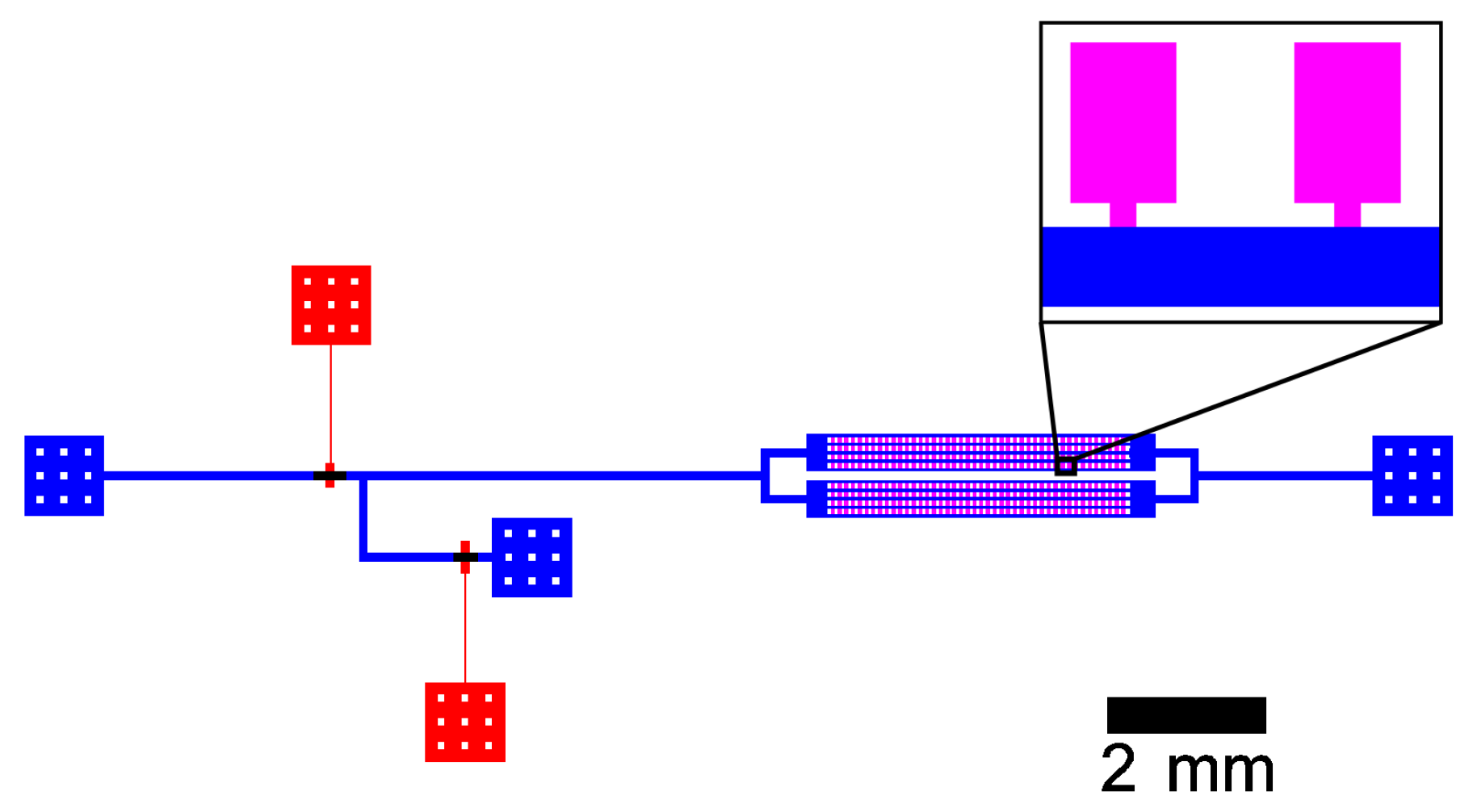
2.2.1. Device Fabrication
2.2.2. Device Operation and Microscopic Imaging
2.2.3. Data Analysis
3. Results and Discussion
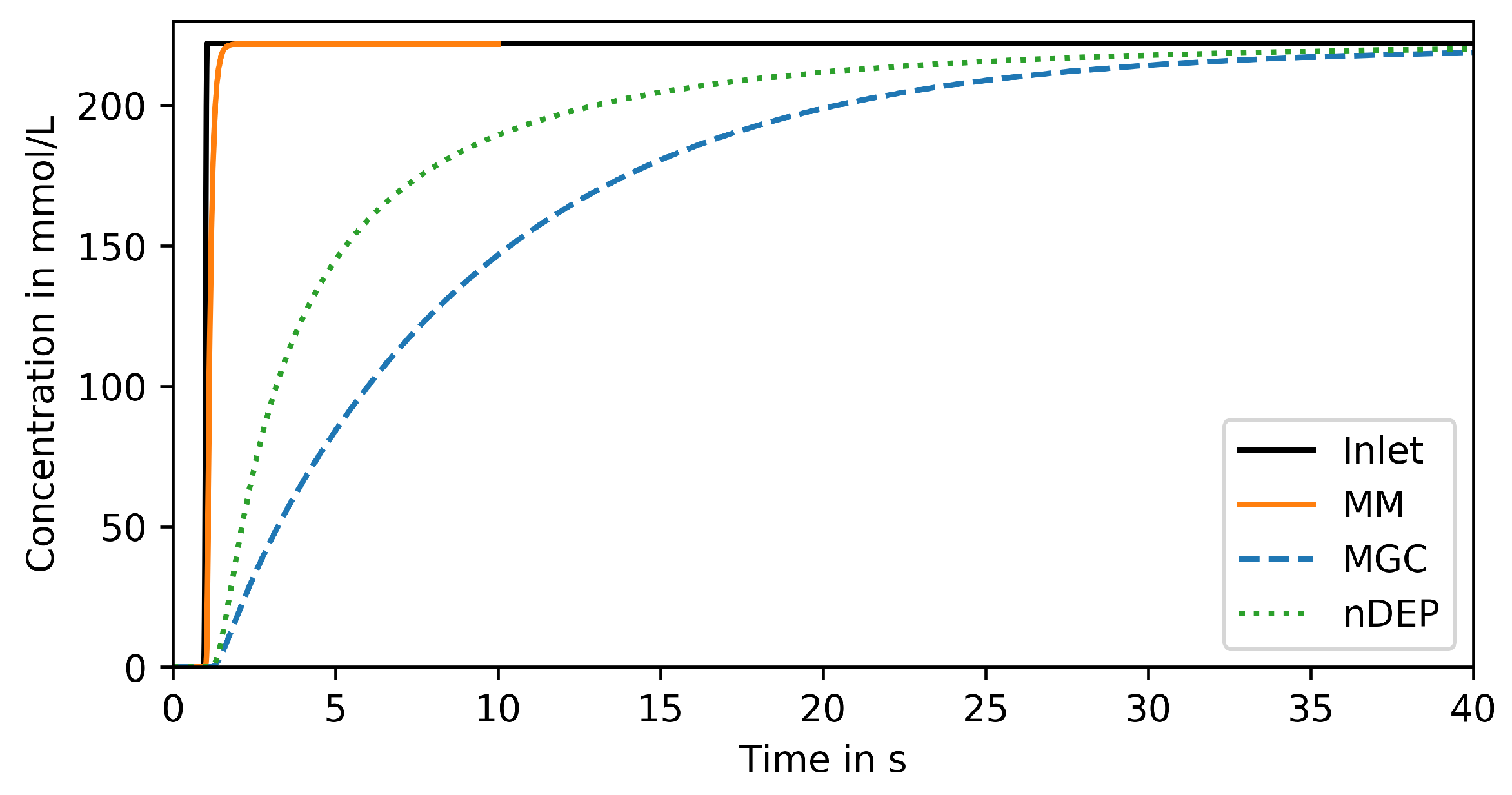
3.1. Step Change
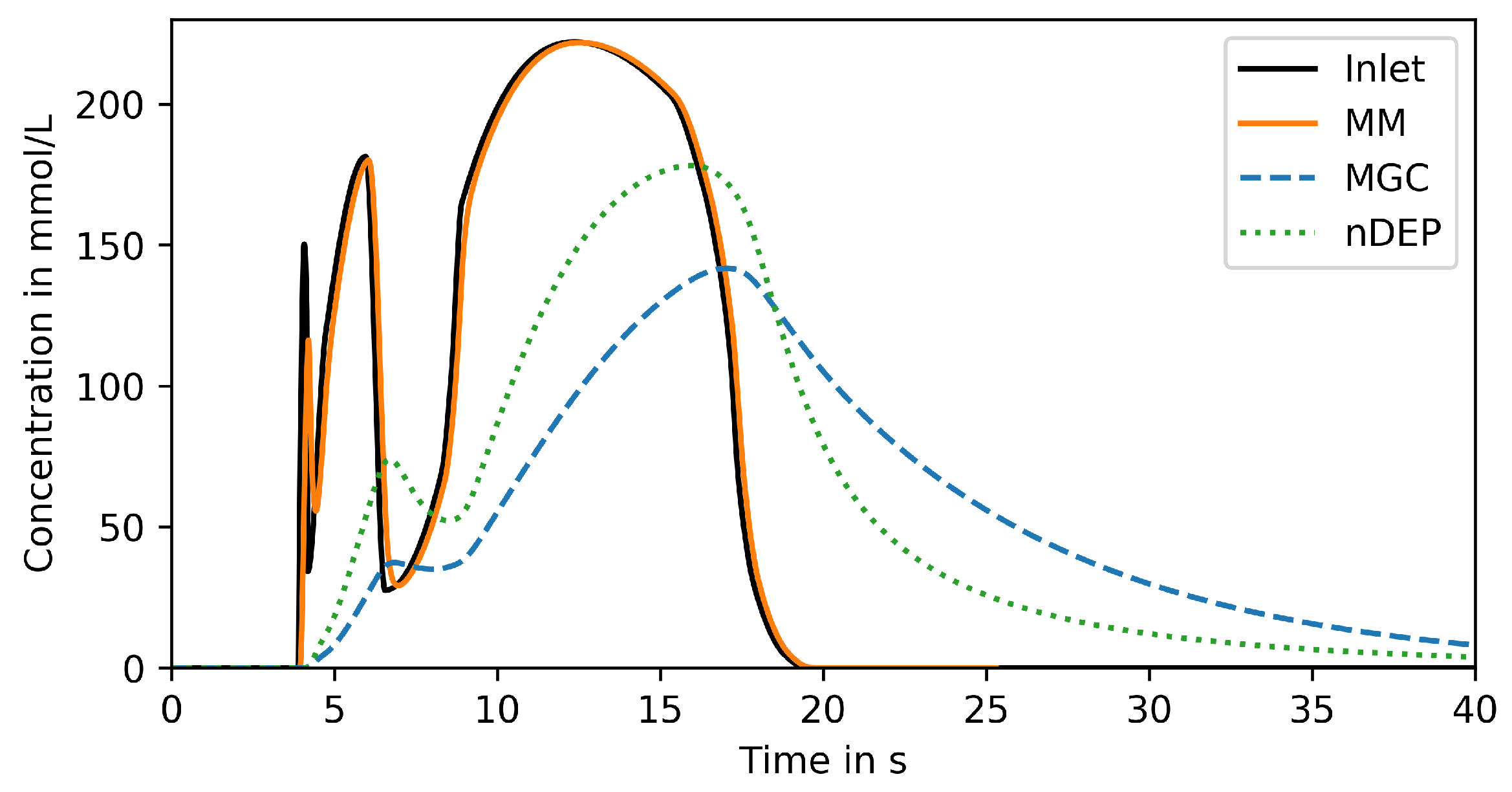
3.2. Life Line
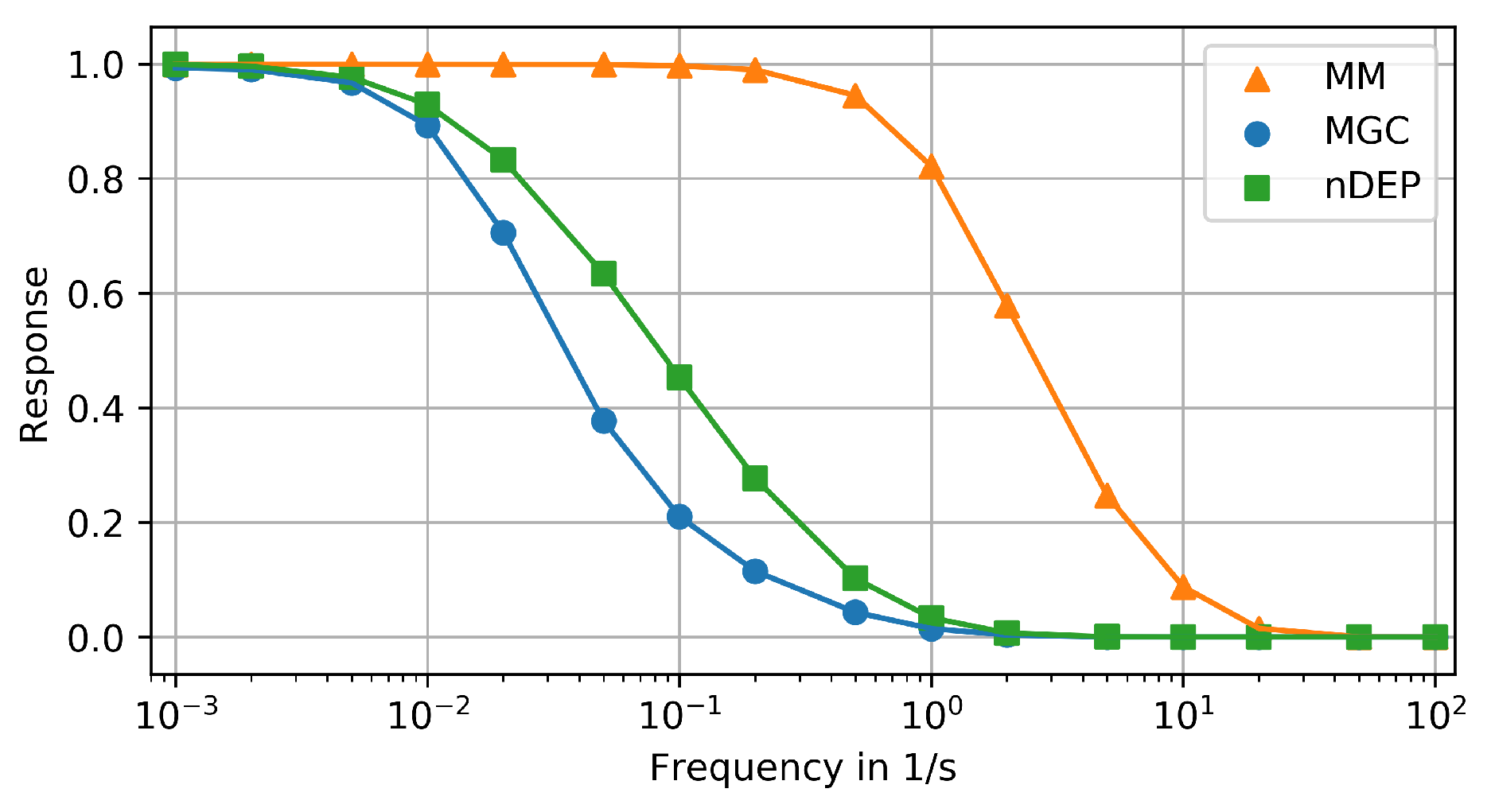
3.3. Frequency Response Analysis
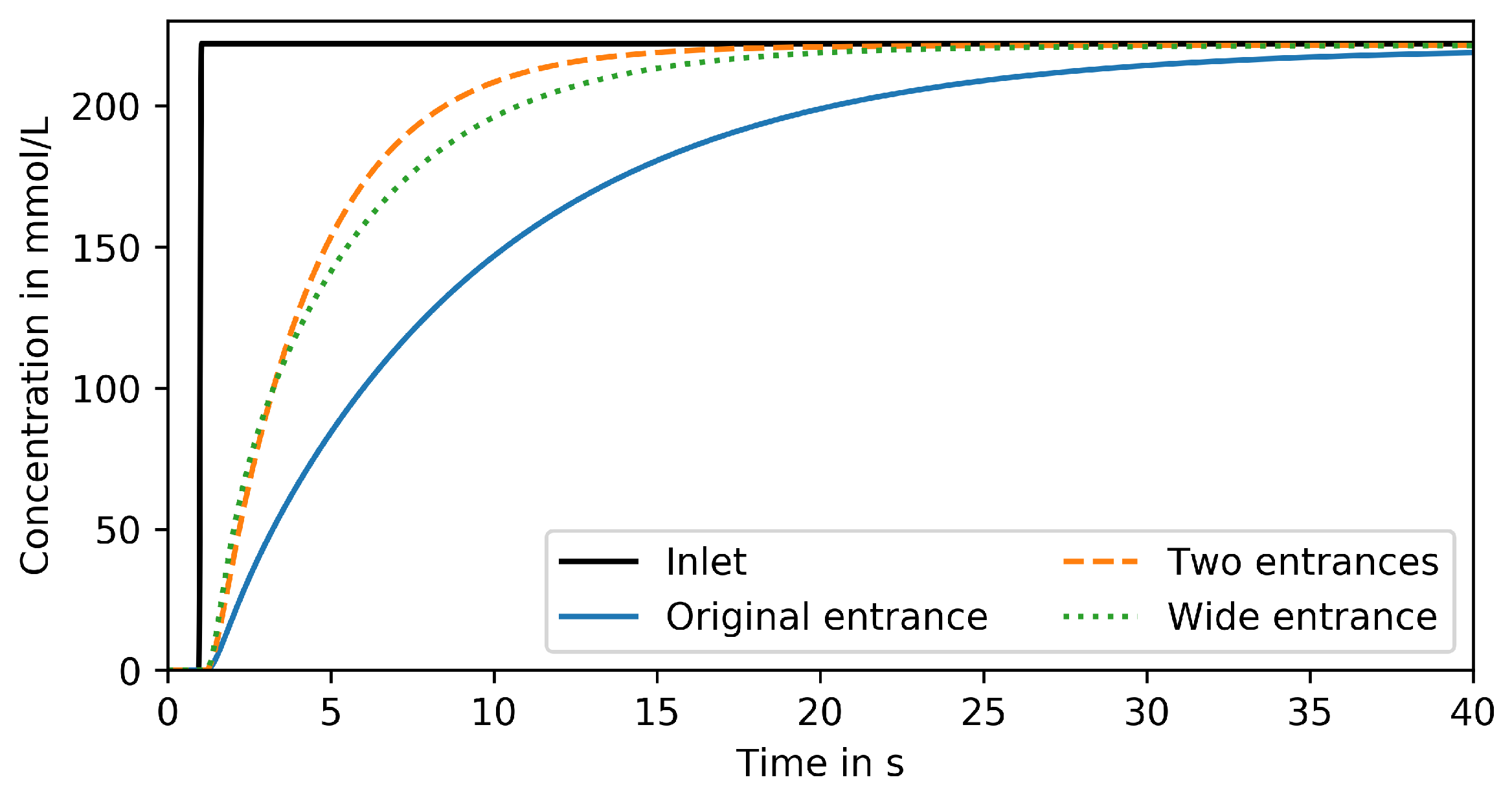
3.4. Design Optimization
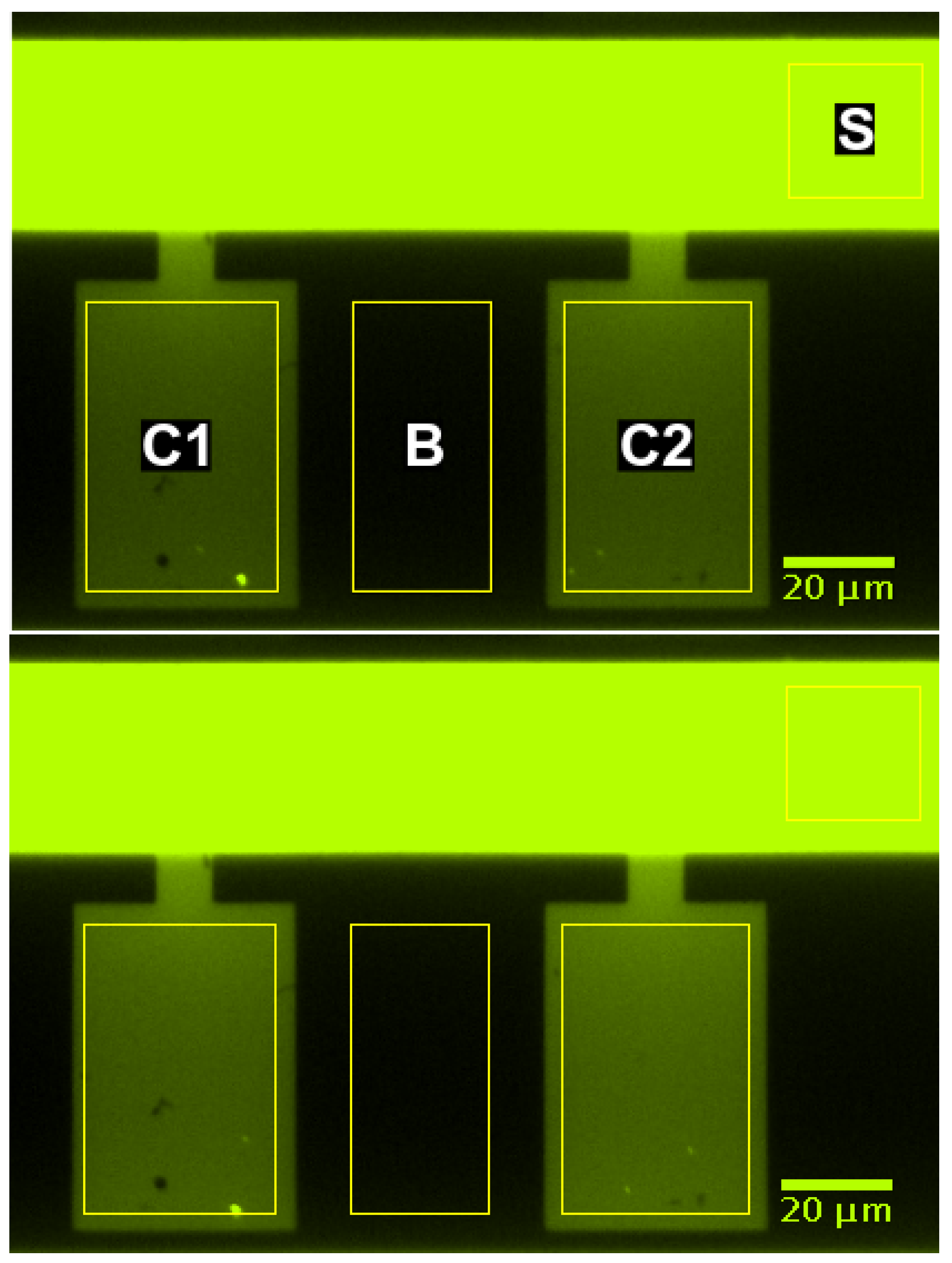
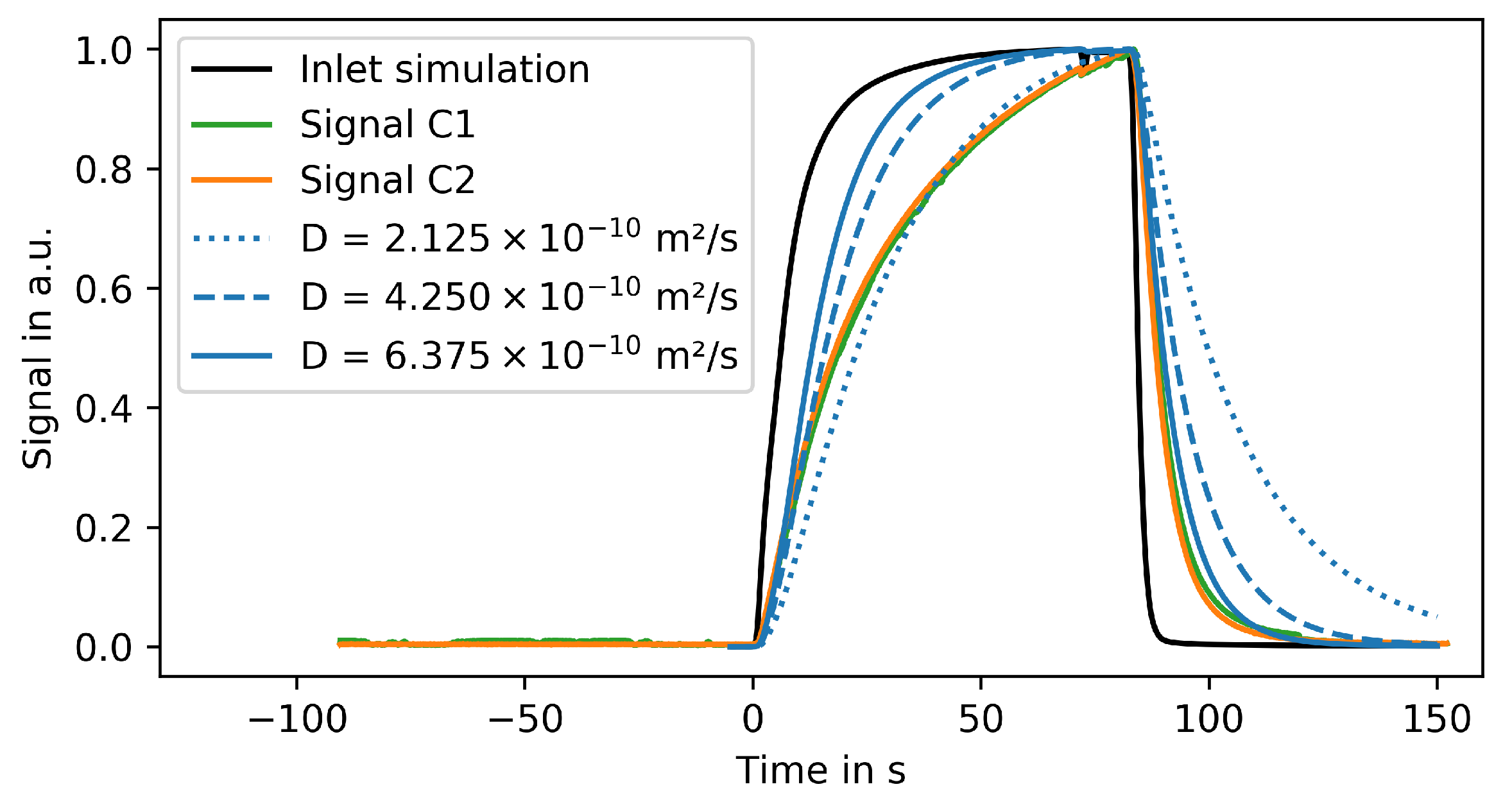
3.5. Experimental Validation
4. Conclusions and Outlook
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Laminar Flow
Appendix B. Dominant Mass Transfer
Appendix C. Mesh and Uptake Model Details
Appendix D. Process Parameters Photolithography
Appendix D.1. Top Layer Master Mold Fabrication
- Wafer dehydration in an oven at 200 for 10
- Spin-Coating of SU-8 photoresist (SU-8 2010, Microchemicals GmbH, Ulm, Germany) at 3500 rpm. Final resist thickness: 10
- Soft bake on a hotplate at 65 for , then at 95 for
- UV light exposure (Karl Suss MA4, Süss Micro Tec, Garching bei München, Germany) for 4 (wavelength, soft vacuum contact mode)
- Post exposure bake on a hotplate at 65 for 3 , then at 95 for 3
- Two-Step development in mr-Dev 600 (Microchemicals GmbH, Ulm, Germany) for 45 + 60 , then cleaning in 2-Propanol for 20
- Hardbake on a hotplate at 150 for 6
Appendix D.2. Bottom Layer Master Mold Fabrication
- Wafer dehydration in an oven at 200 for 10
- Spin-Coating of SU-8 photoresist (SU-8 2000.5 and 2010, mixing ratio 12:88) at 2000 rpm. Final resist thickness: 1
- Soft bake on a hotplate at 65 for 1 , then at 95 for 1
- UV light exposure (Karl Suss MA4, Süss Micro Tec, Garching bei München, Germany) for (wavelength, vacuum contact mode)
- Post exposure bake on a hotplate at 65 for 1 , then at 95 for 1
- Two-Step development in mr-Dev 600 (Microchemicals GmbH, Ulm, Germany) for , then cleaning in 2-Propanol for 20
- Hardbake on a hotplate at 150 for 10
- Spin-Coating of SU-8 photoresist (SU-8 2010) at 3500 rpm. Final resist thickness: 10
- Soft bake on a hotplate at 65 for , then at 95 for
- UV light exposure (Karl Suss MA4, Süss Micro Tec, Garching bei München, Germany) for 4 (wavelength, soft vacuum contact mode)
- Post exposure bake on a hotplate at 65 for 3 , then at 95 for 3
- Two-Step development in mr-Dev 600 for , then cleaning in 2-Propanol for 20
- Hardbake on a hotplate at 150 for 6
- Application of hexamethyldisilazane (HDMS) adhesion promoter
- Spin-Coating of SPR 220-7 photoresist (Microchemicals GmbH, Ulm, Germany) at 3000 rpm. Final resist thickness: 7
- Soft bake on a hotplate at 105 for 4
- UV light exposure (Karl Suss MA4, Süss Micro Tec, Garching bei München, Germany) for 1 (wavelength, soft vacuum contact mode)
- Post exposure bake on a hotplate at 65 for 1 , then at 95 for 1
- Two-Step development in MF-D 26 (Dow Chemical, Midland, MI, USA) for 1
- Hardbake on a hotplate at 120 for 15
Appendix E. Soft Lithography and Multilayer Chip Assembly
- Preparation of a 7:1 (base:curing agent) mixture of PDMS (Sylgard 184 Silicone Elastomer kit, Dow Corning Corporation, Midland, MI, USA)
- Preparation of a 20:1 (base:curing agent) mixture of PDMS
- Degassing of both mixtures in a desiccator for 30
- Top layer molding
- (a)
- Application of the 7:1 PDMS mixture on the top layer master mold
- (b)
- Baking in an oven at 80 for 40
- (c)
- Releasing hardened PDMS mold
- (d)
- Cutting chips, punching inlets
- Bottom layer molding
- (a)
- Application of the 20:1 PDMS mixture on the bottom layer master mold
- (b)
- Spin-coating at 2300 rpm for 60 , ramp 200 rpm/
- (c)
- Relaxation time 20
- (d)
- Baking in an oven at 80 for 20
- Layer bonding
- (a)
- Alignment of the top layer to the bottom layer under a microscope
- (b)
- Bonding in an oven at 80 for 1
- Chip bonding
- (a)
- Release of the bonded PDMS layers from the bottom layer master mold
- (b)
- Punching inlets and outlets using a punching tool (size: , World Precision Instruments, Sarasota, FL, USA)
- (c)
- Bonding of the PDMS chips to a glass substrate (170 ) by exposure to oxygen plasma (Femto Plasma Cleaner, Diener Electronics, Ebhausen, Germany) at an oxygen flow rate of 20 sccm for 25
References
- Noorman, H. An industrial perspective on bioreactor scale-down: What we can learn from combined large-scale bioprocess and model fluid studies. Biotechnol. J. 2011, 6, 934–943. [Google Scholar] [CrossRef] [PubMed]
- Enfors, S.O.; Jahic, M.; Rozkov, A.; Xu, B.; Hecker, M.; Jürgen, B.; Krüger, E.; Schweder, T.; Hamer, G.; O’Beirne, D.; et al. Physiological responses to mixing in large scale bioreactors. J. Biotechnol. 2001, 85, 175–185. [Google Scholar] [CrossRef]
- Neubauer, P.; Junne, S. Scale-down simulators for metabolic analysis of large-scale bioprocesses. Curr. Opin. Biotechnol. 2010, 21, 114–121. [Google Scholar] [CrossRef] [PubMed]
- Lara, A.R.; Taymaz-Nikerel, H.; Mashego, M.R.; van Gulik, W.M.; Heijnen, J.J.; Ramírez, O.T.; van Winden, W.A. Fast dynamic response of the fermentative metabolism of Escherichia coli to aerobic and anaerobic glucose pulses. Biotechnol. Bioeng. 2009, 104, 1153–1161. [Google Scholar] [CrossRef]
- Delvigne, F.; Takors, R.; Mudde, R.; van Gulik, W.; Noorman, H. Bioprocess scale-up/down as integrative enabling technology: From fluid mechanics to systems biology and beyond. Microb. Biotechnol. 2017, 10, 1267–1274. [Google Scholar] [CrossRef] [PubMed]
- Käß, F.; Junne, S.; Neubauer, P.; Wiechert, W.; Oldiges, M. Process inhomogeneity leads to rapid side product turnover in cultivation of Corynebacterium glutamicum. Microb. Cell Fact. 2014, 13, 6. [Google Scholar] [CrossRef]
- Lemoine, A.; Maya Martinez-Iturralde, N.; Spann, R.; Neubauer, P.; Junne, S. Response of Corynebacterium glutamicum exposed to oscillating cultivation conditions in a two- and a novel three-compartment scale-down bioreactor. Biotechnol. Bioeng. 2015, 112, 1220–1231. [Google Scholar] [CrossRef]
- Lapin, A.; Müller, D.; Reuss, M. Dynamic Behavior of Microbial Populations in Stirred Bioreactors Simulated with Euler-Lagrange Methods: Traveling along the Lifelines of Single Cells. Ind. Eng. Chem. Res. 2004, 43, 4647–4656. [Google Scholar] [CrossRef]
- Haringa, C.; Tang, W.; Deshmukh, A.T.; Xia, J.; Reuss, M.; Heijnen, J.J.; Mudde, R.F.; Noorman, H.J. Euler-Lagrange computational fluid dynamics for (bio)reactor scale down: An analysis of organism lifelines. Eng. Life Sci. 2016, 16, 652–663. [Google Scholar] [CrossRef]
- Haringa, C.; Tang, W.; Wang, G.; Deshmukh, A.T.; van Winden, W.A.; Chu, J.; van Gulik, W.M.; Heijnen, J.J.; Mudde, R.F.; Noorman, H.J. Computational fluid dynamics simulation of an industrial P. chrysogenum fermentation with a coupled 9-pool metabolic model: Towards rational scale-down and design optimization. Chem. Eng. Sci. 2017, 175, 12–24. [Google Scholar] [CrossRef]
- Grünberger, A.; Wiechert, W.; Kohlheyer, D. Single-cell microfluidics: Opportunity for bioprocess development. Curr. Opin. Biotechnol. 2014, 29, 15–23. [Google Scholar] [CrossRef] [PubMed]
- Hümmer, D.; Kurth, F.; Naredi-Rainer, N.; Dittrich, P.S. Single cells in confined volumes: Microchambers and microdroplets. Lab Chip 2016, 16, 447–458. [Google Scholar] [CrossRef] [PubMed]
- Rosenthal, K.; Oehling, V.; Dusny, C.; Schmid, A. Beyond the bulk: Disclosing the life of single microbial cells. FEMS Microbiol. Rev. 2017, 41, 751–780. [Google Scholar] [CrossRef]
- Hashimoto, M.; Nozoe, T.; Nakaoka, H.; Okura, R.; Akiyoshi, S.; Kaneko, K.; Kussell, E.; Wakamoto, Y. Noise-driven growth rate gain in clonal cellular populations. Proc. Natl. Acad. Sci. USA 2016, 113, 3251–3256. [Google Scholar] [CrossRef] [PubMed]
- Mannik, J.; Wu, F.; Hol, F.J.H.; Bisicchia, P.; Sherratt, D.J.; Keymer, J.E.; Dekker, C. Robustness and accuracy of cell division in Escherichia coli in diverse cell shapes. Proc. Natl. Acad. Sci. USA 2012, 109, 6957–6962. [Google Scholar] [CrossRef]
- Mustafi, N.; Grünberger, A.; Mahr, R.; Helfrich, S.; Nöh, K.; Blombach, B.; Kohlheyer, D.; Frunzke, J. Application of a genetically encoded biosensor for live cell imaging of L-valine production in pyruvate dehydrogenase complex-deficient Corynebacterium glutamicum strains. PLoS ONE 2014, 9, e85731. [Google Scholar] [CrossRef]
- Bamford, R.A.; Smith, A.; Metz, J.; Glover, G.; Titball, R.W.; Pagliara, S. Investigating the physiology of viable but non-culturable bacteria by microfluidics and time-lapse microscopy. BMC Biol. 2017, 15, 121. [Google Scholar] [CrossRef]
- Haringa, C.; Mudde, R.F.; Noorman, H.J. From industrial fermentor to CFD-guided downscaling: What have we learned? Biochem. Eng. J. 2018, 140, 57–71. [Google Scholar] [CrossRef]
- Uhlendorf, J.; Miermont, A.; Delaveau, T.; Charvin, G.; Fages, F.; Bottani, S.; Batt, G.; Hersen, P. Long-term model predictive control of gene expression at the population and single-cell levels. Proc. Natl. Acad. Sci. USA 2012, 109, 14271–14276. [Google Scholar] [CrossRef]
- Kaiser, M.; Jug, F.; Julou, T.; Deshpande, S.; Pfohl, T.; Silander, O.K.; Myers, G.; van Nimwegen, E. Monitoring single-cell gene regulation under dynamically controllable conditions with integrated microfluidics and software. Nat. Commun. 2018, 9, 212. [Google Scholar] [CrossRef]
- Wang, P.; Robert, L.; Pelletier, J.; Dang, W.L.; Taddei, F.; Wright, A.; Jun, S. Robust growth of Escherichia coli. Curr. Biol. 2010, 20, 1099–1103. [Google Scholar] [CrossRef] [PubMed]
- Long, Z.; Nugent, E.; Javer, A.; Cicuta, P.; Sclavi, B.; Cosentino Lagomarsino, M.; Dorfman, K.D. Microfluidic chemostat for measuring single cell dynamics in bacteria. Lab Chip 2013, 13, 947–954. [Google Scholar] [CrossRef]
- Grünberger, A.; Paczia, N.; Probst, C.; Schendzielorz, G.; Eggeling, L.; Noack, S.; Wiechert, W.; Kohlheyer, D. A disposable picolitre bioreactor for cultivation and investigation of industrially relevant bacteria on the single cell level. Lab Chip 2012, 12, 2060–2068. [Google Scholar] [CrossRef] [PubMed]
- Grünberger, A.; Probst, C.; Helfrich, S.; Nanda, A.; Stute, B.; Wiechert, W.; von Lieres, E.; Nöh, K.; Frunzke, J.; Kohlheyer, D. Spatiotemporal microbial single-cell analysis using a high-throughput microfluidics cultivation platform. Cytom. Part A 2015, 87, 1101–1115. [Google Scholar] [CrossRef] [PubMed]
- Ullman, G.; Wallden, M.; Marklund, E.G.; Mahmutovic, A.; Razinkov, I.; Elf, J. High-throughput gene expression analysis at the level of single proteins using a microfluidic turbidostat and automated cell tracking. Philos. Trans. R. Soc. B Biol. Sci. 2012, 368. [Google Scholar] [CrossRef] [PubMed]
- Westerwalbesloh, C.; Grünberger, A.; Stute, B.; Weber, S.; Wiechert, W.; Kohlheyer, D.; von Lieres, E. Modeling and CFD simulation of nutrient distribution in picoliter bioreactors for bacterial growth studies on single-cell level. Lab Chip 2015, 15, 4177–4186. [Google Scholar] [CrossRef]
- Fritzsch, F.S.O.; Blank, L.M.; Dusny, C.; Schmid, A. Miniaturized octupole cytometry for cell type independent trapping and analysis. Microfluid. Nanofluid. 2017, 21, 845. [Google Scholar] [CrossRef]
- Fritzsch, F.S.O.; Rosenthal, K.; Kampert, A.; Howitz, S.; Dusny, C.; Blank, L.M.; Schmid, A. Picoliter nDEP traps enable time-resolved contactless single bacterial cell analysis in controlled microenvironments. Lab Chip 2013, 13, 397–408. [Google Scholar] [CrossRef]
- Westerwalbesloh, C.; Grünberger, A.; Wiechert, W.; Kohlheyer, D.; von Lieres, E. Coarse-graining bacteria colonies for modelling critical solute distributions in picolitre bioreactors for bacterial studies on single-cell level. Microb. Biotechnol. 2017, 10, 845–857. [Google Scholar] [CrossRef]
- Unthan, S.; Grünberger, A.; van Ooyen, J.; Gätgens, J.; Heinrich, J.; Paczia, N.; Wiechert, W.; Kohlheyer, D.; Noack, S. Beyond growth rate 0.6: What drives Corynebacterium glutamicum to higher growth rates in defined medium. Biotechnol. Bioeng. 2014, 111, 359–371. [Google Scholar] [CrossRef]
- Deen, W.M. Analysis of Transport Phenomena; Topics in Chemical Engineering; Oxford University Press: New York, NY, USA, 1998. [Google Scholar]
- Comesaña, J.F.; Otero, J.J.; García, E.; Correa, A. Densities and Viscosities of Ternary Systems of Water + Glucose + Sodium Chloride at Several Temperatures. J. Chem. Eng. Data 2003, 48, 362–366. [Google Scholar] [CrossRef]
- Gladden, J.K.; Dole, M. Diffusion in Supersaturated Solutions. II. Glucose Solutions. J. Am. Chem. Soc. 1953, 75, 3900–3904. [Google Scholar] [CrossRef]
- Monod, J. The Growth of Bacterial Cultures. Ann. Rev. Microbiol. 1949, 3, 371–394. [Google Scholar] [CrossRef]
- Wendisch, V.F.; de Graaf, A.A.; Sahm, H.; Eikmanns, B.J. Quantitative determination of metabolic fluxes during coutilization of two carbon sources: Comparative analyses with Corynebacterium glutamicum during growth on acetate and/or glucose. J. Bacteriol. 2000, 182, 3088–3096. [Google Scholar] [CrossRef] [PubMed]
- Probst, C.; Grünberger, A.; Wiechert, W.; Kohlheyer, D. Microfluidic growth chambers with optical tweezers for full spatial single-cell control and analysis of evolving microbes. J. Microbiol. Methods 2013, 95, 470–476. [Google Scholar] [CrossRef] [PubMed]
- Dusny, C.; Schmid, A. Microfluidic single-cell analysis links boundary environments and individual microbial phenotypes. Environ. Microbiol. 2015, 17, 1839–1856. [Google Scholar] [CrossRef] [PubMed]
- Unger, M.A.; Chou, H.P.; Thorsen, T.; Scherer, A.; Quake, S.R. Monolithic Microfabricated Valves and Pumps by Multilayer Soft Lithography. Science 2000, 288, 113–116. [Google Scholar] [CrossRef]
- Grünberger, A.; Probst, C.; Heyer, A.; Wiechert, W.; Frunzke, J.; Kohlheyer, D. Microfluidic Picoliter Bioreactor for Microbial Single-cell Analysis: Fabrication, System Setup, and Operation. J. Vis. Exp. 2013, 82, e50560. [Google Scholar] [CrossRef]
- Schindelin, J.; Arganda-Carreras, I.; Frise, E.; Kaynig, V.; Longair, M.; Pietzsch, T.; Preibisch, S.; Rueden, C.; Saalfeld, S.; Schmid, B.; et al. Fiji: An open-source platform for biological-image analysis. Nat. Methods 2012, 9, 676–682. [Google Scholar] [CrossRef]
- Yarlagadda, R.R. Analog and Digital Signals and Systems; Springer: Berlin/Heidelberg, Germany, 2010; Volume 1. [Google Scholar]
- Culbertson, C.T.; Jacobson, S.C.; Ramsey, J.M. Diffusion coefficient measurements in microfluidic devices. Talanta 2002, 56, 365–373. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ho, P.; Westerwalbesloh, C.; Kaganovitch, E.; Grünberger, A.; Neubauer, P.; Kohlheyer, D.; Lieres, E.v. Reproduction of Large-Scale Bioreactor Conditions on Microfluidic Chips. Microorganisms 2019, 7, 105. https://doi.org/10.3390/microorganisms7040105
Ho P, Westerwalbesloh C, Kaganovitch E, Grünberger A, Neubauer P, Kohlheyer D, Lieres Ev. Reproduction of Large-Scale Bioreactor Conditions on Microfluidic Chips. Microorganisms. 2019; 7(4):105. https://doi.org/10.3390/microorganisms7040105
Chicago/Turabian StyleHo, Phuong, Christoph Westerwalbesloh, Eugen Kaganovitch, Alexander Grünberger, Peter Neubauer, Dietrich Kohlheyer, and Eric von Lieres. 2019. "Reproduction of Large-Scale Bioreactor Conditions on Microfluidic Chips" Microorganisms 7, no. 4: 105. https://doi.org/10.3390/microorganisms7040105
APA StyleHo, P., Westerwalbesloh, C., Kaganovitch, E., Grünberger, A., Neubauer, P., Kohlheyer, D., & Lieres, E. v. (2019). Reproduction of Large-Scale Bioreactor Conditions on Microfluidic Chips. Microorganisms, 7(4), 105. https://doi.org/10.3390/microorganisms7040105








