Plasmids Increase the Competitive Ability of Plasmid-Bearing Cells Even When Transconjugants Are Poor Donors, as Shown by Computer Simulations
Abstract
1. Introduction
2. Materials and Methods
2.1. Initial Conditions
2.2. Flow of the Model
2.3. Fitness Analysis
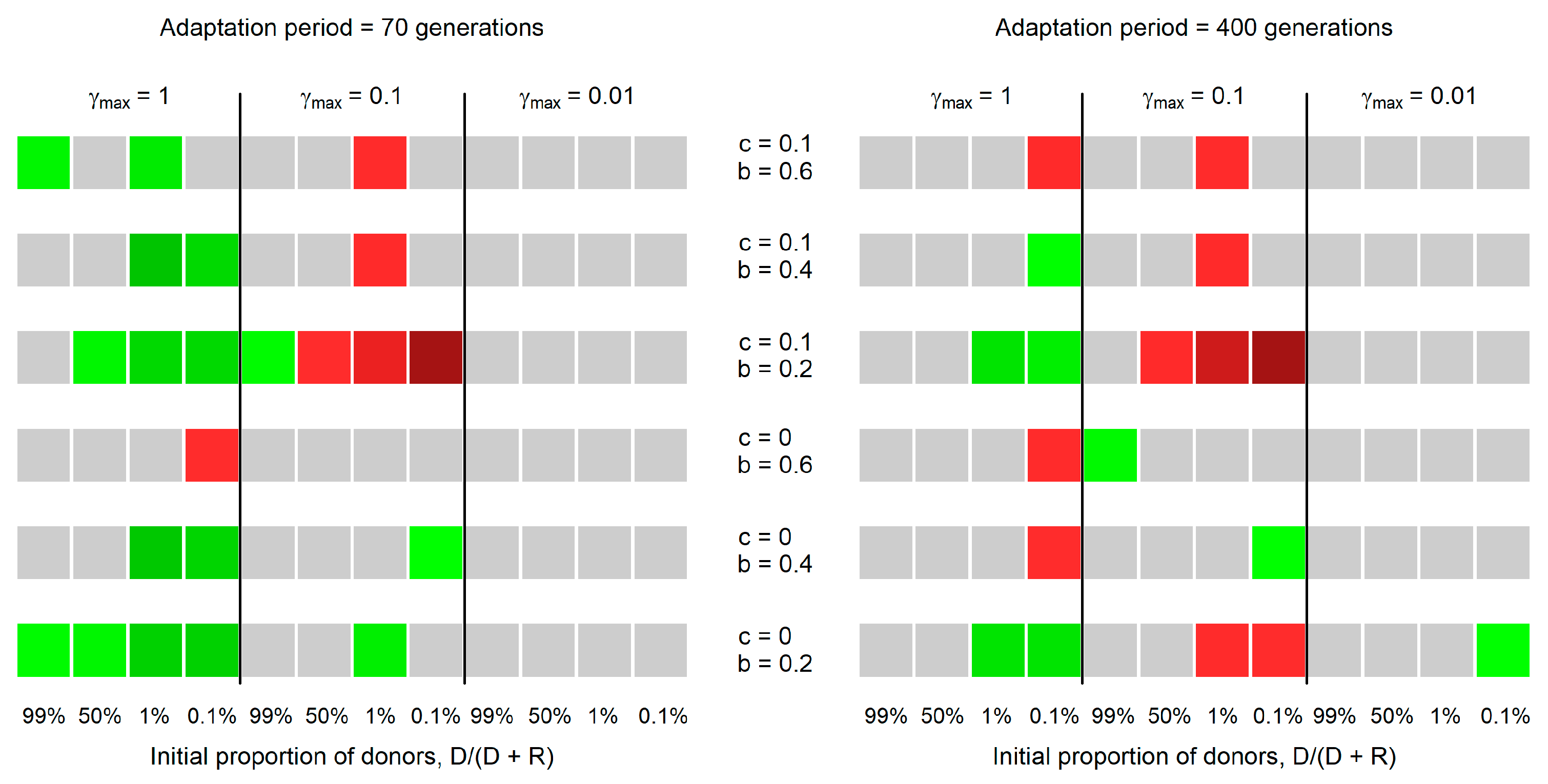
3. Results
4. Discussion
- (i)
- We always considered that compensatory mutations occurred in chromosomes. In another work submitted elsewhere [43], we study the validity of this hypothesis when compensatory mutations occur in plasmids. To our surprise, the effect is almost the same irrespective of the replicon where compensatory mutations occur. The two main reasons are that the period before compensatory mutations occur is the most significant and that transfer events of mutated plasmids usually occur in sites far from the original donors.
- (ii)
- Both plasmids and chromosomes may evolve, and we have already considered the appearance of compensatory mutations, but other mutations may occur during the 1000 bacterial generations considered in this study. These mutations may also help plasmids to survive. For example, plasmids may have the opportunity to receive antibiotic-resistance genes in a transposon that originates from the chromosome or another plasmid present in the same cell. However, plasmids must survive while these genes, compensatory mutations in the plasmid itself or chromosome, or other types do not arise (for example, genes encoding for H-NS proteins that silence horizontally acquired DNA with an AT content higher than that of the chromosome [44,45]). The model/mechanism considered here and elsewhere [17,43] gives plasmids the necessary conditions and time to wait for those advantageous changes. Moreover, plasmids sometimes confer no cost [27], so their maintenance deserves no more explanations. In these cases where the cost is null in a specific environment, there is no guarantee that the plasmid is also costless in other environments; if it is costly in other environments, some mechanism must ensure and explain their maintenance, e.g., the one discussed here or in [46].
- (iii)
- We assumed that the plasmid transfer rate did not change. Bacterial conjugation is often tightly regulated: plasmids frequently encode genes whose function is to decrease their transfer rate. Plasmids in which these genes are mutated transfer more efficiently than the wild-type plasmid. For example, the IncFII R1drd19 plasmid is the corresponding derepressed mutant of the wild-type (repressed) R1 plasmid [47], and the transfer rate between Escherichia coli K12 MG16555 cells of the former plasmid is about 1000 times higher than that of the latter plasmid [20]. Repressed plasmids express lower levels of sex-pili, becoming less susceptible to the so-called male-specific-phages: bacteriophages that infect bacteria precisely through these sex-pili, a hypothesis first proposed by Anderson already in 1968 [48] (see also a refinement of this hypothesis in [49]). Later Lundquist and Levin found that some plasmids become transitory derepressed after a few transfers [50]. In principle, transitory derepression would weaken the hypothesis of the present study because, with transitory derepression, many more transfer events would occur further away from the original donor cells. Some genes are involved in transitory derepression (e.g., the products of the finO and finP genes repress conjugation). However, one cannot be sure that transitory derepression would work in different strains. Moreover, as argued above, the hypothesis discussed in the present study aims to explain how plasmids are maintained before these other genes arise or while these systems are not helpful.
- (iv)
- A limitation of this study is that it is based on a mathematical model [17] and computer simulations ([17] and the present study), rather than on experimental results. We base our simulations on previous studies that have constructed and adjusted the computer model and its parameters to ensure that computer results match those obtained in laboratory experiments [22,23,24]. Moreover and most importantly, simulations allowed us to test hundreds of different conditions and parameters, putatively simulating different bacteria and plasmid types.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Murray, C.J.; Ikuta, K.S.; Sharara, F.; Swetschinski, L.; Aguilar, G.R.; Gray, A.; Han, C.; Bisignano, C.; Rao, P.; Wool, E.; et al. Global Burden of Bacterial Antimicrobial Resistance in 2019: A Systematic Analysis. Lancet 2022, 399, 629–655. [Google Scholar] [CrossRef] [PubMed]
- Cassini, A.; Hogberg, L.D.; Plachouras, D.; Quattrocchi, A.; Hoxha, A.; Simonsen, G.S.; Colomb-Cotinat, M.; Kretzschmar, M.E.; Devleesschauwer, B.; Cecchini, M.; et al. Attributable Deaths and Disability-Adjusted Life-Years Caused by Infections with Antibiotic-Resistant Bacteria in the EU and the European Economic Area in 2015: A Population-Level Modelling Analysis. Lancet 2019, 19, 56–66. [Google Scholar] [CrossRef] [PubMed]
- Dionisio, F.; Baquero, F.; Fuertes, M. Psychological and Cultural Factors Influencing Antibiotic Prescription. Trends Microbiol. 2023. [Google Scholar] [CrossRef]
- Fuertes, M.; Gonçalves, J.L.; Faria, A.; Lopes-dos-Santos, P.; Conceição, I.C.; Dionisio, F. Maternal Sensitivity and Mother-Infant Attachment Are Associated with Antibiotic Uptake in Infancy. J. Health Psychol. 2022, 27, 2197–2210. [Google Scholar] [CrossRef] [PubMed]
- Fuertes, M.; Faria, A.; Gonçalves, J.L.; Antunes, S.; Dionisio, F. The Association between Prematurity, Antibiotic Consumption, and Mother-Infant Attachment in the First Year of Life. Antibiotics 2023, 12, 309. [Google Scholar] [CrossRef]
- Carattoli, A. Plasmids and the Spread of Resistance. Int. J. Med. Microbiol. IJMM 2013, 303, 298–304. [Google Scholar] [CrossRef]
- San Millan, A. Evolution of Plasmid-Mediated Antibiotic Resistance in the Clinical Context. Trends Microbiol. 2018, 26, 978–985. [Google Scholar] [CrossRef]
- Laxminarayan, R. The Overlooked Pandemic of Antimicrobial Resistance. Lancet 2022, 399, 606–607. [Google Scholar] [CrossRef]
- Bojer, M.S.; Frees, D.; Ingmer, H. SosA in Staphylococci: An Addition to the Paradigm of Membrane-Localized, SOS-Induced Cell Division Inhibition in Bacteria. Curr. Genet. 2020, 66, 495–499. [Google Scholar] [CrossRef]
- Jones, C.; Holland, I.B. Role of the SulB (FtsZ) Protein in Division Inhibition during the SOS Response in Escherichia Coli: FtsZ Stabilizes the Inhibitor SulA in Maxicells. Proc. Natl. Acad. Sci. USA 1985, 82, 6045–6049. [Google Scholar] [CrossRef]
- Jain, R.; Rivera, M.C.; Lake, J.A. Horizontal Gene Transfer among Genomes: The Complexity Hypothesis. Proc. Natl. Acad. Sci. USA 1999, 96, 3801–3806. [Google Scholar] [CrossRef] [PubMed]
- San Millan, A.; MacLean, R.C. Fitness Costs of Plasmids: A Limit to Plasmid Transmission. Microbiol. Spectr. 2017, 5. [Google Scholar] [CrossRef] [PubMed]
- Brockhurst, M.A.; Harrison, E. Ecological and Evolutionary Solutions to the Plasmid Paradox. Trends Microbiol. 2022, 30, 534–543. [Google Scholar] [CrossRef] [PubMed]
- Gama, J.A.; Zilhao, R.; Dionisio, F. Multiple Plasmid Interference-Pledging Allegiance to My Enemy’s Enemy. Plasmid 2017, 93, 17–23. [Google Scholar] [CrossRef]
- Gama, J.A.; Zilhão, R.; Dionisio, F. Co-Resident Plasmids Travel Together. Plasmid 2017, 93, 24–29. [Google Scholar] [CrossRef]
- Gama, J.A.; Zilhão, R.; Dionisio, F. Conjugation Efficiency Depends on Intra and Intercellular Interactions between Distinct Plasmids: Plasmids Promote the Immigration of Other Plasmids but Repress Co-Colonizing Plasmids. Plasmid 2017, 93, 6–16. [Google Scholar] [CrossRef]
- Domingues, C.P.F.; Rebelo, J.S.; Monteiro, F.; Nogueira, T.; Dionisio, F. Harmful Behaviour through Plasmid Transfer: A Successful Evolutionary Strategy of Bacteria Harbouring Conjugative Plasmids. Philos. Trans. R. Soc. B Biol. Sci. 2022, 377, 20200473. [Google Scholar] [CrossRef] [PubMed]
- Dionisio, F.; Conceição, I.C.; Marques, A.C.R.; Fernandes, L.; Gordo, I. The Evolution of a Conjugative Plasmid and Its Ability to Increase Bacterial Fitness. Biol. Lett. 2005, 1, 250–252. [Google Scholar] [CrossRef]
- Dahlberg, C.; Chao, L. Amelioration of the Cost of Conjugative Plasmid Carriage in Eschericha Coli K12. Genetics 2003, 165, 1641–1649. [Google Scholar] [CrossRef]
- Dionisio, F.; Matic, I.; Radman, M.; Rodrigues, O.R.; Taddei, F. Plasmids Spread Very Fast in Heterogeneous Bacterial Communities. Genetics 2002, 162, 1525–1532. [Google Scholar] [CrossRef]
- Hall, J.P.J.; Wood, A.J.; Harrison, E.; Brockhurst, M.A. Source-Sink Plasmid Transfer Dynamics Maintain Gene Mobility in Soil Bacterial Communities. Proc. Natl. Acad. Sci. USA 2016, 113, 8260–8265. [Google Scholar] [CrossRef] [PubMed]
- Krone, S.M.; Lu, R.; Fox, R.; Suzuki, H.; Top, E.M. Modelling the Spatial Dynamics of Plasmid Transfer and Persistence. Microbiology 2007, 153, 2803–2816. [Google Scholar] [CrossRef] [PubMed]
- Fox, R.E.; Zhong, X.; Krone, S.M.; Top, E.M. Spatial Structure and Nutrients Promote Invasion of IncP-1 Plasmids in Bacterial Populations. ISME J. 2008, 2, 1024–1039. [Google Scholar] [CrossRef] [PubMed]
- Zhong, X.; Droesch, J.; Fox, R.; Top, E.M.; Krone, S.M. On the Meaning and Estimation of Plasmid Transfer Rates for Surface-Associated and Well-Mixed Bacterial Populations. J. Theor. Biol. 2012, 294, 144–152. [Google Scholar] [CrossRef]
- R Core Team R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2015.
- Gordon, D.M. Rate of Plasmid Transfer among Escherichia-Coli Strains Isolated from Natural-Populations. J. Gen. Microbiol. 1992, 138, 17–21. [Google Scholar] [CrossRef]
- Alonso-del Valle, A.; León-Sampedro, R.; Rodríguez-Beltrán, J.; DelaFuente, J.; Hernández-García, M.; Ruiz-Garbajosa, P.; Cantón, R.; Peña-Miller, R.; San Millán, A. Variability of Plasmid Fitness Effects Contributes to Plasmid Persistence in Bacterial Communities. Nat. Commun. 2021, 12, 2653. [Google Scholar] [CrossRef]
- Dionisio, F. Selfish and Spiteful Behaviour through Parasites and Pathogens. Evol. Ecol. Res. 2007, 9, 1199–1210. [Google Scholar]
- Rozsa, L. Spite, Xenophobia, and Collaboration between Hosts and Parasites. Oikos 91: 396–400. Oikos 2000, 91, 396–400. [Google Scholar] [CrossRef]
- Brown, S.P.; Le Chat, L.; De Paepe, M.; Taddei, F. Ecology of Microbial Invasions: Amplification Allows Virus Carriers to Invade More Rapidly When Rare. Curr. Biol. CB 2006, 16, 2048–2052. [Google Scholar] [CrossRef]
- Gama, J.A.; Reis, A.M.; Domingues, I.; Mendes-Soares, H.; Matos, A.M.; Dionisio, F. Temperate Bacterial Viruses as Double-Edged Swords in Bacterial Warfare. PLoS ONE 2013, 8, e59043. [Google Scholar] [CrossRef]
- Joo, J.; Gunny, M.; Cases, M.; Hudson, P.; Albert, R.; Harvill, E. Bacteriophage-Mediated Competition in Bordetella Bacteria. Proc. Biol. Sci. 2006, 273, 1843–1848. [Google Scholar] [CrossRef] [PubMed]
- Bossi, L.; Fuentes, J.A.; Mora, G.; Figueroa-Bossi, N. Prophage Contribution to Bacterial Population Dynamics. J. Bacteriol. 2003, 185, 6467–6471. [Google Scholar] [CrossRef] [PubMed]
- Erickson, M.; Newman, D.; Helm, R.A.; Dino, A.; Calcutt, M.; French, W.; Eisenstark, A. Competition among Isolates of Salmonella Enterica Ssp. Enterica Serovar Typhimurium: Role of Prophage/Phage in Archived Cultures. FEMS Microbiol. Lett. 2009, 294, 37–44. [Google Scholar] [CrossRef] [PubMed]
- Campbell, A.M. Bacteriophages. In Escherichia coli and Salmonella-Cellular and Molecular Biology, 2nd ed.; Neidhart, F.C., Curtiss, R., Ingraham, J.L., Lin, E.C.C., Low, K.B., Magasanik, B., Reznikoff, W.S., Riley, M., Schaechter, M., Umbarger, H.E., Eds.; American Society for Microbiology: Washinghton, DC, USA, 1996. [Google Scholar]
- Abedon, S.T. Phage Evolution and Ecology. Adv. Appl. Microbiol. 2009, 67, 1–45. [Google Scholar] [CrossRef] [PubMed]
- Howard-Varona, C.; Hargreaves, K.R.; Abedon, S.T.; Sullivan, M.B. Lysogeny in Nature: Mechanisms, Impact and Ecology of Temperate Phages. ISME J. 2017, 11, 1511–1520. [Google Scholar] [CrossRef] [PubMed]
- Abedon, S.T. (Ed.) Bacteriophage Ecology: Population Growth, Evolution, and Impact of Bacterial Viruses; Advances in Molecular and Cellular Microbiology; Cambridge University Press: Cambridge, UK, 2008; ISBN 978-0-521-85845-8. [Google Scholar]
- Weitz, J. Quantitative Viral Ecology; Monographs in Population Biology; Princeton University Press: Princeton, NJ, USA, 2016; ISBN 978-0-691-16154-9. [Google Scholar]
- Pfeifer, E.; Moura de Sousa, J.A.; Touchon, M.; Rocha, E.P.C. Bacteria Have Numerous Distinctive Groups of Phage–Plasmids with Conserved Phage and Variable Plasmid Gene Repertoires. Nucleic Acids Res. 2021, 49, 2655–2673. [Google Scholar] [CrossRef] [PubMed]
- Baquero, F.; Martínez, J.L.; Lanza, V.F.; Rodríguez-Beltrán, J.; Galán, J.C.; San Millán, A.; Cantón, R.; Coque, T.M. Evolutionary Pathways and Trajectories in Antibiotic Resistance. Clin. Microbiol. Rev. 2021, 34, e00050-19. [Google Scholar] [CrossRef]
- Lopez, J.G.; Donia, M.S.; Wingreen, N.S. Modeling the Ecology of Parasitic Plasmids. ISME J. 2021, 25, 2843–2852. [Google Scholar] [CrossRef]
- Rebelo, J.S.; Domingues, C.P.F.; Dionisio, F. Plasmid Costs Explain Plasmid Maintenance, Irrespective of the Nature of Compensatory Mutations. Antibiotics 2023, 12, 841. [Google Scholar] [CrossRef]
- Vial, L.; Hommais, F. Plasmid-Chromosome Cross-Talks. Environ. Microbiol. 2020, 22, 540–556. [Google Scholar] [CrossRef]
- Piña-Iturbe, A.; Suazo, I.D.; Hoppe-Elsholz, G.; Ulloa-Allendes, D.; González, P.A.; Kalergis, A.M.; Bueno, S.M. Horizontally Acquired Homologs of Xenogeneic Silencers: Modulators of Gene Expression Encoded by Plasmids, Phages and Genomic Islands. Genes 2020, 11, 142. [Google Scholar] [CrossRef] [PubMed]
- Harrison, E.; Hall, J.P.J.; Brockhurst, M.A. Migration Promotes Plasmid Stability under Spatially Heterogeneous Positive Selection. Proc. Biol. Sci. 2018, 285, 20180324. [Google Scholar] [CrossRef] [PubMed]
- Meynell, E.; Datta, N. Mutant Drug Resistant Factors of High Transmissibility. Nature 1967, 214, 885–887. [Google Scholar] [CrossRef]
- Anderson, E.S. The Ecology of Transferable Drug Resistance in the Enterobacteria. Annu. Rev. Microbiol. 1968, 22, 131–180. [Google Scholar] [CrossRef] [PubMed]
- Dionisio, F. Plasmids Survive despite Their Cost and Male-Specific Phages Due to Heterogeneity of Bacterial Populations. Evol. Ecol. Res. 2005, 7, 1089–1107. [Google Scholar]
- Lundquist, P.D.; Levin, B.R. Transitory Derepression and the Maintenance of Conjugative Plasmids. Genetics 1986, 113, 483–497. [Google Scholar] [CrossRef]
- Domingues, C.P.F.; Rebelo, J.S.; Pothier, J.; Monteiro, F.; Nogueira, T.; Dionisio, F. The Perfect Condition for the Rising of Superbugs: Person-to-Person Contact and Antibiotic Use Are the Key Factors Responsible for the Positive Correlation between Antibiotic Resistance Gene Diversity and Virulence Gene Diversity in Human Metagenomes. Antibiotics 2021, 10, 605. [Google Scholar] [CrossRef]
- Darmancier, H.; Domingues, C.P.F.; Rebelo, J.S.; Amaro, A.; Dionísio, F.; Pothier, J.; Serra, O.; Nogueira, T. Are Virulence and Antibiotic Resistance Genes Linked? A Comprehensive Analysis of Bacterial Chromosomes and Plasmids. Antibiotics 2022, 11, 706. [Google Scholar] [CrossRef]
| c = 0.1; b = 0.4; = 0.1 * | c = 0; b = 0.4; = 1 | |||||
|---|---|---|---|---|---|---|
| Transfer from transconjugants? | Yes | No | Difference | Yes | No | Difference |
| Recipients | 13.73 | 15.26 | 1.53 | 5.35 | 7.03 | 1.68 |
| Donors | 13.98 | 14.27 | 0.29 | 7.67 | 20.79 | 13.12 |
| Transconjugants | 4.29 | 2.53 | −1.76 | 19.17 | 4.52 | −14.65 |
| Adapted transconjugants | 0 | 0 | 0 | 6.43 | 0 | −6.43 |
| Segregants | 0.32 | 0.27 | −0.05 | 0.08 | 0.11 | 0.03 |
| Distance to nearest donor | 2.17 | 1.89 | −0.28 | 27.69 | 1.43 | −26.26 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rebelo, J.S.; Domingues, C.P.F.; Nogueira, T.; Dionisio, F. Plasmids Increase the Competitive Ability of Plasmid-Bearing Cells Even When Transconjugants Are Poor Donors, as Shown by Computer Simulations. Microorganisms 2023, 11, 1238. https://doi.org/10.3390/microorganisms11051238
Rebelo JS, Domingues CPF, Nogueira T, Dionisio F. Plasmids Increase the Competitive Ability of Plasmid-Bearing Cells Even When Transconjugants Are Poor Donors, as Shown by Computer Simulations. Microorganisms. 2023; 11(5):1238. https://doi.org/10.3390/microorganisms11051238
Chicago/Turabian StyleRebelo, João S., Célia P. F. Domingues, Teresa Nogueira, and Francisco Dionisio. 2023. "Plasmids Increase the Competitive Ability of Plasmid-Bearing Cells Even When Transconjugants Are Poor Donors, as Shown by Computer Simulations" Microorganisms 11, no. 5: 1238. https://doi.org/10.3390/microorganisms11051238
APA StyleRebelo, J. S., Domingues, C. P. F., Nogueira, T., & Dionisio, F. (2023). Plasmids Increase the Competitive Ability of Plasmid-Bearing Cells Even When Transconjugants Are Poor Donors, as Shown by Computer Simulations. Microorganisms, 11(5), 1238. https://doi.org/10.3390/microorganisms11051238







