Programmable Stimuli-Responsive Actuators for Complex Motions in Soft Robotics: Concept, Design and Challenges
Abstract
1. Introduction
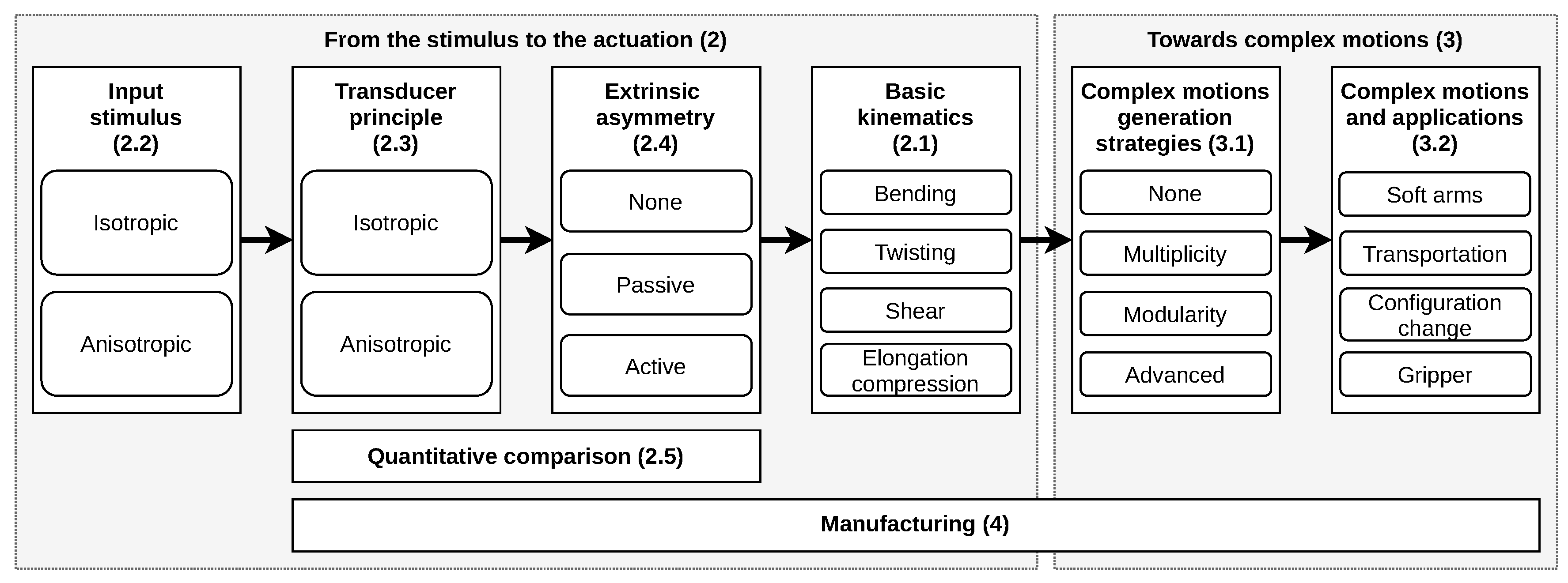
2. From Stimulus to Actuation
2.1. Basic Kinematics
2.2. Input Stimuli
2.3. Transducer Principle
2.3.1. Soft Anisotropic Transducers
2.3.2. Soft Isotropic Transducers
2.3.3. Other Mechanical Transducers
2.3.4. Stiffness Variation Transducers
2.3.5. Nonmechanical Transducers
2.4. Extrinsic Asymmetry
2.4.1. Multi-Material Asymmetry
2.4.2. Geometry
2.4.3. Material Customization
2.4.4. Stiffness Variation
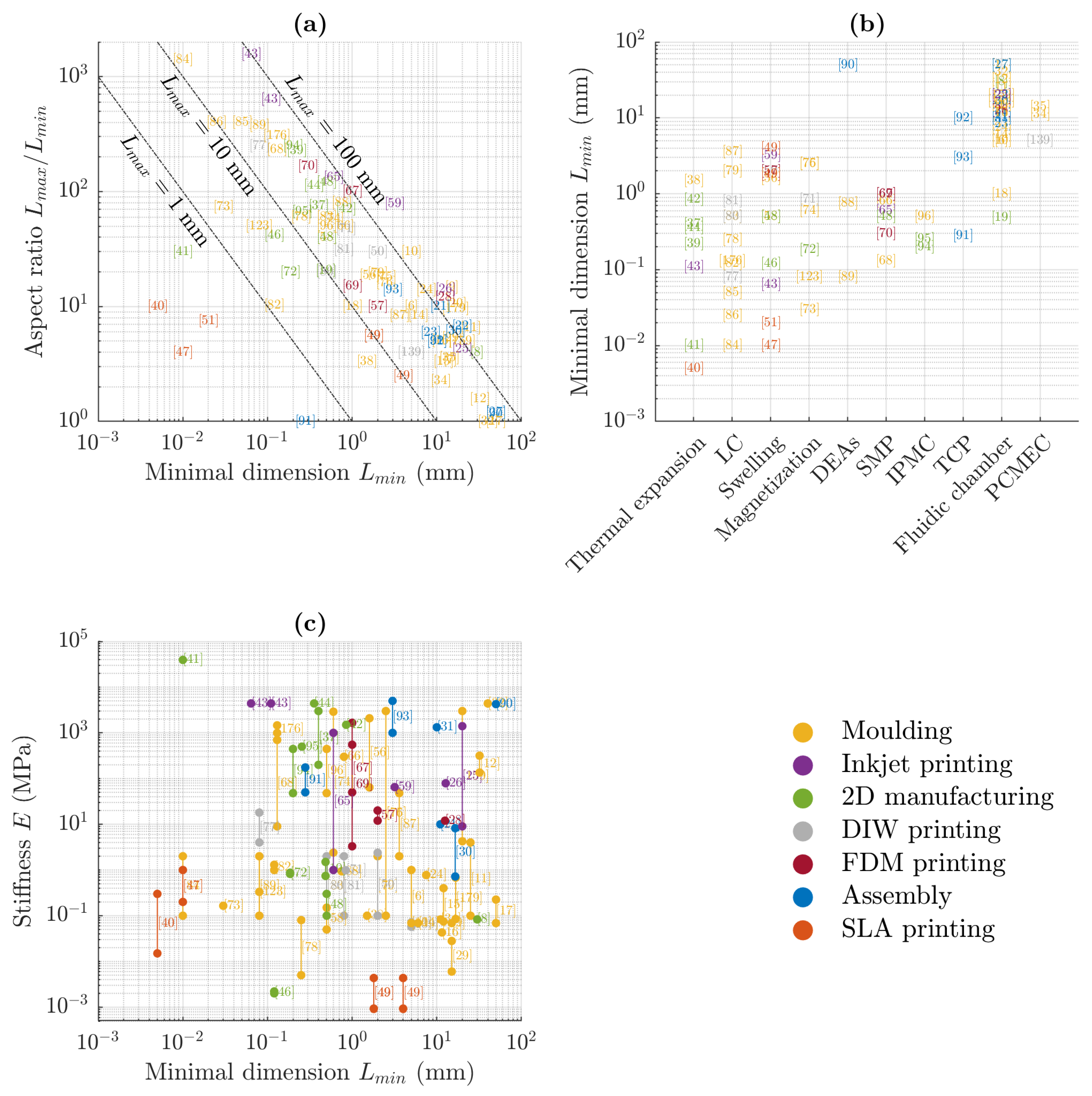
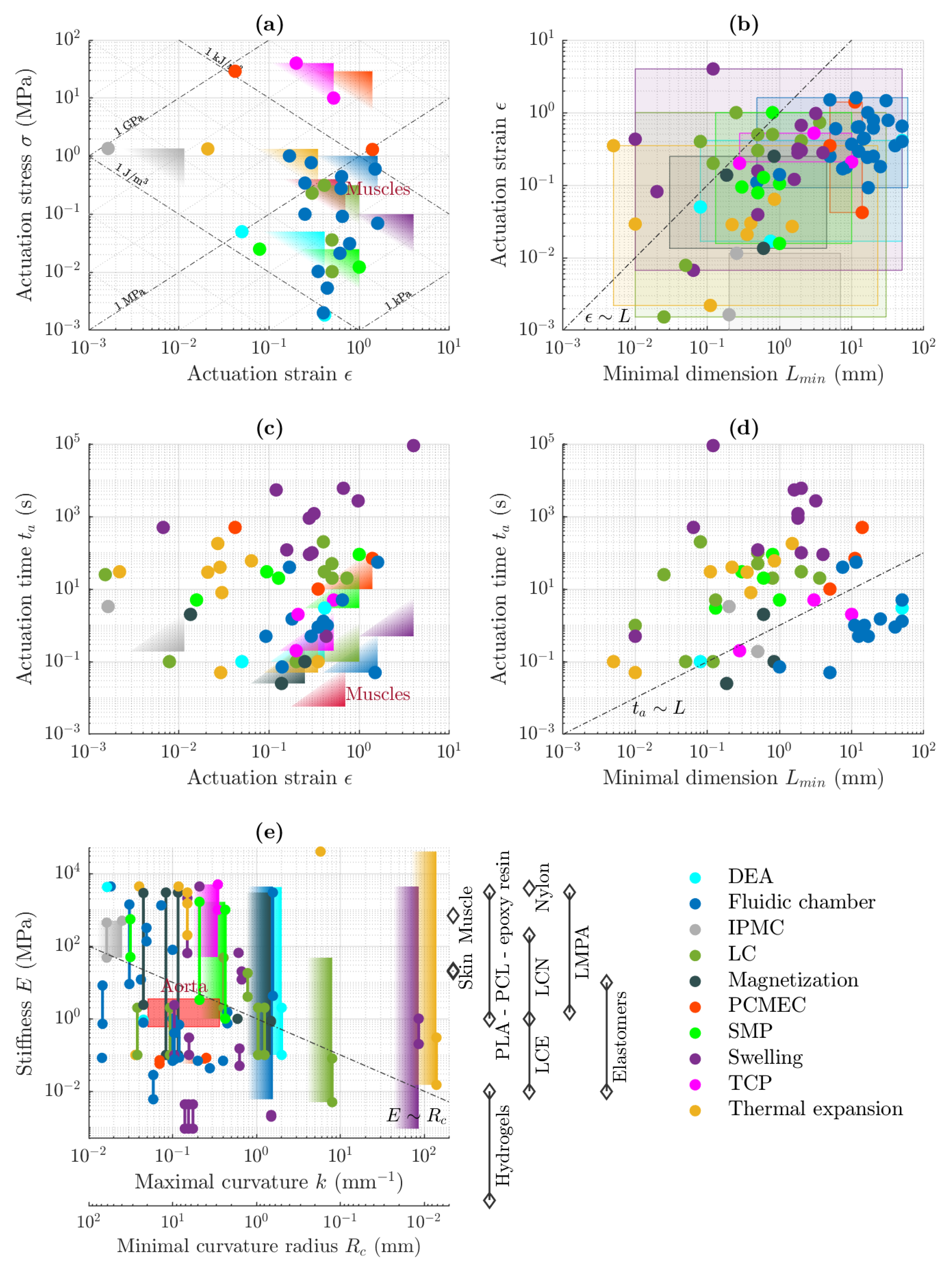
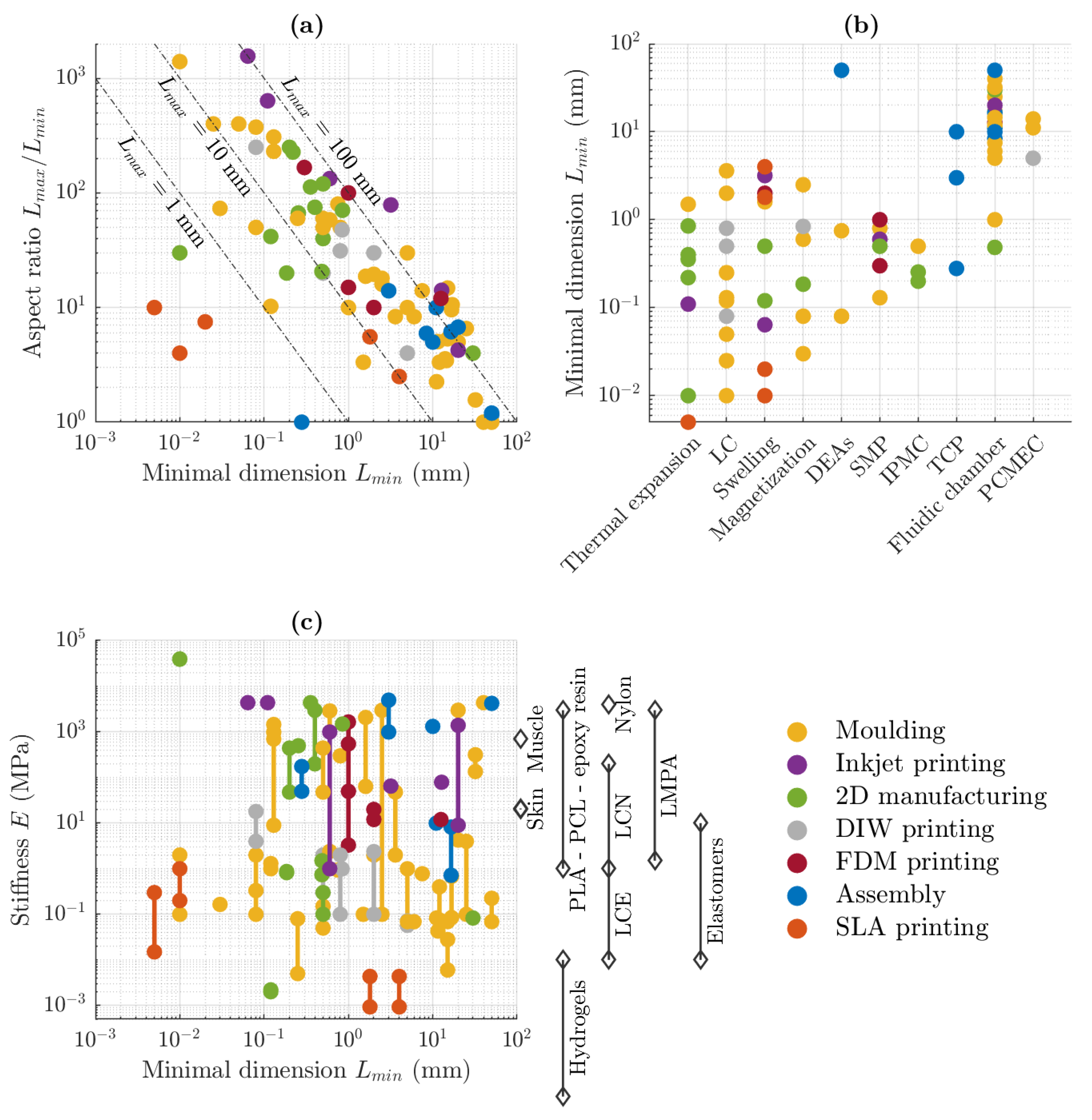
2.5. Overview and Quantitative Comparison of the Transducers
3. Towards Complex Motions
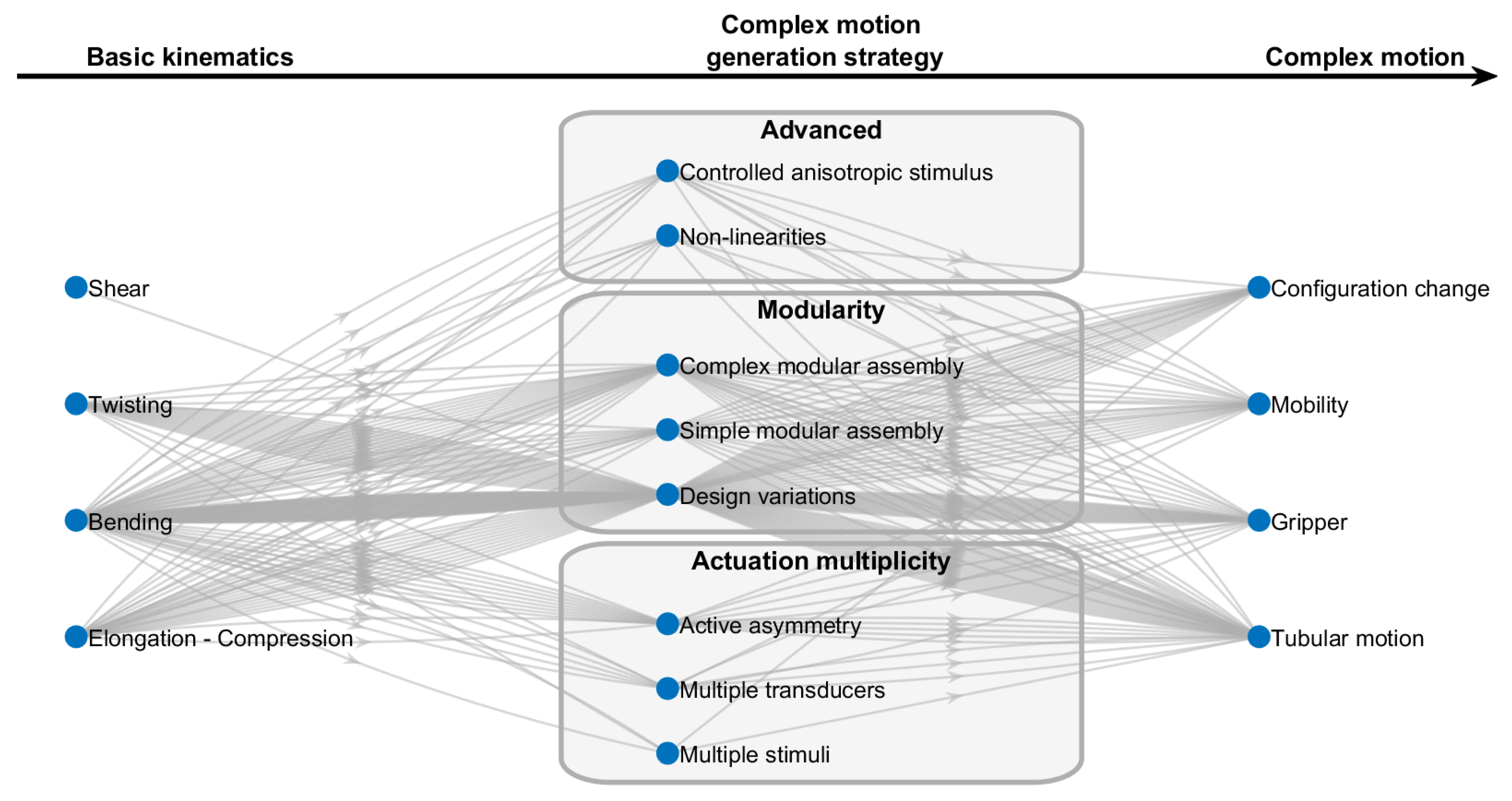
3.1. Complex Motions Generation Strategies
3.1.1. Actuation Multiplicity
3.1.2. Modularity
3.1.3. Advanced Strategies
3.2. Complex Motions and Applications
3.2.1. Soft Arms
3.2.2. Transportation
3.2.3. Grippers
3.2.4. Configuration Change
4. Manufacturing
4.1. 2D Manufacturing
4.2. Moulding
4.3. Assembly
4.4. 3D Printing
4.5. Overview and Comparison
5. Perspectives
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| Ag | silver |
| Au | gold |
| CNT | carbon nanotube |
| CTE | Coefficient of Thermal Expansion |
| DEA | Dielectric Elastomer Actuator |
| EAP | electroactive polymers |
| DIW | Direct Ink Writing |
| FDM | Fused Deposition Modelling |
| IPMC | Ionic Polymer Metal Composite |
| IR | Infrared |
| LC | Liquid Crystal |
| LCE | Liquid Crystal Elastomer |
| LCN | Liquid Crystal Network |
| LCP | Liquid Crystal Polymer |
| LMPA | Low Melting Point Alloy |
| MPCL | Methacrylated Polycaprolactone |
| MWCNT | Multi-Walled Carbon Nanotube |
| NPs | Nanoparticles |
| PCL | Polycaprolactone |
| PCMEC | Phase Change Material—Elastomer Composite |
| PDMS | Polydimethylsiloxane |
| PLA | Polylactide |
| PVA | poly(vinyl alcohol) |
| PUR | Polyurethane |
| SLA | Stereolithography |
| SLS | Selective Laser Sintering |
| SMA | Shape Memory Alloy |
| SMP | Shape Memory Polymer |
| TCP | Twisted and Coiled Polymer |
Appendix A

| Comparison Quantities | Units |
|---|---|
| Generated linear force/blocking force | |
| Actuation stress * | |
| Generated displacement/bending angle/curvature * | // |
| Actuation strain * | – |
| Generated work/power | / |
| Energy density/specific energy density | / |
| Stimulus intensity | Depends on stimulus |
| Energy conversion efficiency | % |
| Actuation time * | |
| Dimensions * | |
| Aspect ratio * | – |
| Stiffness * | |
| Number of cycles | – |
| Weight | kg |
| Density | |
| Other Criteria | Description |
| Reprogrammability | Ability to reprogram the kinematics |
| Possibility of remote actuation | Need of leads/connections (tethered/untethered) |
| Working environment | Typically air or water |
| Stimulus multiplicity | Possibility to actuate using different stimulus |
| Other capabilities | Sensing, self-healing, stiffness variation, etc. |
| Fabrication possibilities | See Section 4 |
References
- Rus, D.; Tolley, M.T. Design, Fabrication and Control of Soft Robots. Nature 2015, 521, 467–475. [Google Scholar] [CrossRef] [PubMed]
- Majidi, C. Soft-Matter Engineering for Soft Robotics. Adv. Mater. Technol. 2019, 4, 1800477. [Google Scholar] [CrossRef]
- Hines, L.; Petersen, K.; Lum, G.Z.; Sitti, M. Soft Actuators for Small-Scale Robotics. Adv. Mater. 2017, 29, 1603483. [Google Scholar] [CrossRef] [PubMed]
- Cianchetti, M.; Laschi, C.; Menciassi, A.; Dario, P. Biomedical Applications of Soft Robotics. Nat. Rev. Mater. 2018, 3, 143–153. [Google Scholar] [CrossRef]
- Shintake, J.; Cacucciolo, V.; Floreano, D.; Shea, H. Soft Robotic Grippers. Adv. Mater. 2018, 30, 1707035. [Google Scholar] [CrossRef]
- Decroly, G.; Mertens, B.; Lambert, P.; Delchambre, A. Design, Characterization and Optimization of a Soft Fluidic Actuator for Minimally Invasive Surgery. Int. J. CARS 2020, 15, 333–340. [Google Scholar] [CrossRef]
- Abidi, H.; Gerboni, G.; Brancadoro, M.; Fras, J.; Diodato, A.; Cianchetti, M.; Wurdemann, H.; Althoefer, K.; Menciassi, A. Highly Dexterous 2-Module Soft Robot for Intra-Organ Navigation in Minimally Invasive Surgery. Int. J. Med. Robot. Comput. Assist. Surg. 2018, 14, e1875. [Google Scholar] [CrossRef]
- Jin, L.; Forte, A.E.; Deng, B.; Rafsanjani, A.; Bertoldi, K. Kirigami-Inspired Inflatables with Programmable Shapes. Adv. Mater. 2020, 32, 2001863. [Google Scholar] [CrossRef]
- Milana, E.; Gorissen, B.; De Voider, M.; Reynaerts, D. Design of a Bi-Segmented Soft Actuator with Hardware Encoded Quasi-Static Inflation Sequence. In Proceedings of the 2018 IEEE International Conference on Soft Robotics (RoboSoft), Livorno, Italy, 24–28 April 2018; pp. 108–113. [Google Scholar] [CrossRef]
- Pal, A.; Goswami, D.; Martinez, R.V. Elastic Energy Storage Enables Rapid and Programmable Actuation in Soft Machines. Adv. Funct. Mater. 2020, 30, 1906603. [Google Scholar] [CrossRef]
- Rafsanjani, A.; Zhang, Y.; Liu, B.; Rubinstein, S.M.; Bertoldi, K. Kirigami Skins Make a Simple Soft Actuator Crawl. Sci. Robot. 2018, 3, eaar7555. [Google Scholar] [CrossRef]
- Ranzani, T.; Gerboni, G.; Cianchetti, M.; Menciassi, A. A Bioinspired Soft Manipulator for Minimally Invasive Surgery. Bioinspir. Biomim. 2015, 10, 035008. [Google Scholar] [CrossRef] [PubMed]
- Sui, X.; Cai, H.; Bie, D.; Zhang, Y.; Zhao, J.; Zhu, Y. Automatic Generation of Locomotion Patterns for Soft Modular Reconfigurable Robots. Appl. Sci. 2019, 10, 294. [Google Scholar] [CrossRef]
- Sun, Y.; Song, S.; Liang, X.; Ren, H. A Miniature Soft Robotic Manipulator Based on Novel Fabrication Methods. IEEE Robot. Autom. Lett. 2016, 1, 617–623. [Google Scholar] [CrossRef]
- Sun, Y.; Yap, H.K.; Liang, X.; Guo, J.; Qi, P.; Ang, M.H.; Yeow, C.H. Stiffness Customization and Patterning for Property Modulation of Silicone-Based Soft Pneumatic Actuators. Soft Robot. 2017, 4, 251–260. [Google Scholar] [CrossRef] [PubMed]
- Han, J.; Jiang, W.; Niu, D.; Li, Y.; Zhang, Y.; Lei, B.; Liu, H.; Shi, Y.; Chen, B.; Yin, L.; et al. Untethered Soft Actuators by Liquid–Vapor Phase Transition: Remote and Programmable Actuation. Adv. Intell. Syst. 2019, 1, 1900109. [Google Scholar] [CrossRef]
- Zou, J.; Lin, Y.; Ji, C.; Yang, H. A Reconfigurable Omnidirectional Soft Robot Based on Caterpillar Locomotion. Soft Robot. 2018, 5, 164–174. [Google Scholar] [CrossRef]
- Gorissen, B.; De Volder, M.; Reynaerts, D. Chip-on-Tip Endoscope Incorporating a Soft Robotic Pneumatic Bending Microactuator. Biomed. Microdev. 2018, 20, 73. [Google Scholar] [CrossRef]
- Sinatra, N.R.; Ranzani, T.; Vlassak, J.J.; Parker, K.K.; Wood, R.J. Nanofiber-Reinforced Soft Fluidic Micro-Actuators. J. Micromech. Microeng. 2018, 28, 084002. [Google Scholar] [CrossRef]
- Furukawa, S.; Wakimoto, S.; Kanda, T.; Hagihara, H. A Soft Master-Slave Robot Mimicking Octopus Arm Structure Using Thin Artificial Muscles and Wire Encoders. Actuators 2019, 8, 40. [Google Scholar] [CrossRef]
- Gorissen, B.; Milana, E.; Baeyens, A.; Broeders, E.; Christiaens, J.; Collin, K.; Reynaerts, D.; Volder, M. Hardware Sequencing of Inflatable Nonlinear Actuators for Autonomous Soft Robots. Adv. Mater. 2019, 31, 1804598. [Google Scholar] [CrossRef]
- Guan, Q.; Sun, J.; Liu, Y.; Wereley, N.M.; Leng, J. Novel Bending and Helical Extensile/Contractile Pneumatic Artificial Muscles Inspired by Elephant Trunk. Soft Robot. 2020. [Google Scholar] [CrossRef] [PubMed]
- Kawamura, S.; Sudani, M.; Deng, M.; Noge, Y.; Wakimoto, S. Modeling and System Integration for a Thin Pneumatic Rubber 3-DOF Actuator. Actuators 2019, 8, 32. [Google Scholar] [CrossRef]
- Matsuoka, H.; Kanda, T.; Wakimoto, S.; Suzumori, K.; Lambert, P. Development of a Rubber Soft Actuator Driven with Gas/Liquid Phase Change. Int. J. Autom. Technol. 2016, 10, 517–524. [Google Scholar] [CrossRef]
- Zhang, Y.F.; Zhang, N.; Hingorani, H.; Ding, N.; Wang, D.; Yuan, C.; Zhang, B.; Gu, G.; Ge, Q. Fast-Response, Stiffness-Tunable Soft Actuator by Hybrid Multimaterial 3D Printing. Adv. Funct. Mater. 2019, 29, 1806698. [Google Scholar] [CrossRef]
- Cappello, L.; Galloway, K.C.; Sanan, S.; Wagner, D.A.; Granberry, R.; Engelhardt, S.; Haufe, F.L.; Peisner, J.D.; Walsh, C.J. Exploiting Textile Mechanical Anisotropy for Fabric-Based Pneumatic Actuators. Soft Robot. 2018, 5, 662–674. [Google Scholar] [CrossRef]
- Yang, H.D.; Greczek, B.T.; Asbeck, A.T. Modeling and Analysis of a High-Displacement Pneumatic Artificial Muscle With Integrated Sensing. Front. Robot. AI 2019, 5, 136. [Google Scholar] [CrossRef]
- Hu, W.; Alici, G. Bioinspired Three-Dimensional-Printed Helical Soft Pneumatic Actuators and Their Characterization. Soft Robot. 2020, 7, 267–282. [Google Scholar] [CrossRef]
- Yuk, H.; Lin, S.; Ma, C.; Takaffoli, M.; Fang, N.X.; Zhao, X. Hydraulic Hydrogel Actuators and Robots Optically and Sonically Camouflaged in Water. Nat. Commun. 2017, 8, 14230. [Google Scholar] [CrossRef]
- Terryn, S.; Roels, E.; Brancart, J.; Van Assche, G.; Vanderborght, B. Self-Healing and High Interfacial Strength in Multi-Material Soft Pneumatic Robots via Reversible Diels–Alder Bonds. Actuators 2020, 9, 34. [Google Scholar] [CrossRef]
- Liao, B.; Zang, H.; Liu, Y.; Wang, Y.; Lang, X.; Jin, J.; Zhu, N.; Yin, Q. Programmable Design of Soft Actuators and Robots. In Proceedings of the 2019 WRC Symposium on Advanced Robotics and Automation (WRC SARA), Beijing, China, 21–22 August 2019; pp. 222–227. [Google Scholar] [CrossRef]
- Lin, Y.; Yang, G.; Liang, Y.; Zhang, C.; Wang, W.; Qian, D.; Yang, H.; Zou, J. Controllable Stiffness Origami “Skeletons” for Lightweight and Multifunctional Artificial Muscles. Adv. Funct. Mater. 2020, 30, 2000349. [Google Scholar] [CrossRef]
- Baumgartner, M.; Hartmann, F.; Drack, M.; Preninger, D.; Wirthl, D.; Gerstmayr, R.; Lehner, L.; Mao, G.; Pruckner, R.; Demchyshyn, S.; et al. Resilient yet Entirely Degradable Gelatin-Based Biogels for Soft Robots and Electronics. Nat. Mater. 2020, 19, 1102–1109. [Google Scholar] [CrossRef] [PubMed]
- Miriyev, A.; Stack, K.; Lipson, H. Soft Material for Soft Actuators. Nat. Commun. 2017, 8, 596. [Google Scholar] [CrossRef] [PubMed]
- Lipton, J.I.; Angle, S.; Banai, R.E.; Peretz, E.; Lipson, H. Electrically Actuated Hydraulic Solids: Electrically Actuated Hydraulic Solids. Adv. Eng. Mater. 2016, 18, 1710–1715. [Google Scholar] [CrossRef]
- Li, L.; Scheiger, J.M.; Levkin, P.A. Design and Applications of Photoresponsive Hydrogels. Adv. Mater. 2019, 31, 1807333. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Liu, C.; Fan, S. Programmable and Functional Electrothermal Bimorph Actuators Based on Large-Area Anisotropic Carbon Nanotube Paper. Nanotechnology 2018, 29, 175503. [Google Scholar] [CrossRef]
- Taniguchi, T.; Blanc, L.; Asahi, T.; Koshima, H.; Lambert, P. Statistical Modeling of Photo-Bending Actuation of Hybrid Silicones Mixed with Azobenzene Powder. Actuators 2019, 8, 68. [Google Scholar] [CrossRef]
- Yao, S.; Cui, J.; Cui, Z.; Zhu, Y. Soft Electrothermal Actuators Using Silver Nanowire Heaters. Nanoscale 2017, 9, 3797–3805. [Google Scholar] [CrossRef]
- Hippler, M.; Blasco, E.; Qu, J.; Tanaka, M.; Barner-Kowollik, C.; Wegener, M.; Bastmeyer, M. Controlling the Shape of 3D Microstructures by Temperature and Light. Nat. Commun. 2019, 10, 232. [Google Scholar] [CrossRef]
- Zhu, Y.; Birla, M.; Oldham, K.R.; Filipov, E.T. Elastically and Plastically Foldable Electrothermal Micro-Origami for Controllable and Rapid Shape Morphing. Adv. Funct. Mater. 2020, 2003741. [Google Scholar] [CrossRef]
- Sachyani Keneth, E.; Scalet, G.; Layani, M.; Tibi, G.; Degani, A.; Auricchio, F.; Magdassi, S. Pre-Programmed Tri-Layer Electro-Thermal Actuators Composed of Shape Memory Polymer and Carbon Nanotubes. Soft Robot. 2020, 7, 123–129. [Google Scholar] [CrossRef]
- Shigemune, H.; Maeda, S.; Hara, Y.; Hosoya, N.; Hashimoto, S. Origami Robot: A Self-Folding Paper Robot With an Electrothermal Actuator Created by Printing. IEEE/ASME Trans. Mechatron. 2016, 21, 2746–2754. [Google Scholar] [CrossRef]
- Hu, Y.; Xu, A.; Liu, J.; Yang, L.; Chang, L.; Huang, M.; Gu, W.; Wu, G.; Lu, P.; Chen, W.; et al. Multifunctional Soft Actuators Based on Anisotropic Paper/Polymer Bilayer Toward Bioinspired Applications. Adv. Mater. Technol. 2019, 4, 1800674. [Google Scholar] [CrossRef]
- Gunes, I.S.; Cao, F.; Jana, S.C. Evaluation of Nanoparticulate Fillers for Development of Shape Memory Polyurethane Nanocomposites. Polymer 2008, 49, 2223–2234. [Google Scholar] [CrossRef]
- Cangialosi, A.; Yoon, C.; Liu, J.; Huang, Q.; Guo, J.; Nguyen, T.D.; Gracias, D.H.; Schulman, R. DNA Sequence–Directed Shape Change of Photopatterned Hydrogels via High-Degree Swelling. Science 2017, 357, 1126–1130. [Google Scholar] [CrossRef] [PubMed]
- Hu, Y.; Wang, Z.; Jin, D.; Zhang, C.; Sun, R.; Li, Z.; Hu, K.; Ni, J.; Cai, Z.; Pan, D.; et al. Botanical-Inspired 4D Printing of Hydrogel at the Microscale. Adv. Funct. Mater. 2020, 30, 1907377. [Google Scholar] [CrossRef]
- Huang, L.; Jiang, R.; Wu, J.; Song, J.; Bai, H.; Li, B.; Zhao, Q.; Xie, T. Ultrafast Digital Printing toward 4D Shape Changing Materials. Adv. Mater. 2017, 29, 1605390. [Google Scholar] [CrossRef]
- Odent, J.; Vanderstappen, S.; Toncheva, A.; Pichon, E.; Wallin, T.J.; Wang, K.; Shepherd, R.F.; Dubois, P.; Raquez, J.M. Hierarchical Chemomechanical Encoding of Multi-Responsive Hydrogel Actuators Via 3D Printing. J. Mater. Chem. A 2019, 7, 15395–15403. [Google Scholar] [CrossRef]
- Zheng, S.Y.; Shen, Y.; Zhu, F.; Yin, J.; Qian, J.; Fu, J.; Wu, Z.L.; Zheng, Q. Programmed Deformations of 3D-Printed Tough Physical Hydrogels with High Response Speed and Large Output Force. Adv. Funct. Mater. 2018, 28, 1803366. [Google Scholar] [CrossRef]
- Guo, Y.; Shahsavan, H.; Sitti, M. 3D Microstructures of Liquid Crystal Networks with Programmed Voxelated Director Fields. Adv. Mater. 2020, 2002753. [Google Scholar] [CrossRef]
- Kalita, H.; Mandal, M.; Karak, N. Biodegradable Solvent-Induced Shape-Memory Hyperbranched Polyurethane. J. Polym. Res. 2012, 19, 9982. [Google Scholar] [CrossRef]
- Lu, H.; Liu, Y.; Leng, J.; Du, S. Qualitative Separation of the Effect of the Solubility Parameter on the Recovery Behavior of Shape-Memory Polymer. Smart Mater. Struct. 2009, 18, 085003. [Google Scholar] [CrossRef]
- Yu, K.; Zhang, Z.; Liu, Y.; Leng, J. Carbon Nanotube Chains in a Shape Memory Polymer/Carbon Black Composite: To Significantly Reduce the Electrical Resistivity. Appl. Phys. Lett. 2011, 98, 074102. [Google Scholar] [CrossRef]
- Bai, Y.; Chen, Y.; Wang, Q.; Wang, T. Poly(Vinyl Butyral) Based Polymer Networks with Dual-Responsive Shape Memory and Self-Healing Properties. J. Mater. Chem. A 2014, 2, 9169. [Google Scholar] [CrossRef]
- Toncheva, A.; Willocq, B.; Khelifa, F.; Douheret, O.; Lambert, P.; Dubois, P.; Raquez, J.M. Bilayer Solvent and Vapor-Triggered Actuators Made of Cross-Linked Polymer Architectures via Diels–Alder Pathways. J. Mater. Chem. B 2017, 5, 5556–5563. [Google Scholar] [CrossRef]
- Baker, A.B.; Bates, S.R.; Llewellyn-Jones, T.M.; Valori, L.P.; Dicker, M.P.; Trask, R.S. 4D Printing with Robust Thermoplastic Polyurethane Hydrogel-Elastomer Trilayers. Mater. Des. 2019, 163, 107544. [Google Scholar] [CrossRef]
- Alexander, S.L.M.; Ahmadmehrabi, S.; Korley, L.T.J. Programming Shape and Tailoring Transport: Advancing Hygromorphic Bilayers with Aligned Nanofibers. Soft Matter 2017, 13, 5589–5596. [Google Scholar] [CrossRef]
- Zhang, H.; Guo, X.; Wu, J.; Fang, D.; Zhang, Y. Soft Mechanical Metamaterials with Unusual Swelling Behavior and Tunable Stress-Strain Curves. Sci. Adv. 2018, 4, eaar8535. [Google Scholar] [CrossRef]
- Du, H.; Zhang, J. Solvent Induced Shape Recovery of Shape Memory Polymer Based on Chemically Cross-Linked Poly(Vinyl Alcohol). Soft Matter 2010, 6, 3370. [Google Scholar] [CrossRef]
- Qi, X.; Yao, X.; Deng, S.; Zhou, T.; Fu, Q. Water-Induced Shape Memory Effect of Graphene Oxide Reinforced Polyvinyl Alcohol Nanocomposites. J. Mater. Chem. A 2014, 2, 2240–2249. [Google Scholar] [CrossRef]
- Zhu, Y.; Hu, J.; Luo, H.; Young, R.J.; Deng, L.; Zhang, S.; Fan, Y.; Ye, G. Rapidly Switchable Water-Sensitive Shape-Memory Cellulose/Elastomer Nano-Composites. Soft Matter 2012, 8, 2509. [Google Scholar] [CrossRef]
- Quitmann, D.; Gushterov, N.; Sadowski, G.; Katzenberg, F.; Tiller, J.C. Solvent-Sensitive Reversible Stress-Response of Shape Memory Natural Rubber. ACS Appl. Mater. Interfaces 2013, 5, 3504–3507. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Q.; Dunlop, J.W.C.; Qiu, X.; Huang, F.; Zhang, Z.; Heyda, J.; Dzubiella, J.; Antonietti, M.; Yuan, J. An Instant Multi-Responsive Porous Polymer Actuator Driven by Solvent Molecule Sorption. Nat. Commun. 2014, 5, 4293. [Google Scholar] [CrossRef] [PubMed]
- Ding, Z.; Yuan, C.; Peng, X.; Wang, T.; Qi, H.J.; Dunn, M.L. Direct 4D Printing via Active Composite Materials. Sci. Adv. 2017, 3, e1602890. [Google Scholar] [CrossRef] [PubMed]
- Toncheva, A.; Khelifa, F.; Paint, Y.; Voué, M.; Lambert, P.; Dubois, P.; Raquez, J.M. Fast IR-Actuated Shape-Memory Polymers Using in Situ Silver Nanoparticle-Grafted Cellulose Nanocrystals. ACS Appl. Mater. Interfaces 2018, 10, 29933–29942. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Wang, Z.; Song, Z.; Ren, L.; Liu, Q.; Ren, L. Biomimetic Shape–Color Double-Responsive 4D Printing. Adv. Mater. Technol. 2019, 4, 1900293. [Google Scholar] [CrossRef]
- Liu, J.A.C.; Gillen, J.H.; Mishra, S.R.; Evans, B.A.; Tracy, J.B. Photothermally and Magnetically Controlled Reconfiguration of Polymer Composites for Soft Robotics. Sci. Adv. 2019, 5, eaaw2897. [Google Scholar] [CrossRef]
- Bodaghi, M.; Damanpack, A.; Liao, W. Adaptive Metamaterials by Functionally Graded 4D Printing. Mater. Des. 2017, 135, 26–36. [Google Scholar] [CrossRef]
- Zolfagharian, A.; Kaynak, A.; Khoo, S.Y.; Kouzani, A. Pattern-Driven 4D Printing. Sens. Actuators A Phys. 2018, 274, 231–243. [Google Scholar] [CrossRef]
- Kim, Y.; Yuk, H.; Zhao, R.; Chester, S.A.; Zhao, X. Printing Ferromagnetic Domains for Untethered Fast-Transforming Soft Materials. Nature 2018, 558, 274–279. [Google Scholar] [CrossRef]
- Hu, W.; Lum, G.Z.; Mastrangeli, M.; Sitti, M. Small-Scale Soft-Bodied Robot with Multimodal Locomotion. Nature 2018, 554, 81–85. [Google Scholar] [CrossRef]
- Zhang, J.; Diller, E. Untethered Miniature Soft Robots: Modeling and Design of a Millimeter-Scale Swimming Magnetic Sheet. Soft Robot. 2018, 5, 761–776. [Google Scholar] [CrossRef] [PubMed]
- Ze, Q.; Kuang, X.; Wu, S.; Wong, J.; Montgomery, S.M.; Zhang, R.; Kovitz, J.M.; Yang, F.; Qi, H.J.; Zhao, R. Magnetic Shape Memory Polymers with Integrated Multifunctional Shape Manipulation. Adv. Mater. 2020, 32, 1906657. [Google Scholar] [CrossRef]
- Chautems, C.; Tonazzini, A.; Boehler, Q.; Jeong, S.H.; Floreano, D.; Nelson, B.J. Magnetic Continuum Device with Variable Stiffness for Minimally Invasive Surgery. Adv. Intell. Syst. 2020, 2, 1900086. [Google Scholar] [CrossRef]
- Chautems, C.; Tonazzini, A.; Floreano, D.; Nelson, B.J. A Variable Stiffness Catheter Controlled with an External Magnetic Field. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 181–186. [Google Scholar] [CrossRef]
- Ambulo, C.P.; Burroughs, J.J.; Boothby, J.M.; Kim, H.; Shankar, M.R.; Ware, T.H. Four-Dimensional Printing of Liquid Crystal Elastomers. ACS Appl. Mater. Interfaces 2017, 9, 37332–37339. [Google Scholar] [CrossRef] [PubMed]
- Barnes, M.; Verduzco, R. Direct Shape Programming of Liquid Crystal Elastomers. Soft Matter 2019, 15, 870–879. [Google Scholar] [CrossRef] [PubMed]
- He, Q.; Wang, Z.; Wang, Y.; Minori, A.; Tolley, M.T.; Cai, S. Electrically Controlled Liquid Crystal Elastomer—Based Soft Tubular Actuator with Multimodal Actuation. Sci. Adv. 2019, 5, eaax5746. [Google Scholar] [CrossRef] [PubMed]
- Kotikian, A.; McMahan, C.; Davidson, E.C.; Muhammad, J.M.; Weeks, R.D.; Daraio, C.; Lewis, J.A. Untethered Soft Robotic Matter with Passive Control of Shape Morphing and Propulsion. Sci. Robot. 2019, 4, eaax7044. [Google Scholar] [CrossRef] [PubMed]
- López-Valdeolivas, M.; Liu, D.; Broer, D.J.; Sánchez-Somolinos, C. 4D Printed Actuators with Soft-Robotic Functions. Macromol. Rapid Commun. 2018, 39, 1700710. [Google Scholar] [CrossRef]
- Palagi, S.; Mark, A.G.; Reigh, S.Y.; Melde, K.; Qiu, T.; Zeng, H.; Parmeggiani, C.; Martella, D.; Sanchez-Castillo, A.; Kapernaum, N.; et al. Structured Light Enables Biomimetic Swimming and Versatile Locomotion of Photoresponsive Soft Microrobots. Nat. Mater 2016, 15, 647–653. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, Z.; He, Q.; Iyer, P.; Cai, S. Electrically Controlled Soft Actuators with Multiple and Reprogrammable Actuation Modes. Adv. Intell. Syst. 2020, 2, 1900177. [Google Scholar] [CrossRef]
- Zeng, H.; Wani, O.M.; Wasylczyk, P.; Priimagi, A. Light-Driven, Caterpillar-Inspired Miniature Inching Robot. Macromol. Rapid Commun. 2018, 39, 1700224. [Google Scholar] [CrossRef] [PubMed]
- Lahikainen, M.; Zeng, H.; Priimagi, A. Design Principles for Non-Reciprocal Photomechanical Actuation. Soft Matter 2020, 16, 5951–5958. [Google Scholar] [CrossRef] [PubMed]
- Ryabchun, A.; Li, Q.; Lancia, F.; Aprahamian, I.; Katsonis, N. Shape-Persistent Actuators from Hydrazone Photoswitches. J. Am. Chem. Soc. 2019, 141, 1196–1200. [Google Scholar] [CrossRef] [PubMed]
- Yu, L.; Peng, R.; Rivers, G.; Zhang, C.; Si, P.; Zhao, B. Multifunctional Liquid Crystal Polymer Network Soft Actuators. J. Mater. Chem. A 2020, 8, 3390–3396. [Google Scholar] [CrossRef]
- Hajiesmaili, E.; Clarke, D.R. Reconfigurable Shape-Morphing Dielectric Elastomers Using Spatially Varying Electric Fields. Nat. Commun. 2019, 10, 183. [Google Scholar] [CrossRef]
- Davidson, Z.S.; Shahsavan, H.; Aghakhani, A.; Guo, Y.; Hines, L.; Xia, Y.; Yang, S.; Sitti, M. Monolithic Shape-Programmable Dielectric Liquid Crystal Elastomer Actuators. Sci. Adv. 2019, 5, eaay0855. [Google Scholar] [CrossRef] [PubMed]
- Xing, Z.; Zhang, J.; McCoul, D.; Cui, Y.; Sun, L.; Zhao, J. A Super-Lightweight and Soft Manipulator Driven by Dielectric Elastomers. Soft Robot. 2020, 7, 512–520. [Google Scholar] [CrossRef]
- Haines, C.S.; Lima, M.D.; Li, N.; Spinks, G.M.; Foroughi, J.; Madden, J.D.W.; Kim, S.H.; Fang, S.; Jung de Andrade, M.; Goktepe, F.; et al. Artificial Muscles from Fishing Line and Sewing Thread. Science 2014, 343, 868–872. [Google Scholar] [CrossRef]
- Sun, J.; Tighe, B.; Liu, Y.; Zhao, J. Twisted-and-Coiled Actuators with Free Strokes Enable Soft Robots with Programmable Motions. Soft Robot. 2020. [Google Scholar] [CrossRef]
- Wu, C.; Zheng, W. A Modeling of Twisted and Coiled Polymer Artificial Muscles Based on Elastic Rod Theory. Actuators 2020, 9, 25. [Google Scholar] [CrossRef]
- Chang, L.; Yu, L.; Li, C.; Niu, Q.; Hu, Y.; Lu, P.; Zhu, Z.; Wu, Y. Ionic Polymer with Single-Layered Electrodes: A Novel Strategy for Ionic Actuator Design. Smart Mater. Struct. 2018, 27, 105046. [Google Scholar] [CrossRef]
- Tripathi, A.S.; Chattopadhyay, B.P.; Das, S. Cost-Effective Fabrication of Ionic Polymer Based Artificial Muscles for Catheter-Guidewire Maneuvering Application. Microsyst. Technol. 2019, 25, 1129–1136. [Google Scholar] [CrossRef]
- Zhu, Z.; Bian, C.; Ru, J.; Bai, W.; Chen, H. Rapid Deformation of IPMC under a High Electrical Pulse Stimulus Inspired by Action Potential. Smart Mater. Struct. 2018, 28, 01LT01. [Google Scholar] [CrossRef]
- Hao, M.; Wang, Y.; Zhu, Z.; He, Q.; Zhu, D.; Luo, M. A Compact Review of IPMC as Soft Actuator and Sensor: Current Trends, Challenges, and Potential Solutions From Our Recent Work. Front. Robot. AI 2019, 6, 129. [Google Scholar] [CrossRef]
- Yang, Y.; Wu, Y.; Li, C.; Yang, X.; Chen, W. Flexible Actuators for Soft Robotics. Adv. Intell. Syst. 2020, 2, 1900077. [Google Scholar] [CrossRef]
- Coyle, S.; Majidi, C.; LeDuc, P.; Hsia, K.J. Bio-Inspired Soft Robotics: Material Selection, Actuation, and Design. Extrem. Mech. Lett. 2018, 22, 51–59. [Google Scholar] [CrossRef]
- McCracken, J.M.; Donovan, B.R.; White, T.J. Materials as Machines. Adv. Mater. 2020, 32, 1906564. [Google Scholar] [CrossRef] [PubMed]
- Boyraz, P.; Runge, G.; Raatz, A. An Overview of Novel Actuators for Soft Robotics. Actuators 2018, 7, 48. [Google Scholar] [CrossRef]
- Palagi, S.; Fischer, P. Bioinspired Microrobots. Nat. Rev. Mater. 2018, 3, 113–124. [Google Scholar] [CrossRef]
- Rich, S.I.; Wood, R.J.; Majidi, C. Untethered Soft Robotics. Nat. Electron. 2018, 1, 102–112. [Google Scholar] [CrossRef]
- Lui, Y.S.; Sow, W.T.; Tan, L.P.; Wu, Y.; Lai, Y.; Li, H. 4D Printing and Stimuli-Responsive Materials in Biomedical Aspects. Acta Biomater. 2019, 92, 19–36. [Google Scholar] [CrossRef] [PubMed]
- Laschi, C.; Mazzolai, B.; Cianchetti, M. Soft Robotics: Technologies and Systems Pushing the Boundaries of Robot Abilities. Sci. Robot. 2016, 1, eaah3690. [Google Scholar] [CrossRef] [PubMed]
- McEvoy, M.A.; Correll, N. Materials That Couple Sensing, Actuation, Computation, and Communication. Science 2015, 347. [Google Scholar] [CrossRef] [PubMed]
- Koshima, H. (Ed.) Mechanically Responsive Materials for Soft Robotics, 1st ed.; Wiley: Hoboken, NJ, USA, 2020. [Google Scholar] [CrossRef]
- Sun, L.; Huang, W.M.; Ding, Z.; Zhao, Y.; Wang, C.C.; Purnawali, H.; Tang, C. Stimulus-Responsive Shape Memory Materials: A Review. Mater. Des. 2012, 33, 577–640. [Google Scholar] [CrossRef]
- Sokolowski, W.; Metcalfe, A.; Hayashi, S.; Yahia, L.; Raymond, J. Medical Applications of Shape Memory Polymers. Biomed. Mater. 2007, 2, S23–S27. [Google Scholar] [CrossRef] [PubMed]
- Ware, T.; Simon, D.; Hearon, K.; Liu, C.; Shah, S.; Reeder, J.; Khodaparast, N.; Kilgard, M.P.; Maitland, D.J.; Rennaker, R.L.; et al. Three-Dimensional Flexible Electronics Enabled by Shape Memory Polymer Substrates for Responsive Neural Interfaces. Macromol. Mater. Eng. 2012, 297, 1193–1202. [Google Scholar] [CrossRef]
- Lu, H.; Yu, K.; Liu, Y.; Leng, J. Sensing and Actuating Capabilities of a Shape Memory Polymer Composite Integrated with Hybrid Filler. Smart Mater. Struct. 2010, 19, 065014. [Google Scholar] [CrossRef]
- Santo, L.; Quadrini, F.; Accettura, A.; Villadei, W. Shape Memory Composites for Self-Deployable Structures in Aerospace Applications. Procedia Eng. 2014, 88, 42–47. [Google Scholar] [CrossRef]
- Mao, Y.; Yu, K.; Isakov, M.S.; Wu, J.; Dunn, M.L.; Jerry Qi, H. Sequential Self-Folding Structures by 3D Printed Digital Shape Memory Polymers. Sci. Rep. 2015, 5, 13616. [Google Scholar] [CrossRef]
- Pandini, S.; Passera, S.; Messori, M.; Paderni, K.; Toselli, M.; Gianoncelli, A.; Bontempi, E.; Riccò, T. Two-Way Reversible Shape Memory Behaviour of Crosslinked Poly(ϵ-Caprolactone). Polymer 2012, 53, 1915–1924. [Google Scholar] [CrossRef]
- Ishida, K.; Yoshie, N. Two-Way Conversion between Hard and Soft Properties of Semicrystalline Cross-Linked Polymer. Macromolecules 2008, 41, 4753–4757. [Google Scholar] [CrossRef]
- Chung, T.; Romo-Uribe, A.; Mather, P.T. Two-Way Reversible Shape Memory in a Semicrystalline Network. Macromolecules 2008, 41, 184–192. [Google Scholar] [CrossRef]
- Qin, H.; Mather, P.T. Combined One-Way and Two-Way Shape Memory in a Glass-Forming Nematic Network. Macromolecules 2009, 42, 273–280. [Google Scholar] [CrossRef]
- Pilate, F.; Toncheva, A.; Dubois, P.; Raquez, J.M. Shape-Memory Polymers for Multiple Applications in the Materials World. Eur. Polym. J. 2016, 80, 268–294. [Google Scholar] [CrossRef]
- Scalet, G. Two-Way and Multiple-Way Shape Memory Polymers for Soft Robotics: An Overview. Actuators 2020, 9, 10. [Google Scholar] [CrossRef]
- Xia, Y.; He, Y.; Zhang, F.; Liu, Y.; Leng, J. A Review of Shape Memory Polymers and Composites: Mechanisms, Materials, and Applications. Adv. Mater. 2020, 2000713. [Google Scholar] [CrossRef]
- Yang, Z.; Zhang, L. Magnetic Actuation Systems for Miniature Robots: A Review. Adv. Intell. Syst. 2020, 2000082. [Google Scholar] [CrossRef]
- Sitti, M.; Wiersma, D.S. Pros and Cons: Magnetic versus Optical Microrobots. Adv. Mater. 2020, 32, 1906766. [Google Scholar] [CrossRef]
- Xu, T.; Zhang, J.; Salehizadeh, M.; Onaizah, O.; Diller, E. Millimeter-Scale Flexible Robots with Programmable Three-Dimensional Magnetization and Motions. Sci. Robot. 2019, 4. [Google Scholar] [CrossRef]
- O’Halloran, A.; O’Malley, F.; McHugh, P. A Review on Dielectric Elastomer Actuators, Technology, Applications, and Challenges. J. Appl. Phys. 2008, 104, 071101. [Google Scholar] [CrossRef]
- Ohm, C.; Brehmer, M.; Zentel, R. Liquid Crystalline Elastomers as Actuators and Sensors. Adv. Mater. 2010, 22, 3366–3387. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Z.C.; Xiao, Y.Y.; Zhao, Y. Shining Light on Liquid Crystal Polymer Networks: Preparing, Reconfiguring, and Driving Soft Actuators. Adv. Opt. Mater. 2019, 7, 1900262. [Google Scholar] [CrossRef]
- Ge, F.; Zhao, Y. Microstructured Actuation of Liquid Crystal Polymer Networks. Adv. Funct. Mater. 2020, 30, 1901890. [Google Scholar] [CrossRef]
- Suo, Z. Theory of Dielectric Elastomers. Acta Mech. Solida Sin. 2010, 23, 549–578. [Google Scholar] [CrossRef]
- Gupta, U.; Qin, L.; Wang, Y.; Godaba, H.; Zhu, J. Soft Robots Based on Dielectric Elastomer Actuators: A Review. Smart Mater. Struct. 2019, 28, 103002. [Google Scholar] [CrossRef]
- Duduta, M.; Hajiesmaili, E.; Zhao, H.; Wood, R.J.; Clarke, D.R. Realizing the Potential of Dielectric Elastomer Artificial Muscles. Proc. Natl. Acad. Sci. USA 2019, 116, 2476–2481. [Google Scholar] [CrossRef]
- Gorissen, B.; Reynaerts, D.; Konishi, S.; Yoshida, K.; Kim, J.W.; De Volder, M. Elastic Inflatable Actuators for Soft Robotic Applications. Adv. Mater. 2017, 29, 1604977. [Google Scholar] [CrossRef]
- Polygerinos, P.; Correll, N.; Morin, S.A.; Mosadegh, B.; Onal, C.D.; Petersen, K.; Cianchetti, M.; Tolley, M.T.; Shepherd, R.F. Soft Robotics: Review of Fluid-Driven Intrinsically Soft Devices; Manufacturing, Sensing, Control, and Applications in Human-Robot Interaction: Review of Fluid-Driven Intrinsically Soft Robots. Adv. Eng. Mater. 2017, 19, 1700016. [Google Scholar] [CrossRef]
- Lambert, P.; Szewczyk, J.; Renaud, P. Actionneurs Non Conventionnels Pour la Robotique. Techniques de l’ingénieur Conception, modélisation et Commande en Robotique. 2016, p. s7769. Available online: https://www.techniques-ingenieur.fr/base-documentaire/automatique-robotique-th16/conception-modelisation-et-commande-en-robotique-42398210/actionneurs-non-conventionnels-pour-la-robotique-s7769/ (accessed on 2 August 2020).
- Walker, J.; Zidek, T.; Harbel, C.; Yoon, S.; Strickland, F.S.; Kumar, S.; Shin, M. Soft Robotics: A Review of Recent Developments of Pneumatic Soft Actuators. Actuators 2020, 9, 3. [Google Scholar] [CrossRef]
- Mustaza, S.M.; Elsayed, Y.; Lekakou, C.; Saaj, C.; Fras, J. Dynamic Modeling of Fiber-Reinforced Soft Manipulator: A Visco-Hyperelastic Material-Based Continuum Mechanics Approach. Soft Robot. 2019, 6, 305–317. [Google Scholar] [CrossRef]
- Joshi, S.; Paik, J. Pneumatic Supply System Parameter Optimization for Soft Actuators. Soft Robot. 2020. [Google Scholar] [CrossRef] [PubMed]
- Wehner, M.; Truby, R.L.; Fitzgerald, D.J.; Mosadegh, B.; Whitesides, G.M.; Lewis, J.A.; Wood, R.J. An Integrated Design and Fabrication Strategy for Entirely Soft, Autonomous Robots. Nature 2016, 536, 451–455. [Google Scholar] [CrossRef] [PubMed]
- Miriyev, A.; Caires, G.; Lipson, H. Functional Properties of Silicone/Ethanol Soft-Actuator Composites. Mater. Des. 2018, 145, 232–242. [Google Scholar] [CrossRef]
- Li, X.; Duan, H.; Lv, P.; Yi, X. Soft Actuators Based on Liquid–Vapor Phase Change Composites. Soft Robot. 2020. [Google Scholar] [CrossRef] [PubMed]
- Miriyev, A.; Trujillo, C.; Caires, G.; Lipson, H. Rejuvenation of Soft Material–Actuator. MRS Commun. 2018, 8, 556–561. [Google Scholar] [CrossRef]
- Tian, Y.; Li, Y.T.; Tian, H.; Yang, Y.; Ren, T.L. Recent Progress of Soft Electrothermal Actuators. Soft Robot. 2020. [Google Scholar] [CrossRef] [PubMed]
- Koetting, M.C.; Peters, J.T.; Steichen, S.D.; Peppas, N.A. Stimulus-Responsive Hydrogels: Theory, Modern Advances, and Applications. Mater. Sci. Eng. R Rep. 2015, 93, 1–49. [Google Scholar] [CrossRef]
- Mohd Jani, J.; Leary, M.; Subic, A.; Gibson, M.A. A Review of Shape Memory Alloy Research, Applications and Opportunities. Mater. Des. 2014, 56, 1078–1113. [Google Scholar] [CrossRef]
- Haga, Y.; Mizushima, M.; Matsunaga, T.; Totsu, K.; Esashi, M. Active Bending Ileus Tube Using Shape Memory Alloy for Treatment of Intestinal Obstruction. In Proceedings of the 2005 3rd IEEE/EMBS Special Topic Conference on Microtechnology in Medicine and Biology, Oahu, HI, USA, 12–15 May 2005; pp. 249–252. [Google Scholar] [CrossRef]
- Kianzad, S.; Amini, A.; Karkouti, S.O. Force Control of Laparoscopy Grasper Using Antagonistic Shape Memory Alloy. In Proceedings of the 2011 1st Middle East Conference on Biomedical Engineering, Sharjah, UAE, 21–24 February 2011; pp. 335–338. [Google Scholar] [CrossRef]
- Gao, X.; Yang, J.; Wu, J.; Xin, X.; Li, Z.; Yuan, X.; Shen, X.; Dong, S. Piezoelectric Actuators and Motors: Materials, Designs, and Applications. Adv. Mater. Technol. 2020, 5, 1900716. [Google Scholar] [CrossRef]
- Deng, T.; Wang, H.; Chen, W.; Wang, X.; Pfeifer, R. Development of a New Cable-Driven Soft Robot for Cardiac Ablation. In Proceedings of the 2013 IEEE International Conference on Robotics and Biomimetics (ROBIO), Shenzhen, China, 12–14 December 2013; pp. 728–733. [Google Scholar] [CrossRef]
- Gerboni, G.; Henselmans, P.W.J.; Arkenbout, E.A.; van Furth, W.R.; Breedveld, P. HelixFlex: Bioinspired Maneuverable Instrument for Skull Base Surgery. Bioinspir. Biomim. 2015, 10, 066013. [Google Scholar] [CrossRef]
- Feng, F.; Hong, W.; Xie, L. Design of 3D-Printed Flexible Joints With Presettable Stiffness for Surgical Robots. IEEE Access 2020, 8, 79573–79585. [Google Scholar] [CrossRef]
- Dupont, P.E.; Lock, J.; Itkowitz, B.; Butler, E. Design and Control of Concentric-Tube Robots. IEEE Trans. Robot. 2010, 26, 209–225. [Google Scholar] [CrossRef] [PubMed]
- Qiu, T.; Palagi, S.; Mark, A.G.; Melde, K.; Adams, F.; Fischer, P. Wireless Actuation with Functional Acoustic Surfaces. Appl. Phys. Lett. 2016, 109, 191602. [Google Scholar] [CrossRef]
- Taniguchi, T.; Sugiyama, H.; Uekusa, H.; Shiro, M.; Asahi, T.; Koshima, H. Walking and Rolling of Crystals Induced Thermally by Phase Transition. Nat. Commun. 2018, 9, 538. [Google Scholar] [CrossRef] [PubMed]
- Appiah, C.; Arndt, C.; Siemsen, K.; Heitmann, A.; Staubitz, A.; Selhuber-Unkel, C. Living Materials Herald a New Era in Soft Robotics. Adv. Mater. 2019, 31, 1807747. [Google Scholar] [CrossRef]
- Webster-Wood, V.A.; Akkus, O.; Gurkan, U.A.; Chiel, H.J.; Quinn, R.D. Organismal Engineering: Toward a Robotic Taxonomic Key for Devices Using Organic Materials. Sci. Robot. 2017, 2, eaap9281. [Google Scholar] [CrossRef]
- Blanc, L.; Delchambre, A.; Lambert, P. Flexible Medical Devices: Review of Controllable Stiffness Solutions. Actuators 2017, 6, 23. [Google Scholar] [CrossRef]
- Kuder, I.K.; Arrieta, A.F.; Raither, W.E.; Ermanni, P. Variable Stiffness Material and Structural Concepts for Morphing Applications. Prog. Aerosp. Sci. 2013, 63, 33–55. [Google Scholar] [CrossRef]
- Loeve, A.; Breedveld, P.; Dankelman, J. Scopes Too Flexible...and Too Stiff. IEEE Pulse 2010, 1, 26–41. [Google Scholar] [CrossRef]
- Manti, M.; Cacucciolo, V.; Cianchetti, M. Stiffening in Soft Robotics: A Review of the State of the Art. IEEE Robot. Autom. Mag. 2016, 23, 93–106. [Google Scholar] [CrossRef]
- Yoshida, S.; Morimoto, Y.; Zheng, L.; Onoe, H.; Takeuchi, S. Multipoint Bending and Shape Retention of a Pneumatic Bending Actuator by a Variable Stiffness Endoskeleton. Soft Robot. 2018, 5, 718–725. [Google Scholar] [CrossRef] [PubMed]
- Cartolano, M.; Xia, B.; Miriyev, A.; Lipson, H. Conductive Fabric Heaters for Heat-Activated Soft Actuators. Actuators 2019, 8, 9. [Google Scholar] [CrossRef]
- Bilodeau, R.A.; Miriyev, A.; Lipson, H.; Kramer-Bottiglio, R. All-Soft Material System for Strong Soft Actuators. In Proceedings of the 2018 IEEE International Conference on Soft Robotics (RoboSoft), Livorno, Italy, 24–28 April 2018; pp. 288–294. [Google Scholar] [CrossRef]
- Mishra, S.R.; Tracy, J.B. Sequential Actuation of Shape-Memory Polymers through Wavelength-Selective Photothermal Heating of Gold Nanospheres and Nanorods. ACS Appl. Nano Mater. 2018, 1, 3063–3067. [Google Scholar] [CrossRef]
- Nguyen, B.H.; Nguyen, V.H.; Tran, H.N. Rich Variety of Substrates for Surface Enhanced Raman Spectroscopy. Adv. Nat. Sci. Nanosci. Nanotechnol. 2016, 7, 033001. [Google Scholar] [CrossRef]
- Li, J.F.; Li, Z.Y. Manipulation of Plasmonic Wavefront and Light—Matter Interaction in Metallic Nanostructures: A Brief Review. Chin. Phys. B 2014, 23, 047305. [Google Scholar] [CrossRef]
- Luo, H.; Li, Z.; Yi, G.; Wang, Y.; Zu, X.; Wang, H.; Huang, H.; Liang, Z. Temperature Sensing of Conductive Shape Memory Polymer Composites. Mater. Lett. 2015, 140, 71–74. [Google Scholar] [CrossRef]
- Luo, H.; Li, Z.; Yi, G.; Zu, X.; Wang, H.; Wang, Y.; Huang, H.; Hu, J.; Liang, Z.; Zhong, B. Electro-Responsive Silver Nanowire-Shape Memory Polymer Composites. Mater. Lett. 2014, 134, 172–175. [Google Scholar] [CrossRef]
- Weems, A.C.; Raymond, J.E.; Easley, A.D.; Wierzbicki, M.A.; Gustafson, T.; Monroe, M.B.B.; Maitland, D.J. Shape Memory Polymers with Visible and Near-Infrared Imaging Modalities: Synthesis, Characterization and in Vitro Analysis. RSC Adv. 2017, 7, 19742–19753. [Google Scholar] [CrossRef]
- Yang, L.; Lu, X.; Wang, Z.; Xia, H. Diels–Alder Dynamic Crosslinked Polyurethane/Polydopamine Composites with NIR Triggered Self-Healing Function. Polym. Chem. 2018, 9, 2166–2172. [Google Scholar] [CrossRef]
- Zhang, H.; Zhao, Y. Polymers with Dual Light-Triggered Functions of Shape Memory and Healing Using Gold Nanoparticles. ACS Appl. Mater. Interfaces 2013, 5, 13069–13075. [Google Scholar] [CrossRef]
- Fang, T.; Cao, L.; Chen, S.; Fang, J.; Zhou, J.; Fang, L.; Lu, C.; Xu, Z. Preparation and Assembly of Five Photoresponsive Polymers to Achieve Complex Light-Induced Shape Deformations. Mater. Des. 2018, 144, 129–139. [Google Scholar] [CrossRef]
- Zhang, Z.X.; Dou, J.X.; He, J.H.; Xiao, C.X.; Shen, L.Y.; Yang, J.H.; Wang, Y.; Zhou, Z.W. Electrically/Infrared Actuated Shape Memory Composites Based on a Bio-Based Polyester Blend and Graphene Nanoplatelets and Their Excellent Self-Driven Ability. J. Mater. Chem. C 2017, 5, 4145–4158. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, J.; Tong, X.; Ma, D.; Zhao, Y. Light Polarization-Controlled Shape-Memory Polymer/Gold Nanorod Composite. Macromol. Rapid Commun. 2013, 34, 1575–1579. [Google Scholar] [CrossRef] [PubMed]
- Lu, H.; Zhu, S.; Yang, Y.; Huang, W.M.; Leng, J.; Du, S. Surface Grafting of Carbon Fibers with Artificial Silver-Nanoparticle-Decorated Graphene Oxide for High-Speed Electrical Actuation of Shape-Memory Polymers. J. Appl. Polym. Sci. 2014. [Google Scholar] [CrossRef]
- Lu, H.; Liang, F.; Gou, J.; Leng, J.; Du, S. Synergistic Effect of Ag Nanoparticle-Decorated Graphene Oxide and Carbon Fiber on Electrical Actuation of Polymeric Shape Memory Nanocomposites. Smart Mater. Struct. 2014, 23, 085034. [Google Scholar] [CrossRef]
- Li, J.; Sun, M.; Wu, Z. Design and Fabrication of a Low-Cost Silicone and Water-Based Soft Actuator with a High Load-to-Weight Ratio. Soft Robot. 2020. [Google Scholar] [CrossRef]
- Zhao, T.; Dou, W.; Hu, Z.; Hou, W.; Sun, Y.; Lv, J.A. Reconfigurable Soft Actuators with Multiple-Stimuli Responses. Macromol. Rapid Commun. 2020, 41, 2000313. [Google Scholar] [CrossRef]
- Armon, S.; Efrati, E.; Kupferman, R.; Sharon, E. Geometry and Mechanics in the Opening of Chiral Seed Pods. Science 2011, 333, 1726–1730. [Google Scholar] [CrossRef]
- Connolly, F.; Walsh, C.J.; Bertoldi, K. Automatic Design of Fiber-Reinforced Soft Actuators for Trajectory Matching. Proc. Natl. Acad. Sci. USA 2017, 114, 51–56. [Google Scholar] [CrossRef]
- Connolly, F.; Polygerinos, P.; Walsh, C.J.; Bertoldi, K. Mechanical Programming of Soft Actuators by Varying Fiber Angle. Soft Robot. 2015, 2, 26–32. [Google Scholar] [CrossRef]
- Paez, L.; Agarwal, G.; Paik, J. Design and Analysis of a Soft Pneumatic Actuator with Origami Shell Reinforcement. Soft Robot. 2016, 3, 109–119. [Google Scholar] [CrossRef]
- Wang, Z.; Polygerinos, P.; Overvelde, J.T.B.; Galloway, K.C.; Bertoldi, K.; Walsh, C.J. Interaction Forces of Soft Fiber Reinforced Bending Actuators. IEEE/ASME Trans. Mechatronics 2017, 22, 717–727. [Google Scholar] [CrossRef]
- Lazeroms, M.; La Haye, A.; Sjoerdsma, W.; Schreurs, W.; Jongkind, W.; Honderd, G.; Grimbergen, C. A Hydraulic Forceps with Force-Feedback for Use in Minimally Invasive Surgery. Mechatronics 1996, 6, 437–446. [Google Scholar] [CrossRef]
- Huber, J.E.; Fleck, N.A.; Ashby, M.F. The Selection of Mechanical Actuators Based on Performance Indices. Proc. R. Soc. Lond. A 1997, 453, 2185–2205. [Google Scholar] [CrossRef]
- Miriyev, A. A Focus on Soft Actuation. Actuators 2019, 8, 74. [Google Scholar] [CrossRef]
- Blanc, L. Controllable Stiffness Mechanisms for Endoscopic Catheters. Ph.D. Thesis, Université libre de Bruxelles, Bruxelles, Belgium, 2019. [Google Scholar]
- McKee, C.T.; Last, J.A.; Russell, P.; Murphy, C.J. Indentation Versus Tensile Measurements of Young’s Modulus for Soft Biological Tissues. Tissue Eng. Part B Rev. 2011, 17, 155–164. [Google Scholar] [CrossRef]
- Liu, J.; Sidiropoulos, A.; Konertz, W. Minimally Invasive Aortic Valve Replacement (AVR) Compared to Standard AVR. Eur. J. Cardiothorac. Surg. 1999, 16, S80–S83. [Google Scholar] [CrossRef]
- Shah, D.; Yang, B.; Kriegman, S.; Levin, M.; Bongard, J.; Kramer-Bottiglio, R. Shape Changing Robots: Bioinspiration, Simulation, and Physical Realization. Adv. Mater. 2020, 2002882. [Google Scholar] [CrossRef]
- Odent, J.; Toncheva, A.; Dubois, P.; Raquez, J.M. From 3D to 4D-Printing: On the Road to Smart 3D-Printed Polymer Devices. In How Smart Are the Polymers? Polymer Science and Technology, Nova Science Publishers: New York, NY, USA, 2018. [Google Scholar]
- Allen, E.; Swensen, J. Directional Stiffness Control Through Geometric Patterning and Localized Heating of Field’s Metal Lattice Embedded in Silicone. Actuators 2018, 7, 80. [Google Scholar] [CrossRef]
- Bertoldi, K.; Vitelli, V.; Christensen, J.; van Hecke, M. Flexible Mechanical Metamaterials. Nat. Rev. Mater. 2017, 2, 17066. [Google Scholar] [CrossRef]
- Ren, X.; Das, R.; Tran, P.; Ngo, T.D.; Xie, Y.M. Auxetic Metamaterials and Structures: A Review. Smart Mater. Struct. 2018, 27, 023001. [Google Scholar] [CrossRef]
- Fischer, S.C.L.; Hillen, L.; Eberl, C. Mechanical Metamaterials on the Way from Laboratory Scale to Industrial Applications: Challenges for Characterization and Scalability. Materials 2020, 13, 3605. [Google Scholar] [CrossRef] [PubMed]
- Nam, S.; Pei, E. A Taxonomy of Shape-Changing Behavior for 4D Printed Parts Using Shape-Memory Polymers. Prog. Addit. Manuf. 2019, 4, 167–184. [Google Scholar] [CrossRef]
- Kim, S.; Laschi, C.; Trimmer, B. Soft Robotics: A Bioinspired Evolution in Robotics. Trends Biotechnol. 2013, 31, 287–294. [Google Scholar] [CrossRef] [PubMed]
- Shie, M.Y.; Shen, Y.F.; Astuti, S.D.; Lee, A.K.X.; Lin, S.H.; Dwijaksara, N.L.B.; Chen, Y.W. Review of Polymeric Materials in 4D Printing Biomedical Applications. Polymers 2019, 11, 1864. [Google Scholar] [CrossRef]
- Ashuri, T.; Armani, A.; Jalilzadeh Hamidi, R.; Reasnor, T.; Ahmadi, S.; Iqbal, K. Biomedical Soft Robots: Current Status and Perspective. Biomed. Eng. Lett. 2020, 10, 369–385. [Google Scholar] [CrossRef]
- Runciman, M.; Darzi, A.; Mylonas, G.P. Soft Robotics in Minimally Invasive Surgery. Soft Robot. 2019, 6, 423–443. [Google Scholar] [CrossRef]
- De Greef, A.; Lambert, P.; Delchambre, A. Towards Flexible Medical Instruments: Review of Flexible Fluidic Actuators. Precis. Eng. 2009, 33, 311–321. [Google Scholar] [CrossRef]
- Field, R.D.; Anandakumaran, P.N.; Sia, S.K. Soft Medical Microrobots: Design Components and System Integration. Appl. Phys. Rev. 2019, 6, 041305. [Google Scholar] [CrossRef]
- Hughes, J.; Culha, U.; Giardina, F.; Guenther, F.; Rosendo, A.; Iida, F. Soft Manipulators and Grippers: A Review. Front. Robot. AI 2016, 3. [Google Scholar] [CrossRef]
- Fenci, G.E.; Currie, N.G. Deployable Structures Classification: A Review. Int. J. Space Struct. 2017, 32, 112–130. [Google Scholar] [CrossRef]
- Chowdhary, G.; Gazzola, M.; Krishnan, G.; Soman, C.; Lovell, S. Soft Robotics as an Enabling Technology for Agroforestry Practice and Research. Sustainability 2019, 11, 6751. [Google Scholar] [CrossRef]
- Arezzo, A.; Mintz, Y.; Allaix, M.E.; Arolfo, S.; Bonino, M.; Gerboni, G.; Brancadoro, M.; Cianchetti, M.; Menciassi, A.; Wurdemann, H.; et al. Total Mesorectal Excision Using a Soft and Flexible Robotic Arm: A Feasibility Study in Cadaver Models. Surg. Endosc. 2017, 31, 264–273. [Google Scholar] [CrossRef] [PubMed]
- Yeung, C.K.; Cheung, J.L.; Sreedhar, B. Emerging Next-Generation Robotic Colonoscopy Systems towards Painless Colonoscopy. J. Dig. Dis. 2019, 20, 196–205. [Google Scholar] [CrossRef] [PubMed]
- Rus, D.; Tolley, M.T. Design, Fabrication and Control of Origami Robots. Nat. Rev. Mater. 2018, 3, 101–112. [Google Scholar] [CrossRef]
- van Manen, T.; Janbaz, S.; Zadpoor, A.A. Programming the Shape-Shifting of Flat Soft Matter. Mater. Today 2018, 21, 144–163. [Google Scholar] [CrossRef]
- Joshi, S.; Rawat, K.; Karunakaran, C.; Rajamohan, V.; Mathew, A.T.; Koziol, K.; Kumar Thakur, V.; A. S.S, B. 4D Printing of Materials for the Future: Opportunities and Challenges. Appl. Mater. Today 2020, 18, 100490. [Google Scholar] [CrossRef]
- Mitchell, A.; Lafont, U.; Hołyńska, M.; Semprimoschnig, C. Additive Manufacturing—A Review of 4D Printing and Future Applications. Addit. Manuf. 2018, 24, 606–626. [Google Scholar] [CrossRef]
- Huang, X.; Ford, M.; Patterson, Z.J.; Zarepoor, M.; Pan, C.; Majidi, C. Shape Memory Materials for Electrically-Powered Soft Machines. J. Mater. Chem. B 2020, 8, 4539–4551. [Google Scholar] [CrossRef]
- Wallin, T.J.; Pikul, J.; Shepherd, R.F. 3D Printing of Soft Robotic Systems. Nat. Rev. Mater. 2018, 3, 84–100. [Google Scholar] [CrossRef]
- Truby, R.L.; Lewis, J.A. Printing Soft Matter in Three Dimensions. Nature 2016, 540, 371–378. [Google Scholar] [CrossRef] [PubMed]
- Gul, J.Z.; Sajid, M.; Rehman, M.M.; Siddiqui, G.U.; Shah, I.; Kim, K.H.; Lee, J.W.; Choi, K.H. 3D Printing for Soft Robotics—A Review. Sci. Technol. Adv. Mater. 2018, 19, 243–262. [Google Scholar] [CrossRef] [PubMed]








| Classification | Typical Main Materials | |
|---|---|---|
| Isotropic – undirected | Fluidic chamber | Elastomers (Ecoflex [6,7,8,9,10,11,12,13,14,15,16], Dragon Skin [17], Sylgard 184 [18,19], other [20,21,22,23,24,25]), fabric [15,26,27], Filaflex [28], hydrogels [29], Diels-Alder polymer [30], polypropylene [31], FC72 fluid [24], ethanol [16], paper [32], urethane [27], gelatin-based biogel [33] |
| Phase Change Material Elastomer Composite (PCMEC) | Elastomers [34,35,36], phase change material (wax [35], ethanol [34]) | |
| Thermal expansion | Elastomers [37,38,39], resin [40,41], SMP (MPCL) [42], other polymer [43], paper [43,44], micro- and nanofillers [45] | |
| Swelling | Hydrogels [46,47,48,49,50], paper [43], LCN [51], SMP [48,52,53,54,55], cross-linked PCL [56], other polymers [43,57,58,59,60,61,62,63,64] | |
| Anisotropic – directed | Shape Memory Polymer (SMP) | Resins [65], functionalized PCL [66], functionalized PLA [67], polyurethan, wax [48], DiAPLEX [68], other polymers [69,70] |
| Magnetization | Elastomers [71,72,73], resin [74], SMP (DiAPLEX [68], other [74]), low melting point alloy (LMPA) (Cerrolow 117) [75], magnet [75,76], magnetic particles [68,71,72,73,74] | |
| Liquid Crystal (LC) | LCE [77,78,79,80,81,82,83,84], LCN [85,86,87] | |
| Dielectric Elastomer Actuator (DEA) | Elastomers [88], LCE [89], polyethylene [90] | |
| Twisted and Coiled Polymer (TCP) | Nylon 6,6 [91,92,93], polyethylene [91] | |
| Ionic Polymer Metal Composite (IPMC) | Electrolyte membrane (Nafion [94,95,96], Flemion [97], Aciplex [97]), electrode (gold [94], gold-chromium [95], palladium [96], platinum [97]) | |
| Classification | Description | Examples | |
|---|---|---|---|
| None | |||
| Passive | Multi-material | Creating/increasing anisotropy by using material with different properties | Bilayers [10,19,26,37,38,39,40,41,42,43,44,46,49,56,57,59,70,175,176] Strain limiting fibres [6,14,19,31,177] Reinforcement [15,21,22,178,179,180] Kirigami [8,11] |
| Geometry | Creating/increasing anisotropy by changing the geometrical properties of a single material | Patterns [50,77,80,81] Eccentricity[7,16,18,20,23,79,90,92] Swelling rate gradient [49] Bellows [9,24,28,29,30] | |
| Material customization | Creating/increasing anisotropy by customizing the material properties locally | Prestrain [65,69,78] Magnetic profile [71,72,73,123] Gradient [47,48,49] Anisotropic stiffness [89] Local fibre alignment [51,58,84] | |
| Active | Stiffness variation | Creating/increasing anisotropy by controlling the stiffness of on part of the structure | [12,25,32,68,74,75,159] |
| Classification | Description | Examples | |
|---|---|---|---|
| None | Simple kinematics only | [6,14,18,24,95,152] | |
| Actuation multiplicity | Multiple stimuli | Several stimuli per transducers | [86,176,189] |
| Multiple transducers | Several transducers per actuator | [42,44,46,49,85] | |
| Active asymmetry | Stiffness variation | [12,32,68,74,75,159,190] | |
| Modularity | Design variations | Modified actuator design to achieve a given task | [8,15,37,39,48,51,58,71,77,81] |
| Simple modular assembly | Reproduction of a given module, controlling the assembly with a single stimulus | Hinges [41,57,80] Tubular segments [9,40,178,179] Metamaterials [59,71,81] Other [91] | |
| Complex modular assembly | Reproduction of a given module, controlling the assembly with one stimulus per module | Tubular segments [7,12,22,75,90] Voxels [13,17,32,94] Hinges [70] Rigid base [28,30,79] Other [92] | |
| Advanced | Non linearities | Exploitation of a nonlinear transducer response | [9,10,16,21,41,67] |
| Controlled anisotropic stimulus | Variable or structured controlled stimulus | Light [82] Magnetic field [59,72,75,123] | |
| Classification | Example | Typical Application | |
|---|---|---|---|
| Soft arm | Simple bending |  | Surgical device [6,7,12,14,18,75,95] Manipulator [10,15,22,28,44,90,92,159] Microfluidic [40,44] Assistive device [26] Agroforestery [203] Not specified [85,94,178] |
| Multiple curvature |  | ||
| Helixing |  | ||
| Finger/trunk/octopus |  | ||
| Transportation | Walking/inching |  | Locomotion [11,13,17,21,71,80,82,84,179] Drug delivery [72] |
| Inchworm/crawling |  | ||
| Jumping/Rolling |  | ||
| Swimming |  | ||
| Gripper | Star gripper |  | Manipulators [28,37,74,139] Drug delivery [47] Micromanipulation [47,71,123] |
| Finger gripper |  | ||
| Other gripper |  | ||
| Configuration change and other motions | Shape mimicking/self-folding |  | Optics [44,81] Self-assembly—reconfigurable structures [8,41,43,48,57,65,69,80,88,88] Tunable material [59,71] Surgical sutures [66,69] Not specified [89] |
| Origami rigid self-folding |  | ||
| Self-tightening knot |  | ||
| Active metamaterials |  | ||
| Muscle like |  | ||
| Gaussian curvature |  | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Decroly, G.; Toncheva, A.; Blanc, L.; Raquez, J.-M.; Lessinnes, T.; Delchambre, A.; Lambert, P. Programmable Stimuli-Responsive Actuators for Complex Motions in Soft Robotics: Concept, Design and Challenges. Actuators 2020, 9, 131. https://doi.org/10.3390/act9040131
Decroly G, Toncheva A, Blanc L, Raquez J-M, Lessinnes T, Delchambre A, Lambert P. Programmable Stimuli-Responsive Actuators for Complex Motions in Soft Robotics: Concept, Design and Challenges. Actuators. 2020; 9(4):131. https://doi.org/10.3390/act9040131
Chicago/Turabian StyleDecroly, Gilles, Antoniya Toncheva, Loïc Blanc, Jean-Marie Raquez, Thomas Lessinnes, Alain Delchambre, and Pierre Lambert. 2020. "Programmable Stimuli-Responsive Actuators for Complex Motions in Soft Robotics: Concept, Design and Challenges" Actuators 9, no. 4: 131. https://doi.org/10.3390/act9040131
APA StyleDecroly, G., Toncheva, A., Blanc, L., Raquez, J.-M., Lessinnes, T., Delchambre, A., & Lambert, P. (2020). Programmable Stimuli-Responsive Actuators for Complex Motions in Soft Robotics: Concept, Design and Challenges. Actuators, 9(4), 131. https://doi.org/10.3390/act9040131







