Real-Time Implementation of a New MPPT Control Method for a DC-DC Boost Converter Used in a PEM Fuel Cell Power System
Abstract
1. Introduction
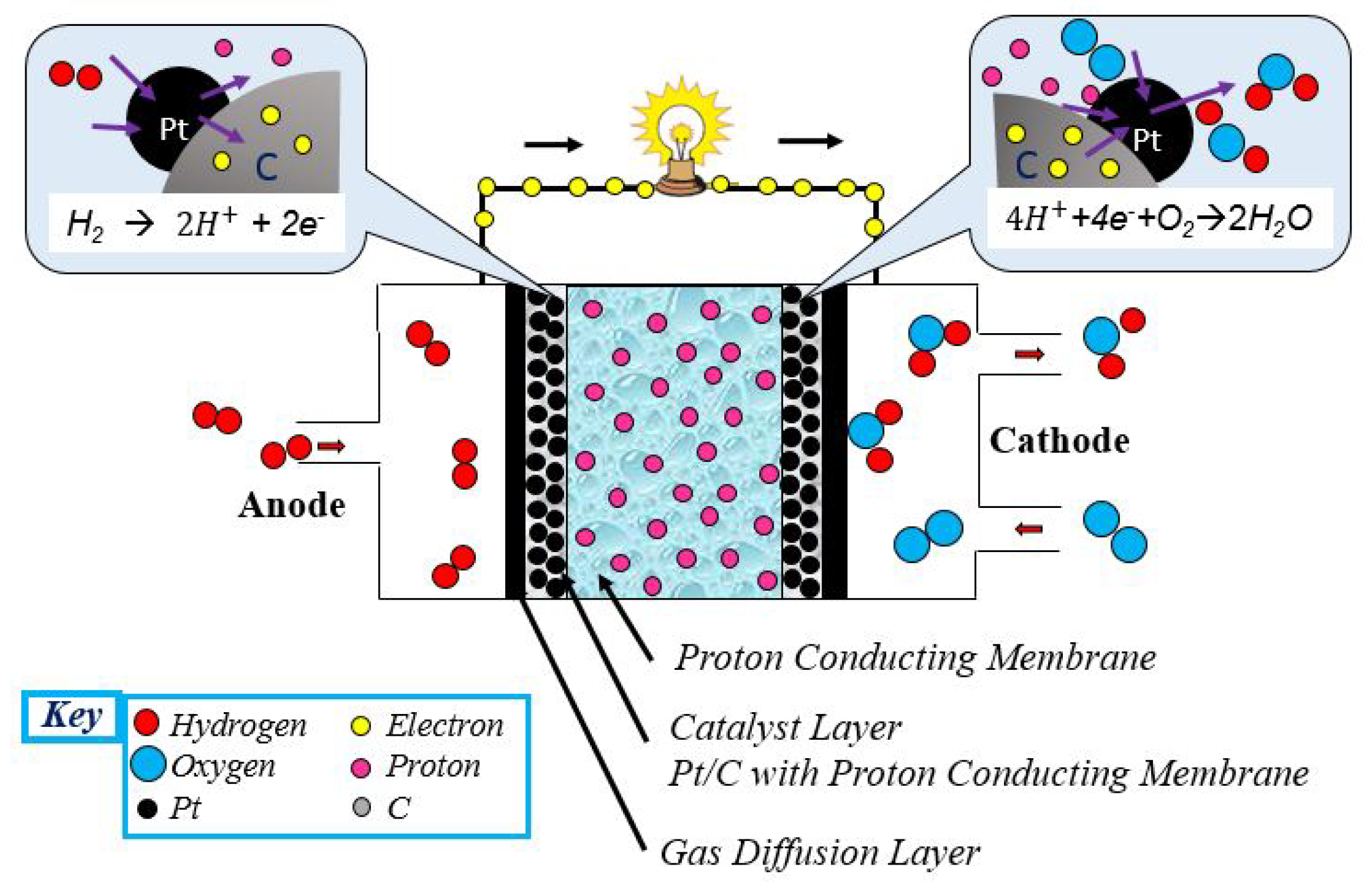
2. PEM Fuel Cell Stack
2.1. Operating Principle
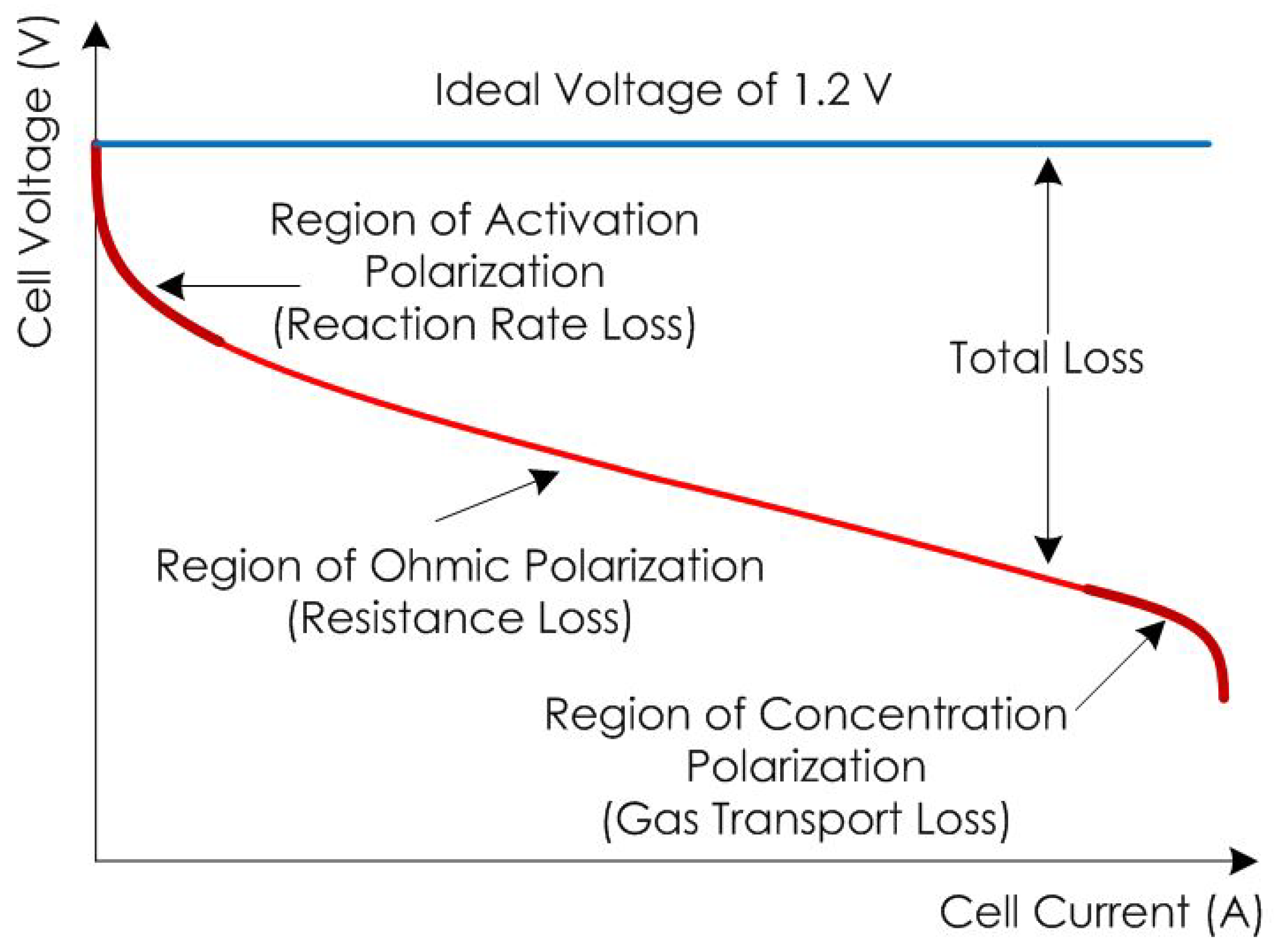
2.2. Model and Analysis
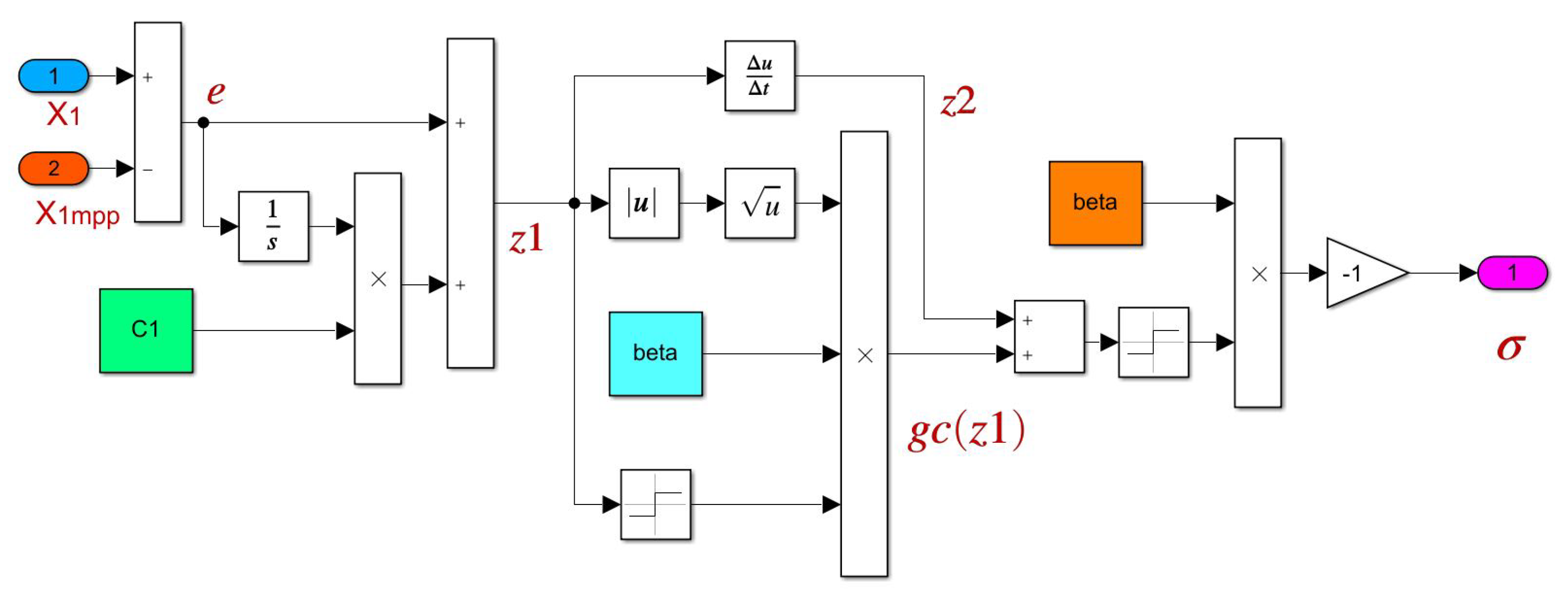
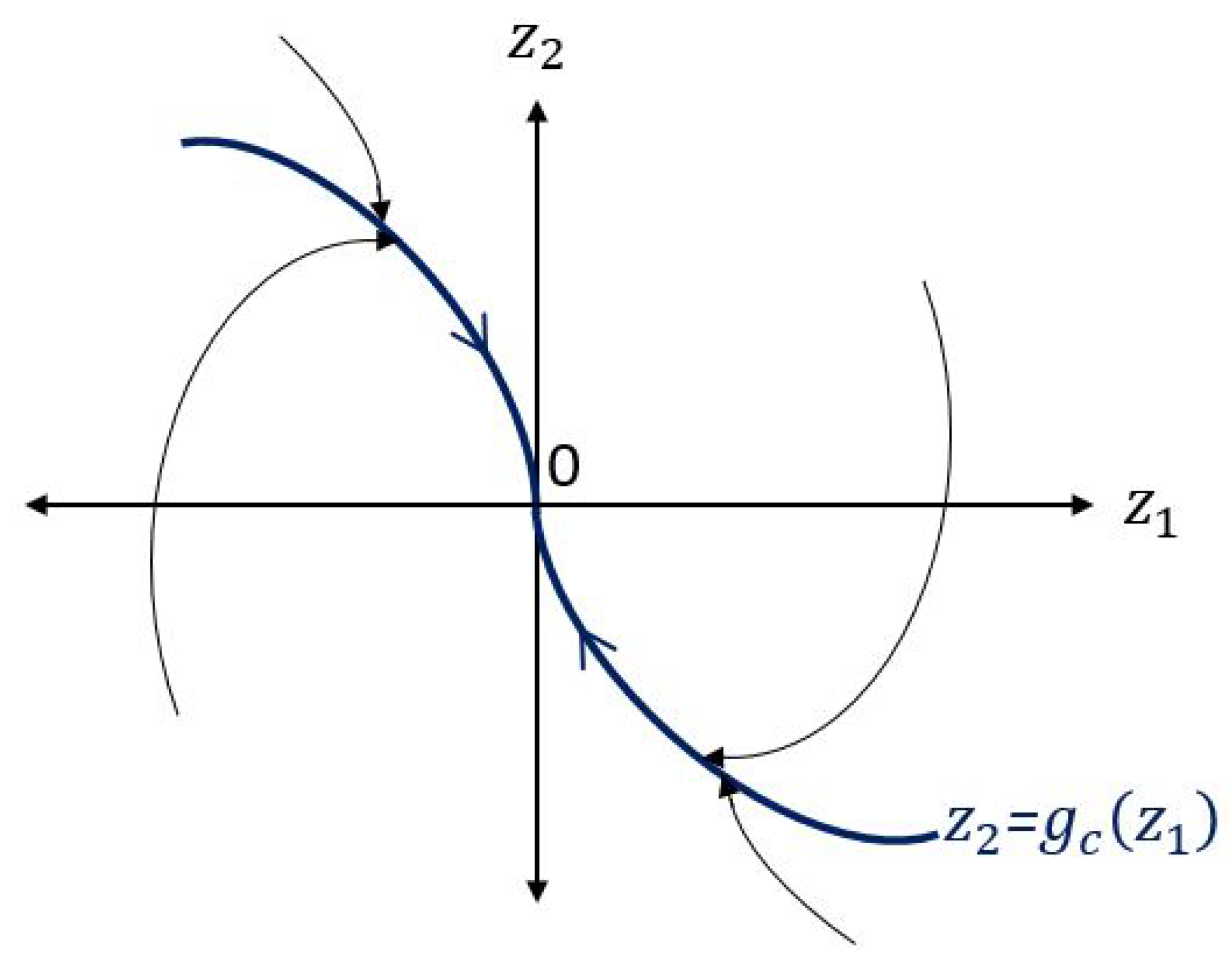
3. MPPT Control Design
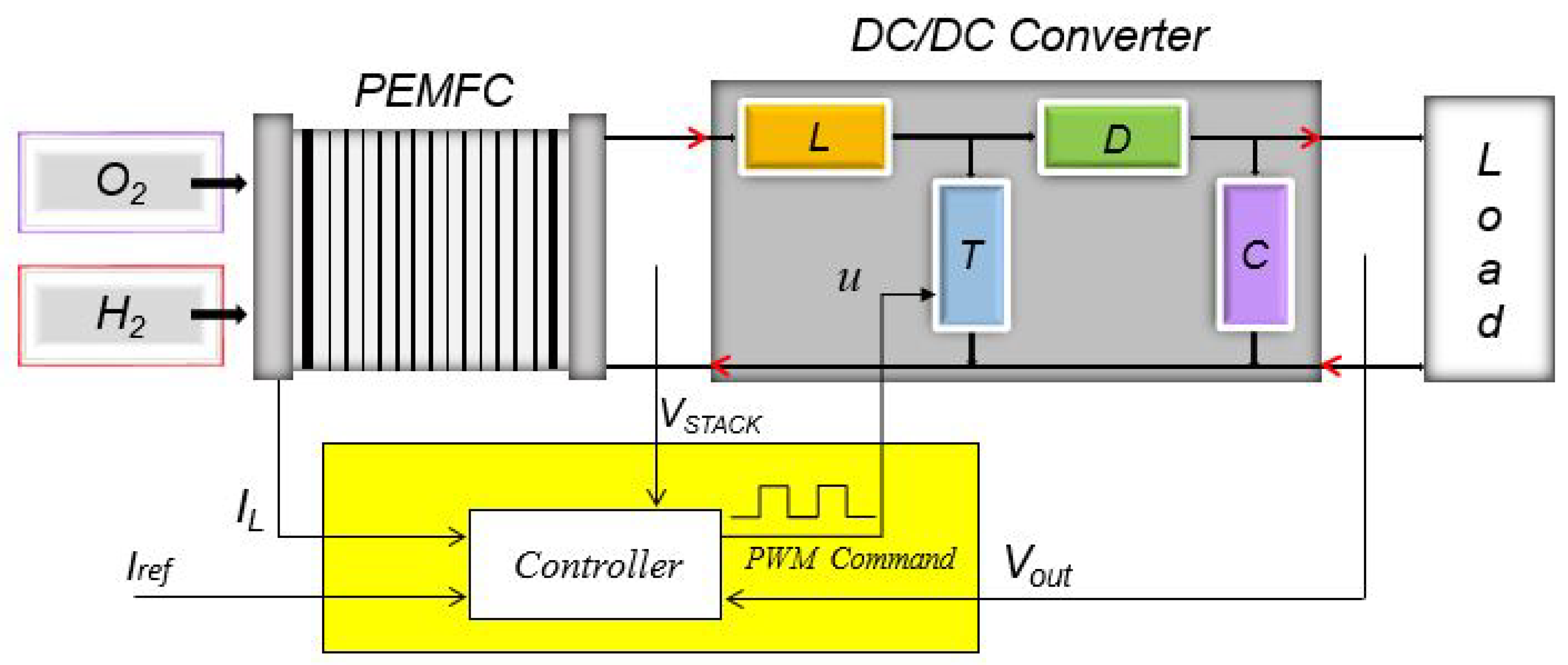
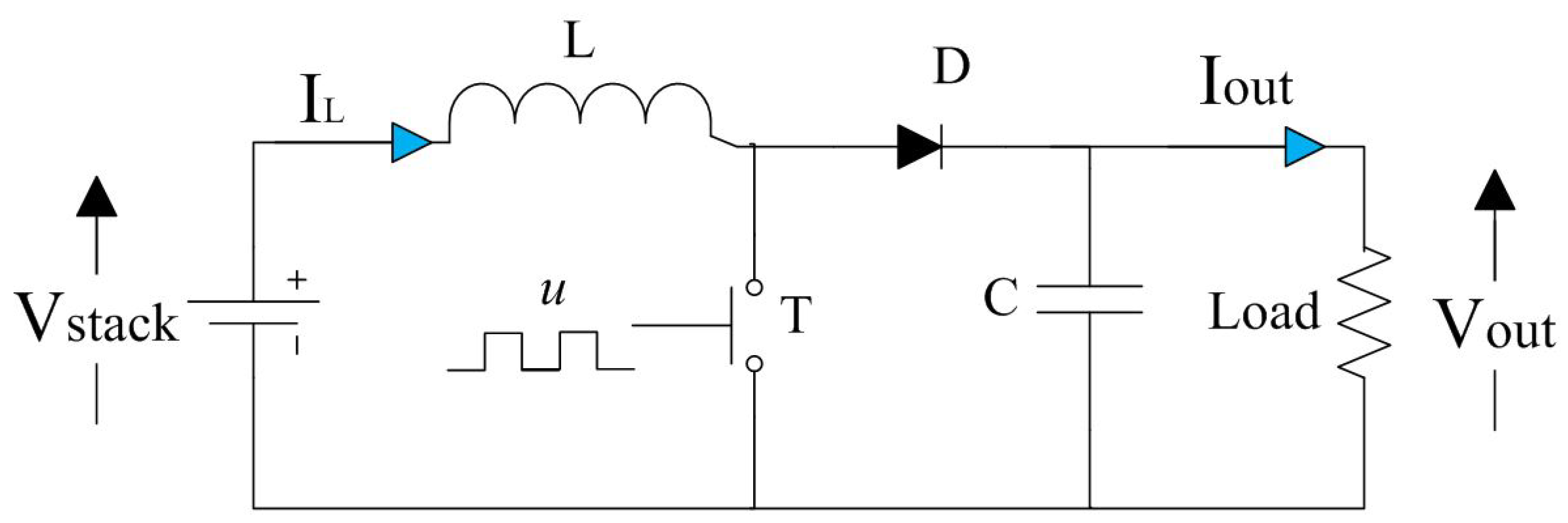
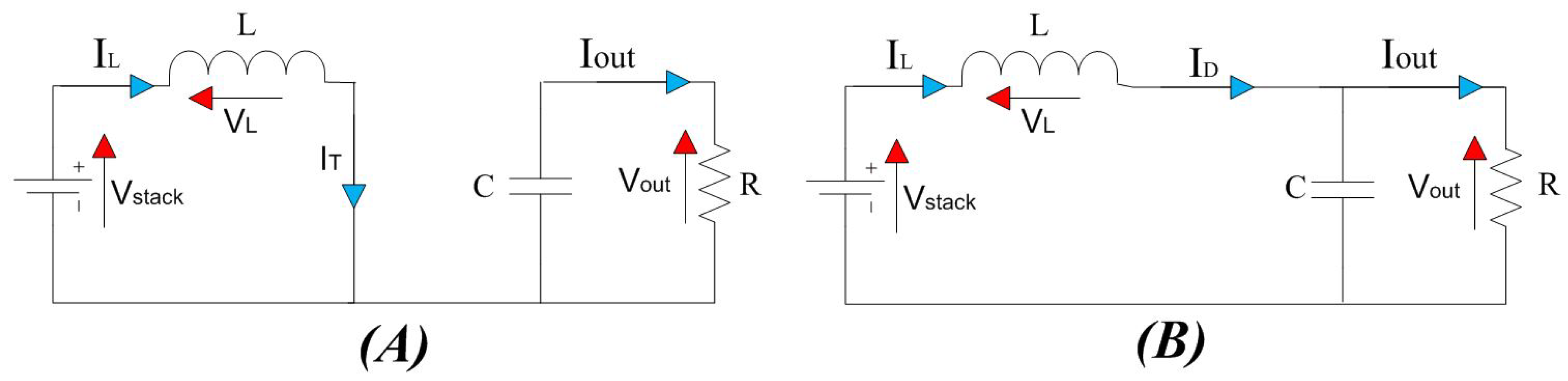
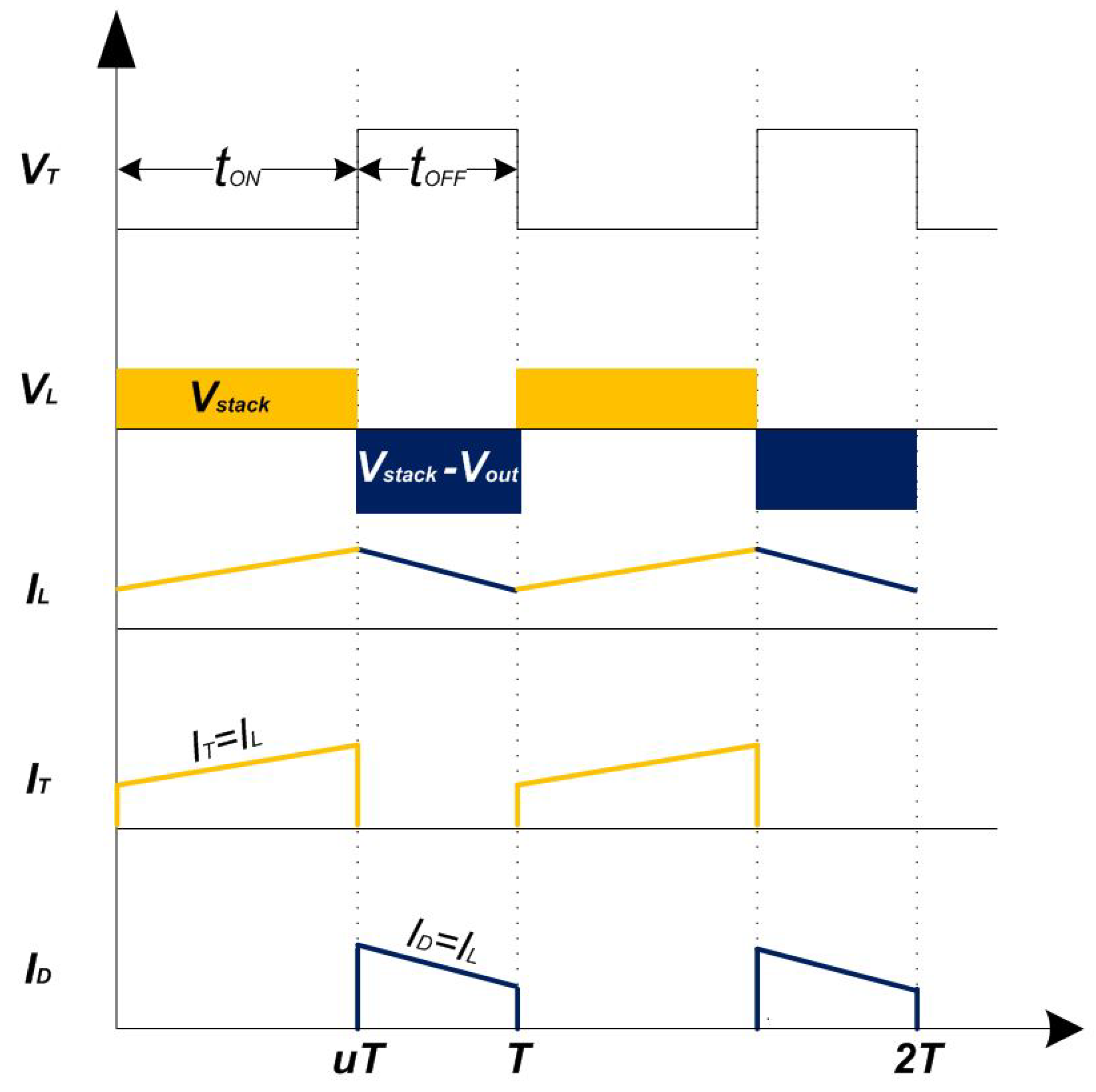
3.1. DC/DC Boost Converter
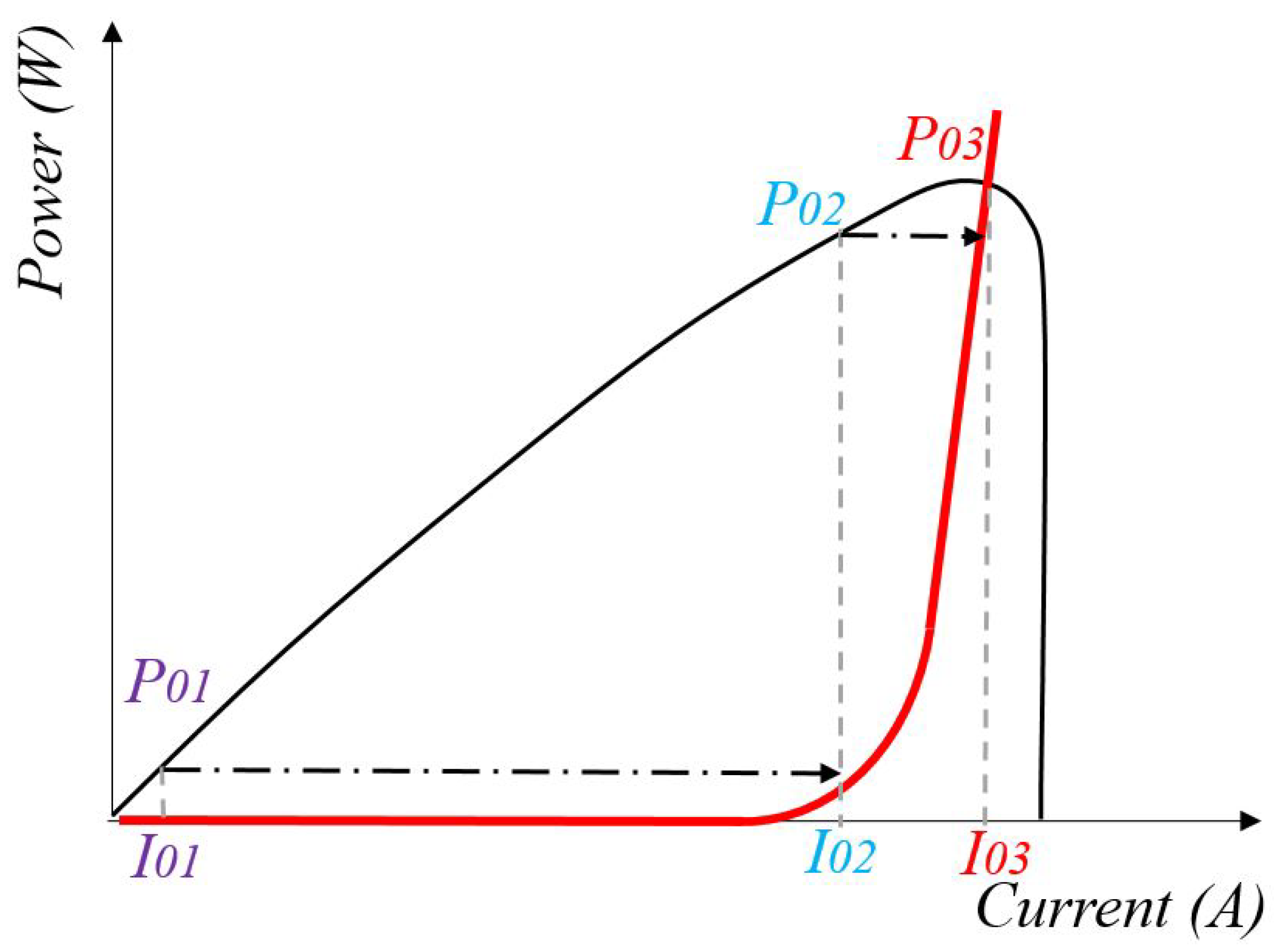
3.2. Reference Current Estimator
- Gather the data of and for each P-I polarization curve in two vectors and load this data at the MATLAB command line. The experimental data obtained from the FC-42 Evaluation Kit is enlisted in Table 1.
- Execute CFT by entering the function “sftool” or “cftool” in the Command Window.
- Select as X data, and as Y data so as to import the database. The CFT will create a default interpolation to fit the loaded data.
- Using the fit category drop-down list (Interpolant, Polynomial, Fourier, Gaussian, Weibull…), select various types and try to find the best curve by comparing the graphical and numerical fit results including fitted coefficients and the goodness of fit (GOF). Regarding to the latter mentioned, it includes the sum of squared due to error (SSE), the R-square, the adjusted R-square and the root mean squared error (RMSE); these metrics are tools that contribute to find the best curve that fits the data, for instance, a small SSE indicates a good fitting.
- Export the best fit to the Matlab workspace.
3.3. Current Regulation
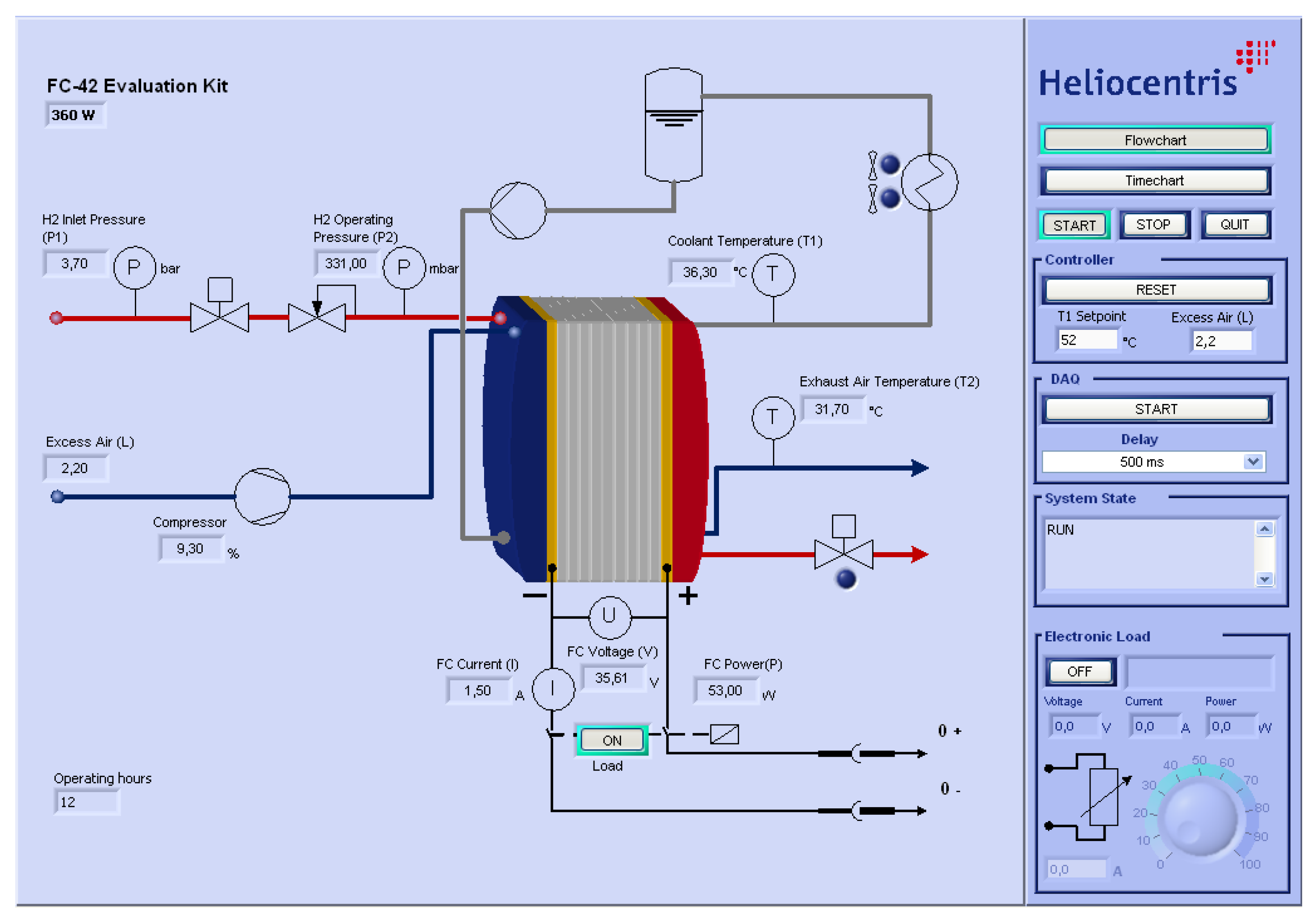
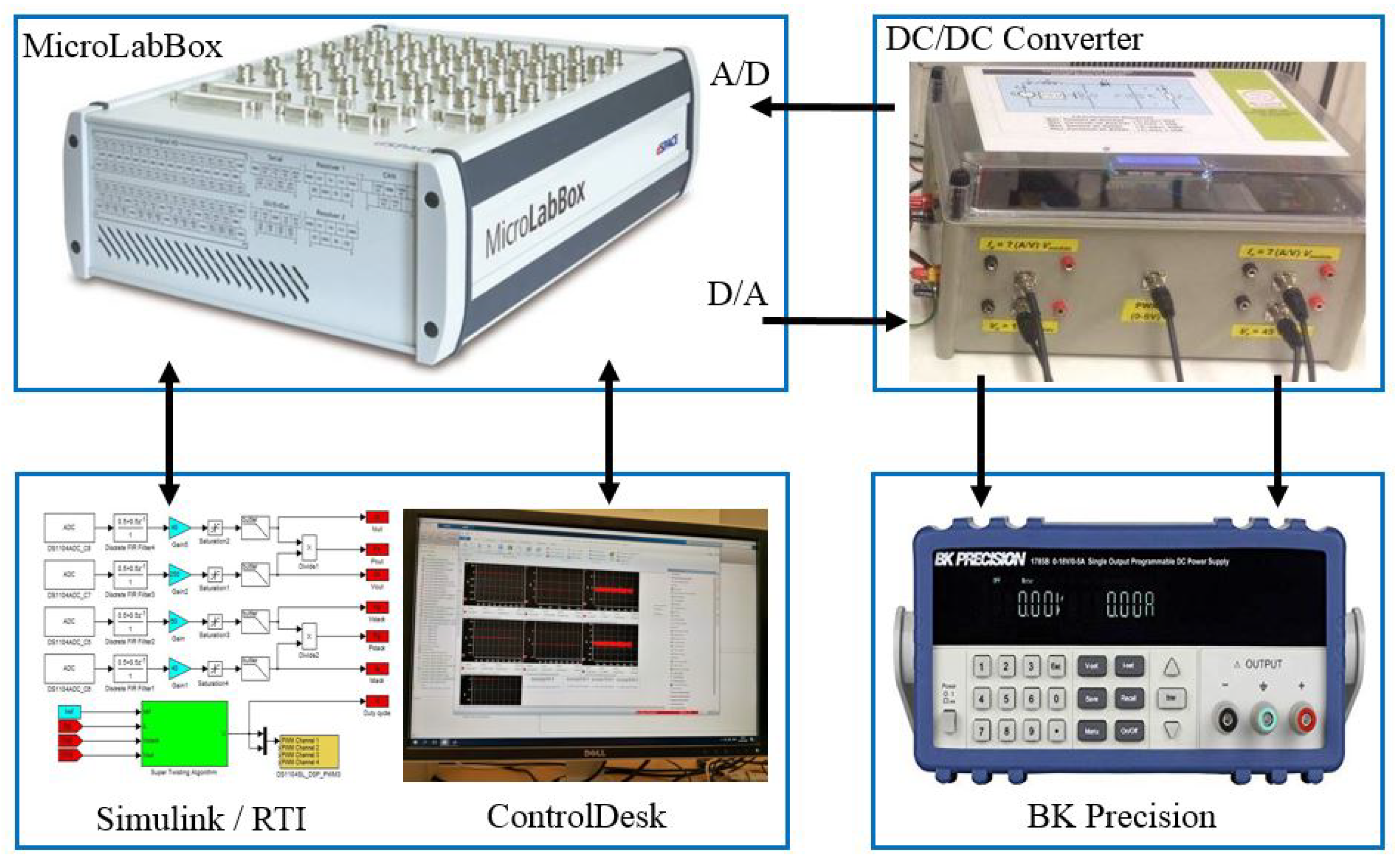
4. Description of the Experimental System
- Stack current (with an accuracy of 0.8 A)
- Stack voltage (with an accuracy of 0.1 A)
- Stack power (calculated)
- Cooling temperature (with an accuracy of )
- Exhaust air temperature (with an accuracy of )
- hydrogen inlet pressure
- hydrogen operating pressure
- Excess air (calculated)
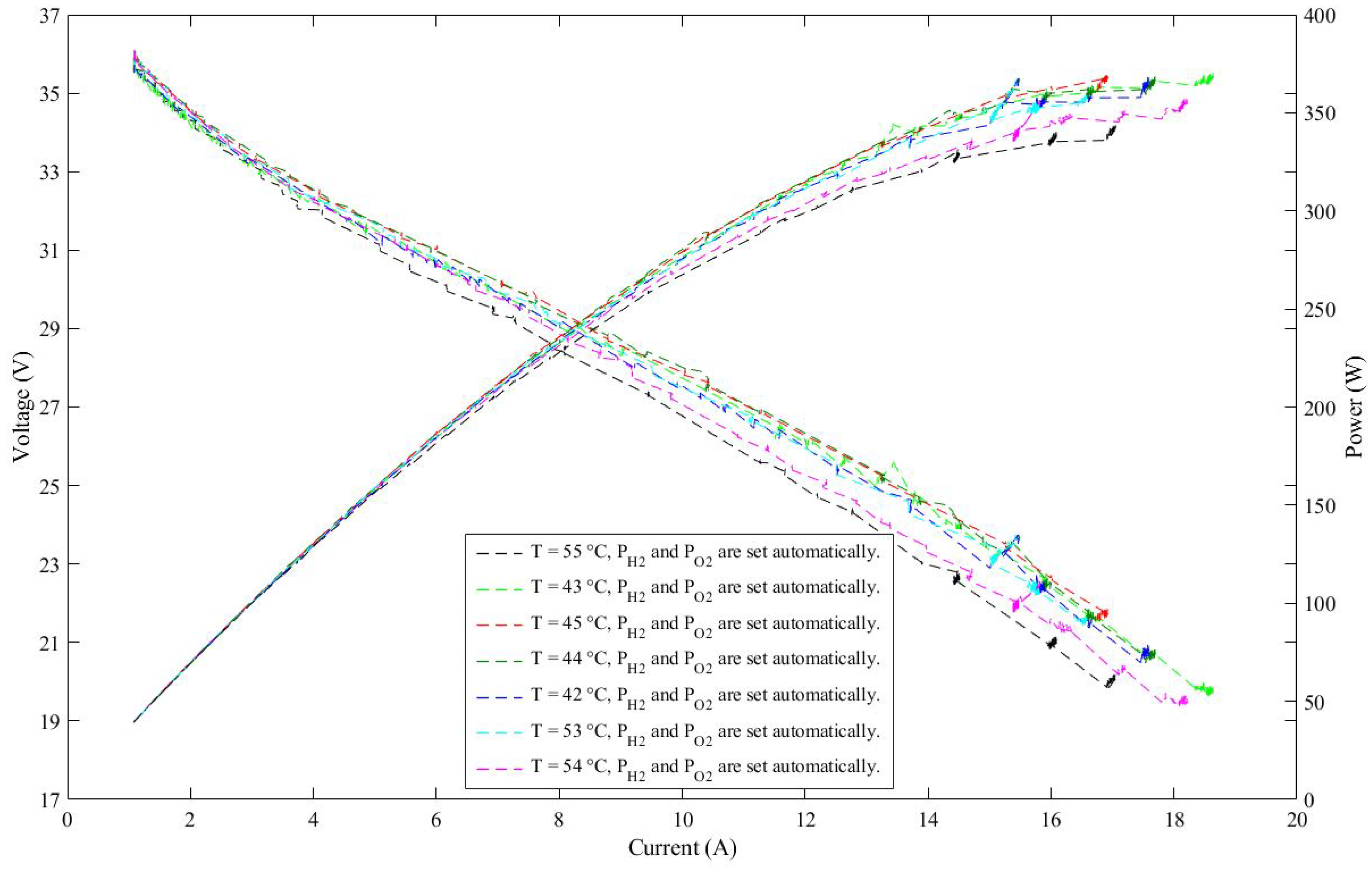
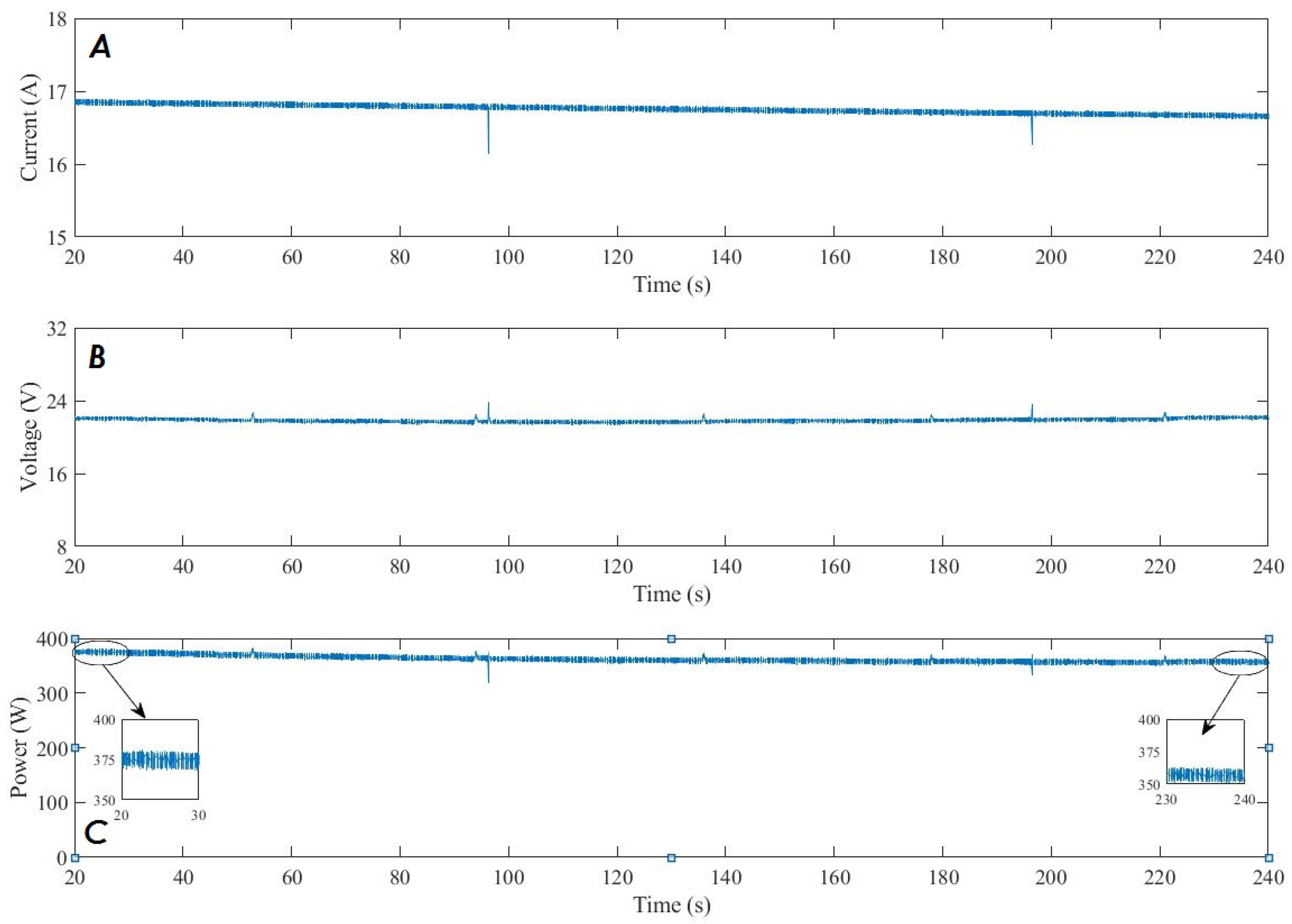
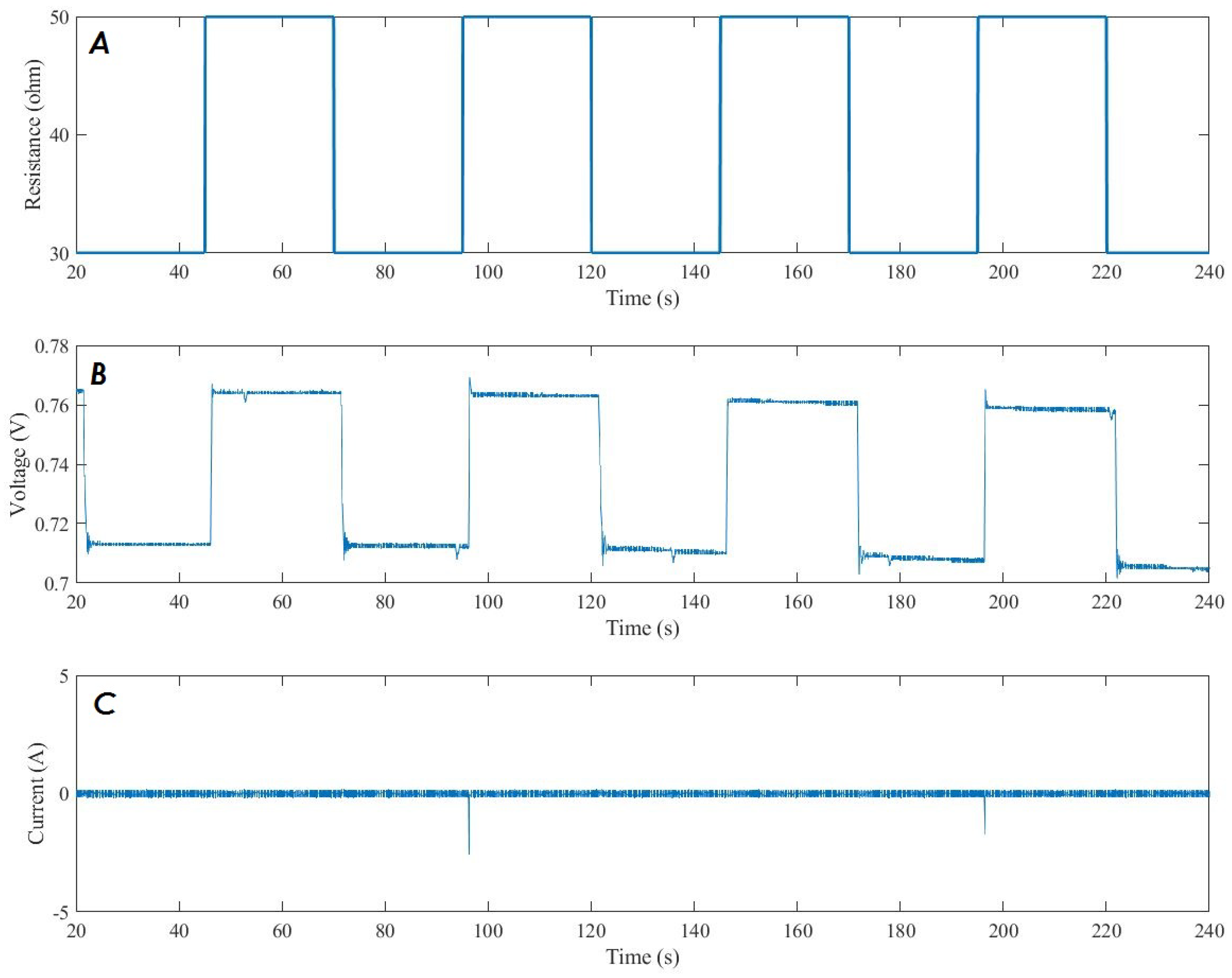
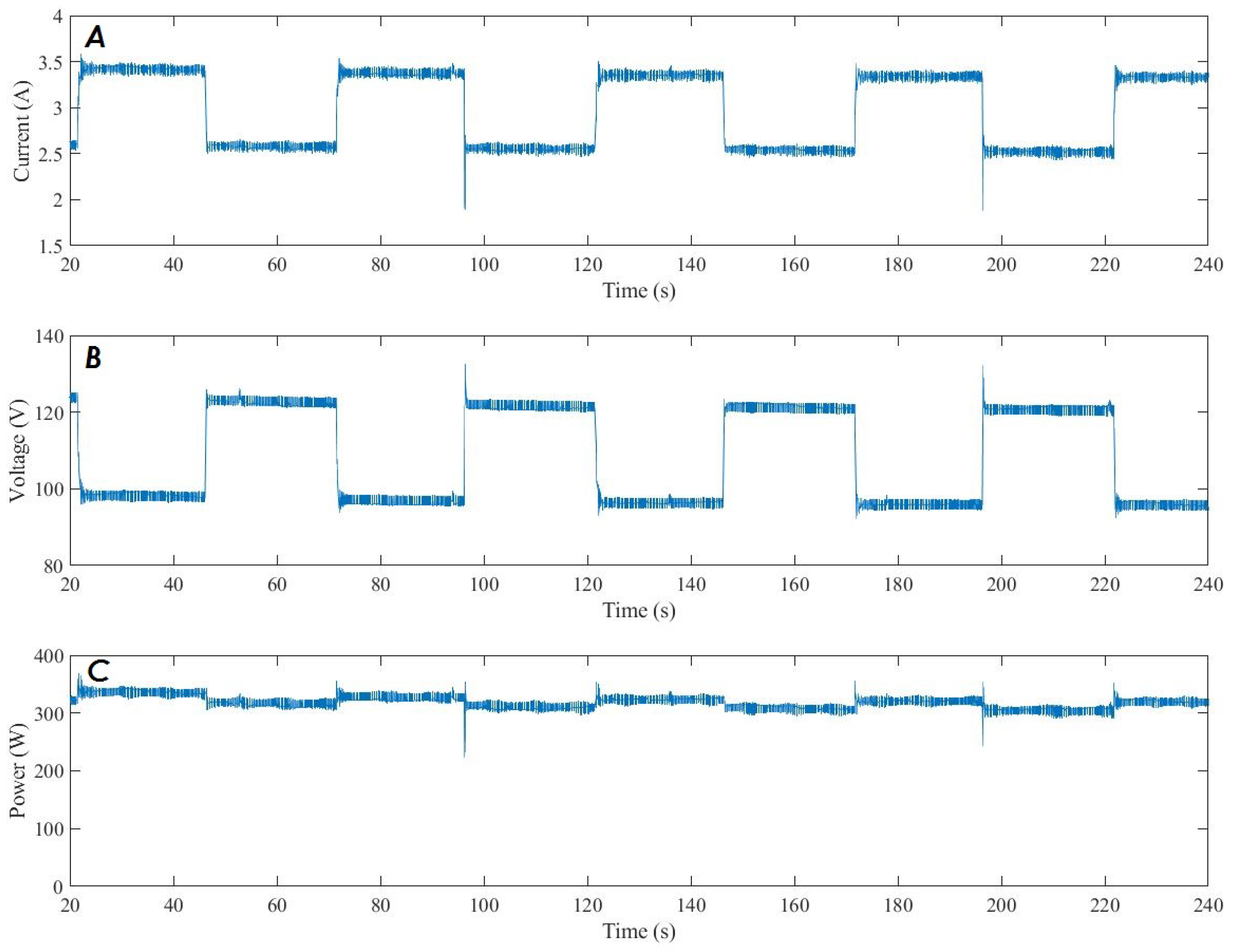
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| PEM | Proton Exchange Membrane |
| MPPT | Maximum Power Point Tracker |
| HOSM | High-order sliding mode |
| RCE | Reference Current Estimator |
| HO-PCL | High-Order Prescribed Convergence Law |
| FOCV | Fractional Open Circuit Voltage |
| HC | Hill Climbing |
| P&O | Perturb and Observation |
| IC | Incremental Conductance |
| GSS | Golden Section Search |
| NQI | Newton’s Quadratic Interpolation |
| ESC | Extremum Seeking Control |
| SMC | Sliding Mode Control |
| MPC | Model Predictive Control |
| FLC | Fuzzy Logic Control |
| BSA | Backstepping Algorithm |
| GAs | Genetic Algorithms |
| PSO | Particle Swarm Optimization |
| CS | Cuckoo Search |
| NIA | Nature-Inspired Algorithms |
| RLGA | Recurrent Learning Gradient Algorithm |
| FPA | Flower Pollination Algorithm |
| NNC | Neural Network Control |
| CPSO | Chaotic Particle Swarm Optimization |
| MPC | Model Predictive Control |
| NGMPC | Neural Generalized MPC |
| MPP | Maximum Power Point |
| PID | Proportional-Integral Derivative |
| GWO | Grey Wolf Optimizer |
| SSA | Slap Swarm Algorithm |
| GAO | Grey Antlion Optimization |
| IRA | Incremental Resistance algorithm |
| MBA | Mine Blast Algorithm |
| PI | Proportional-Integral |
| CCM | Continuous-Conduction Mode |
| DCM | Discontinuous-Conduction Mode |
| CFT | Curve Fitting Toolbox |
| GOF | Goodness Of Fit |
| SSE | Sum of Squared due to Error |
| RMSE | Root Mean Squared Error |
| RTI | Real-Time Interface |
| ADC | Analog to Digital Converter |
| PEL | programmable electronic load |
| UPV | Universidad del Pais Vasco |
| EHU | Euskal Herriko Uniberstsitatea |
References
- Charaabi, A.; Barambones, O.; Zaidi, A.; Zanzouri, N. A Novel Two Stage Controller for a DC-DC Boost Converter to Harvest Maximum Energy from the PV Power Generation. Actuators 2020, 9, 29. [Google Scholar] [CrossRef]
- Boschetto, A.; Bottini, L.; Costanza, G.; Tata, M.E. Shape Memory Activated Self-Deployable Solar Sails: Small-Scale Prototypes Manufacturing and Planarity Analysis by 3D Laser Scanner. Actuators 2019, 8, 38. [Google Scholar] [CrossRef]
- Lampreia, S.; Vairinhos, V.; Lobo, V.; Requeijo, J. A Statistical State Analysis of a Marine Gas Turbine. Actuators 2019, 8, 54. [Google Scholar] [CrossRef]
- Matuszewska, D.; Kuta, M.; Olczak, P. Techno-Economic Assessment of Mobilized Thermal Energy Storage System Using Geothermal Source in Polish Conditions. Energies 2020, 13, 3404. [Google Scholar] [CrossRef]
- Vargas, C.A.; Tinoco, H.A. Electrical Performance of a Piezo-inductive Device for Energy Harvesting with Low-Frequency Vibrations. Actuators 2019, 8, 55. [Google Scholar] [CrossRef]
- Ai, R.; Monteiro, L.L.S.; Monteiro, P.C.C., Jr.; Pacheco, P.M.C.L.; Savi, M.A. Piezoelectric Vibration-Based Energy Harvesting Enhancement Exploiting Nonsmoothness. Actuators 2019, 8, 25. [Google Scholar] [CrossRef]
- Wei, W.; Li, Q.; Xu, F.; Zhang, X.; Jin, J.; Sun, F. Research on an Electromagnetic Actuator for Vibration Suppression and Energy Regeneration. Actuators 2020, 9, 42. [Google Scholar] [CrossRef]
- Boukrich, N.; Derbeli, M.; Farhat, M.; Sbita, L. Smart auto-tuned regulators in electric vehicule PMSM drives. In Proceedings of the 2017 International Conference on Green Energy Conversion Systems (GECS), Hammamet, Tunisia, 23–25 March 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Silaa, M.Y.; Derbeli, M.; Barambones, O.; Cheknane, A. Design and Implementation of High Order Sliding Mode Control for PEMFC Power System. Energies 2020, 13, 4317. [Google Scholar] [CrossRef]
- Derbeli, M.; Barambones, O.; Sbita, L. A Robust Maximum Power Point Tracking Control Method for a PEM Fuel Cell Power System. Appl. Sci. 2018, 8, 2449. [Google Scholar] [CrossRef]
- Yaacoubi, S.; McKeon, P.; Ke, W.; Declercq, N.F.; Dahmene, F. Towards an Ultrasonic Guided Wave Procedure for Health Monitoring of Composite Vessels: Application to Hydrogen-Powered Aircraft. Materials 2017, 10, 1097. [Google Scholar] [CrossRef]
- Mohamed, A.-A.A.; Ali, S.; Alkhalaf, S.; Senjyu, T.; Hemeida, A.M. Optimal Allocation of Hybrid Renewable Energy System by Multi-Objective Water Cycle Algorithm. Sustainability 2019, 11, 6550. [Google Scholar] [CrossRef]
- Atawi, I.E.; Kassem, A.M.; Zaid, S.A. Modeling, Management, and Control of an Autonomous Wind/Fuel Cell Micro-Grid System. Processes 2019, 7, 85. [Google Scholar] [CrossRef]
- Derbeli, M.; Barambones, O.; Farhat, M.; Ramos, J.A.; Sbita, L. Robust high order sliding mode control for performance improvement of PEM fuel cell power systems. Int. J. Hydrogen Energy 2020. [Google Scholar] [CrossRef]
- Wilberforce, T.; Alaswad, A.; Palumbo, A.; Dassisti, M.; Olabi, A.G. Advances in stationary and portable fuel cell applications. Int. J. Hydrogen Energy 2016, 41, 16509–16522. [Google Scholar] [CrossRef]
- Boulmrharj, S.; Khaidar, M.; Bakhouya, M.; Ouladsine, R.; Siniti, M.; Zine-dine, K. Performance Assessment of a Hybrid System with Hydrogen Storage and Fuel Cell for Cogeneration in Buildings. Sustainability 2020, 12, 4832. [Google Scholar] [CrossRef]
- Bass, P.S.; Zhang, L.; Tu, M.; Cheng, Z. Enhancement of Biodegradable Poly(Ethylene Oxide) Ionic–Polymer Metallic Composite Actuators with Nanocrystalline Cellulose Fillers. Actuators 2018, 7, 72. [Google Scholar] [CrossRef]
- Kweon, B.C.; Sohn, J.S.; Ryu, Y.; Cha, S.W. Energy Harvesting of Ionic Polymer-Metal Composites Based on Microcellular Foamed Nafion in Aqueous Environment. Actuators 2019, 9, 71. [Google Scholar] [CrossRef]
- Torki, W.; Derbeli, M. Modeling and control of a stand-alone PEMFC for AC load-PMSM application. In Proceedings of the 2017 International Conference on Green Energy Conversion Systems (GECS), Hammamet, Tunisia, 23–25 March 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Derbeli, M.; Mrad, I.; Sbita, L.; Barambones, O. PEM fuel cell efficiency boosting—Robust MPP tracking. In Proceedings of the 2018 9th International Renewable Energy Congress (IREC), Hammamet, Tunisia, 20–22 March 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Lin, C.-L.; Hung, H.-C.; Li, J.-C. Active Control of Regenerative Brake for Electric Vehicles. Actuators 2018, 7, 84. [Google Scholar] [CrossRef]
- Chen, E.-P.; Cheng, J.; Tu, J.-H.; Lin, C.-L. Sensorless Driving/Braking Control for Electric Vehicles. Actuators 2020, 9, 22. [Google Scholar] [CrossRef]
- Lund, S.H.J.; Billeschou, P.; Larsen, L.B. High-Bandwidth Active Impedance Control of the Proprioceptive Actuator Design in Dynamic Compliant Robotics. Actuators 2019, 8, 71. [Google Scholar] [CrossRef]
- Ko, J.-S.; Huh, J.-H.; Kim, J.-C. Overview of Maximum Power Point Tracking Methods for PV System in Micro Grid. Electronics 2020, 9, 816. [Google Scholar] [CrossRef]
- Pathy, S.; Subramani, C.; Sridhar, R.; Thamizh Thentral, T.M.; Padmanaban, S. Nature-Inspired MPPT Algorithms for Partially Shaded PV Systems: A Comparative Study. Energies 2019, 12, 1451. [Google Scholar] [CrossRef]
- Kim, J.-C.; Huh, J.-H.; Ko, J.-S. Optimization Design and Test Bed of Fuzzy Control Rule Base for PV System MPPT in Micro Grid. Sustainability 2020, 12, 3763. [Google Scholar] [CrossRef]
- Rezk, H.; Fathy, A. Performance Improvement of PEM Fuel Cell Using Variable Step-Size Incremental Resistance MPPT Technique. Sustainability 2020, 12, 5601. [Google Scholar] [CrossRef]
- Andrean, V.; Chang, P.C.; Lian, K.L. A Review and New Problems Discovery of Four Simple Decentralized Maximum Power Point Tracking Algorithms—Perturb and Observe, Incremental Conductance, Golden Section Search, and Newton’s Quadratic Interpolation. Energies 2018, 11, 2966. [Google Scholar] [CrossRef]
- Mahmod Mohammad, A.N.; Mohd Radzi, M.A.; Azis, N.; Shafie, S.; Atiqi Mohd Zainuri, M.A. A Novel Hybrid Approach for Maximizing the Extracted Photovoltaic Power under Complex Partial Shading Conditions. Sustainability 2020, 12, 5786. [Google Scholar] [CrossRef]
- Ahmed, M.; Abdelrahem, M.; Kennel, R. Highly Efficient and Robust Grid Connected Photovoltaic System Based Model Predictive Control with Kalman Filtering Capability. Sustainability 2020, 12, 4542. [Google Scholar] [CrossRef]
- Hadji, S.; Gaubert, J.-P.; Krim, F. Real-Time Genetic Algorithms-Based MPPT: Study and Comparison (Theoretical an Experimental) with Conventional Methods. Energies 2018, 11, 459. [Google Scholar] [CrossRef]
- Basha, C.H.; Rani, C. Different Conventional and Soft Computing MPPT Techniques for Solar PV Systems with High Step-Up Boost Converters: A Comprehensive Analysis. Energies 2020, 13, 371. [Google Scholar] [CrossRef]
- Viloria-Porto, J.; Robles-Algarín, C.; Restrepo-Leal, D. A Novel Approach for an MPPT Controller Based on the ADALINE Network Trained with the RTRL Algorithm. Energies 2018, 11, 3407. [Google Scholar] [CrossRef]
- Yousri, D.; Babu, T.S.; Allam, D.; Ramachandaramurthy, V.K.; Beshr, E.; Eteiba, M.B. Fractional Chaos Maps with Flower Pollination Algorithm for Partial Shading Mitigation of Photovoltaic Systems. Energies 2019, 12, 3548. [Google Scholar] [CrossRef]
- Derbeli, M.; Sbita, L.; Farhat, M.; Barambones, O. Proton exchange membrane fuel cell—A smart drive algorithm. In Proceedings of the 2017 International Conference on Green Energy Conversion Systems (GECS), Hammamet, Tunisia, 23–25 March 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Harrag, A.; Messalti, S. How fuzzy logic can improve PEM fuel cell MPPT performances? Int. J. Hydrogen Energy 2018, 43, 537–550. [Google Scholar] [CrossRef]
- Derbeli, M.; Barambones, O.; Farhat, M.; Sbita, L. Efficiency Boosting for Proton Exchange Membrane Fuel Cell Power System Using New MPPT Method. In Proceedings of the 10th International Renewable Energy Congress (IREC), Sousse, Tunisia, 26–28 March 2019; pp. 1–4. [Google Scholar] [CrossRef]
- Derbeli, M.; Charaabi, A.; Barambones, O.; Sbita, L. Optimal Energy Control of a PEM Fuel Cell/Battery Storage System. In Proceedings of the 10th International Renewable Energy Congress (IREC), Sousse, Tunisia, 26–28 March 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Reddy, K.J.; Sudhakar, N. High voltage gain interleaved boost converter with neural network based MPPT controller for fuel cell based electric vehicle applications. IEEE Access 2018, 6, 3899–3908. [Google Scholar] [CrossRef]
- Al-Araji, A.S.; Dhahad, H.A.; Jaber, E.A. A Neural Networks based Predictive Voltage-Tracking Controller Design for Proton Exchange Membrane Fuel Cell Model. J. Eng. 2019, 25, 26–48. [Google Scholar] [CrossRef]
- Pereira, D.F.; da Costa Lopes, F.; Watanabe, E.H. Neural Generalized Predictive Control for Tracking Maximum Efficiency and Maximum Power Points of PEM Fuel Cell Stacks. In Proceedings of the IECON 2018 44th Annual Conference of the IEEE Industrial Electronics Society, Washington, DC, USA, 21–23 October 2018; pp. 1878–1883. [Google Scholar] [CrossRef]
- Luta, D.N.; Raji, A.K. Fuzzy rule-based and particle swarm optimisation MPPT techniques for a fuel cell stack. Energies 2019, 12, 936. [Google Scholar] [CrossRef]
- Harrag, A.; Bahri, H. A Novel Single Sensor Variable Step Size Maximum Power Point Tracking for Proton Exchange Membrane Fuel Cell Power System. Fuel Cells 2019, 19, 177–189. [Google Scholar] [CrossRef]
- Bizon, N.; Thounthong, P. Energy efficiency and fuel economy of a fuel cell/renewable energy sources hybrid power system with the load-following control of the fueling regulators. Mathematics 2020, 8, 151. [Google Scholar] [CrossRef]
- Rana, K.P.S.; Kumar, V.; Sehgal, N.; George, S. A Novel dPdI feedback based control scheme using GWO tuned PID controller for efficient MPPT of PEM fuel cell. ISA Trans. 2019, 93, 312–324. [Google Scholar] [CrossRef]
- Fathy, A.; Abdelkareem, M.A.; Olabi, A.G.; Rezk, H. A novel strategy based on salp swarm algorithm for extracting the maximum power of proton exchange membrane fuel cell. Int. J. Hydrogen Energy 2020, 8, 2449. [Google Scholar] [CrossRef]
- Derbeli, M.; Farhat, M.; Barambones, O.; Sbita, L. A robust MPP tracker based on backstepping algorithm for Proton Exchange Membrane Fuel Cell power system. In Proceedings of the 2017 11th IEEE International Conference on Compatibility, Power Electronics and Power Engineering (CPE-POWERENG), Cadiz, Spain, 4–6 April 2017; pp. 424–429. [Google Scholar] [CrossRef]
- Derbeli, M.; Barambones, O.; Ramos-Hernanz, J.A.; Sbita, L. Real-Time Implementation of a Super Twisting Algorithm for PEM Fuel Cell Power System. Energies 2019, 12, 1594. [Google Scholar] [CrossRef]
- Derbeli, M.; Farhat, M.; Barambones, O.; Sbita, L. Control of Proton Exchange Membrane Fuel Cell (PEMFC) power system using PI controller. In Proceedings of the 2017 International Conference on Green Energy Conversion Systems (GECS), Hammamet, Tunisia, 23–25 March 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Derbeli, M.; Sbita, L.; Farhat, M.; Barambones, O. PEM fuel cell green energy generation—SMC efficiency optimization. In Proceedings of the 2017 International Conference on Green Energy Conversion Systems (GECS), Hammamet, Tunisia, 23–25 March 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Amphlett, J.C.; Baumert, R.M.; Mann, R.F.; Peppley, B.A.; Roberge, P.R.; Harris, T.J. Performance modeling of the Ballard Mark IV solid polymer electrolyte fuel cell II. Empirical model development. J. Electrochem. Soc. 1995, 142, 9. [Google Scholar] [CrossRef]
- Kim, J.; Lee, S.M.; Srinivasan, S.; Chamberlin, C.E. Modeling of proton exchange membrane fuel cell performance with an empirical equation. J. Electrochem. Soc. 1995, 142, 2670. [Google Scholar] [CrossRef]
- Derbeli, M.; Farhat, M.; Barambones, O.; Sbita, L. Control of PEM fuel cell power system using sliding mode and super-twisting algorithms. Int. J. Hydrogen Energy 2017, 42, 8833–8844. [Google Scholar] [CrossRef]
- Davoudi, A.; Jatskevich, J.; De Rybel, T. Numerical state-space average-value modeling of PWM DC-DC converters operating in DCM and CCM. IEEE Trans. Power Electron. 2006, 21, 1003–1012. [Google Scholar] [CrossRef]
- Amir, S.; van der Zee, R.; Nauta, B. An improved modeling and analysis technique for peak current-mode control-based boost converters. IEEE Trans. Power Electron. 2014, 30, 5309–5317. [Google Scholar] [CrossRef]
- Kazimierczuk, M.K. Pulse-Width Modulated DC-DC Power Converters; John Wiley & Sons: Hoboken, NJ, USA, 2015; p. 960. [Google Scholar]
- Suntio, T. Average and small-signal modeling of self-oscillating flyback converter with applied switching delay. IEEE Trans. Power Electron. 2006, 21, 479–486. [Google Scholar] [CrossRef]
- Cheng, C.H.; Chen, C.J.; Wang, S.S. Small-signal model of flyback converter in continuous-conduction mode with peak-current control at variable switching frequency. IEEE Trans. Power Electron. 2017, 33, 4145–4156. [Google Scholar] [CrossRef]
- Luchetta, A.; Manetti, S.; Piccirilli, M.C.; Reatti, A.; Kazimierczuk, M.K. Comparison of DCM operated PWM DC-DC converter modelling methods including the effects of parasitic components on duty ratio constraint. In Proceedings of the 2015 IEEE 15th International Conference on Environment and Electrical Engineering (EEEIC), Rome, Italy, 10–13 June 2015; pp. 766–771. [Google Scholar] [CrossRef]
- Fridman, L.; Levant, A. High-Order Sliding Modes Sliding Modes Control in Engineering; Perruquetti, W., Barbot, J.P., Eds.; Marcel Dekker: New York, NY, USA, 2002. [Google Scholar]
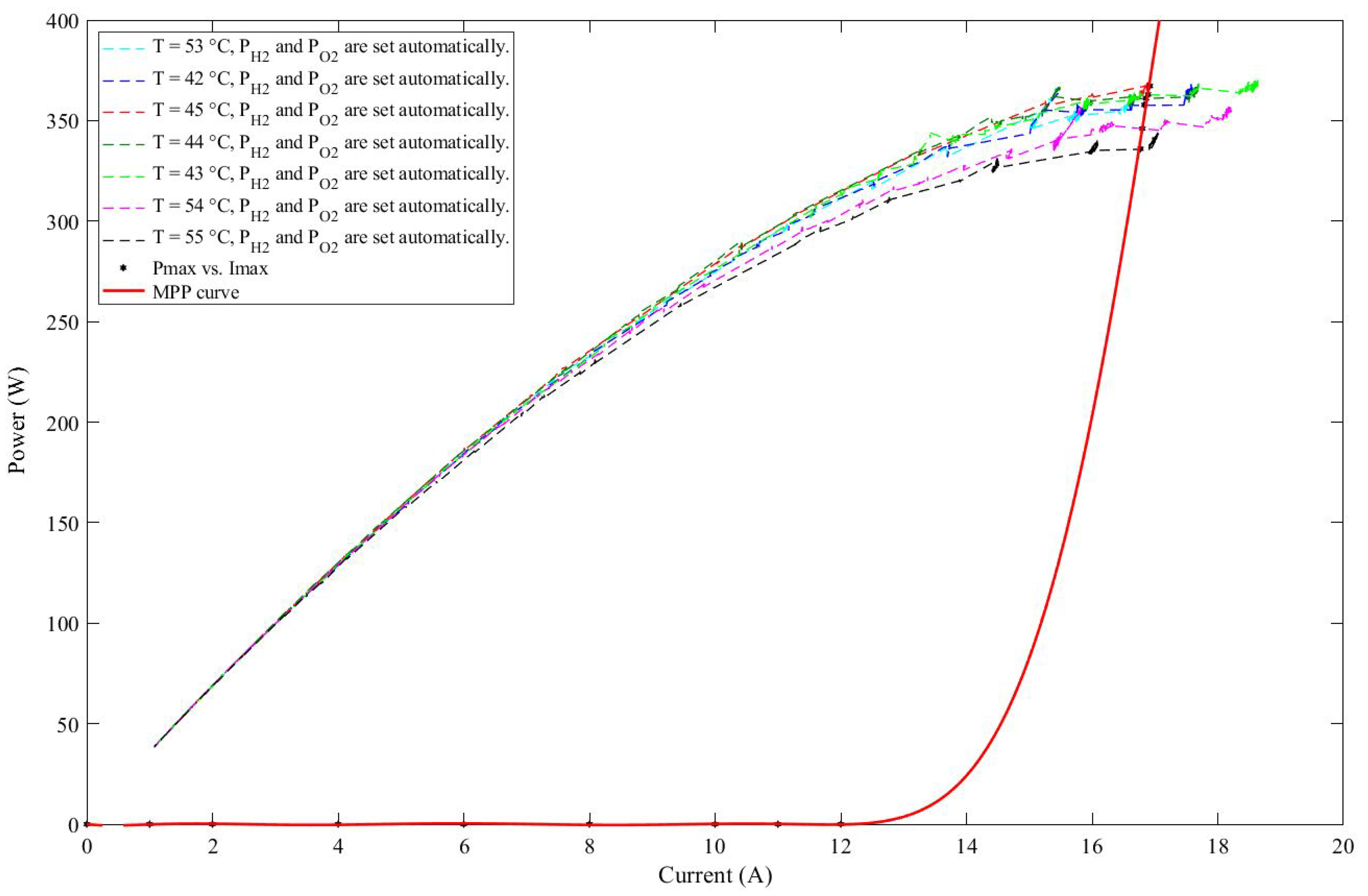

| Pmax | 363 | 361 | 336 | 346 | |||
| Imax |
| Goodness of the fit | ||||
| SSE: | R-square: | Adjusted R-square: | RMSE: | |
| Coefficients with 95% confidence bounds | ||||
| General Properties | Electrical Properties | ||
| Type | FC-42/HLC (42 cells) | Operating voltage | 20–45 V |
| Cooling | Liquid (drinking water) | Open-circuit voltage | 36–42 V |
| Fuel | Hydrogen | Nominal stack voltage | 24 V |
| Service life | >1500 h | Booster voltage | 12 V (11–14 V) |
| W× D× H (mm) | 168 × 230 × 115 | Operating current | 0–30 A |
| Total weight | 17.1 kg | Nominal stack current | 15 A |
| Starting time | 2 min | Nominal stack power | 360 W |
| Noise | Max 65 dB | Power consumption | 70 W |
| Thermal Properties | Fuel Properties | ||
| Max. temperature of the surface | 60 | inlet pressure | 1–11 bar |
| Exhaust air temperature | 10–60 | operating pressure | 50–360 mbar |
| Ambient temperature | 10–30 | Purity of | 99.99% |
| Coolant temperature | 10–57 | Consumption | 0–4 L/min |
| Cooling capacity | 400 W @ 25 | Air volume flow rate | 65 L/min |
| Coolant volume flow rate | 240 L/h | Air pressure | 400 mbar |
| Coolant pressure | 320 mbar | Excess air | 1.50–4.00 |
| Parameter | Description |
|---|---|
| Switching frequency | 20 KHz |
| Schottky diode | 2MURF1560 GT, 0.4 V, 10 A, 600 V, 15 A/150 |
| Capacitances | 2TK Series, = 1500 and = 3000 |
| Inductance | 6PCV2-564-08 94 H, 7 A, 42 m |
| IGBT | 1HGT40N60B3, 600 V, 40 A, 1.5 V, 150 |
| Maximum input values | = 60 V, = 30 A |
| Maximum output values | = 250 V, = 30 A |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Derbeli, M.; Barambones, O.; Silaa, M.Y.; Napole, C. Real-Time Implementation of a New MPPT Control Method for a DC-DC Boost Converter Used in a PEM Fuel Cell Power System. Actuators 2020, 9, 105. https://doi.org/10.3390/act9040105
Derbeli M, Barambones O, Silaa MY, Napole C. Real-Time Implementation of a New MPPT Control Method for a DC-DC Boost Converter Used in a PEM Fuel Cell Power System. Actuators. 2020; 9(4):105. https://doi.org/10.3390/act9040105
Chicago/Turabian StyleDerbeli, Mohamed, Oscar Barambones, Mohammed Yousri Silaa, and Cristian Napole. 2020. "Real-Time Implementation of a New MPPT Control Method for a DC-DC Boost Converter Used in a PEM Fuel Cell Power System" Actuators 9, no. 4: 105. https://doi.org/10.3390/act9040105
APA StyleDerbeli, M., Barambones, O., Silaa, M. Y., & Napole, C. (2020). Real-Time Implementation of a New MPPT Control Method for a DC-DC Boost Converter Used in a PEM Fuel Cell Power System. Actuators, 9(4), 105. https://doi.org/10.3390/act9040105






