1. Introduction
Creating nature-like compliant and autonomous robots has been one of the main aims of robotics. A combination of compliance and self-awareness in robots may allow for proper human–robot interaction, required for co-working with people. The ability of such robots to optimally interact with their environment and humans depends to a large extent on their embodiment, namely the morphology and the materials comprising them [
1]. In the past decade, soft robotics research has been focused both on the morphological aspect—namely the design of soft robots, soft sensing and actuation—and on the development of advanced materials for providing compliance and resilience [
2,
3]. In the soft actuation domain only, more than half of the recent research papers involve material development [
4]. The materials used in soft actuation are mostly based on various types of polymers and their composites, responsive to one or several stimuli. Among others, these materials comprise dielectric elastomer actuators [
5], ionic polymer–metal composite actuators [
6], hydrogel actuators [
7], liquid crystal elastomer (LCE) and LCE-composite actuators [
8], and shape memory polymers (SMP) and SMP-composite actuators [
9].
In their matrix-filler combinations, composite material actuators, on the one hand, intertwine stimulus-responsiveness with mechanical robustness or additional physical properties; on the other hand, they require compatibility with each other and sometimes limit the final actuator properties. For instance, LCE composites typically include rigid filler particles providing the LCE matrix with electrical and thermal conductivity, but limiting their shape-morphing capabilities. To address this problem, Ford et al. have recently replaced rigid fillers with deformable liquid metal inclusions, forming novel compliant LCE/liquid metal composite actuators [
10]. Lipton et al. have added a paraffin wax filler to a silicone rubber matrix to allow for shape expansion caused by paraffin’s solid–liquid phase transition upon heating [
11]. The silicone/paraffin composite has shown significant actuation force, while the actuation strain remained below 5%.
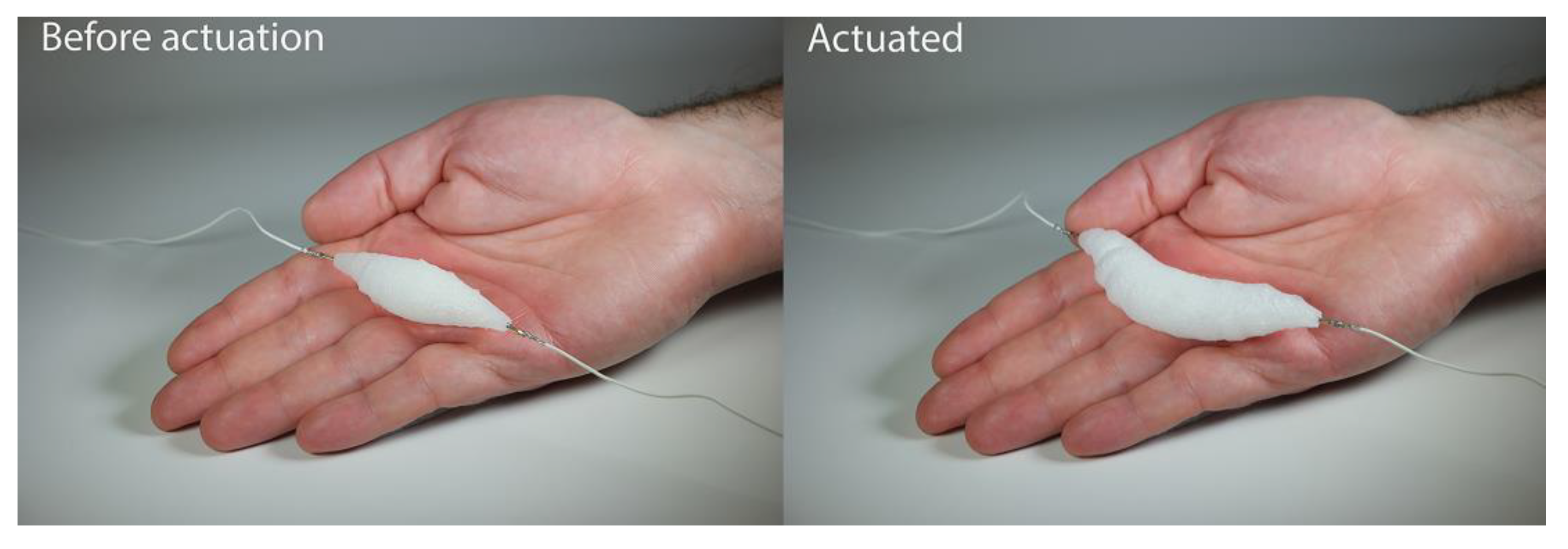
To overcome this limitation, Miriyev et al. utilized the liquid–vapor phase transition of ethanol, distributed throughout a silicone rubber matrix in micron-scale pores (
Figure 1) [
12]. Upon heating to the boiling point of ethanol (78.32 °C), the composite would volumetrically expand up to 900%. The 3D-printable silicone/ethanol composite material [
13] combined both high actuation stress and very high actuation strain, which was applied to creating soft-bodied locomotion, gripping, and soft artificial muscle.
Silicone/ethanol artificial muscle was reported to lift weight corresponding to >1000 times that of its own and was capable of multi-cyclic actuation. However, prolonged actuation by Joule heating negatively affects the performance due to the escape of ethanol and temperature build-up in the actuator [
14]. A method of rejuvenating the artificial muscle by dipping it in ethanol was developed [
15]. Although this method allowed the restoration of most of the material-actuator/muscle functionality, prolonged actuation by Joule heating using Ni-Cr alloy spiral irreversibly damaged the silicone matrix, leading to the degradation of the composite structure. Alternative Joule heaters based on silicone/expanded intercalated graphite composites [
16] and conductive fabric heaters with kirigami design [
17] have been developed to allow better heat distribution.
As the actuation of the silicone/ethanol composite is achieved by heating, the heat distribution aspect has a significant effect on the actuator speed, durability, and reliability. The typical actuation/de-actuation cycle for thermally-driven actuators is relatively long, resulting in low actuation frequency [
18]. For silicone/ethanol actuators, the actuation/de-actuation cycle lasts for roughly 120–400 s, depending on the actuation power, the heater type, and the actuator size. Silicone rubber has a low thermal conductivity (typically, <0.2 W/mK), thus during actuation the areas closer to the heater (for example, the Ni-Cr wire) are heated much faster than other areas, resulting in non-uniform heating. Various fillers were reported to increase the thermal conductivity of silicones. Zhou et al. [
19] reported that adding 40 vol.% boron nitride powder to silicone rubber, on the one hand, increased the thermal conductivity of the material to 0.8–1 W/mK (for various particle sizes). On the other hand, it decreased the maximal strain. Xue et al. [
20] processed methyl vinyl silicone rubber with vertically-aligned boron nitride powder to achieve high through-plane thermal conductivity. The authors reported thermal conductivity of 5.4 W/mK for 40 vol.% filler concentration. Adding 50 vol.% silicone nitride with silicone carbide whiskers hybrid filler was reported to result in thermal conductivity of 1.48 W/mK [
21]. In addition, various types of highly thermally conductive nanoparticle-based fillers, such as powders and pastes, are commercially available.
However, a significant increase in thermal conductivity is usually reached by adding large amounts of thermally-conductive fillers, which leads to stiffening of the soft-material matrices and reducing their elasticity. To avoid this, Bartlett et al. [
22] proposed using liquid metal inclusions, which allowed obtaining highly thermally-conductive silicone composite (9.8 W/mK) that possesses the maximal strain limit of >600%. Multiple recent works were reported on using liquid metal in Soft Robotics [
10,
22,
23,
24,
25,
26]. Despite significant improvement of thermal conductivity along with high elasticity, implementing this solution in silicone/ethanol composites might be challenging due to the presence of ethanol, which potentially interferes with the proper distribution of liquid metal inclusions in the silicone matrix. An additional limitation might be the handling and distribution of liquid metal in bulk specimens, such as silicone/ethanol material actuators and artificial muscles.
Poor heat distribution affects not only the actuation speed of silicone/ethanol composites, but also negatively contributes to their durability and reliability by the uneven thermal degradation of the silicone matrix in the vicinity of heaters. One of the main measures of the actuator durability is multi-cyclic actuation testing. It allows us to examine the actuator performance over multiple actuation cycles and prolonged working times at various conditions, providing an overall reliability assessment. For material-actuators, multi-cyclic actuation testing allows for the evaluation of material stability and may indicate structural and property changes. On the material structure level, morphological and spectroscopic analysis may be used in addition to the multi-cyclic test observations. For instance, scanning electron microscopy (SEM) [
14,
27,
28,
29] and Fourier transform infrared spectroscopy (FTIR) [
29,
30] have been employed for the characterization of silicone composites with various fillers and form factors. In [
12,
14], the silicone/ethanol material-actuator’s multi-cyclic actuation testing was performed, showing a few tens of actuation cycles with an increase in cycle duration for each subsequent actuation cycle. This has been attributed to poor heat distribution and heat-induced permanent damage to the silicone matrix, which shortens the actuator’s life and negatively affects the actuator’s reliability.
In this paper, we studied the effect of adding relatively small amounts of a highly thermally-conductive diamond nanoparticle-based filler (0–20 wt.%) on the thermal and mechanical properties and the multi-cyclic performance of silicone/ethanol material-actuator. We showed that a slight increase in thermal conductivity already allows a notable increase in actuation speed, and we found the “sweet spot”, after which adding more filler deteriorates the mechanical properties. We performed multi-cyclic actuation tests to evaluate the durability of the actuator with the chosen filler concentration. In addition, for the first time, we successfully implemented a long short-term memory (LSTM) neural network model for the prediction of the actuation/de-actuation behavior of material-actuators in a uniform cyclic actuation experiment.
2. Results and Discussion
Increasing the thermal conductivity of the silicone/ethanol material-actuator has several advantages: the material will dissipate heat more efficiently; the maximum temperature around the heating element will decrease (alleviating thermal degradation); the cooling process will be accelerated. For this purpose, we added the diamond-nanoparticle-based thermally-conductive grease to the silicone/ethanol composite in various filler/matrix ratios.
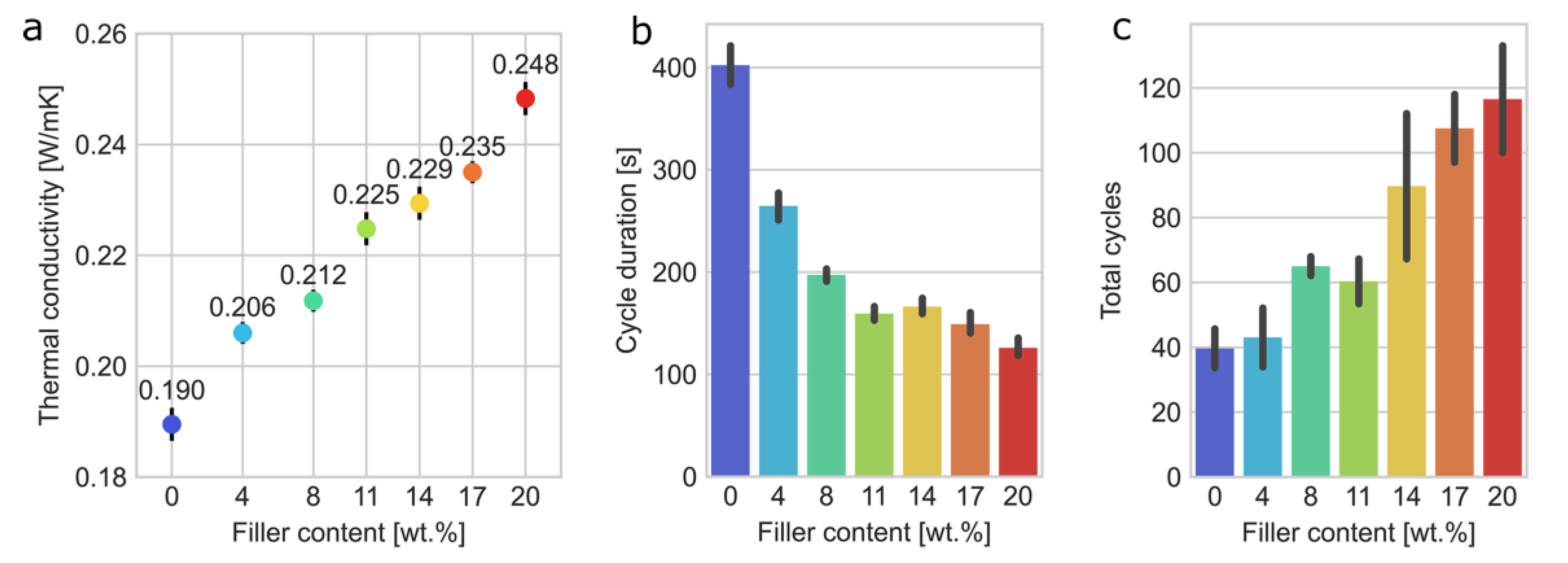
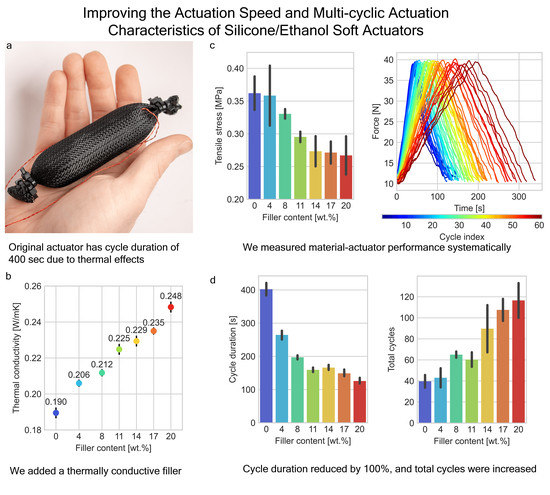
Figure 2a shows the effect of the filler concentration on the thermal conductivity of silicone/ethanol composite. It was observed that the thermal conductivity increases linearly with filler content from 0.190 ± 0.003 W/mK for 0 wt.% to 0.248 ± 0.003 W/mK for 20 wt.%. Simultaneously, the average actuation/de-actuation operation cycle duration decreases with increasing filler content: it was measured at 402 ± 55 s for 0 wt.%, 197 ± 18 s for 8 wt.%, and at 125 ± 26 s for 20 wt.% filler material (
Figure 2b). In addition, the total amount of cycles performed by 8 wt.% filler material-actuator was increased as compared to the 0 wt.% filler material (65 ± 2 cycles vs. 40 ± 7 cycles, accordingly) (
Figure 2c). Material-actuators with higher filler concentration (14–20 wt.%) showed a significantly higher maximal number of actuation cycles while exhibiting a non-uniform result distribution, reflected in a high standard deviation.
However, adding fillers to elastomers typically affects their mechanical properties [
19,
21,
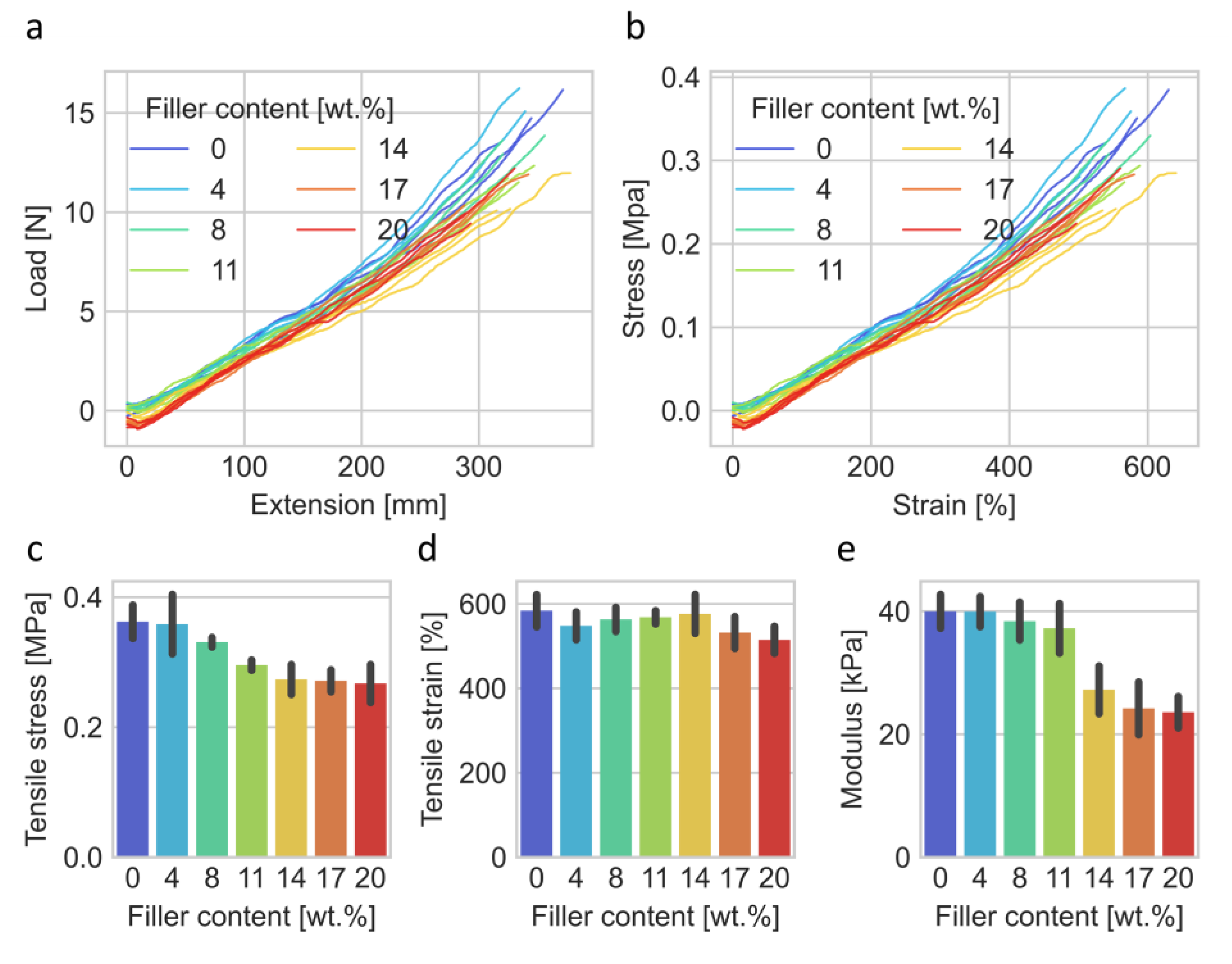
22], which in turn may be reflected in their performance in soft robotics. Mechanical testing results of the silicone/ethanol composite material with various concentrations of diamond nanoparticle grease are shown in
Figure 3. The load vs. extension is plotted in
Figure 3a and the stress vs. strain in
Figure 3b.
Figure 3c–e show the maximal stress, maximal strain, and strain at 100% elongation, respectively. It may be seen that filler concentration of ≥11 wt.% significantly affects the mechanical properties of the composite, resulting in lower maximal stress (
Figure 3c) and modulus at 100% elongation (
Figure 3e). The higher the filler concentration, the more pronounced the decrease in mechanical properties. For instance, tensile strength at failure for composite with 20 wt.% filler and 0 wt.% filler were 0.267 ± 0.036 MPa and 0.362 ± 0.031 MPa, respectively.
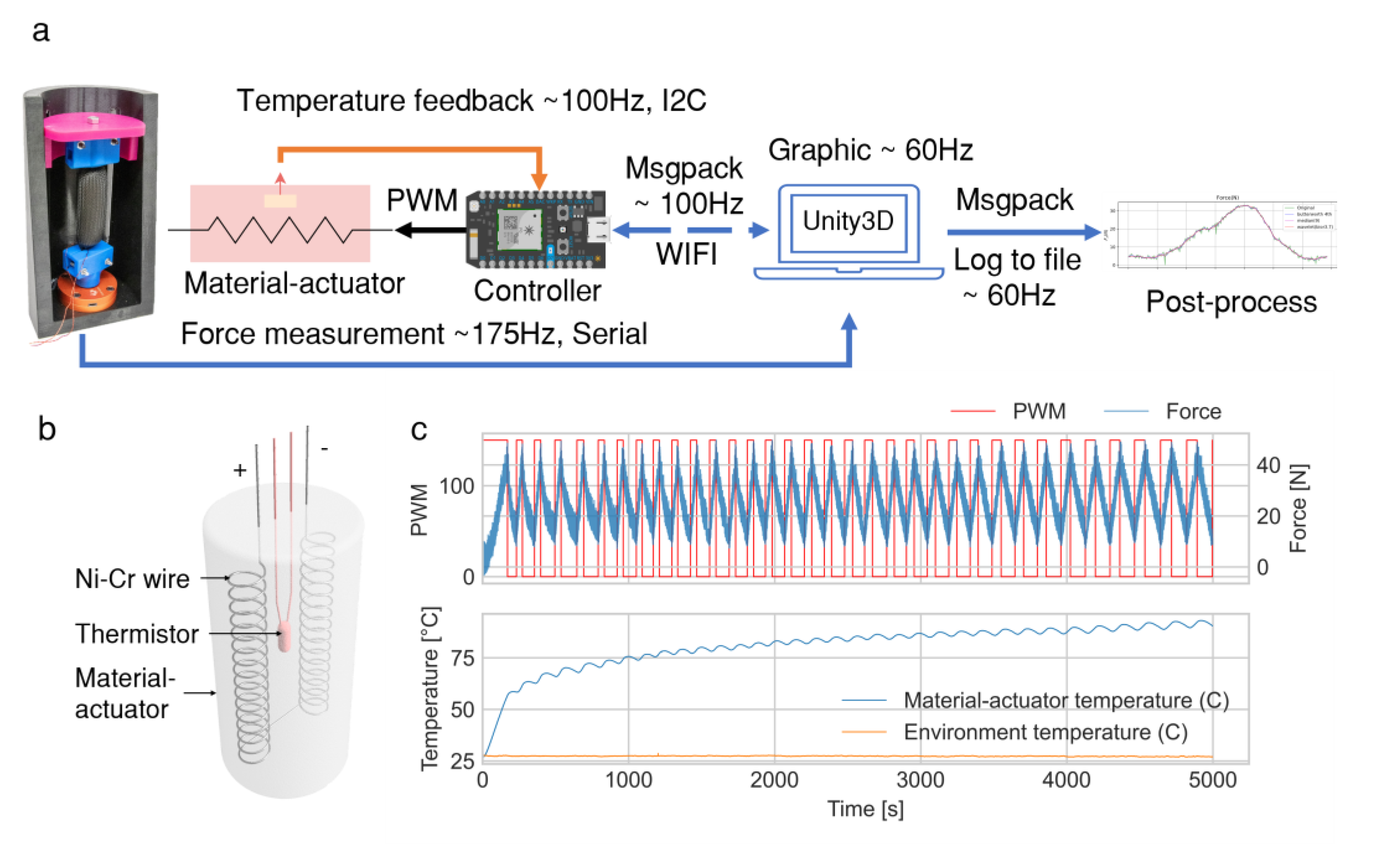
A superposition of the measured thermal characteristics, cycle duration, maximal achieved number of cycles, and mechanical properties reveals that composites with 8 wt.% filler concentration provide improved thermal conductivity with minimal effect on the mechanical properties, and increase the actuation speed and the total amount of operation cycles. We evaluated the multi-cyclic behavior of the silicone/ethanol material-actuator with 8 wt.% filler. For this, we built an automated multi-cyclic actuation testing unit (
Figure 4a), in which soft material-actuator specimens (
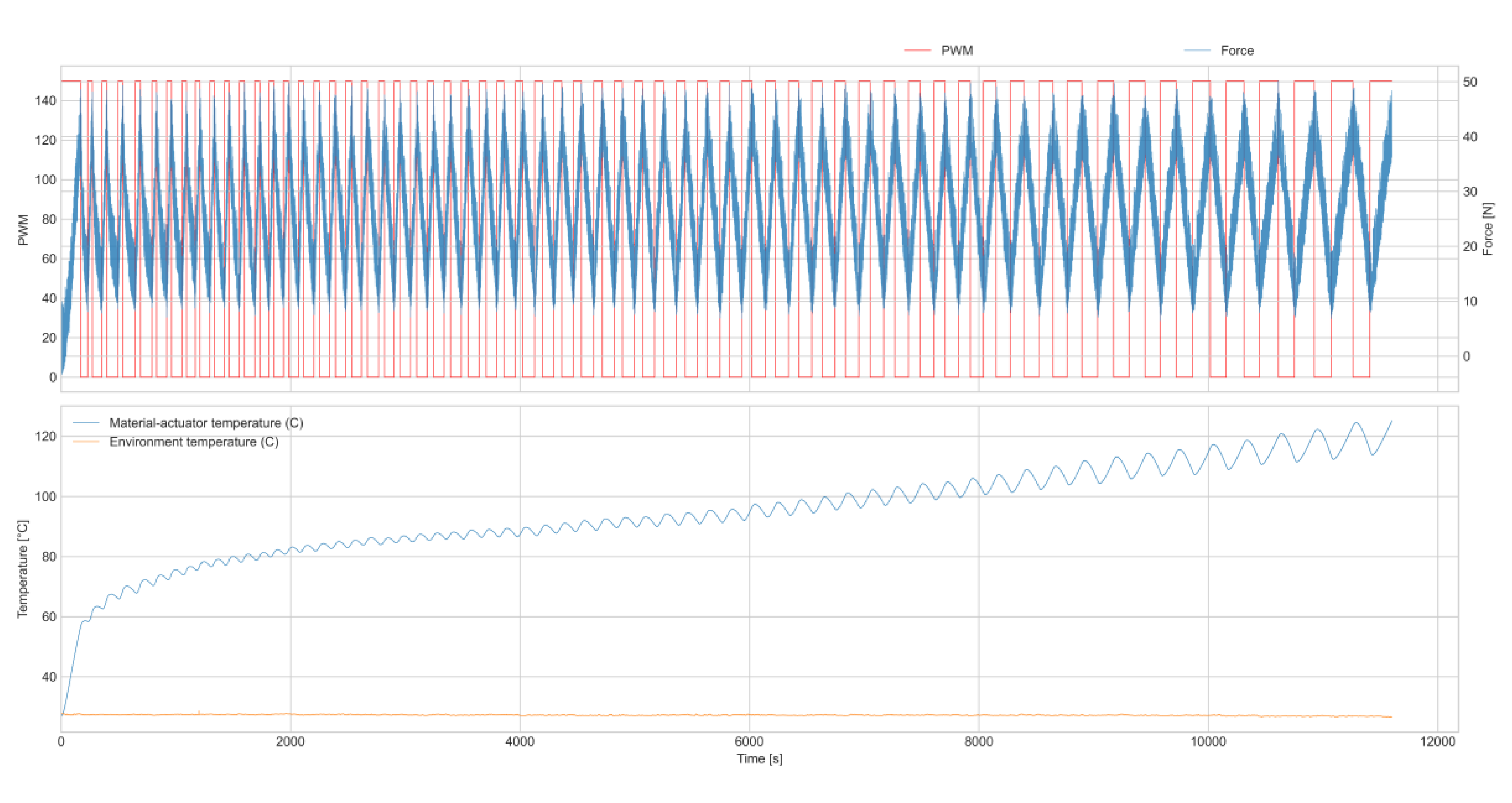
Figure 4b) may be continuously and automatically actuated to a certain force, and subsequently de-actuated. The actuation force, internal material-actuator temperature, environment temperature, and the pulse-width modulation (PWM) data were collected from the 8 wt.% composite material-actuator over time (
Figure 4c) and subsequently analyzed.
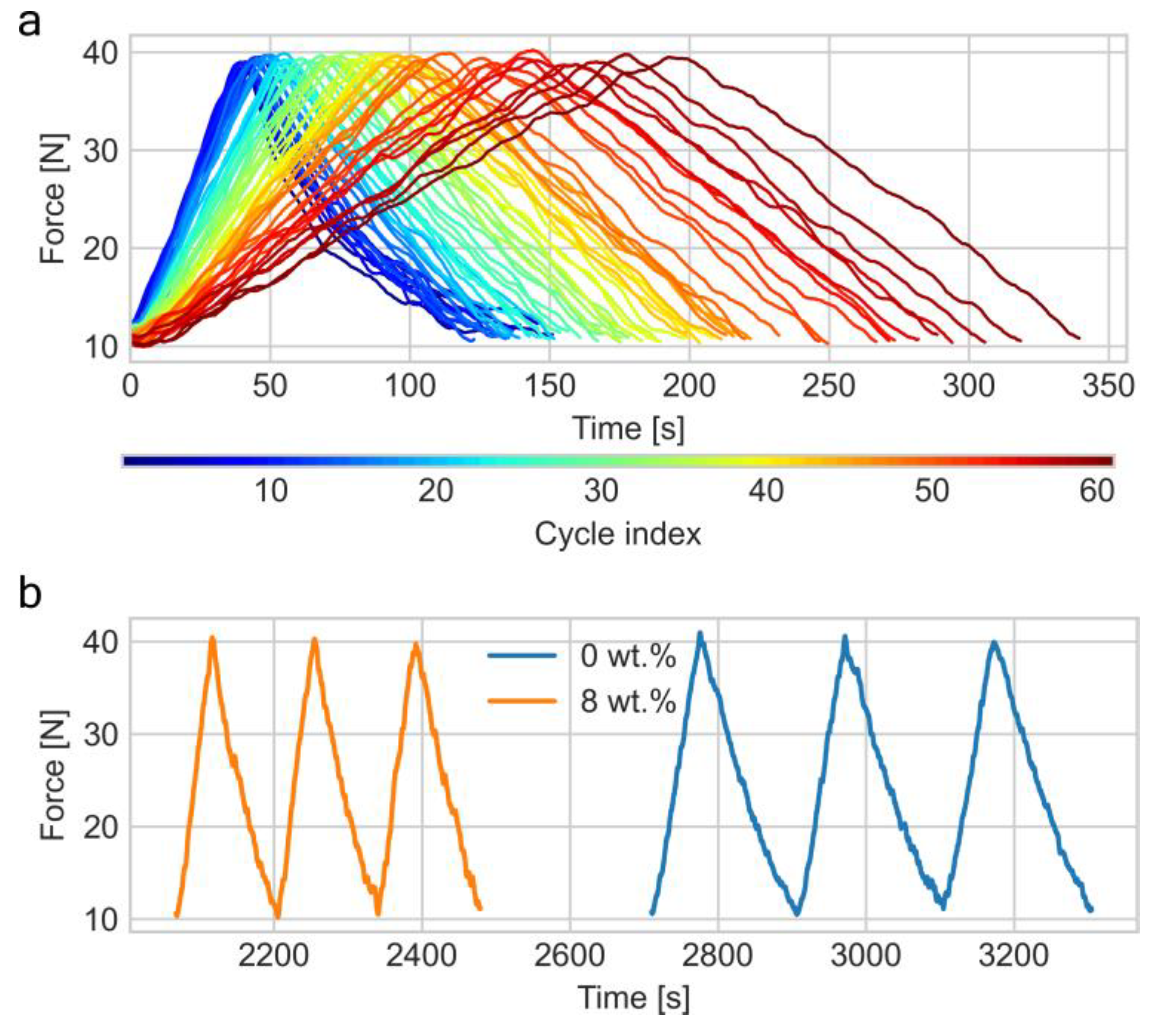
Figure 5a shows the force-time operation cycle curves of the 8 wt.% filler material-actuator for 61 cycles in an overlapping representation (each operation cycle consists of the actuation and de-actuation part). In each cycle, the material-actuator was actuated via Joule heating to exert a force of 40 N, and then de-actuated by an ambient cooling until the exerted force decreased to 10 N. Further decrease to 0 N was avoided as it would require cooling the material-actuator to room temperature, which is significantly time-consuming. It may be seen that the actuation duration, namely the time required to reach the force of 40 N, increased with the operation cycles. This may be attributed to the loss of ethanol, due to the diffusion of ethanol vapors through the silicone rubber matrix to the environment during the operation; besides, the silicone matrix may deteriorate due to thermal damage (
Figure A2) [
14].
Conducting such multi-cycle actuation experiments for reliability evaluation of thermally-driven actuators in a statistically-satisfactory amount is a complex and time- and resource-consuming task. Thus, the ability to use computational methods to predict the actuator behavior based on a small amount of experimental data has been much demanded. Up to now, machine learning methods have been used in soft actuation, mainly for the automation and optimization of control (reinforcement learning [
31], deep neural network [
32]) and for modeling the kinematics of unknown soft actuators and estimating the interaction forces with external items (long short-term memory (LSTM) recurrent neural network) [
33]). In Materials Science, machine learning methods have been utilized for predicting material properties that are hard to evaluate empirically or calculate using conventional computer simulations [
34,
35], as well as for developing new materials [
36] and evaluating structure–property relationships [
37]. To the best of our knowledge, no previous works exist on the prediction of the force/time/temperature behavior of soft material-actuators using machine learning.
Previously, the fast deterioration of plain (0 wt.% filler) material-actuators over multiple cycles hindered collecting enough reliable data for machine learning methods to predict the actuation behavior. Increasing the amount of operation cycles per actuator may allow collecting sufficient data for applying machine learning methods to predict actuation behavior.
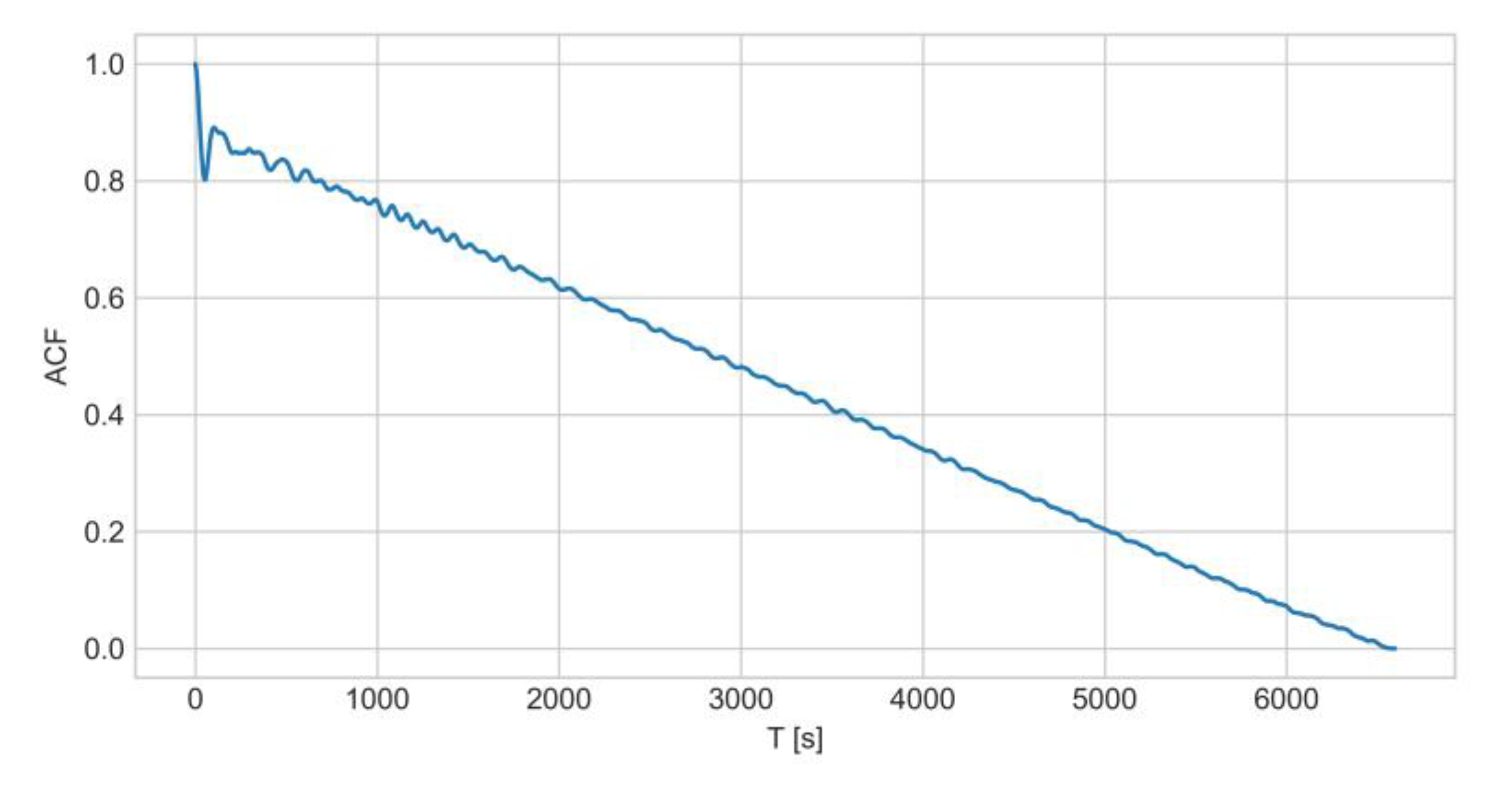
Figure 5b shows the comparison of the actuation behavior of a plain (no filler added) specimen and one with 8 wt.% filler for actuation cycles #15 to #18, emphasizing much faster actuation of the 8 wt.% filler specimens during multi-cyclic operation. The improved actuation speed of the material-actuator with 8 wt.% filler, along with grater total number of cycles, enabled the application of supervised machine learning for predicting the time-series actuation cycle pattern. Autocorrelation function validation is provided in
Appendix A and
Figure A4, which revealed the predictability of the actuation.
The time-series data, namely the force and temperature data points indexed in time, reflect the material-actuator performance during multi-cyclic operation. The task of predicting the future performance of the material-actuator may be solved as a supervised machine learning problem: at time
, predict the material-actuator’s future force output
(i.e.,
time steps later), given a sequence of material-actuator temperatures
, the environment temperatures
, the material-actuator’s raw force values
, 2.5-second-window rolling-average force values
, and PWM input at times
. As the force is changing relative slowly, we chose to predict the force output at 20 s in the future (
), in which the root-mean-squared error (RMSE) between
and
is 5.0 N. As shown in
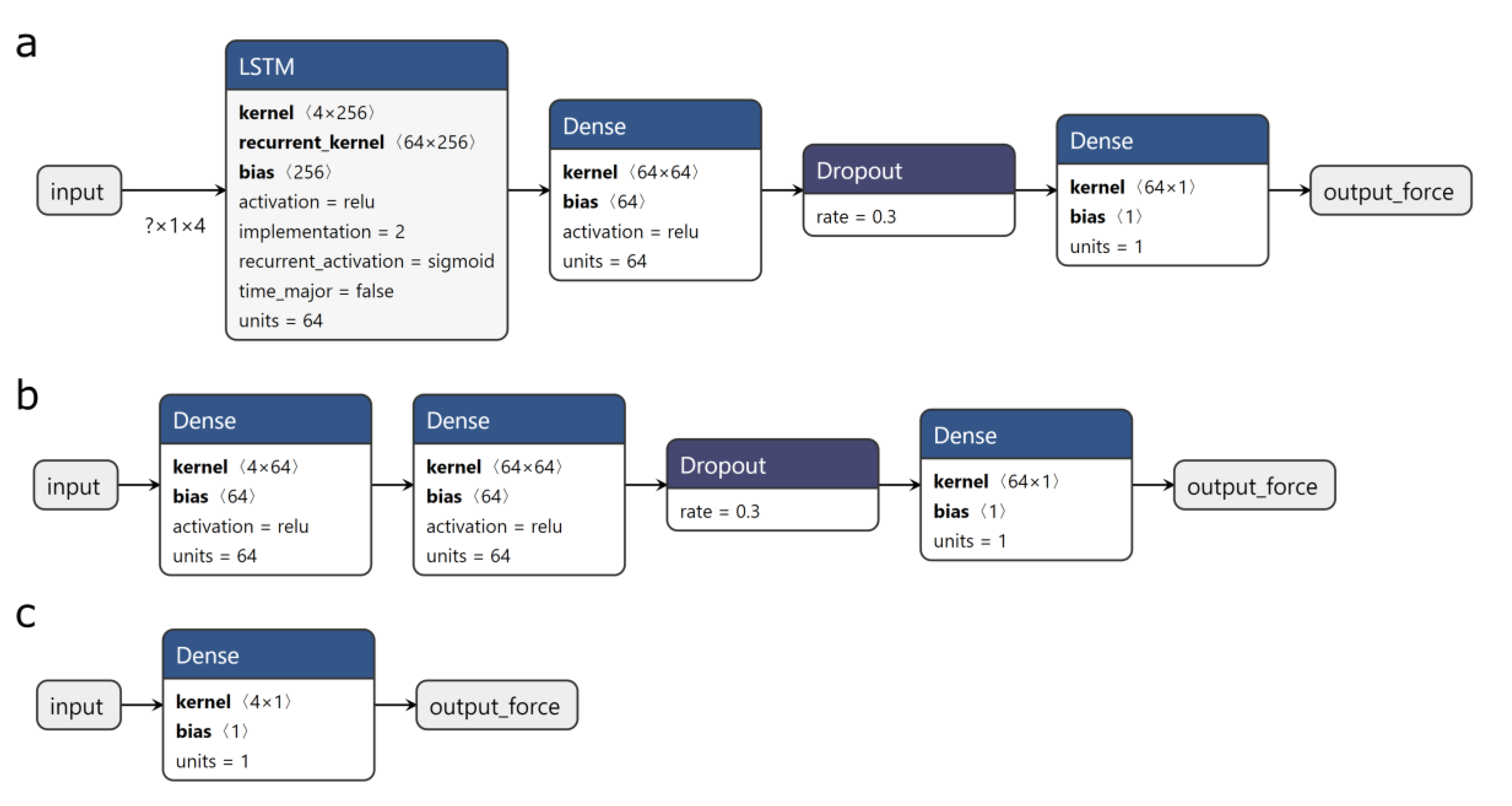
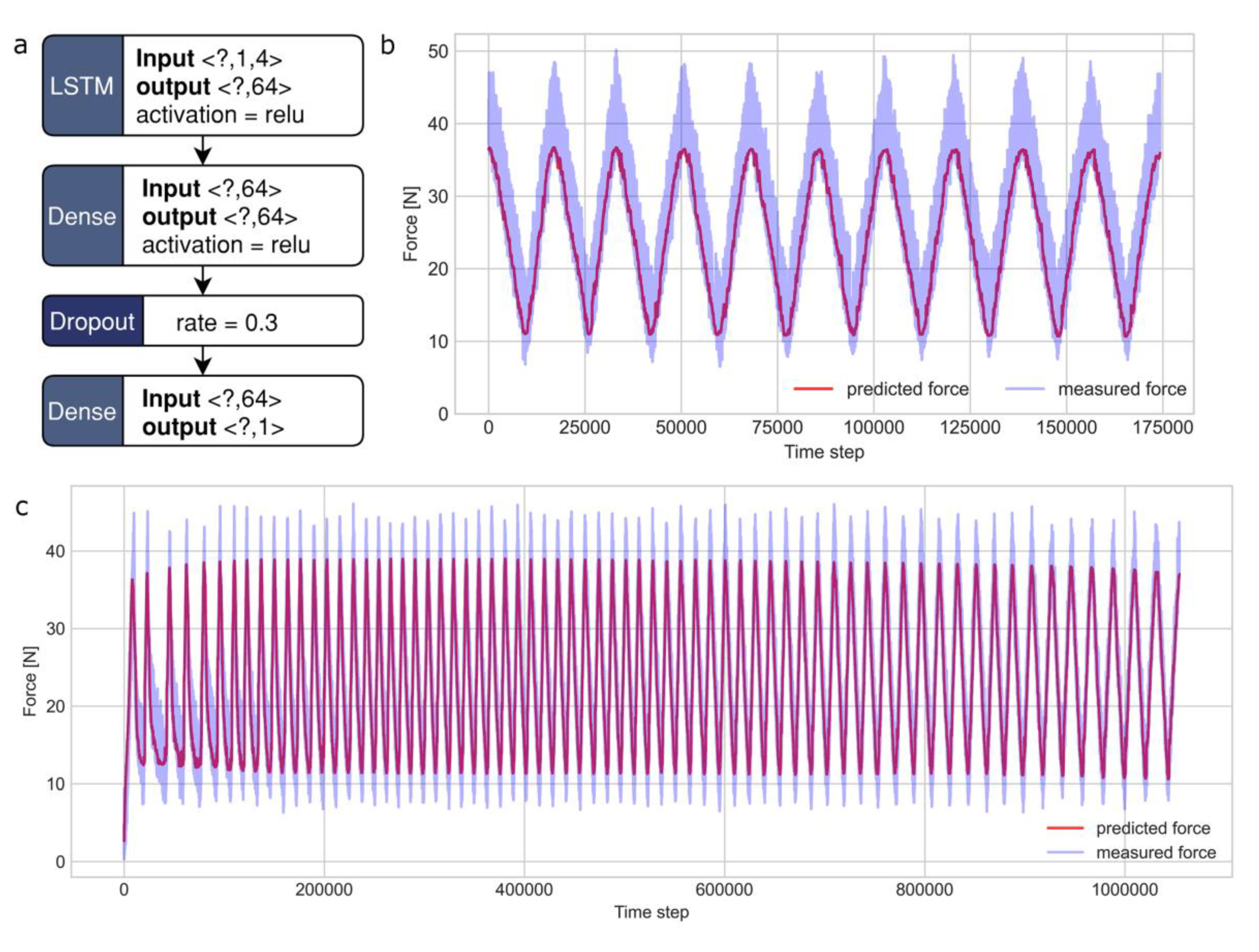
Figure 6a, we used a long short-term memory neural network model (LSTM) to predict the force
. The first layer of the model has 64 LSTM cells, which are connected to a dense layer with ReLU activation, a dropout layer, and a final dense layer. The mean squared error (MSE) was used as a loss function. For comparison, a baseline model was trained by replacing the LSTM layer with a dense layer (ReLU activation) of 64 cells. A much simpler linear regression model was also trained. The models are shown in detail in
Figure A6.
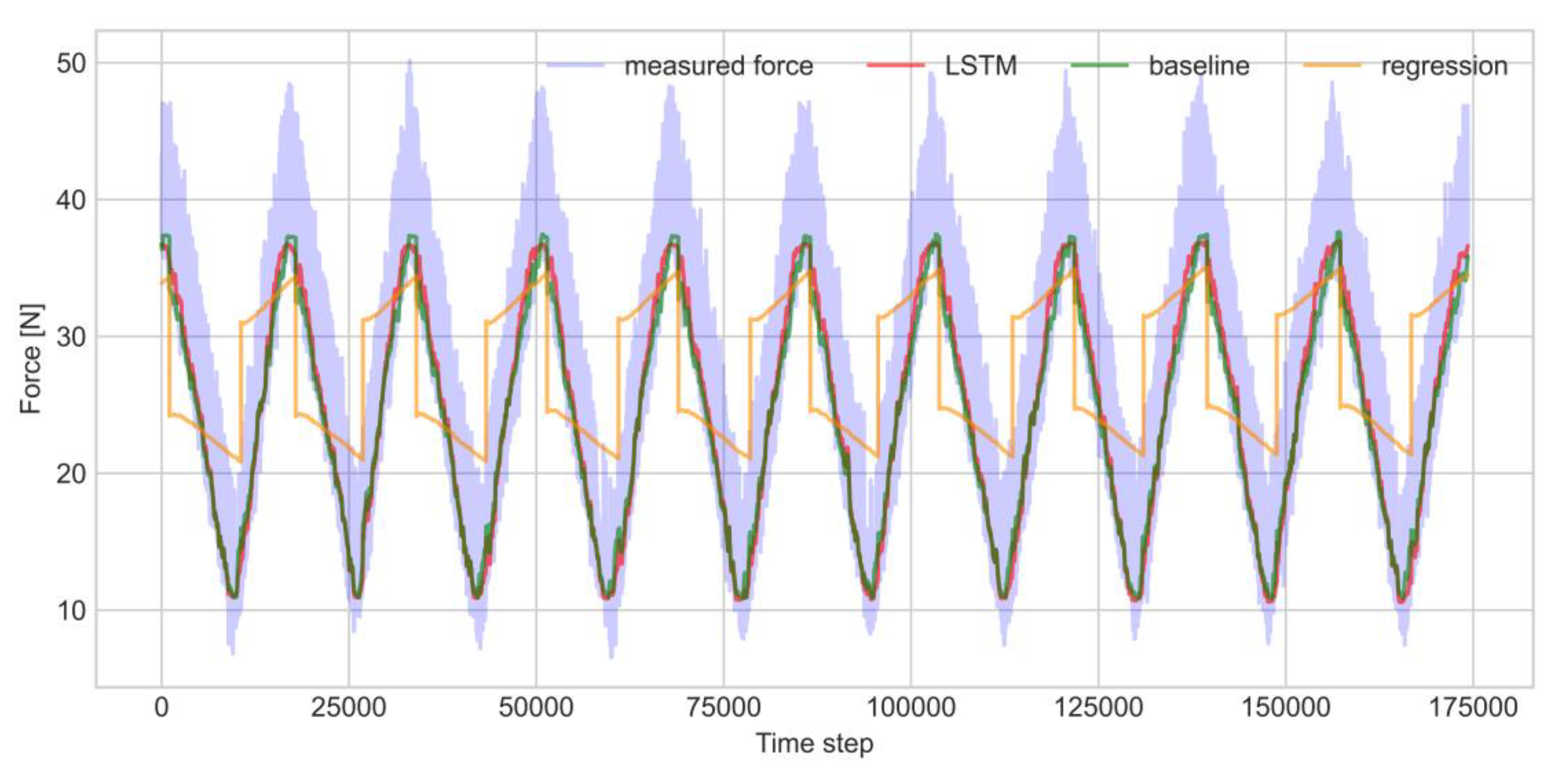
The models were trained for 40 epochs (batch size: 8192) using a material-actuator specimen recording of 61 operation cycles. The data were split into training (the first 64% data), validation (the next 16% data), and test (the last 20% data) time-series datasets. The actual and predicted operation cycles of the material-actuator are shown in
Figure 6b (here, the training, validation, and test sets belong to the same specimen). The trained LSTM model performed slightly better (validation RMSE: 1.7 N, test RMSE: 1.8 N) compared to the alternative baseline model (validation RMSE: 1.9 N, test RMSE: 2.0 N); they both greatly outperformed the linear regression model (validation RMSE: 7.6 N, test RMSE: 7.9 N). A comparison of the model predictions of the test data can be found in
Figure A7. Given that the force sensor measurement has a ±2 N error bound, a strong similarity between the real and the predicted cycles was obtained. Thus, for the first time, the actuation of soft composite material-actuator was successfully predicted by LSTM recurrent neural network.
In addition, we demonstrated cross-specimen predictions on three 8 wt.% filler specimens using the same neural network model (here, the train and test sets belong to different specimens: 6 train-test pairs in total). The prediction of one test set is shown in
Figure 6c. The model was trained on the complete time-series data of one specimen for 40 epochs (batch size: 8192) and tested on the complete time-series data of a different specimen. Again, the LSTM model performed slightly better with an RMSE of 2.7 ± 0.7 N; the baseline model had an RMSE of 2.9 ± 0.7 N; the linear regression had an RMSE of 5.5 ± 0.7 N. The results showed that the 8 wt.% filler material-actuator has good predictability and repeatability. It also showed that the LSTM model has learned generalized actuation characteristics and could predict the actuation reasonably well. Despite the slight advantage shown by the LSTM model over the baseline model, we expect LSTM to fit well to the advanced task of predicting random actuation behavior.
4. Materials and Methods
4.1. Materials
The soft material-actuator used in the present paper is based on the original silicone/ethanol composite described in [
12]. The original silicone/ethanol composite has two components: a platinum-catalyzed two-part silicone rubber matrix (Ecoflex 00-35 Fast, Smooth-On, PA, USA) and ethanol (≥99.5%; Sigma Aldrich, MO, USA) as the active phase-change material. Each material-actuator specimen was equipped with double-coiled 30 AWG Ni-Cr alloy wire (Remington Industries, Johnsburg, IL, USA) for heat-induced actuation, and with a negative temperature coefficient (NTC) thermistor as an internal temperature sensor (
Figure 4b). For the evaluation of mechanical properties and multi-cyclic testing, the material-actuator of a cylindrical shape was prepared (diameter of 25.4 mm, height 76.2 mm), and placed inside a braided mesh sleeving (diameter 25.4 mm, model: Techflex Flexo, Techflex, Sparta, NJ, USA). Prior to placing it in the sleeving, the material was lubricated using WD-40 (WD-40 Company, San Diego, CA, USA) to reduce friction (between the material and the braided sleeving). The material-actuator was prepared according to the following steps:
Hand-wind a U-shaped 30 Ohm double-coiled Ni-Cr wire.
Mix 40 vol.% Ecoflex 00-35 part-A, 40 vol% Ecoflex 00-35 part-B, and 20 vol% ethanol for 30 s (here performed using a wood stick attached to an electric drill at its full speed (model: DW235G, DeWalt, Baltimore, MD, USA).
Pour the mixture into a 3D-printed mold (cylindrical container; polylactic acid (PLA) material) designed to cast a 76.2-mm long and 25.4-mm diameter material-actuator. Immediately insert the double-coiled Ni-Cr wire into the mixture in the mold (position it in the center of the mold). Leave the material inside the mold for curing and take it out of the mold after five min.
Use a sewing needle to punch a hole on the top face of the material-actuator, and then use a tweezer to insert the thermistor. The thermistor should not touch the Ni-Cr wire.
Solder both the thermistor and the Ni-Cr wire, respectively, with 30 AWG enameled copper wire (Remington Industries, IL, USA). These two pairs of copper wires will be used to connect the Ni-Cr wire and the thermistor to the controller.
Lubricate the material-actuator by spraying the WD-40 on its surface, and place it inside the 25.4-mm diameter braided mesh sleeving. Seal both ends of the mesh sleeving using plastic zip ties, such that the material-actuator is in firm contact with the sleeving.
For improvement of the material-actuator’s thermal properties, MasterGel Maker Nano thermal compound (Cooler Master, Taiwan, China; thermal conductivity, according to the manufacturer: 11 W/mK) was added as a thermally conductive filler to the silicone/ethanol composite. Preparation of the material-actuator with enhanced thermal conductivity includes the same steps described above, except for a different procedure for step 1: prepare 40 vol.% Ecoflex 00-35 part-A, 40 vol.% Ecoflex 00-35 part-B and 20 vol.% ethanol. First, thoroughly mix the filler with Ecoflex 00-35 part-A, then mix with Ecoflex 00-35 part-B for 30 s. Specimens with 4, 8, 11, 14, 17 and 20 wt.% (1.3, 2.7, 3.8, 5, 6.2, 7.5 vol.%, accordingly) filler concentration were prepared and tested.
4.2. Mechanical Testing
The mechanical properties of the material-actuator were tested using the Instron 5569A Table Mounted Materials Testing System (Instron, Norwood, MA, USA), equipped with the Instron BlueHill software (Instron, Norwood, MA, USA). Testing specimens were prepared according to the dimensions provided in the ASTM D-412 standard (Standard Test Methods for Vulcanized Rubber and Thermoplastic Elastomers-Tension) for the Die A dumbbell specimen. The prepared material was cast into molds, which were 3D-printed on a Stratasys J750 printer (Stratasys, Rehovot, Israel) using the Vero-Blue acrylic material. The cast silicone/ethanol material is assumed as isotropic. The tests were performed on four specimens for each test batch at a strain rate of 500 mm/min.
4.3. Thermal Properties Assessment
The thermal conductivity was measured using a custom-built guarded hot plate device (guarded zone: 50 × 50 mm
2, measuring zone: 25 × 25 mm
2) designed for small specimens of low thermal conductivity materials [
38]. Thermal conductivity test specimens and setup are shown in
Figure A5. The tests were performed on specimens enclosed in identically sealed polyethylene bags to prevent affecting the results by ethanol evaporation.
4.4. Characterization Hardware and Software
To test the actuation characteristics of the material-actuator, we produced a testing unit that automates the actuation (suitable for actuation resulting in either material compression or extension).
Figure A1a shows the mechanical part of the testing unit. The 3D-printed housing of the testing unit is 20 cm in height. A Variense FSE1001 Digital and Miniature Uniaxial Force Sensor (Variense, Montreal, QC, Canada) with range ±250 N was attached at the base of the housing. A top (pink) moving plate slides vertically along the guide rails on the housing to allow for the material-actuator to move as it actuates. The material-actuator was attached to a set of 3D printed clamps at both ends. The clamps were connected to the moving plate and the force sensor, respectively.
Figure A1b shows the electronics of the testing unit. There are three ADS1115 analog-to-digital converters (Texas Instruments, Dallas, TX, USA) on the circuit board that measure the resistance of the two thermistors using Wheatstone bridges. One of the thermistors was located inside the muscle, and the other was exposed to the ambient environment. The ADS1115 communicated with a Photon microcontroller (Particle, San Francisco, CA, USA) at 100 Hz using the I2C protocol. A PWM controlled MOSFET module was connected to the material-actuator’s heating element. The controller communicated with a master computer via WiFi, where it accepted PWM commands from the computer and sent the temperature readout using Msgpack binary format at a speed of 60 Hz.
We developed a Unity3D graphics interface (GUI) on the master computer to monitor and automatically control the testing (shown in
Figure A1c). The program monitored the temperature of the material-actuator, the ambient temperature, the PWM voltage input, and the force sensor output. The force sensor communicated directly with the Unity program at 175 Hz via a serial connection.
Figure 4a summarizes the controlling scheme.
4.5. Characterization Criteria
The process of setting up an automatic actuation testing was as follows: First, set an upper bound force , a lower bound force , and a PWM voltage. For each cycle, the material-actuator was actuated until it produced a force , then the actuation was terminated, and the material-actuator was passively cooled down in open air until the force output reached the level . The cyclic actuation experiment continued until the expiration criteria were triggered, where either the actuator temperature exceeded a predefined maximum temperature (145 °C), or the heating time exceeded twice the initial cycle duration, which is an indicator of ethanol evaporation and the usability of the material-actuator.