Understanding the Behavior of Fully Non-Toxic Polypyrrole-Gelatin and Polypyrrole-PVdF Soft Actuators with Choline Ionic Liquids
Abstract
1. Introduction
2. Materials and Methods
2.1. Preparation of PPy-Gelatin Actuators
2.1.1. Preparation of Gelatin Membranes
2.1.2. Electrochemical Synthesis of PPy Electrodes
2.2. Electro-Chemo-Mechanical Characterization of PPy-Gelatin Actuators
2.3. Microbial Compatibility of PPy-Gelatin Actuators
2.4. Computational
2.4.1. Molecular Dynamics Simulations
2.4.2. Partial Charges
2.4.3. Molar Volume of Ions
3. Results and Discussion
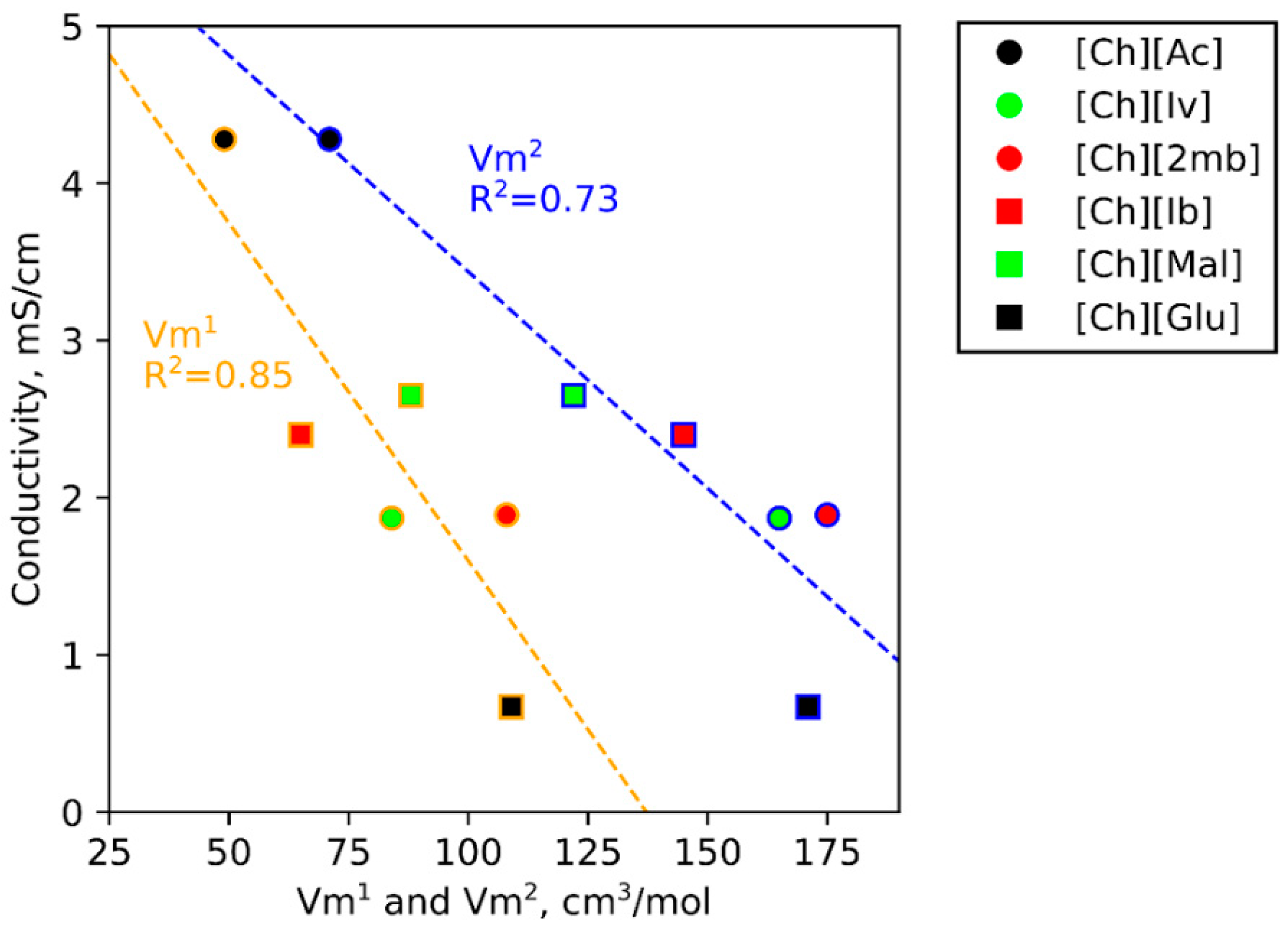
3.1. Ionic Conductivities of Choline ILs in Gelatin Membranes
3.2. Structure and Morphology of PPy-Gelatin Actuators
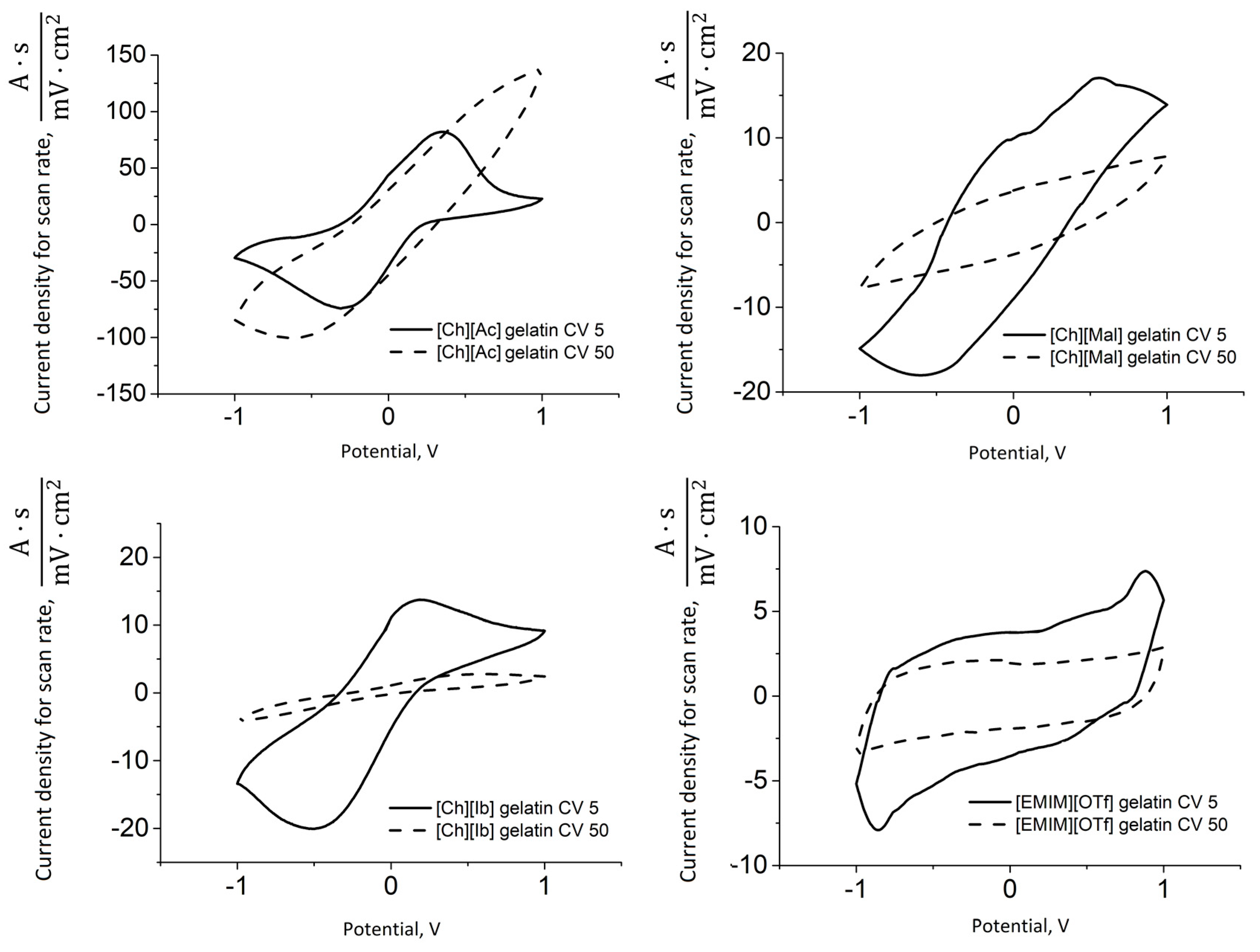
3.3. Electro-Chemo-Mechanical Properties of PPy-Gelatin Actuators
3.4. Biological Impact of PPy-Gelatin Actuators
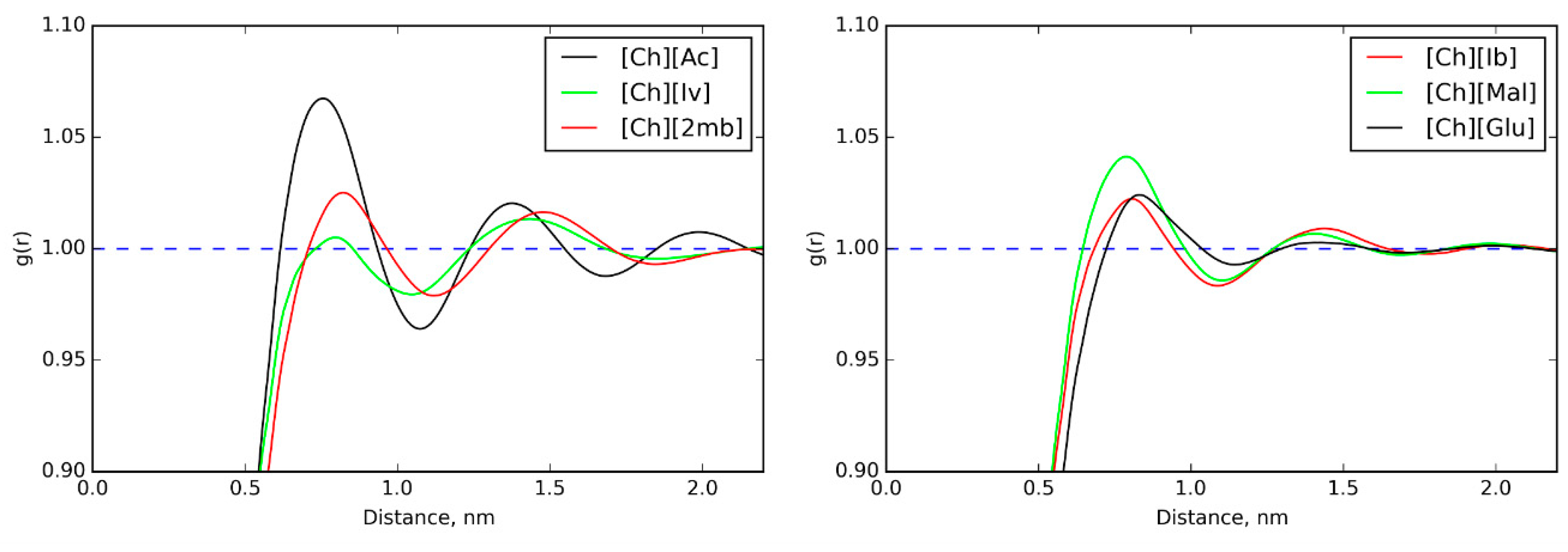
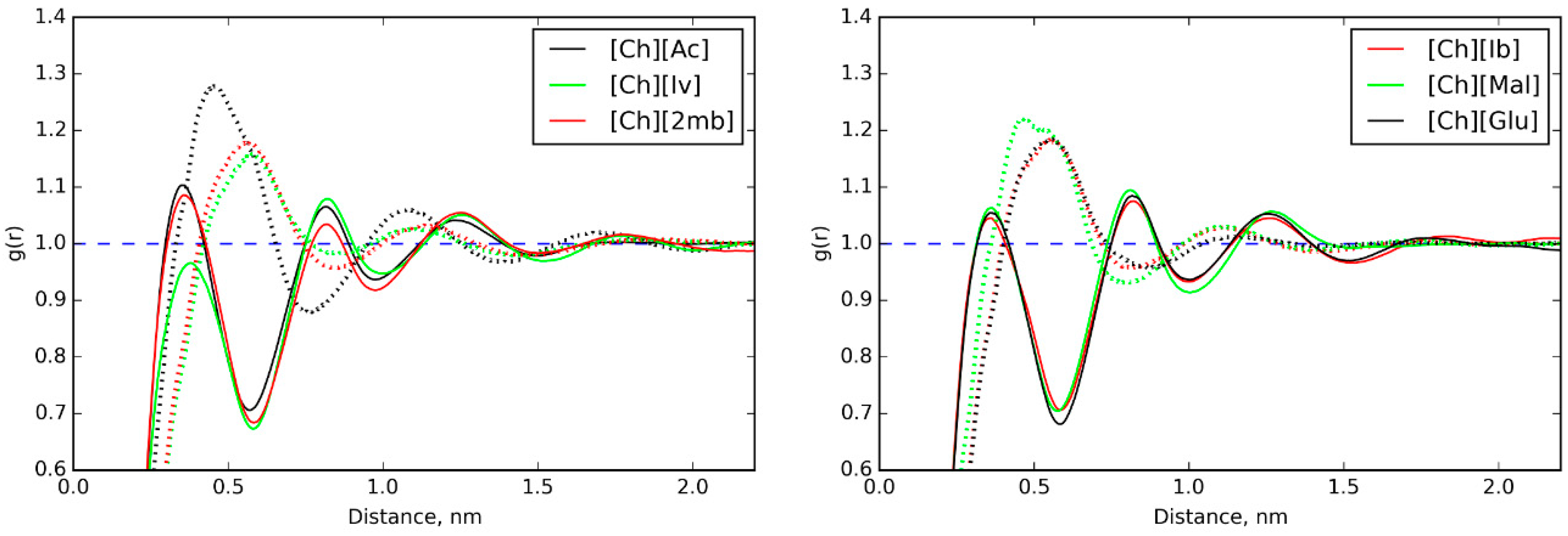
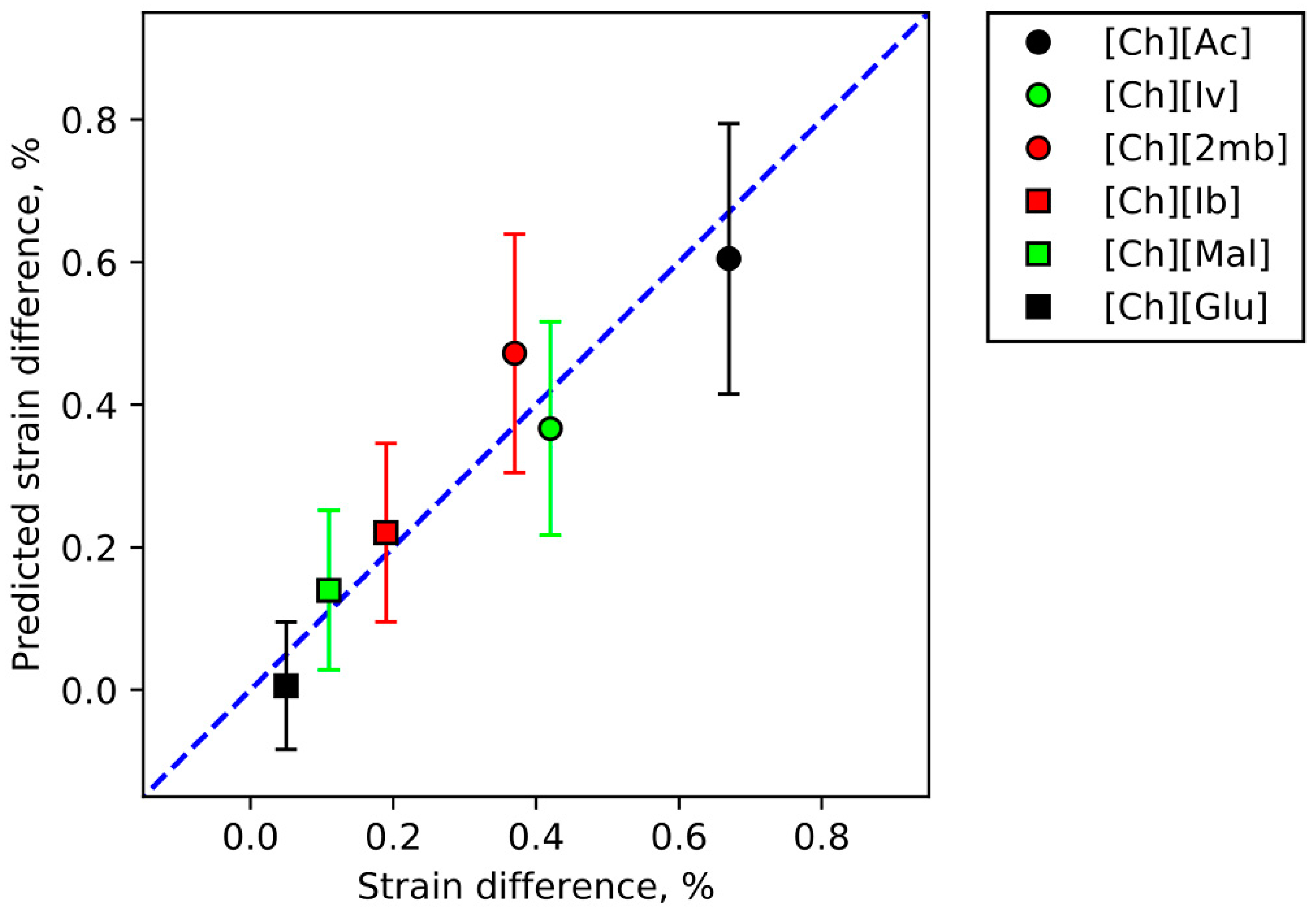
3.5. IL Properties Governing Actuation
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Temmer, R.; Maziz, A.; Plesse, C.; Aabloo, A.; Vidal, F.; Tamm, T. In search of better electroactive polymer actuator materials: PPy versus PEDOT versus PEDOT–PPy composites. Smart Mater. Struct. 2013, 22, 104006. [Google Scholar] [CrossRef]
- Maziz, A.; Plesse, C.; Soyer, C.; Cattan, E.; Vidal, F. Top-down Approach for the Direct Synthesis, Patterning, and Operation of Artificial Micromuscles on Flexible Substrates. ACS Appl. Mater. Interfaces 2016, 8, 1559–1564. [Google Scholar] [CrossRef] [PubMed]
- Yan, Y.; Santaniello, T.; Bettini, L.G.; Minnai, C.; Bellacicca, A.; Porotti, R.; Denti, I.; Faraone, G.; Merlini, M.; Lenardi, C.; et al. Electroactive Ionic Soft Actuators with Monolithically Integrated Gold Nanocomposite Electrodes. Adv. Mater. 2017, 29, 1606109. [Google Scholar] [CrossRef] [PubMed]
- Mirfakhrai, T.; Madden, J.D.; Baughman, R.H. Polymer artificial muscles. Mater. Today 2007, 10, 30–38. [Google Scholar] [CrossRef]
- Kruusamäe, K.; Punning, A.; Aabloo, A.; Asaka, K. Self-Sensing Ionic Polymer Actuators: A Review. Actuators 2015, 4, 17–38. [Google Scholar] [CrossRef]
- Bar-Cohen, Y. Artificial Muscles Using Electroactive Polymers (EAP): Capabilities, Challenges and Potential; Jet Propulsion Laboratory, National Aeronautics and Space Administration: Pasadena, CA, USA, 2005; pp. 1–14. [Google Scholar]
- Chambers, L.D.; Winfield, J.; Ieropoulos, I.; Rossiter, J. Biodegradable and edible gelatine actuators for use as artificial muscles. In Electroactive Polymer Actuators and Devices (EAPAD) 2014; Bar-Cohen, Y., Ed.; International Society for Optics and Photonics: San Diego, CA, USA, 2014; p. 90560B. [Google Scholar]
- Cai, Z.; Kim, J. Characterization and electromechanical performance of cellulose–chitosan blend electro-active paper. Smart Mater. Struct. 2008, 17, 035028. [Google Scholar] [CrossRef]
- Kim, J.; Yun, S.; Mahadeva, S.K.; Yun, K.; Yang, S.Y.; Maniruzzaman, M. Paper Actuators Made with Cellulose and Hybrid Materials. Sensors 2010, 10, 1473–1485. [Google Scholar] [CrossRef]
- Kai, D.; Prabhakaran, M.P.; Jin, G.; Ramakrishna, S. Biocompatibility evaluation of electrically conductive nanofibrous scaffolds for cardiac tissue engineering. J. Mater. Chem. B 2013, 1, 2305. [Google Scholar] [CrossRef]
- Siimon, K.; Siimon, H.; Järvekülg, M. Mechanical characterization of electrospun gelatin scaffolds cross-linked by glucose. J. Mater. Sci. Mater. Med. 2015, 26. [Google Scholar] [CrossRef]
- Wang, X.; Gu, X.; Yuan, C.; Chen, S.; Zhang, P.; Zhang, T.; Yao, J.; Chen, F.; Chen, G. Evaluation of biocompatibility of polypyrrole in vitro and in vivo. J. Biomed. Mater. Res. A 2004, 68, 411–422. [Google Scholar] [CrossRef]
- George, P.M.; Lyckman, A.W.; LaVan, D.A.; Hegde, A.; Leung, Y.; Avasare, R.; Testa, C.; Alexander, P.M.; Langer, R.; Sur, M. Fabrication and biocompatibility of polypyrrole implants suitable for neural prosthetics. Biomaterials 2005, 26, 3511–3519. [Google Scholar] [CrossRef] [PubMed]
- Egorova, K.S.; Ananikov, V.P. Toxicity of Ionic Liquids: Eco(cyto)activity as Complicated, but Unavoidable Parameter for Task-Specific Optimization. ChemSusChem 2014, 7, 336–360. [Google Scholar] [CrossRef] [PubMed]
- Elhi, F.; Priks, H.; Rinne, P.; Kaldalu, N.; Žusinaite, E.; Johanson, U.; Aabloo, A.; Tamm, T.; Põhako-Esko, K. Electromechanically active polymer actuators based on biofriendly choline ionic liquids. Smart Mater. Struct. 2020. [Google Scholar] [CrossRef]
- Kaynak, A.; Yang, C.; Lim, Y.C.; Kouzani, A. Electrochemical fabrication and modelling of mechanical behavior of a tri-layer polymer actuator. Mater. Chem. Phys. 2011, 125, 113–117. [Google Scholar] [CrossRef]
- Liu, S.; Masurkar, N.; Varma, S.; Avrutsky, I.; Reddy Arava, L.M. Experimental Studies and Numerical Simulation of Polypyrrole Trilayer Actuators. ACS Omega 2019, 4, 6436–6442. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, C.H.; Alici, G.; Wallace, G.G. Modelling trilayer conjugated polymer actuators for their sensorless position control. Sens. Actuators Phys. 2012, 185, 82–91. [Google Scholar] [CrossRef]
- Farajollahi, M.; Madden, J.D.W.; Sassani, F. Non-linear time variant model intended for polypyrrole-based actuators. In Electroactive Polymer Actuators and Devices (EAPAD) 2014; Bar-Cohen, Y., Ed.; International Society for Optics and Photonics: San Diego, CA, USA, 2014; p. 90561T. [Google Scholar]
- Ikushima, K.; John, S.; Yokoyama, K.; Nagamitsu, S. A practical multilayered conducting polymer actuator with scalable work output. Smart Mater. Struct. 2009, 18, 095022. [Google Scholar] [CrossRef]
- Lopez Cascales, J.J.; Otero, T.F. Understanding the structural changes that take place in a polypyrrole film during its oxi-reduction process: A molecular dynamics simulation study. In Nanotechnology II; Lugli, P., Kish, L.B., Mateos, J., Eds.; International Society for Optics and Photonics: Sevilla, Spain, 2005; p. 258. [Google Scholar]
- López Cascales, J.J.; Otero, T.F. Molecular dynamic simulation of the hydration and diffusion of chloride ions from bulk water to polypyrrole matrix. J. Chem. Phys. 2004, 120, 1951–1957. [Google Scholar] [CrossRef]
- Otero, T.F.; Lopez Cascales, J.J. Modeling the Polypyrrole Water Interface by Molecular Dynamics Simulation; Bar-Cohen, Y., Ed.; International Society for Optics and Photonics: San Diego, CA, USA, 2004; p. 164. [Google Scholar]
- López Cascales, J.J.; Fernández, A.J.; Otero, T.F. Characterization of the Reduced and Oxidized Polypyrrole/Water Interface: A Molecular Dynamics Simulation Study. J. Phys. Chem. B 2003, 107, 9339–9343. [Google Scholar] [CrossRef]
- Takeuchi, I.; Asaka, K.; Kiyohara, K.; Sugino, T.; Terasawa, N.; Mukai, K.; Fukushima, T.; Aida, T. Electromechanical behavior of fully plastic actuators based on bucky gel containing various internal ionic liquids. Electrochim. Acta 2009, 54, 1762–1768. [Google Scholar] [CrossRef]
- Kwon, K.-S.; Ng, T.N. Improving electroactive polymer actuator by tuning ionic liquid concentration. Org. Electron. 2014, 15, 294–298. [Google Scholar] [CrossRef]
- Davidson, J.D.; Goulbourne, N.C. Boundary layer charge dynamics in ionic liquid-ionic polymer transducers. J. Appl. Phys. 2011, 109, 014909. [Google Scholar] [CrossRef]
- Siimon, K.; Mõisavald, K.; Siimon, H.; Järvekülg, M. Increasing mechanical strength of electrospun gelatin nanofibers by the addition of aluminum potassium sulfate. J. Appl. Polym. Sci. 2015, 132, 1–5. [Google Scholar] [CrossRef]
- Temmer, R.; Must, I.; Kaasik, F.; Aabloo, A.; Tamm, T. Combined chemical and electrochemical synthesis methods for metal-free polypyrrole actuators. Sens. Actuators B Chem. 2012, 166–167, 411–418. [Google Scholar] [CrossRef]
- Sugino, T.; Kiyohara, K.; Takeuchi, I.; Mukai, K.; Asaka, K. Actuator properties of the complexes composed by carbon nanotube and ionic liquid: The effects of additives. Sens. Actuators B Chem. 2009, 141, 179–186. [Google Scholar] [CrossRef]
- Klesewetter, L.; Houdeau, D.; Steckenbom, A. Determination of Young’s moduli of micromechanical thin films using the resonance method. Sens. Actuators Phys. 1992, 32, 153–159. [Google Scholar] [CrossRef]
- Bauer, A.W.; Kirby, W.M.M.; Sherris, J.C.; Turck, M. Antibiotic Susceptibility Testing by a Standardized Single Disk Method. Am. J. Clin. Pathol. 1966, 45, 493–496. [Google Scholar] [CrossRef]
- Hudzicki, J. Kirby-Bauer Disk Diffusion Susceptibility Test Protocol; American Society for Microbiology: Washington, DC, USA, 2009. [Google Scholar]
- Abraham, M.J.; Murtola, T.; Schulz, R.; Páll, S.; Smith, J.C.; Hess, B.; Lindahl, E. GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX 2015, 1–2, 19–25. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Maxwell, D.S.; Tirado-Rives, J. Development and Testing of the OPLS All-Atom Force Field on Conformational Energetics and Properties of Organic Liquids. J. Am. Chem. Soc. 1996, 118, 11225–11236. [Google Scholar] [CrossRef]
- Martínez, L.; Andrade, R.; Birgin, E.G.; Martínez, J.M. PACKMOL: A package for building initial configurations for molecular dynamics simulations. J. Comput. Chem. 2009, 30, 2157–2164. [Google Scholar] [CrossRef]
- Darden, T.; York, D.; Pedersen, L. Particle mesh Ewald: An N⋅log(N) method for Ewald sums in large systems. J. Chem. Phys. 1993, 98, 10089–10092. [Google Scholar] [CrossRef]
- Berendsen, H.J.C.; Postma, J.P.M.; van Gunsteren, W.F.; DiNola, A.; Haak, J.R. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 1984, 81, 3684–3690. [Google Scholar] [CrossRef]
- Breneman, C.M.; Wiberg, K.B. Determining atom-centered monopoles from molecular electrostatic potentials. The need for high sampling density in formamide conformational analysis. J. Comput. Chem. 1990, 11, 361–373. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef] [PubMed]
- Weigend, F. Accurate Coulomb-fitting basis sets for H to Rn. Phys. Chem. Chem. Phys. 2006, 8, 1057–1065. [Google Scholar] [CrossRef]
- Neese, F. The ORCA program system. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2012, 2, 73–78. [Google Scholar] [CrossRef]
- Grimme, S.; Bannwarth, C.; Shushkov, P. A Robust and Accurate Tight-Binding Quantum Chemical Method for Structures, Vibrational Frequencies, and Noncovalent Interactions of Large Molecular Systems Parametrized for All spd-Block Elements (Z = 1–86). J. Chem. Theory Comput. 2017, 13, 1989–2009. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Peterson, G.A.; et al. Gaussian 09; Gaussian, Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Bondi, A. van der Waals Volumes and Radii. J. Phys. Chem. 1964, 68, 441–451. [Google Scholar] [CrossRef]
- Karu, K.; Elhi, F.; Põhako-Esko, K.; Ivaništšev, V. Predicting Melting Points of Biofriendly Choline-Based Ionic Liquids with Molecular Dynamics. Appl. Sci. 2019, 9, 5367. [Google Scholar] [CrossRef]
- Russina, O.; Santis, S.D.; Gontrani, L. Micro-and mesoscopic structural features of a bio-based choline- amino acid ionic liquid. RSC Adv. 2016, 6, 34737–34743. [Google Scholar] [CrossRef]
- Knorr, A.; Fumino, K.; Bonsa, A.-M.; Ludwig, R. Spectroscopic evidence of cholinium ‘jumping and pecking’ and H-bond enhanced cation-cation interaction in ionic liquids. Phys. Chem. Chem. Phys. 2015, 17, 30978–30982. [Google Scholar] [CrossRef]
- Knorr, A.; Ludwig, R. Cation-cation clusters in ionic liquids: Cooperative hydrogen bonding overcomes like-charge repulsion. Sci. Rep. 2015, 5, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Campetella, M.; Le Donne, A.; Daniele, M.; Gontrani, L.; Lupi, S.; Bodo, E.; Leonelli, F. Hydrogen Bonding Features in Cholinium-Based Protic Ionic Liquids from Molecular Dynamics Simulations. J. Phys. Chem. B 2018, 122, 2635–2645. [Google Scholar] [CrossRef]
- Le Donne, A.; Adenusi, H.; Porcelli, F.; Bodo, E. Hydrogen Bonding as a Clustering Agent in Protic Ionic Liquids: Like-Charge vs. Opposite-Charge Dimer Formation. ACS Omega 2018, 3, 10589–10600. [Google Scholar] [CrossRef]
- Gamrad, W.; Dreier, A.; Goddard, R.; Pörschke, K.-R. Selbstassoziation organischer Kationen über N-C-H⋅⋅⋅O-Wasserstoffbrückenbindungen. Angew. Chem. 2015, 127, 4564–4569. [Google Scholar] [CrossRef]


| Ionic Liquid | Anion Structure |
|---|---|
| choline acetate ([Ch][Ac]) | 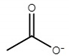 |
| choline isobutyrate ([Ch][Ib]) |  |
| choline isovalerate ([Ch][Iv]) | 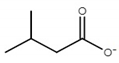 |
| choline 2-methylbutyrate ([Ch][2mb]) |  |
| choline malonate ([Ch][Mal]) | 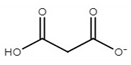 |
| choline glutarate ([Ch][Glu]) | 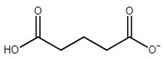 |
| Ionic Liquid | Ionic Conductivity of ILs in Membranes κ/mS·cm−1 | |
|---|---|---|
| Gelatin | Gelatin, 10 min | |
| [Ch][Ac] | 0.48 | 1.65 |
| [Ch][Ib] | 0.06 | 0.28 |
| [Ch][Iv] | 0.06 | 0.18 |
| [Ch][2mb] | 0.01 | 0.40 |
| [Ch][Mal] | 0.05 | 0.26 |
| [Ch][Glu] | 0.00 | 0.16 |
| Ionic Liquid | PPy-Gelatin | PPy-PVdF | ||||||
|---|---|---|---|---|---|---|---|---|
| Strain Difference/% | Elastic Modulus/MPa | Strain Difference/% [15] | Elastic Modulus/MPa | |||||
| sq | CV 5 | CV 50 | sq | CV 5 | CV 50 | |||
| [Ch][Ac] | 0.62 ± 0.12 | 1.35 ± 0.13 | 0.17 ± 0.03 | 61 | 0.67 ± 0.09 | 0.65 ± 0.05 | 0.30 ± 0.03 | 186 |
| [Ch][Ib] | 0.29 ± 0.12 | 1.79 ± 0.14 | 0.34 ± 0.07 | 94 | 0.19 ± 0.08 | 0.49 ± 0.07 | 0.15 ± 0.05 | 221 |
| [Ch][Mal] | 0.18 ± 0.09 | 0.09 ± 0.01 | 0.03 ± 0.01 | 301 | 0.11 ± 0.02 | 0.06 ± 0.01 | 0.02 ± 0.00 | 990 |
| [EMIM][OTf] | 0.07 ± 0.01 | 0.05 ± 0.01 | 0.03 ± 0.00 | 222 | 0.16 ± 0.02 | 0.05 ± 0.01 | 0.04 ± 0.01 | 914 |
| Ionic Liquid | PPy-PVdF sq | PPy-PVdF CV 5 | PVdF-CV CV 50 | PPy-Gelatin sq | PPy-Gelatin CV 5 | Gelatin-CV CV 50 |
|---|---|---|---|---|---|---|
| [Ch][Ac] | 10 | 11 | 12 | 16 | 74 | 77 |
| [Ch][Ib] | 5 | 11 | 12 | 13 | 81 | 85 |
| [Ch][Mal] | 3 | 3 | 2 | 2 | 5 | 4 |
| [EMIM][OTf] | 5 | 5 | 5 | 6 | 8 | 8 |
| Ion | Vm1 (cm3·mol−1) | Vm2 (cm3·mol−1) | x (Å) | y (Å) | z (Å) |
|---|---|---|---|---|---|
| [Glu]− | 109 | 171 | 5.50 | 6.78 | 7.60 |
| [2mb]− | 108 | 175 | 5.31 | 6.60 | 8.27 |
| [Mal]− | 88 | 122 | 4.55 | 5.78 | 7.68 |
| [Ch]+ | 84 | 179 | 6.05 | 6.32 | 7.78 |
| [Iv]− | 84 | 165 | 5.45 | 5.92 | 8.47 |
| [Ib]− | 65 | 145 | 5.27 | 6.72 | 6.78 |
| [OTf]− | 63 | 107 | 5.66 | 5.52 | 5.71 |
| [Ac]− | 49 | 71 | 4.09 | 5.31 | 5.42 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elhi, F.; Karu, K.; Rinne, P.; Nadel, K.-A.; Järvekülg, M.; Aabloo, A.; Tamm, T.; Ivaništšev, V.; Põhako-Esko, K. Understanding the Behavior of Fully Non-Toxic Polypyrrole-Gelatin and Polypyrrole-PVdF Soft Actuators with Choline Ionic Liquids. Actuators 2020, 9, 40. https://doi.org/10.3390/act9020040
Elhi F, Karu K, Rinne P, Nadel K-A, Järvekülg M, Aabloo A, Tamm T, Ivaništšev V, Põhako-Esko K. Understanding the Behavior of Fully Non-Toxic Polypyrrole-Gelatin and Polypyrrole-PVdF Soft Actuators with Choline Ionic Liquids. Actuators. 2020; 9(2):40. https://doi.org/10.3390/act9020040
Chicago/Turabian StyleElhi, Fred, Karl Karu, Pille Rinne, Kadi-Anne Nadel, Martin Järvekülg, Alvo Aabloo, Tarmo Tamm, Vladislav Ivaništšev, and Kaija Põhako-Esko. 2020. "Understanding the Behavior of Fully Non-Toxic Polypyrrole-Gelatin and Polypyrrole-PVdF Soft Actuators with Choline Ionic Liquids" Actuators 9, no. 2: 40. https://doi.org/10.3390/act9020040
APA StyleElhi, F., Karu, K., Rinne, P., Nadel, K.-A., Järvekülg, M., Aabloo, A., Tamm, T., Ivaništšev, V., & Põhako-Esko, K. (2020). Understanding the Behavior of Fully Non-Toxic Polypyrrole-Gelatin and Polypyrrole-PVdF Soft Actuators with Choline Ionic Liquids. Actuators, 9(2), 40. https://doi.org/10.3390/act9020040






