Multi-Physical Design and Resonant Controller Based Trajectory Tracking of the Electromagnetically Driven Fast Tool Servo
Abstract
1. Introduction
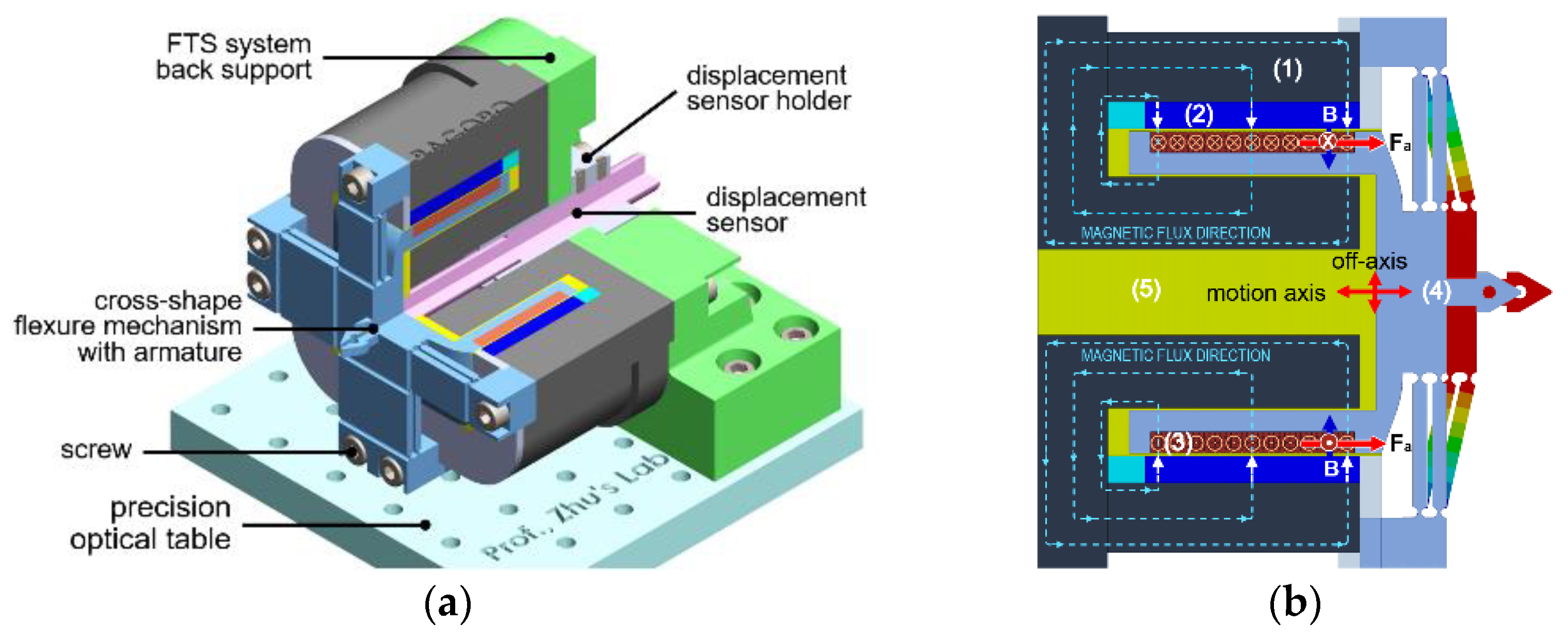
2. Architecture of the VCM Actuated FTS System
2.1. Design of the Voice Coil Motor
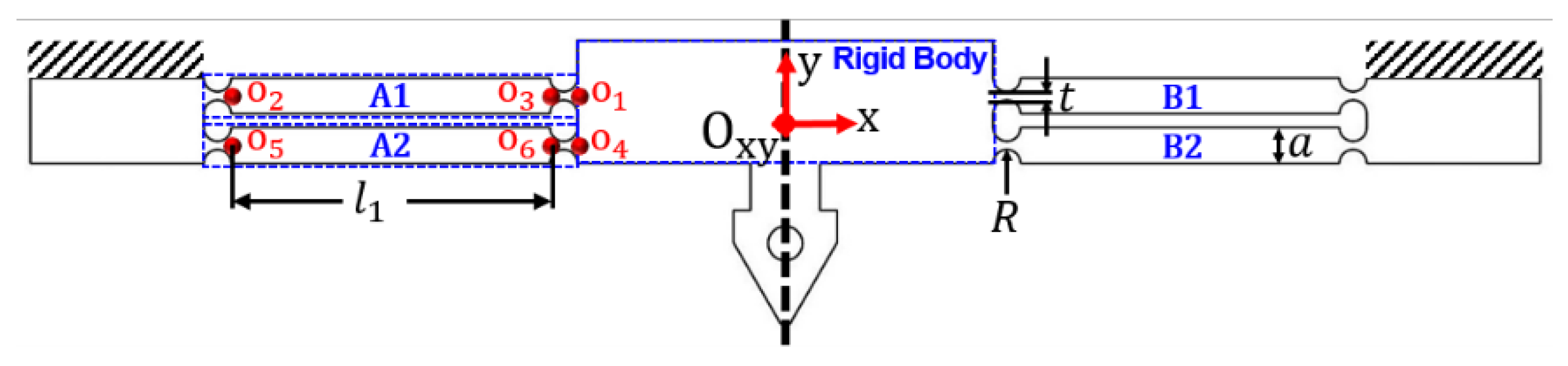
2.2. Design of the Flexure Mechanism
3. Modeling and Verification of the VCM Actuated FTS System
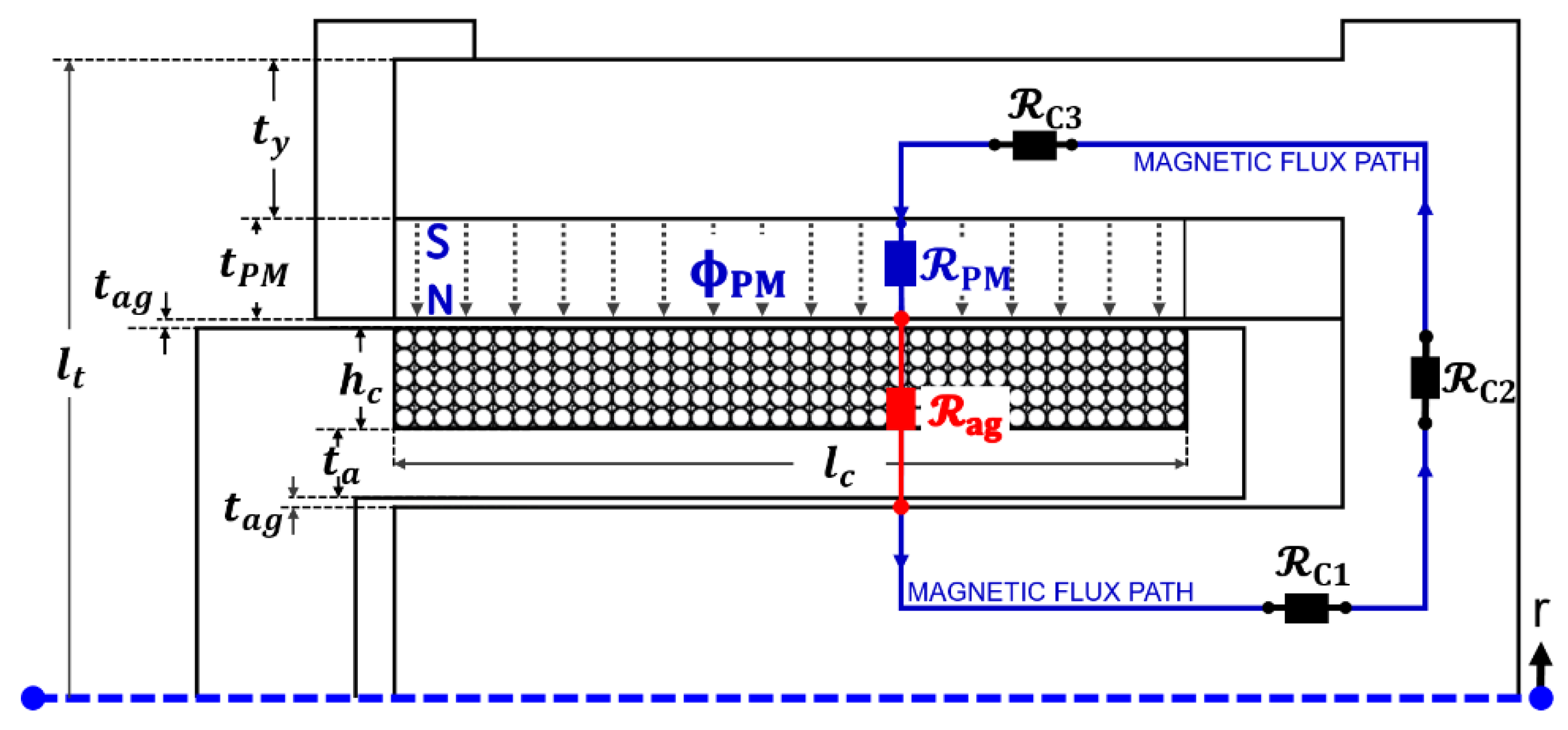
3.1. Magnetic Equivalent Circuit Modeling
3.2. Modeling of Flexure Mechanism
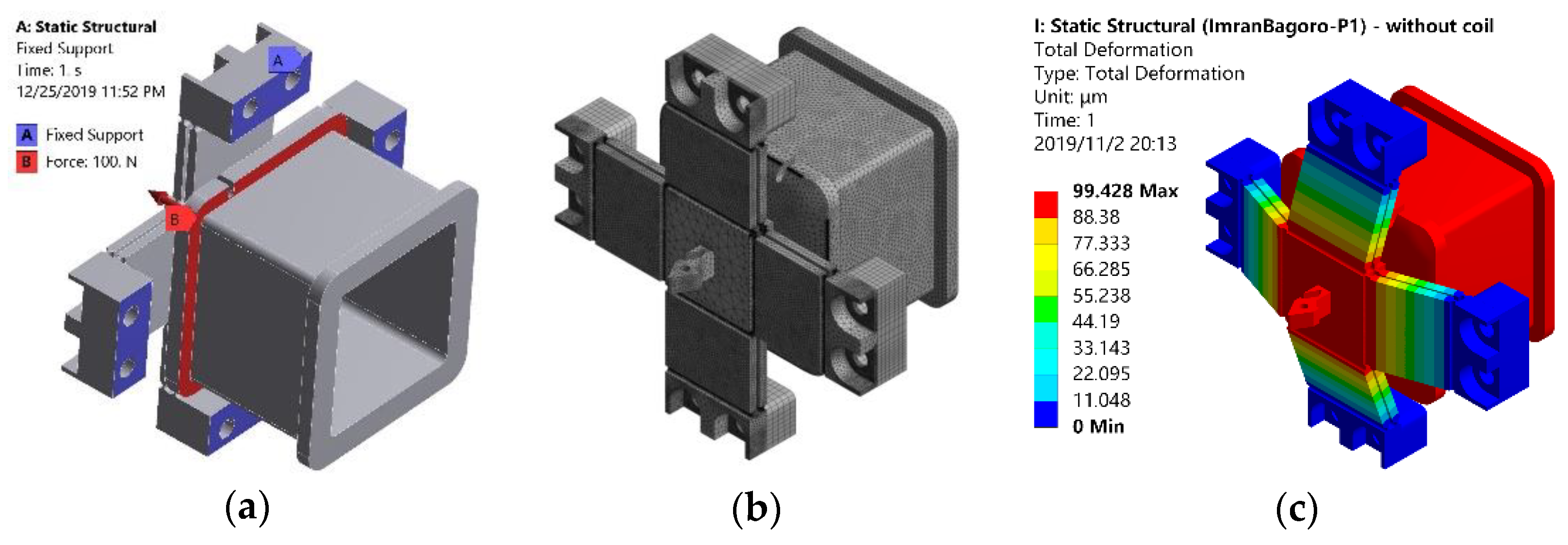
3.3. Finite Element Analysis Validation
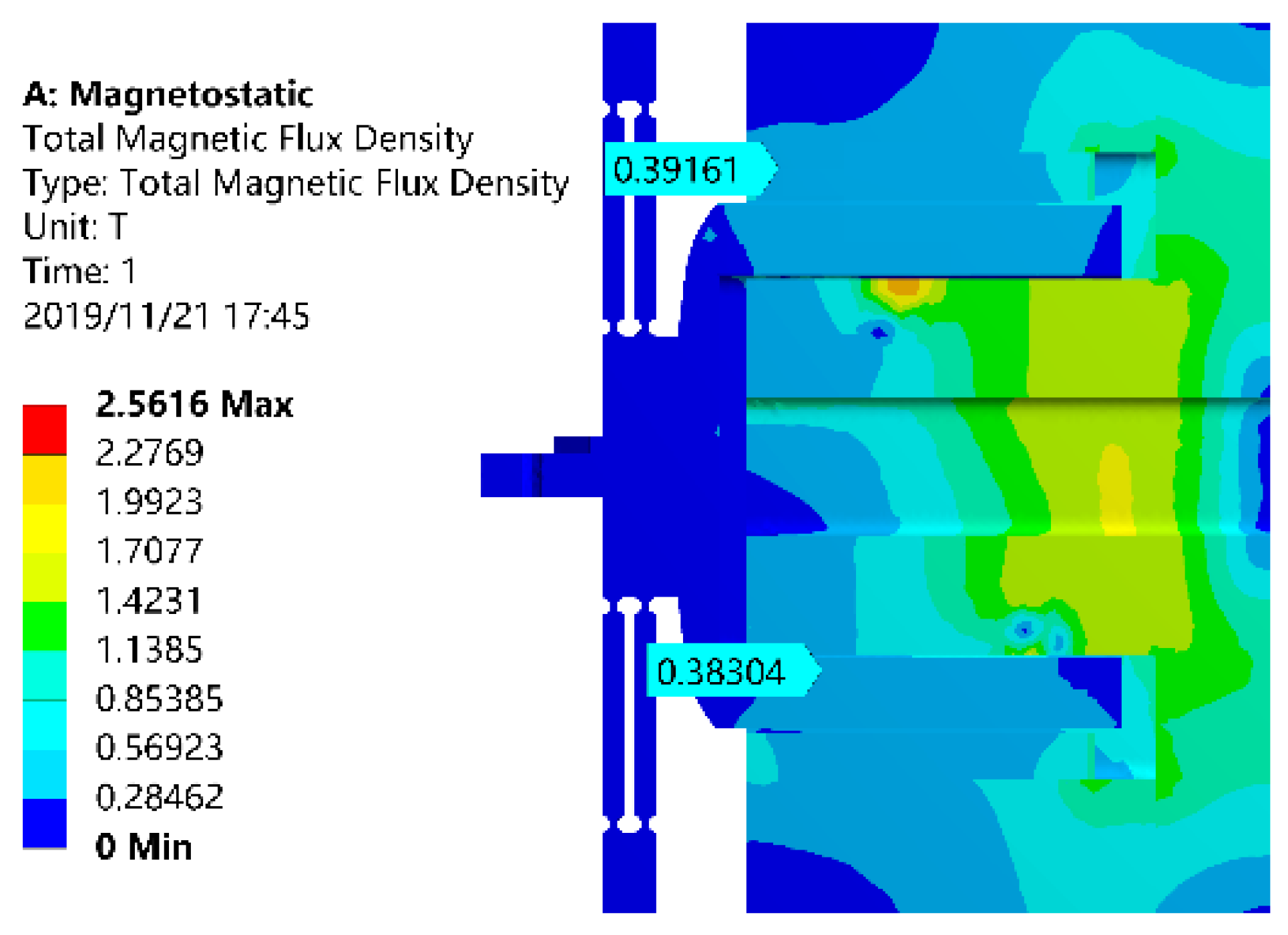
3.3.1. Electromagnetic Verification of the VCM
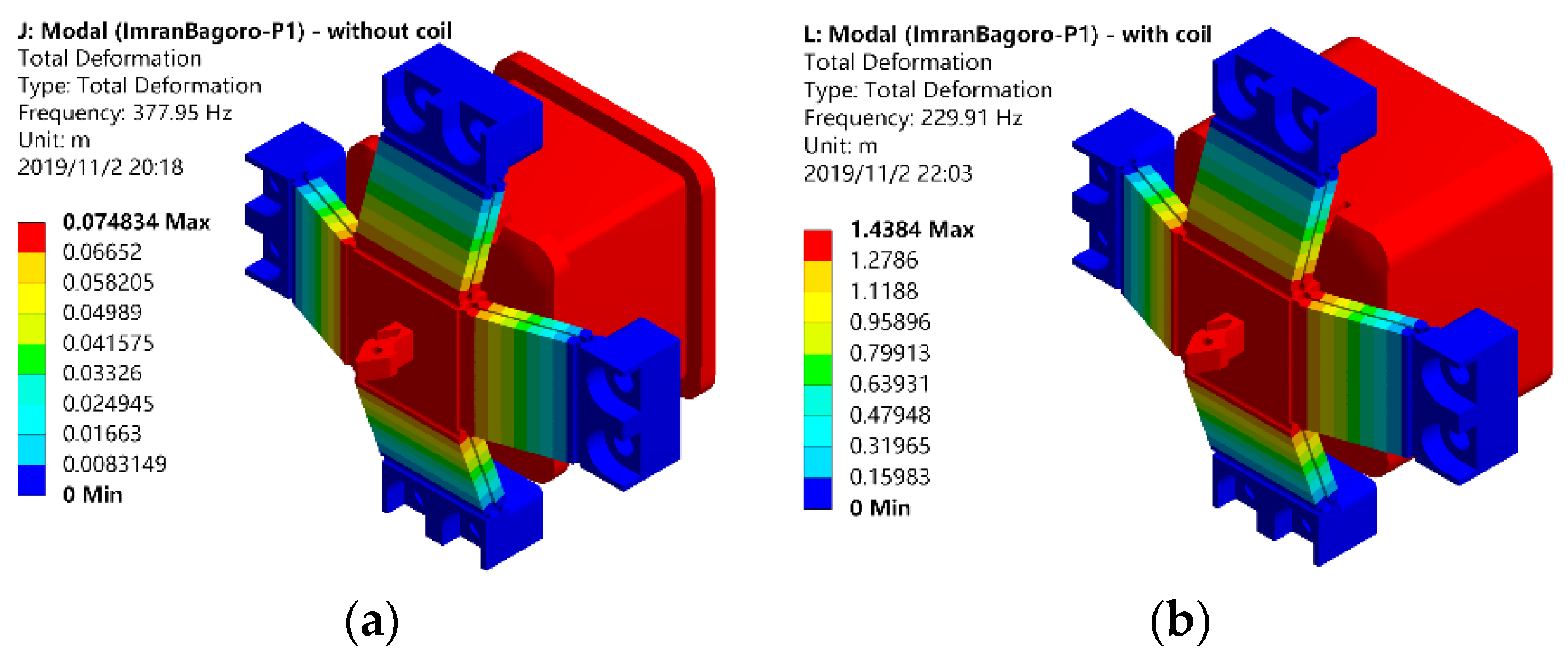
3.3.2. Mechanical Verification of Flexure Mechanism
4. Controller Design for the Fast Tool Servo System
4.1. PID Controller
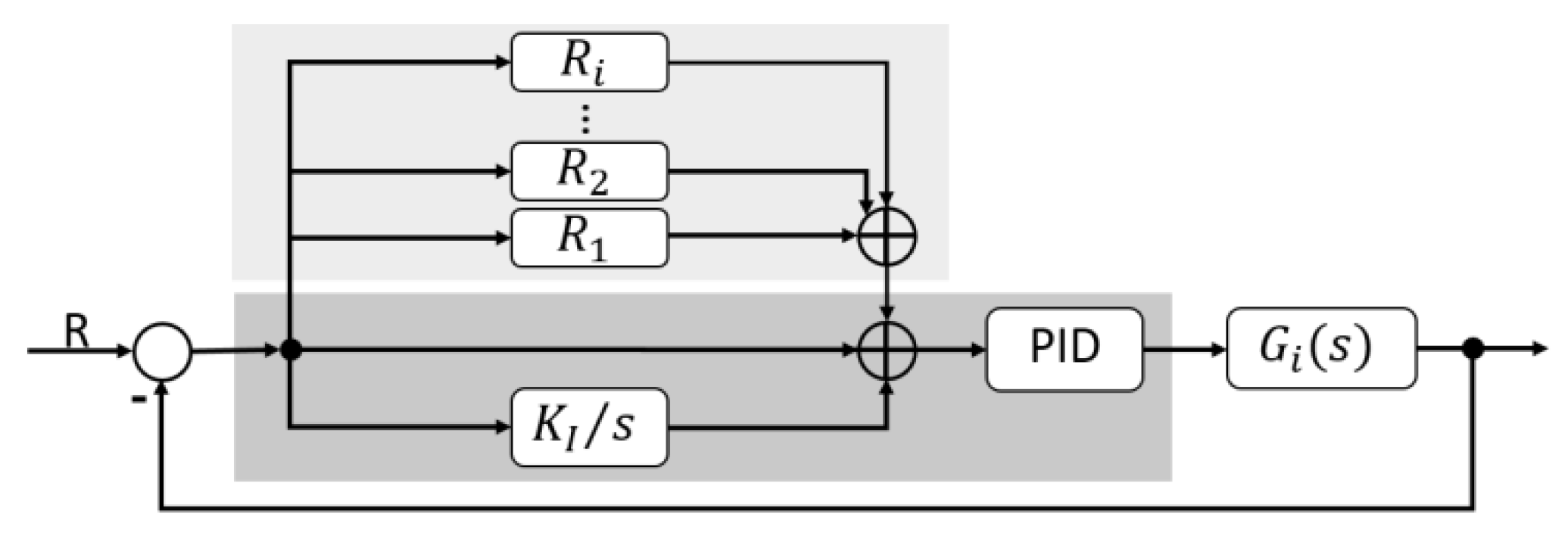
4.2. Resonant Controller
5. Experimental Testing and Results
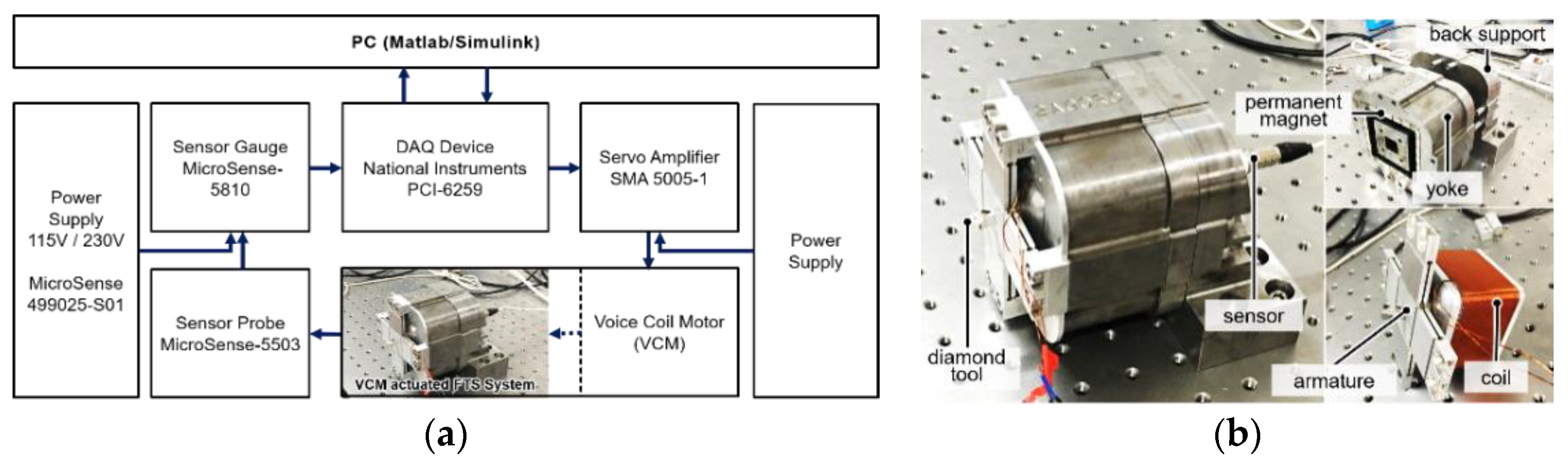
5.1. Experimental Setup
5.2. Experimental Results
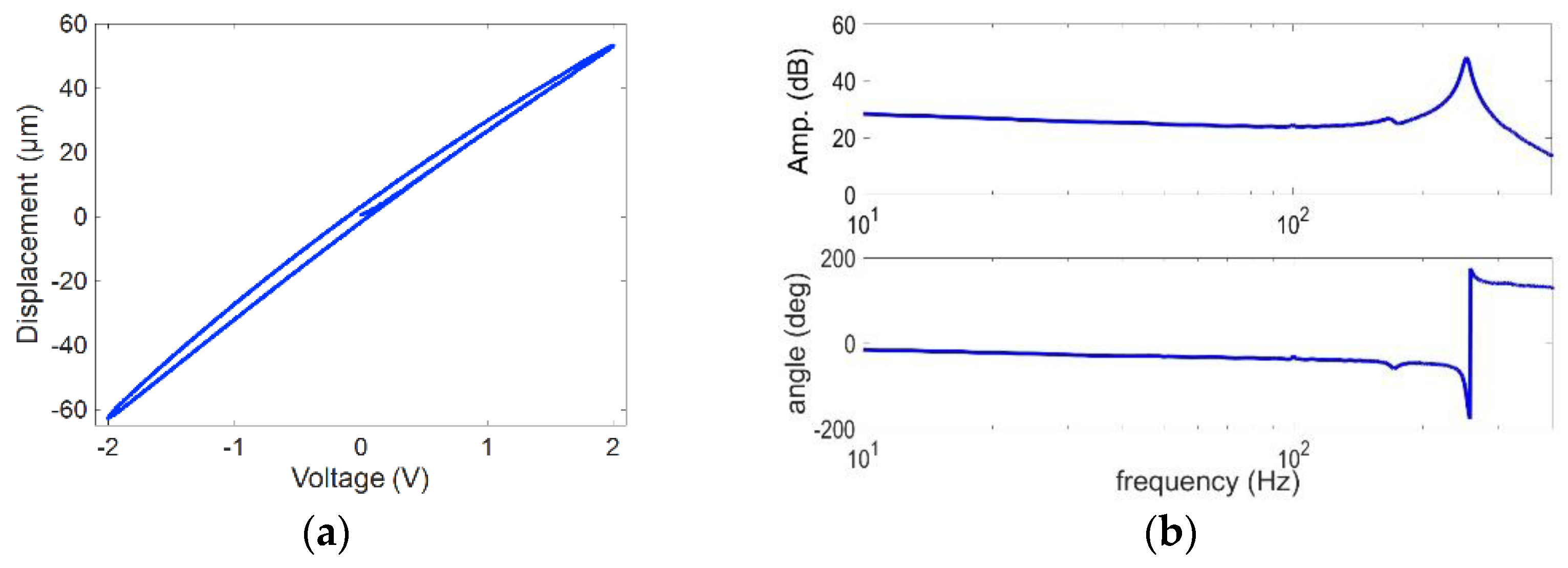
5.2.1. Static and Dynamic Performance Testing
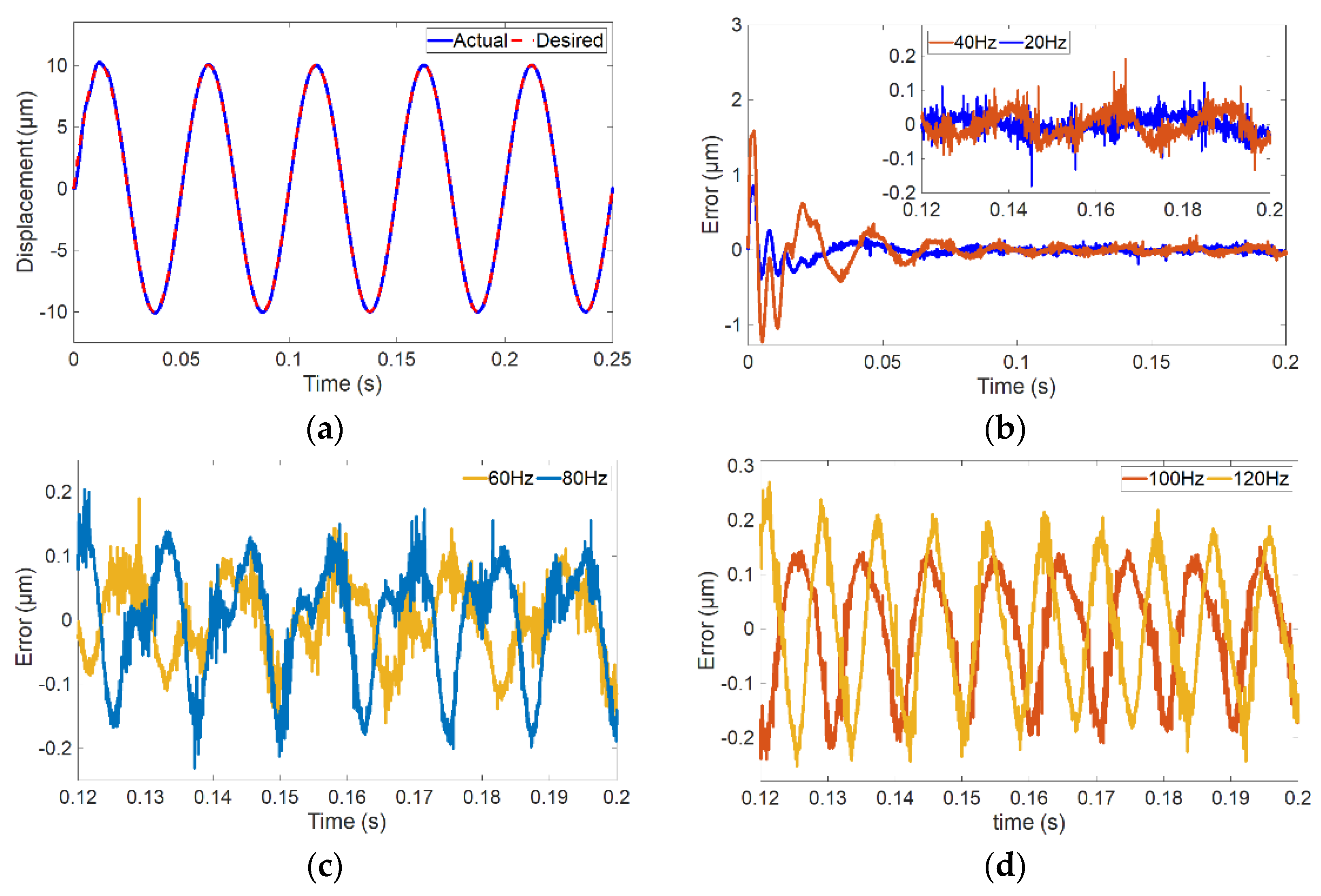
5.2.2. Control Performance Testing
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Rakuff, S.; Cuttino, J.F. Design and testing of a long-range, precision fast tool servo system for diamond turning. Precis. Eng. 2009, 33, 18–25. [Google Scholar] [CrossRef]
- Zhu, W.-L.; Yang, X.; Duan, F.; Zhu, Z.; Ju, B.-F. Design and adaptive terminal sliding mode control of a fast tool servo system for diamond machining of freeform surfaces. IEEE Trans. Ind. Electron. 2019, 66, 4912–4922. [Google Scholar] [CrossRef]
- Zhu, Z.; Zhou, X.; Liu, Z.; Wang, R.; Zhu, L. Development of a piezoelectrically actuated two-degree-of-freedom fast tool servo with decoupled motions for micro-/nanomachining. Precis. Eng. 2014, 38, 809–820. [Google Scholar] [CrossRef]
- Liu, Q.; Zhou, X.; Lin, J.; Xu, P.; Zhu, Z. A Quasiphysics Intelligent Model for a Long Range Fast Tool Servo. Sci. World J. 2013, 2013. [Google Scholar] [CrossRef] [PubMed]
- Liu, Q.; Zhou, X.; Liu, Z.; Lin, C.; Ma, L. Long-stroke fast tool servo and a tool setting method for freeform optics fabrication. Opt. Eng. 2014, 53, 092005. [Google Scholar] [CrossRef]
- Byl, M.F. Design and Control of a Long Stroke Fast Tool Servo. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2005. [Google Scholar]
- Crudele, M.; Kurfess, T.R. Implementation of a fast tool servo with repetitive control for diamond turning. Mechatronics 2003, 13, 243–257. [Google Scholar] [CrossRef]
- Byl, M.F.; Ludwick, S.J.; Trumper, D.L. A loop shaping perspective for tuning controllers with adaptive feedforward cancellation. Precis. Eng. 2005, 29, 27–40. [Google Scholar] [CrossRef]
- Lu, X. Electromagnetically-Driven Ultra-Fast Tool Servos for Diamond Turning. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2005. [Google Scholar]
- Brauer, J.R. Magnetic Actuators and Sensors; John Wiley & Sons: New York, NY, USA, 2006. [Google Scholar]
- Okyay, A.; Khamesee, M.B.; Erkorkmaz, K. Design and optimization of a voice coil actuator for precision motion applications. IEEE Trans. Magn. 2014, 51, 1–10. [Google Scholar] [CrossRef]
- Parmar, G.; Hiemstra, D.B.; Chen, Y.; Awtar, S. A moving magnet actuator for large range nanopositioning. In Proceedings of the ASME 2011 Dynamic Systems and Control Conference and Bath/ASME Symposium on Fluid Power and Motion Control, Arlington, VA, USA, 31 October–2 November 2011. [Google Scholar]
- Zhu, Z.; Zhou, X.; Wang, R.; Liu, Q. A simple compliance modeling method for flexure hinges. Sci. China Technol. Sci. 2015, 58, 56–63. [Google Scholar] [CrossRef]
- Wu, Y.; Zhou, Z. Design calculations for flexure hinges. Rev. Sci. Instrum. 2002, 73, 3101–3106. [Google Scholar] [CrossRef]
- Koseki, Y.; Tanikawa, T.; Koyachi, N.; Arai, T. Kinematic analysis of a translational 3-dof micro-parallel mechanism using the matrix method. Adv. Robot. 2002, 16, 251–264. [Google Scholar] [CrossRef]
- Zhu, Z.; Zhou, X.; Liu, Q.; Zhao, S. Multi-objective optimum design of fast tool servo based on improved differential evolution algorithm. J. Mech. Sci. Technol. 2011, 25, 3141–3149. [Google Scholar] [CrossRef]
- Sadeghpour, M.; De Oliveira, V.; Karimi, A. A toolbox for robust PID controller tuning using convex optimization. IFAC Proc. Vol. 2012, 45, 158–163. [Google Scholar] [CrossRef]
| Symbol | Description | Turns/Layers | Value |
|---|---|---|---|
| lc | Length for multiple turns | 64 | 37 mm |
| hc | height for multiple turns | 8 | 4.5 mm |
| NT | Total number of turns | 64 × 8 | 512 |
| Parts | Geometric Parameters | Symbols | Value |
|---|---|---|---|
| Stator | thickness (outer side of yoke) | ty | 10 |
| thickness (central iron core) | tcr | 12 | |
| PM | length | lc + 3 | 40 |
| thickness (magnetization direction) | tPM | 5 | |
| width | w | 50 | |
| Armature | thickness | ta | 4.5 |
| Air-gap | thickness | tag | 0.5 |
| R | t | a | b | |
|---|---|---|---|---|
| 1 | 0.6 | 28 | 2.6 | 30 |
| kin (N⁄μm) | fo (Hz) | B (T) | Fa (N) | s (μm) | ||
|---|---|---|---|---|---|---|
| Without Coil | With Coil | |||||
| Ana. | 1.10 | 395.51 | 240.51 | 0.432 | 132.7 | 120.63 |
| FEA | 1.01 | 377.95 | 229.91 | 0.383 | 117.6 | 116.49 |
| Error | 8.91% | 4.65% | 4.61% | 12.79% | 12.78% | 3.55% |
| Freq. (Hz) | 20 | 40 | 60 | 80 | 100 | 120 |
| Error (μm) | ±0.040 | ±0.067 | ±0.100 | ±0.128 | ±0.144 | ±0.200 |
| Percentage | ±0.02% | ±0.034% | ±0.05% | ±0.64% | ±0.72% | ±1.00% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hussain, I.; Xia, W.; Zhao, D.; Huang, P.; Zhu, Z. Multi-Physical Design and Resonant Controller Based Trajectory Tracking of the Electromagnetically Driven Fast Tool Servo. Actuators 2020, 9, 28. https://doi.org/10.3390/act9020028
Hussain I, Xia W, Zhao D, Huang P, Zhu Z. Multi-Physical Design and Resonant Controller Based Trajectory Tracking of the Electromagnetically Driven Fast Tool Servo. Actuators. 2020; 9(2):28. https://doi.org/10.3390/act9020028
Chicago/Turabian StyleHussain, Imran, Wei Xia, Dongpo Zhao, Peng Huang, and Zhiwei Zhu. 2020. "Multi-Physical Design and Resonant Controller Based Trajectory Tracking of the Electromagnetically Driven Fast Tool Servo" Actuators 9, no. 2: 28. https://doi.org/10.3390/act9020028
APA StyleHussain, I., Xia, W., Zhao, D., Huang, P., & Zhu, Z. (2020). Multi-Physical Design and Resonant Controller Based Trajectory Tracking of the Electromagnetically Driven Fast Tool Servo. Actuators, 9(2), 28. https://doi.org/10.3390/act9020028





