1. Introduction
Magnetic actuators that produce forces based on attraction of permeable iron to an electromagnet are fundamentally quadratic in their force response to coil currents. Among other things, this means that a single pole electromagnet can only pull a permeable target toward it. This fact necessitates the use of electromagnet arrays to produce forces in multiple directions as are required by many practical applications such as magnetic bearings [
1] or more general magnetic levitation systems [
2,
3].
The coil currents of many such arrays may be coordinated in such a manner that the force response is linear with respect to specific coil current combinations. Such an approach is sometimes referred to as bias linearization. While
ad hoc methods of bias linearization have existed since at least the first emergence of magnetic bearing technology [
4], these
ad hoc methods rely on specific structural symmetries in the electromagnet array. These symmetries are usually easy to design into the structure but there are several circumstances under which this symmetry cannot be obtained. One such circumstance is when a highly optimized design is sought where the poles in specific directions are sized tightly to directional load capacity requirements. Another circumstance of substantial importance is when symmetry is disturbed by faults in the coils or the coil drives.
These problems led to definition of the generalized bias current linearization problem [
5]. The goal of generalized bias current linearization is to select actuator currents consisting of a set of bias currents and a set of control currents in each actuator force direction such that the current required to realize an arbitrary commanded force is a linear combination of those currents, even though the current–to–force relationships are quadratic.The generalized bias current linearization problem for actuators described by a quadratic current–to–force relationship has been considered by numerous researchers over the last three decades. Na and Palazzolo [
6,
7] extended the numerical solutions of Reference [
5] to produce solutions optimized for specific objectives.
Much of the work since Reference [
5] has been directed at the fault tolerance motivation. Here, the goal is to continue to bias linearize the electromagnet array after failure of one or more of the electromagnet coils or its driver. This subsequent work has explored various aspects of fault tolerance through generalized bias linearization. Examples include Reference [
8], which explored many aspects of potential failures in magnetic bearing systems, including the use of generalized bias linearization provide tolerance of coil or amplifier failures, Reference [
9], which examined a range of implementation aspects of this approach, Reference [
10], which specifically examined the problem of robust fault detection prior to action, [
6] which included finite magnetic permeability and the effect of leakage into the generalized bias linearization formulation, Reference [
11], which introduced the math to enable use of reduced controller outputs in generalized bias linearization, and Reference [
12], which examined how controller parameters might need to be modified with faults under generalized bias linearization. Experimental results are provided in Reference [
13], which documents an early application of generalized fault tolerance to a rotor test rig, in Reference [
14], which applied the approach to the design of magnetic bearings for turbo–molecular results, and in Reference [
15], which compared theoretical results to physical experiments.
Of course, such actuators can be controlled in a more general fashion than using bias linearization and numerous researchers have eschewed bias linearization in favor of nonlinear methods because the latter offer lower power operation at potentially the same level of performance [
16,
17,
18,
19]. A key value of bias linearization to the broader structural or rotordynamic control problem in which the actuator is embedded is that bias linearization converts the otherwise quadratic actuator to a linear element (whose properties may even be invariant under partial fault conditions) thereby simplifying the broader control problem. This motivated the original
ad hoc bias linearization methods as well as the generalized bias linearization methods.
Although previous works produced practical solutions to the generalized bias current linearization problem, those solutions were typically the result of computationally intensive numerical algorithms. For a twelve–pole magnetic bearing system, the solution requires solving a nonlinear problem in 36 variables. As an indicator of typical solution effort, the code provided in Reference [
20] requires about 3.5 s to compute solutions starting from 1000 randomly selected starting points on a modern computer with a 3GHz clock speed. The quality and properties of such solutions (which are not unique) depend strongly on the initial guess, so several minutes of processor time may be required to consider enough starting points to ensure a near-optimal solution. The high computational cost of finding these solutions does not affect their utility in real–time control as the solutions are computed off–line, are compact, and are stored in memory for real–time use. The real deficiency associated with this costly solution is the inability to adequately characterize the solution space and obtain solutions optimized for various design conditions. Some headway toward this design optimality was explored in Reference [
7], but the computational complexity and non–convexity of the solution space remains a hindrance to truly optimal solutions.
This work presents a closed–form solution to the generalized bias current linearization problem. Manifolds of solutions to the bias current linearization problem are defined via a small number of arbitrarily selected parameters. To motivate the solution, the force on a magnetically permeable sphere in free space subject to the magnetic field from an array of coils will first be considered. Selecting the currents to produce a desired force for this case is mathematically the same problem as bias current linearization, but the problem naturally has a form that yields a parameterized representation of bias current linearization solutions. Only the solution to a straightforward linear algebra problem is needed to generate the bias current linearization for the permeable sphere problem. Next, a magnetic bearing with sinusoidally distributed flux density is considered. The current–to–force relationship has a similar form to the permeable sphere, and it suggests an approach for treating a magnetic bearing with discrete poles. Last, radial magnetic bearings with an even number of evenly spaced, equal–sized poles are considered. This problem can also be converted to the same convenient form as the permeable sphere, resulting in a manifold of parameterized solutions. Several examples are then considered, showing that the method can produce solutions for magnetic bearings under normal operating conditions and under faulted coil conditions.
2. Force on a Magnetically Permeable Sphere
To aid in the understanding of the proposed approach to bias current linearization of radial magnetic bearings, the mathematically related problem of force on a magnetically permeable sphere is first considered. This problem arises in the literature in the context of manipulating microbots with an array of magnetic coils [
21] and
in vivo magnetically guided brain surgery [
22]. A typical configuration is shown in
Figure 1. Although only four coils are shown in the figure for the purposes of illustration, a stationary array typically consisting of six or more coils is arranged about a movable soft iron or permanent magnet particle. One then seeks the coil currents needed to apply a desired magnetic force to the particle, given a specific position of the particle. The quadratic form of the current–to–force problem for the permeable sphere (a soft iron particle) is similar to the bias current linearization problem for radial magnetic bearings. However, the physics of the permeable sphere problem naturally produces an asymmetric form of the problem that can be intuitively understood and that is easy to solve. The goal is then to find a way to cast the bias linearization for radial magnetic bearings into the same easy–to–solve asymmetric form,
that is, the subject of later sections of this work.
As shown in
Figure 1, the sphere is located by position vector
x, defining the sphere’s location relative to the origin of the fixed
c reference frame. Since the sphere is small in comparison to the dimensions of the device, it is typical to idealize the sphere as a point dipole as in Reference [
21]. In this case, the sphere’s dipole moment,
m is related to the magnetic flux density,
, produced by the coils at
x in the absence of the sphere by [
23]:
where
r is the radius of the sphere,
is the magnetic permeability of free space, and it is assumed that the sphere’s relative permeability is
. The boldface type of
m,
x, and
B denotes that these are all vector quantities.
The force on a magnetic dipole,
f, is defined in [
24] as:
As in Reference [
22],
m can be represented by a three–component column matrix,
m, where the elements of
m represent the components of
m along the fixed
,
, and
axes shown in
Figure 1, that is,:
Similarly, the components of the flux density, force, and sphere position are represented by column matrices B, f, and x, respectively.
The coil currents in the device can be succinctly represented by the column matrix of coil currents,
i, defined as:
where
n is the total number of coils in the device.
For the purposes of this example, it is assumed that the coils are air–cored. Per the Biot–Savart law [
24], the field at the sphere’s position in the absence of the sphere is the linear superposition of field contributions created by each of the coils, and the contribution of any particular coil is linearly proportional to the current in that coil. The dipole moment,
m, can then be related to the coil currents by a
matrix,
M, as
The term in each column of M represents the per–unit current contribution of a corresponding coil to the flux density (and therefore, the sphere’s dipole moment) at the sphere’s location.
The derivatives of flux density with respect to position can then be represented in terms of contributions from each of the coils in the machine by
matrices
,
, and
, defined as:
The matrix for of the dipole force Equation (
2) can then be summarized in matrix notation as:
Equation (
8) shows that the force in each direction is quadratic in coil current. Note that the
matrix that forms the core of each quadratic force expression is
not symmetric. An equivalent symmetric form that would produce the same forces is
, but the “natural” non–symmetric form lends itself to a very convenient decomposition:
To solve for the currents needed to produce a desired force at position
x, dipole moment
m is first selected arbitrarily. Once
m is selected, coil currents can be computed by solving a linear problem to determine
i. For convenience (
9) can be represented more succinctly as:
There are six rows in
G, but many designs (e.g., Reference [
21]) use more than six coil currents to avoid singularities. The solution for the current is:
where
is the pseudo–inverse of
G, since the system may be under–determined. If there are only six currents,
. Note that for
m and
f to be selected arbitrarily, the rank of
G must be at least six. For cases in which the rank of
G is less than six, the range of valid combinations of
f and
m is limited to those that fall within the column space of
G.
Equation (
11) is a bias linearization solution because the coil currents depend linearly on each desired force component and have a bias component dictated by the choice of
m. Since
m is chosen
a priori (thereby selecting the solution for
),
i depends temporally only on the temporal value of
f. The decomposition into the form of (
9) converts a difficult simultaneous quadratic problem into a simple linear problem, and the choice of
m parameterizes all solutions for coil current. The rows of
M could be thought of as spanning a space of possible bias currents, and the choice of
m selects which bias vector is actually employed in that space. In the case of the permeable sphere, the bias space arises naturally because the sphere’s dipole moment is only a function of the three flux density components at the sphere’s location. The force is produced by the gradients of flux acting on the selected dipole moment.
The usual ways of generating the current–to–force relationships for radial magnetic bearings (see Reference [
5]) result in a quadratic system of equations typically represented as:
where
and
are indefinite symmetric matrices. Previously, computation of bias linearization strategies has been approached by assuming that:
and solving a problem equivalent to (
12) for a
bias linearization matrix
C that satisfies:
Numerically intensive procedures are typically used to find solutions to (
14). However, if the force matrices could either be derived in or converted to the same form as (
8), computation of bias linearization current sets for radial magnetic bearings would be a simple computation, that is, (
11).
3. Radial Magnetic Bearing with Sinusoidal Flux Variation
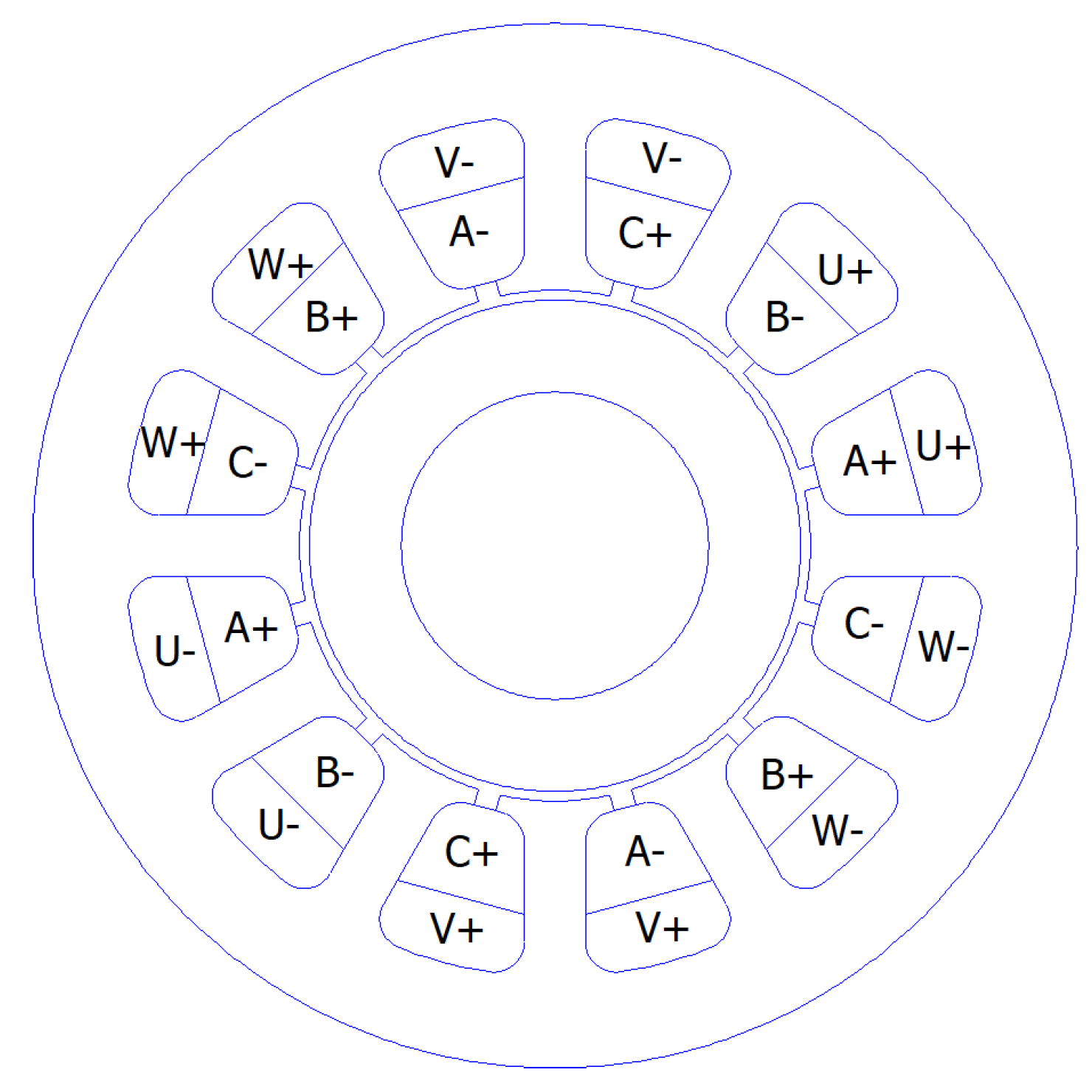
As an intermediate step between force on a permeable sphere and force on a radial magnetic bearing with an even number of poles, the special case of a radial magnetic bearing with sinusoidally distributed flux on the surface of the rotor will be considered. This arrangement often arises in “bearingless” induction motors. These motors use a primary sinusoidal winding to generate torque and a secondary sinusoidal winding to produce a different harmonic of flux density that controls the motor’s bearing forces. The history of this sort of motor is reviewed in Reference [
25]. A representative layout is shown in
Figure 2. With reference to
Figure 2, the ABC winding is the primary three–phase, four–pole winding, and the UVW winding is the secondary three–phase, two–pole winding. The purpose of examining this motor is that its bearing force equations can be “naturally” derived in a form similar to (
8). This derivation suggests the method of converting the equations for a radial magnetic bearing with discrete poles into the form of (
8).
Force on the rotor of a magnetic bearing is typically computed using Maxwell’s Stress Tensor [
26]. Assuming that the rotor’s relative magnetic permeability is
, all flux passes normal to the rotor, and the differential force on the surface of the rotor is:
where
is the magnetic permeability of free space and
is a unit vector pointing outward normal to the rotor. The total force can be obtained
where
h and
R are the axial length and radius of the rotor, respectively. Consider the case where the flux density is composed of two sinusoidal components from different harmonics:
in which
j and
k are positive-valued integers. In a typical bearingless motor,
and
with the sinusoidal flux created by windings distributed in an approximately sinusoidal pattern in a large number of stator slots. Substituting (
17) into (
16) and evaluating the resulting integrals yields:
Through orthogonality of sines and cosines (as shown for continuous functions in Reference [
27] and for discrete vectors of sines and cosines in
Appendix A), harmonics only interact to produce force if the difference in the order of the harmonics is exactly one.
Equation (
18) can be recognized as a bias linearization solution for the selection of flux components needed to produce any desired force. The magnitudes of the
j component can be held constant, and the amplitudes of the
k component are linearly proportional to the desired force (or vice versa). For example, if
, the relationship between flux and force can be written in the same form as (
8),
where
m and
b are assumed to be as defined in (
20) and (
21):
and (
22) follows directly from (
20) and (
21)
By inspection of (
18), the
and
matrices are then defined by:
In this case, flux density column matrix
b substitutes for current
i because (
18) is posed in terms of flux densities rather than currents.
More generally, the implication of (
18) is that the harmonics of flux density can be broken up into even– and odd–numbered harmonics. Even–numbered harmonics can never interact with other even–numbered harmonics because the difference in order of the harmonics is never equal to one. Similarly, odd–numbered harmonics never interact with other odd–numbered harmonics. Therefore, even–numbered harmonics can be used for biasing and odd–numbered harmonics for control (or vice versa). The interactions of the harmonics can be cast into the same form as (
19)–(
21) where the sizes of the matrices grow to incorporate the extra harmonics considered. If additional harmonics are used, the problem to be solved becomes under–determined and has many solutions in addition to the arbitrary choice of amplitude of the biasing components. Essentially, posing the problem of force on a radial magnetic bearing in terms of interacting harmonics allows the problem to be decomposed into the easy-to-solve form of (
19).
4. Current–Controlled Radial Magnetic Bearing
Although the results from the previous section in terms of rotor flux density harmonics shed light on how a radial magnetic bearing can be decomposed into an easily bias–linearizable form, radial magnetic bearings are typically idealized as contributions from a number of “point” poles located at even intervals over the surface of the rotor rather than as a flux density that varies smoothly over the surface of the rotor. Furthermore, magnetic bearings are typically controlled by imposing currents in the bearing coils, not by directly driving flux density in the gaps. The objective of this section is to derive a separation that is equivalent to (
9) for a magnetic bearing with evenly spaced and sized discrete poles by recasting the values of flux density at the bearing’s discrete poles into odd and even harmonics, then tying that gap flux density back to coil currents.
Consider a non–dimensionalized symmetric magnetic bearing with an even number of poles (similar to the non–dimensionalization described in Reference [
20]) where the relationships between dimensional current, gap flux density, and force are related to non–dimensional quantities by:
In (
25) through (
27),
N is the number of turns per pole;
g is the nominal air gap length;
a is the projected pole area; and
is the saturation flux density in the bearing iron. A common magnetic bearing geometry is shown below in
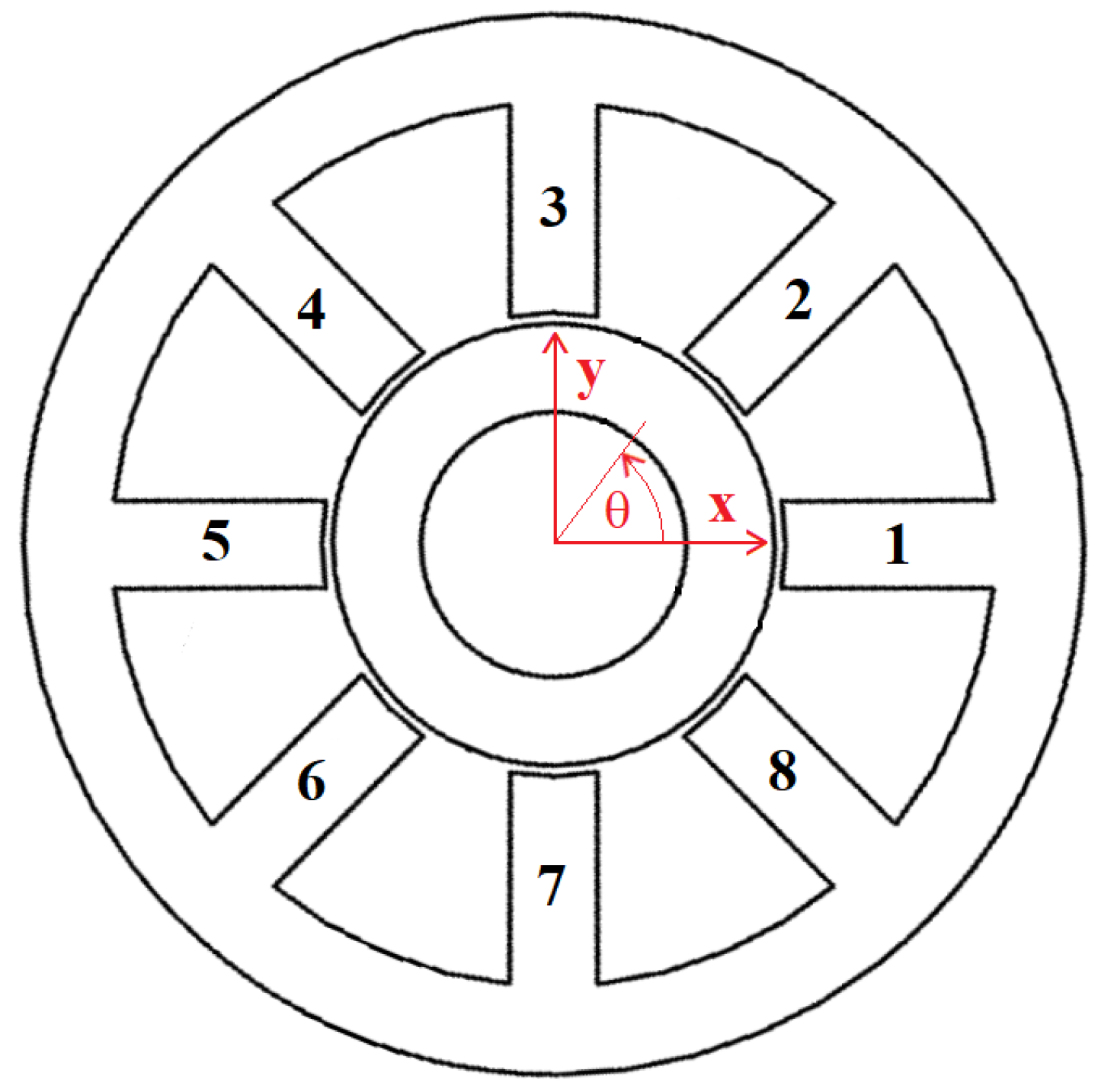
Figure 3.
Pole angle
is defined as a row vector with
n elements indicating the locations of all of the bearing’s poles:
where
n denotes the number of poles in the bearing. Here,
n is assumed to be an even number. Since there is a set of discrete poles, force can be evaluated via Maxwell’s Stress Tensor by summing the contributions from all the poles. This summation is written in matrix form as:
in which
b is a column vector with
n elements denoting the nondimensional flux densities at each pole, and
and
are
diagonal matrices that indicate the contribution of each pole to forces in the
x- and
y-directions respectively:
Because the bearing’s poles are evenly spaced and of the same size, one can define matrix
P to be an orthonormal matrix of normalized Discrete Fourier Transform (DFT) basis functions [
28] that maps flux density at each of the poles onto the amplitudes of the sine and cosine components at each harmonic:
where
is a single row associated with common mode flux;
is a set of rows associated with even–numbered harmonics; and
is a set of rows associated with odd–numbered harmonics.
The rows of
P are straightforward to write, having one of the following two forms:
or
depending on whether the row is computing the amplitude of the cosine or sine component of the
harmonic. As described in Reference [
28], the
k can range from 0 to
(i.e., due to the Sampling Theorem, higher values of
k alias to lower values). However, if there were rows in
P for both sine and cosine from
, there would be
rows in
P rather than a full–rank
matrix. This dilemma is resolved by noting that both
and
are exactly equal to zero for an even–numbed
n. Those corresponding zero rows are neglected in
P, leaving a square matrix with
n rows. The harmonics are arranged so that the first row is the common mode,
; the second set of rows forms
, the mappings for even–numbered harmonics with
; and the last set of rows forms
, the mapping for odd–numbered harmonics. For example, for an 8–pole bearing, the full–rank
P matrix is:
Since
is the identity matrix, it can be inserted into (
29) without affecting the computed forces:
Considering just the inner part of each force relationship and expanding in terms of the common mode, even, and odd harmonic mappings yields:
Through orthogonality of DFT sinusoids (see
Appendix A),
,
,
and
are all zero matrices:
Rolling up the result from (
37) into (
35) and exploiting the linear relationship between flux density
b and coil currents
i (see Reference [
20]):
yields a complete force expression relating current to force:
However, Gauss’s law [
24] says that the flux through any closed volume must sum to zero. For a radial magnetic bearing with equally sized poles, Gauss’s law means that the common mode flux (equal amounts of flux going onto the rotor from each bearing pole) must be zero. Therefore, the product
must be zero, which is a mathematical way of saying that there is no set of coil currents that can create a common–mode flux. Since
, (
39) simplifies to:
and similarly for the y–direction:
The current–to–force relationships from (
40) and (
41) can now be trivially decomposed into the form of (
19). The decomposition can be done in two different ways, depending on whether the even– or odd–numbered harmonics are select to form the biasing currents:
And again, the linear problem to be solved for current to get the desired force is:
where the
m vector of biasing components can be selected arbitrarily. Equation (
43) defines a manifold of possible bias–linearizing solutions depending on the choice of
m and the choice of weighting factors used in building the pseudo–inverse needed to solve the typically under–constrained linear problem. While the dimension of the parameter space may be high, every choice of parameters leads to a valid control scheme. Since every choice of parameters yields is a valid solution, searching through solutions to find one that optimizes performance with respect to some metric (e.g., lowest power or highest load capacity) is simpler and more reliable than previous numerical schemes that must simultaneously generate and optimize valid bias linearizing solutions.
5. Eight–Pole Radial Magnetic Bearing Example
As a specific example, consider the bias linearization of the 8–pole bearing pictured in
Figure 3. This bearing has previously been considered in Reference [
20]. The bearing example is non–dimensionalized using (
25)–(
27), so no bearing dimensions are needed in this example. For this analysis, it is assumed that the rotor is centered within the stator. As in Reference [
20], the relationship between current applied to the coils and flux in the air gaps for a centered rotor is defined by matrix
:
The matrix is close to the identity matrix, but it screens out common mode current due to Gauss’s law. Since flux through any closed volume must add up to zero, the only solution for the case in which all poles are trying to push equal flux onto the rotor is for the flux to be zero in all gaps.
As shown in
Figure 3, the pole locations are defined as:
With these pole locations, the even and odd harmonic mapping matrices can be defined as in (
34):
The mapping is then constructed by evaluating (
42), where for this example, even–numbered harmonics are used as the bias space:
The resulting version of (
43) is under–determined with five linear equations for eight unknowns. This means that the solution of (
43) requires the choice of three parameters in
m, plus specification of three more constraints. These constraint equations could be selected to minimize power; accommodate failures; or enforce configuration constraints like winding coils in series. In any case, any choice of parameters and constraints leads to a valid solution.
As an example solution, consider the
case. This choice of
m leads to a NSNS biasing scheme for the bearing, whereas
turns out to produce a NNSS scheme. To obtain a power–optimizing solution for the under–determined system, the Moore–Penrose inverse [
29] is employed, yielding the power and load capacity optimizing solution presented in References [
20,
23]:
6. Fault Tolerance
Equation (
43) can also be used to determine sets of bias linearizing currents that accommodate the failure of one or more coils. Since (
43) is under–determined, extra equations can be added to the equation to force the current in the failed coils to be zero in the bias linearization solution. Equation (
52) is a modified version of (
43) that incorporates the constraint matrix
A defining the failed coil currents:
Continuing the eight–pole example, consider the case in which poles 1, 2, and 4 have failed. In this case, the
A matrix denoting the faulted coils is:
Although (
52) has eight equations for eight unknowns in this case, there is still a manifold of possible solutions defined by the arbitrary choice of
m. (Solutions are possible for at least one case of more than three failed coils in an eight–pole bearing with a constrained choice of
m: See
Appendix C.)
A reasonable way to select
m is to pick its elements to minimize power throughout an entire rotor revolution. The bearing force for this example is assumed to be the combination of a steady–state gravitational load and a rotating imbalance load about half the magnitude of the gravitational load:
In practice, the ratio between steady–state and dynamic load will be implementation–specific.
A cost function is formed by integrating the squared current through an entire rotation.
For ease of evaluation, cost function
W can be analytically integrated over
(see
Appendix B). Minimization of
W can then proceed using the function minimization routines built into standard numerical analysis tools. Solutions that minimize
W starting from randomly selected initial guesses are collected in
Table 1. The solution space is well–behaved, converging to a small number of minima. For any particular minimum
,
is also a minimum with the same properties. However, some of the minima are local rather than global: the minimization should be run multiple times to make sure that the best power–minimizing solution is obtained.
The solution for coil current as a function of force using the first solution in
Table 1 is: