Experimental Assessment of Fractional-Order PDD1/2 Control of a Brushless DC Motor with Inertial Load
Abstract
1. Introduction
- after a more detailed discussion of their performances in terms of settling time, rise time, overshoot and settling energy: in case of step response, the three controllers are compared by simulation, while keeping the overshoot constant (Section 5);
- then, the comparison is extended to the response in case of trapezoidal speed law, which is commonly used as reference signal for finite displacements of mechatronic systems, again by adopting a non-dimensional approach (Section 6); and,
- finally, the effects of discrete-time digital implementation of the controller with finite sampling time and short memory effect, suitable for limited capacity microcontrollers, are investigated both by simulations and by experimental tests on a real-world mechatronic test-bench: a position-controlled rotor actuated by a DC brushless motor (Section 7).
2. The Integro-Differential Operator: Definition and Numerical Computation
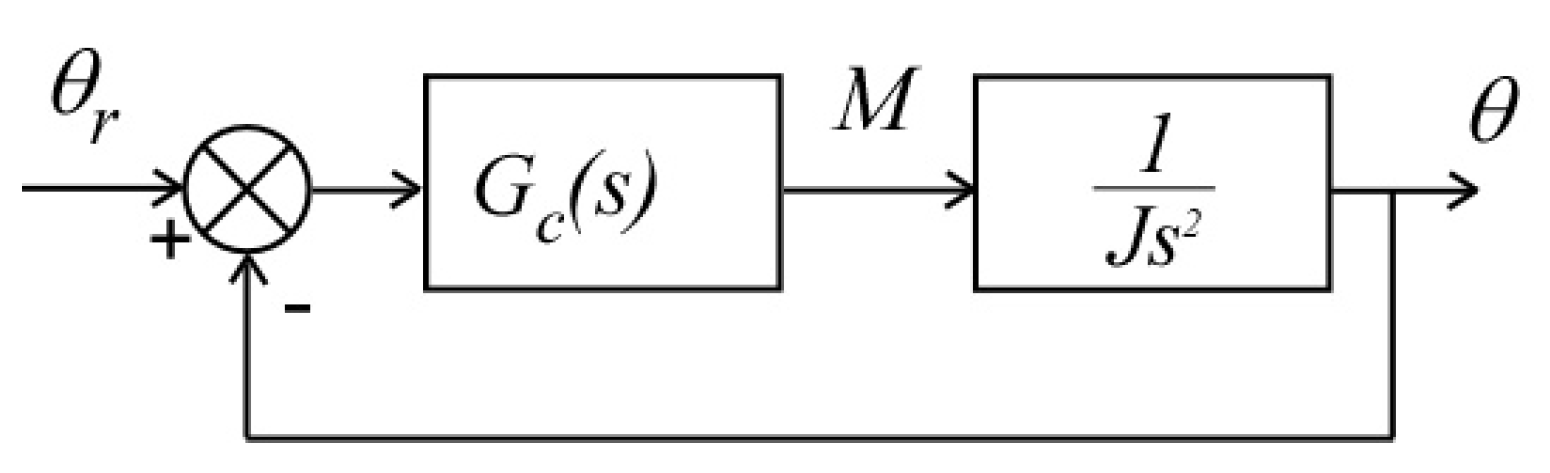
3. Second-Order Linear System with Fractional-Order Control
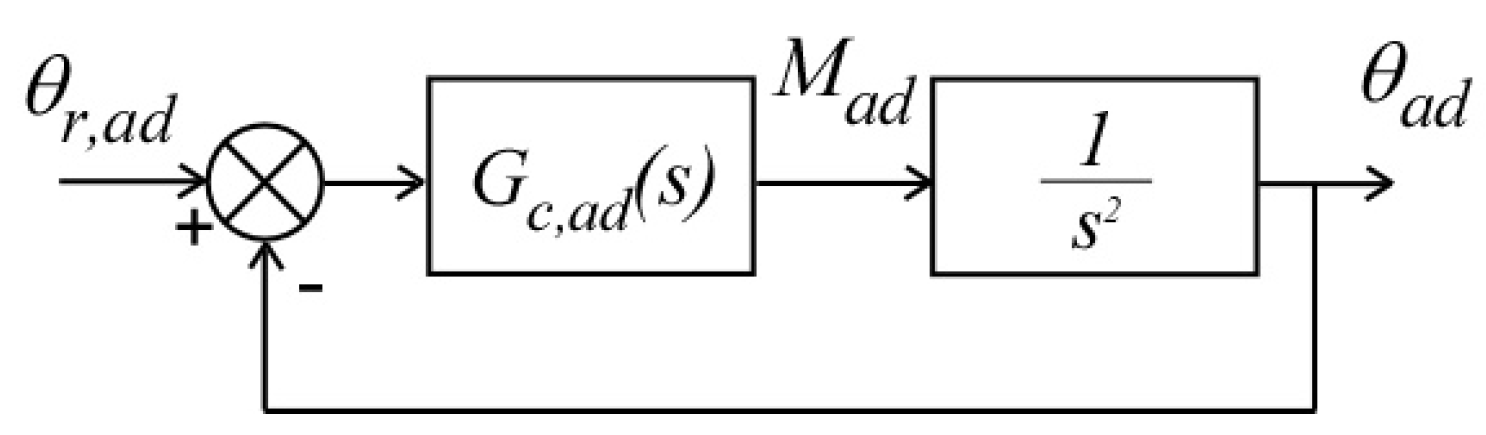
4. Non-Dimensional Model
- when µ = 1 the PDµ controller is a PD controller with ζ = ϕ/2; and,
- when µ = 1/2 the PDµ controller is a PD1/2 controller with φ = ψ
- PD, PDµ, and PDD1/2 controls are compared non-dimensionally by simulation while considering the response to a step input (Section 5);
- the non-dimensional comparison by simulation is then extended to the response to a set-point with trapezoidal speed law, suitable for position control of mechatronic devices (Section 6); and,
- finally, the tuned PD, PDµ, and PDD1/2 controllers are experimentally validated on a mechatronic test bench, with a discrete-time digital implementation that is suited to be executed by microcontrollers with limited computing power (Section 7).
5. Step Response
- settling time to within 2% band;
- rise time from 10% to 90% of the final value;
- overshoot (%); and,
- dimensionless settling energy, being defined as follows [31]:
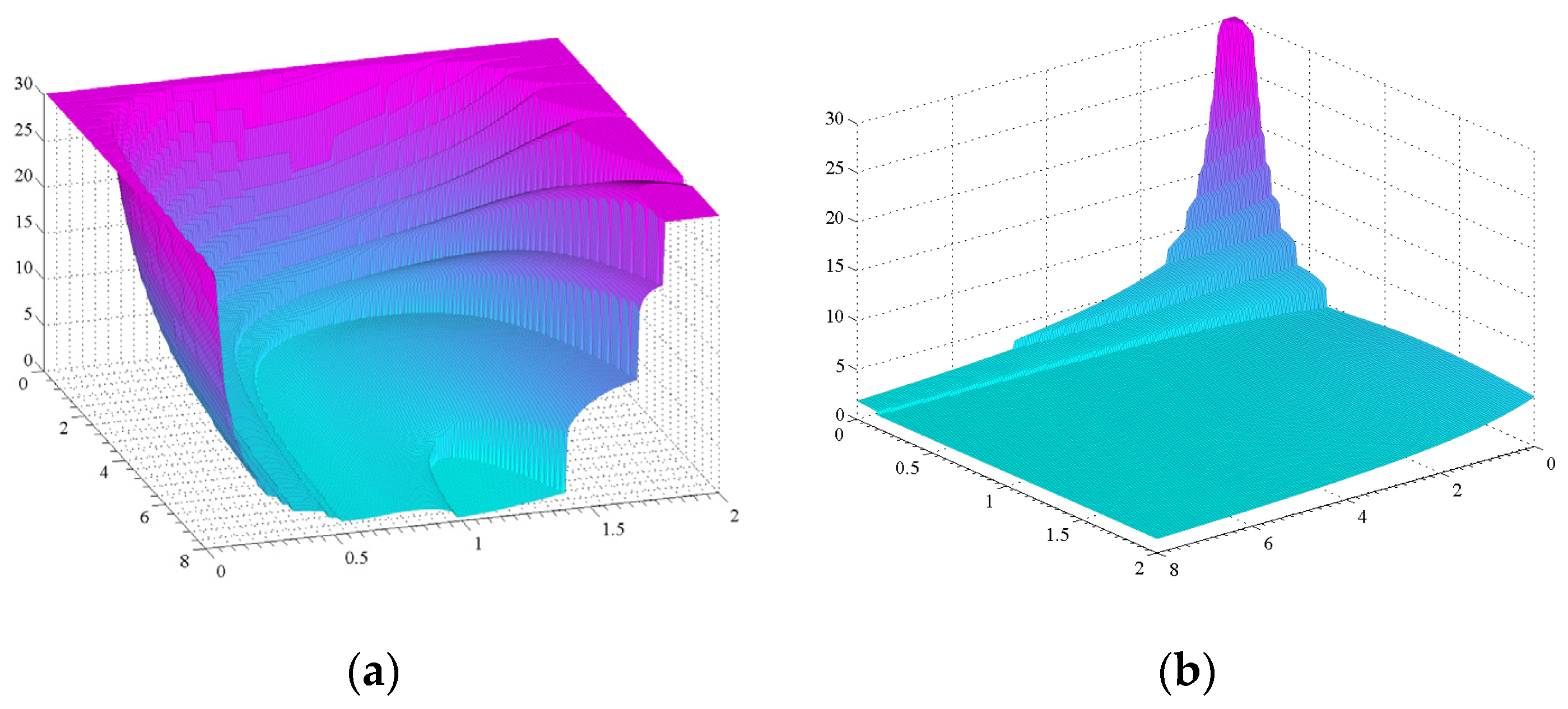
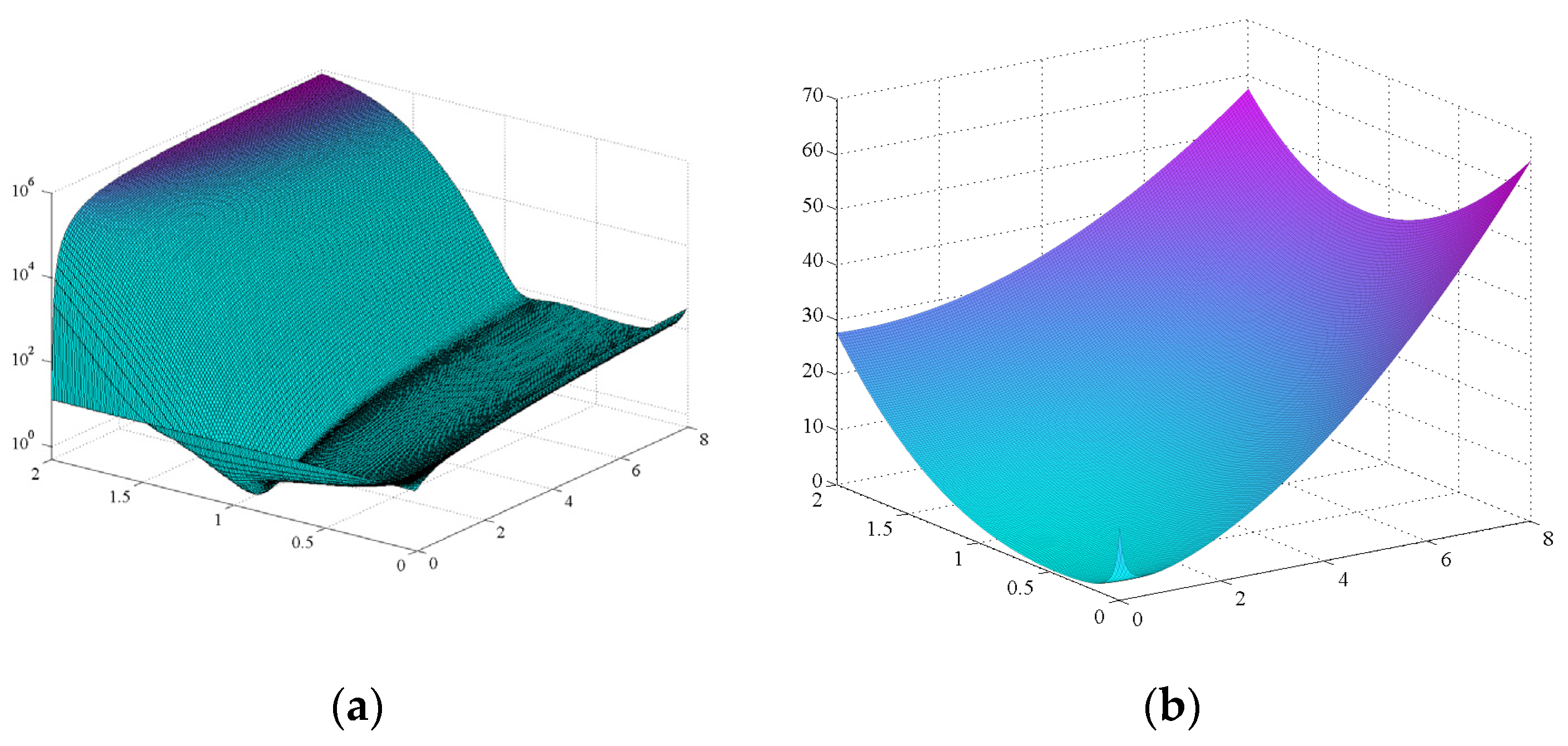
- the 3D surfaces representing the settling time are characterized by discontinuities, which are related to the number of oscillations, which are performed before reaching the 2% band; for the PDµ control, the number of oscillations increases if φ tends to zero or if µ is distant from the unit value; for PDD1/2 this number increases if both ζ and ψ tend to zero (absence of damping);
- overshoot is 100% without any damping (φ = 0 for PDµ, ζ = ψ = 0 for PDD1/2); this graph can be used to impose a lower limit to the total damping: φ for PDµ, the combination of ζ and ψ for PDD1/2; and,
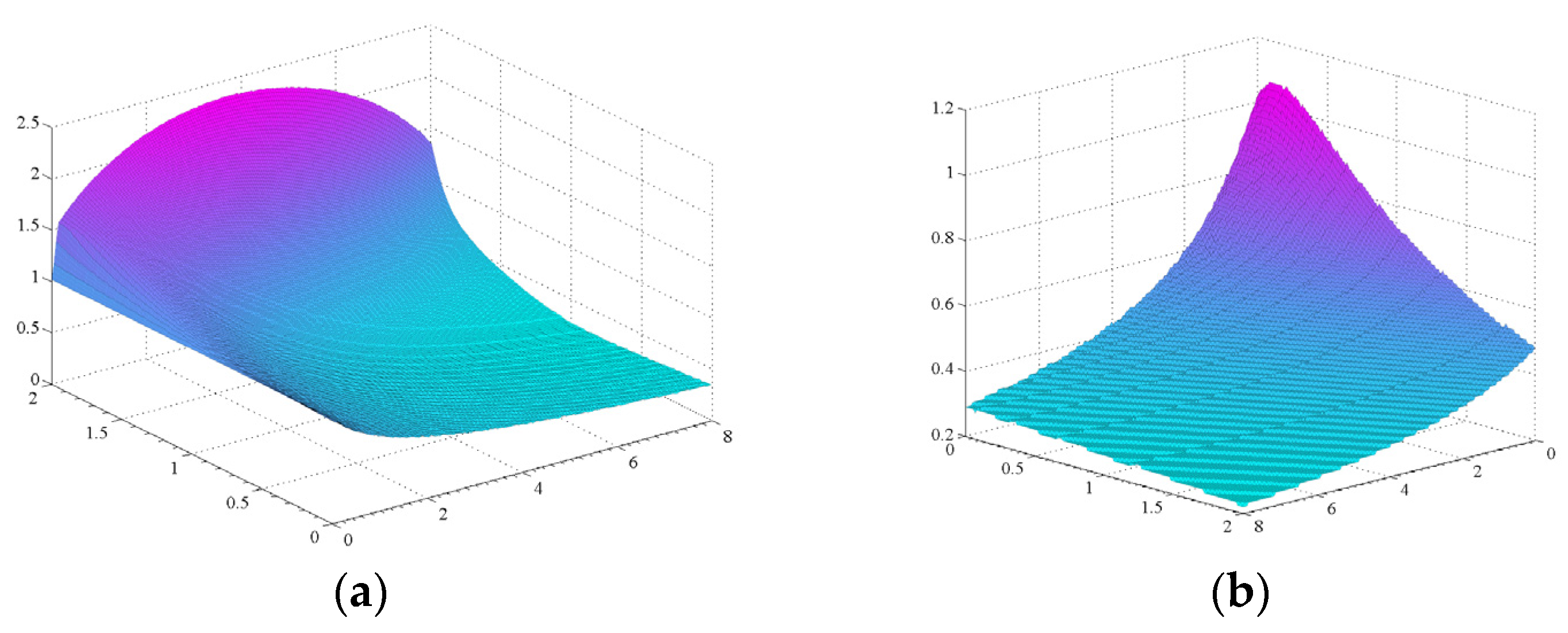
- for the PDµ control, the three-dimensional (3D) graph of the settling energy show that the derivation order should range around the unit value, with an upper limit for φ; for PDD1/2, this graph can be used to impose an upper limit to the total damping (the combination of ζ and ψ).
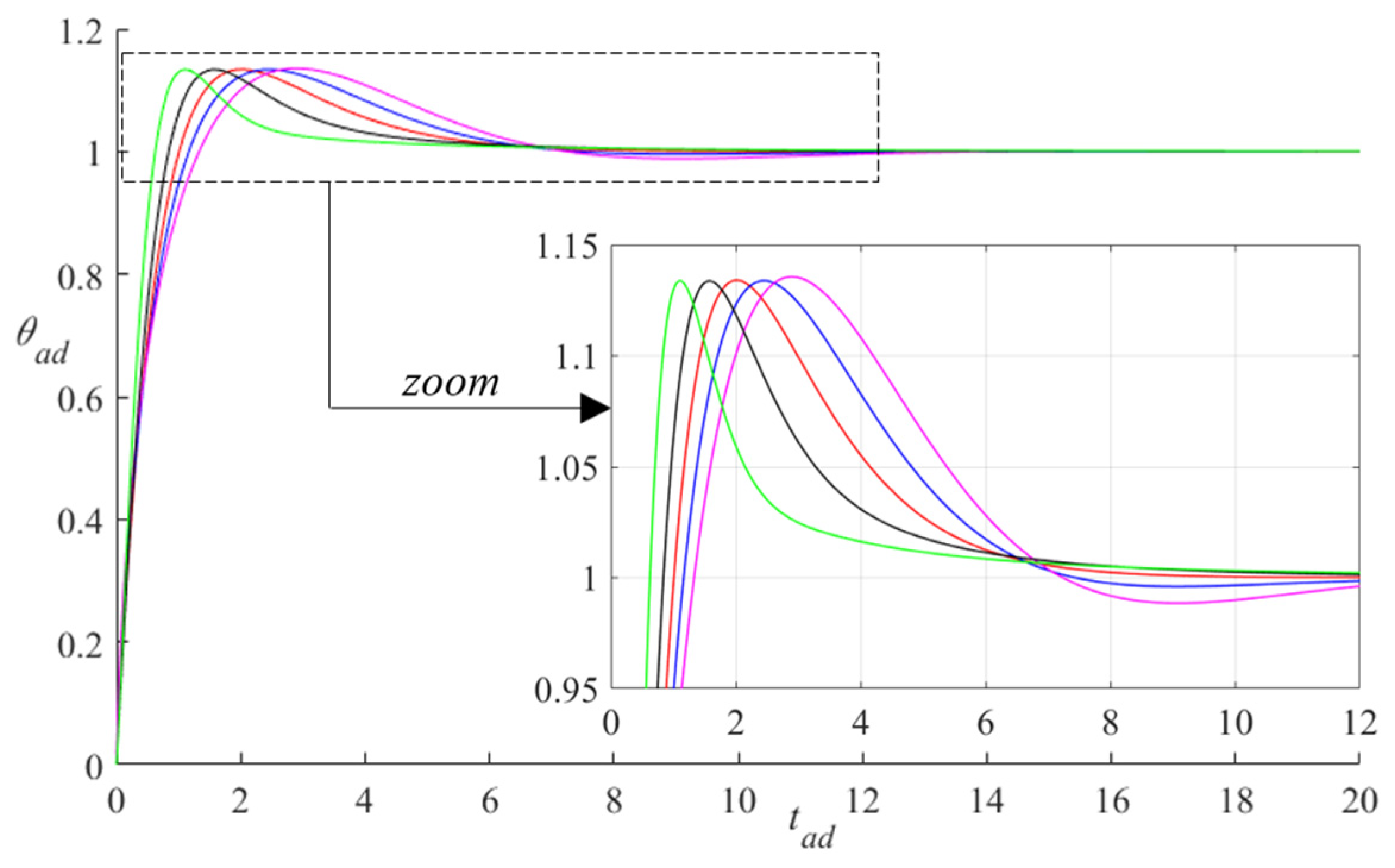
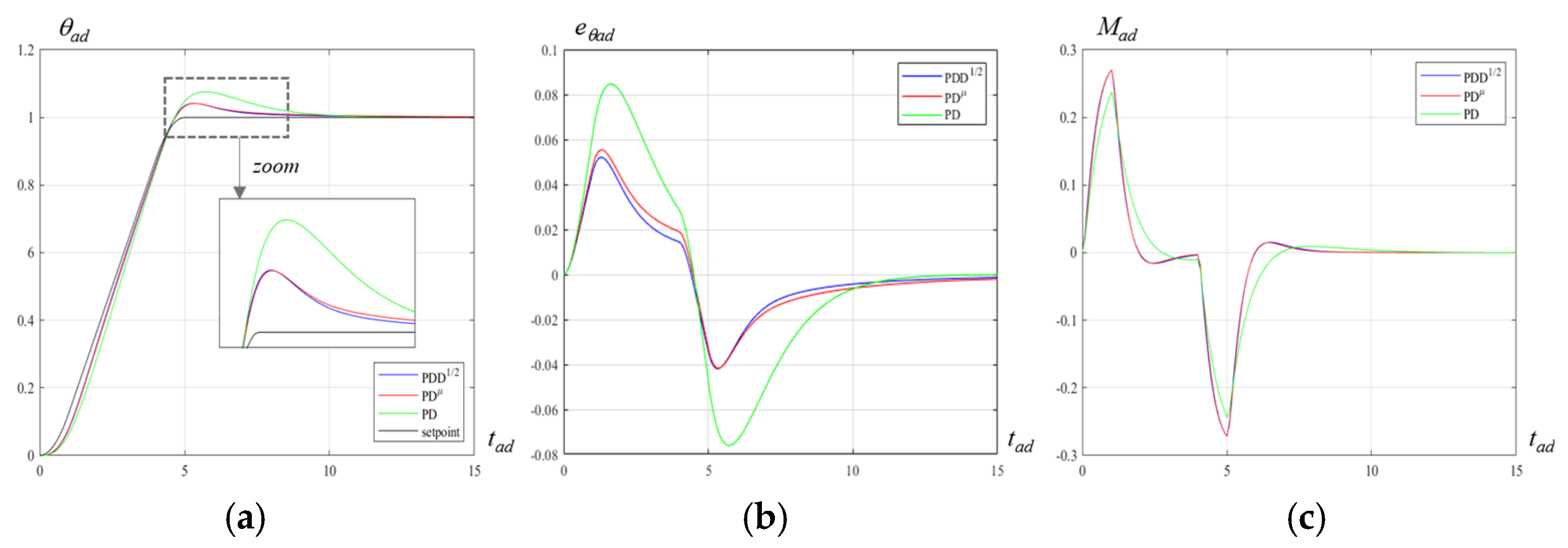
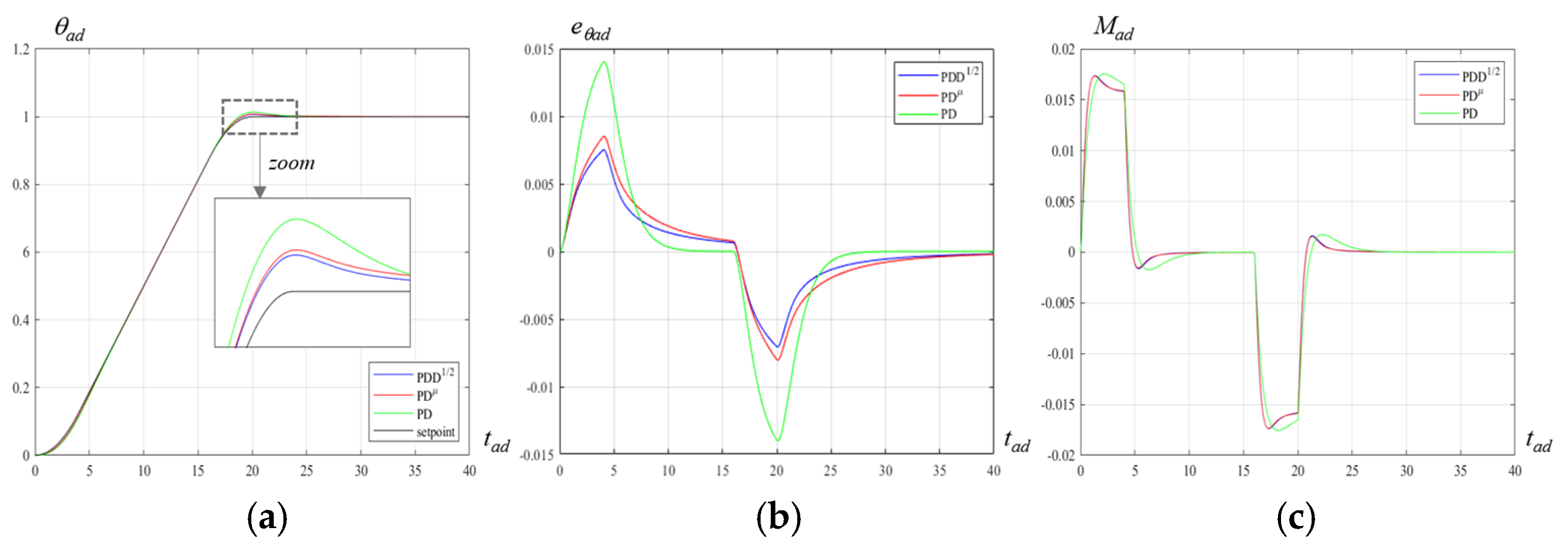
6. Trapezoidal Speed Law Response
- the total dimensionless rotation θad has unit value; and,
- in the first and third phases, acceleration and deceleration are equal in magnitude, and consequently also the duration of these phases is equal; if the total dimensionless duration of the three phases is tad,fin, the duration of the first and third phases is α tad,fin, with 0 < α < 0.5; consequently, the second phase duration is (1–2α) tad,fin.
- by carrying out simulations with discrete-time, limited memory implementations of the controllers: in such a case, the control laws are implemented with sampling time Ts by digital filters with finite memory length n, with Ts, and n limited by the computational power of the controller hardware; and,
- by experimental tests on a physical prototype, to validate the possibility of obtaining the expected performance improvement also in real applications.
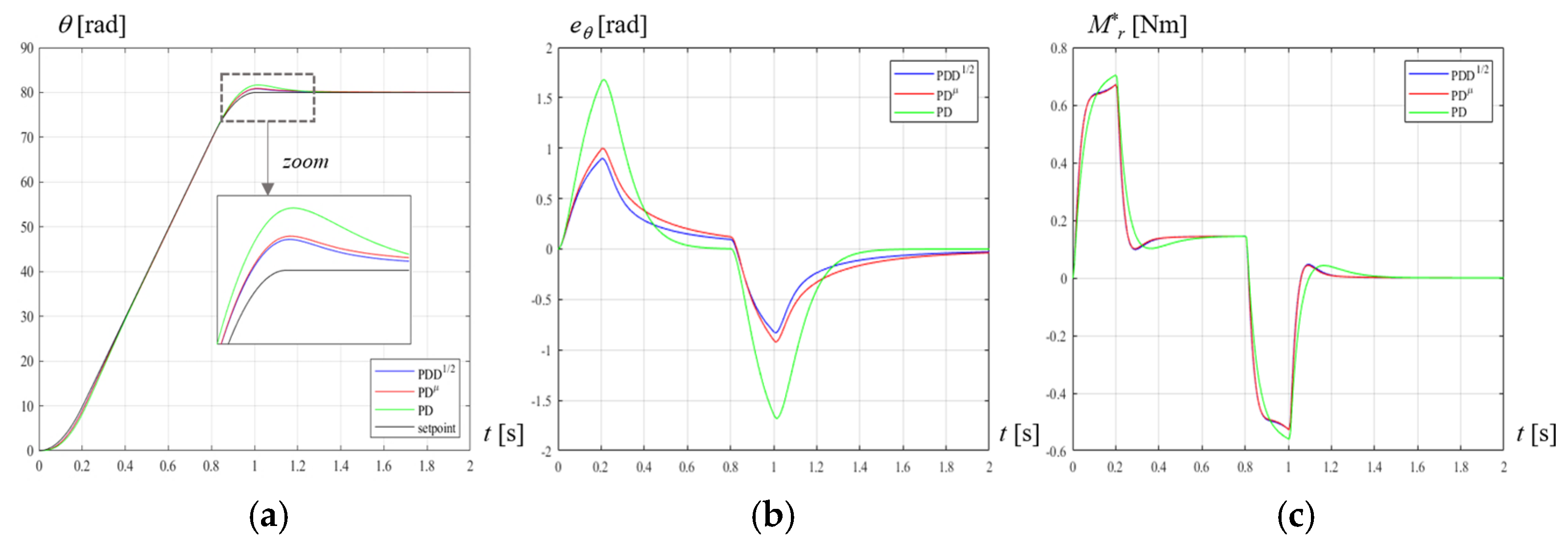
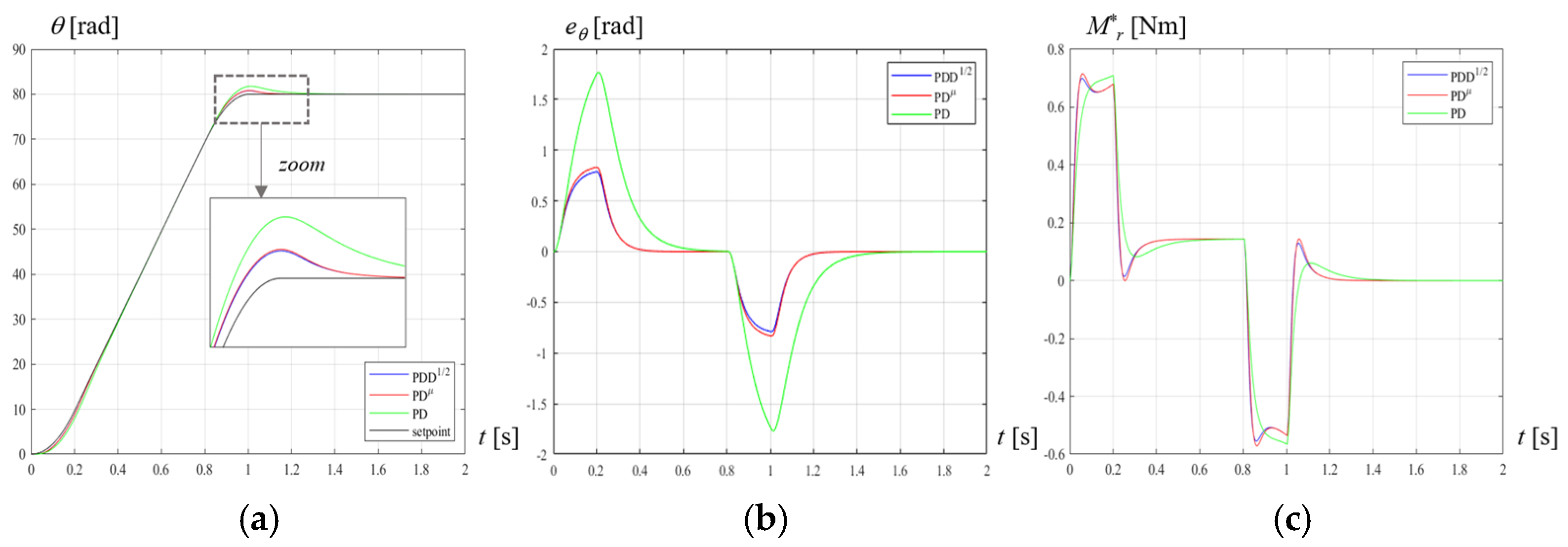
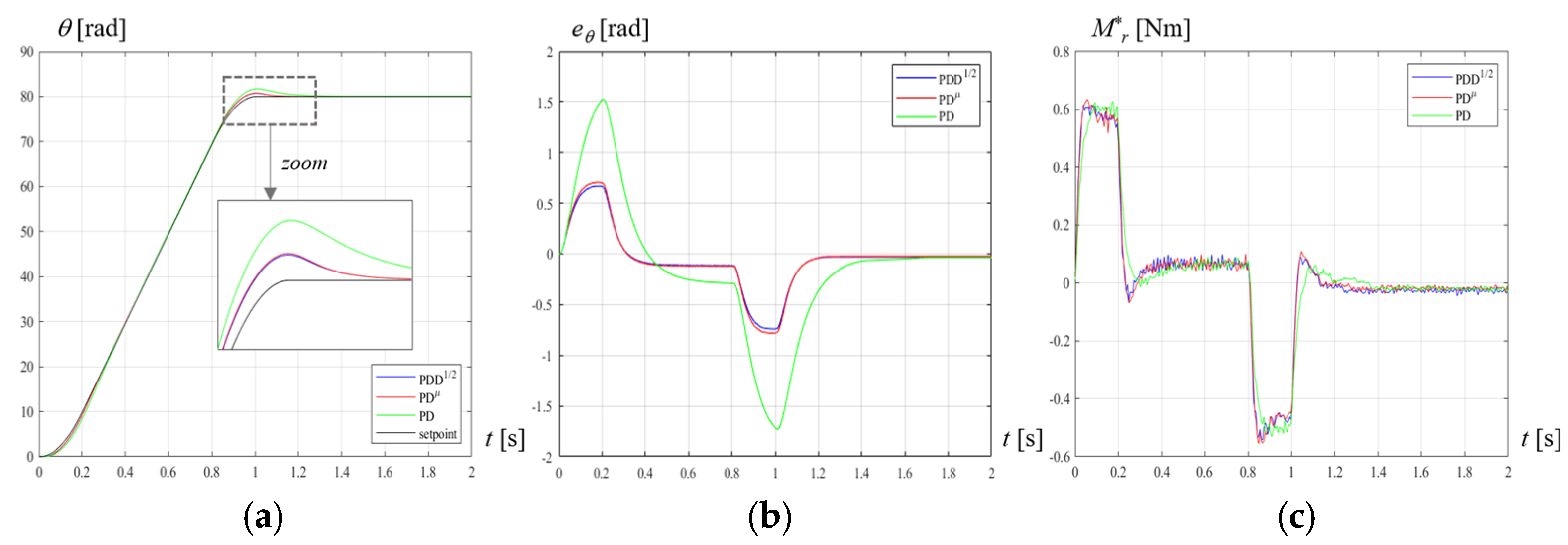
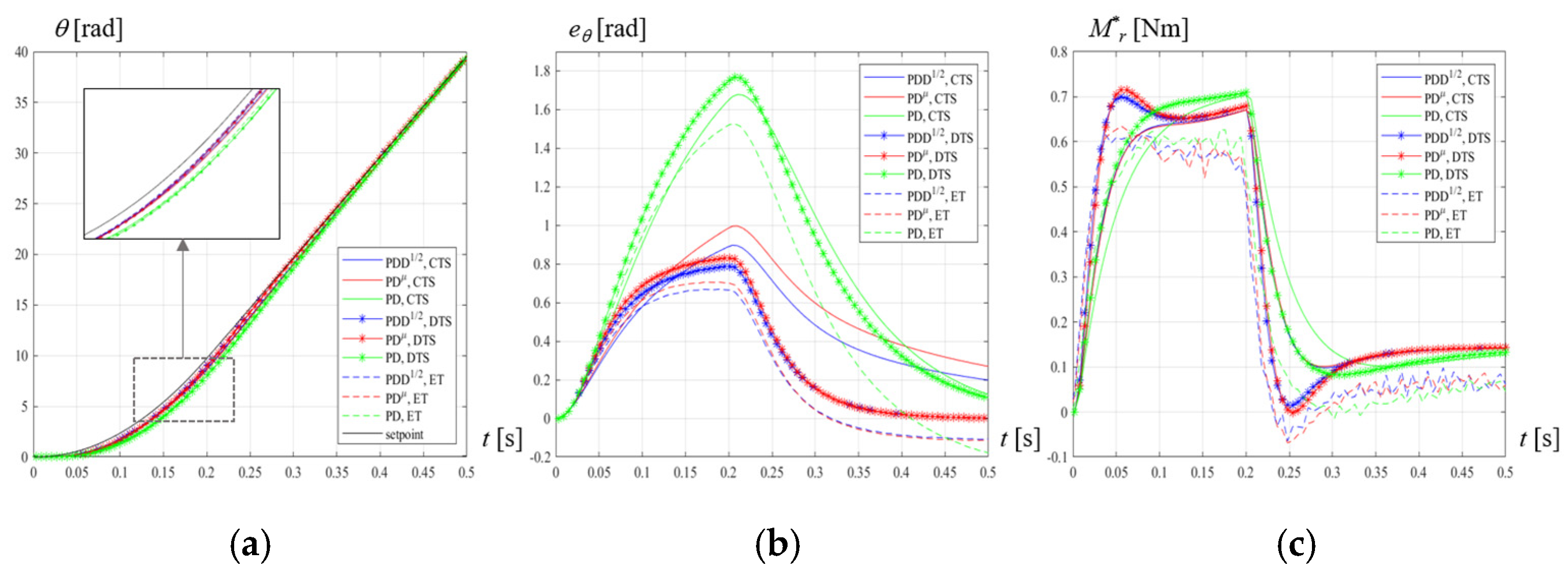
7. Discrete-Time Implementation and Experimental Validation
- The simulated dynamics of the system with the discrete-time digital implementation of the FO controllers exhibits the same advantage with respect to the integer-order controller, which has been evidenced by the continuous-time model, as shown in Figure 16, Figure 17 and Figure 19: the peak tracking error is strongly reduced, and the improvement is even greater than in continuous time (−47% for PDD1/2 and −41% for PDµ in CTS, −55% for PDD1/2, and −53% for PDµ in DTS).
- The percentage decrease of the mean tracking error with respect to PD is similar to the decrease of the maximum tracking error: (−45% for PDD1/2 and −38% for PDµ in CTS, −56% for PDD1/2, and −53% for PDµ in DTS).
- On the other hand, the maximum peak torque is similar or even lower (−4.7% for PDD1/2 and −4.8% for PDµ in C.T.S., −1.5% for PDD1/2 and +0.7% for PDµ in DTS); also the settling energies are similar (−1.4% for PDD1/2 and −1.7% for PDµ in C.T.S., +1.8% for PDD1/2 and +3.1% for PDµ in DTS).
- Discrete-time simulation results and experimental data are in good agreement: the reduction of the peak tracking error with respect to PD is −57% for PDD1/2 and −55% for PDµ; the reduction of the mean tracking error with respect to PD is −53% for PDD1/2 and −50% for PDµ; the variation of maximum peak torque with respect to PD is −1.7% for PDD1/2 and +1.3% for PDµ; and, the variation of settling energy with respect to PD is +0.6% for PDD1/2 and +1.4% for PDµ.
- CTS and DTS both highlight the benefits of FO controllers and can be considered valuable tools for their tuning.
- The difference between PDµ and PDD1/2 is small, but, in the discrete-time implementation, PDD1/2 exhibits slightly better performances, both in simulations and in experimental tests, since it provides slightly lower maximum and mean errors, with lower maximum torque and settling energy.
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; John Wiley & Sons: New York, NY, USA, 1993. [Google Scholar]
- Hilfer, R. Applications of Fractional Calculus in Physics; World Scientific: Singapore, 2000. [Google Scholar]
- Bard, A.J.; Faulkner, L.R. Electrochemical Methods: Fundamentals and Applications, 2nd ed.; John Wiley & Sons: New York, NY, USA, 2001. [Google Scholar]
- Rihan, F.A. Numerical Modeling of Fractional-Order Biological Systems. Abstr. Appl. Anal. 2013, 2013, 816803. [Google Scholar] [CrossRef]
- Gutiérrez, R.E.; Rosário, J.M.; Machado, J.T. Fractional Order Calculus: Basic Concepts and Engineering Applications. Math. Probl. Eng. 2010, 2010, 375858. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional-order systems and PIλDμ controllers. IEEE Trans. Autom. Control 1999, 44, 208–213. [Google Scholar] [CrossRef]
- Yeroglu, C.; Tan, N. Note on fractional-order proportional-integral-differential controller design. IET Control Theory Appl. 2012, 5, 1978–1989. [Google Scholar] [CrossRef]
- Duma, R.; Dobra, P.; Trusca, M. Embedded application of fractional order control. Electron. Lett. 2012, 48, 1526–1528. [Google Scholar] [CrossRef]
- Beschi, M.; Padula, F.; Visioli, A. The generalised isodamping approach for robust fractional PID controllers design. Int. J. Control 2015, 90, 1157–1164. [Google Scholar] [CrossRef]
- Sondhi, S.; Hote, Y.V. Fractional order PID controller for perturbed load frequency control using Kharitonov’s theorem. Electr. Power Energy Syst. 2016, 78, 884–896. [Google Scholar] [CrossRef]
- Kesarkar, A.A.; Selvaganesan, N. Tuning of optimal fractional-order PID controller using an artificial bee colony algorithm. Syst. Sci. Control Eng. 2015, 3, 99–105. [Google Scholar] [CrossRef]
- Khubalkar, S.; Chopade, A.; Junghare, A.; Aware, M.; Das, S. Design and Realization of Stand-Alone Digital Fractional Order PID Controller for Buck Converter Fed DC Motor. Circuits Syst. Signal Process. 2016, 35, 2189–2211. [Google Scholar] [CrossRef]
- Saidi, B.; Amairi, M.; Najar, S.; Aoun, M. Bode shaping-based design methods of a fractional order PID controller for uncertain systems. Nonlinear Dyn. 2015, 80, 1817–1838. [Google Scholar] [CrossRef]
- Anantachaisilp, P.; Lin, Z. Fractional Order PID Control of Rotor Suspension by Active Magnetic Bearings. Actuators 2017, 6, 4. [Google Scholar] [CrossRef]
- Yang, J.; Dong, L.; Liao, X. Fractional order PD controller based on ADRC algorithm for DC motor. In Proceedings of the IEEE Transportation Electrification Conference and Expo, ITEC Asia-Pacific 2014, Beijing, China, 31 August–3 September 2014. [Google Scholar]
- Jin, Y.; Luo, Y.; Wang, C.; Chen, Y.Q. LabView Based Experimental Validation of Fractional Order Motion Controllers. In Proceedings of the 2009 Chinese Control and Decision Conference, Guilin, China, 17–19 January 2009; pp. 323–328. [Google Scholar]
- Dimeas, I.; Petras, I.; Psychalinos, C. New analog implementation technique for fractional-order controller: A DC motor control. AEU Int. J. Electron. Commun. 2017, 78, 192–200. [Google Scholar] [CrossRef]
- Sun, G.; Ma, Z.; Yu, J. Discrete-Time Fractional Order Terminal Sliding Mode Tracking Control for Linear Motor. IEEE Trans. Ind. Electron. 2018, 65, 3386–3394. [Google Scholar] [CrossRef]
- Haji, V.; Monje, C. Fractional-order PID control of a chopper-fed DC motor drive using a novel firefly algorithm with dynamic control mechanism. Soft Comput. 2018, 22, 6135–6146. [Google Scholar] [CrossRef]
- Chen, S.Y.; Li, T.H.; Chang, C.H. Intelligent fractional-order backstepping control for an ironless linear synchronous motor with uncertain nonlinear dynamics. ISA Trans. 2019, 89, 218–232. [Google Scholar] [CrossRef] [PubMed]
- Hekimoglu, B. Optimal Tuning of Fractional Order PID Controller for DC Motor Speed Control via Chaotic Atom Search Optimization Algorithm. IEEE Access 2019, 7, 38100–38114. [Google Scholar] [CrossRef]
- Puangdownreong, D. Fractional order PID controller design for DC motor speed control system via flower pollination algorithm. Trans. Electr. Eng. Electron. Commun. 2019, 17, 14–23. [Google Scholar] [CrossRef]
- Zheng, W.; Luo, Y.; Pi, Y.; Chen, Y. Improved frequency-domain design method for the fractional order proportional-integral-derivative controller optimal design: A case study of permanent magnet synchronous motor speed control. IET Control Theory Appl. 2018, 12, 2478–2487. [Google Scholar] [CrossRef]
- Lino, P.; Maione, G. Cascade Fractional-Order PI Control of a Linear Positioning System. IFAC PapersOnLine 2018, 51, 557–562. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, X.; Xia, J.; Shen, H.; Meng, B. Adaptive sliding mode output tracking control based-FODOB for a class of uncertain fractional-order nonlinear time-delayed systems. Sci. China Technol. Sci. 2020. [Google Scholar] [CrossRef]
- Meng, B.; Wang, X.; Zhang, Z.; Wang, Z. Necessary and sufficient conditions for normalization and sliding mode control of singular fractional-order systems with uncertainties. Sci. China Inf. Sci. 2020. [Google Scholar] [CrossRef]
- Bruzzone, L.; Bozzini, G. Application of the PDD1/2 algorithm to position control of serial robots. In Proceedings of the 28th IASTED International Conference Modelling, Identification and Control (MIC 2009), Innsbruck, Austria, 16–18 February 2009; pp. 225–230. [Google Scholar]
- Bruzzone, L.; Bozzini, G. PDD1/2 control of purely inertial systems: Nondimensional analysis of the ramp response. In Proceedings of the 30th IASTED International Conference Modelling, Identification, and Control (MIC 2011), Innsbruck, Austria, 14–16 February 2011; pp. 308–315. [Google Scholar]
- Bruzzone, L.; Fanghella, P. Fractional order control of the 3-CPU parallel kinematics Machine. In Proceedings of the 32nd IASTED International Conference Modelling, Identification and Control (MIC 2013), Innsbruck, Austria, 11–13 February 2013; pp. 286–292. [Google Scholar]
- Bruzzone, L.; Fanghella, P. Fractional-order control of a micrometric linear axis. J. Control Sci. Eng. 2013, 2013, 947428. [Google Scholar] [CrossRef]
- Bruzzone, L.; Fanghella, P. Comparison of PDD1/2 and PDμ position controls of a second order linear system. In Proceedings of the 33rd IASTED International Conference on Modelling, Identification and Control (MIC 2014), Innsbruck, Austria, 17–19 February 2014; pp. 182–188. [Google Scholar]
- Corinaldi, D.; Palpacelli, M.; Carbonari, L.; Bruzzone, L.; Palmieri, G. Experimental analysis of a fractional-order control applied to a second order linear system. In Proceedings of the 10th IEEE/ASME International Conference on Mechatronic and Embedded Systems and Applications (MESA 2014), Senigallia, Italy, 10–12 September 2014. [Google Scholar]
- Machado, J.T. Fractional-order derivative approximations in discrete-time control systems. J. Syst. Anal. Model. Simul. 1999, 34, 419–434. [Google Scholar]
- Xue, D. FOTF Toolbox for Fractional-Order Control Systems. In Applications in Control; Petráš, I., Ed.; De Gruyter: Berlin, Germany; Boston, MA, USA, 2019; pp. 237–266. [Google Scholar]
- Das, S. Functional Fractional Calculus; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Matusu, R.; Senol, B.; Pekar, L. Robust stability of Fractional-Order Linear Time-Invariant systems: Parametric versus unstructured uncertainty models. Complexity 2018, 2018, 8073481. [Google Scholar] [CrossRef]
- Lu, J.-G.; Chen, G. Robust stability and stabilization of Fractional-Order interval systems: An LMI approach. IEEE Trans. Autom. Control 2009, 54, 1294–1298. [Google Scholar]
- Mohsenipour, R.; Jegarkandi, M.F. Robust stability analysis of fractional-order interval systems with multiple time delays. Int. J. Robust Nonlinear Control 2019, 29, 1823–1839. [Google Scholar] [CrossRef]

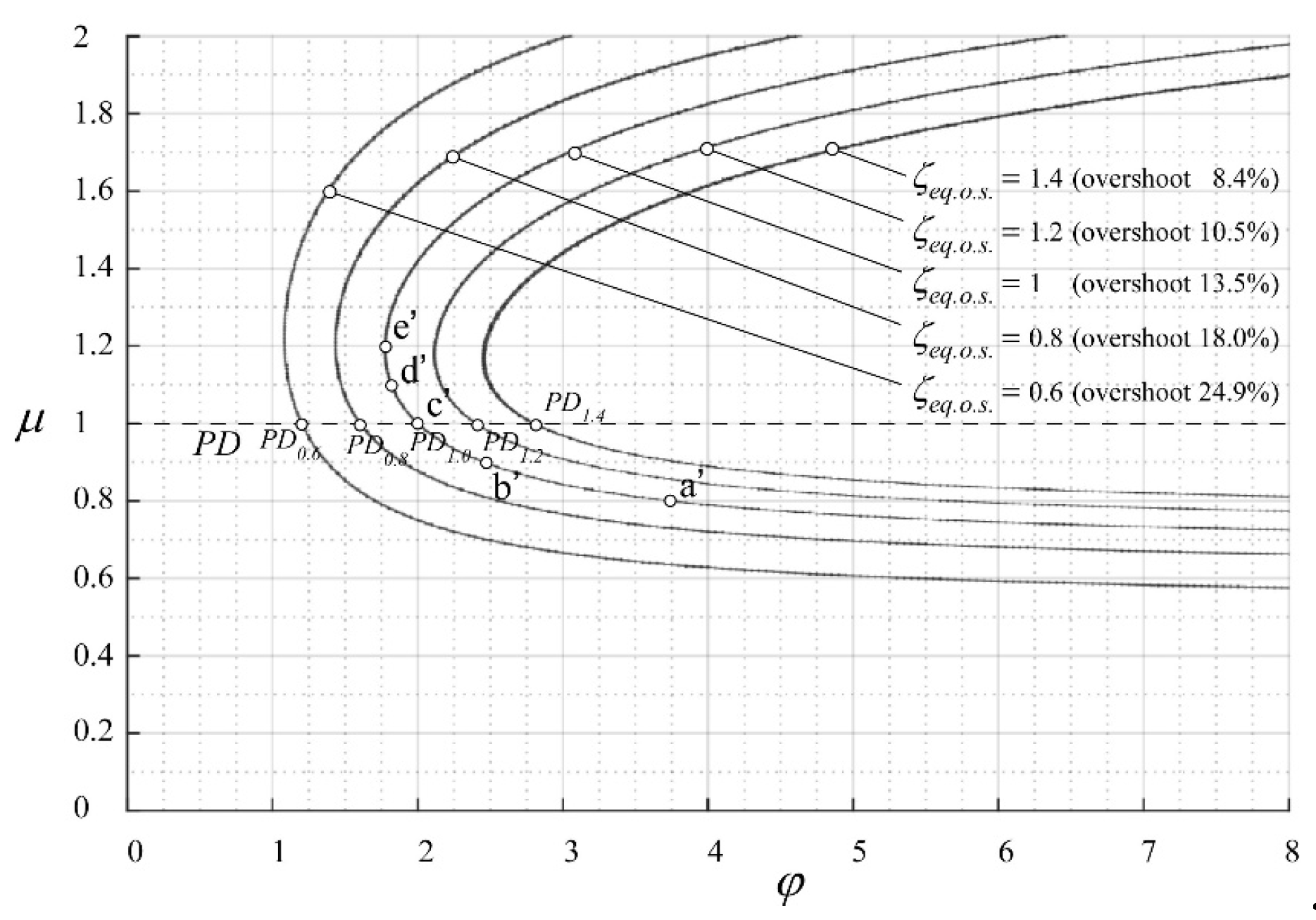
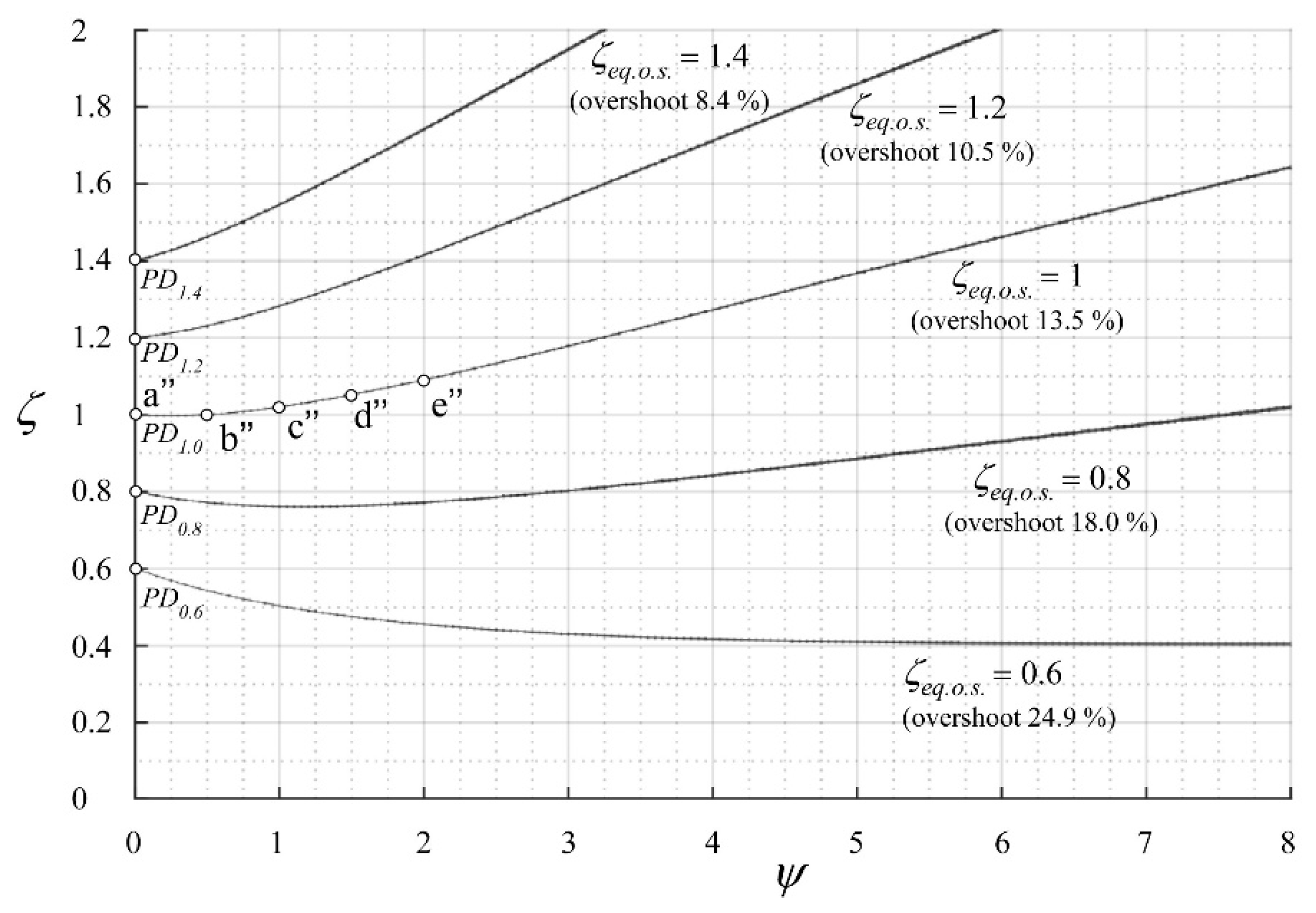





| Parameter Set | Colour in Figure 9 | µ | φ | Dimensionless Settling Energy | Dimensionless Settling Time | Dimensionless Rise Time |
|---|---|---|---|---|---|---|
| a’ (PDµ) | 0.8 | 3.75 | 17.84 | 3.46 | 0.46 | |
| b’ (PDµ) | 0.9 | 2.46 | 5.28 | 4.78 | 0.62 | |
| c’ (PD, ζ = 1) | 1 | 2 | 3.14 | 5.41 | 0.73 | |
| d’ (PDµ) | 1.1 | 1.82 | 22.60 | 5.87 | 0.84 | |
| e’ (PDµ) | 1.2 | 1.76 | 137.28 | 6.28 | 0.95 |
| Parameter Set | Colour in Figure 10 | ζ | ψ | Dimensionless Settling Energy | Dimensionless Settling Time | Dimensionless Rise Time |
|---|---|---|---|---|---|---|
| a’’ (PD, ζ = 1) | 1 | 0 | 3.14 | 5.41 | 0.73 | |
| b’’ (PDD1/2) | 1 | 0.5 | 3.36 | 4.66 | 0.63 | |
| c’’ (PDD1/2) | 1.02 | 1 | 4.08 | 4.07 | 0.57 | |
| d’’ (PDD1/2) | 1.05 | 1.5 | 5.25 | 3.58 | 0.51 | |
| e’’ (PDD1/2) | 1.09 | 2 | 6.83 | 3.19 | 0.46 |
| Kp [Nm/rad] | Kd [Nms/rad] | Khd [Nms1/2/rad] | Kfd [Nms0.8/rad] | Total Rotation θr [rad] | Rotation Time tfin [s] | Sample Time Ts [s] | |
|---|---|---|---|---|---|---|---|
| PD | 0.25 | 3.236 × 10−2 | - | - | 80 | 1 | 0.006 |
| PDD1/2 | 3.527 × 10−2 | 0.127 | - | ||||
| PDµ | - | - | 0.105 |
| eθ,max [rad] | eθ,mean [rad] | M*max [Nm] | Es [N2m2s] | ||
|---|---|---|---|---|---|
| PD | CTS | 1.679 | 0.624 | 0.704 | 22.016 |
| DTS | 1.769 | 0.632 | 0.710 | 23.774 | |
| ET | 1.732 | 0.626 | 0.627 | 18.217 | |
| PDD1/2 | CTS | 0.897 | 0.346 | 0.671 | 21.699 |
| DTS | 0.789 | 0.279 | 0.699 | 24.201 | |
| ET | 0.741 | 0.296 | 0.616 | 18.319 | |
| PDµ | CTS | 0.997 | 0.386 | 0.670 | 21.631 |
| DTS | 0.832 | 0.294 | 0.715 | 24.508 | |
| ET | 0.782 | 0.313 | 0.635 | 18.477 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bruzzone, L.; Fanghella, P.; Baggetta, M. Experimental Assessment of Fractional-Order PDD1/2 Control of a Brushless DC Motor with Inertial Load. Actuators 2020, 9, 13. https://doi.org/10.3390/act9010013
Bruzzone L, Fanghella P, Baggetta M. Experimental Assessment of Fractional-Order PDD1/2 Control of a Brushless DC Motor with Inertial Load. Actuators. 2020; 9(1):13. https://doi.org/10.3390/act9010013
Chicago/Turabian StyleBruzzone, Luca, Pietro Fanghella, and Mario Baggetta. 2020. "Experimental Assessment of Fractional-Order PDD1/2 Control of a Brushless DC Motor with Inertial Load" Actuators 9, no. 1: 13. https://doi.org/10.3390/act9010013
APA StyleBruzzone, L., Fanghella, P., & Baggetta, M. (2020). Experimental Assessment of Fractional-Order PDD1/2 Control of a Brushless DC Motor with Inertial Load. Actuators, 9(1), 13. https://doi.org/10.3390/act9010013







