Damage Detection Using d15 Piezoelectric Sensors in a Laminate Beam Undergoing Three-Point Bending
Abstract
1. Introduction
2. Theoretical Background
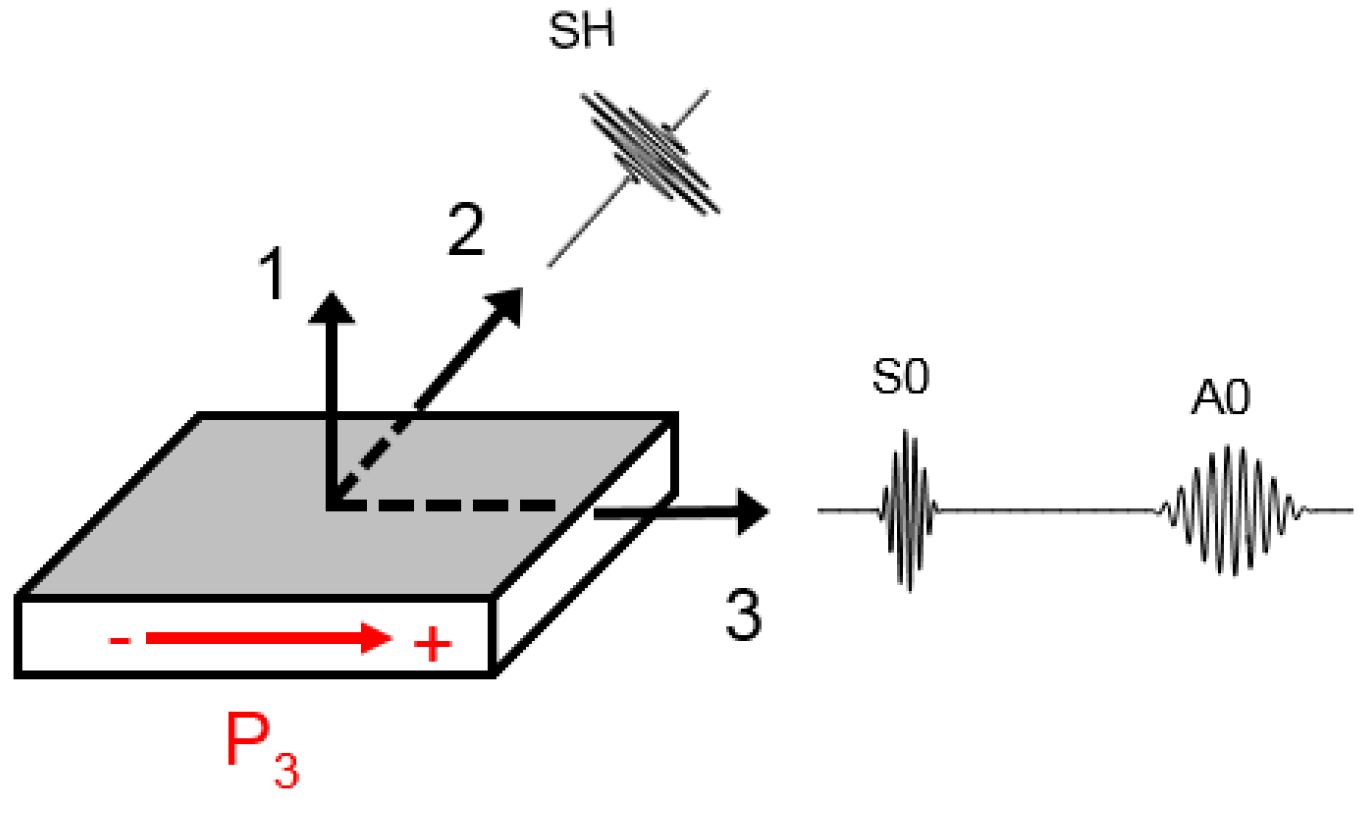
2.1. Shear-Mode (d15) PZTs
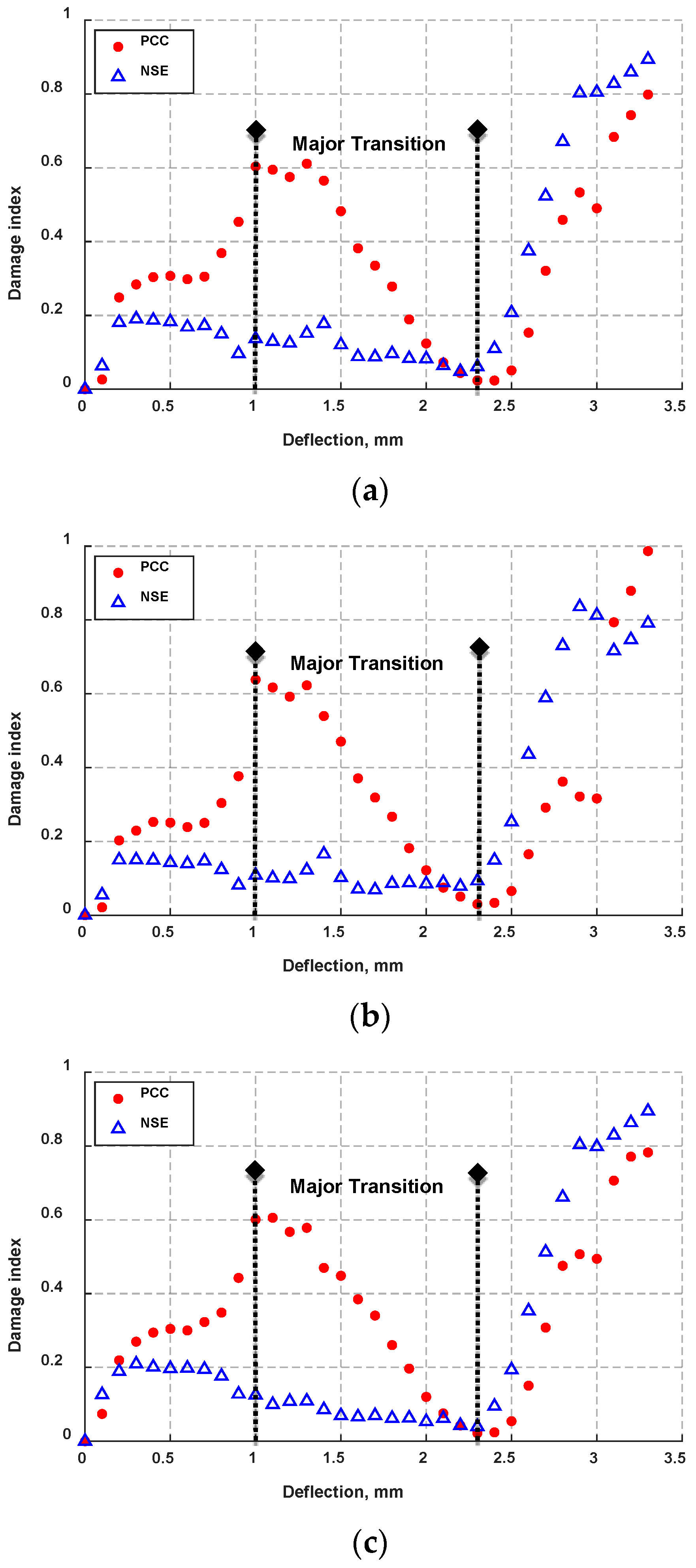
2.2. Damage Index
3. Experiment
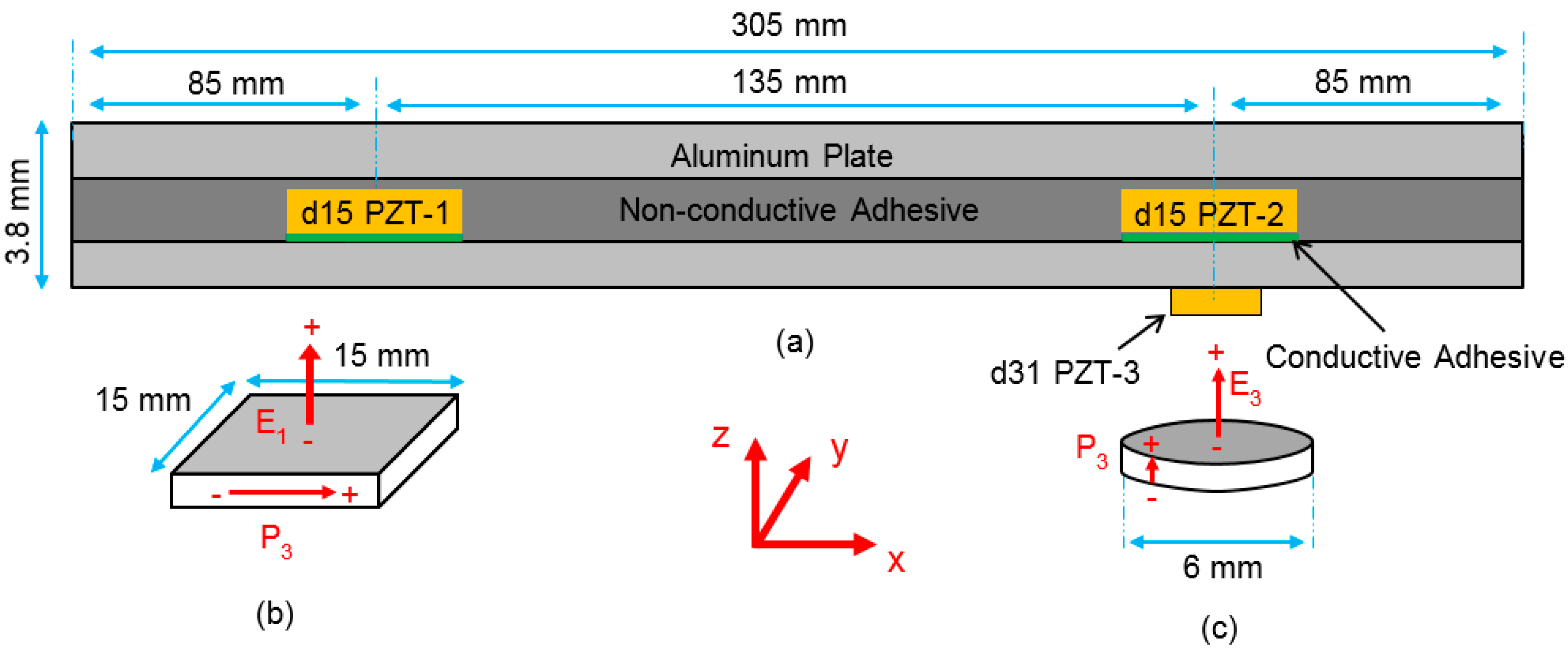
3.1. Specimen Design and Fabrication
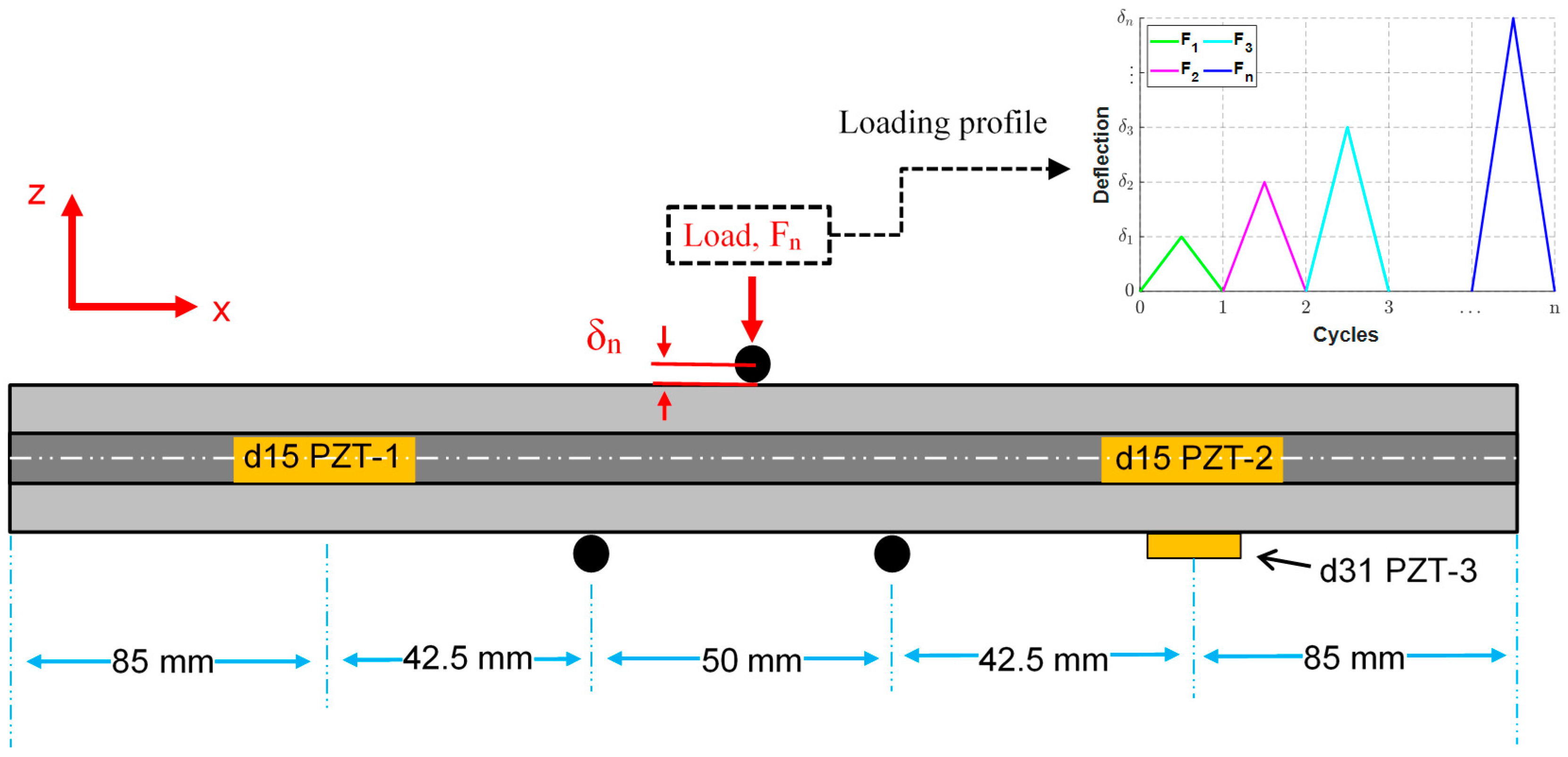
3.2. Quasi-Static Three-Point Bending
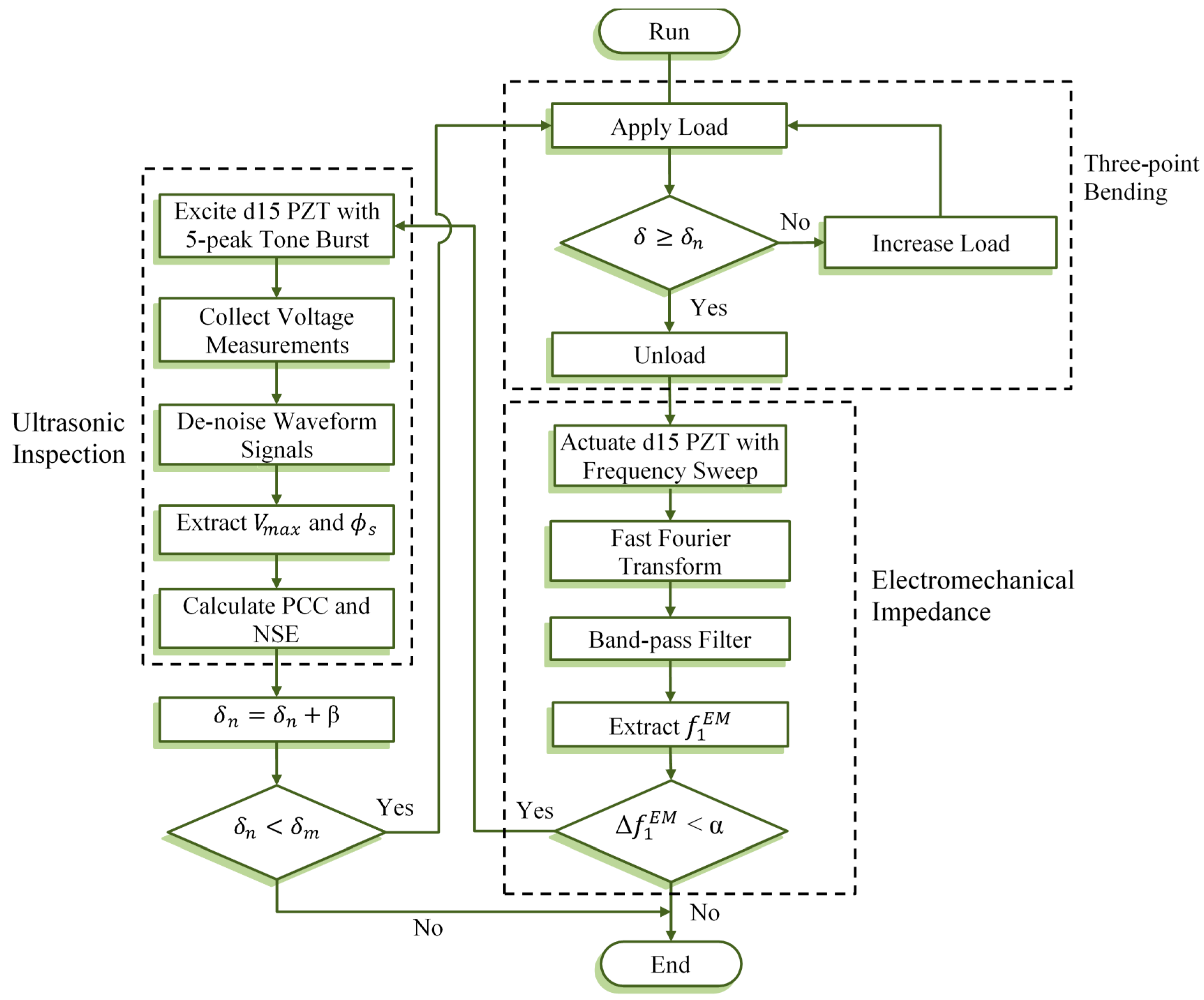
3.3. Experimental Method
- Apply an increasing quasi-static load on the specimen until mid-span deflection reaches δn, then remove the applied mid-span load.
- At no-load condition state, actuate d15 PZTs with a voltage frequency sweep (Vi) from 200 kHz to 1600 kHz by measuring the voltage (Vo) across a sensing resistor (Rs = 100 Ω) and the PZT element, then calculate the impedance, .
- Apply fast Fourier transform method and band-pass filter to the harmonic signals and identify the first resonance frequency, , for each d15 PZT.
- Continue the test if the difference between the baseline resonant peak and the measured resonant is less than α, which is set as 1% of the baseline resonant peak.
- Perform ultrasonic inspection by actuating bondline-embedded d15 PZTs. The excitation signal shown in Figure 6 is a five-peak sine signal centered at 30 kHz and modulated by a Hann window, , where is the length of the window.
- Denoise senor signals using discrete wavelet transform with Coiflet wavelet performed at level six wavelet decomposition and applying the universal threshold , to the wavelet coefficients.
- Determine the maximum voltage, Vmax of the first arrival in sensor signals and the phase shift, ϕmax with respect to baseline signals.
- Calculate damage index values based on PCC and NSE methods using Equations (6) and (7), respectively.
- Repeat loading the specimen at a higher mid-span deflection by β increment, 0.1 mm herein.
- Stop the test when mid-span deflection reaches δm that is calculated based on flexural rigidity of the laminate specimen.
4. Results and Discussion
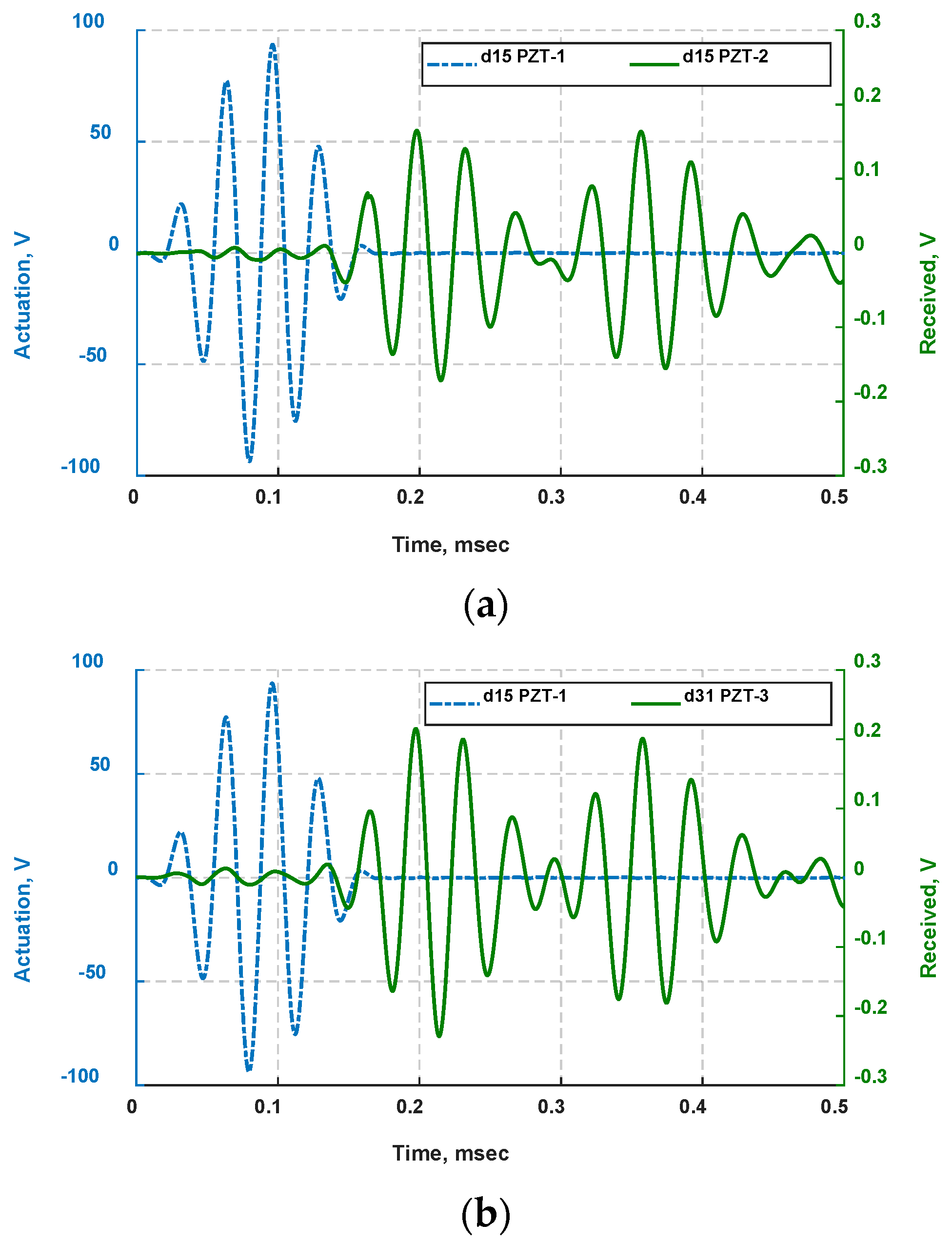
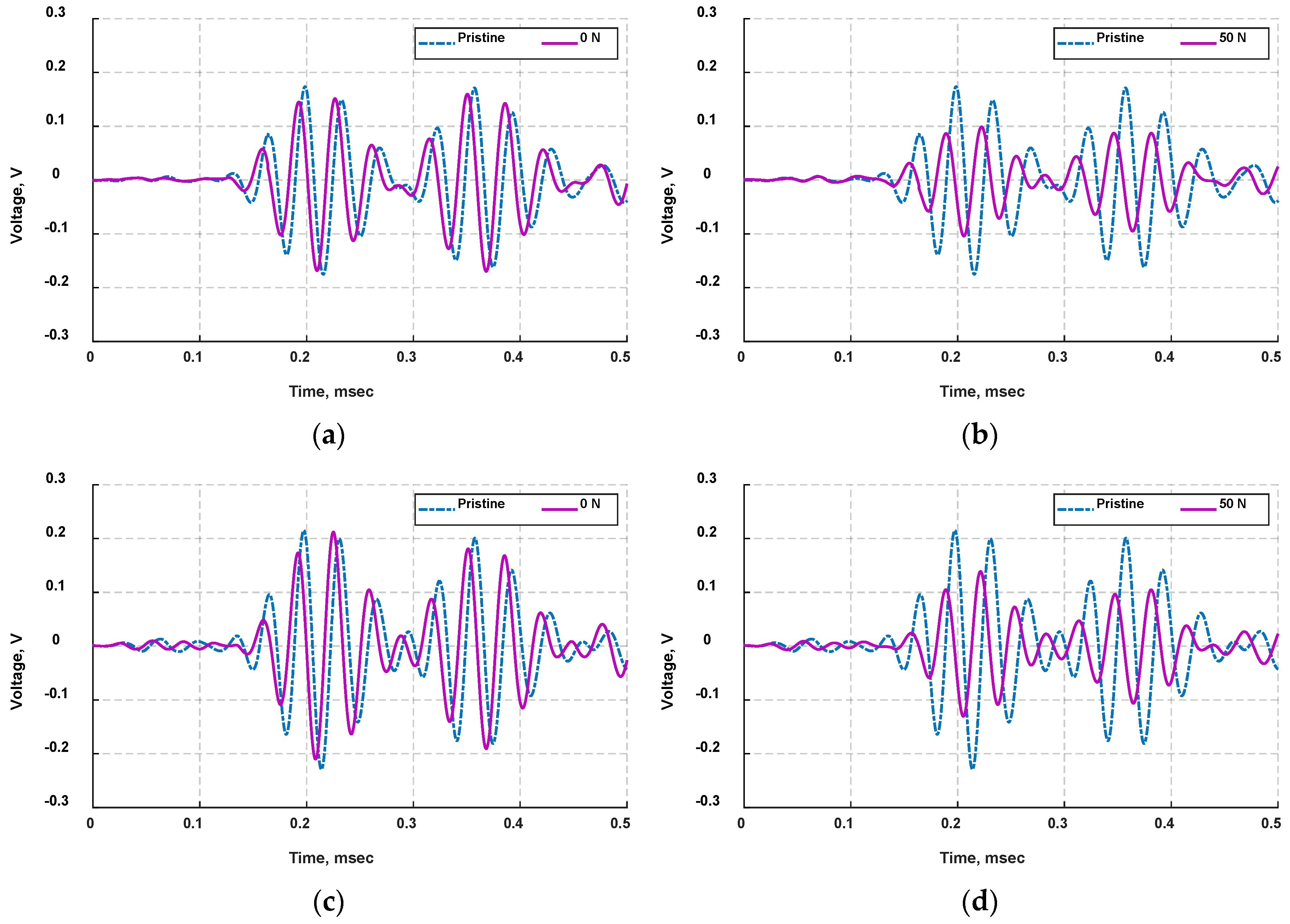
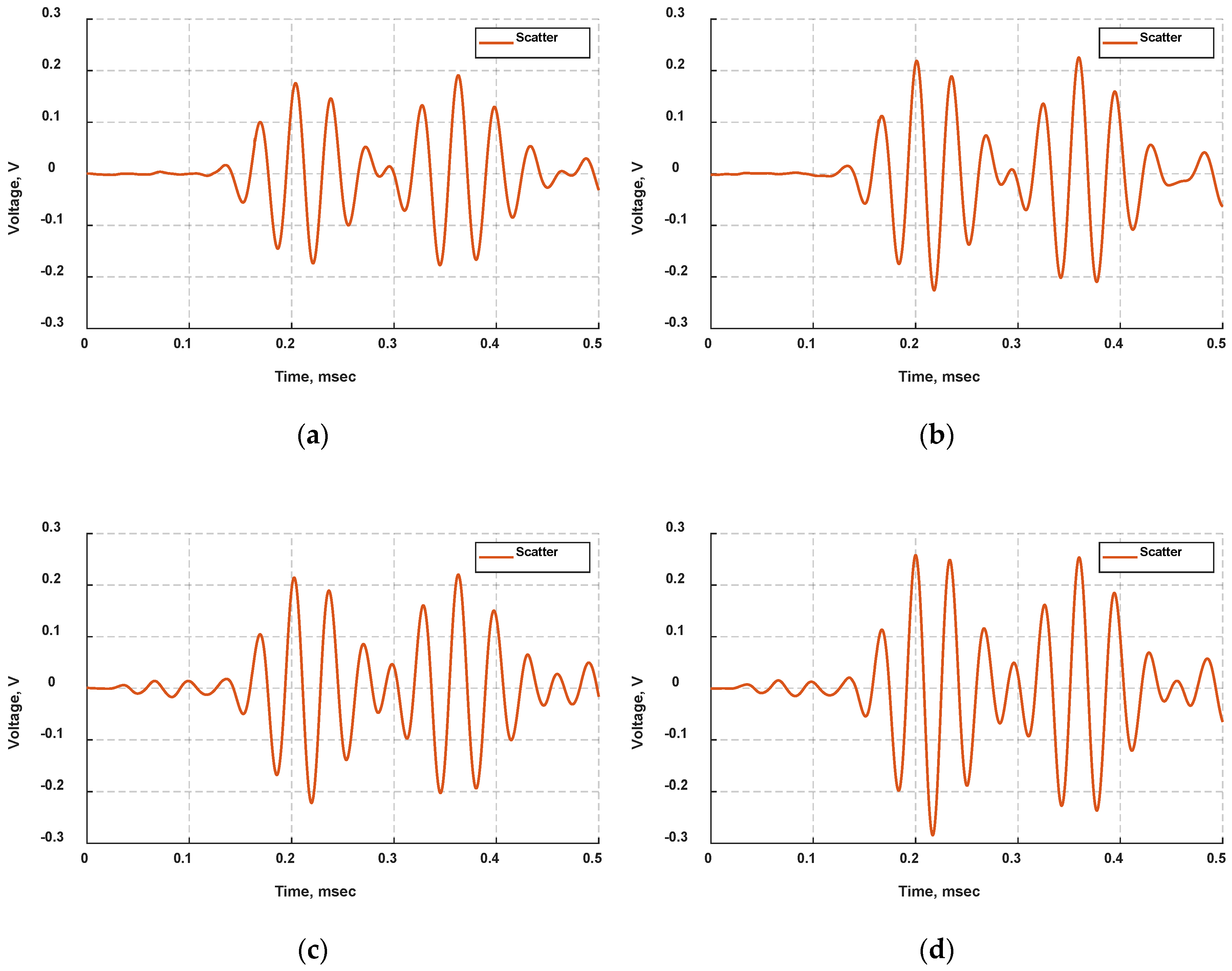
4.1. Wave Propagation Analysis
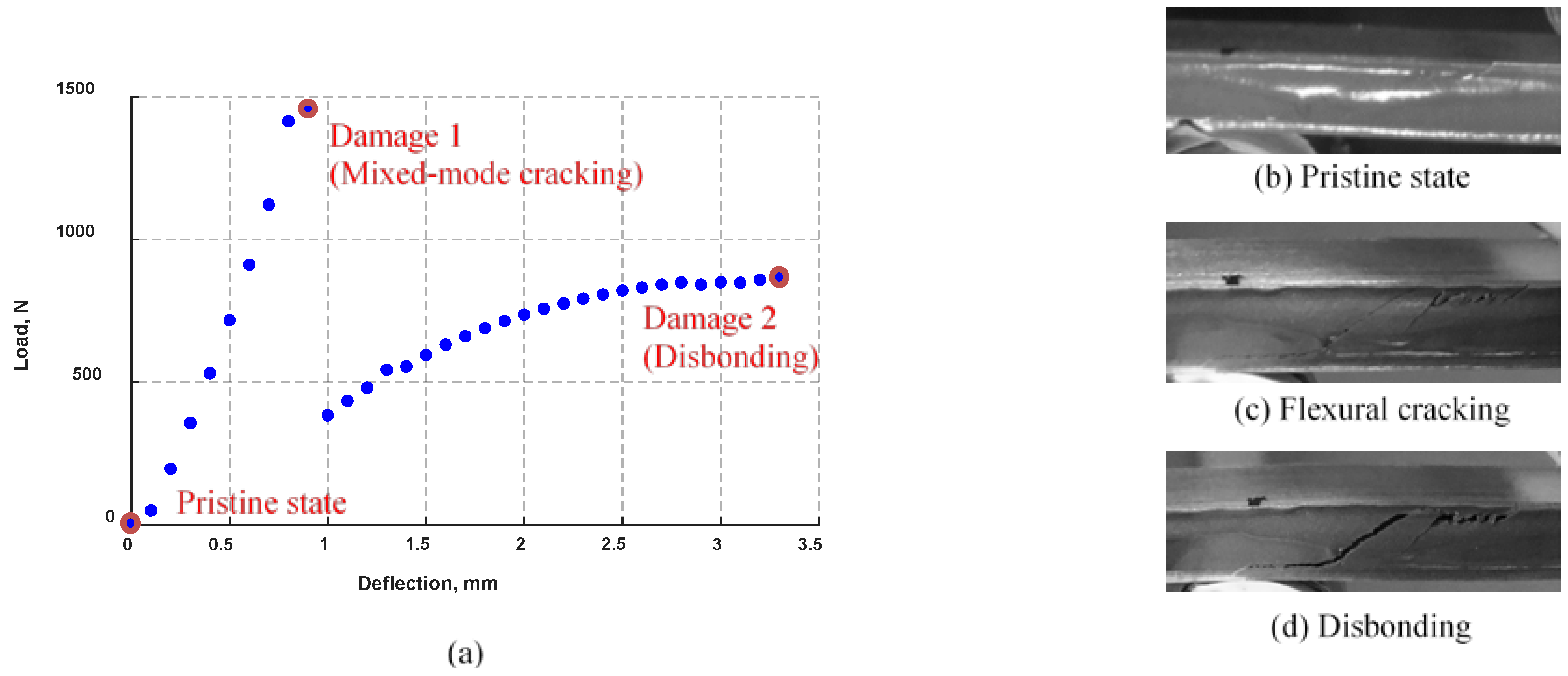
4.2. Joint Degradation
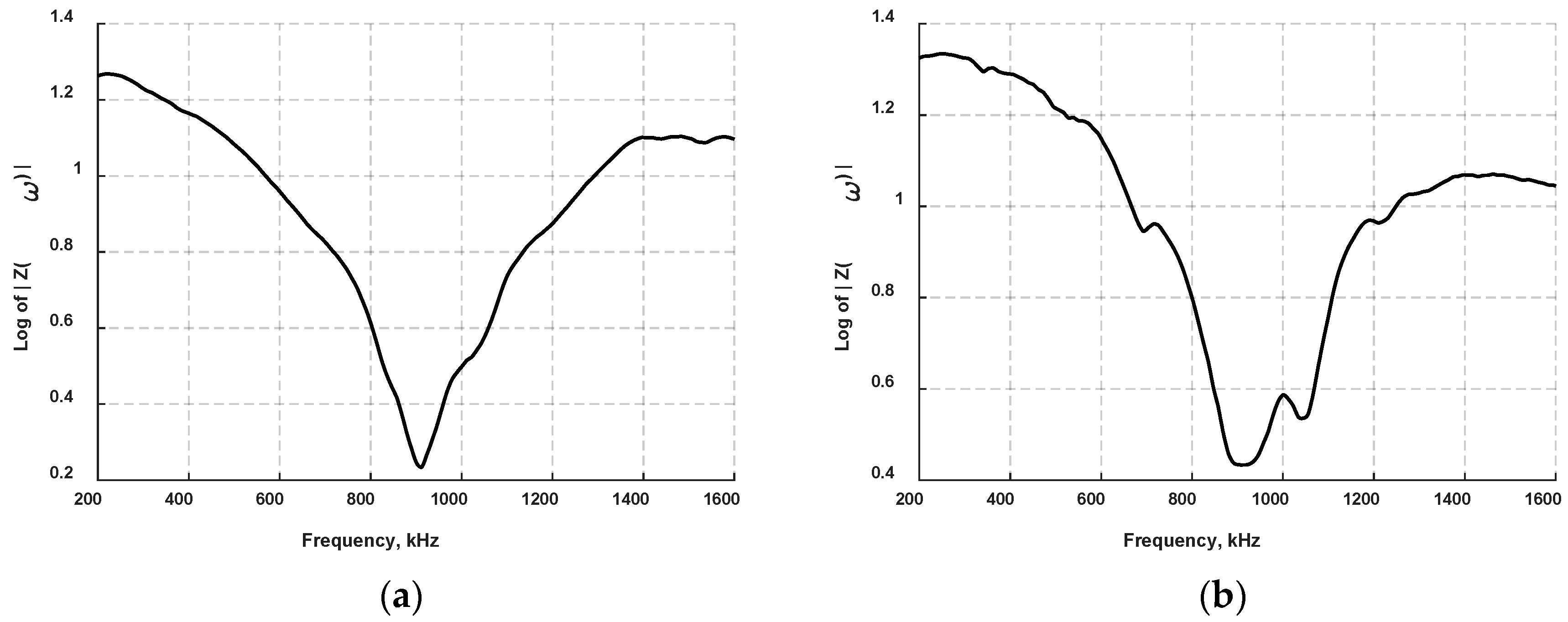
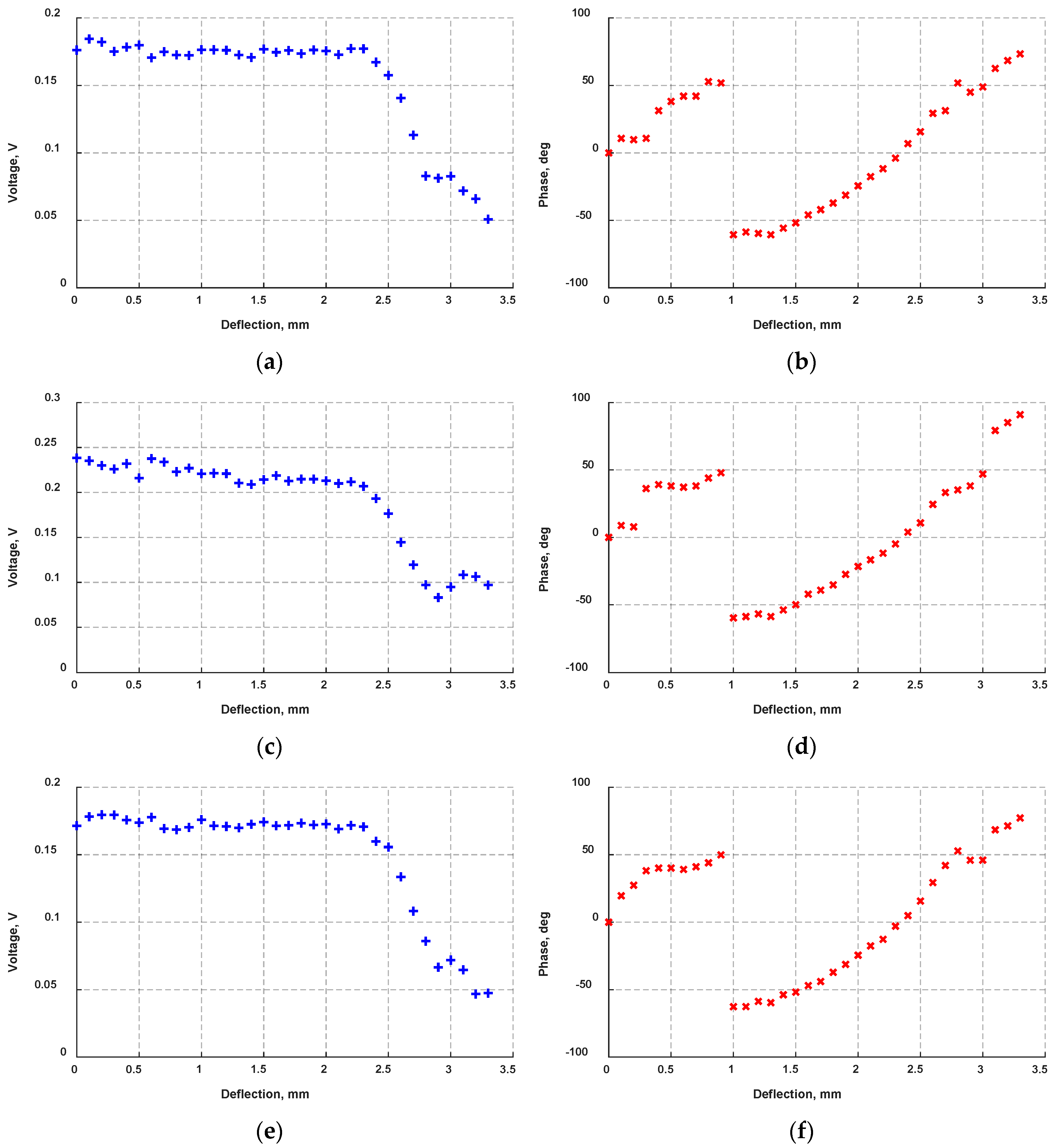
4.3. Electromechanical Impedance
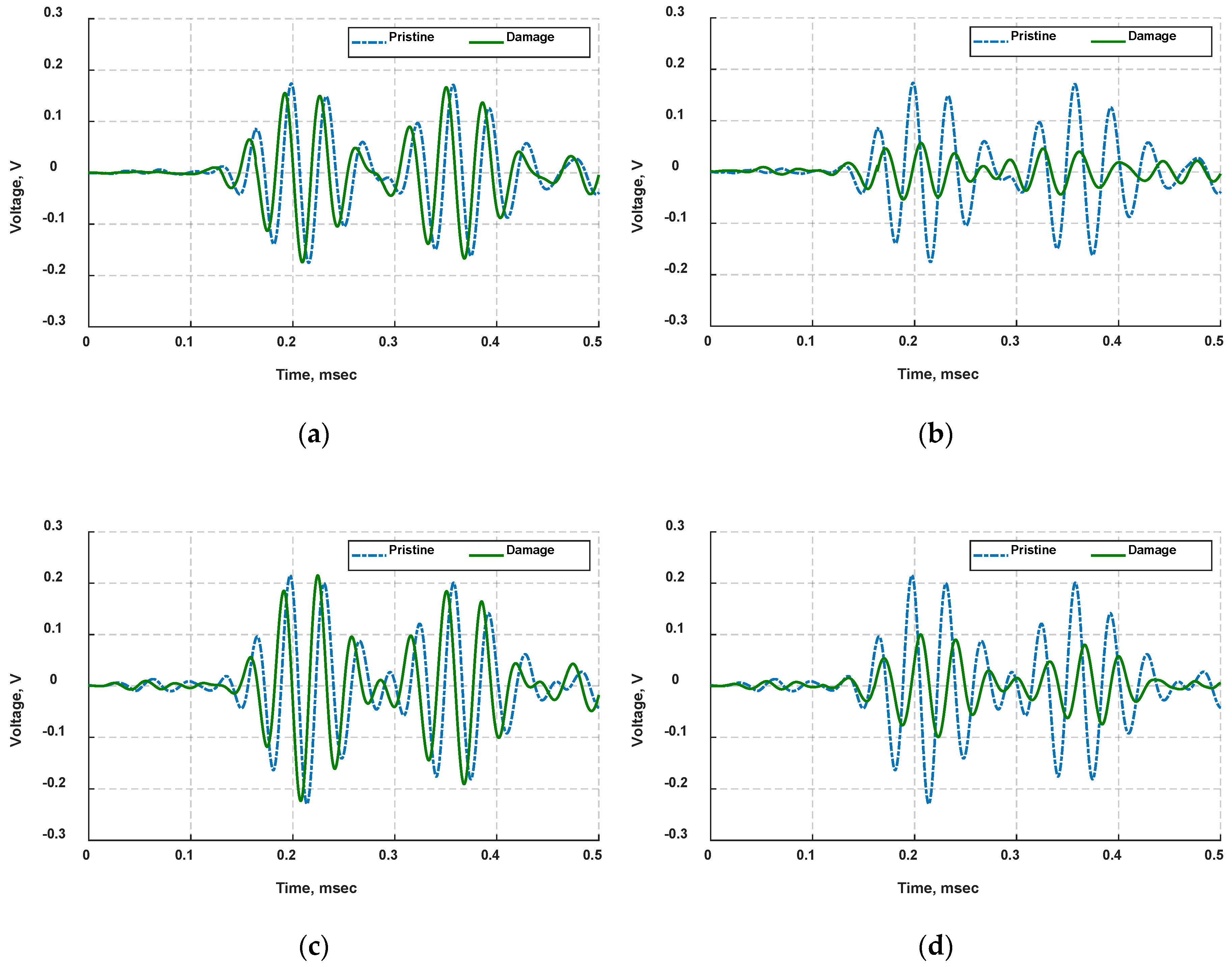
4.4. Ultrasonic Inspection
4.5. Influence of Preload Condition
5. Conclusions
6. Future Work
Author Contributions
Funding
Conflicts of Interest
References
- Structural Integrity and Durability of Advanced Composites: Innovative Modelling Methods and Intelligent Design; Beaumont, P.W.R., Soutis, C., Hodzic, A., Eds.; Woodhead Publishing: Sawston, UK; Cambridge, UK, 2015; ISBN 978-0-08-100137-0. [Google Scholar]
- Dugnani, R.; Zhuang, Y.; Kopsaftopoulos, F.; Chang, F.-K. Adhesive bond-line degradation detection via a cross-correlation electromechanical impedance–based approach. Struct. Health Monit. 2016, 15, 650–667. [Google Scholar] [CrossRef]
- Zhuang, Y.; Li, Y.-H.; Kopsaftopoulos, F.; Chang, F.-K. A self-diagnostic adhesive for monitoring bonded joints in aerospace structures. In Proceedings of the Sensors and Smart Structures Technologies for Civil, Mechanical, and Aerospace Systems, Las Vegas, NV, USA, 20 April 2016. [Google Scholar]
- Nagy, P.B. Ultrasonic detection of kissing bonds at adhesive interfaces. J. Adhes. Sci. Technol. 1991, 5, 619–630. [Google Scholar] [CrossRef]
- Kundu, T.; Maji, A.; Ghosh, T.; Maslov, K. Detection of kissing bonds by Lamb waves. Ultrasonics 1998, 35, 573–580. [Google Scholar] [CrossRef]
- Ramadas, C.; Balasubramaniam, K.; Joshi, M.; Krishnamurthy, C.V. Numerical and experimental studies on propagation of A0mode in a composite plate containing semi-infinite delamination: Observation of turning modes. Compos. Struct. 2011, 93, 1929–1938. [Google Scholar] [CrossRef]
- Masserey, B.; Raemy, C.; Fromme, P. High-frequency guided ultrasonic waves for hidden defect detection in multi-layered aircraft structures. Ultrasonics 2014, 54, 1720–1728. [Google Scholar] [CrossRef] [PubMed]
- Zhang, K.; Zhou, Z. Quantitative characterization of disbonds in multilayered bonded composites using laser ultrasonic guided waves. NDT E Int. 2018, 97, 42–50. [Google Scholar] [CrossRef]
- Guo, N.; Cawley, P. Lamb wave propagation in composite laminates and its relationship with acousto-ultrasonics. NDT E Int. 1993, 26, 75–84. [Google Scholar] [CrossRef]
- Ramadas, C.; Balasubramaniam, K.; Joshi, M.; Krishnamurthy, C.V. Characterisation of rectangular type delaminations in composite laminates through B- and D-scan images generated using Lamb waves. NDT E Int. 2011, 44, 281–289. [Google Scholar] [CrossRef]
- Altammar, H.; Kaul, S.; Dhingra, A.K. Use of wavelets for damage diagnostics in truss structures. Int. J. Struct. Integr. 2017, 8, 373–391. [Google Scholar] [CrossRef]
- Mix, P.E. Introduction to Nondestructive Testing: A Training Guide; John Wiley & Sons: Hoboken, NJ, USA, 2005; ISBN 13 978-0-471-42029-3. [Google Scholar]
- Hellier, C.J. Handbook of Nondestructive Evaluation; McGraw-Hill Education: New York, NY, USA, 2012; Volume 69, ISBN 007139947X. [Google Scholar]
- Gulizzi, V.; Rizzo, P.; Milazzo, A. Electromechanical impedance method for the health monitoring of bonded joints: Numerical modelling and experimental validation. SDHM Struct. Durab. Health Monit. 2014, 10, 19–54. [Google Scholar]
- Malinowski, P.; Wandowski, T.; Ostachowicz, W. The use of electromechanical impedance conductance signatures for detection of weak adhesive bonds of carbon fibre–reinforced polymer. Struct. Health Monit. 2015, 14, 332–344. [Google Scholar] [CrossRef]
- Altammar, H.; Dhingra, A.; Salowitz, N. Initial study of internally embedded shear-mode piezoelectric transducers for the detection of joint defects in laminate structures. J. Intell. Mater. Syst. Struct. 2019, 30, 2314–2330. [Google Scholar] [CrossRef]
- Dı́az Valdés, S.H.; Soutis, C.; Dı́az Valdés, S.H.; Soutis, C.; Diaz Vald, S.H.; Soutis, C. Real-time nondestructive evaluation of fiber composite laminates using low-frequency Lamb waves. J. Acoust. Soc. Am. 2002, 111, 2026–2033. [Google Scholar] [CrossRef] [PubMed]
- Osmont, D.; Devillers, D.; Taillade, F. Health Monitoring of Sandwich Plates Based on the Analysis of the Interaction of Lamb Waves with Damages. Smart Struct. Integr. Syst. 2001, 4327, 290–301. [Google Scholar]
- Wilcox, P.D.; Lee, C.K.; Scholey, J.J.; Friswell, M.I.; Wisnom, M.R.; Drinkwater, B.W. Quantitative structural health monitoring using acoustic emission. SPIE Conf. Proc. 2006, 6173, 61731K. [Google Scholar]
- Pau, A.; Achillopoulou, D.V.; Vestroni, F. Scattering of guided shear waves in plates with discontinuities. NDT E Int. 2016, 84, 67–75. [Google Scholar] [CrossRef]
- Kamal, A.; Giurgiutiu, V. Shear horizontal wave excitation and reception with shear horizontal piezoelectric wafer active sensor (SH-PWAS). Smart Mater. Struct. 2014, 23, 085019. [Google Scholar] [CrossRef]
- Zhou, W.; Li, H.; Yuan, F.G. Guided wave generation, sensing and damage detection using in-plane shear piezoelectric wafers. Smart Mater. Struct. 2013, 23, 015014. [Google Scholar] [CrossRef]
- Hou, S.; Zhang, H.B.; Ou, J.P. A PZT-based smart aggregate for seismic shear stress monitoring. Smart Mater. Struct. 2013, 22, 065012. [Google Scholar] [CrossRef]
- Zhou, W.; Li, H.; Yuan, F.G. Fundamental understanding of wave generation and reception using d36 type piezoelectric transducers. Ultrasonics 2015, 57, 135–143. [Google Scholar] [CrossRef] [PubMed]
- Altammar, H.; Dhingra, A.; Salowitz, N. Ultrasonic Sensing and Actuation in Laminate Structures Using Bondline-Embedded d35 Piezoelectric Sensors. Sensors 2018, 18, 21. [Google Scholar] [CrossRef] [PubMed]
- Köhler, B.; Gaul, T.; Lieske, U.; Schubert, F. Shear horizontal piezoelectric fiber patch transducers (SH-PFP) for guided elastic wave applications. NDT E Int. 2016, 82, 1–12. [Google Scholar] [CrossRef]
- APC International, Ltd. Piezoelectric Ceramics: Principles and Applications, 1st ed.; APC International: Mackeyville, PA, USA, 2002; ISBN 0615565034. [Google Scholar]
- IEEE Standard on Piezoelectricity “ANSI/IEEE Std 176-1987”; The Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 1988; Volume 74.
- Giurgiutiu, V. Structural Health Monitoring With Piezoelectric Wafer Active Sensors, 2nd ed.; Elsevier Inc.: London, UK, 2014; ISBN 9780124186910. [Google Scholar]
- Wu, Z.; Qing, X.P.; Ghosh, K.; Karbhari, V.M.; Chang, F.-K. Health monitoring of bonded composite repair in bridge rehabilitation. Smart Mater. Struct. 2008, 17, 045014. [Google Scholar] [CrossRef]
- Torkamani, S.; Roy, S.; Barkey, M.E.; Sazonov, E.; Burkett, S.; Kotru, S. A novel damage index for damage identification using guided waves with application in laminated composites. Smart Mater. Struct. 2014, 23, 095015. [Google Scholar] [CrossRef]
- Tseng, K.K.-H.; Naidu, A.S.K. Non-parametric damage detection and characterization using smart piezoceramic material. Smart Mater. Struct. 2002, 11, 317–329. [Google Scholar] [CrossRef]
- Methods, S.T. ASTM E 290—Standard Test Methods for Bend Testing of Material for Ductility. Current 1998, 3, 1–10. [Google Scholar]
- Dowling, N.E. Mechanical Behavior of Materials, 4th ed.; Pearson Education, Inc.: Hoboken, NJ, USA, 2013; ISBN 9780131395060. [Google Scholar]
- Broda, D.; Staszewski, W.J.; Martowicz, A.; Uhl, T.; Silberschmidt, V.V. Modelling of nonlinear crack–wave interactions for damage detection based on ultrasound—A review. J. Sound Vib. 2014, 333, 1097–1118. [Google Scholar] [CrossRef]
- Alleyne, D.N.; Cawley, P. The Interaction of Lamb Waves with Defects. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1992, 39, 381–397. [Google Scholar] [CrossRef] [PubMed]
- Greve, D.W.; Tyson, N.; Oppenheim, I.J. Interaction of defects with Lamb waves in complex geometries. Proc. IEEE Ultrason. Symp. 2005, 1, 297–300. [Google Scholar]
- Altammar, H.; Dhingra, A.; Salowitz, N. Investigating the Feasibility of Ultrasonic Shear Actuation for Evaluation of Adhesive Joints in Multilayered Structures: FE Simulation. In Proceedings of the ASNT Annual Conference, Nashville, Tennessee, 30 October–2 November 2017; pp. 25–34. [Google Scholar]
- Salowitz, N.P.; Guo, Z.; Kim, S.J.; Li, Y.H.; Lanzara, G.; Chang, F.K. Microfabricated expandable sensor networks for intelligent sensing materials. IEEE Sens. J. 2014, 14, 2138–2144. [Google Scholar] [CrossRef]
- Salowitz, N.; Guo, Z.; Li, Y.H.; Kim, K.; Lanzara, G.; Chang, F.K. Bio-inspired stretchable network-based intelligent composites. J. Compos. Mater. 2013, 47, 97–105. [Google Scholar] [CrossRef]
- Chalioris, C.E.; Papadopoulos, N.A.; Angeli, G.M.; Karayannis, C.G.; Liolios, A.A.; Providakis, C.P. Damage Evaluation in Shear-Critical Reinforced Concrete Beam using Piezoelectric Transducers as Smart Aggregates. Open Eng. 2015, 5, 373–384. [Google Scholar] [CrossRef]


| Property | Unit | Symbol | PZT-5A | Adhesive | Aluminum |
|---|---|---|---|---|---|
| Young’s Modulus | 109 N/m2 | Y11 | 61.0 | 4.24 | 68.9 |
| 109 N/m2 | Y33 | 53.2 | 4.24 | 68.9 | |
| Shear’s Modulus | 109 N/m2 | G12 | 22.6 | 1.46 | 25.9 |
| 109 N/m2 | G13 | 10.5 | 1.46 | 25.9 | |
| Poisson’s ratio | 1 | v12 | 0.35 | 0.45 | 0.33 |
| 1 | v13 | 0.44 | 0.45 | 0.33 | |
| Density | kg/m3 | ρ | 7600 | 1360 | 2700 |
| Dielectric permittivity | 8.854 µF/m | ε11 | 1851 | ------ | ------ |
| 8.854 µF/m | ε13 | 1581 | ------ | ------ | |
| Piezoelectric coefficient | 10−12 m/V | d15 | 584 | ------ | ------ |
| 10−12 m/V | d31 | −171 | ------ | ------ | |
| 10−12 m/V | d33 | 374 | ------ | ------ |
| Wave Propagation Path | Time of Flight (μs) | Group Velocity (m/s) |
|---|---|---|
| PZT-1 → PZT-2 | 116.6 | 1157.8 |
| PZT-1 → PZT-3 | 118.1 | 1143.1 |
| PZT-2 → PZT-1 | 116.4 | 1159.8 |
| Wave Propagation Path | 0 N | 50 N | ||
|---|---|---|---|---|
| PCC | NSE | PCC | NSE | |
| PZT-1 → PZT-2 | 0.5644 | 0.1790 | 1.2886 | 0.6947 |
| PZT-1 → PZT-3 | 0.5398 | 0.1657 | 1.1829 | 0.6724 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Altammar, H.; Dhingra, A.; Salowitz, N. Damage Detection Using d15 Piezoelectric Sensors in a Laminate Beam Undergoing Three-Point Bending. Actuators 2019, 8, 70. https://doi.org/10.3390/act8040070
Altammar H, Dhingra A, Salowitz N. Damage Detection Using d15 Piezoelectric Sensors in a Laminate Beam Undergoing Three-Point Bending. Actuators. 2019; 8(4):70. https://doi.org/10.3390/act8040070
Chicago/Turabian StyleAltammar, Hussain, Anoop Dhingra, and Nathan Salowitz. 2019. "Damage Detection Using d15 Piezoelectric Sensors in a Laminate Beam Undergoing Three-Point Bending" Actuators 8, no. 4: 70. https://doi.org/10.3390/act8040070
APA StyleAltammar, H., Dhingra, A., & Salowitz, N. (2019). Damage Detection Using d15 Piezoelectric Sensors in a Laminate Beam Undergoing Three-Point Bending. Actuators, 8(4), 70. https://doi.org/10.3390/act8040070






