Space Vector Modulation Strategies for Self-Sensing Three-Phase Radial Active Magnetic Bearings †
Abstract
:1. Introduction
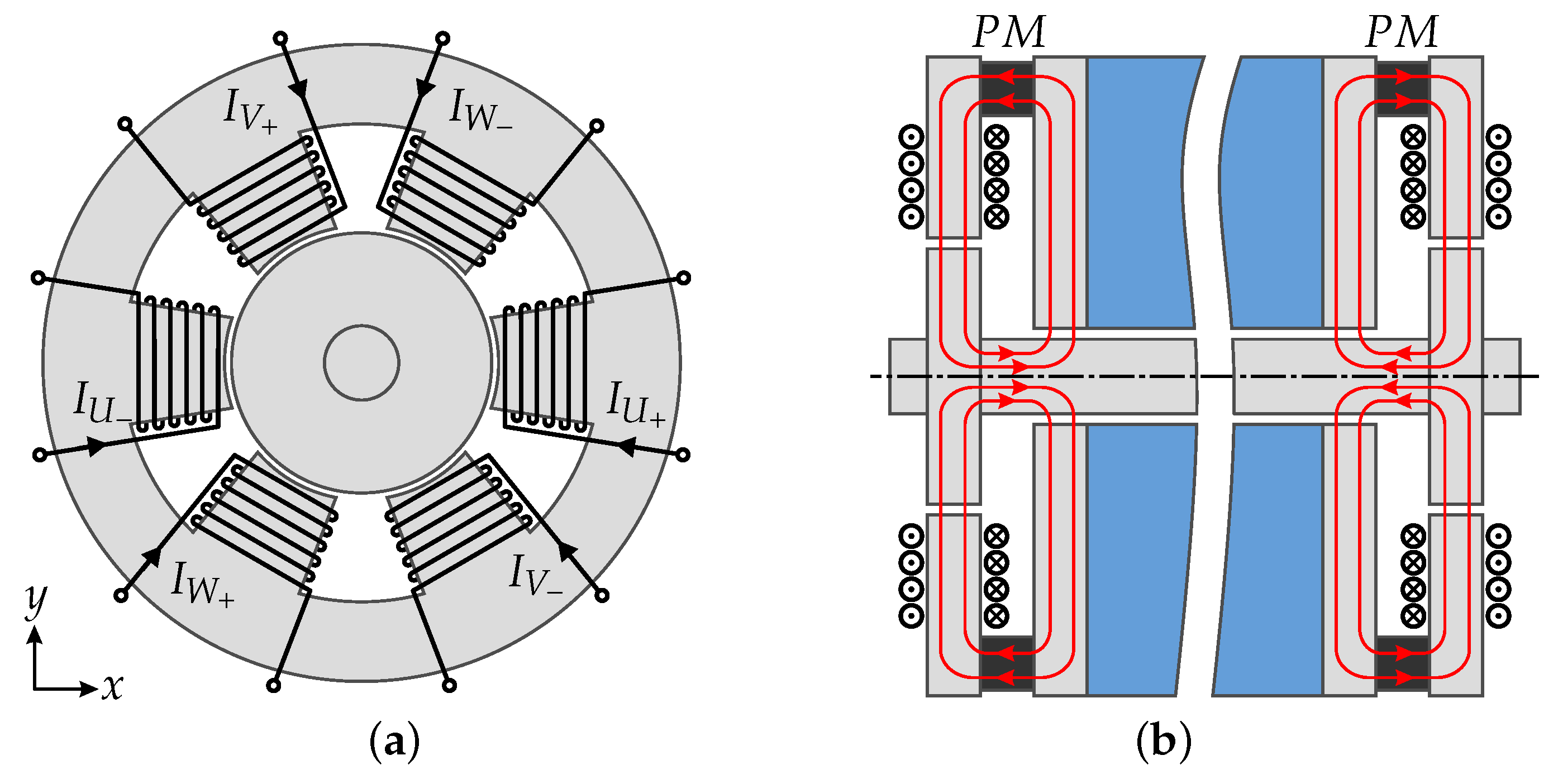
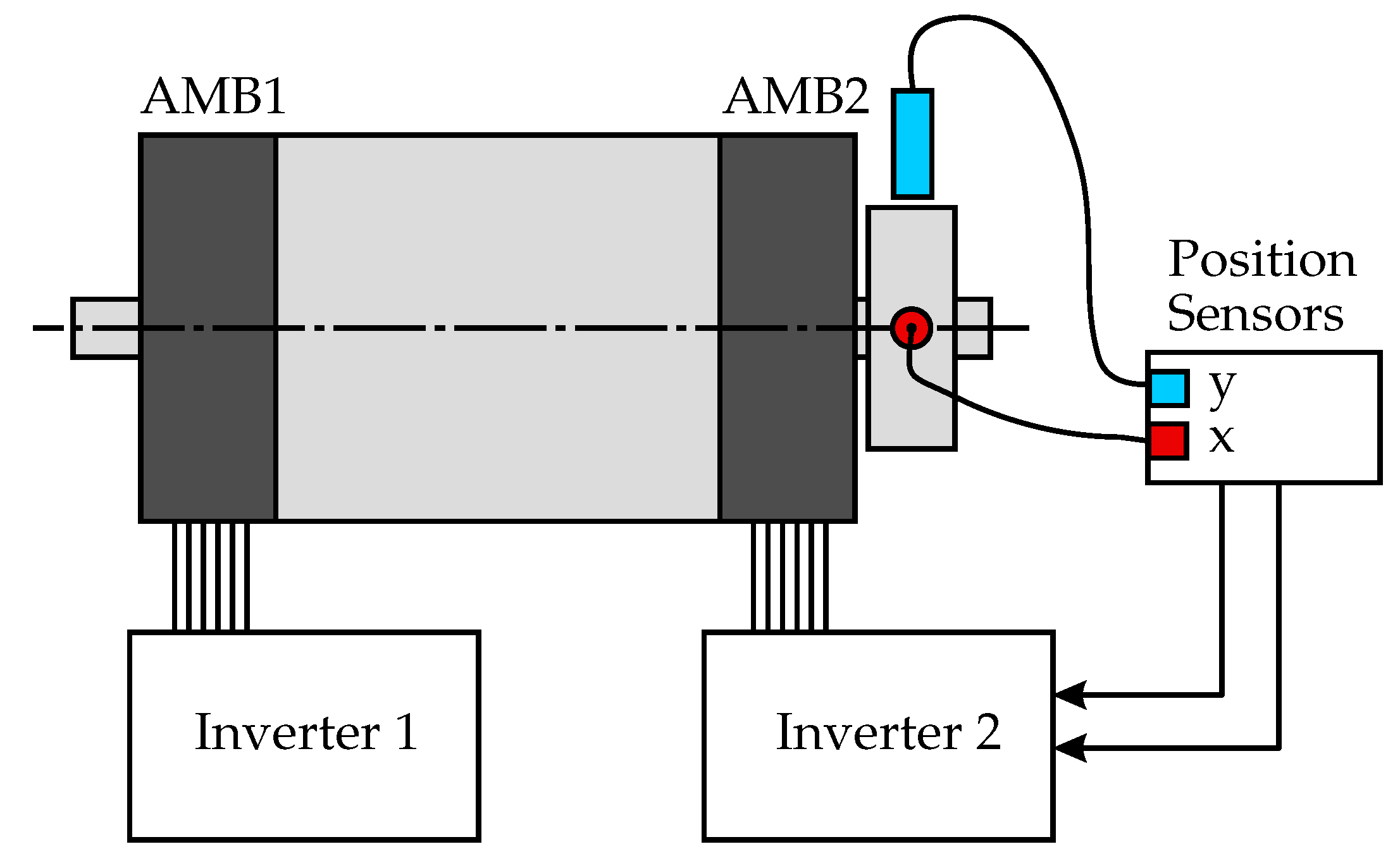
2. Self-Sensing Bearing Setup
3. Problem Formulation
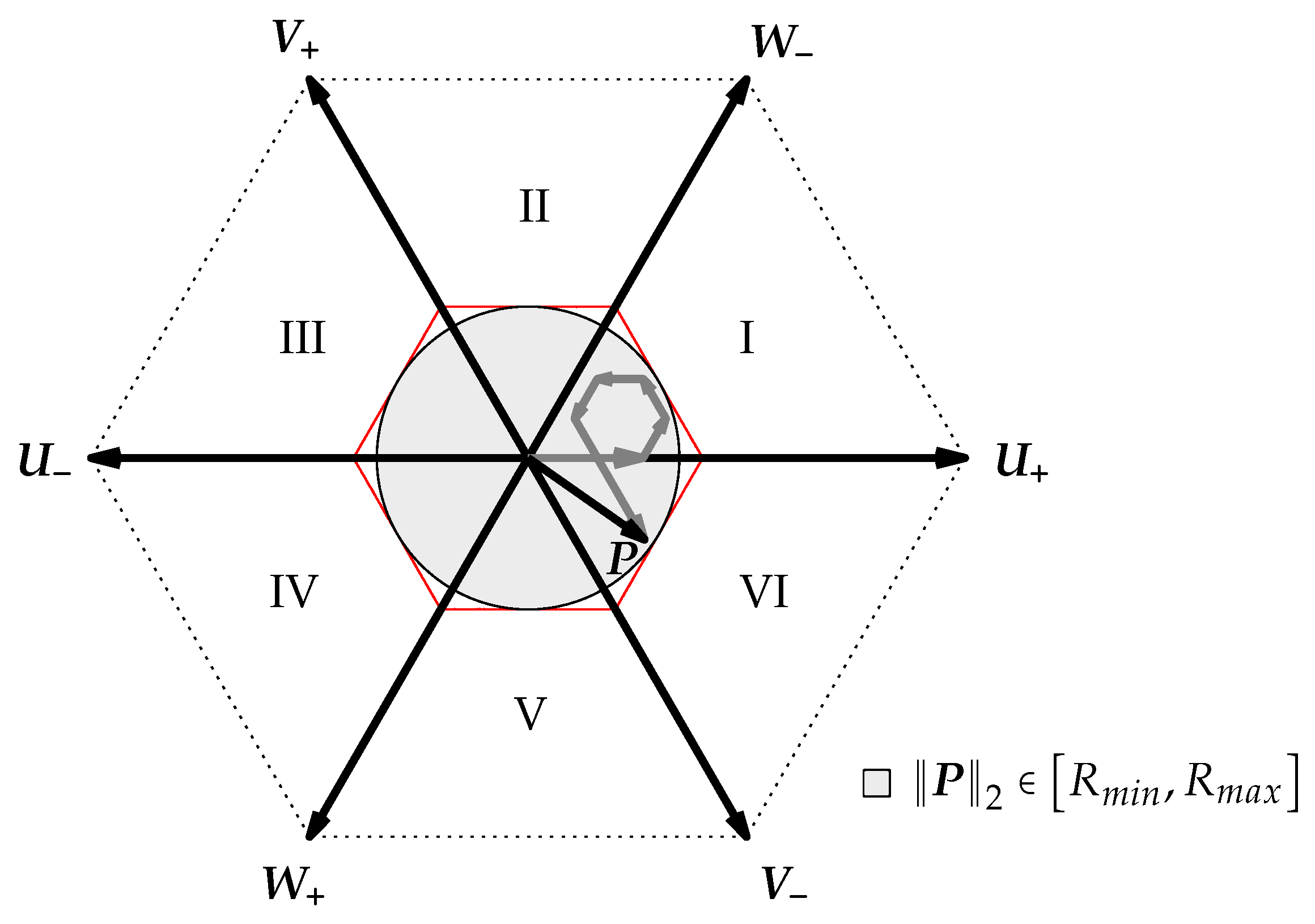
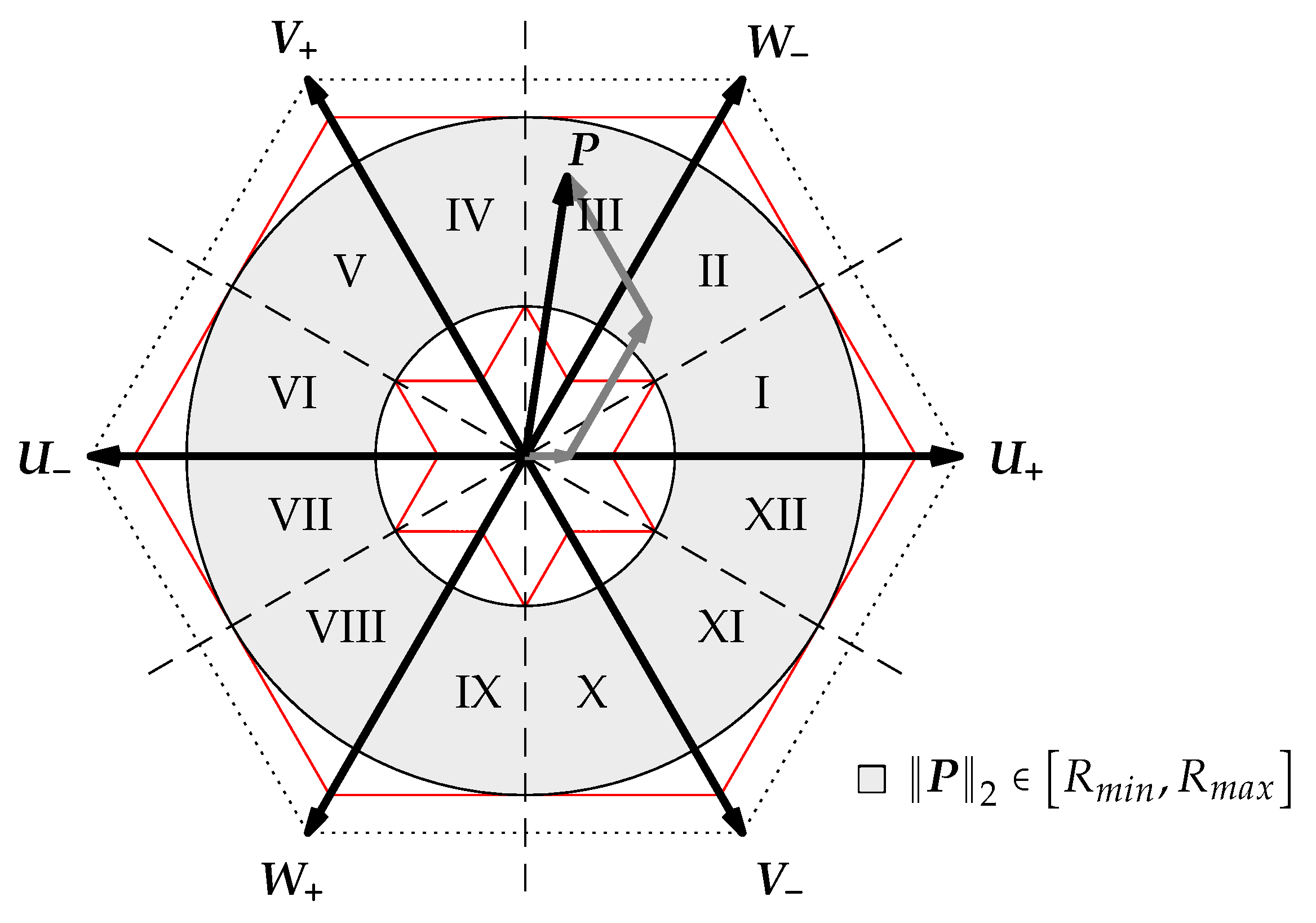
4. Space Vector Modulation
4.1. Design Rules for SVM
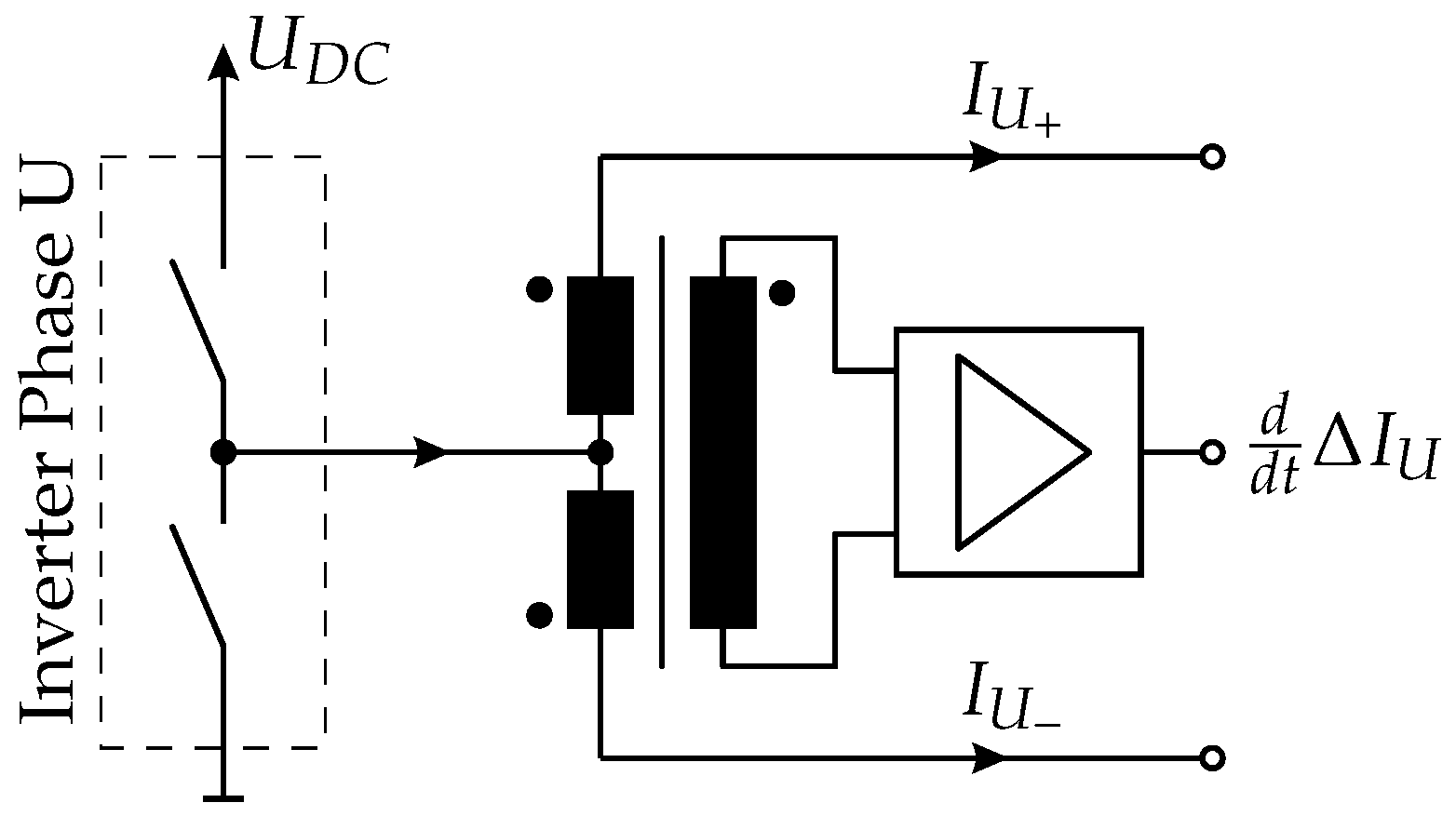
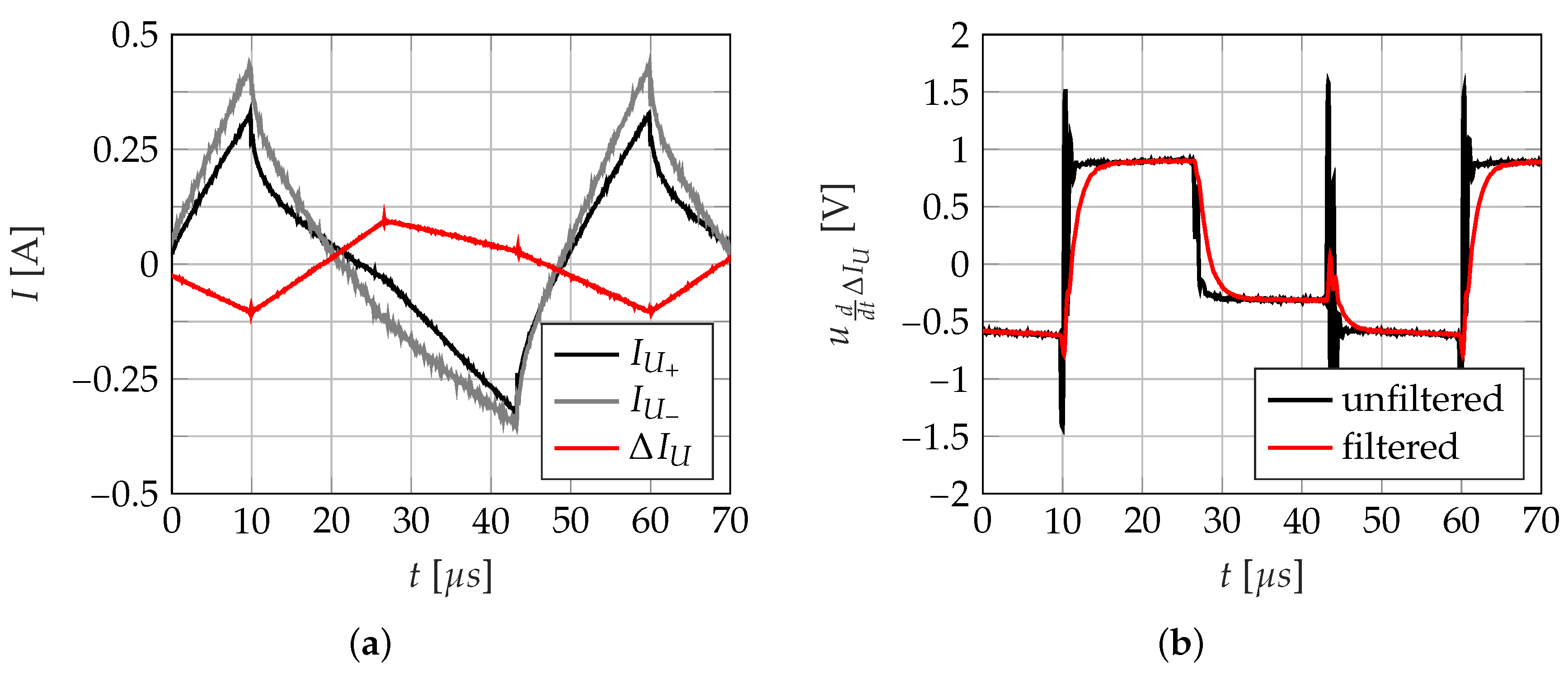
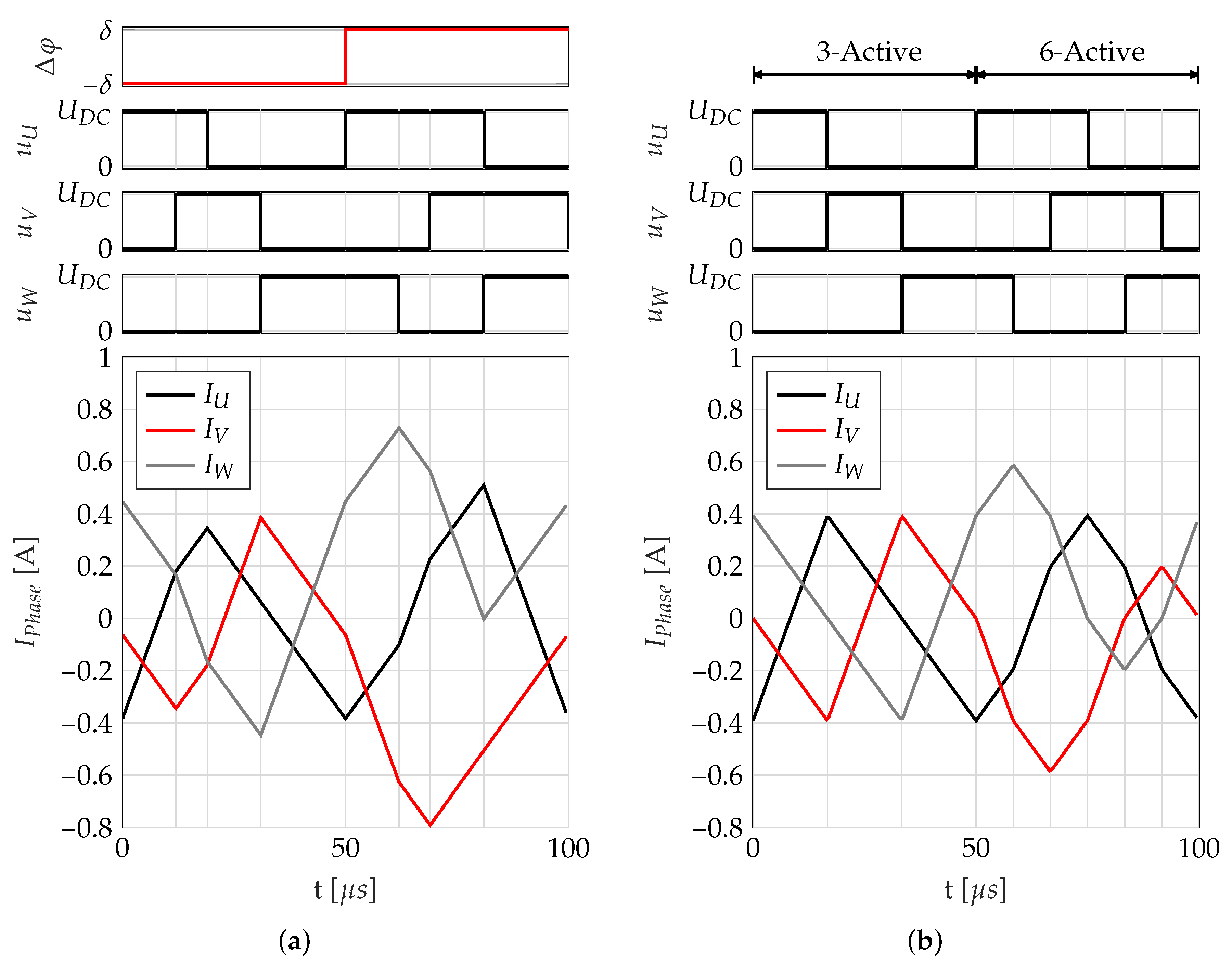
- INFORM method: Theoretically, the current ripple caused by a single voltage pulse contains the whole information of the rotor position. As asymmetries appear in the real system (caused by mechanical, electrical or magnetic deviations), it is beneficial to use the current slope information from independent voltage pulses. Furthermore, the voltage pulses must have a minimal pulse duration , which is given by the settling time of the current slope measurement path (Figure 3b). The duration is defined by the decay of the eddy currents and the settling of the analog filter, which causes a distortion of the differential current slope signal.
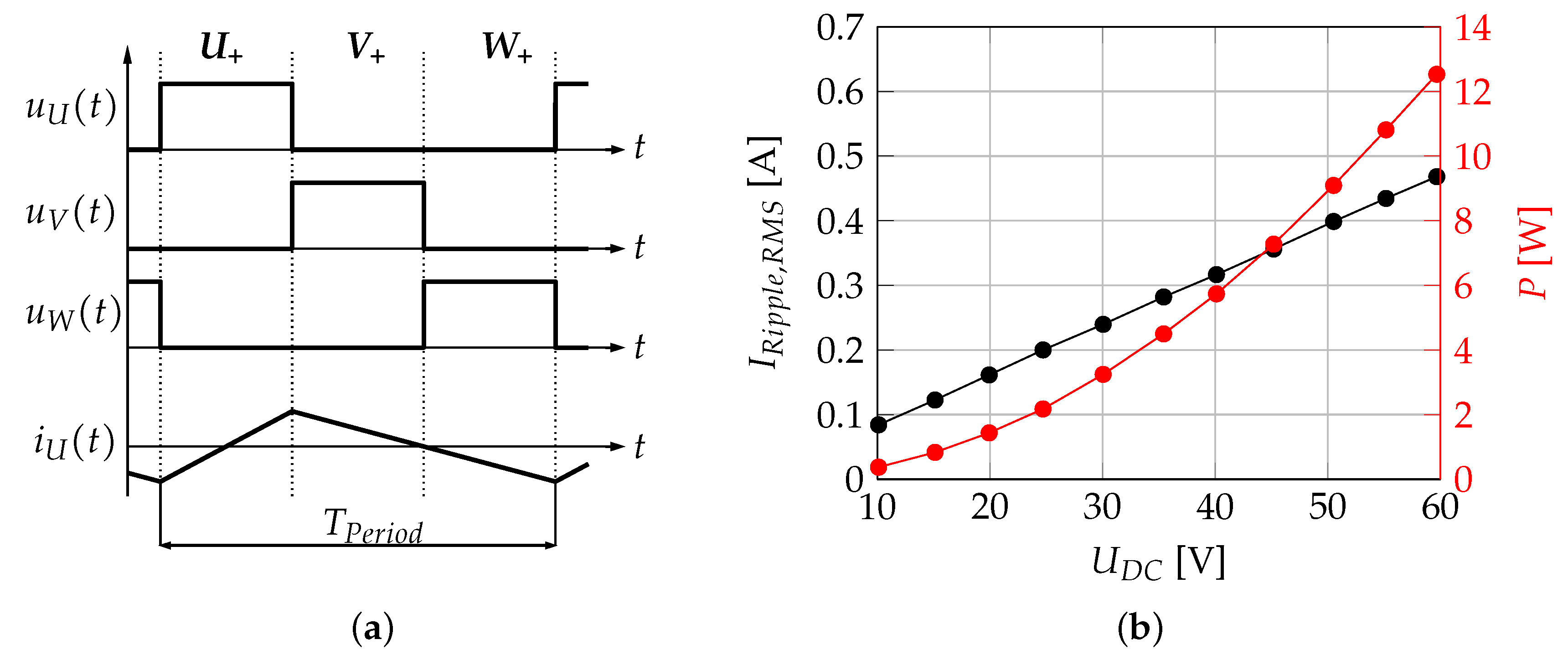
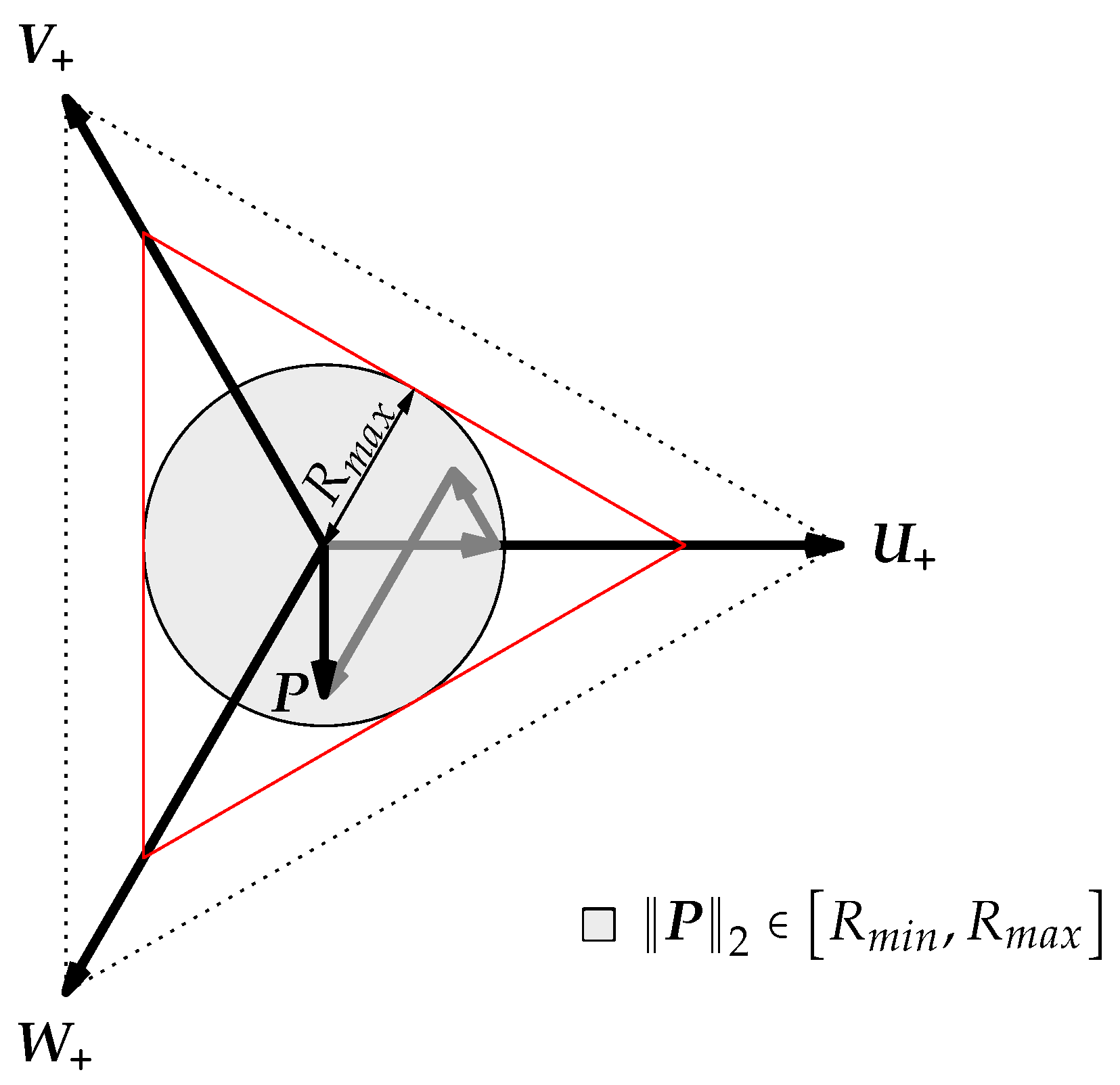
- Modulation amplitude: The modulation amplitude defines the maximum length of a desired voltage space vector. High modulation amplitudes of the desired voltage space vector allow a high dynamic of the current control. For a symmetrical (angle independent) operation of the current controller, it is beneficial to limit the modulation amplitude to the in-circle of the possible modulation area. Theoretically, the symmetrical modulation amplitude can achieve a value of for the given AMB system.
- Inverter: Short pulse lengths could cause problems in semiconductor switches. Hence, the specified recovery time of the switches must be considered in the PWM pattern [22]. Furthermore, a proper operation of a potential charge pump of the gate driver must be ensured. Therefore, the pulse pattern has to provide at least one switching action in each phase.
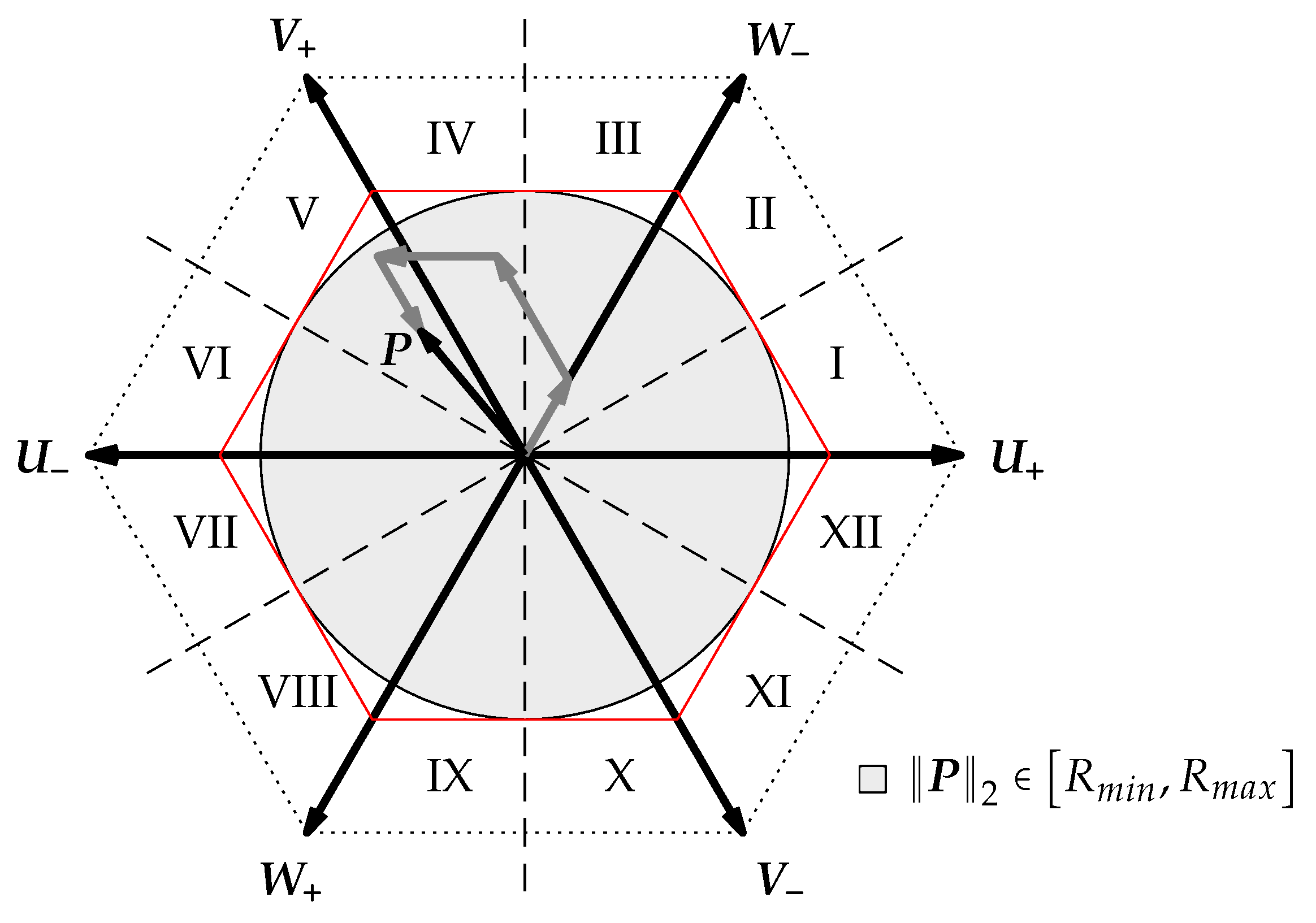
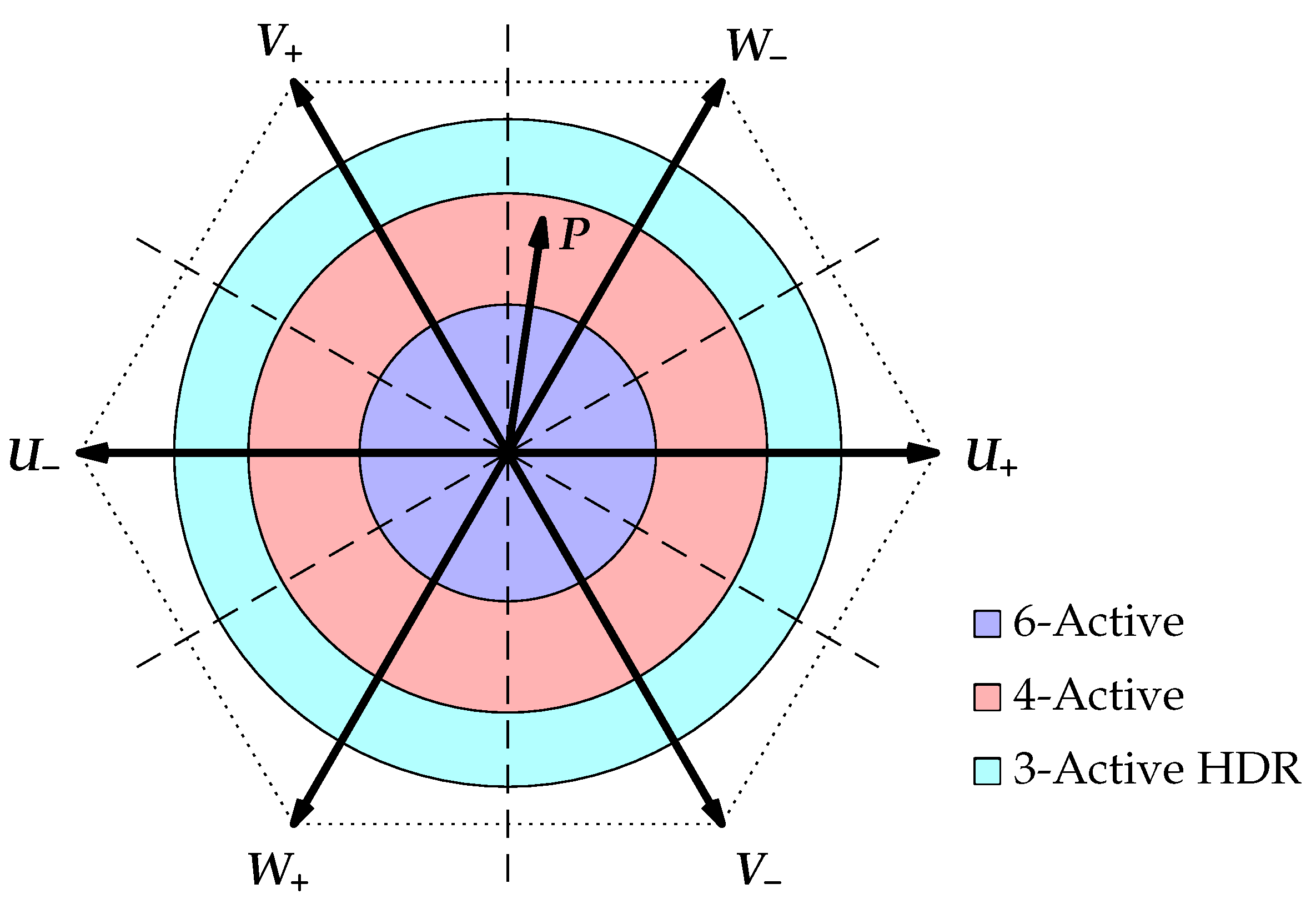
4.2. 6-Active SVM
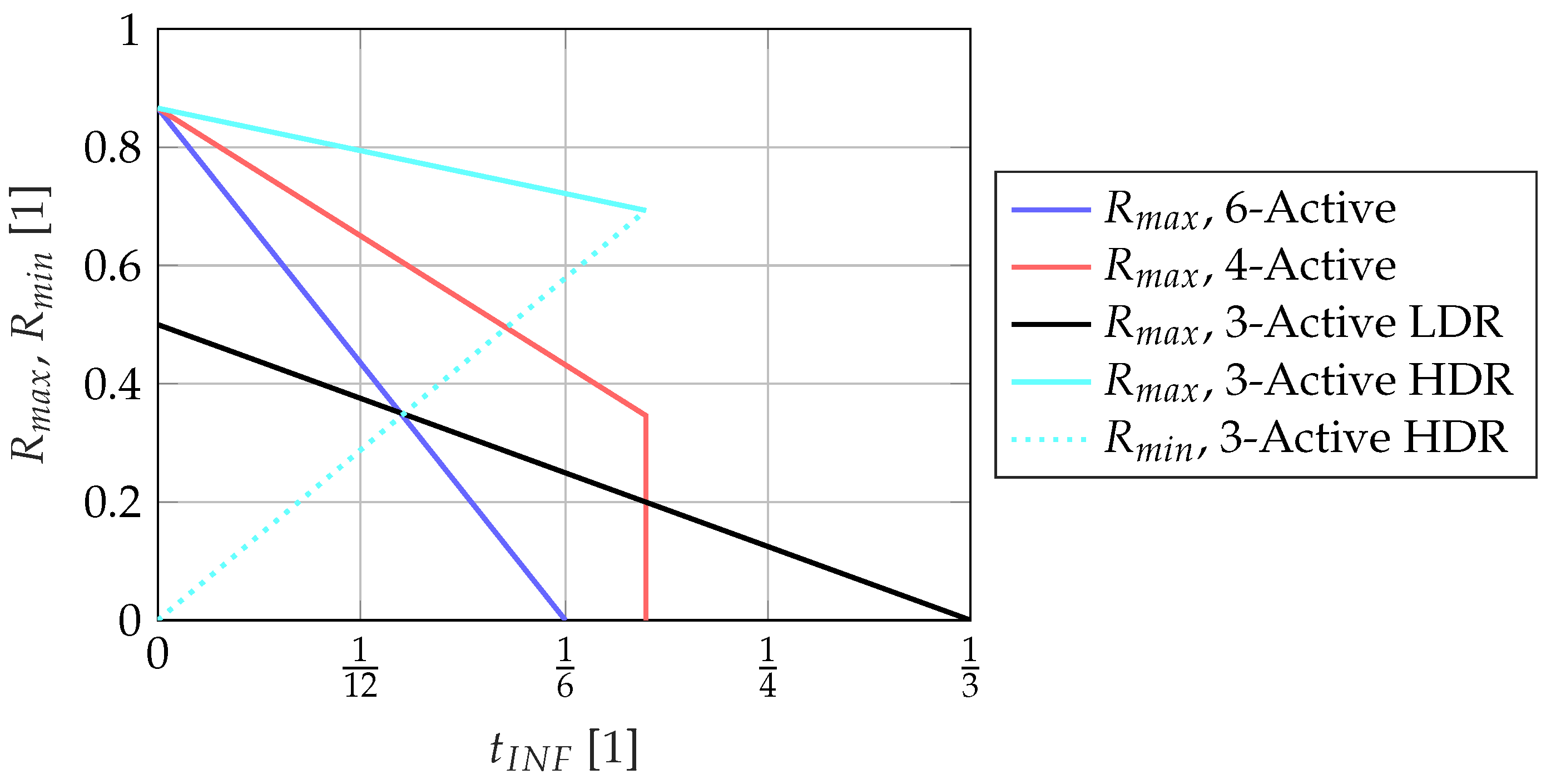
4.3. 3-Active Low Dynamic Range SVM
4.4. 4-Active SVM
4.5. 3-Active High Dynamic Range SVM
4.6. Combination of the SVMs
4.7. SVM Switchover
5. Measurements
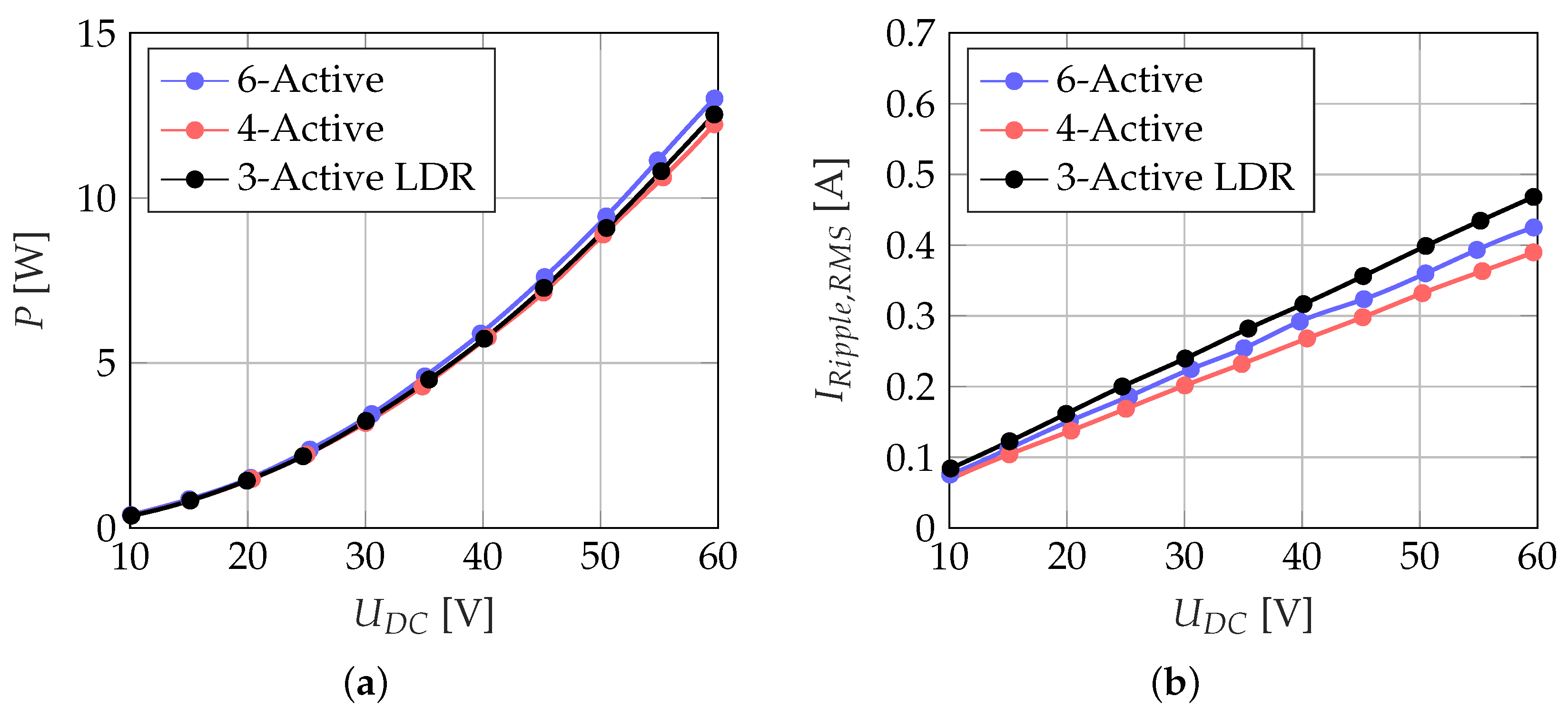
5.1. Power Losses of the SVM Variants
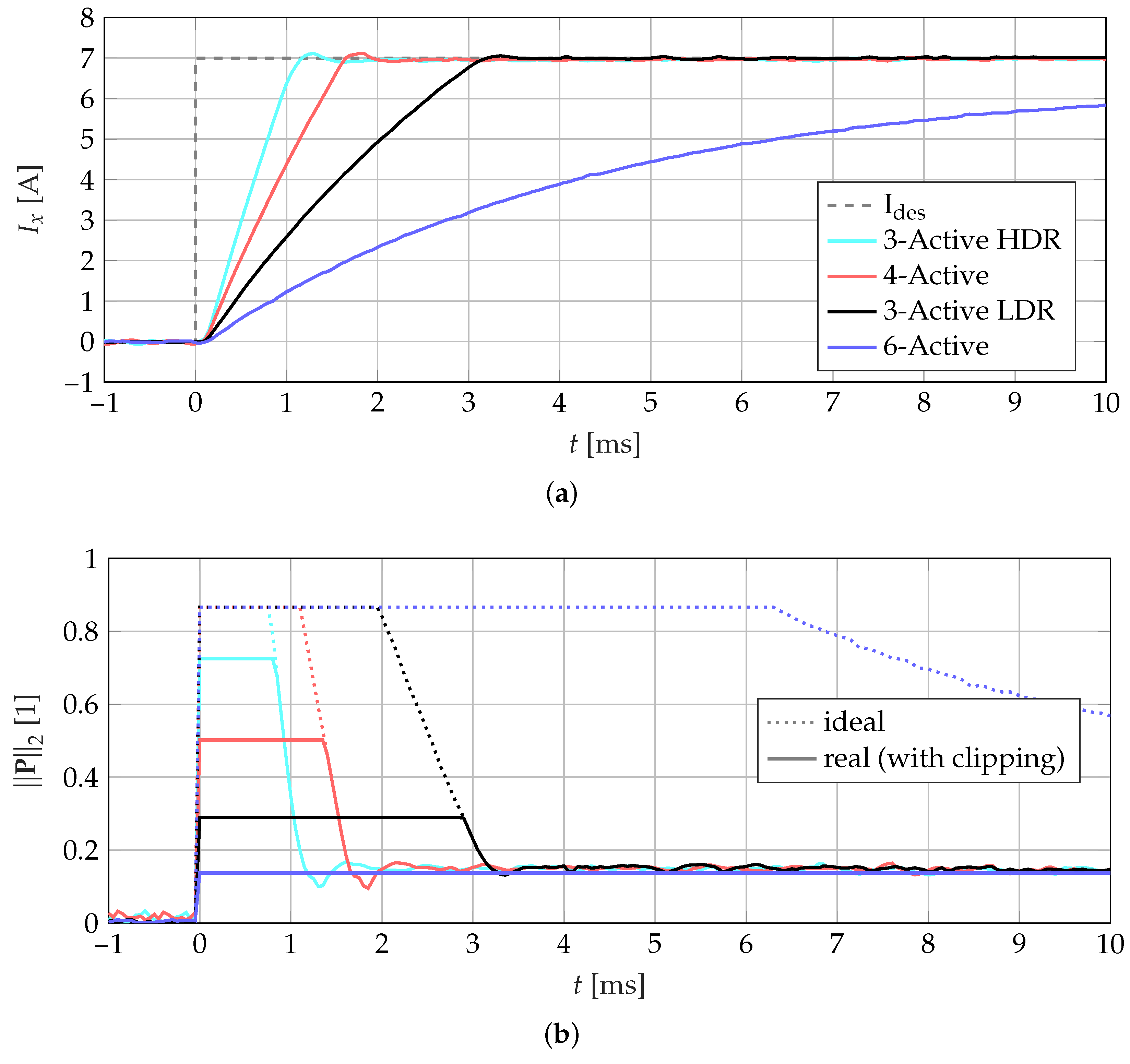
5.2. Dynamic of the Current Controller
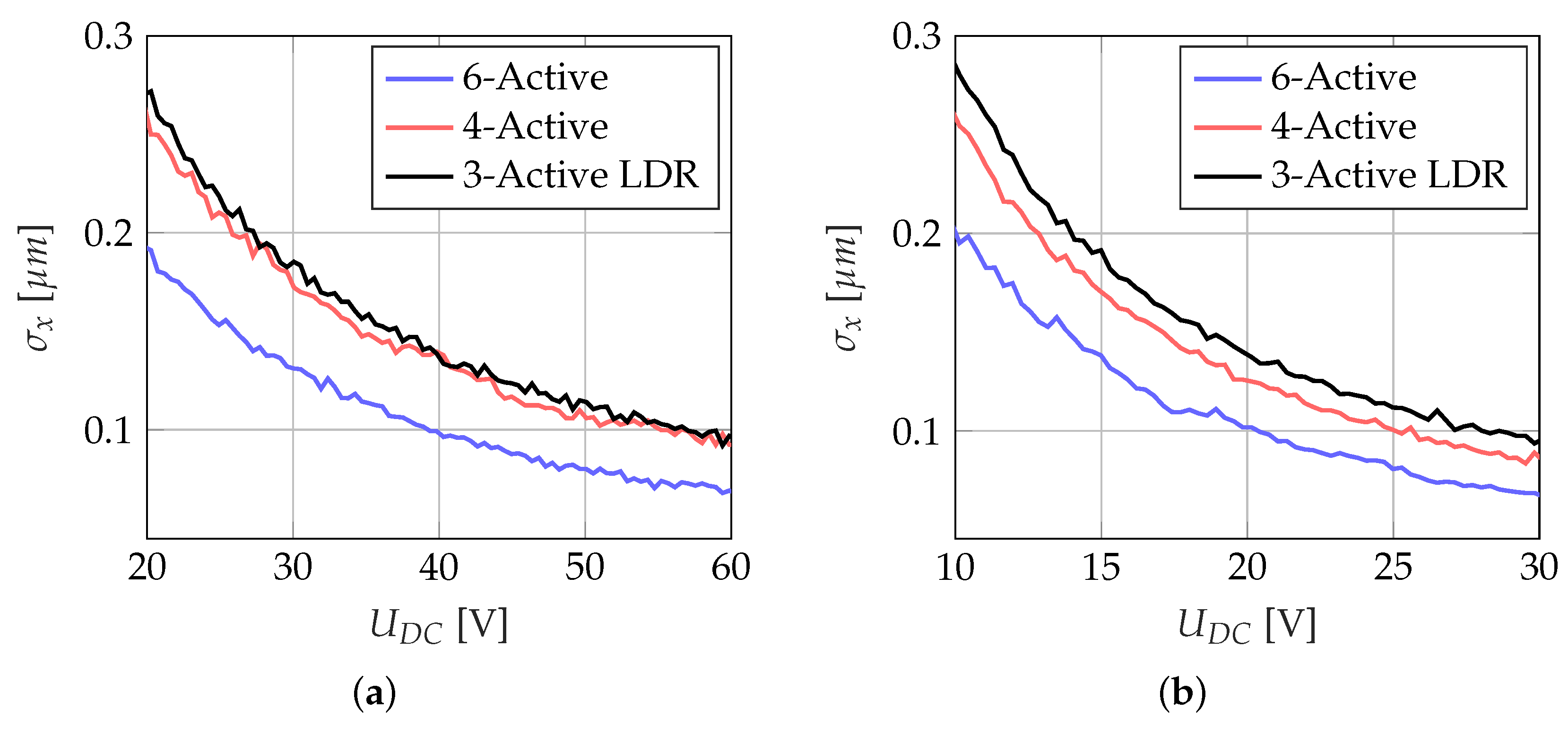
5.3. Noise of the Self-Sensing Method
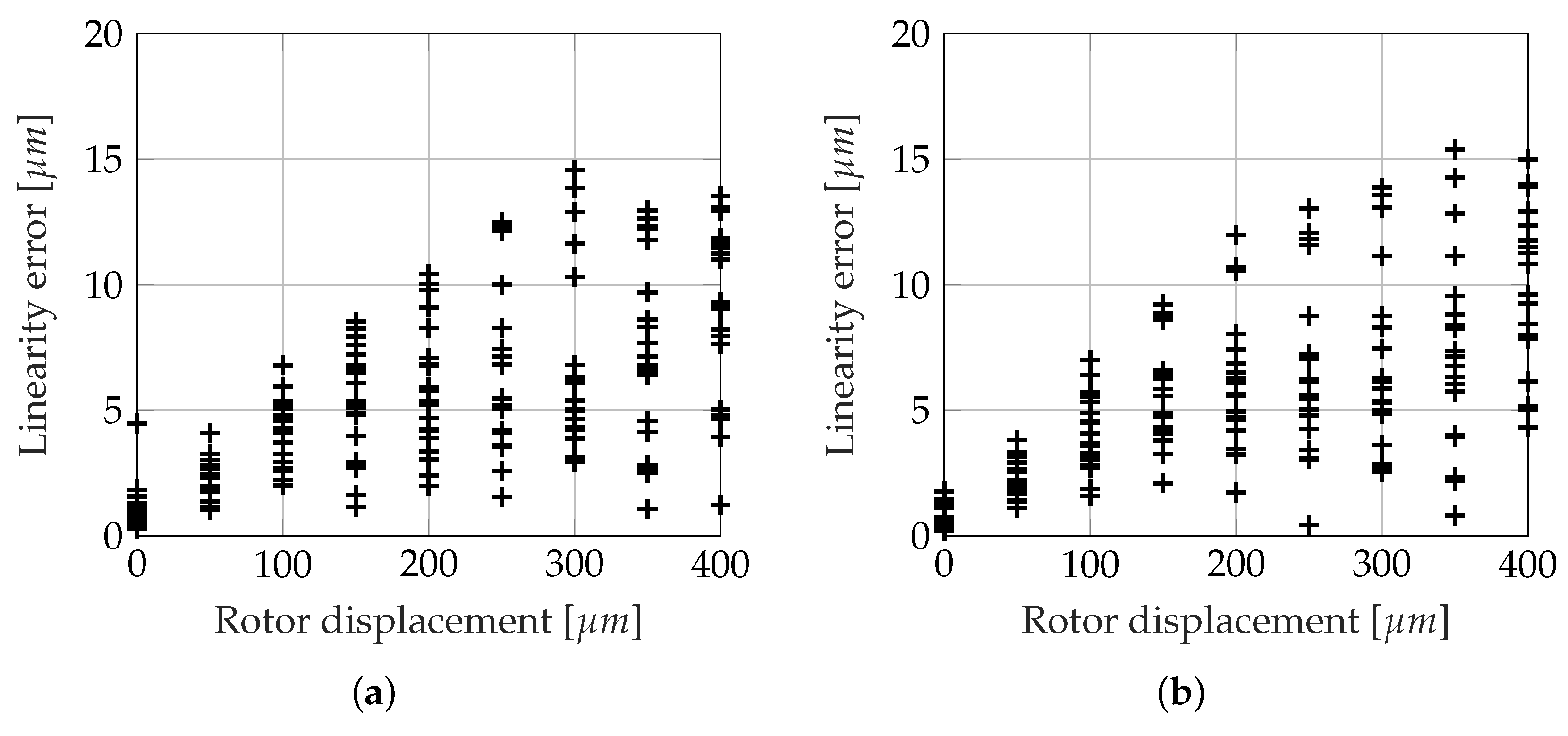
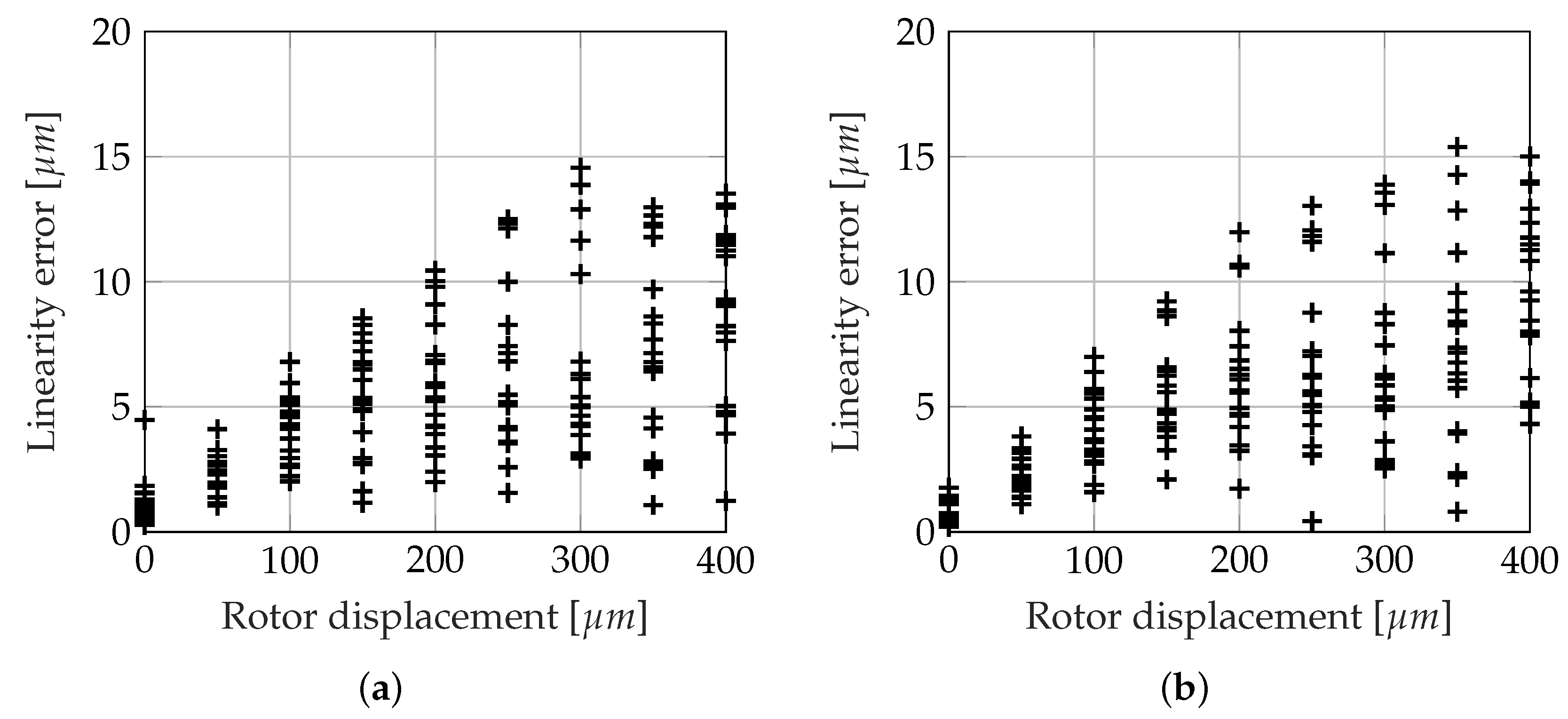
5.4. Linearity of the Self-Sensing Method
5.5. Small Signal Behavior
6. Results
7. Conclusions and Outlook
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| AMB | Active Magnetic Bearing |
| DC | Direct Current |
| HDR | High Dynamic Range |
| LDR | Low Dynamic Range |
| PCB | Printed Circuit Board |
| PM | Permanent Magnet |
| PWM | Pulse Width Modulation |
| SMC | Soft Magnetic Composite |
| SVM | Space Vector Modulation |
References
- Schweitzer, G.; Maslen, E.H. Magnetic Bearings: Theory, Design, and Application to Rotating Machinery; Springer: Berlin, Germany, 2009; pp. 127–145. ISBN 978-3-642-00496-4. [Google Scholar]
- Earnshaw, S. On the Nature of Molecular Forces which Regulate the Constitution of the Lumiferous Ether. Trans. Camb. Philos. Soc. 1842, 7, 97–112. [Google Scholar]
- Sivadasan, K.K. Analysis of Self-Sensing Active Magnetic Bearings Working on Inductance Measurement Principle. IEEE Trans. Magn. 1996, 32, 329–334. [Google Scholar] [CrossRef]
- Maslen, E. Self–sensing for active magnetic bearings: Overview and status. In Proceedings of the 10th International Symposium on Magnetic Bearings (ISMB10), Martigny, Switzerland, 21–23 August 2006. [Google Scholar]
- Schammass, A.; Herzog, R.; Buhler, P.; Bleuler, H. New results for Self-Sensing Active Magnetic Bearings Using Modulation Approach. IEEE Trans. Control. Syst. Technol. 2005, 13, 509–516. [Google Scholar] [CrossRef]
- Hofer, M.; Nenning, T.; Hutterer, M.; Schrödl, M. Current Slope Measurement Strategies for Sensorless Control of a Three Phase Radial Active Magnetic Bearing. In Proceedings of the 22nd International Conference on Magnetic Levitated Systems and Linear Drives (MAGLEV 2014), Rio de Janeiro, Brazil, 28 September–1 October 2014. [Google Scholar]
- Wang, J.; Binder, A. Position estimation for self-sensing magnetic bearings based on the current slope due to the switching amplifier. Eur. Power Electron. Drives (EPE) 2016, 26, 125–141. [Google Scholar] [CrossRef]
- Gruber, W.; Pichler, M.; Rothböck, M.; Amrhein, W. Self-Sensing Active Magnetic Bearing Using 2-Level PWM Current Ripple Demodulation. In Proceedings of the 7th International Conference on Sensing Technology (ICST), Wellington, New Zealand, 3–5 December 2013. [Google Scholar]
- You, S.J.; Ahn, H.J. Position Estimation for Self-Sensing Magnetic Bearings using Artificial Neural Network. In Proceedings of the 16th International Symposium on Magnetic Bearings (ISMB16), Beijing, China, 13–17 August 2018. [Google Scholar]
- Schrödl, M. Sensorless control of permanent-magnet synchronous machines at arbitrary operating points using a modified INFORM flux model. Eur. Trans. Electr. Power ETEP 1993, 3, 277–283. [Google Scholar] [CrossRef]
- Hofer, M.; Hutterer, M.; Nenning, T.; Schrödl, M. Improved Sensorless Control of a Modular Three Phase Radial Active Magnetic Bearing. In Proceedings of the 14th International Symposium on Magnetic Bearings (ISMB14), Linz, Austria, 11–14 August 2014. [Google Scholar]
- Nenning, T.; Hofer, M.; Hutterer, M.; Schrödl, M. Setup with two Self-Sensing Magnetic Bearings using Differential 3-Active INFORM. In Proceedings of the 14th International Symposium on Magnetic Bearings (ISMB14), Linz, Austria, 11–14 August 2014. [Google Scholar]
- Schöb, R.; Redemann, C.; Gempp, T. Radial Active Magnetic Bearing for Operation with a 3-Phase Power Converter. In Proceedings of the ISMST4, Gifu City, Japan, 30 October–1 November 1997; pp. 111–124. [Google Scholar]
- Ahn, H.J.; Jeong, S.N. Driving an AMB system using a 2D space vector modulation of three-leg voltage source converters. J. Mech. Sci. Technol. 2011, 25, 239–246. [Google Scholar] [CrossRef]
- Hofer, M.; Hutterer, M.; Schrödl, M. PCB Integrated Differential Current Slope Measurement for Position-Sensorless Controlled Radial Active Magnetic Bearings. In Proceedings of the 15th International Symposium on Magnetic Bearings (ISMB15), Kitakyushu, Japan, 3–6 August 2016. [Google Scholar]
- Hofer, M.; Wimmer, D.; Schrödl, M. Analysis of a Current Biased Eight-Pole Radial Active Magnetic Bearing Regarding Self-Sensing. In Proceedings of the 16th International Symposium on Magnetic Bearings (ISMB16), Beijing, China, 13–17 August 2018. [Google Scholar]
- Herzog, R.; Vullioud, S.; Amstad, R.; Galdo, G.; Muellhaupt, P.; Longchamp, R. Self-Sensing of Non-Laminated Axial Magnetic Bearings: Modelling and Validation. J. Syst. Des. Dyn. 2009, 3, 443–452. [Google Scholar] [CrossRef]
- Hofer, M.; Hutterer, M.; Schrödl, M. Application of Soft Magnetic Composites (SMCs) in Position-Sensorless Controlled Radial Active Magnetic Bearings. In Proceedings of the 15th International Symposium on Magnetic Bearings (ISMB15), Kitakyushu, Japan, 3–6 August 2016. [Google Scholar]
- Gua, Y.; Zhu, J.G. Application of Soft Magnetic Composite Materials in Electrical Machines. Aust. J. Electr. Electron. Eng. 2006, 3, 37–46. [Google Scholar] [CrossRef]
- Van der Broeck, H.W.; Skudelny, H.-C.; Stanke, G.V. Analysis and Realization of a Pulsewidth Modulator Based on Voltage Space Vectors. IEEE Trans. Ind. Appl. 1988, 24, 142–150. [Google Scholar] [CrossRef]
- Chattopadhyay, S.; Mitra, M.; Sengupta, S. Electric Power Quality; Springer: Berlin, Germany, 2011; pp. 89–96. ISBN 978-94-007-0634-7. [Google Scholar]
- Quang, N.P.; Dittrich, J.A. Vector Control of Three-Phase AC Machines: System Development in Practice; Springer: Berlin, Germany, 2015; pp. 17–59. ISBN 978-3-662-46915-6. [Google Scholar]
- Hutterer, M.; Schrödl, M. Control of Active Magnetic Bearings in Turbomolecular Pumps for Rotors with Low Resonance Frequencies of the Blade Wheel. Lubricants 2017, 5, 26. [Google Scholar] [CrossRef]
- Nerg, J.; Pöllänen, R.; Pyrhönen, J. Modelling the Force versus Current Characteristics, Linearized Parameters and Dynamic Inductance of Radial Active Magnetic Bearings Using Different Numerical Calculation Methods. WSEAS Trans. Circuits Syst. 2005, 4, 551–559. [Google Scholar]
- Maslen, E.; Montie, D.; Iwasaki, T. Robustness Of Self Sensing Magnetic Bearings Using Amplifier Switching Ripple. In Proceedings of the 9th International Symposium on Magnetic Bearings (ISMB9), Lexington, KY, USA, 3–6 August 2004. [Google Scholar]
- Hutterer, M.; Hofer, M.; Schrödl, M. New Results on the Robustness of Selfsensing Magnetic Bearings. In Proceedings of the 15th International Symposium on Magnetic Bearings (ISMB15), Kitakyushu, Japan, 3–6 August 2016. [Google Scholar]

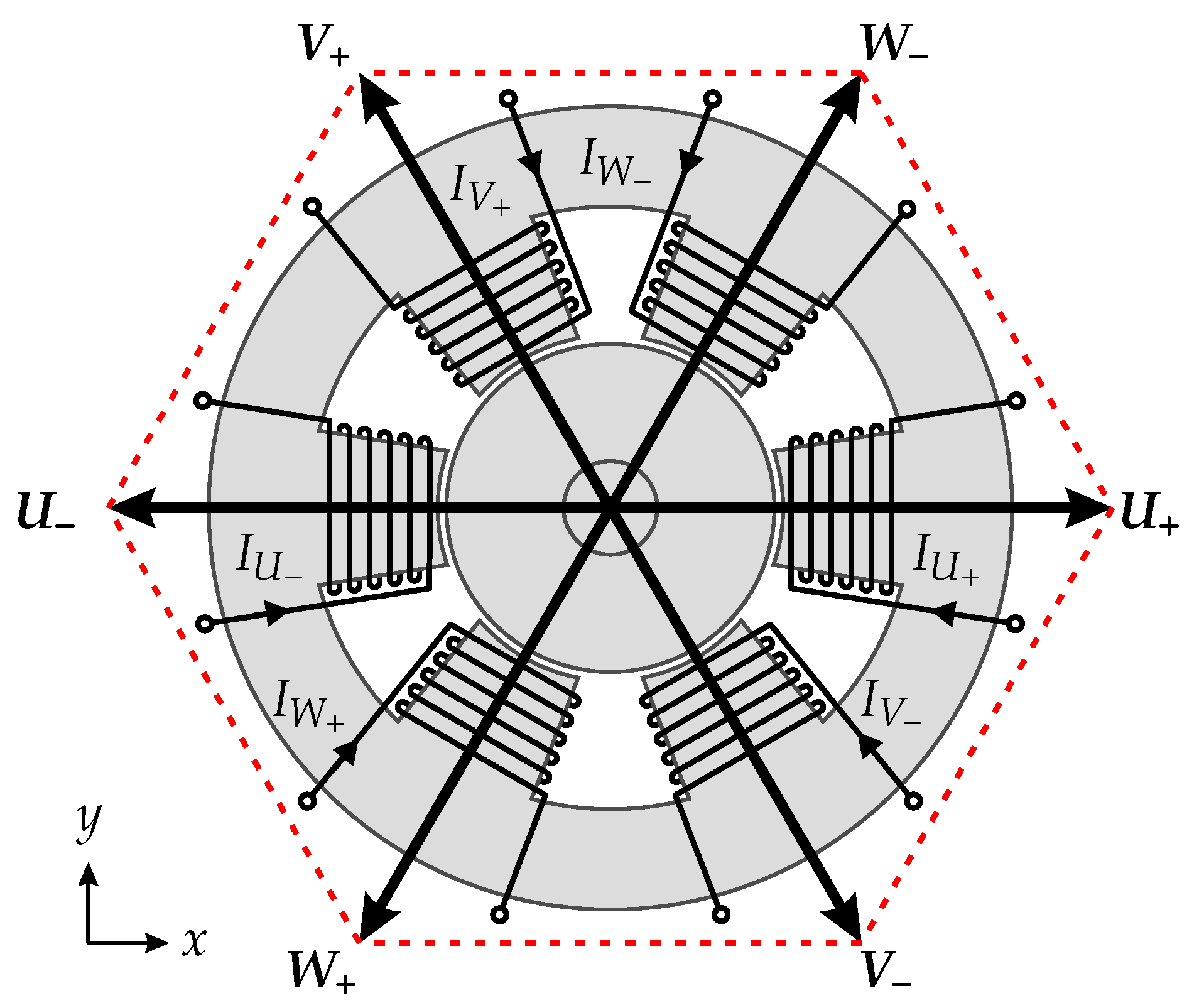

| Phase | Switch | Voltage Space Vector | |||||||
|---|---|---|---|---|---|---|---|---|---|
| U | HS | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 |
| U | LS | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 1 |
| V | HS | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 |
| V | LS | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 1 |
| W | HS | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 |
| W | LS | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wimmer, D.; Hutterer, M.; Hofer, M.; Schrödl, M. Space Vector Modulation Strategies for Self-Sensing Three-Phase Radial Active Magnetic Bearings. Actuators 2019, 8, 41. https://doi.org/10.3390/act8020041
Wimmer D, Hutterer M, Hofer M, Schrödl M. Space Vector Modulation Strategies for Self-Sensing Three-Phase Radial Active Magnetic Bearings. Actuators. 2019; 8(2):41. https://doi.org/10.3390/act8020041
Chicago/Turabian StyleWimmer, Dominik, Markus Hutterer, Matthias Hofer, and Manfred Schrödl. 2019. "Space Vector Modulation Strategies for Self-Sensing Three-Phase Radial Active Magnetic Bearings" Actuators 8, no. 2: 41. https://doi.org/10.3390/act8020041
APA StyleWimmer, D., Hutterer, M., Hofer, M., & Schrödl, M. (2019). Space Vector Modulation Strategies for Self-Sensing Three-Phase Radial Active Magnetic Bearings. Actuators, 8(2), 41. https://doi.org/10.3390/act8020041





