Measurement of a Temperature Field Generated by a Synthetic Jet Actuator using Digital Holographic Interferometry
Abstract
1. Introduction
2. Digital Holographic Interferometry
Temperature Field Measurements
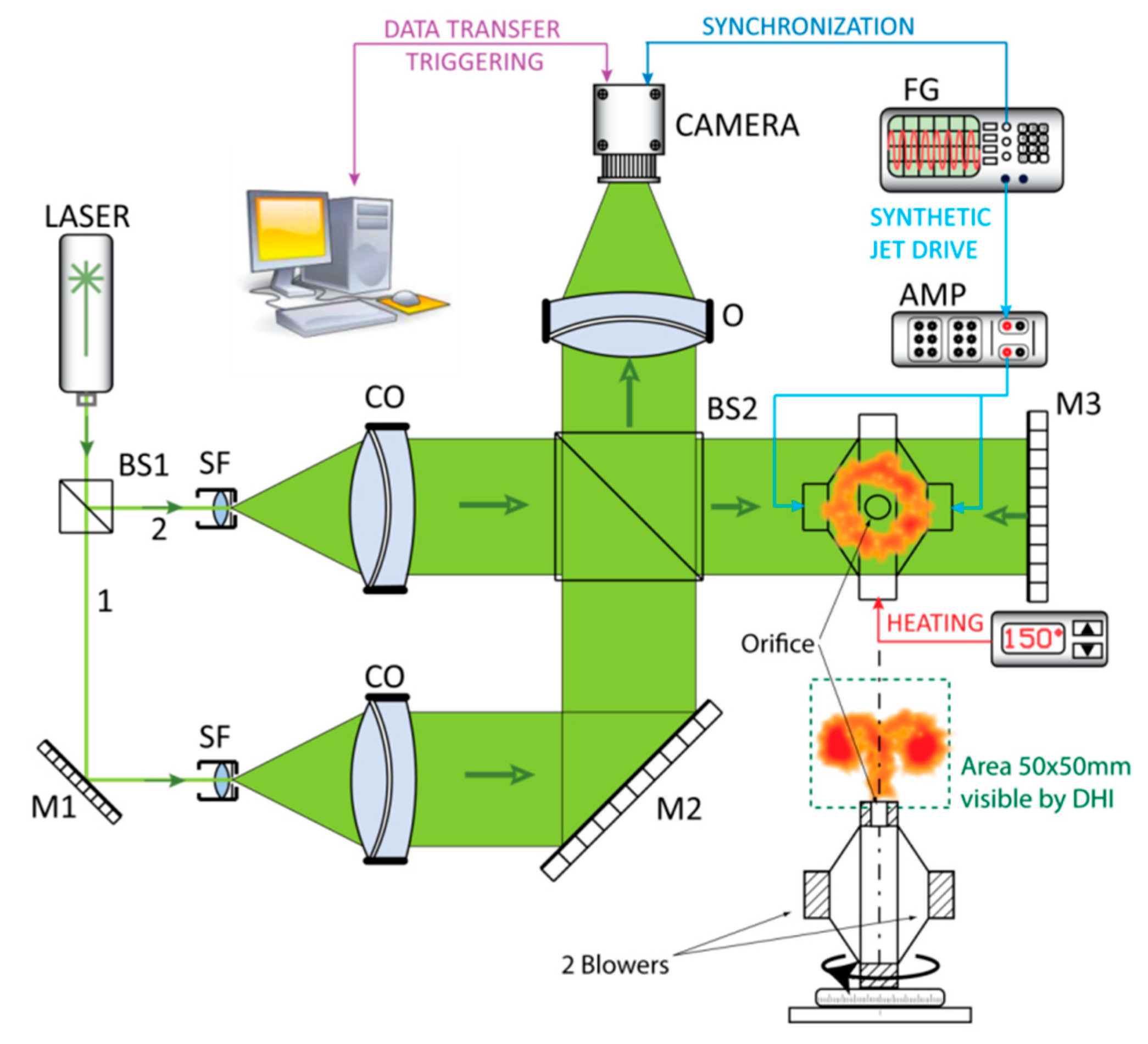
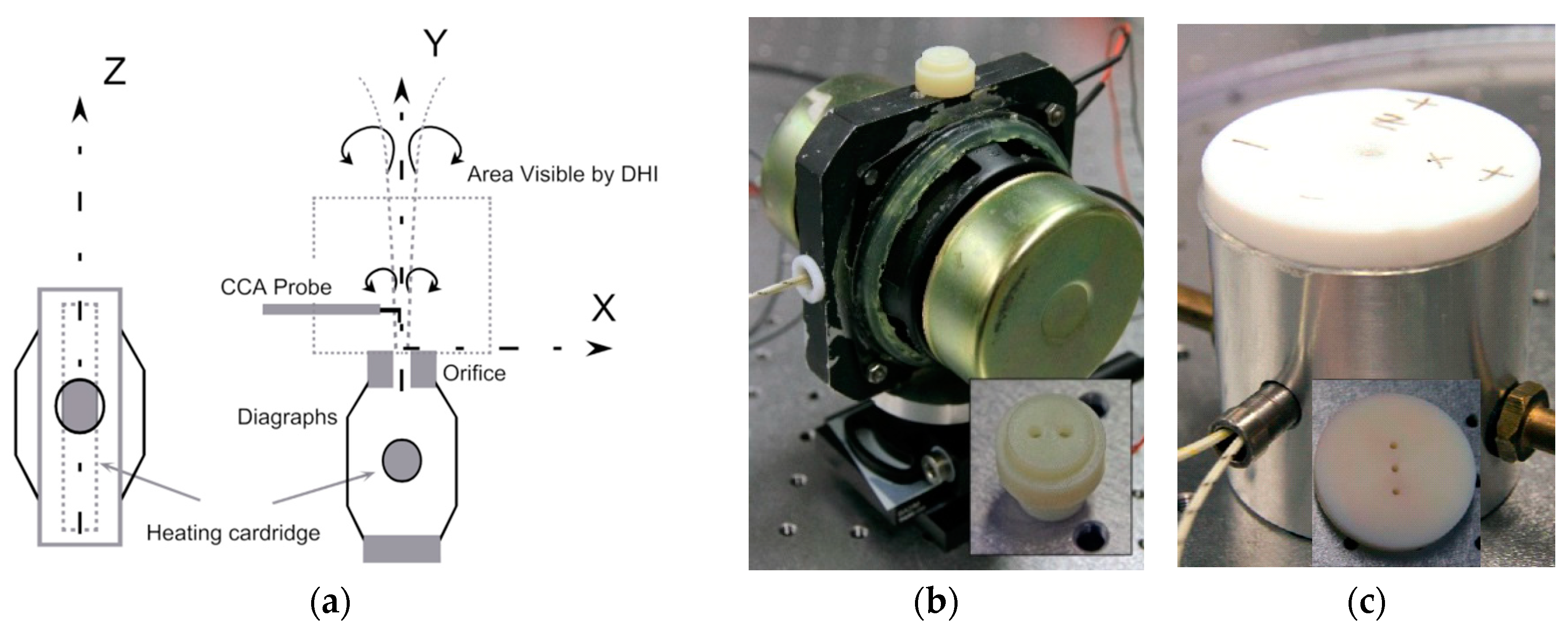
3. Experimental Setup
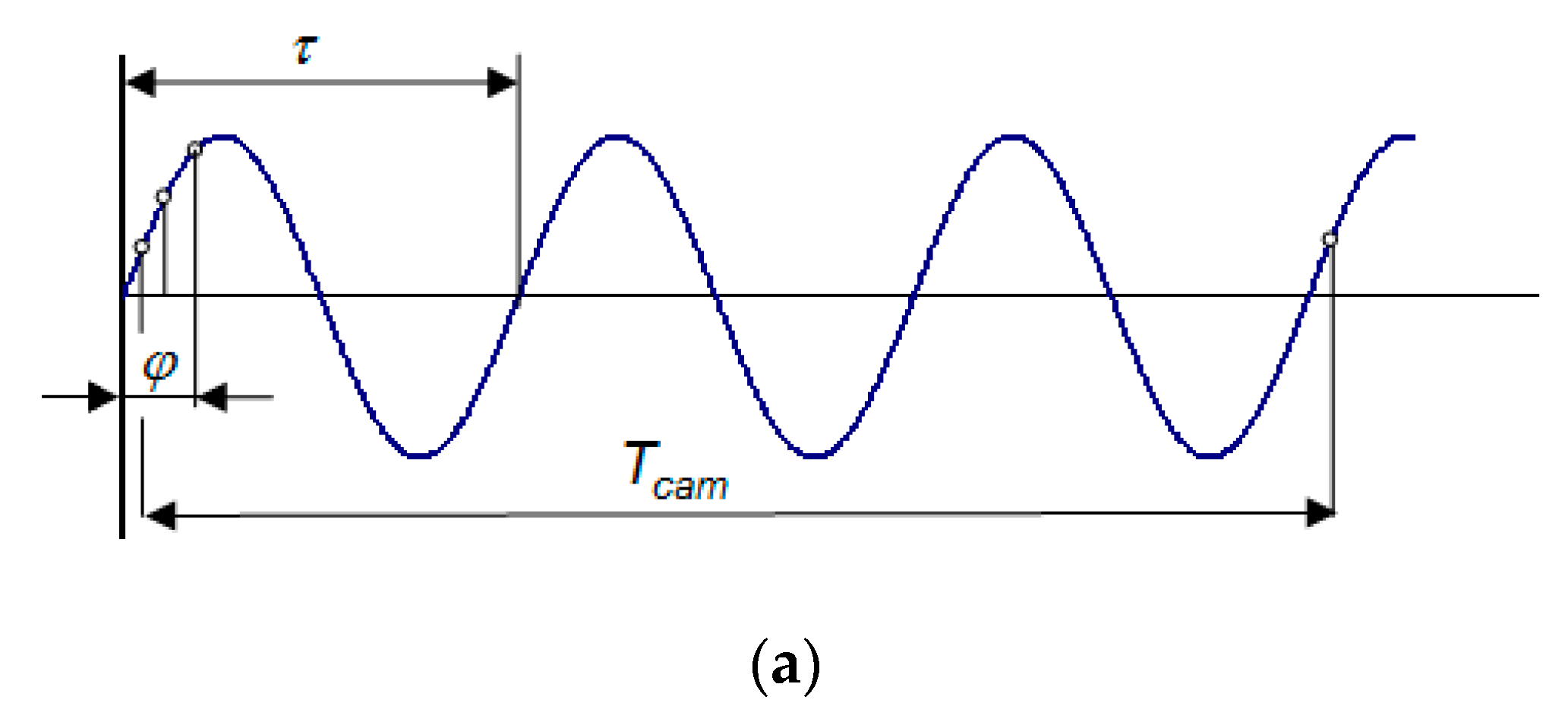
System Synchronization
4. Results
4.1. Validation of Camera Synchronization and 2D Digital Holographic Interferometry
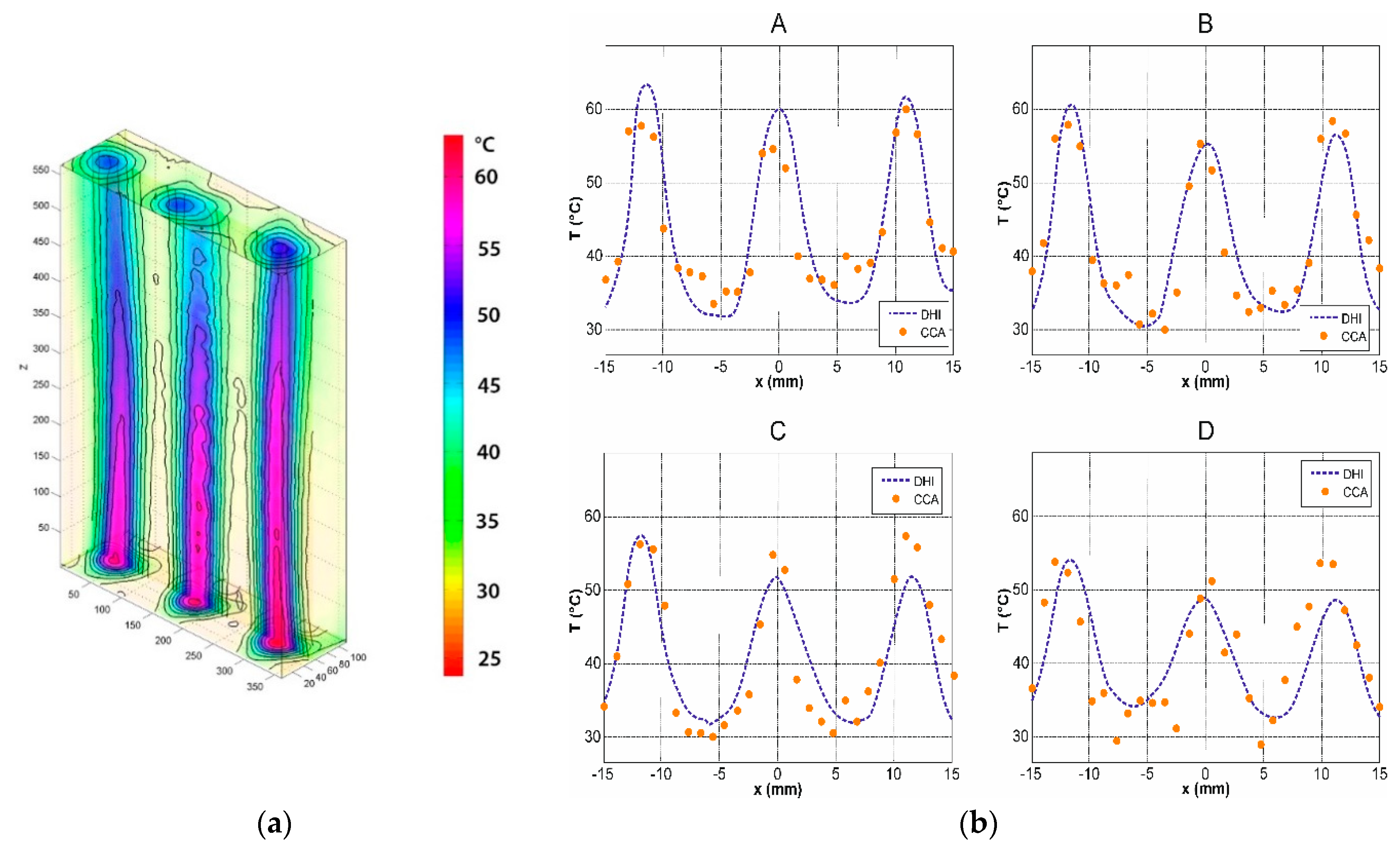
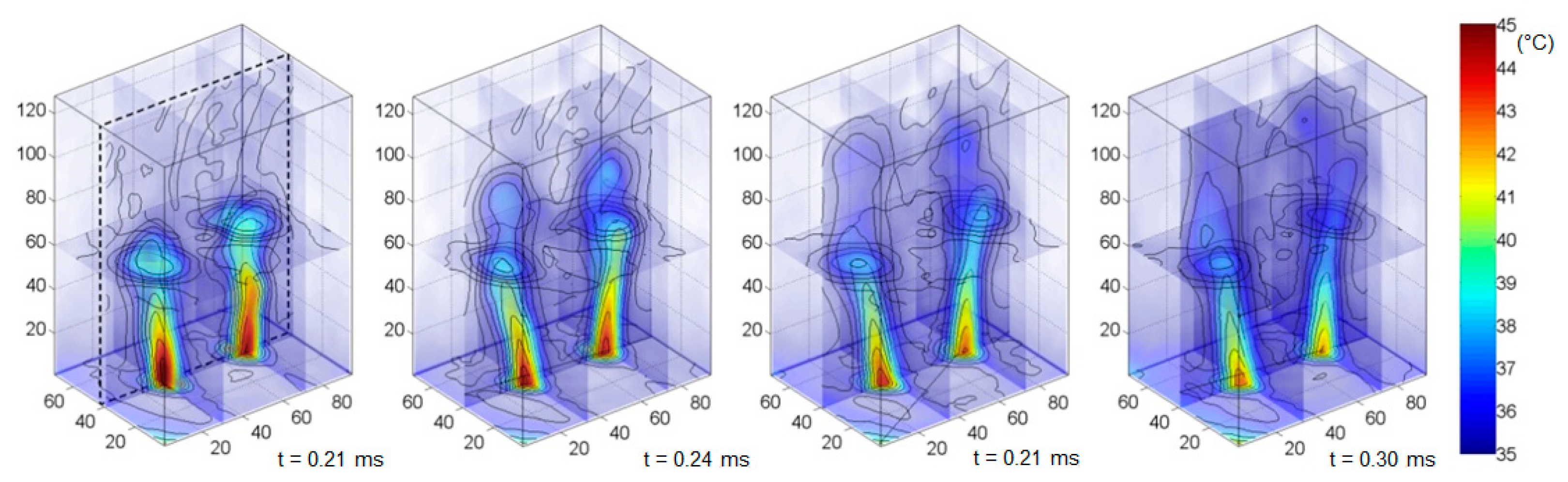
4.2. DHI Validation of the Tomographic Measurement of the 3D Temperature Field by DHI Steady Flow
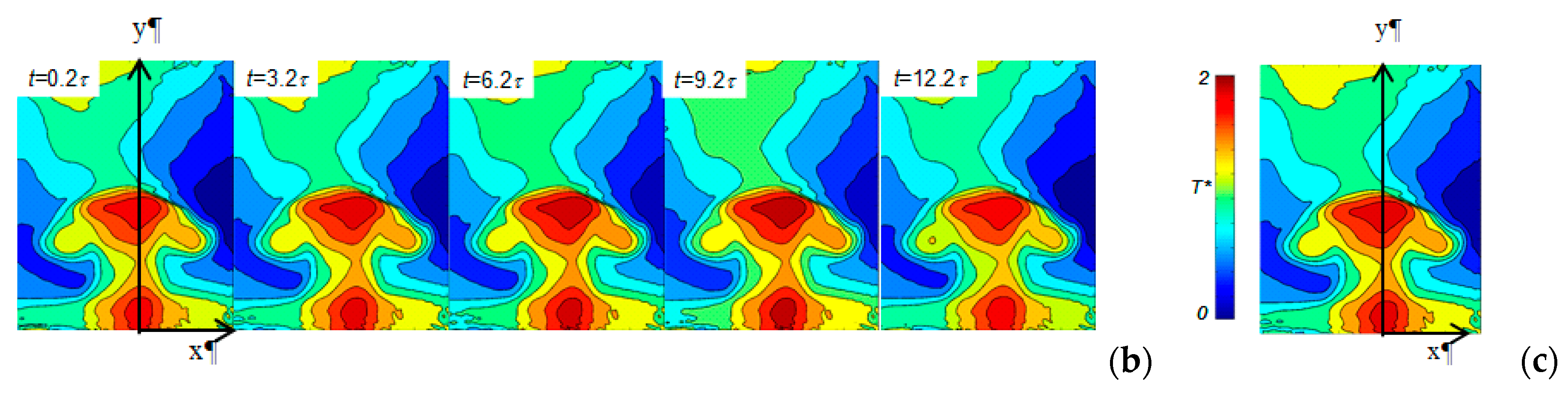
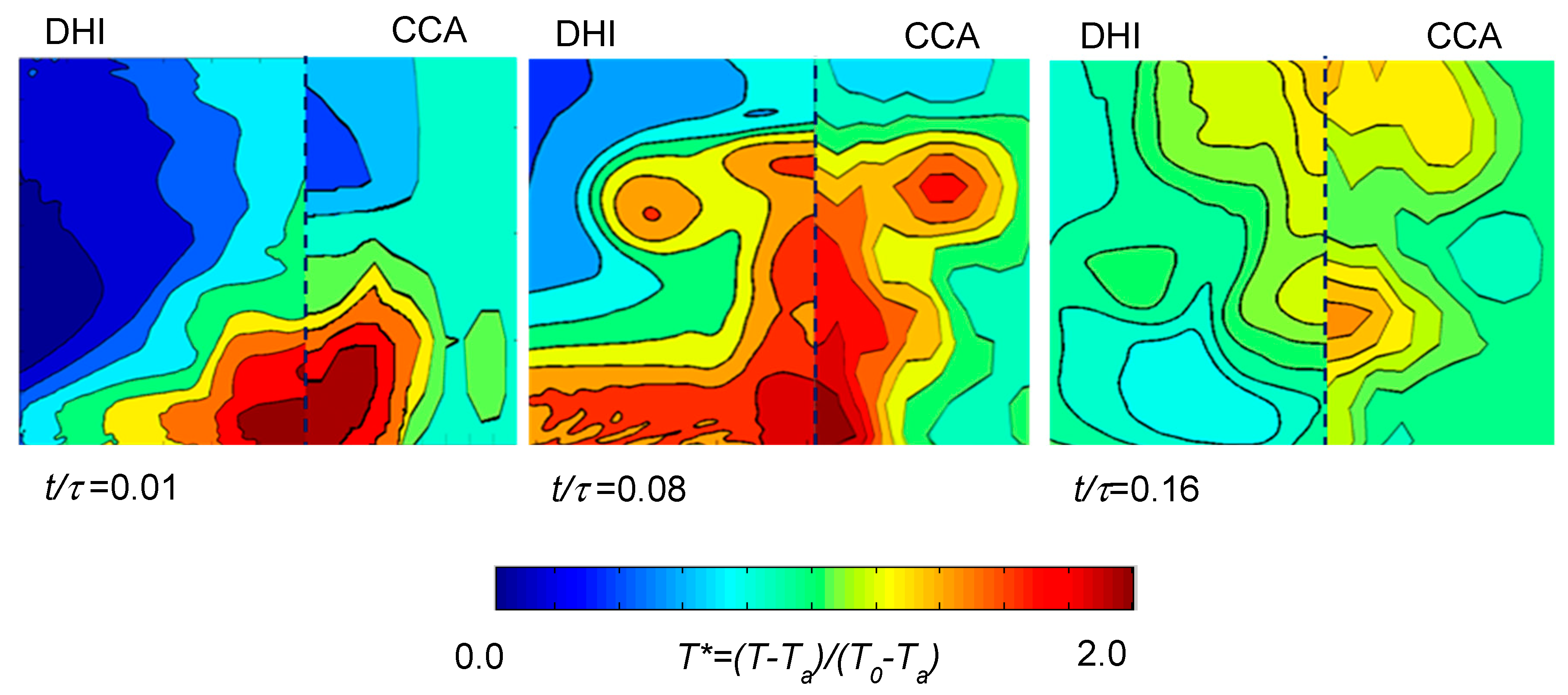
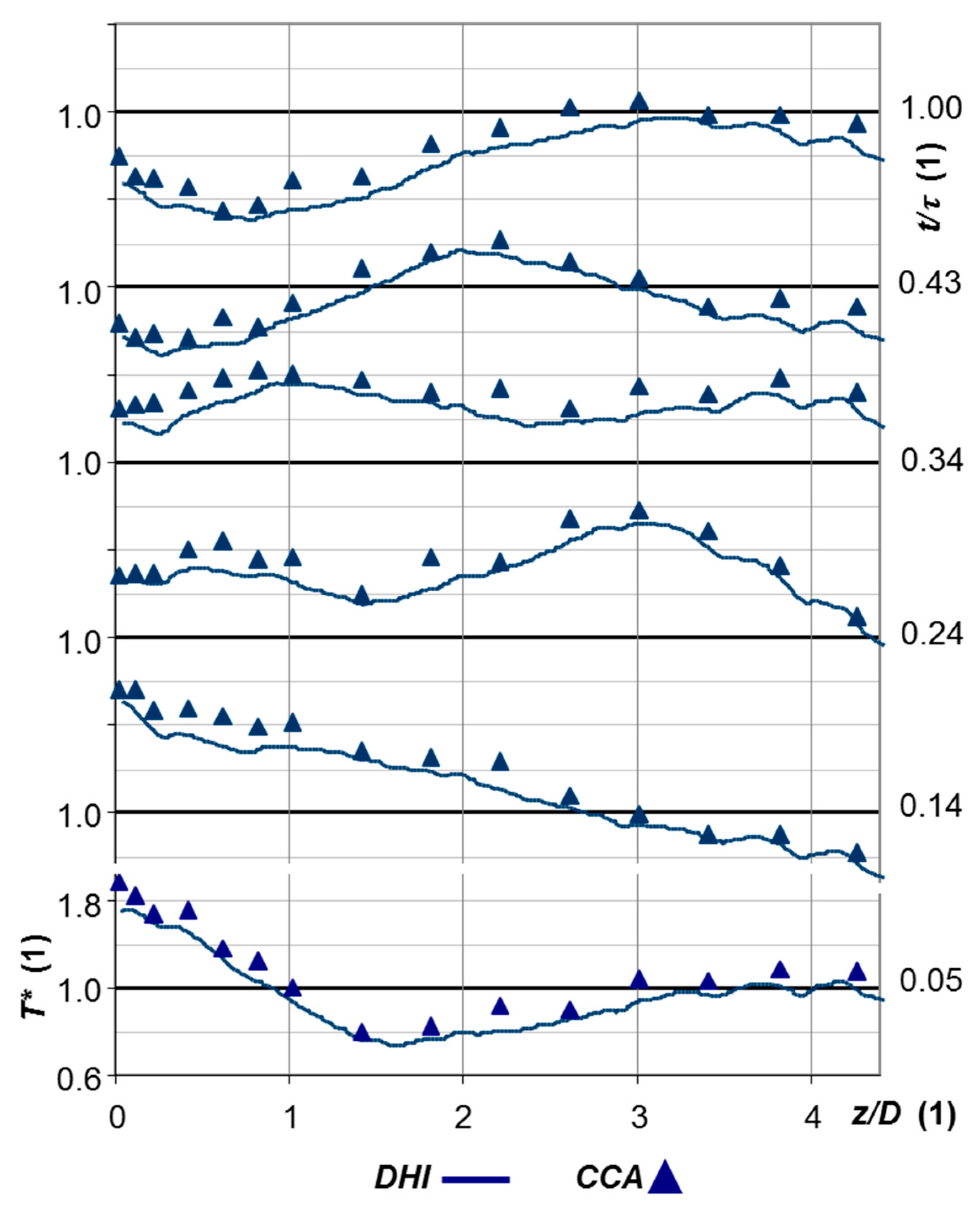
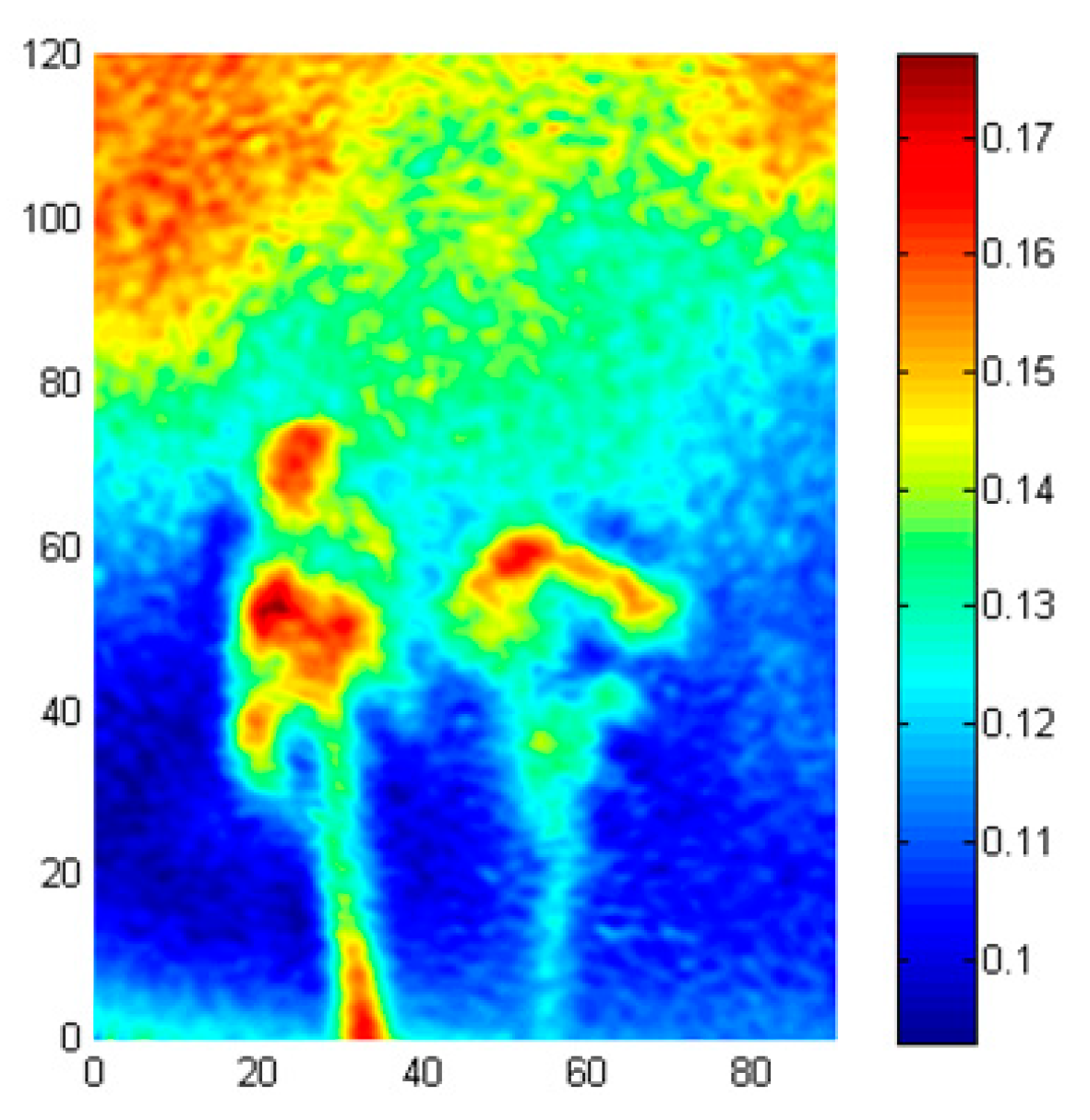
4.3. DHI Measurements of the Dynamic Asymmetrical Temperature Field—Synthetic Jets
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Liu, S.; Sakr, M. A comprehensive review on passive heat transfer enhancements in pipe exchangers. Renew. Sustain. Energy Rev. 2013, 19, 64–81. [Google Scholar] [CrossRef]
- Vasiliev, L.L. Heat pipes in modern heat exchangers. Appl. Therm. Eng. 2005, 25, 1–19. [Google Scholar] [CrossRef]
- Straka, P.; Prihoda, J.; Kozisek, M.; Furst, J. Simulation of transitional flows through a turbine blade cascade with heat transfer for various flow conditions. Eur. Phys. J. Conf. 2017, 143, 02118. [Google Scholar] [CrossRef]
- Verstraete, T.; Alsalihi, Z.; Van den Braembussche, R.A. Numerical Study of the Heat Transfer in Micro Gas Turbines. J. Turbomach. 2006, 129, 835–841. [Google Scholar] [CrossRef]
- Xiao, G.; Yang, T.; Liu, H.; Ni, D.; Ferrari, M.L.; Li, M.; Luo, Z.; Cen, K.; Ni, M. Recuperators for micro gas turbines: A review. Appl. Energy 2017, 197, 83–99. [Google Scholar] [CrossRef]
- Verstraete, D.; Bowkett, C. Impact of heat transfer on the performance of micro gas turbines. Appl. Energy 2015, 138, 445–449. [Google Scholar] [CrossRef]
- Hasnain, S.M. Review on sustainable thermal energy storage technologies, Part I: Heat storage materials and techniques. Energy Convers. Manag. 1998, 39, 1127–1138. [Google Scholar] [CrossRef]
- Hanchen, M.; Brückner, S.; Steinfeld, A. High-temperature thermal storage using a packed bed of rocks—Heat transfer analysis and experimental validation. Appl. Therm. Eng. 2011, 31, 1798–1806. [Google Scholar] [CrossRef]
- Agyenim, F.; Hewitt, N.; Eames, P.; Smyth, M. A review of materials, heat transfer and phase change problem formulation for latent heat thermal energy storage systems. Renew. Sustain. Energy Rev. 2010, 14, 615–628. [Google Scholar] [CrossRef]
- Krishnamurthy, M.R.; Prasannakumara, B.C.; Gireesha, B.J.; Gorla, R.S.R. Effect of chemical reaction on MHD boundary layer flow and melting heat transfer of Williamson nanofluid in porous medium. Eng. Sci. Technol. Int. J. 2016, 19, 53–61. [Google Scholar] [CrossRef]
- Khan, W.A.; Irfan, M.; Khan, M.; Alshomrani, A.S.; Alzahrani, A.K.; Alghamdi, M.S. Impact of chemical processes on magneto nanoparticle for the generalized Burgers fluid. J. Mol. Liq. 2017, 234, 201–208. [Google Scholar] [CrossRef]
- Venkateswarlu, B.; Satya Narayana, P.V. Chemical reaction and radiation absorption effects on the flow and heat transfer of a nanofluid in a rotating system. Appl. Nanosci. 2015, 5, 351–360. [Google Scholar] [CrossRef]
- Zhao, J.; Huang, S.; Gong, L.; Huang, Z. Numerical study and optimizing on micro square pin-fin heat sink for electronic cooling. Appl. Therm. Eng. 2016, 93, 1347–1359. [Google Scholar] [CrossRef]
- Abdoli, A.; Jimenez, G.; Dulikravich, G.S. Thermo-fluid analysis of micro pin-fin array cooling configurations for high heat fluxes with a hot spot. Int. J. Therm. Sci. 2015, 90, 290–297. [Google Scholar] [CrossRef]
- Liu, D.; Zhao, F.Y.; Yang, H.X.; Tang, G.F. Thermoelectric mini cooler coupled with micro thermosiphon for CPU cooling system. Energy 2015, 83, 29–36. [Google Scholar] [CrossRef]
- Sohel Murshed, S.M.; Nieto de Castro, C.A. A critical review of traditional and emerging techniques and fluids for electronics cooling. Renew. Sustain. Energy Rev. 2017, 78, 821–833. [Google Scholar] [CrossRef]
- Dancova, P. Experimental Investigation of Synthetic Jets in a Laminar Channel Flow. Ph.D. Thesis, Technical University of Liberec, Liberec, Czech Republic, 2012. [Google Scholar]
- Dancova, P.; Travnicek, Z.; Vit, T. Experimental Investigation of a Synthetic Jet Array in a Laminar Channel Flow. Eur. Phys. J. Conf. 2013, 45, 01002. [Google Scholar] [CrossRef]
- Timchenko, V.; Reizes, J.A.; Leonardi, E. An Evaluation of Synthetic Jets for Heat Transfer Enhancement in Air Cooled Micro-Channels. Int. J. Numer. Methods Heat Fluid Flow 2007, 17, 263–283. [Google Scholar] [CrossRef]
- Travnicek, Z.; Dancova, P.; Lam, J.H.; Timchenko, V.; Reizes, J. Numerical and experimental studies of a channel flow with multiple circular synthetic jets. Eur. Phys. J. Conf. 2012, 25, 01094. [Google Scholar] [CrossRef]
- Chaudhari, M.; Puranik, B.; Agrawal, A. Multiple orifice synthetic jet for improvement in impingement heat transfer. Int. J. Heat Mass Transf. 2011, 54, 2056–2065. [Google Scholar] [CrossRef]
- Al-Asadi, M.T.; Alkasmoul, F.S.; Wilson, M.C.T. Heat transfer enhancement in a micro-channel cooling system using cylindrical vortex generators. Int. Commun. Heat Mass Transf. 2016, 74, 40–47. [Google Scholar] [CrossRef]
- Chen, C.; Teng, J.T.; Cheng, C.H.; Jin, S.; Huang, S.; Liu, C.; Lee, M.T.; Pan, H.H.; Greif, R. A study on fluid flow and heat transfer in rectangular microchannels with various longitudinal vortex generators. Int. J. Heat Mass Transf. 2014, 69, 203–214. [Google Scholar] [CrossRef]
- Al-Asadi, M.T.; Alkasmoul, F.S.; Wilson, M.C.T. Benefits of spanwise gaps in cylindrical vortex generators for conjugate heat transfer enhancement in micro-channels. Appl. Therm. Eng. 2018, 130, 571–586. [Google Scholar] [CrossRef]
- Smith, B.L.; Glezer, A. The formation and evolution of synthetic jets. Phys. Fluids 1998, 10, 2281–2297. [Google Scholar] [CrossRef]
- Holman, R.; Utturkar, Y. Formation Criterion for Synthetic Jets. AIAA J. 2005, 43, 2110–2116. [Google Scholar] [CrossRef]
- Cater, J.E.; Soria, J. The evolution of round zero-net-mass-flux jets. J. Fluid Mech. 2002, 472, 167–200. [Google Scholar] [CrossRef]
- Glezer, A.; Amitay, M. Synthetic jets. Annu. Rev. Fluid Mech. 2002, 34, 503–529. [Google Scholar] [CrossRef]
- Chiatto, M.; Capuano, F.; de Luca, L. Numerical and experimental characterization of a double-orifice synthetic jet actuator. Meccanica 2018, 53, 2883–2896. [Google Scholar] [CrossRef]
- Mallinson, S.G.; Reizes, J.A.; Hong, G.; Westbury, P.S. Analysis of hot-wire anemometry data obtained in a synthetic jet flow. Exp. Fluid Sci. 2004, 28, 265–272. [Google Scholar] [CrossRef]
- Bruun, H.H. Hot Wire Anemometry; Oxford Univ. Press: Oxford, NY, USA, 1995. [Google Scholar]
- Childs, P.R.N.; Greenwood, J.R.; Long, C.A. Review of temperature measurement. Rev. Sci. Instrum. 2000, 71, 2959–2978. [Google Scholar] [CrossRef]
- Hall, R.J.; Bonczyk, P.A. Sooting Flame Thermometry Using Emission/Absorption Tomography. Appl. Opt. 1990, 29, 4590–4598. [Google Scholar] [CrossRef]
- Kampmann, S.; Leipertz, A.; Döbbeling, K.; Haumann, J.; Sattelmayer, T. Two-dimensional temperature measurements in a technical combustor with laser Rayleigh scatterin. Appl. Opt. 1993, 32, 6167–6172. [Google Scholar] [CrossRef]
- Feldmann, O.; Mayinger, F. Optical Measurements—Techniques and Applications; Springer: Berlin, Germany, 2001. [Google Scholar]
- Dancova, P. Analysis of the “Synthetic Jet”. Master’s Thesis, Technical University of Liberec, Liberec, Czech Republic, 2006. [Google Scholar]
- Gabor, D. A new microscopic principle. Nature 1948, 161, 777–778. [Google Scholar] [CrossRef]
- Leith, E.N.; Upatnieks, J. Wavefront Reconstruction with Diffused Illumination and Three-Dimensional Objects. J. Opt. Soc. Am. 1964, 54, 1295. [Google Scholar] [CrossRef]
- Lohmann, A.W.; Paris, D.P. Binary Fraunhofer Holograms, Generated by Computer. Appl. Opt. 1967, 6, 1739. [Google Scholar] [CrossRef]
- Lee, W.H. Binary Synthetic Holograms. Appl. Opt. 1974, 13, 1677–1682. [Google Scholar] [CrossRef]
- Lee, W.H. Sampled Fourier Transform Hologram Generated by Computer. Appl. Opt. 1970, 9, 639–643. [Google Scholar] [CrossRef]
- Heanue, F.; Bashaw, M.C.; Hesselink, L. Volume holographic storage and retrieval of digital data. Science 1994, 265, 749–752. [Google Scholar] [CrossRef]
- Powell, R.L.; Stetson, K.A. Interferometric Vibration Analysis by Wavefront Reconstruction. J. Opt. Soc. Am. 1965, 55, 1593–1598. [Google Scholar] [CrossRef]
- Stetson, K.A.; Powell, R.L. Interferometric Hologram Evaluation and Real-Time Vibration Analysis of Diffuse Objects. J. Opt. Soc. Am. 1965, 55, 1694–1695. [Google Scholar] [CrossRef]
- Brooks, R.E.; Heflinger, L.O.; Wuerker, R.F. Interferometry with a Holographically Reconstructed Comparison Beam. Appl. Phys. Lett. 1965, 7, 248–249. [Google Scholar] [CrossRef]
- Haines, K.A.; Hildebrand, B.P. Surface-Deformation Measurement using the Wavefront Reconstruction Technique. Appl. Opt. 1966, 5, 595–602. [Google Scholar] [CrossRef] [PubMed]
- Hildebrand, B.P.; Haines, K.A. The generation of three-dimensional contour maps by wavefront reconstruction. Phys. Lett. 1966, 21, 422–423. [Google Scholar] [CrossRef]
- Heflinger, L.O.; Wuerker, R.F. Holographic Contouring via Multifrequency Lasers. Appl. Phys. Lett. 1969, 15, 28–30. [Google Scholar] [CrossRef]
- Horman, M.H. An Application of Wavefront Reconstruction to Interferometry. Appl. Opt. 1965, 4, 333–336. [Google Scholar] [CrossRef]
- Sweeney, D.W.; Vest, C.M. Reconstruction of Three-Dimensional Refractive Index Fields from Multidirectional Interferometric Data. Appl. Opt. 1973, 12, 2649–2664. [Google Scholar] [CrossRef] [PubMed]
- Lira, I.H.; Vest, C.M. Refraction correction in holographic interferometry and tomography of transparent objects. Appl. Opt. 1987, 26, 3919–3928. [Google Scholar] [CrossRef]
- Goodman, J.W.; Lawrence, R.W. Digital Image Formation from Electronically Detected Holograms. Appl. Phys. Lett. 1967, 11, 176–181. [Google Scholar] [CrossRef]
- Kronrod, M.A.; Yaroslavsky, L.P.; Merzlyakov, N.S. Reconstruction of holograms with a computer. Sov. Phys. Technol. Phys. 1972, 17, 333–334. [Google Scholar]
- Schnars, U.; Jüptner, W. Direct recording of holograms by a CCD target and numerical reconstruction. Appl. Opt. 1994, 33, 179–181. [Google Scholar] [CrossRef]
- Zou, Y.; Pedrini, G.; Tiziani, H. Surface contouring in a video frame by changing the wavelength of a diode laser. Opt. Eng. 1996, 35, 1074–1079. [Google Scholar] [CrossRef]
- Kreis, T. Handbook of Holographic Interferometry, Optical and Digital Methods; Wiley: Berlin, Germany, 2004. [Google Scholar]
- Schnars, U.; Jueptner, W. Digital Holography: Digital Hologram Recording, Numerical Reconstruction, and Related Techniques; Springer: Berlin, Germany, 2004. [Google Scholar]
- Kim, M.K. Principles and techniques of digital holographic microscopy. J. Photonics Energy 2010, 1, 18005. [Google Scholar] [CrossRef]
- Garcia-Sucerquia, J.; Xu, W.; Jericho, S.K.; Klages, P.; Jericho, M.H.; Kreuzer, H.J. Digital in-line holographic microscopy. Appl. Opt. 2006, 45, 836–850. [Google Scholar] [CrossRef] [PubMed]
- Takaki, Y.; Ohzu, H. Fast Numerical Reconstruction Technique for High-Resolution Hybrid Holographic Microscopy. Appl. Opt. 1999, 38, 2204–2211. [Google Scholar] [CrossRef] [PubMed]
- Dubois, F.; Joannes, L.; Legros, J.C. Improved Three-Dimensional Imaging with a Digital Holography Microscope with a Source of Partial Spatial Coherence. Appl. Opt. 1999, 38, 7085–7094. [Google Scholar] [CrossRef] [PubMed]
- Vit, T.; Ledl, V.; Dolecek, R.; Psota, P. The Possibility of Visualizing Temperature Fields Using Digital Holographic Interferometry. Appl. Mech. Mater. 2013, 284, 988–995. [Google Scholar] [CrossRef]
- Ledl, V.; Vit, T.; Dolecek, R.; Psota, P. Digital holographic interferometry used for identification of 2D temperature field. Eur. Phys. J. Conf. 2012, 25, 02014. [Google Scholar] [CrossRef]
- Dolecek, R.; Psota, P.; Ledl, V.; Vit, T.; Václavik, J.; Kopecky, V. General temperature field measurement by digital holography. Appl. Opt. 2013, 52, A319–A325. [Google Scholar] [CrossRef] [PubMed]
- Dancova, P.; Vit, T.; Ledl, V.; Travnicek, Z.; Dolecek, R. Holographic interferometry as a tool for visualization of temperature fields in air. Eng. Mech. 2013, 20, 205–212. [Google Scholar]
- Ledl, V.; Psota, P.; Dolecek, R.; Vit, T. Digital holographic setups for phase object measurements in micro and macro scale. Eur. Phys. J. Conf. 2015, 92, 01001. [Google Scholar] [CrossRef]
- Dancova, P.; Dolecek, R.; Ledl, V. Experimental investigation of temperature fields in a synthetic jet. MATEC Web Conf. 2014, 18, 03001. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dancova, P.; Psota, P.; Vit, T. Measurement of a Temperature Field Generated by a Synthetic Jet Actuator using Digital Holographic Interferometry. Actuators 2019, 8, 27. https://doi.org/10.3390/act8010027
Dancova P, Psota P, Vit T. Measurement of a Temperature Field Generated by a Synthetic Jet Actuator using Digital Holographic Interferometry. Actuators. 2019; 8(1):27. https://doi.org/10.3390/act8010027
Chicago/Turabian StyleDancova, Petra, Pavel Psota, and Tomas Vit. 2019. "Measurement of a Temperature Field Generated by a Synthetic Jet Actuator using Digital Holographic Interferometry" Actuators 8, no. 1: 27. https://doi.org/10.3390/act8010027
APA StyleDancova, P., Psota, P., & Vit, T. (2019). Measurement of a Temperature Field Generated by a Synthetic Jet Actuator using Digital Holographic Interferometry. Actuators, 8(1), 27. https://doi.org/10.3390/act8010027



