Car Soundproof Improvement through an SMA Adaptive System †
Abstract
:1. Introduction
- the development and integration of dedicated noise and vibration control strategies (f.i., embedded piezoelectric-based solutions developed by Bein et al. in the abovementioned CO2NTROL project [16], piezo shunted resonators assessed by Liao and Sodano [17] or Ciminello et al. [18], SMA-based architectures for dynamic structural response modulation introduced by Ameduri et al. [19]).
2. Seal Adhesion Problem and System Specifications
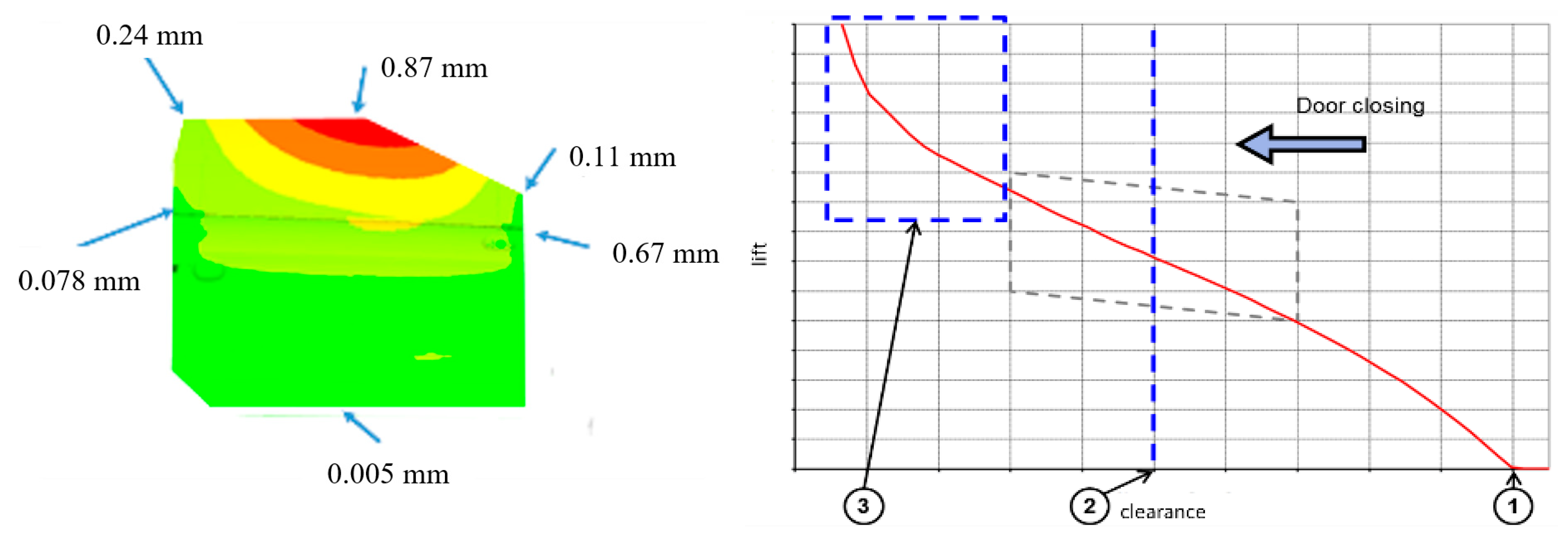
- Seals gap should not exceed 1.0 mm (by engineering specs, derived from design constraints); in turn, as aerodynamic action is considered, this constraint implies the gap to be retrieved is lower than 2 mm;
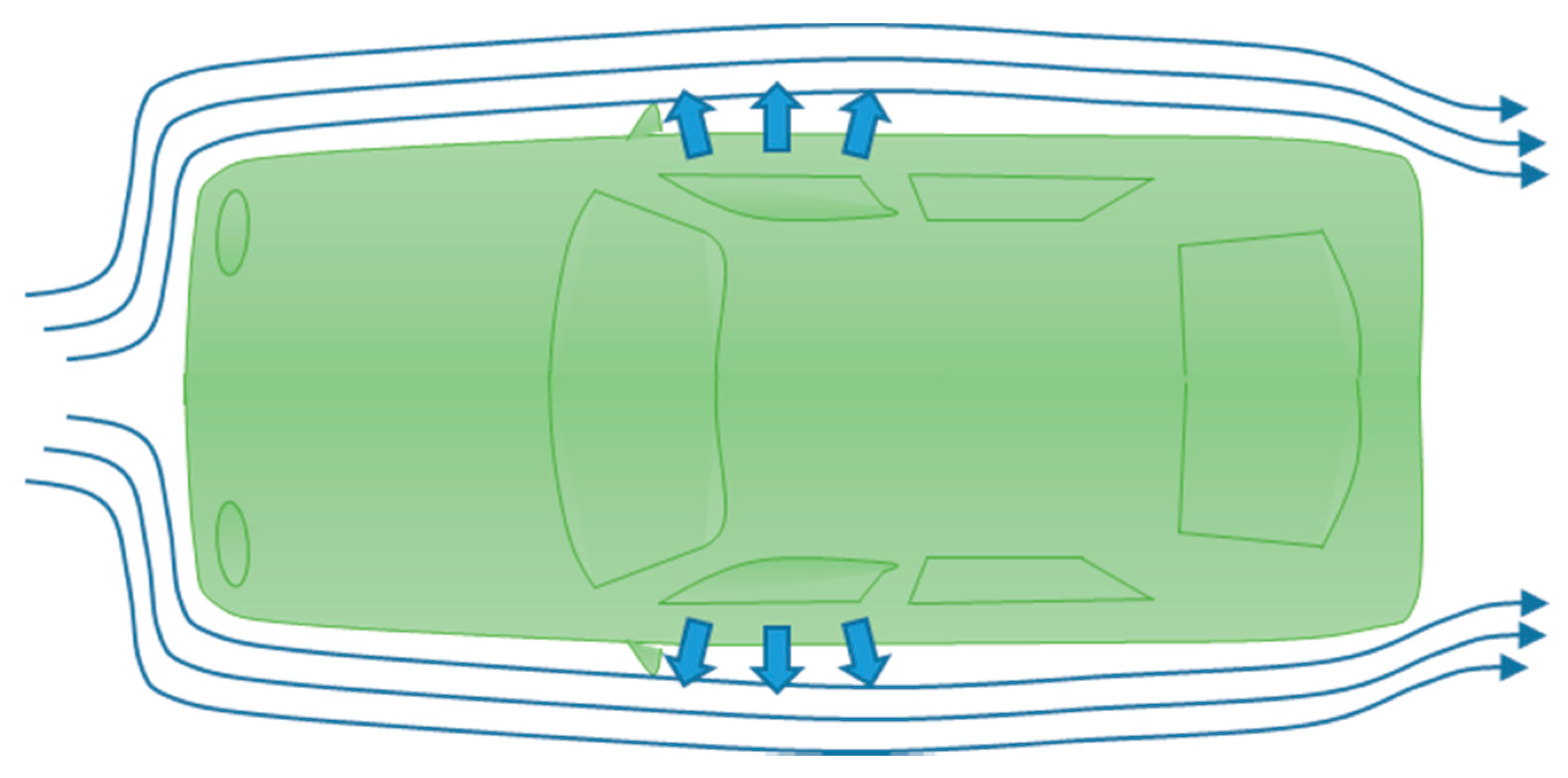
- the main interest zone, as usual for this kind of problems, was at the forward top corner edge of the two front doors, Figure 2;
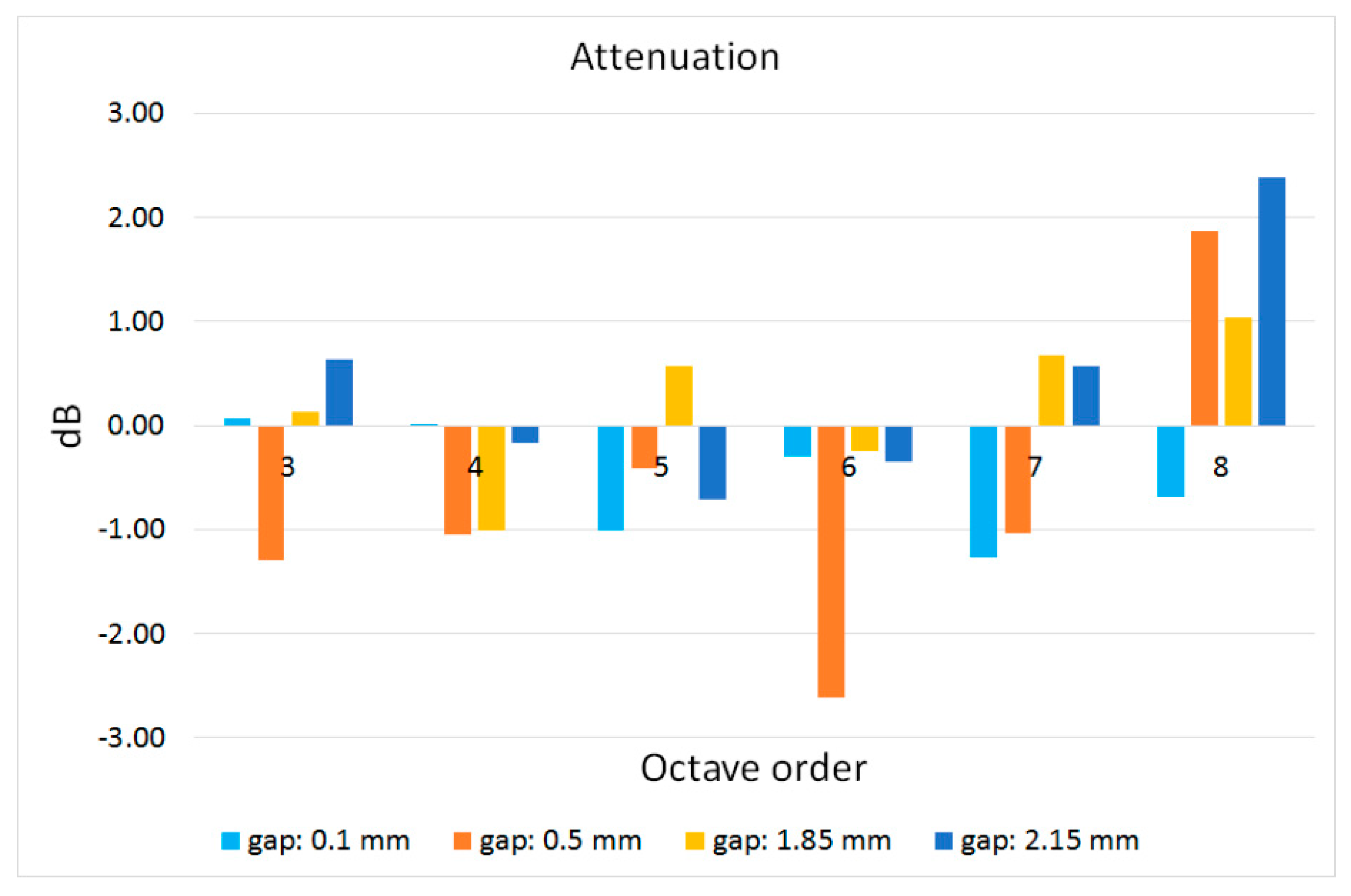
- to be appreciable, SPL abatement should be higher than 3 dB over the frequency band of interest;
- the temperature operational range should be considered between −50 °C and +80 °C;
- the proposed system should be designed to be turned on during high-speed cruise segments only; its full activation should be completed within 1 s;
- the electrical and thermal insulation should be ensured between the SMA system and the relaxed seal; and
- the power consumption should not exceed 5 W per door, according to standards for such kinds of additional systems, commonly adopted on the car class herein considered.
3. Concept, Integration, and Working Phases
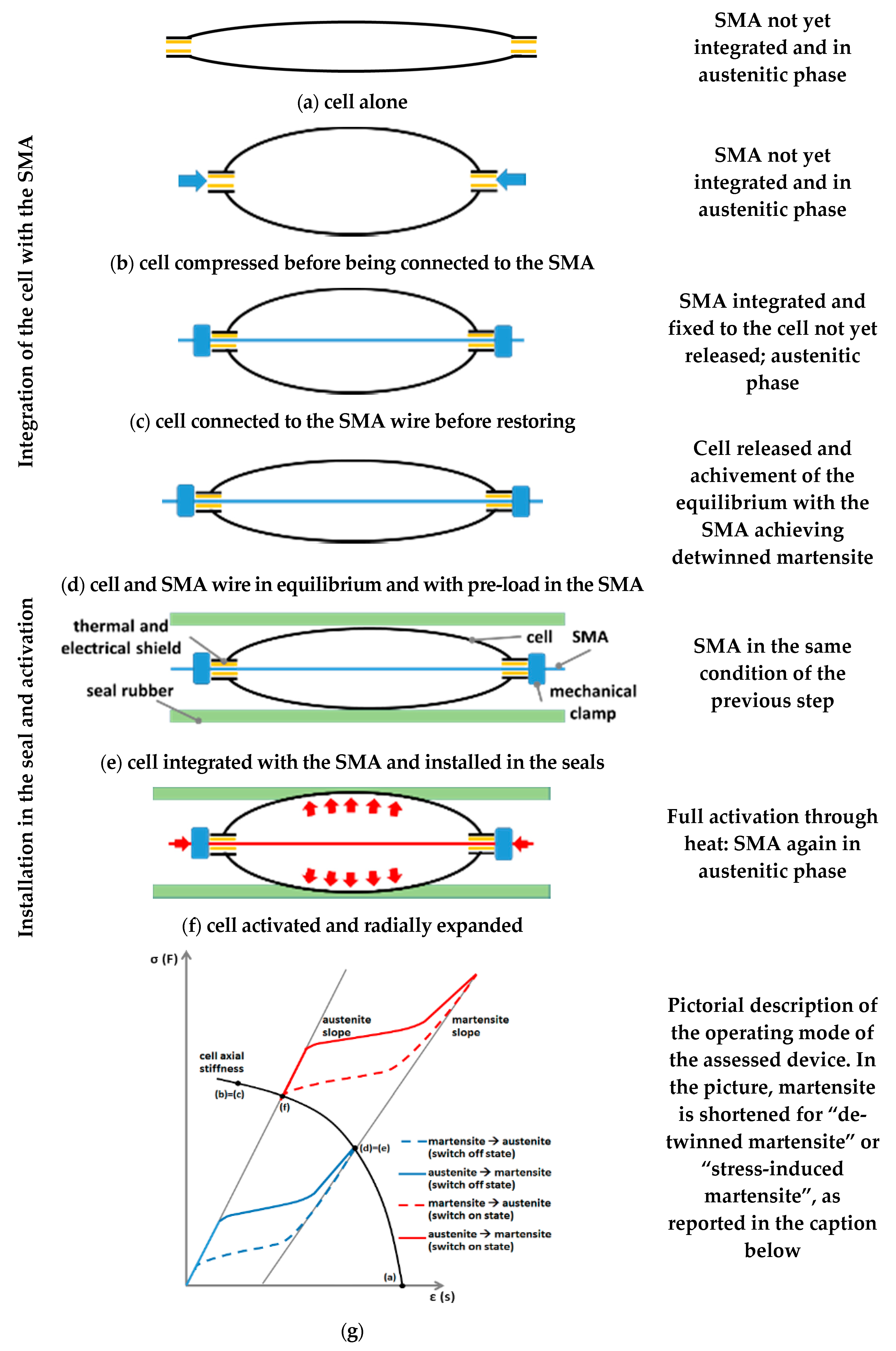
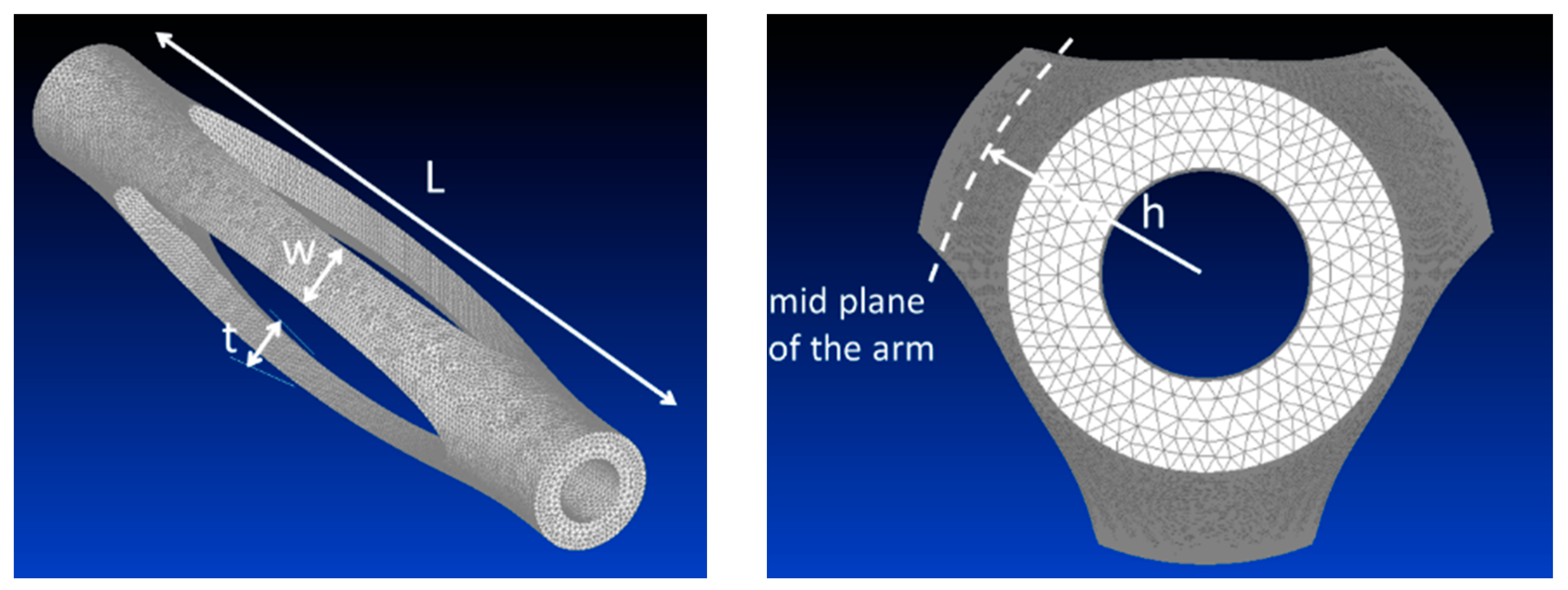
- A shell-like mechanical structure (“the cell”): A device that hosted a longitudinal SMA active element inside, converting its axial action into transversal displacements with the effect of pushing the seal against the door and its frame. Such a component, which was slender ellipsoid shaped, was deployed within the seal, taking advantage of its natural cavity;
- the SMA actuator, a pre-stressed wire, linked to the cell axial extremities and equilibrated by its elastic reaction. When heated by using the Joule effect, the wire shrunk (strain recovery) and compressed the cell longitudinally, inducing in turn a transversal expansion (something similar to the Poisson’s effect); and
- mechanical, thermal, and electrical interfaces: They assured effective mechanical transmission between the wire and the cell, provided a thermal shield between the SMA hot surface, and the cell and the seal rubber, respectively, and limited electrical dispersions.
4. System Design
- Assuring full integrability within the hollowed seal, in both on and off states;
- guaranteeing an extended contact area with the seal to maximize interactions and distribute the load uniformly;
- establishing a sufficient length to reduce interaction losses and minimize side effects at the connection with the SMA-wire; and
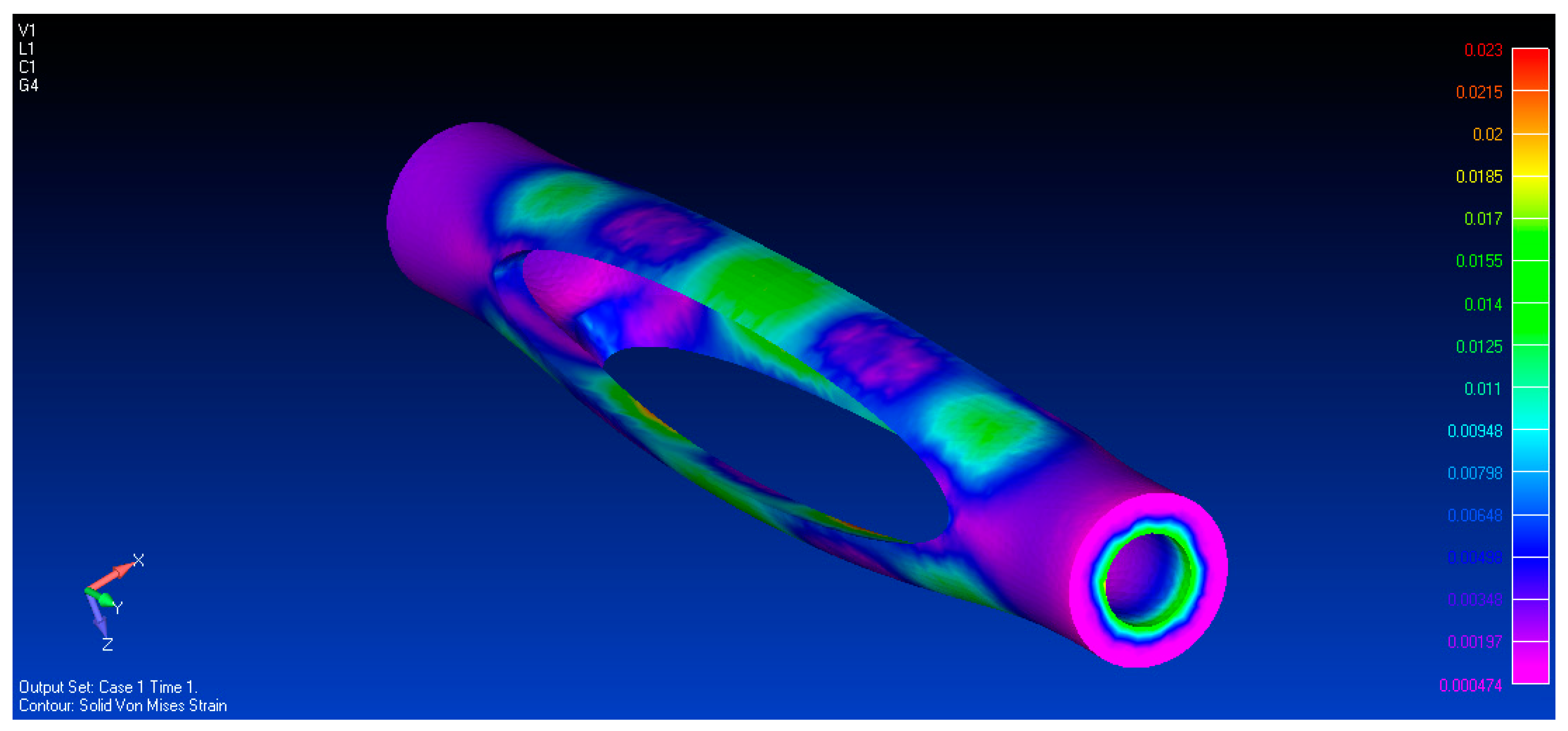
- keeping the stress and strain levels under certain thresholds to mitigate fatigue problems.
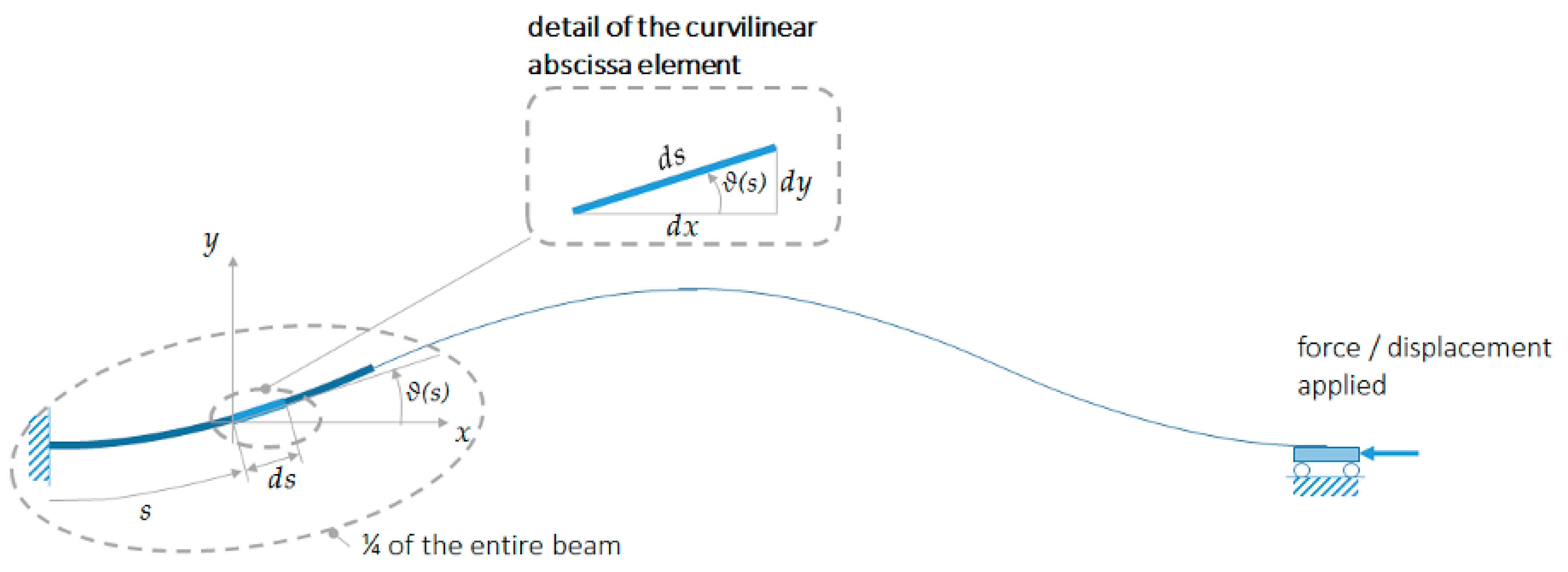
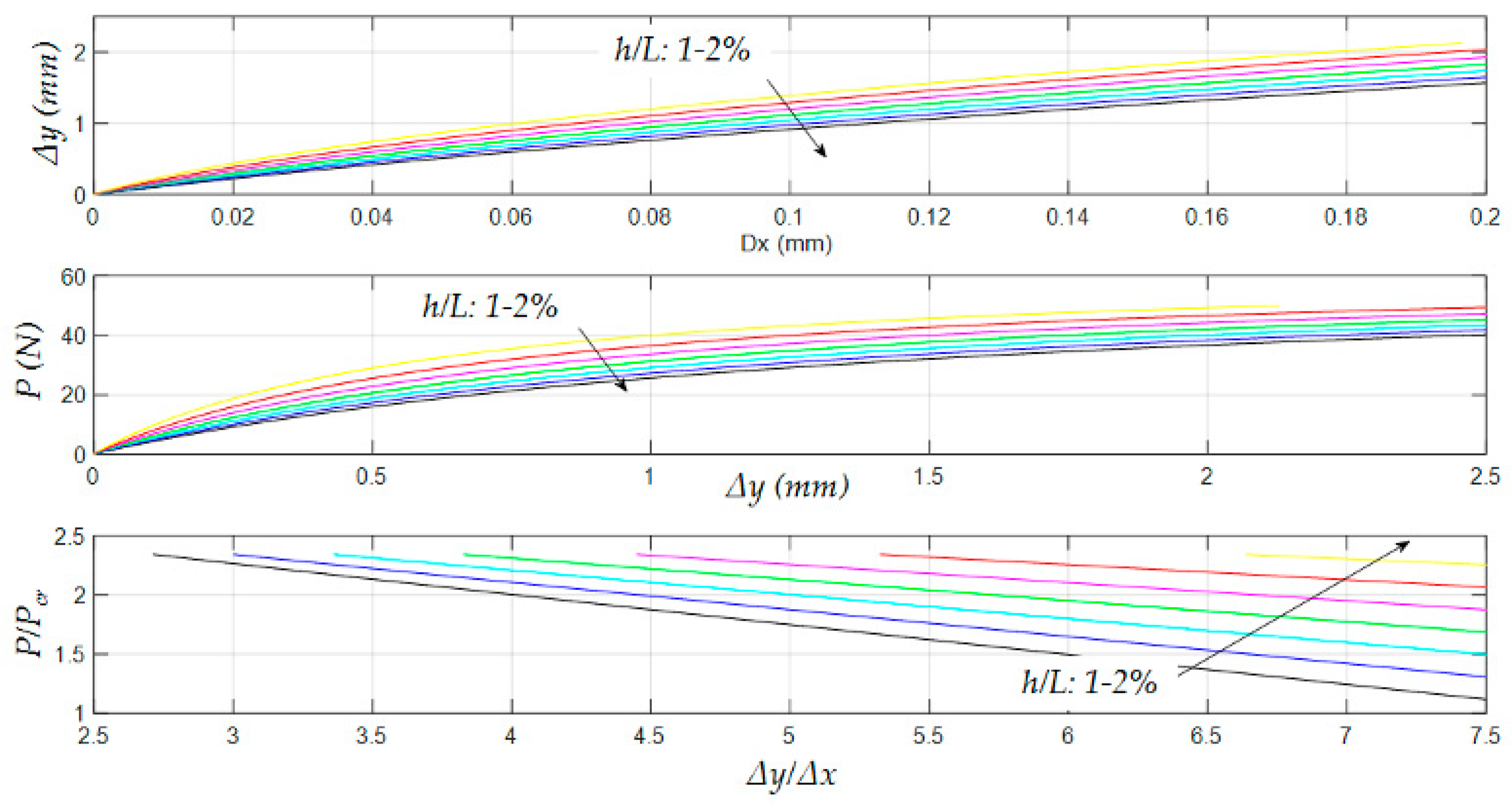
4.1. Cell Modelling and Sizing
- ; (clamped at one edge);
- ; (inflection point—curvature inversion at a quarter of the total length, L).
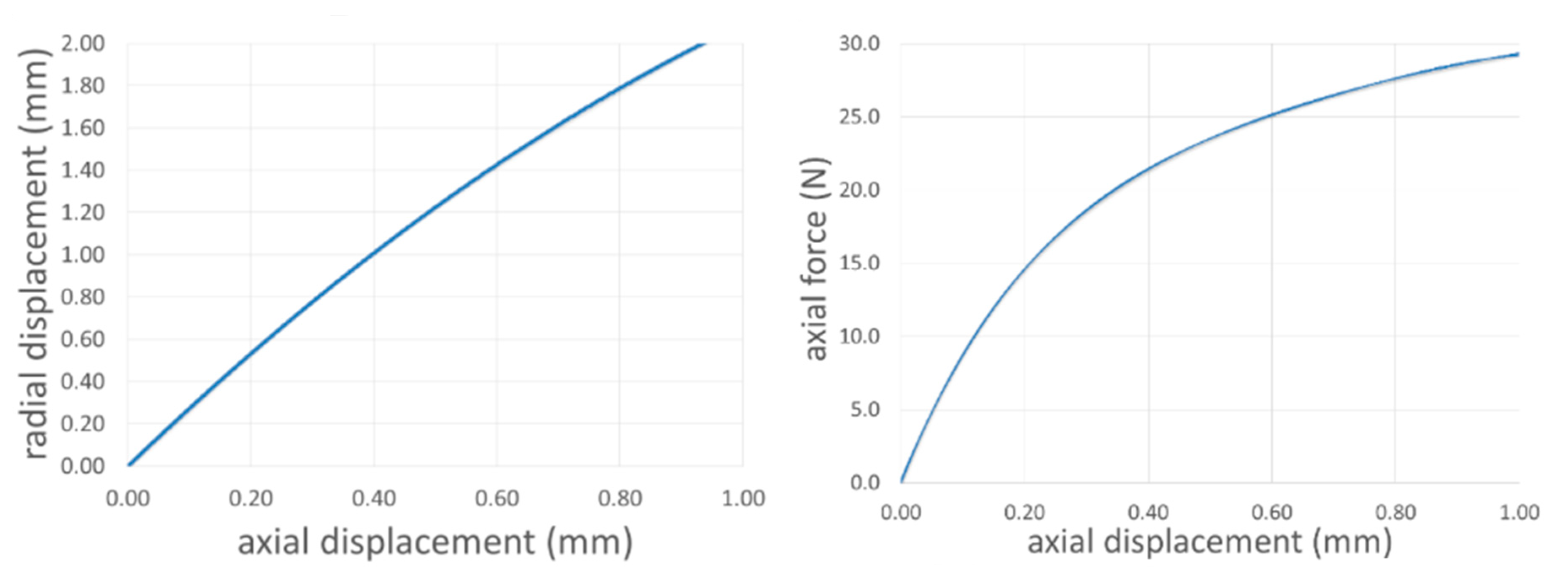
4.2. SMA Wire Modelling and Cell System Integration
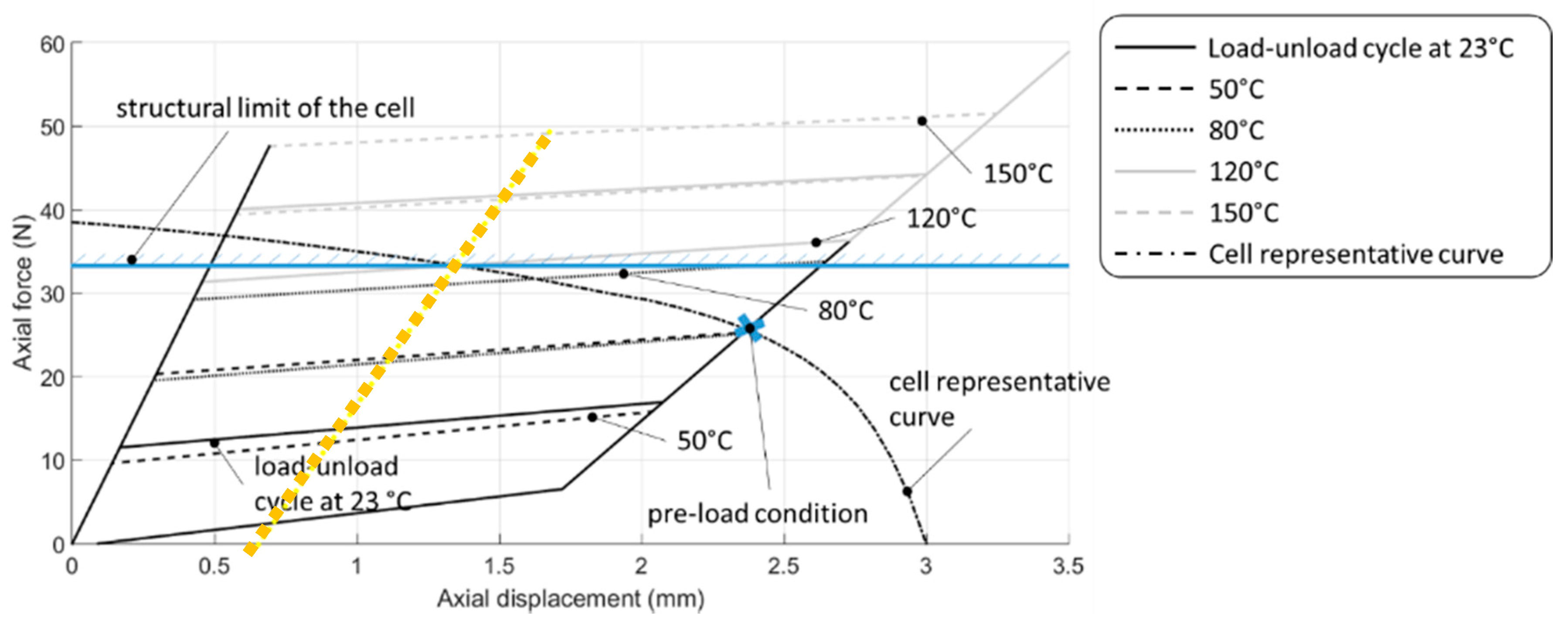
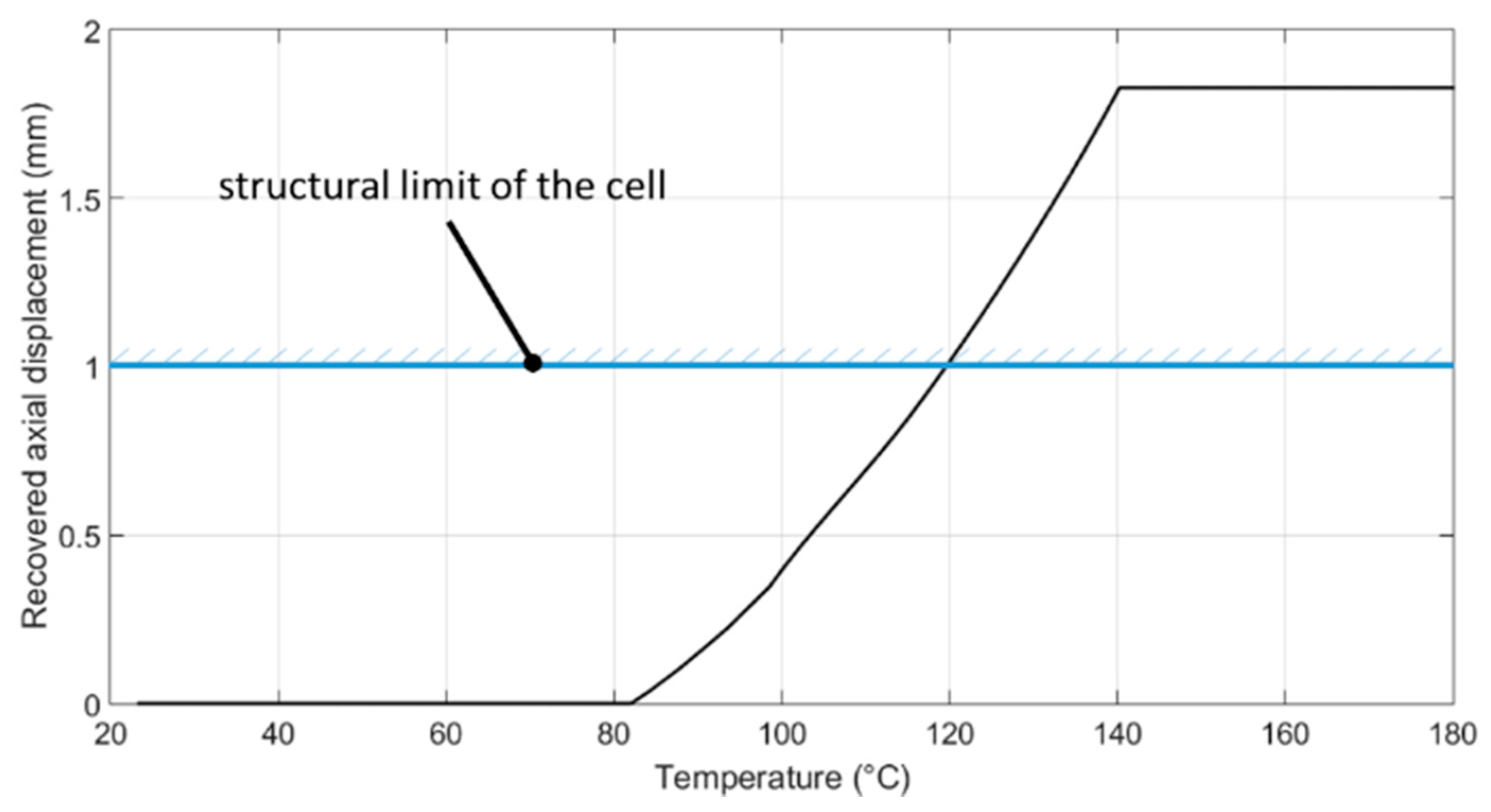
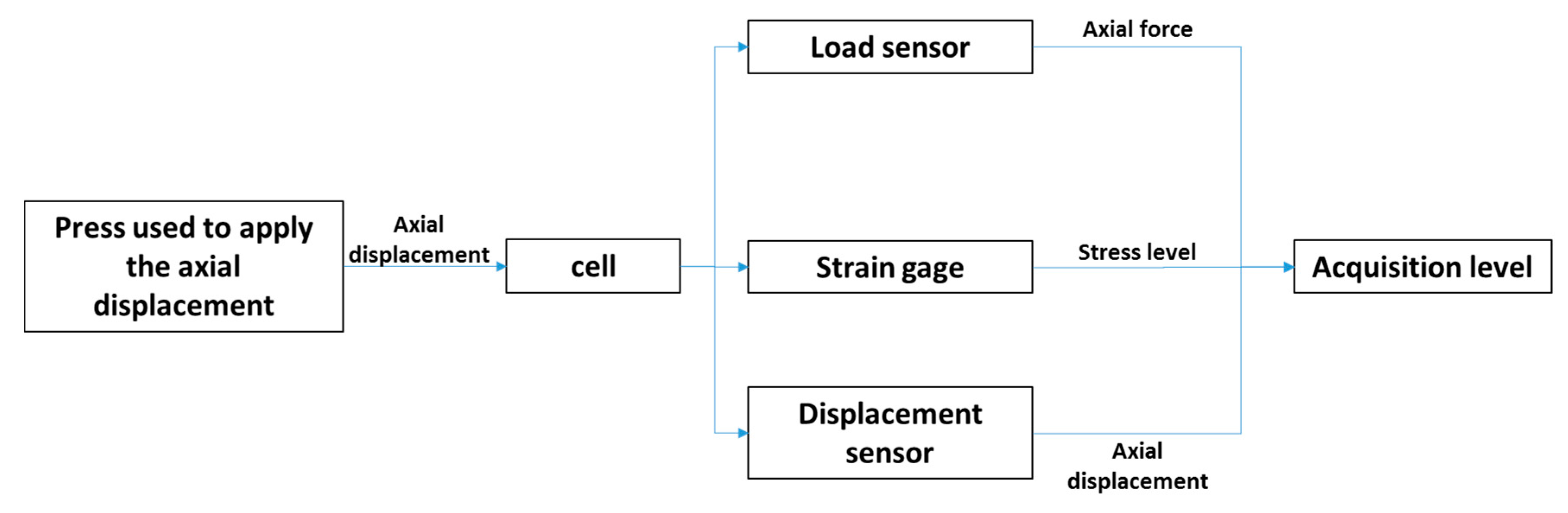
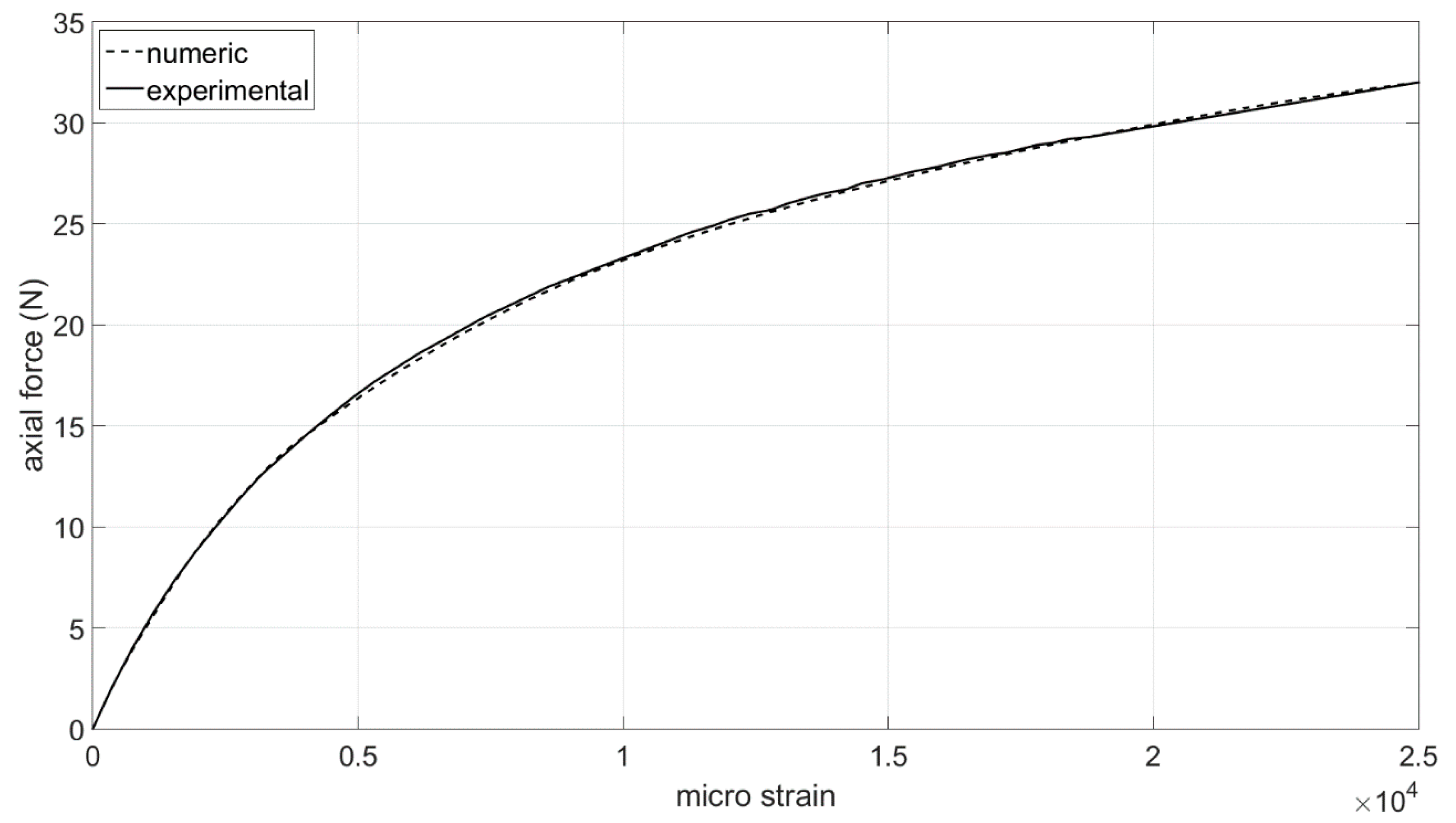
5. Prototyping and Validation
- Cronos PL8 acquisition system, handling strain gages, linear variable differential transformer (LVDT) and load sensors;
- a mechanical press to apply axial loads to the cell system;
- a single Vishay Micro-Measurements EP-08-125BT strain gage;
- an LVDT sensor, for measuring cell axial displacements (compression); and
- a load cell, to record actual longitudinal load, arisen by the press action.
6. Installation and Acoustic Tests
7. Conclusions and Further Steps
Author Contributions
Funding
Conflicts of Interest
References
- Hooftman, N.; Messagie, M.; Van Mierlo, J.; Coosemans, T. A review of the European passenger car regulations—Real driving emissions vs local air quality. Renew. Sustain. Energy Rev. 2018, 86, 1–21. [Google Scholar] [CrossRef]
- Five Trends Transforming the Automotive Industry. Available online: www.pwc.com/auto (accessed on 26 October 2018).
- Yadav, P.; Shinde, A.; Gangurde, Y.; Patil, P. Review on Weight Reduction in Automobile. Int. J. Adv. Technol. Eng. Sci. 2016, 4, 478–483. [Google Scholar]
- Simpkin, R.; D’Ambrosio, C.; Simonsson, J.; Abele, M.; Ferrè, A.; Rollenitz, L.; Estrada Vasquez, R.; Boldea, I.; Scridon, S. Energy Efficient Vehicles for Road Transport. Procedia Soc. Behav. Sci. 2018, 48, 3613–3621. [Google Scholar] [CrossRef]
- Inomata, S.; Yamada, H.; Tanimoto, H. Investigation on VOC Emissions from Automobile Sources by Means of Online Mass Spectrometry. Curr. Pollut. Rep. 2016, 2, 188–199. [Google Scholar] [CrossRef] [Green Version]
- Patil, A.V.; Kumar, B.; Barjibhe, R.B. An Extensive Review on the Use of Acoustic Emission Technique for Continuous Monitoring. Int. Res. J. Eng. Technol. 2016, 3, 137–140. [Google Scholar]
- Integrated Solutions for Noise and Vibration Control in Vehicles. Available online: https://cordis.europa.eu/project/rcn/92595_en.html (accessed on 26 October 2018).
- Intelligent Materials for Active Noise Reduction. Available online: https://cordis.europa.eu/result/rcn/47813_en.html (accessed on 26 October 2018).
- Ecochamps. Available online: http://www.ecochamps.eu/project (accessed on 26 October 2018).
- Panda, K.C. Dealing with Noise and Vibration in Automotive Industry. Procedia Eng. 2016, 144, 1167–1174. [Google Scholar] [CrossRef]
- Genuit, K.; Bray, W.R. A Virtual Car: Prediction of Sound and Vibration in an Interactive Simulation Environment. J. Passeng. Cars Mech. Syst. J. 2001, 110, 1748–1754. [Google Scholar]
- Schulte-Werning, B.; Asmussen, B.; Behr, W.; Degen, K.; Garburg, R. Advancements in Noise and Vibration Abatement to Support the Noise Reduction Strategy of Deutsche Bahn. In Noise and Vibration Mitigation for Rail Transportation Systems; Springer: Berlin, Germany, 2012. [Google Scholar] [CrossRef]
- Razak, N.F.D.; Sani, M.S.M.; Azmi, W.H.; Zhang, B. Noise and vibration analysis for automotive radiator cooling fan. In Proceedings of the 4th International Conference on Mechanical Engineering Research (ICMER2017), Pahang, Malaysia, 1–2 August 2017; 2017; Volume 257, p. 012083. [Google Scholar] [CrossRef]
- Duffy, K.P.; Padula, S.P.; Scheiman, D.A. Damping of high-temperature shape memory alloys. Proc. SPIE Int. Soc. Opt. Eng. 2008. [Google Scholar] [CrossRef]
- Davino, D.; Giustiniani, A.; Visone, C.; Adly, A. Experimental analysis of vibrations damping due to magnetostrictive based energy harvesting. J. Appl. Phys. 2011, 109, 07E509. [Google Scholar] [CrossRef]
- Bein, T.; Elliot, S.; Ferralli, L.; Casella, M.; Meschke, J.; Saemann, E.U.; Nielsen, F.K.; Kropp, W. Integrated solutions for Noise and Vibration control in vehicles. Proc. Soc. Behav. Sci. 2012, 48, 919–931. [Google Scholar] [CrossRef]
- Liao, Y.; Sodano, H.A. Piezoelectric Damping of Resistively Shunted Beams and Optimal Parameters for Maximum Damping. J. Vib. Acoust. 2010, 132, 041014. [Google Scholar] [CrossRef]
- Ciminello, M.; Ameduri, S.; Concilio, A. FE Modeling of an Innovative Vibration Control Shunt Technique. J. Intell. Mater. Syst. Struct. 2007, 19, 875–887. [Google Scholar] [CrossRef]
- Ameduri, S.; Diodati, G.; Concilio, A. SMA Embedded Panel Optimized Through a Genetic Approach. J. Intell. Mater. Syst. Struct. 2009, 20, 1529–1540. [Google Scholar] [CrossRef]
- Bettini, P.; Riva, M.; Sala, G.; Di Landro, L.; Airoldi, A.; Cucco, J. Carbon Fiber Reinforced Smart Laminates with Embedded SMA Actuators—Part I: Embedding Techniques and Interface Analysis. J. Mater. Eng. Perform. 2009, 18, 664–671. [Google Scholar] [CrossRef]
- Spaggiari, A.; Dragoni, E. Analytical and numerical modeling of shape memory alloy Negator springs for constant-force, long-stroke actuators. J. Intell. Mater. Syst. Struct. 2013, 25, 1139–1148. [Google Scholar] [CrossRef]
- Reynaerts, D.; Van Brussel, H. Design aspects of shape memory actuators. Mechatronics 1998, 8, 635–656. [Google Scholar] [CrossRef]
- Nespoli, A.; Besseghini, S.; Pittaccio, S.; Villa, E.; Viscuso, S. The high potential of shape memory alloys in developing miniature mechanical devices: A review on shape memory alloy mini-actuators. Sens. Actuators A Phys. 2010, 158, 149–160. [Google Scholar] [CrossRef]
- Ishii, H.; Ting, K.L. SMA actuated compliant bistable mechanisms. Mechatronics 2004, 14, 421–437. [Google Scholar] [CrossRef]
- Zisser, H.C. The OmniPod Insulin Management System: The latest innovation in insulin pump therapy. Diabetes Ther. 2010, 1, 10–24. [Google Scholar] [CrossRef]
- Kuszneruk, P. SMA Valve Assembly for Controlling Pressurized Air Supply to Air Cells in a Vehicle Seat. European Patent Application, NO. EP3281821A1, 8 August 2016. [Google Scholar]
- Williams, E.A.; Shaw, G.; Elahinia, M. An Automotive SMA Mirror Actuator: Modeling, Design, and Experimental Evaluation. Mechatronics 2010, 20, 527–534. [Google Scholar] [CrossRef]
- Kazi, A.; Honold, M.; Rimkus, W.; Lokner, T.; Baeuml, M.; Koepfer, M. SMA Actuator for Optical Image Stabilization, Paper C5.1, Actuator 2018, Bremen (D). In Proceedings of the ACTUATOR 2018, 16th International Conference on New Actuators, Bremen, Germany, 25–27 June 2018; pp. 375–378. [Google Scholar]
- Frangibolt. Available online: https://tiniaerospace.com/products/space-frangibolt/ (accessed on 20 November 2018).
- Butera, F. SmartFlex Springs and SmartFlex Wires, by SAES Getter. Available online: https://docplayer.net/23849945-Smas-for-industrial-applications-from-first-nitinol-to-a-big-success.html (accessed on 20 November 2018).
- Ameduri, S.; Brindisi, A.; Ciminello, M.; Concilio, A.; Quaranta, V.; Brandizzi, M. An SMA Sealing System for Enhanced Door Soundproof Performance: Design, Prototyping and Testing. In Proceedings of the ACTUATOR 2018, 16th International Conference on New Actuators, Bremen, Germany, 25–27 June 2018; pp. 379–383. [Google Scholar]
- Jani, J.M.; Leary, M.; Subic, A. Shape Memory Alloys in Automotive Applications. Appl. Mech. Mater. 2014, 663, 248–253. [Google Scholar] [CrossRef]
- Ameduri, S.; Concilio, A.; Pecora, R.; Karagiannis, D. A Single Slotted Morphing Flap Based on SMA Technology. Smart Struct. Syst. 2016, 17, 819–835. [Google Scholar] [CrossRef]
- Lecce, L.; Concilio, A. (Eds.) Shape Memory Alloys Engineering for Aeronautical, Medical and Civil Applications; Butterworth-Heinemann: Oxford, UK, 2014; 448p, ISBN 978-0-08-099920-3. [Google Scholar] [CrossRef]
- Concilio, A.; Ameduri, S. Influence of structural architecture on linear shape memory alloy actuator performance and morphing system layout optimization. J. Intell. Mater. Syst. Struct. 2013, 25, 2037–2051. [Google Scholar] [CrossRef]
- Jani, J.M. Design Optimisation of Shape Memory Alloy Linear Actuator Applications. Ph.D. Thesis, RMIT University, Melbourne, Australia, 2016. [Google Scholar]
- Timoshenko, S.P.; Gere, J.M. Theory of Elastic Stability, 2nd ed.; International Student Edition; Mc Graw-Hill International Book Company: New York, NY, USA, 1985; pp. 76–82. ISBN 0-07-Y85821-7. [Google Scholar]
- Mirzaeifar, R.; DesRoches, R.; Yavari, A. A combined analytical, numerical, and experimental study of shape-memory-alloy helical springs. Int. J. Solids Struct. 2011, 48, 611–624. [Google Scholar] [CrossRef]
- Liang, C.; Rogers, C.A. A multi-dimensional constitutive model for shape-memory alloys. J. Eng. Math. 1992, 26, 429–443. [Google Scholar] [CrossRef]
- Huang, M.S.; Brinson, L.C. A multivariant model for single crystal shape memory alloy behavior. J. Mech. Phys. Solids 1998, 16, 1379–1409. [Google Scholar] [CrossRef]
- Patoor, E.; Lagoudas, D.C.; Entchev, P.; Brinson, L.C.; Gao, X. Shape-memory alloys, part I: General properties and modeling of single crystal. Mech. Mater. 2006, 38, 391–429. [Google Scholar] [CrossRef]
- Mehrabi, R.; Masood, T.A.; Elahinia, M.; Kadkhodaeid, M. Anisotropic behavior of superelastic NiTi shape memory alloys; an experimental investigation and constitutive modeling. Mech. Mater. 2014, 77, 110–124. [Google Scholar] [CrossRef]
- Andani, M.T.; Elahinia, M. A rate dependent tension–torsion constitutive model for superelastic nitinol under non-proportional loading; a departure from von Mises equivalency. Smart Mater. Struct. 2014, 23, 015012. [Google Scholar] [CrossRef]
- Ameduri, S.; Concilio, A. An SMA Torsion Actuator for Static Blade Twist. In Proceedings of the ICAST2018: 29th International Conference on Adaptive Structures and Technologies, Seoul, Korea, 30 September–4 October 2018. [Google Scholar]
- Funakubo, M. Shape Memory Alloys; Taylor & Francis: Abingdon, UK, 1987; 276p, ISBN1 2881241360. ISBN2 9782881241369. [Google Scholar]
- Introduction to Nitinol; Memry Corporation: Bethel, CT, USA, 28 December 2017.
- Malka, Y.; Shilo, D. A fast and powerful release mechanism based on pulse heating of shape memory wires. Smart Mater. Struct. 2017, 26, 095061. [Google Scholar] [CrossRef]
- Motzki, P.; Gorges, T.; Kappel, M.; Schmidt, M.; Rizzello, G.; Seelecke, S. High-Speed and High-Efficiency Shape Memory Alloy Actuation. Smart Mater. Struct. 2018, 27, 075047. [Google Scholar] [CrossRef]
- Vibro-Acoustic Characterisation Laboratory. Available online: https://www.cira.it/en/research-infrastructures/vibro-acoustic-characterisation-laboratory (accessed on 7 December 2018).
- Browne, A.L.; Johnson, N.L.; Mc Knight, G.P.; Keefe, A.C.; Herrera, G.A. Reconfigurable Bi-Stable Device. US Application NO. US 20130081933 A1, 4 April 2013. [Google Scholar]
- Motzki, P.; Seelecke, S. Bistable actuator device having a shape memory element. World Intellectual Property Organization Patent NO. WO 2017/194591 AI, 16 November 2017. [Google Scholar]
- Morgen, R.; Yee, H.H. Electro-Thermal Bi-Stable Actuator. US Grant US5977858A, 2 November 1999. [Google Scholar]



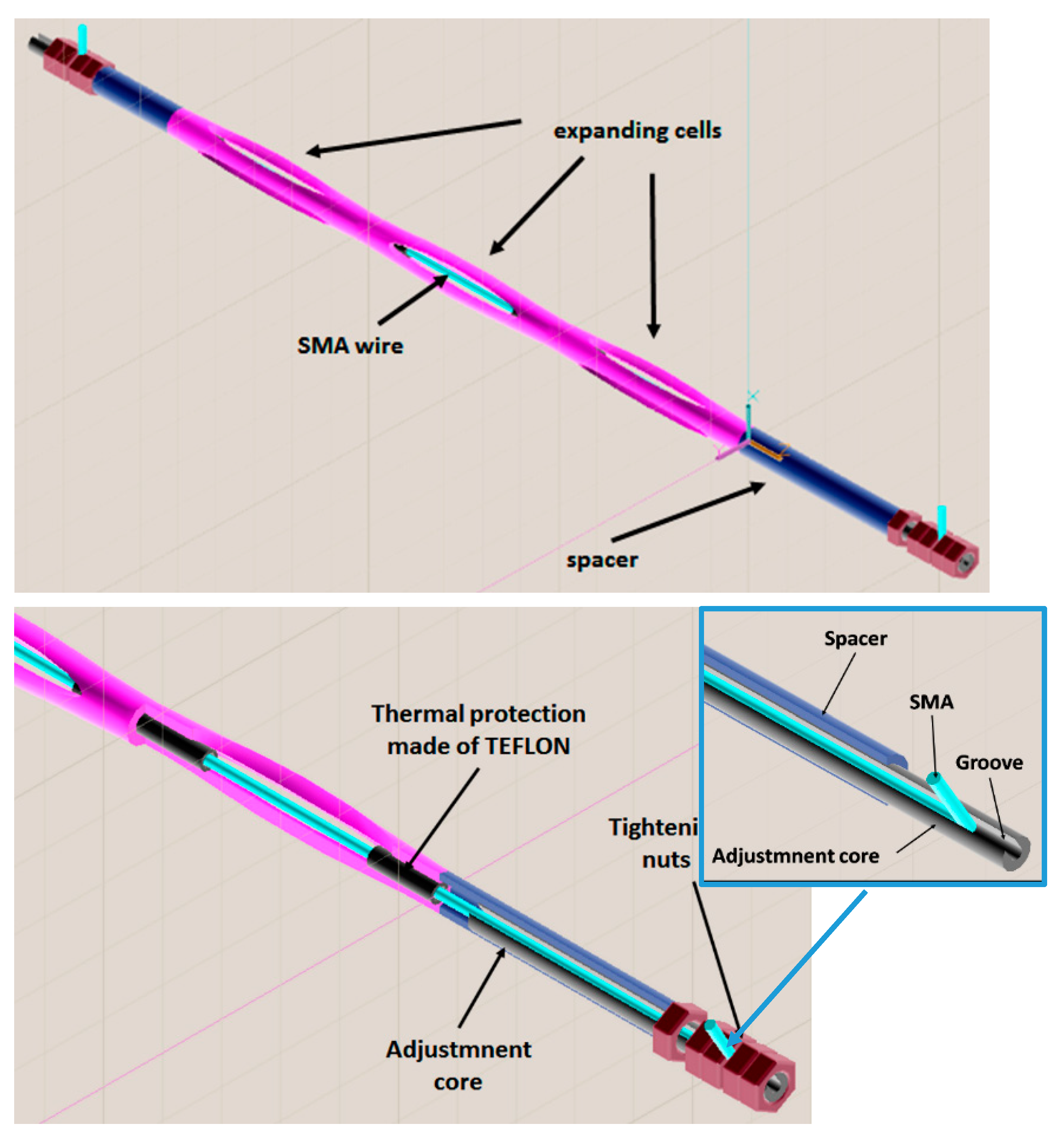
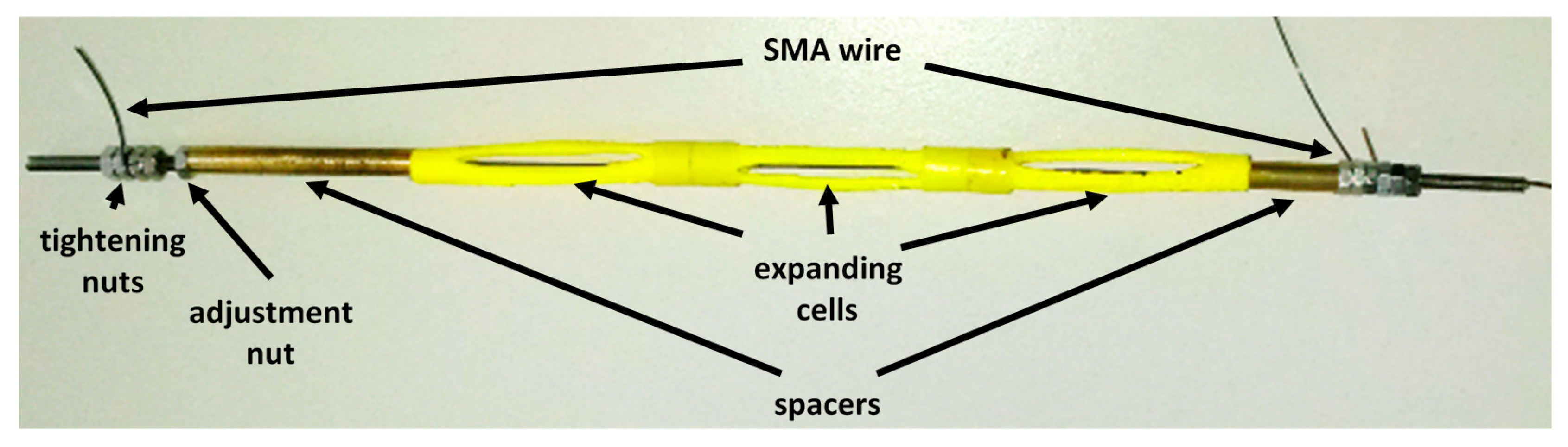




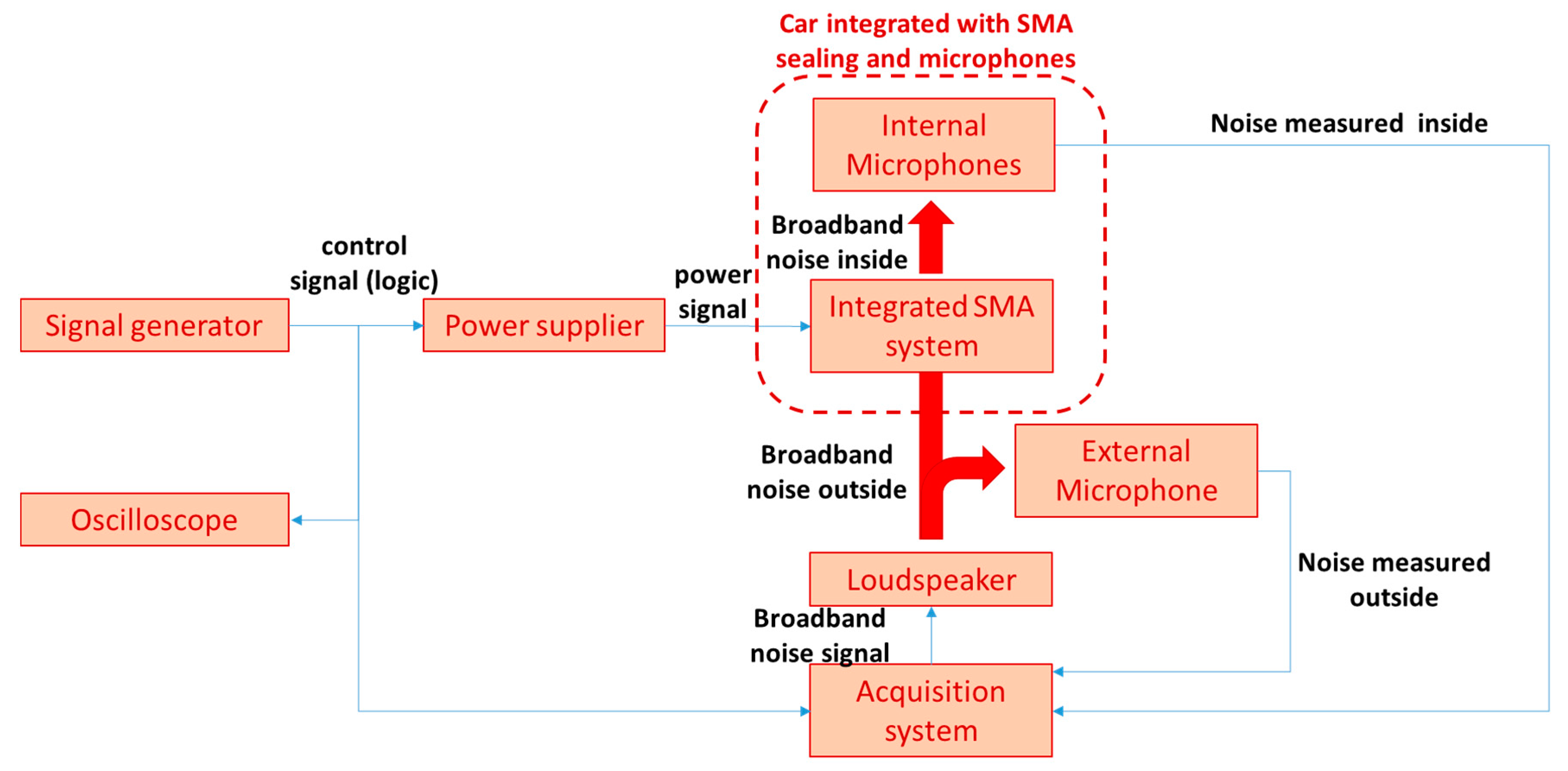

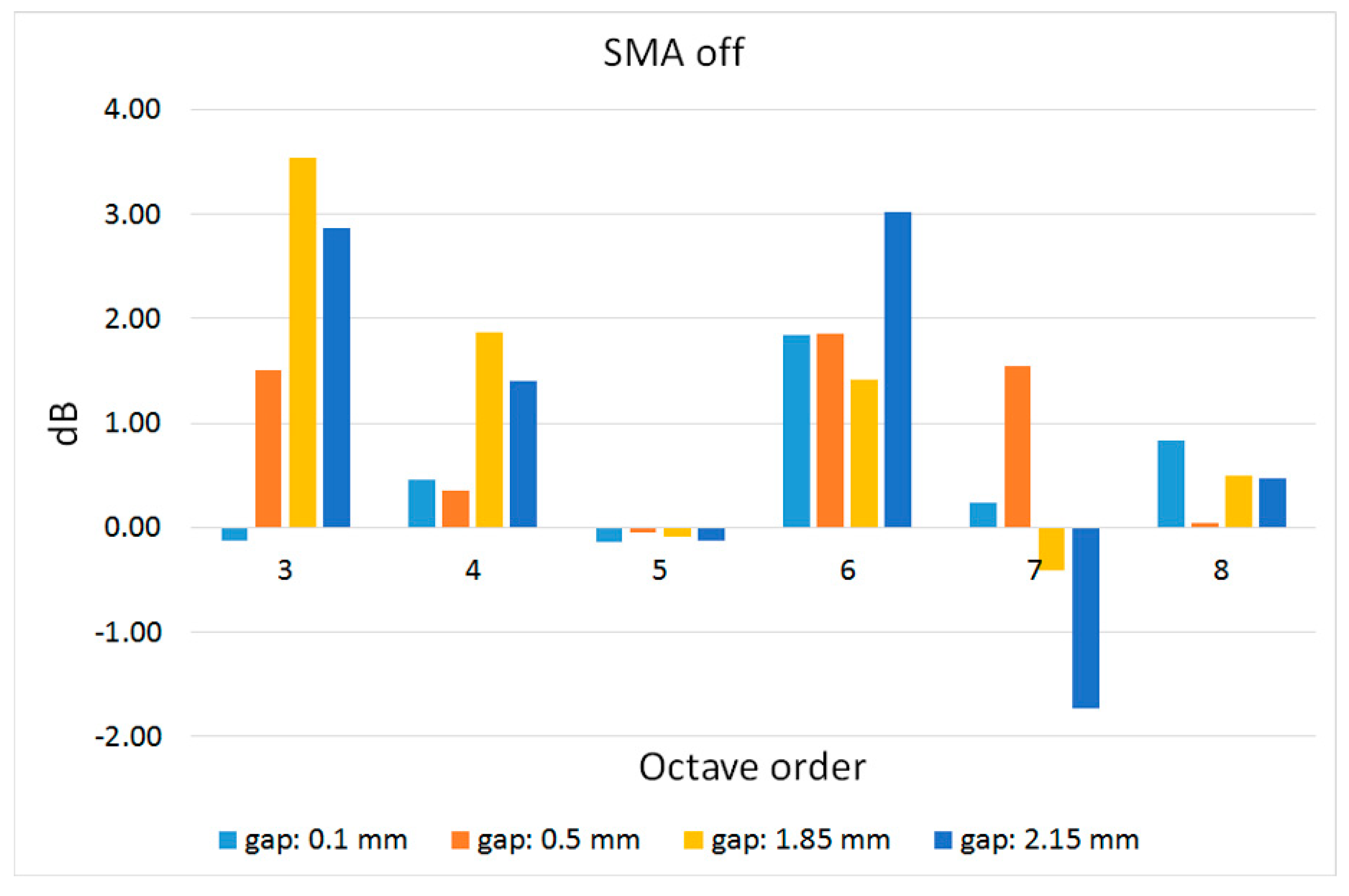
| Length (mm) | Transversal Size (mm) | Number of Arms | Arms Thickness (Average Value, mm) | Arms Width (Average Value, mm) | Elements | Nodes | Young’s Modulus (GPa) | Poisson’s Ratio (-) |
|---|---|---|---|---|---|---|---|---|
| 50 | 5 | 3 | 1.5 | 2.6 | 175930 | 37947 | 2.3 | 0.32 |
| Wire Length (mm) | Diameter (mm) | Young’s Modulus (GPa) | Poisson’s Ratio (-) | Transformation Temperatures (°C) | Maximum Recoverable Strain (%) | ||||
|---|---|---|---|---|---|---|---|---|---|
| Mf0 | Ms0 | As0 | Af0 | ||||||
| 50 | 0.25 | 15 | 25 | 0.32 | −24.9 | −8.5 | 5.7 | 24.0 | 3.0 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ameduri, S.; Brindisi, A.; Ciminello, M.; Concilio, A.; Quaranta, V.; Brandizzi, M. Car Soundproof Improvement through an SMA Adaptive System. Actuators 2018, 7, 88. https://doi.org/10.3390/act7040088
Ameduri S, Brindisi A, Ciminello M, Concilio A, Quaranta V, Brandizzi M. Car Soundproof Improvement through an SMA Adaptive System. Actuators. 2018; 7(4):88. https://doi.org/10.3390/act7040088
Chicago/Turabian StyleAmeduri, Salvatore, Angela Brindisi, Monica Ciminello, Antonio Concilio, Vincenzo Quaranta, and Marco Brandizzi. 2018. "Car Soundproof Improvement through an SMA Adaptive System" Actuators 7, no. 4: 88. https://doi.org/10.3390/act7040088
APA StyleAmeduri, S., Brindisi, A., Ciminello, M., Concilio, A., Quaranta, V., & Brandizzi, M. (2018). Car Soundproof Improvement through an SMA Adaptive System. Actuators, 7(4), 88. https://doi.org/10.3390/act7040088








