Abstract
In a plating process, the steel plate is conveyed 20–50 m in the vertical direction for drying, during which it is negligibly supported by rollers and other mechanisms. This produces plating without uniformity owing to the generation of vibration and other factors, which prevent the increase in productivity. We have developed a noncontact guide system for a high-speed traveling elastic steel plate in which electromagnetic forces are applied by actuators at the edges of the plate to control the plate’s position. In this study, we investigated the vibration phenomenon when changing the steady current value of the electromagnet used for controlling the position. In addition, we conducted mode analysis of the steel plate to enable stable control even at low steady current values and verified whether stable guide can be provided by using it together with a permanent magnet. As a result, by arranging the permanent magnets, stable guidance was possible even at a low steady current value. In addition, it became clear that vibration damping performance is also improved.
1. Introduction
Primary products, which are the basic materials for various industrial products such as paper, film, thin steel plates, etc., are several kilometers in length. During the manufacturing process, the primary products are carried in a long continuum of states by a number of rollers. This long manufacturing process consists of many linear parts and the part where traveling direction is changed. For improving the quality of the final product and reducing cost, it is necessary to improve the quality of the primary product. A guidance technique for preventing wrinkles and meandering is proposed. Magnetic guideways that are capable of guiding a target in a noncontact manner, i.e., by utilizing electromagnetic force, have been actively considered for the manufacturing process of a thin steel plate that particularly considers the deterioration of surface quality caused by contact with a roller. In some of the existing techniques, electromagnets are installed on the upper and lower surfaces of a steel plate to support continuous steel plates in a noncontact manner by utilizing an attractive force [1,2,3,4,5]; however, to the best of our knowledge, suppression of out-of-plane vibrations have not been reported. Furthermore, these studies on this subject considered only linearly transported continuous steel plates. The problem of meandering persists due to lack of control in the perpendicular direction compared to that in the running direction of the plane of the steel plate. All studies on this subject considered only linearly transported continuous steel plates. Therefore, it is necessary to consider the noncontact guidance in the part where traveling direction is changed for realization of the noncontact guide system in actual process. Changing the traveling direction leads to a complex behavior of the continuous steel plate because of several factors such as the inertial force, centrifugal force, Coriolis force, etc.
Our current study establishes that a noncontact guideway can be provided on a direction-changing traveling continuous steel plate, and the vibrations outside the plane can be suppressed by applying tension on the steel plate [6]. Although the loop shape of the direction-changing part becomes asymmetric while running, it has been experimentally clarified that the vibrational damping effects can be improved by dynamically relocating the electromagnet according to the shape [7]. In addition, our research group established a method for numerically computing the asymmetric shape of a traveling steel plate using multibody dynamics (MBD) and finite element method (FEM) [8]. Furthermore, structural analysis by FEM reveals that out-of-plane vibrations in the loop-shape part can be suppressed by placing an electromagnet in the area under high stress on the traveling steel plate [9]. In recent years, research on zero power control using permanent magnets has been actively investigated. Thus, we conducted an experiment using permanent magnets in noncontact guideway system. As a result, it was confirmed that vibration can be suppressed by installing a permanent magnet on the continuous steel plate [10]. In this paper, we considered the vibration phenomena that appear when changing the steady current value of the electromagnet used for guiding the steel plate. At that time, to realize stable control with a small control current, we considered whether it can be stabilized by using a permanent magnet in combination.
2. Noncontact Guide System
We supported the continuous steel plate production line with a deflector and a sink roll. As shown in Figure 1, to form a noncontact guideway using an electromagnet for the roll part, we fabricated a device simulating a part through which the continuous steel plate passes through the plating tank. A continuous steel plate was welded to a 6894 mm long, 150 mm wide, and 0.3 mm thick belt made of stainless steel material (SUS632). The width of the steel plate in the current experiments was chosen to reduce the vertical deformation and the elastic vibration of the steel plate plane and to consider the impact of the edge control system on the loop-shaped part. The belt was hung from a pulley with a diameter of 700 mm and a width of 154 mm. A DC servomotor, enabling endless movement of the continuous steel plate, drove the pulley. In addition, electromagnets were installed in two locations when the experiments were conducted. Figure 2 shows schematic illustration of electromagnet. The number of turns of the electromagnet coil is 1005 times, and the material of the E type core is ferrite. The dimensions of the electromagnet are as shown in Figure 2. A noncontact edge control system, which was constructed to perform the active control with the aid of the electromagnet with respect to the edge direction of the running steel plate, was experimentally established. To compensate for the attractive force shortage, the electromagnets were connected in two series connections and arranged to face the adjacent opposite edges of the steel plate. As shown in Figure 3, the permanent magnets were also for the magnetic poles to oppose to each other placed near both the edges of the steel plate.
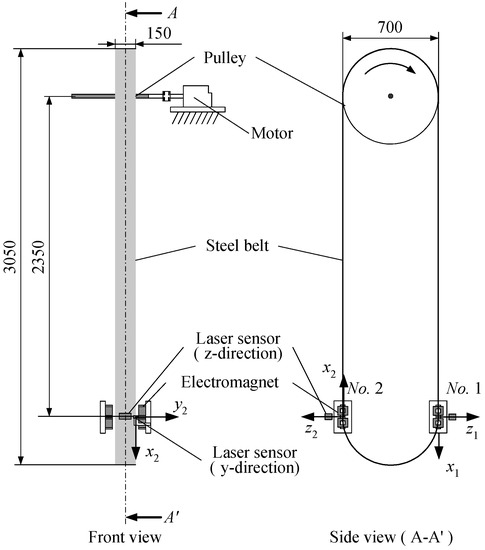
Figure 1.
Non-contact guide system.
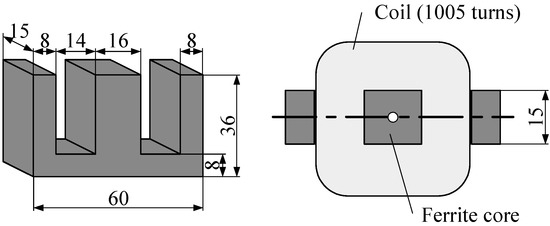
Figure 2.
Schematic illustration of electromagnet.
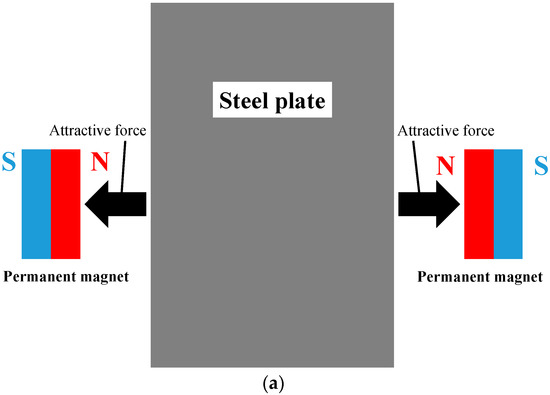
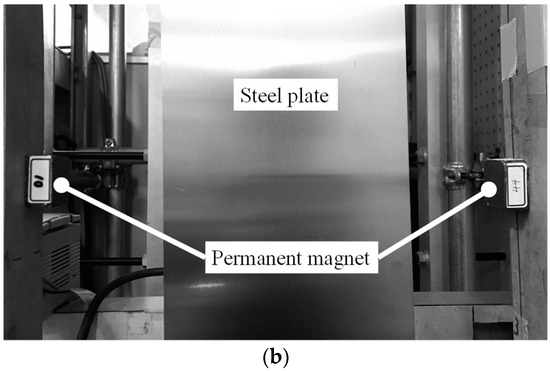
Figure 3.
Permanent magnets placed near both the edges of the steel plate. (a) Schematic drawing; (b) Photograph of arrangement.
3. Noncontact Edge Control System
3.1. Edge Control System
A displacement is caused in the y direction of the continuous steel plate by the active control from electromagnets. The control system is shown in Figure 4. In this experiment, a pair of serially connected electromagnets is placed facing each other near the two edges of the continuous steel plate to supplement for the lack of attractive force. For both the electromagnets, the distance between the electromagnet surface and the edge of the continuous steel plate is maintained at 5 mm. The information on displacement, traveling speed, and current are locally fed back only to the electromagnets. In the z direction, the steel plate is guided from the initial position in the uncontrolled state to the center of the electromagnet. This phenomenon occurs due to the magnetic field generated for positioning control in the y direction. This phenomenon causes as an attractive force on the steel plate that drives it toward the electromagnet center. Thus, it is experimentally confirmed that the range in which this attractive force acts in the z direction of the steel plate is the outermost circumference of the electromagnet coil.
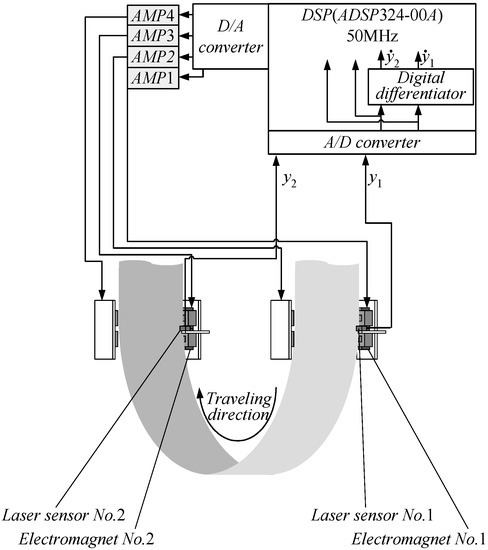
Figure 4.
Control system of noncontact guide.
3.2. Modelling System
The parts where the direction of travel is changed (indicated by curves) and the linear-traveling parts are divided into sections, as shown in Figure 5. Each section is modeled as a target of control. For a model with one degree of freedom where the weight of each section is represented by mn and the control force generated by the electromagnet is represented by fn, the equation of motion is expressed as
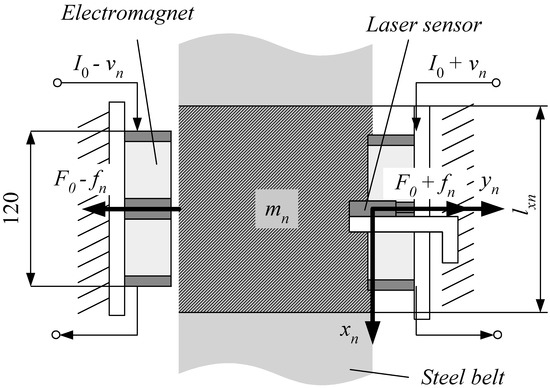
Figure 5.
Model of noncontact guide.
The inductance of the electromagnetic coil is expressed as a sum of the component inversely proportional to the gap between the steel plate and magnet and the component of leakage inductance. If deviation around the static equilibrium state is very small, the characteristic equations of the electromagnet are linearized as
where
F0: magnetic force in the equilibrium state (0.83 N), Γ0: gap between steel plate and electromagnet in the equilibrium state (59 mm), I0: current in the equilibrium state (0.5 A), R: resistance of the coupled magnet coils (10 Ω), yn: horizontal displacement [m], vn: dynamic voltage of the coupled magnets [V], in: dynamic current of the coupled magnets [A].
The state equation of the system is introduced from the from the equation of motion, that is,
where
4. Vibration Phenomenon Accompanying Steady Current Value Change
First, we compared the vibrations of the continuous steel plate caused by the differences in the steady current value. From the basic experiments, it has been confirmed that the steel sheet can be controlled stably for 30 min or more when the steady current is 0.7 A or less. In addition, it was confirmed that steel plates with a traveling velocity of 1000 m/min could be controlled when the steady current is 0.3 A or more. In the experiment, two steady current values of 0.3 A and 0.7 A were used. From the previous study, the static attractive force which the electromagnet generates on the steel plate is 0.1 N when steady current is 0.3 A, and 0.6 N when steady current is 0.7 A [11]. We have confirmed that the RMS in control direction (y-axis) is same in each steady current. When running the experiments, the electromagnet was installed on the loop shaped part of the steel plate. As shown in Figure 6, the laser sensor was installed radially from the center assuming that a pulley is installed under the loop of the steel plate, and it can be measured every 15°. In this section, the sensor was installed at 30°, 45°, 75°, 90°, 135°, and 150° on the lower part of the steel plate, and measured the displacement in the out-of-plane direction for 30 s. The vibration of the steel plate includes various frequency vibration. Therefore, we obtained RMS from measured displacement of the steel plate to evaluate the vibration of the steel plate. During the running experiment, the running speed was 1000 m/min, the data were measured ten times, and then the average was evaluated. Figure 7 shows the amplitude of the measurement point at each steady current value. As a result, it was confirmed that 0.7 A was able to suppress vibration compared to 0.3 A.
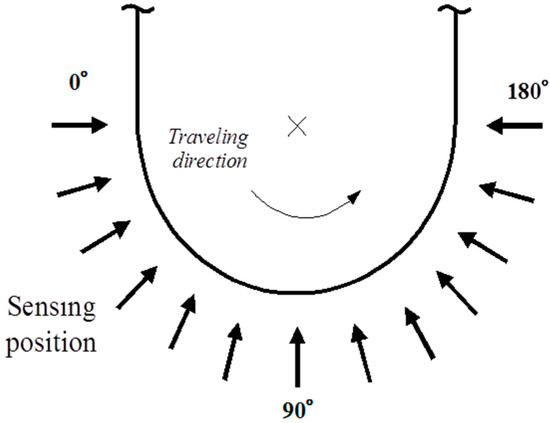
Figure 6.
Sensing position on the lower part of the steel plate.
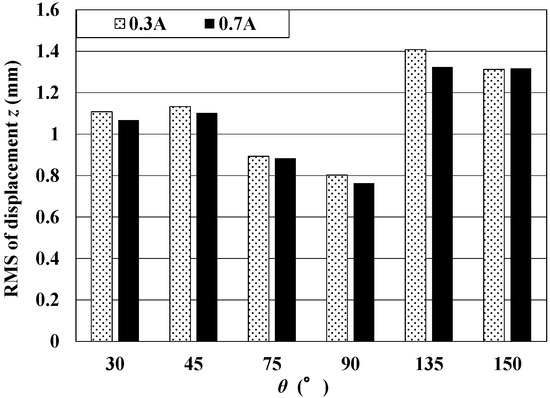
Figure 7.
The RMS of displacement in the z direction of the steel plate at each steady current value.
Therefore, it was confirmed that stable guidance can be performed on the steel plate conveyance with a steady current value of 0.7 A. When the steady current value is strong, stable guidance of the steel sheet can be performed. However, heat was generated in the electromagnet under control due to an increase in the current value. Furthermore, problems such as an increase in the resistance value due to the heat generation of the electromagnet and a decrease in the overall cost performance were noted. Therefore, guidance control in a state where the steady current value is low is desired. Moreover, a stable guidance is desired with small vibration amplitude. Therefore, a permanent magnet was used in combination with a steady current value of 0.3 A. The performance of this combination was then compared with that using a steady current value of 0.7 A, and we investigated whether the performance increased or remained equal.
5. Consideration on Arrangement of Permanent Magnets
5.1. Permanent Magnet Analysis
Until now, we determined the arrangement of electromagnets from the analysis of the stationary shape of the steel plate and we damped the vibration of the steel plate. We investigated the calculation of vibration mode shape of steel plate from the dynamic analysis and placement of permanent magnets at the position which becomes the antinode of the mode shape of the characteristic frequency band. First, electromagnetic analysis software JMAG was used to consider permanent magnets. We analyzed the static characteristics of the permanent magnet acting on the steel plate. The material was set as follows. The steel plate was SS400, the coil was copper, the core was ferrite with TDK PC 47 (remanent flux density Br = 180 mT, coercive Hc = 13 A/m), the permanent magnet was TDK FB5B (remanent flux density Br = 420 mT, coercive Hc = 253 kA/m). The size of the permanent magnet is 30 mm in length, 30 mm in width and 15 mm in thickness. From the analysis result, Figure 8 shows the relationship between the y-axis direction of the steel plate and the attractive force fy acting on the steel plate. As shown in Figure 8, fy has the maximum attractive force acting when the distance from the steel plate is 25 mm, and then the attractive force tends to decrease from 30 mm to 70 mm.
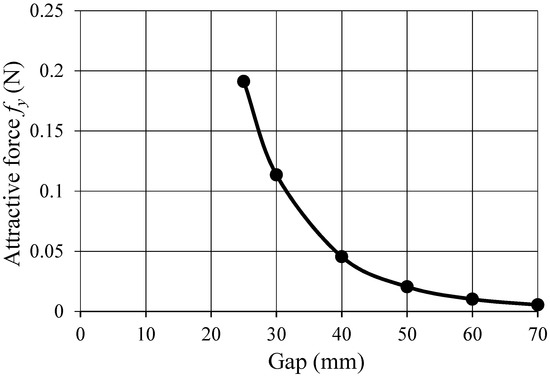
Figure 8.
Relationship attractive force fy of the permanent magnet and gap.
5.2. Permanent Magnet Arrangement Using ANSYS
To conduct a running experiment with permanent magnets in combination, we need to consider the arrangement of permanent magnets for vibration suppression. The running steel plate vibrates in a specific frequency band. If the vibration mode shape of the frequency band can be confirmed, it is possible to suppress the vibration by performing control considering the mode shape. The tension generated in the steel plate during continuous running is calculated from Euler’s friction theory [12]. The calculated tension is applied to the shape of the steel plate obtained from MBD. At this time, we made the steel plate act as loose side tension and pull side tension. From Euler’s friction theory, the effective tension of the running steel plate is Te, the loose side tension is Ts, the pull side tension is Tt and they are expressed by the following equation:
Here, V is the steel plate with running speed (m/min), P is the motor output (W), μ is the coefficient of friction between the steel plate and the pulley, ψ is the winding angle (rad) of the portion where the belt is in contact with the pulley, and m is the mass per unit length of the steel plate (kg/m). In this consideration, the steel plate running speed is set to 1000 m/min. We applied loose side tension Ts and pull side tension Tt at this speed along the surface of the steel plate. Using Equations (9) and (10), Tt and Ts is obtained to 176 N and 113 N. Then, frequency response analysis and modal analysis were performed. The mesh of the model was a shell element whose number is 264, and the place where the steel plate and the pulley contacted was fixed. ANSYS Workbench Mechanical was used for this analysis. Figure 9a shows the spectral waveform at the steady current value of 0.3 A, and Figure 9b shows the result of the frequency response analysis. From the analysis result, the twist modes which include the vibration from 1.5 Hz to 5.0 Hz are confirmed. In the actual experiment, it is considered that these twist modes are suppressed by edge control system. Therefore, we concluded that the resonance of the experiment is the peak of the out-of-plane vibration. This frequency is in the frequency band around 1.048 Hz. The vibration mode shape of this frequency band was calculated by modal analysis. From the result of the modal analysis, permanent magnets were placed in consideration of the vibration mode shape of the steel plate. Figure 10 is a schematic diagram. The permanent magnets were installed at two position 575 mm and 1450 mm from the center of a pulley with a diameter of 700 mm. Therefore, four permanent magnets were installed on each side. A total of eight permanent magnets were installed on both sides on the edge portion of the steel plate.
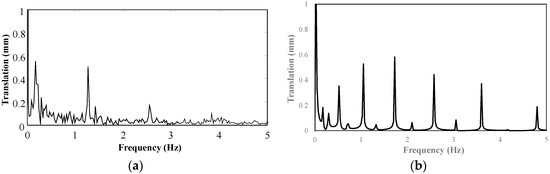
Figure 9.
Frequency response analysis of continuous steel plate. (a) Experiment result; (b) Analysis result.
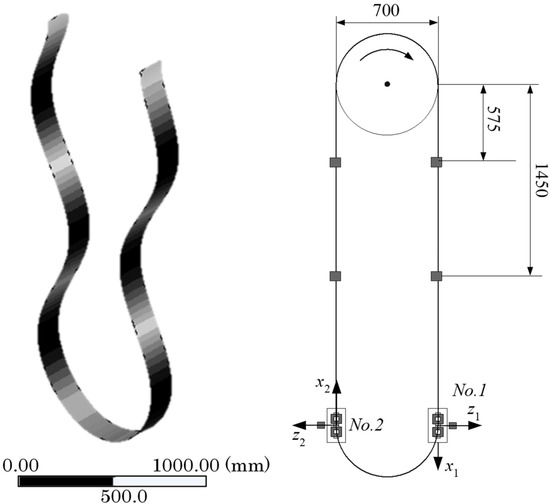
Figure 10.
Mode shape and arrangement of permanent magnets.
6. Steel Plate Traveling Experience
From the results in Section 5.2, we could estimate the placement position of the permanent magnet. This arrangement was confirmed of the vibration suppression performance of steady current value 0.3 A by conducting the experiments. Based on the previous studies, we have confirmed the vibration amplitude of the traveling steel plate without control was approximately 40 mm in y direction and 20 mm in the z direction [6]. Therefore, the experiment was conducted with the electromagnet control in each condition. From the result of basic experiment, when the experiment was carried out with gap 25 mm which the attractive force was maximum, the steel plate and the permanent magnet were in contact with each other, making measurement impossible. Therefore, the experiments were carried with the gap 30 mm which the positioning control can be maintained. The running speed was set to 1000 m/min, similar to that in the experiment in Section 4. The sensor was placed from 0° to 180° at intervals of 15° on the steel plate loop shaped part. The displacement was measured in the z direction, and the displacement was evaluated by using RMS. Figure 11 shows the measurement results of the displacement RMS of displacement obtained from the experiment. From this result, the symbol [●] in Figure 11 shows the measurement of the guideway with a steady current value of 0.7 A and the symbol [■] shows the measurement of the guideway with a steady current value of 0.3 A with the permanent magnet. The symbol [▲] in Figure 11 compares the guideway with a steady current value of 0.3 A and the guideway on which the permanent magnet is placed. In the case where the steady current value is the same, a decrease in the RMS can be confirmed at all measurement points. Thus, it can be confirmed that vibration can be suppressed. Comparing without permanent magnet with steady current 0.7 A and with permanent magnet with steady current 0.3 A, vibration can be suppressed more than 0.7 A by disposing a permanent magnet.
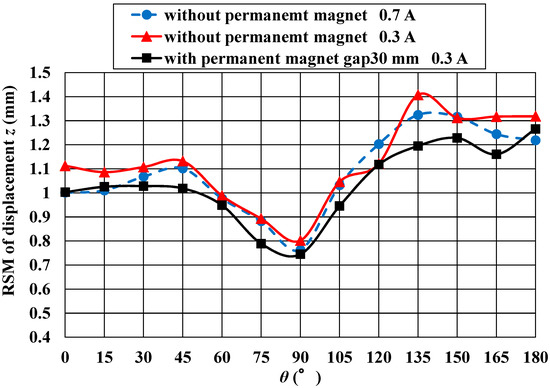
Figure 11.
Experimental results of each guideway.
As a result, it was confirmed that it exceeds the vibration suppression performance of the steady current value of 0.7 A. At 90° of the measurement point in both the figures, it is considered that the vibration reduction amount decreases because the lowest point of the steel plate corresponds to the part where vibration hardly changes.
7. Conclusions
In this research, we analyzed the vibration phenomena when changing the steady current value of the electromagnet used for controlling the traveling steel plate. We confirmed whether the phenomenon can be stable guidance by using permanent magnets with low steady current value. Owing to varying the steady current value, stable guidance was possible in the case of a high steady current value. However, the electromagnet under control has a problem of heat generation due to an increase in current value. Furthermore, there was a possibility that control performance can be deteriorated by an increase in the resistance value. To confirm the vibration suppression performance at a low steady state current value using a permanent magnet, we analyzed the vibration mode of the steel plate by ANSYS. Permanent magnets were placed in consideration of the calculated vibration mode shape and experiments were conducted. As a result, it was found that vibration can be suppressed at all measurement points as compared with the guideway of strong steady current value. The arrangement of the permanent magnets exhibited the damping effect even at the same steady current value. Therefore, it was clarified that the performance of vibration suppression performance is improved by arranging permanent magnets with the low steady current value. In future, we will investigate the optimum gap of permanent magnets to confirm further vibration suppression effects.
Author Contributions
T.B., S.I., Y.N., R.Y., wrote the paper; T.B., S.I., Y.N., R.Y. carried out an experiments; T.B., S.I., Y.N., R.Y. contributed the analyses of the data; and T.N. and H.K. contributed the design of the controller and electric circuit.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest. The founding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, and in the decision to publish the results.
References
- Inoue, A.; Fujioka, H.; Morii, S.; Komori, M. Study on Stability of Steel Strip Under the Electromagnetic Shape Controller. Trans. Jpn. Soc. Mech. Eng. 2008, 74, 52–59. (In Japanese) [Google Scholar] [CrossRef]
- Inoue, A.; Kawanishi, M.; Morii, S.; Komori, M. Study on Shape Control and Vibration Absorber of Steel Strip (1st Report, Result of Experimental Test). J. JSAEM 2009, 17, 79–84. (In Japanese) [Google Scholar]
- Kabeya, K.; Ishida, K.; Suzuki, H.; Ishigaki, Y.; Ishino, K.; Ishii, T. Strip Vibration and Control Using Electromagnets at Gas Wipers in CGL. Tetsu-to-Hagane 2013, 99, 18–24. (In Japanese) [Google Scholar] [CrossRef]
- Sudwilai, P.; Oka, K. The Frequency Response of Vibration Control with a Linear Actuator and a Permanent Magnet. J. SAEM 2012, 20, 216–221. [Google Scholar] [CrossRef]
- Jung, W.; Jang, Y.J.; Lim, S.; Won, S. Active Vibration and Flatness Control of a Strip in a Continuous Galvanizing Line using Positive Position Feedback Control. J. ISIJ Int. 2013, 53, 854–865. [Google Scholar] [CrossRef]
- Ogura, K.; Kashiwabara, K.; Mitsuhashi, Y.; Oshinoya, Y.; Ishibashi, K. Fundamental Consideration of Optimal Relationship between Magnetic Force and Location of Permanent Magnet Installed in Edge Direction of Thin Steel Plate. Proc. Sch. Eng. Tokai Univ. Ser. E 2004, 44, 43–48. (In Japanese) [Google Scholar]
- Narita, T.; Hasegawa, S.; Oshinoya, Y. Non-contact guide system for traveling elastic steel plates (Fundamental considerations on asymmetric placement of electromagnets). In Proceedings of the International Conference on Electrical Engineering, Kanazawa, Japan, 8–12 July 2012; The Institute of Electrical Engineers of Japan: Tokyo, Japan, 2012. [Google Scholar]
- Kawasaki, K.; Sakaba, K.; Kato, H.; Narita, T. Non-contact guide system for traveling elastic steel plate (Optimal placement of electromagnets by analysis of steel plate shape). J. Int. Conf. Counc. Electr. Eng. 2017, 7, 181–187. [Google Scholar] [CrossRef]
- Kawasaki, K.; Narita, T.; Kato, H.; Moriyama, H. Non-Contact Guide for Traveling Elastic Steel Plate Using Electromagnets (Fundamental Consideration of Electromagnet Placement Using FEM). Trans. Mag. Soc. Jpn. Spec. Issues 2017, 1, 181–187. (In Japanese) [Google Scholar] [CrossRef]
- Bessho, T.; Kawasaki, K.; Narita, T.; Kato, H.; Moriyama, H. Noncontact Guide System of Traveling Continuous Steel Plate for Electromagnetic Force (Fundamental Consideration on Vibration Suppression Effect by Permanent Magnet). In Proceedings of the 29th Symposium on Electromagnetics and Dynamics, Kurashiki, Japan, 18–19 May 2017; pp. 65–66. (In Japanese). [Google Scholar]
- Narita, T.; Oshinoya, Y.; Hasegawa, S. Control of electromagnetic levitation transport of flexible steel plate (Fundamental considerations on elastic vibration control under transport). In Proceedings of the International Power Electronics Conference, Sapporo, Japan, 21–24 June 2010. [Google Scholar]
- Koyama, T. Practical Design of Belt Transmission; Yokendo: Tokyo, Japan, 2006; pp. 21–25. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).