1. Introduction
The vibration control of civil structures is a challenging area of research. The solutions devised within this field of knowledge can be deployed into actual buildings leading to safety improvements of both persons and property. One of the main natural events that has a severe impact on the structural integrity of buildings is movements of the Earth’s crust. The classical approach to minimize the effect of this disturbance lies in the proper design of building architecture. However, nowadays, both passive and active control systems can be found, for example, integrated into slender and tall structures, which are used to mitigate vibrations introduced by wind and seismic disturbances.
Research on semi-active control for seismically excited structures has significantly evolved in previous years. Many innovative control and structural health monitoring systems, including wireless sensing, have been proposed for large-scale civil structures, and a large number of research works have been devoted to this field [
1,
2,
3,
4,
5,
6,
7,
8,
9,
10,
11,
12]. Semi-active and hybrid control systems rely on the information provided by current state-of-the-art electronic instrumentation systems in order to provide real-time information regarding civil structure dynamics [
13]. Moreover, due to the crescent ubiquity of digital computer systems, artificial intelligence (AI) and soft computing techniques have been gradually introduced into the context of building vibration and seismic control. For example, in September of 2017, the NTT Facilities Inc. (Minato, Tokyo, Japan) put forward the world’s first artificial intelligence-based system that is able to counteract the effects of earthquakes. The system, designed to control long-period ground motion, analyzes the movements of buildings using AI and artificially vibrates them with actuators to counteract the vibrations imposed by earthquakes.
Effectively, the future trend will be to devise buildings with the ability to dynamically react to seismic or other disturbances through the integration of intelligence into civil structures and by providing the ability of these structures to react through the excitation of building-embedded actuators.
The brain emotional learning (BEL) paradigm positions itself within the universe of computational intelligence techniques and has already been considered within the context of building vibration mitigation. For example, in [
14], the authors presented a study where a BEL-based controller was used to reduce building vibration by reacting over a magneto-rheological damper.
BEL-based controllers have, typically, a large set of coefficients that must be tuned to achieve the best performance. In the abovementioned work, those parameters were obtained using a manual trial and error procedure which would have led to suboptimal performance. The present work follows on from the abovementioned work by presenting an alternative controller parameter tuning using an evolutionary search algorithm. In particular, a particle swarm optimization (PSO) method is integrated into the control loop in order to obtain the set of parameters that minimizes a given performance index.
The present article will be organized in the following way:
Section 2 addresses the actual vibration control problem and presents the fundamental system architecture.
Section 3 is devoted to presenting a brief overview of magneto-rheological dampers and their mathematical modelling.
Section 4 describes the main concepts of a BEL controller, and
Section 5 presents an overview of the PSO algorithm. The details regarding the computer simulation and the obtained results are provided in
Section 6. This article will end with
Section 7 where the final conclusions and remarks are presented.
2. Problem Statement
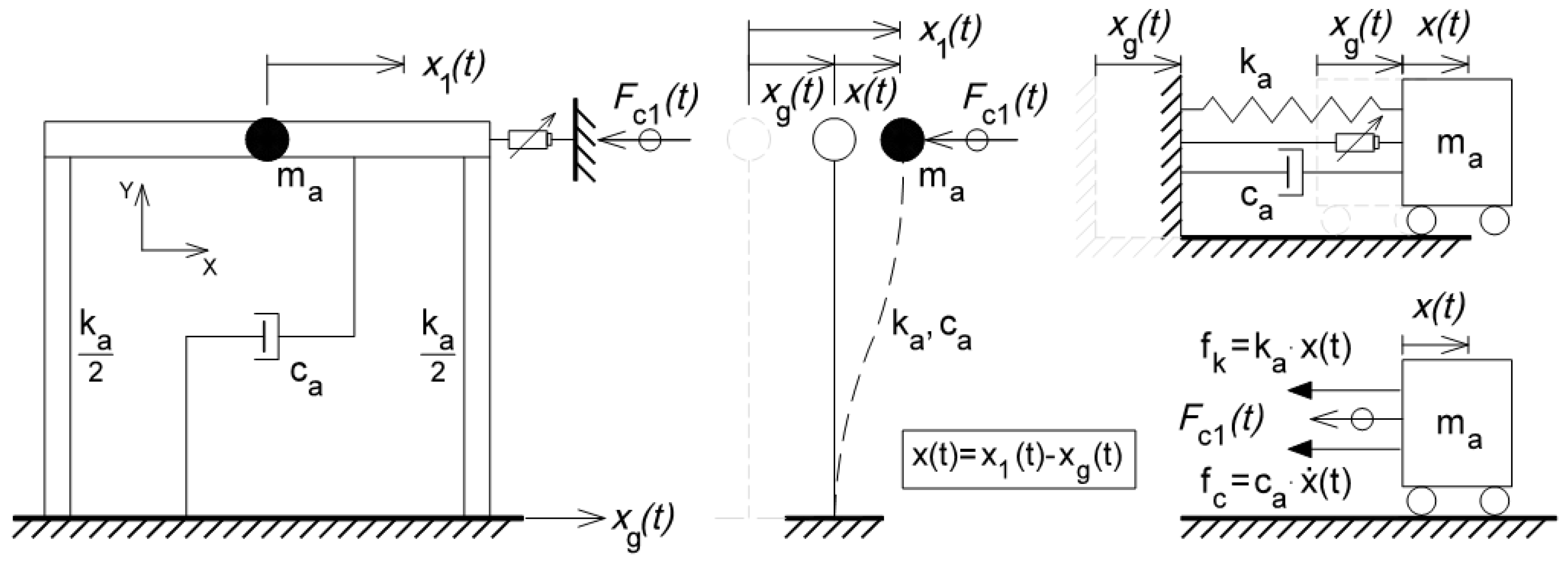
Consider a semi-active, single degree-of-freedom (SDOF), controlled system subjected to an earthquake ground motion with a control force applied to the first mass, as illustrated in
Figure 1.
It is intended that the control force will reduce the response of the system and is achieved placing an actuator between the base and the first mass. The damper force can be changed using a control system comprising a controller that monitors the system’s response and computes the required damping force to be applied to the system in order to improve its structural performance. An effective semi-active control involves an appropriate algorithm that can take advantage of the dissipative properties of the control device.
In the current work, the civil structure was equipped with a passive control system comprising a magneto-rheological damper located between the ground floor and the first floor, which was able to operate in two modes: as a passive energy dissipation device and as a semi-active actuator whose control action was commanded by the controller described in
Section 4.
The building dynamics were modified by a generic actuator whose effect was defined by the control force, , included in the equation of motion. In this case, the actuator was a magneto-rheological damper that was able to be operated as a passive or semi-active device. Details regarding this actuator will be provided in the subsequent section.
3. Magneto-Rheological Actuators
A magneto-rheological (MR) damper is a promising semi-active device that can be found in areas of vibration isolation of suspension systems and civil structures.
As the name suggests, an MR damper is a damping device filled with MR fluid. These are oil-based fluids in which ferric particles are embedded. When subjected to a magnetic field, this type of fluid changes its viscosity up to the point where it becomes a viscoelastic solid. The viscosity value is defined through an externally applied magnetic field. When this fluid is used within a damper, the damping coefficient can be changed by controlling the magnetic field intensity. The magnetic field is generated by an electromagnet device added to the piston body. The intensity of the magnetic field generated by this electromagnet is dependent on the electrical current intensity applied to the coil wires. Due to its properties, the fluid viscosity increases proportionally to the increase in the magnetic field intensity. This allows the damping characteristics of the device to be continuously controlled by means of proper dosing of the electrical current intensity delivered to the electromagnet.
Mathematical Modelling of an MR Damper
The MR damper inherently has hysteresis characteristics during non-linear friction mechanisms, and many efforts have been devoted to the modelling of this non-linear behaviour [
15,
16,
17]. Static or quasi-static models include no dynamics but can express non-linear mapping from the velocity to the damping force [
16,
18,
19]. It is not easy to identify the hysteresis curve by using a small number of model parameters from the actual road surface excitation data. To model the hysteresis dynamics explicitly, the Bouc–Wen model and its variations, in which the input–output relationship is expressed by a set of non-linear differential equations, have also been investigated [
15,
16].
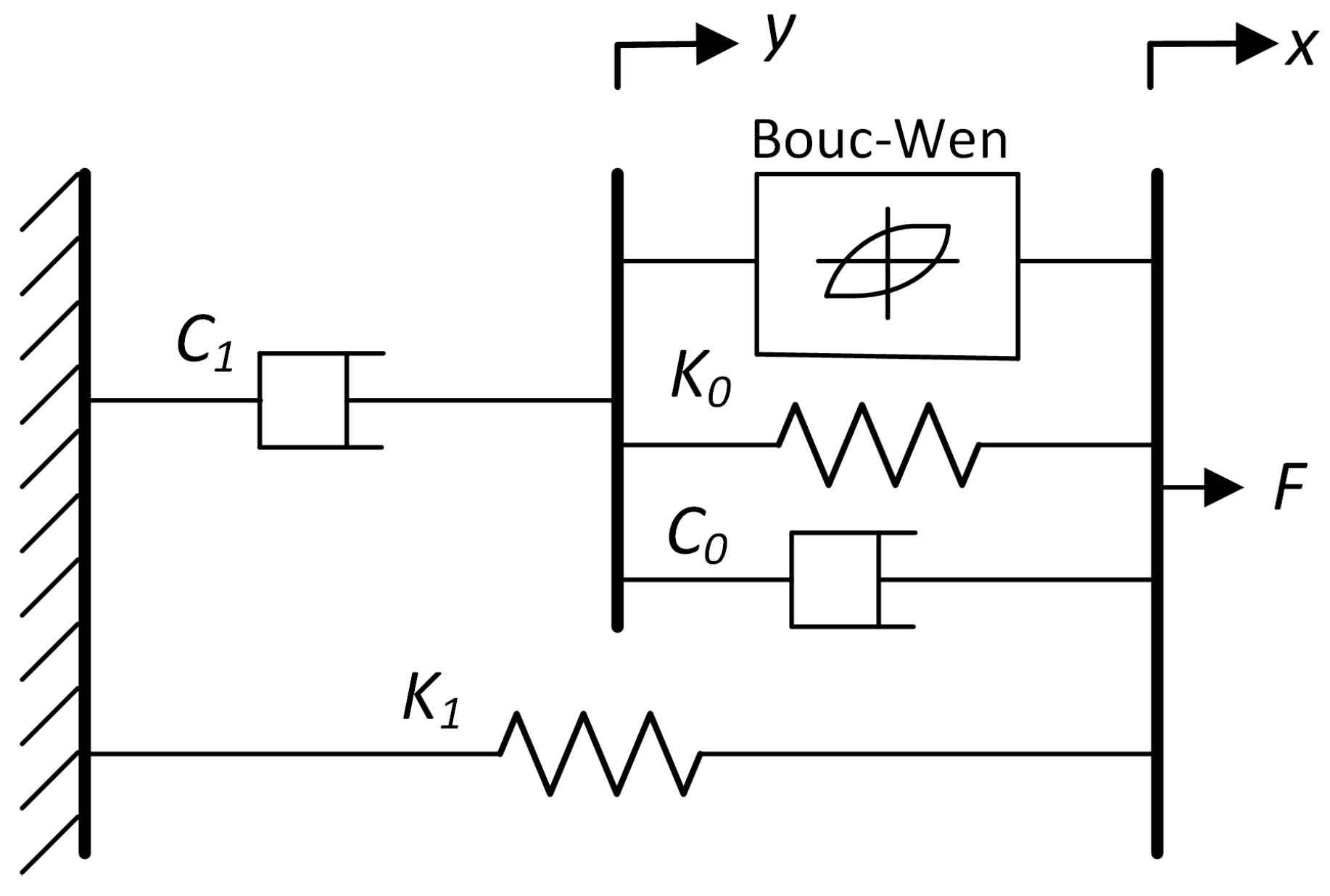
In the current work, the modified Bouc–Wen model was selected to simulate the behaviour of the MR damper.
Figure 2 presents a schematic description of this model.
In this schematic, the force is given by the following first order differential equation:
where,
and,
Some of the model parameters are independent of current, such as , mm, mm, N/mm, N, and .
The intensity of the electrical current delivered to the MR damper is a function of the actual building vibration, measured using sensors scattered along the civil structure and computed by means of a brain emotional learning controller. The following section is devoted to describing the main characteristics and working principles of a BEL controller.
4. The BEL-Based Control System
The BEL controller presents interesting features that can be exploited to design structural control systems for civil engineering applications. The brain emotional learning controller is a relatively recent, bio-inspired control system architecture, based on the emotional learning mechanism of the brain’s limbic system, which has been employed to develop feedback controllers for complex control problems [
20,
21,
22,
23,
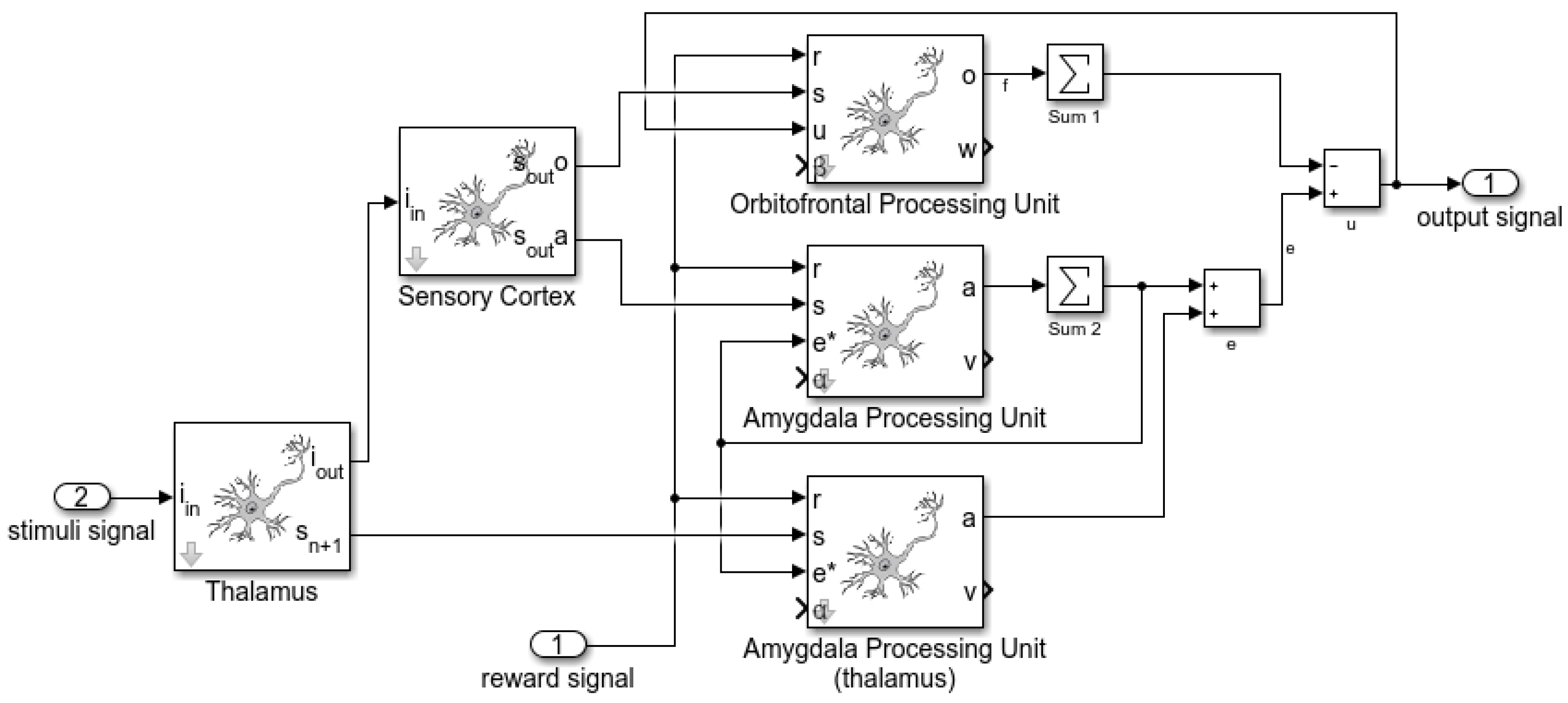
24]. The BEL model, initially proposed by [
25], comprises four main components: the amygdala, the orbitofrontal cortex, the sensory cortex and the thalamus. The amygdala and the orbitofrontal cortex are used to process the emotional incoming signals, while both the sensory cortex and the thalamus receive and processe sensory inputs. The signal processing structure of a BEL model is presented in
Figure 3.
Sensory inputs are processed in the thalamus, initiating the process of response to stimuli and passing those signals to the amygdala and the sensory cortex. Then, the sensory cortex operates by distributing the incoming signals properly between the amygdala and the orbitofrontal cortex. In this controller, the learning procedure is mainly processed in the orbitofrontal cortex and is based on the difference between an expected punishment or reward and the received punishment or reward. The perceived punishment/reward is processed in the brain using learning mechanisms while the received punishment/reward represents an external input. If these signals are not identical, the orbitofrontal cortex inhibits and restrains the emotional response for further learning. This is by no means a through description of the BEL model. For a deeper insight, the reader is advised to refer to [
25].
This limbic-based model can be used within a control system paradigm. This approach was first proposed by [
22], where the control signal is provided by the model output, and the stimuli and reward signals are derived from the system measurements.
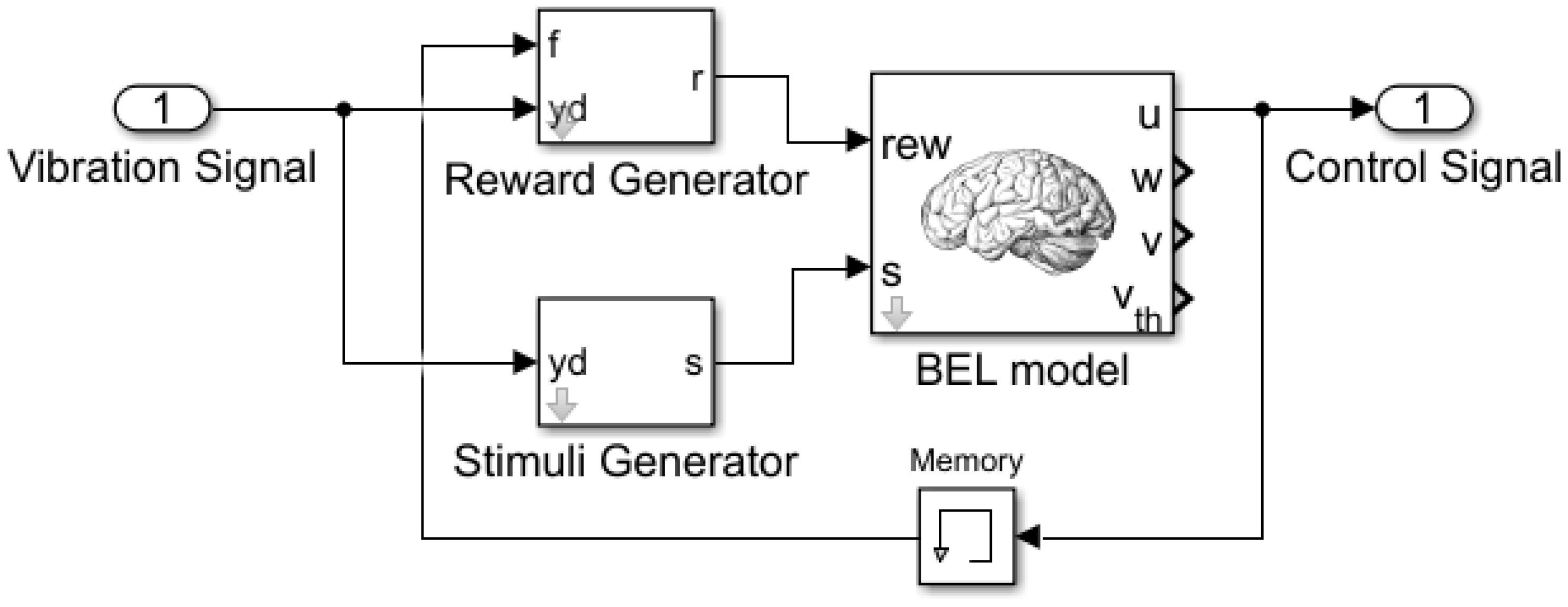
In this work, the stimuli signal was generated from processing the measured building vibration, and the reward signal from both the vibration signal and the latest value of the control signal. This architecture is presented in
Figure 4.
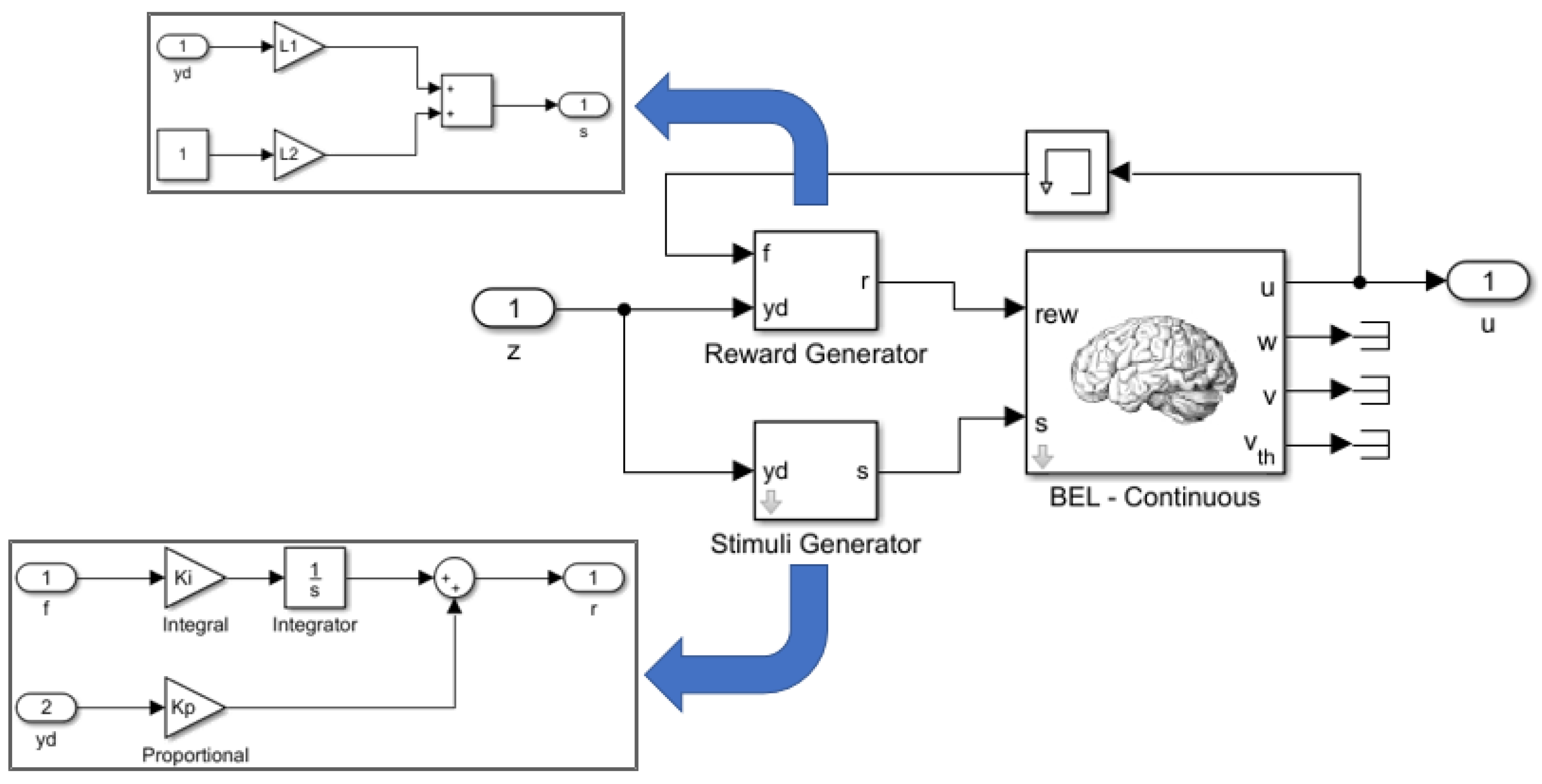
The stimuli signal was obtained from
and the reward signal used
where the
values for
, are weight factors that define the relative importance given to each component,
is the control signal and
is an input signal generated from a scaled version of the square of the measured vibration signal.
The main drawback of the BEL controller is related essentially to the appropriate definition of emotional and sensory signals that are able to represent, with sufficient precision, the system’s state and the control’s objective in order to maximize the performance of the control system. Moreover, several parameters must be defined in order to get the controller to perform well, for example, the learning rate of both the amygdala and orbitofrontal processing units and the reward and stimuli generators. A common approach is to use a trial-and-error procedure. However, other forms have been addressed in the literature, such as the use of Lyapunov theory [
26] or even fuzzy-based tuning [
27]. The use of evolutionary based algorithms is also a common choice. For example, [
28] used a particle swarm optimization algorithm to tune a BEL-Based Intelligent Controller (BELBIC) applied to a voltage regulation problem in a power electronic application. Two years later, [
29] presented a multi-input and multi-output BELBIC-based architecture concerning the control of a highly non-linear coupled distillation columns process. The authors showed that a significant increase in closed-loop performance was achieved by having a particle swarm optimization algorithm to search for the best BELBIC parameters. Those results were corroborated by the more recent work of [
30].
In [
31], a BELBIC-based controller was applied to a single-link, flexible joint manipulator. The controller was tuned using the clonal selection algorithm while seeking to minimize a set of time performance indicators, such as the rise time and overshoot. The clonal selection algorithm, proposed by [
32], is an evolutionary-based algorithm that mimics the immune system’s dynamics.
The work of [
33] also used a particle swarm algorithm in association with a BELBIC controller. They proposed a novel paradigm applied to an inverted pendulum problem, which requires the execution of three steps: First, the BELBIC learns how to reproduce a control signal by imitation of a basic controller. Then, an optimization step improves the stress produced by the emotional cue generator. Finally, the particle swarm optimization seeks a new solution that is able to increase the closed-loop system’s performance.
The BEL model can also be used in other tasks other than control system design, for example, in signal processing and machine learning tasks, such as pattern classification. In regard to this latter application context, [
34] resorted to a genetic algorithm to find the weights and biases of both the amygdala and orbitofrontal cortex in order to improve a BEL-based neural network used to classify human face expressions.
In this work, the BELBIC parameters were also found by means of a particle swarm optimization algorithm. Nevertheless, there were significant differences that distinguish it from the above enumerated research articles. One of the main distinctions concerns the actuator operating regime. In order to keep the actuator away from saturation, the cost function over which the search algorithm looks for a solution was more complex than the usual set-point error function used. Meanwhile, and in order to keep all the relevant information self contained within this article, in the next section, an overview of the particle swarm optimization search method is presented.
5. The Particle Swarm Optimisation Algorithm
The particle swarm optimization algorithm (PSO) has its foundations in attempts to mathematically model the dynamics of the collective behaviour of groups of identical organisms, such as bird flocks [
35]. It was further observed that the base concepts of this modelling paradigm could be used as the core for a new evolutionary-based optimisation method. It has been over two decades since this search method was put forward. From this point forward, it has been used in thousands of different applications where it has proved to be an efficient technique. The reader is referred to the work of [
36,
37] for a review regarding the span of applications using the PSO technique.
As in virtually all evolutionary-based search methods, the PSO algorithm evolves an initial set of admissible solutions, called particles, through the problem search space. The main difference to other existing evolutionary techniques is that the particles’ movement is governed by a set of rules that mimics the social behaviour found in the synchronised movement of some groups of living beings.
At a given evolutionary time,
t, each particle has its own position and momentum. For each particle,
i, in the swarm, the shift on those two physical variables is performed by means of the following equations:
where the vector
describes the velocity of particle
i for each one of the
d dimensions in the problem. The vector
denotes the position of particle
i in the search space.
The first equation describes how the velocity of particle i is updated. As can be seen, the particle’s momentum depends on the value of two additional variables: the cognition-only and social-only components.
The vector
represents the cognition-only component and
represents the social one. The cognition-only component models the fraction of the particle movement that is due to the particle’s own experience. On the other hand, the social-only element takes into consideration the knowledge of the remaining particles in the swarm. Both components are mathematically described by the following two vectorial equations:
where
represents the best achieved position of particle
i from the beginning of the optimization process until the epoch,
t. The vector
indicates the overall best position among the available set of particles for the current iteration.
The coefficients
and
in (
6a) are known as cognitive and social constants, respectively. Usually, their values come from uniformly-distributed random numbers generated between 0 and 2. Those values can be either constant along the full set of epochs or can be generated at each epoch. Moreover, they can be also be
d-dimensional vectors whose component values are individually defined from the abovementioned random generation method.
The above set of four equations are, by no means, a closed subject. Indeed, several modifications have appeared in the literature over time. For example, [
38] incorporated an inertia weight, denoted by
, into (
6a), which led to the following alternative formulation:
A large value for the inertia weight will guide the particles’s movement towards a more global search. Furthermore, a smaller value will lead to a more concentrated search radius. Frequently, this coefficient is adjusted from a larger value to a smaller one along an epoch’s elapsing time. This strategy aims to stimulate the search initially on a broader space grid and focus it as the algorithm converges.
It is commonplace to think about the coefficients
and
and
the belief degree that a given particle has on its actual position, its personal experience, and on the influence of its neighbours position. It is worth mentioning that the neighbourhood of an arbitrary particle is evaluated using a given metric, such as the Euclidean distance [
38].
A simpler version of (
6a) was suggested in [
39], considering
and assuming an intermediate position
between the best individual position
and the overall swarm best
. This assumption leads to the following formulation:
promoting an alternative velocity equation now treated by
Further adjustments to the original formulation were also proposed by [
40], where an additional constriction coefficient was added to (
10), leading to
where the effect of the constriction coefficient,
, is to promote convergence over time. Its value is calculated by
where
and
are suggested as suitable values to be used [
38].
In practice, both velocity and position should be limited in order to prevent particles from searching for solutions outside the admissible region. The position range of the particles is defined according to the addressed optimization problem. In addition, the speed should not be set too high to avoid oscillations, or too low so that the population is prevented from collapsing towards local minimums. Suitable values for both the inertia weight and the maximum allowed velocity were considered in [
40].
In this work, the function particleswarm(), from the
Matlab global optimization toolbox, was used. According to the
MathWorks documentation, the implemented PSO function follows the formulation introduced in the seminal work of [
35] and extends it by taking into consideration the modifications suggested in [
41,
42]. During the simulations carried out in this work, the PSO algorithm was parametrized assuming
. The inertia weight,
, starts with a value of 0.1 and grows up to 1.1 as the number of executed epochs increase. The addressed problem dimension is 6 and a swarm size of 30 particles was found to be suitable. Further details regarding the computer simulations carried out and the obtained results are presented in the following section.
6. Computer Simulations and Obtained Results
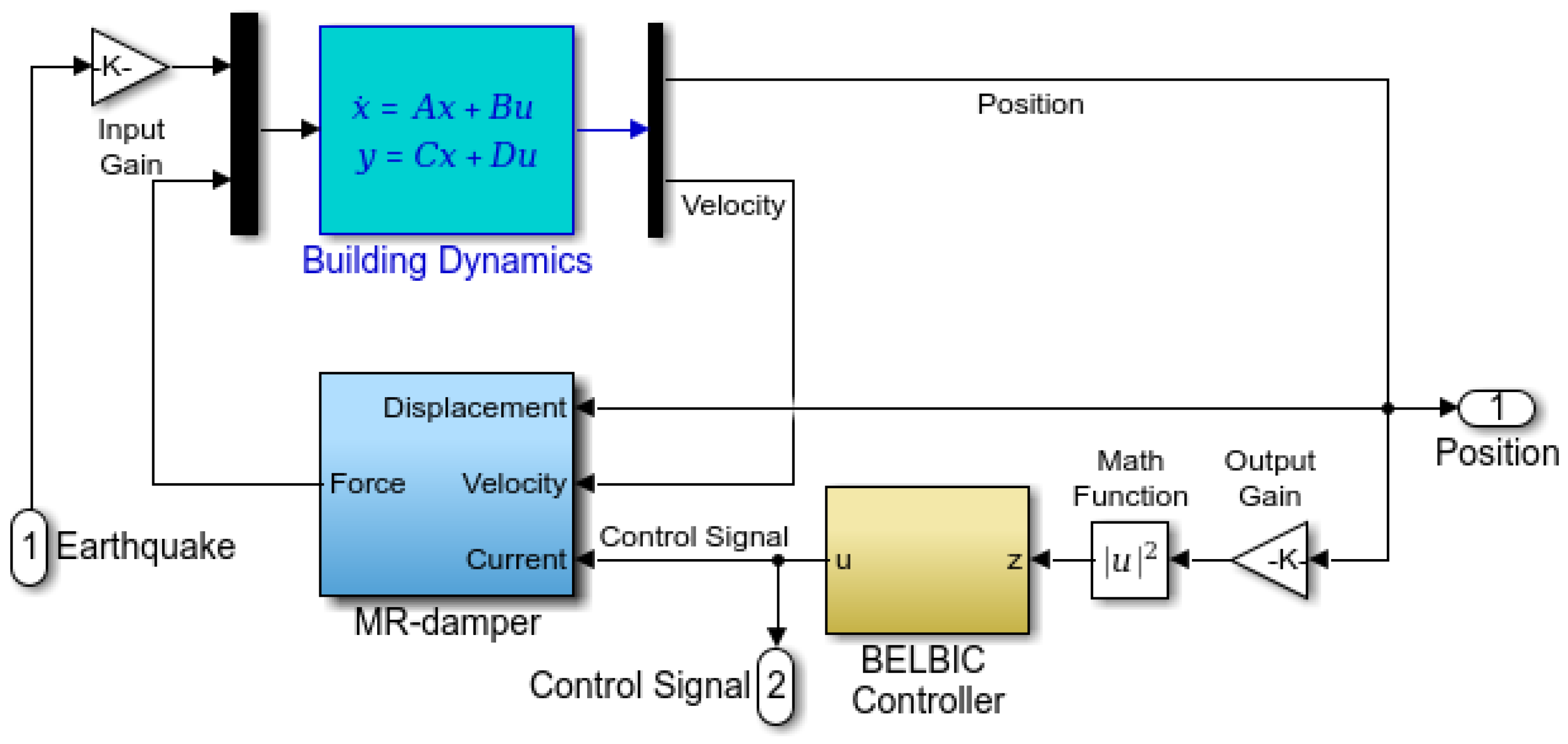
The aim of the current work is to evaluate the ability of a PSO algorithm to automatically parameterize a BEL-based controller. In particular, the addressed problem concerns the vibration improvement of a single degree-of-freedom structural system when excited by a one dimensional earthquake signal.
As seen in
Section 2, building dynamics can be modified by changing the damping ratio of a magneto-rheological actuator. As explained in
Section 3, this change in behaviour can be promoted by means of a suitable injection of electrical current into a piston-embedded electromagnet. The question raised at this point is how to define the correct electromagnet excitation current and how this current should be modulated in order to accomplish a minimum structural vibration in the presence of an earthquake.
In this work, the computation of such electric current was viewed within a closed-loop feedback control strategy. In this type of strategy, the building vibration is measured, for example by means of installed accelerometers or strain gages, and this information is delivered to a controller which is responsible for generating the electrical current profile to excite the MR damper. The controller paradigm considered here, and previously introduced in
Section 4, used a BEL-based controller. The main motivation behind the use of such type of controller was its ability to adapt to changes in the operating conditions. Those changes could be due to several factors, such as the aging of materials or even natural structural dilation and contraction.
The main issue when applying a BEL controller is its parameterization. One of the most promising methods is based on the use of evolutionary-based algorithms. In this framework, an off-line parameter estimation task takes place, where the controller parameters are found through the use of simulation models. One of these evolutionary methods is the PSO algorithm which was addressed in
Section 5. In order to analyse the performance of this type of control system architecture, a
Simulink model (MathWorks, Natick, MA, USA) of the structural BEL-based control system was developed, as can be seen in
Figure 5.
The building dynamics were modelled using a state-space approach and the MR damper, using the model referred to in
Section 3. The BEL-based controller input was obtained from a scaled version of the squared building position variation, and the output was directly fed into the MR electromagnet.
The
Simulink based BELBIC toolbox was used to implement the controller block. In particular, the continuous-time version of the BEL model was considered. Further details regarding this toolbox can be found in [
43].
Figure 6 shows the internal structure of the BELBIC controller of
Figure 5. The stimuli and reward transfer functions blocks were also expanded.
During the simulation, the system was excited using an earthquake input signal, and then, both the building position and computed control signal were used to establish the controller performance. This performance was then used by the PSO algorithm to evaluate the fitness of a given solution. In this work, the performance index used was the following:
where
denotes the controller parameters set, and
denotes the simulation time, which in this case was set to 10 s. It is worth noting that the MR excitation current must be positive and below a given threshold. In the present case, an electric current of 0.5 A was assumed to be the actuator upper saturation level. For this reason,
is a function that penalizes solutions that lead to control signals whose amplitudes are outside the actuator saturation limits. In particular,
is computed with
for
, and
is the simulation time which, in the current case, was set at 10 s.
The PSO algorithm was run several times to search for a suitable solution,
, that minimized
. As previously stated, a swarm size, composed of a total of 30 particles, was used, and the obtained solution converged systematically to
. Parametrizing the controller with these values led to the results presented in
Figure 7,
Figure 8 and
Figure 9.
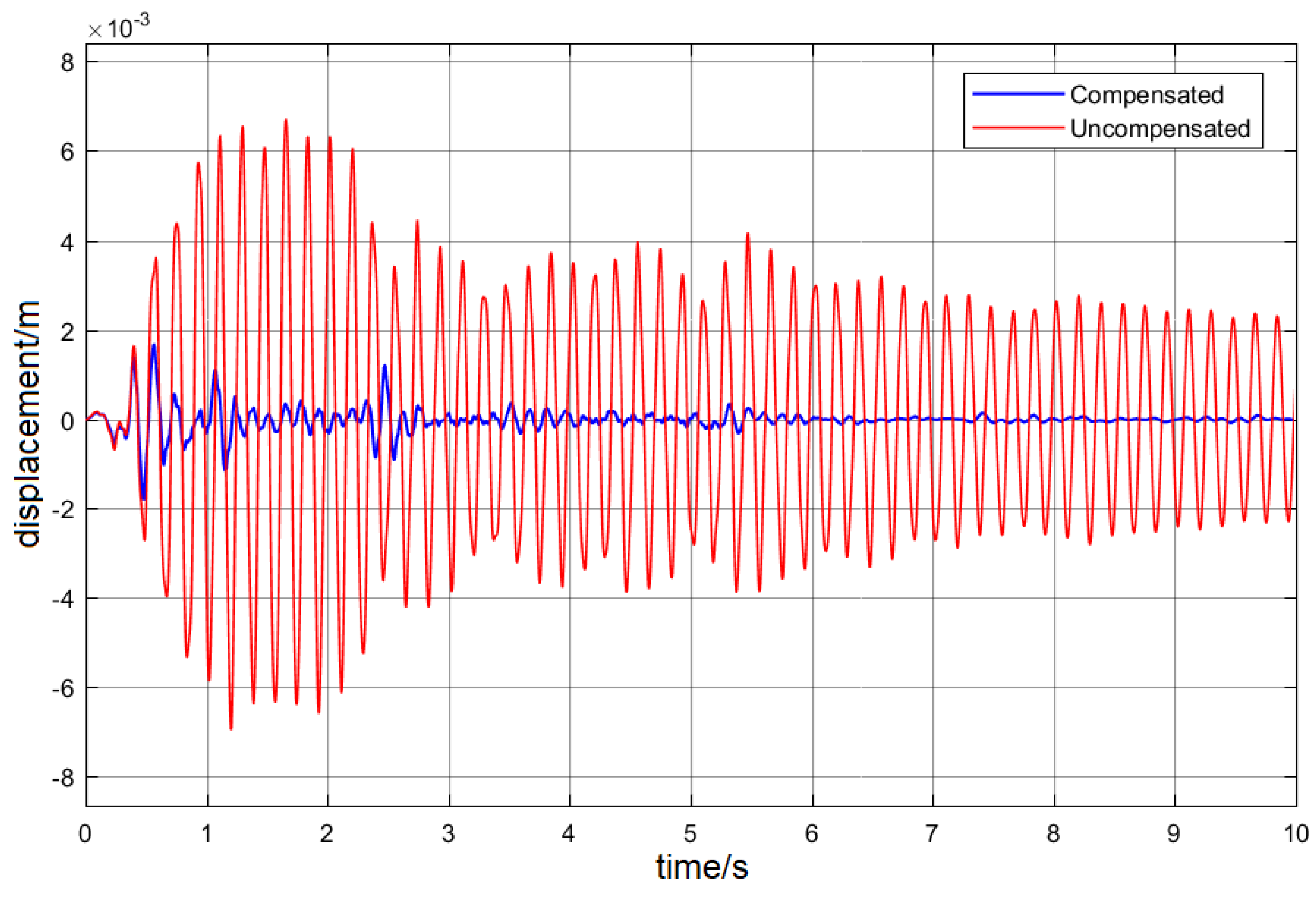
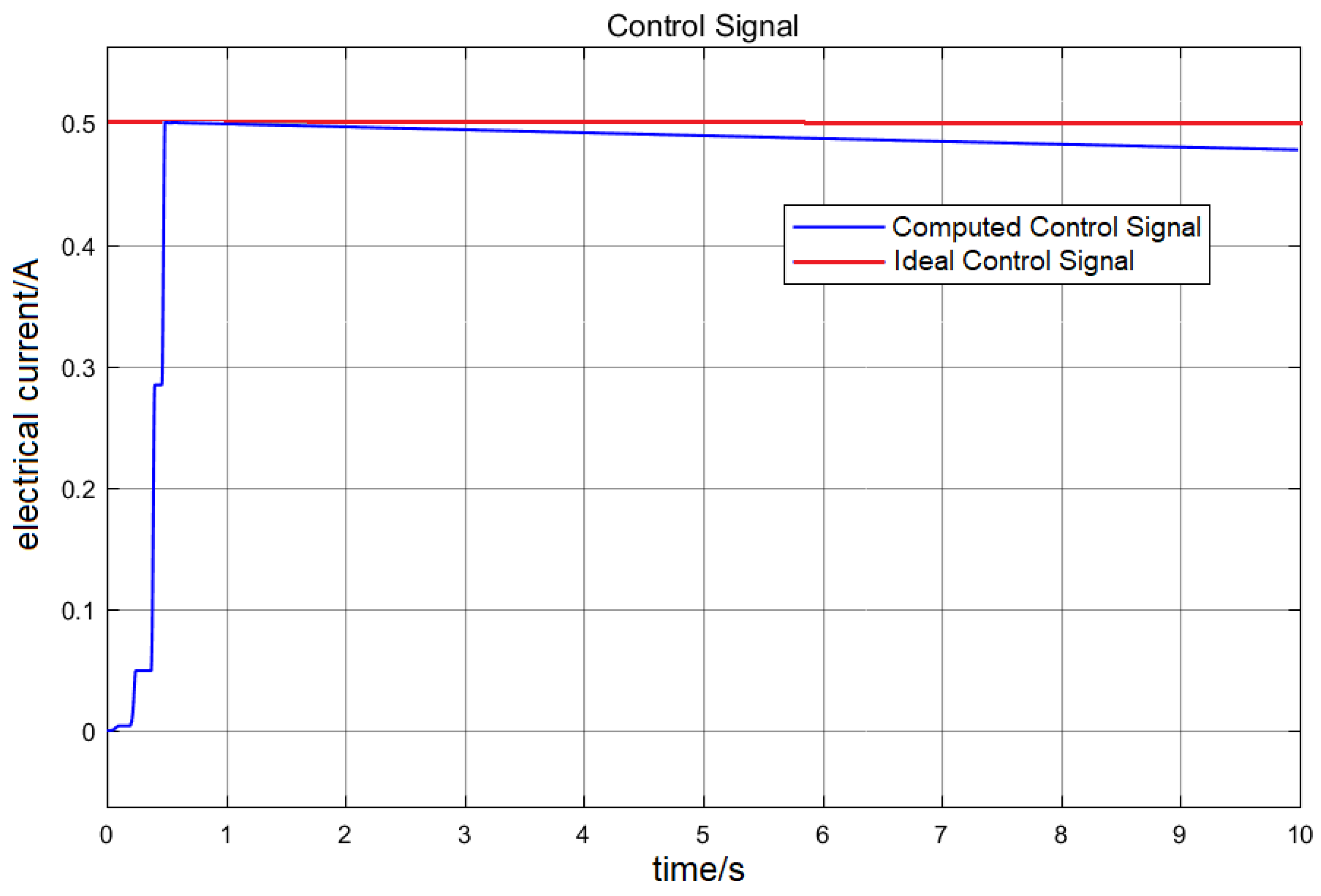
As can be seen from
Figure 7, the use of a semi-active approach in the civil structure was able to severely absorb the oscillations imposed by the earthquake. When comparing the uncompensated with the compensated systems, it is clear that the latter was able to reduce both the oscillation amplitude and its duration which would lead to an increase in a building’s seismic reaction ability. This type of behaviour was also observed when considering the building’s velocity. As can be seen in
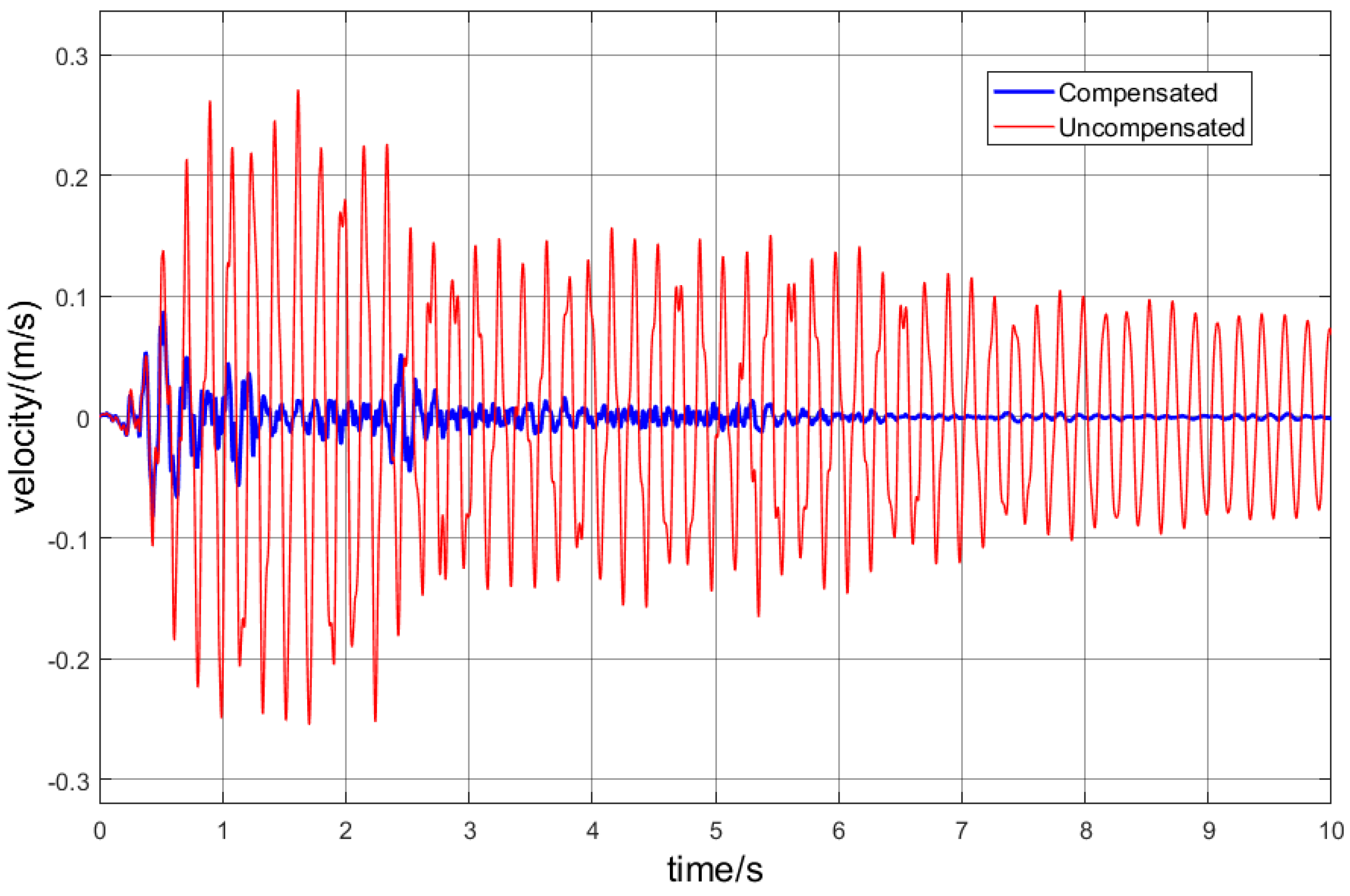
Figure 8, the peak velocity amplitude and its duration were severely damped when the actuator was excited by the control signal. Moreover, as can be seen from
Figure 9, the PSO search algorithm was able to deliver a solution that maintained the control signal within the saturation limits of the actuator. Accomplishing the controller parametrization task by relying solely on human intuition would be a cumbersome, hard or probably impossible, task.
The following section summarizes the current work and provides some future work directions.
7. Conclusions
Maintaining the integrity of civil buildings in the presence of vibrations due to several causes, such as earthquakes, is a major concern. Nowadays, there is a trend towards introducing active or semi-active reaction systems in structures in order to mitigate, among others, the effects of seismic disturbances. The use of magneto-rheological dampers has been proven from computer simulations to be useful in achieving this objective. Due to its non-linearity, computational intelligence-based control methods have been addressed to tackle the problem of damping ratio tuning under building oscillations. One of such methods is based on the BEL model. However, the effective use of this control paradigm requires the tuning of several parameters which is impracticable when viewed as a pure human task. For this reason, the present work presented an automated approach to BEL controller tuning by resorting to a PSO algorithm. The obtained results suggested that an acceptable closed-loop response can be achieved while maintaining the control signal, limited to the dynamic operation range of the actuator. In particular, the obtained peak-to-peak displacement attenuation was higher than 10 dB and the building settling time was attained after less than 10 s. The maximum vibration speed was reduced from 0.3 m/s to less than 0.1 m/s. Moreover, the velocity damping strongly increased and became negligible after six seconds. The control signal was also within the actuator dynamic range. Moreover, the current magnitude decreased slightly over time which is in line with the damping requirement which should be lower as the vibration diminishes. This will lead to a reduction in the energy delivered to the actuator when comparing to a constant current delivery.
The positive results obtained with the present controller design procedure serve as motivation to extend the method for systems with multiple degrees-of-freedom. Additionally, the present research work will be validated using experimental data and also expanded to include multiple degrees-of-freedom (MDOF) systems. Future work includes the performance of small-scale structural control tests on the Quanser Shake Table II system. A real-time data acquisition/actuation system (National Instruments PXI or PCI DAQ running LabVIEW) based on acceleration signals from integrated circuit piezoelectric (ICP) accelerometers and displacement measurements from linear variable differential transformer (LVDTs) will be used to monitor the system’s response. Sensor measurements including the damper force will be also used to characterize the damper state and to estimate the relative velocities and displacements of different stories. Initially, a classical linear quadratic gaussian (LQG) state-space control algorithm will be used to determine control forces for state feedback. The results will be used to calibrate the experimental mockup and to implement the BEL controller.