1. Introduction
Vibration causes oscillation, which may be detrimental to a system. Vibration control systems can be divided into passive, active, and semi-active, depending on the external power required. Though active vibration control systems can act upon broadband load and frequency, they require a large control effort associated with the system [
1]. Moreover, in multiple-degree-of-freedom systems, the actuators and sensors make the control system complex and bulky. This causes problems in some applications, such as magnetic bearings. Reducing the actively controlled degree-of-freedom can lead to miniaturization of the system [
2]. In a vertically active magnetic suspension system operated in the differential mode, vibration is easily induced in the lightly damped lateral directions. Any disturbance in lateral directions can cause the system to oscillate for a long time. Vibration can be suppressed in such systems by varying stiffness, as mentioned in Mizuno et al. [
3] and Javed et al. [
4]. Varying stiffness control was applied in a single-degree-of-freedom system in both cases.
In a magnetic suspension system, when five degrees-of-freedom (DoF) are actively controlled, it achieves high reliability and high stiffness [
5]. Various control strategies can be applied to active magnetic suspension systems, such as PID (proportional-integral-derivative) control [
6] and robust control [
7,
8,
9], to reduce vibration. Robust control can be applied by considering the uncertainties of a magnetic bearing system, such as linearization error, parameter uncertainty, and gyroscopic effect [
10]. Standard control methods may not deal with all factors [
7]. Zhou et al. [
9] applied
µ synthesis to active magnetic bearing system considering parametric uncertainty. Two radial magnetic bearings are used in their system. Gosiewski et al. [
8] designed an H-infinity robust controller. They compared the proposed controller with a PID controller and reported better performance. In their system, two pairs of coils are placed in each direction with a permanent magnet (PM) in the rotor. The performance of the robust control system depends on the proper selection of the weighting function [
8]. The control systems used in [
8,
9] show good performance; however, the design of the systems is complex. In addition, all of them were for actively controlled DoF. Asama et al. [
6] developed a 5-axis actively controlled bearingless PM motor. The axial direction is controlled by thrust magnetic bearing. The radial and tilting motions of the rotor are controlled actively by two bearingless motor units. However, to reduce the size and cost, the actively controlled directions can be reduced. When the radial directions are actively controlled, and the axial and tilting directions are passively stabilized, vibration can be induced easily in these directions. Rao et al. [
11] proposed a permanent free bearingless motor where the radial directions are actively controlled. Axial and tilting directions are passively stabilized by the bias and control fluxes. In their system, the bias current is high in order to create the bias flux. Sugimoto et al. [
5] proposed increasing the damping effect in the axial direction to suppress vibration in two-axis actively controlled bearingless PM motors. In their system, axial displacement of the rotor is measured based on the variation in flux linkage. However, the proposed estimation method and vibration suppression technique are effective for PM bearingless motors. For further reduction of space and cost, a 1-axis actively controlled magnetic bearing [
2] and a bearingless motor [
12] were investigated. In these systems, the axial direction is actively controlled, and the radial and tilting directions are passively controlled. However, the precision machining of the parts is necessary to maintain passive stiffness to facilitate vibration reduction in passively stable radial and tilting vibration [
2]. Applying varying stiffness control requires radial displacement, so different sensing techniques may require miniaturization of the system when applied to these systems.
Varying stiffness control has been studied in order to control vibration by various researchers. Winthrop et al. [
13] gathered data related to various variable stiffness devices and introduced two parameters for comparing the characteristics of those devices. Ledezma-Ramirez et al. [
14] reduced the shock acting on the base of a single-degree-of-freedom system by switching the stiffness strategy. The control in the system was divided into two stages: low stiffness was maintained during shock, and switching stiffness control was applied to suppress the residual vibration. A similar type of set up was used in [
15]. Zhou et al. [
15] developed a tunable vibration isolator with a mechanical spring and electromagnets, and permanent magnets, which possesses high-static-low-dynamic properties. The isolator works passively or semi-actively and suppresses base vibration. The authors of [
14] used nylon wires to attach the floator to the frame, and in [
15], a steel beam supported the isolated mass. Most existing methods, some of which are mentioned in [
6,
8,
9], including switching stiffness control [
14], target the vibration in the normal direction—that is, the direction of force produced by an actuator. This indicates that the number of actuators increases in proportion to the number of degrees-of-freedom to be controlled. In contrast, in the proposed system, two electromagnets (actuators) in the normal direction are used to reduce the vibration in the lateral directions (2-DoF) without any added actuator. In magnetic suspension system, two such electromagnets are commonly used to control 1-DoF motion to generate bidirectional force, as the force of an electromagnet is unidirectional (attractive). The proposed method utilizes this configuration. The motion in the normal direction is not affected, even if switching stiffness control is introduced. This is the main advantage of the proposed method. The only parameter that must be calculated correctly is the current-force coefficient to avoid such interaction. The basic idea of the proposed method was reported in [
3]. Mizuno et al. [
3] reported vibration reduction by switching stiffness in an active magnetic suspension system. In addition, a modified control strategy was introduced in their report. Varying stiffness in attenuating lateral vibration was experimented in a single-degree-of-freedom system in Javed et al. [
4]. A different procedure was applied to estimate the displacement of the floator. However, single-degree-of-freedom was considered to apply stiffness control in these systems [
3,
4]. As for magnetic suspension, the floator was supported with auxiliary mechanical means. Therefore, it is necessary to evaluate the performance of the strategy on a freely suspended floator to find out its interaction with vertical motion. The controller is adjustable by the control current in both of the mentioned strategies and additionally by the steepness parameter in the modified control strategy.
In this paper, a pair of electromagnets positioned in differential mode are used to actively control the vertical direction, as well as to reduce vibration in the lateral directions in a three-degrees-of-freedom (3-DoF) system. The floator is suspended freely without any mechanical support. Varying stiffness control is applied to reduce lateral vibration, maintaining the desired vertical position. This control strategy may be utilized to reduce actively controlled directions and to attenuate vibration.
2. Principle of Suspension and Stiffness Control
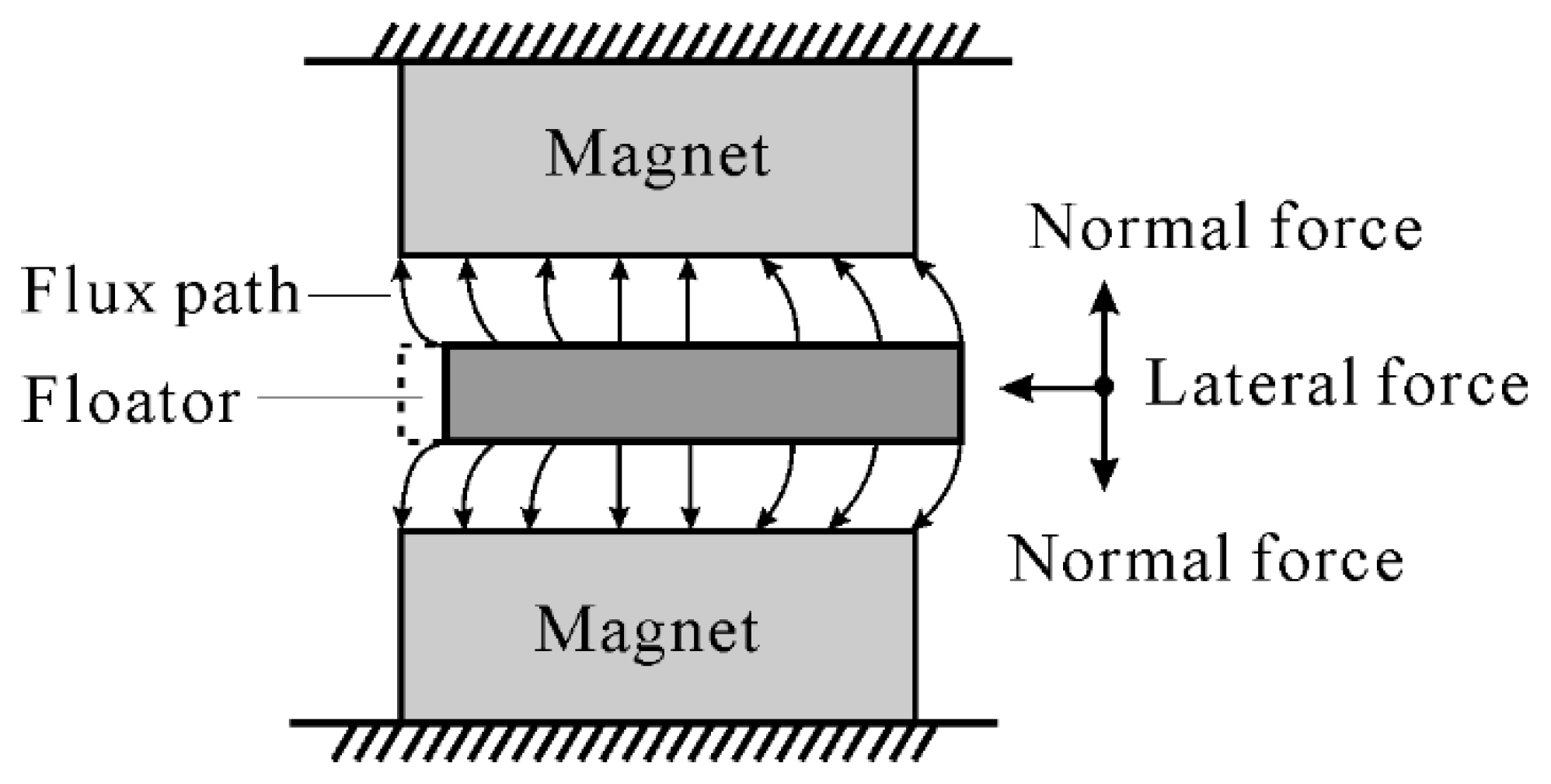
When a ferromagnetic material is placed in a magnetic field, the flux passes through it. When it is moved from its position, a force on the material is realized. The force tries to shorten the flux path, and the flux passes through the path of least reluctance [
16]. This phenomenon is named the edge effect, and is shown in
Figure 1. The forces acting on the moving floator in vertical and horizontal directions are normal and lateral forces, respectively. The lateral forces act to restore the equilibrium position.
The control system can be divided into two stages: (a) suspension of the floator, and (b) application of stiffness control. Both of these are discussed below.
2.1. Suspension of the Floator
In a magnetic suspension system, a controller delivers a control signal based on the difference between the reference and the position of floator measured by sensor. This control signal is fed into a power amplifier to transform it into control current, which is supplied to electromagnets. Proportional-derivative (PD) and PID are commonly used controllers in a magnetic suspension system. Steady-state error occurs in applying PD control. It can be overcome by using PID control integrating feedback [
17].
In the developed system, both of the controls are applied. PID control is applied in the Z-direction of the floator to achieve suspension while varying stiffness control. The gains of the PID controller are determined experimentally through trial and error. At first, PD control is applied to achieve stable levitation, and afterward, the integral control is added to maintain the desired position. Moreover, PD control is applied to determine the properties of the system. The position of the floator is almost in the middle of the two electromagnets in the Z-direction. Permanent magnets are used in both the upper and lower electromagnets to provide bias flux. This lessens the bias current, a high value of which could increase the temperature of the coil of the electromagnets. This bias flux ensures the linearity of control current in the working range.
2.2. Application of Stiffness Control
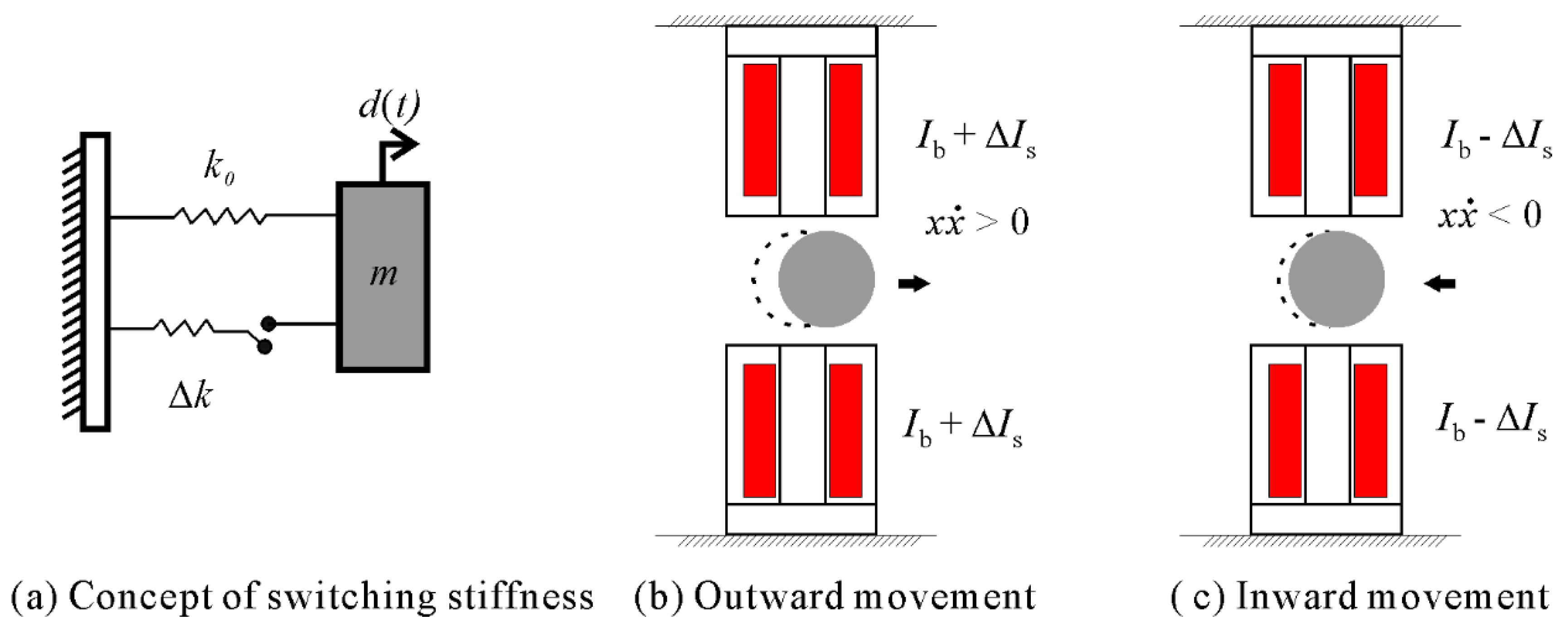
The equation of motion of a single-degree-of-freedom (sdof) system as shown in
Figure 2a can be written as follows:
where
m is mass,
k is the effective stiffness of the system, and
d(t) is displacement with respect to time.
In the case of switching stiffness control, the stiffness of the system can be changed between high and low depending on the product of displacement,
and velocity,
of the floator as mentioned in Equation (2) [
3]:
In a magnetic suspension system, the effective stiffness in the lateral direction is adjusted by varying the bias current of the electromagnets. As written in Equation (3) and depicted in
Figure 2b,c, to attain a high stiffness state when
, the switching current, ∆
Is, is added to the bias current,
Ib. When
the switching current is subtracted from bias current to achieve a low stiffness state.
where
and
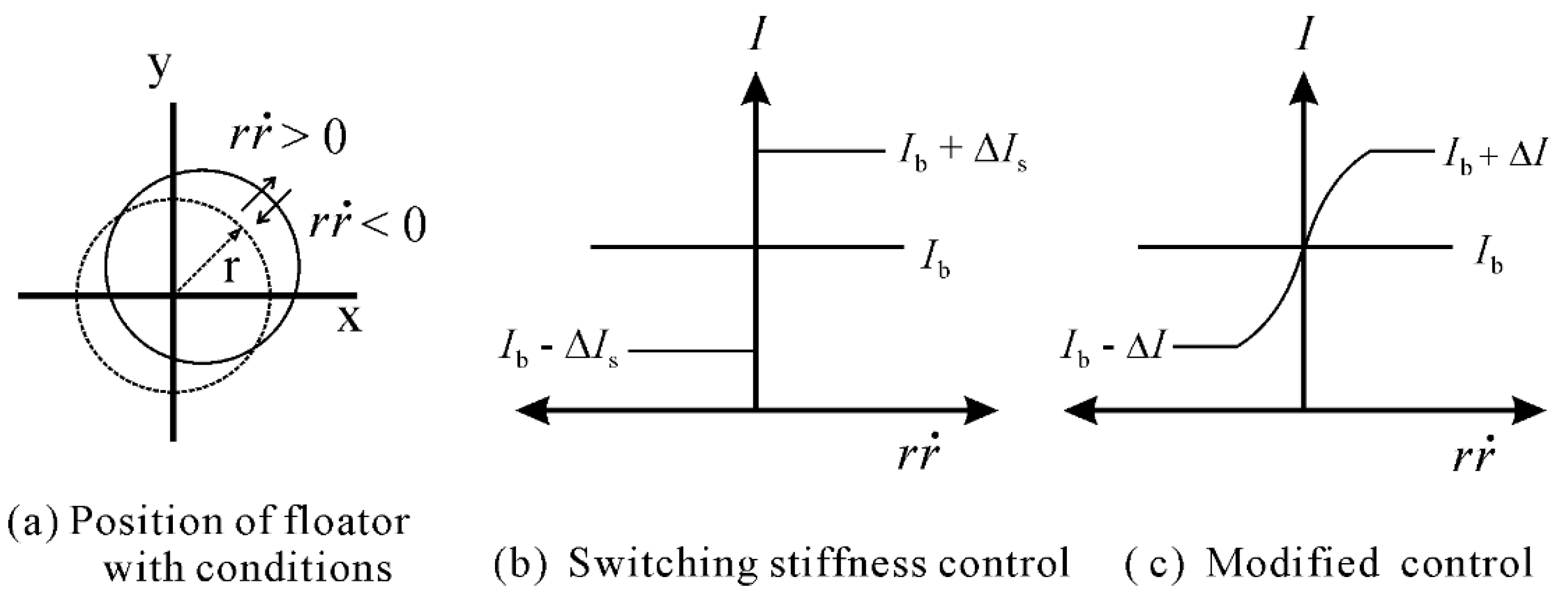
are displacement and velocity with respect to time, respectively. In brief, when the floator is moving out from its equilibrium position, the stiffness is increased, and when moving in to its equilibrium position, the stiffness is decreased. As the stiffness control is intended to apply in a 3-DoF system to reduce lateral vibration, the distance
r of the floator from the reference position is measured as
where
x and
y are the displacements in X- and Y-directions, respectively.
Figure 3a shows the conditions with position of floator. Therefore, the Equation (3) becomes
Another approach to varying the stiffness of a system is mentioned in Mizuno et al. [
3]. An inverse tangent function is introduced in the control current, as shown in Equation (6), to smooth the profile of ∆
I.
where ∆
I is the control current and
q is the parameter to change the steepness of the control current. When
q is increased, the shape of the control current becomes the same as that of the control current of the switching stiffness strategy. This control strategy is referred to as modified stiffness control. The current with respect to
is depicted in
Figure 3b,c for both control strategies [
4].
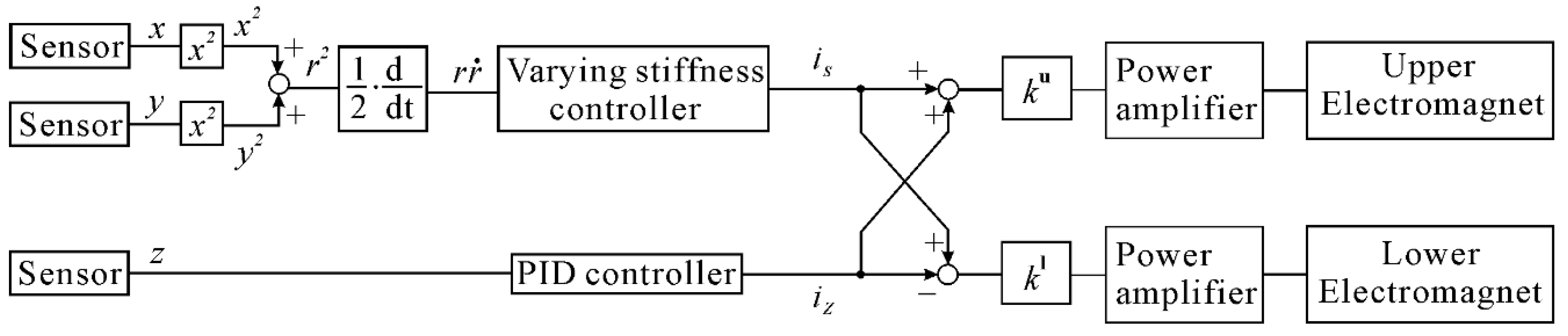
Modal control is applied to distribute the current between the upper and lower electromagnets.
Figure 4 shows the block diagram of modal control.
ku and
kl are the gains of upper and lower electromagnets, respectively, to balance the force in the Z-direction during stiffness control,
iz is the control current to levitate the floator, and
is is the control current to reduce lateral vibration. A filtered derivative is used for differentiation of the signal in the controller, which is realized by digital signal processor (DS1005) with a sampling frequency of 10 kHz. A low-pass filter with a cut-off frequency of 100 Hz is used, which is considered high enough compared to the frequency in the lateral directions. The time delay does not affect the stability in the lateral directions. This is considered to be below the maximum limit, as Ledezma-Ramirez et al. [
21] mentioned in their study that too much time delay could make the system unstable.
4. Parameter Identification
Though the number of turns of the coil of the upper and lower electromagnets is the same, the strengths of the permanent magnets are different. To balance the force during the change of current in varying stiffness control, the current-force coefficients of both electromagnets (EMs) are necessary to determine. Otherwise, vibration will be induced in the Z-direction. This can be realized by considering linear current-force and gap-force coefficient of the electromagnets based on the equation of motion in the Z-direction given by Equation (7). The first two terms come from the upper EM denoted by subscript
u, and the last two terms come from lower EM denoted by subscript
l.
where
m is mass of the ball,
kiu is the current-force coefficient of the upper EM (EM
u),
kzu is the gap-force coefficient of the EM
u and permanent magnet,
kil is the current-force coefficient of the lower EM (EM
l),
kzl is the gap-force coefficient of the EM
l and permanent magnet,
i is the control current, and
z is the displacement in Z-direction.
As the value of
kzu is larger than the
kzl, it is necessary to find out the current-force coefficients of the electromagnets to balance the force of EM
u and EM
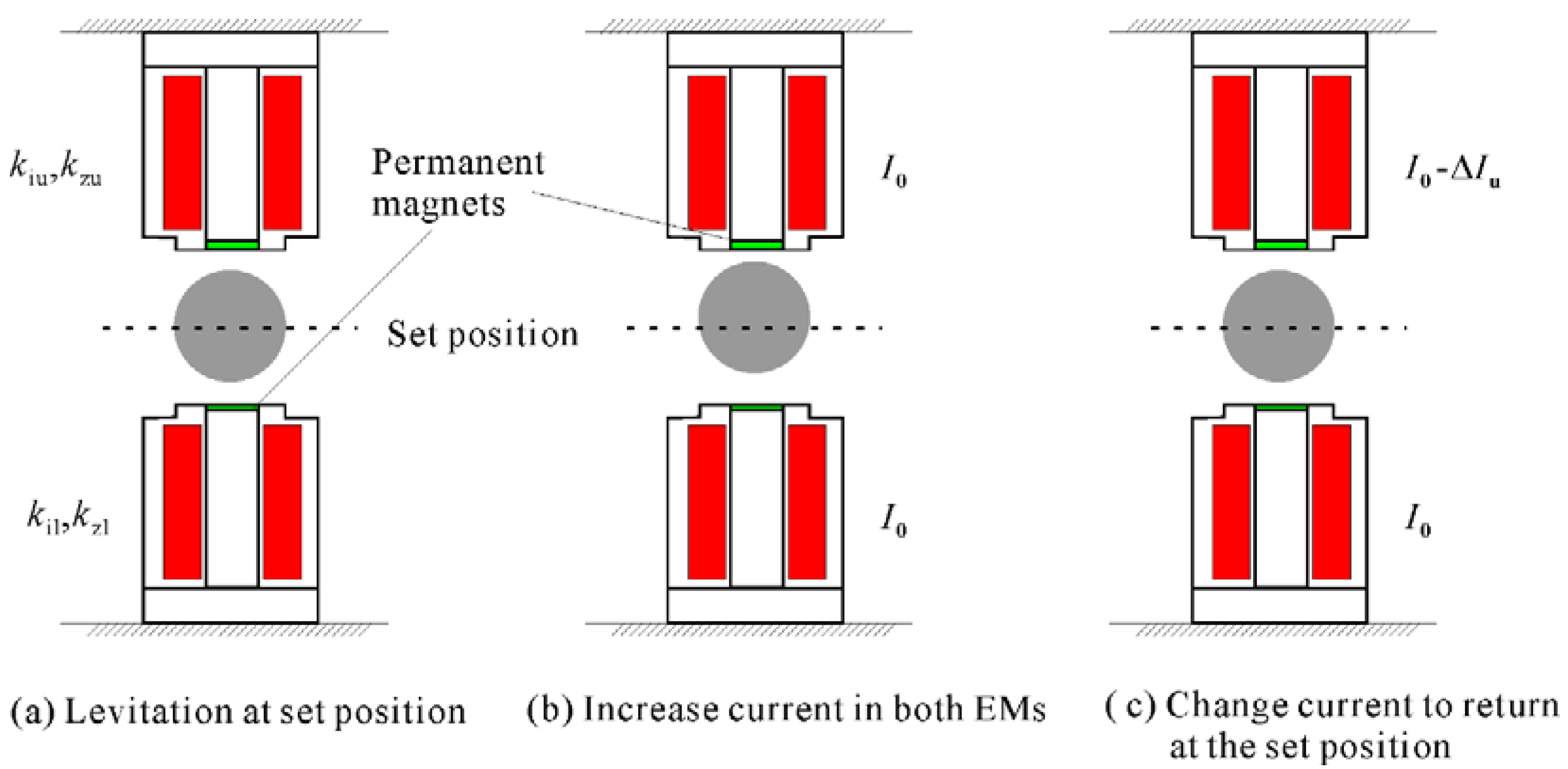
l during control. To find out the ratio of current-force coefficients, at first, the ball is levitated at the set position by PD control, as shown in
Figure 6a. The same amount of current
I0 is added to both EMs. The EM
u generates larger force than the EM
l, as a result, the ball moves upward as shown in
Figure 6b. Either current should be decreased in the EM
u or increased in the EM
l to return the ball to its set position. The procedure is depicted with decreasing the current in EM
u in
Figure 6.
The force is balanced at this set position, and the relation can be written as follows:
where
I0 is the current added to both EMs, ∆
Iu is the current reduced from EM
u to return the ball to the set position.
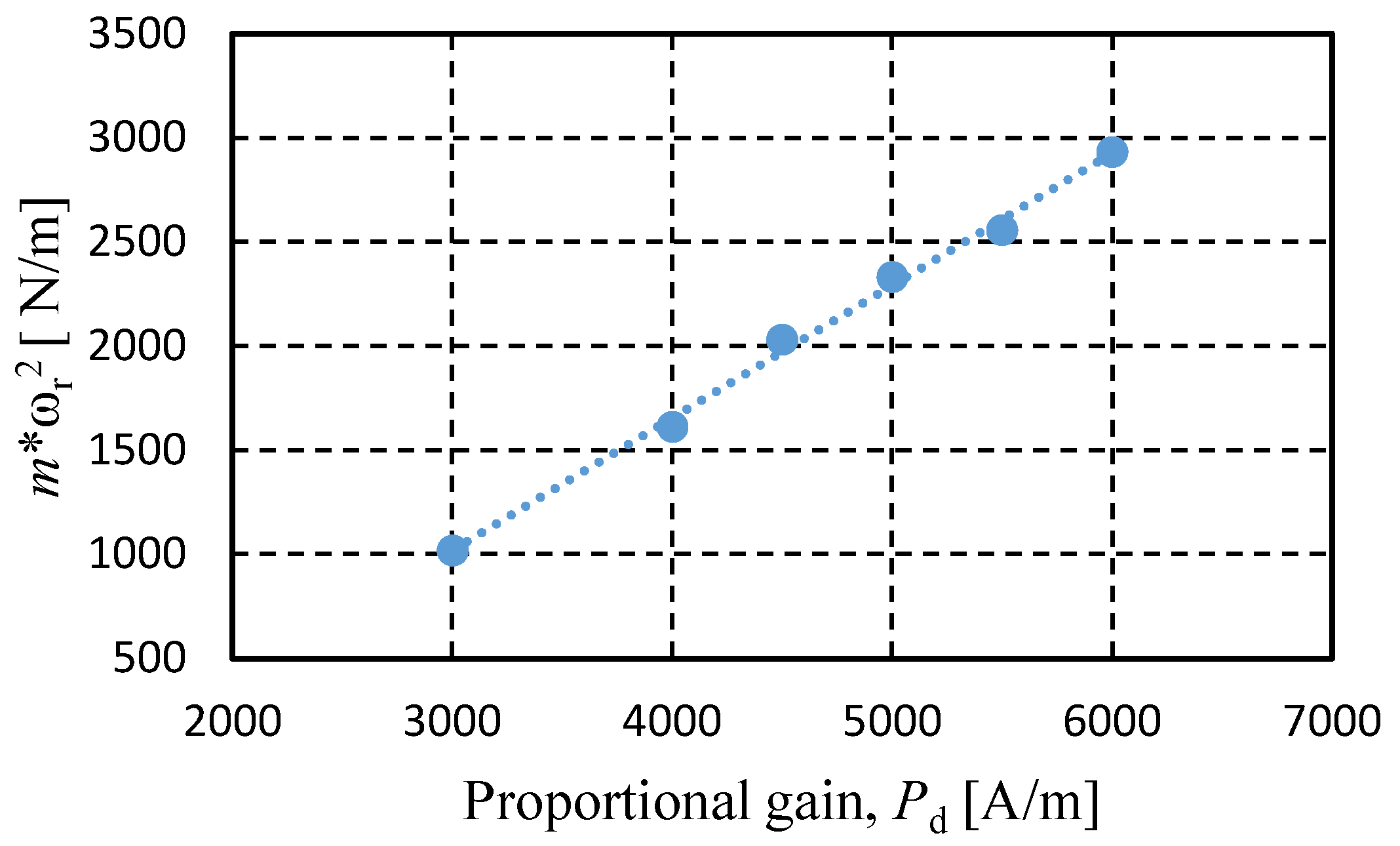
The total
ki of the system is measured by plotting
mω2 versus proportional gain,
Pd of the PD controller [
19].
where
m is the mass of the ball,
ωr is resonant angular frequency of the system in rad/s, and
ks =
kzu +
kzl is gap-force coefficient of the system. The slope of the curve represents the total current-force coefficient of the system. From
Figure 7, it is found that
From Equations (9) and (11) it is found that kiu = 0.405 N/A and kil = 0.23 N/A.
According to the findings, 0.23 N/A and 0.405 N/A are assigned as the gain in EM
u and EM
l, respectively, to balance the force as written in Equation (12).
where
ku and
kl are gains of upper and lower electromagnets, respectively, to balance force in Z-direction.
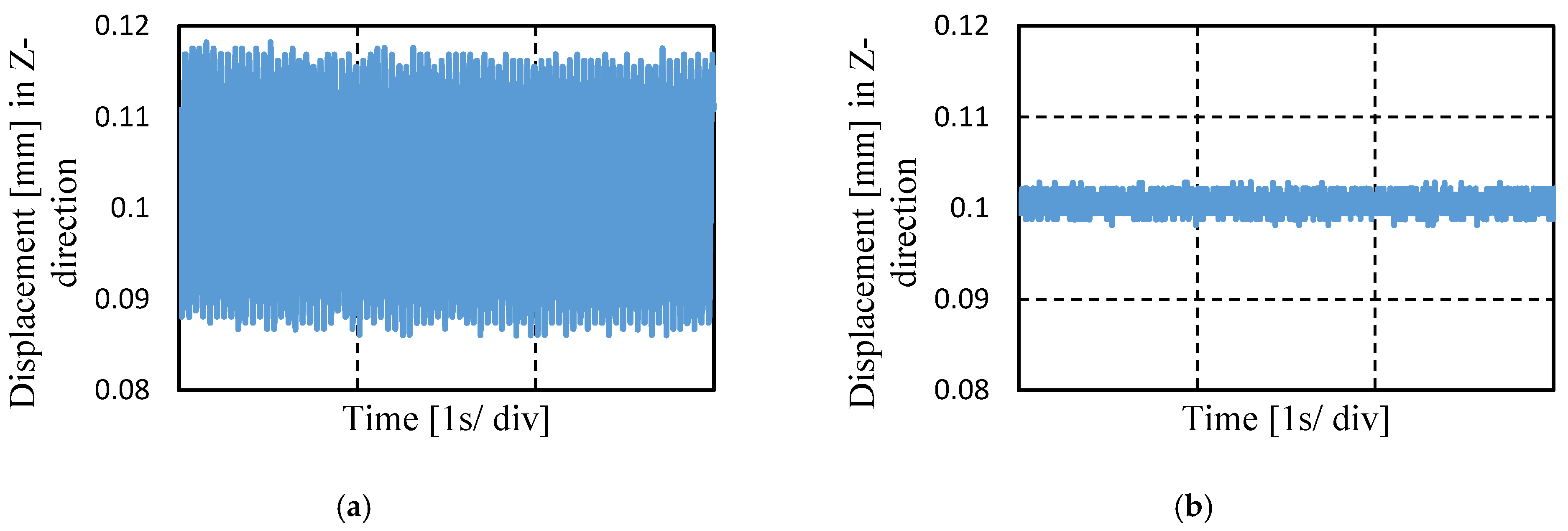
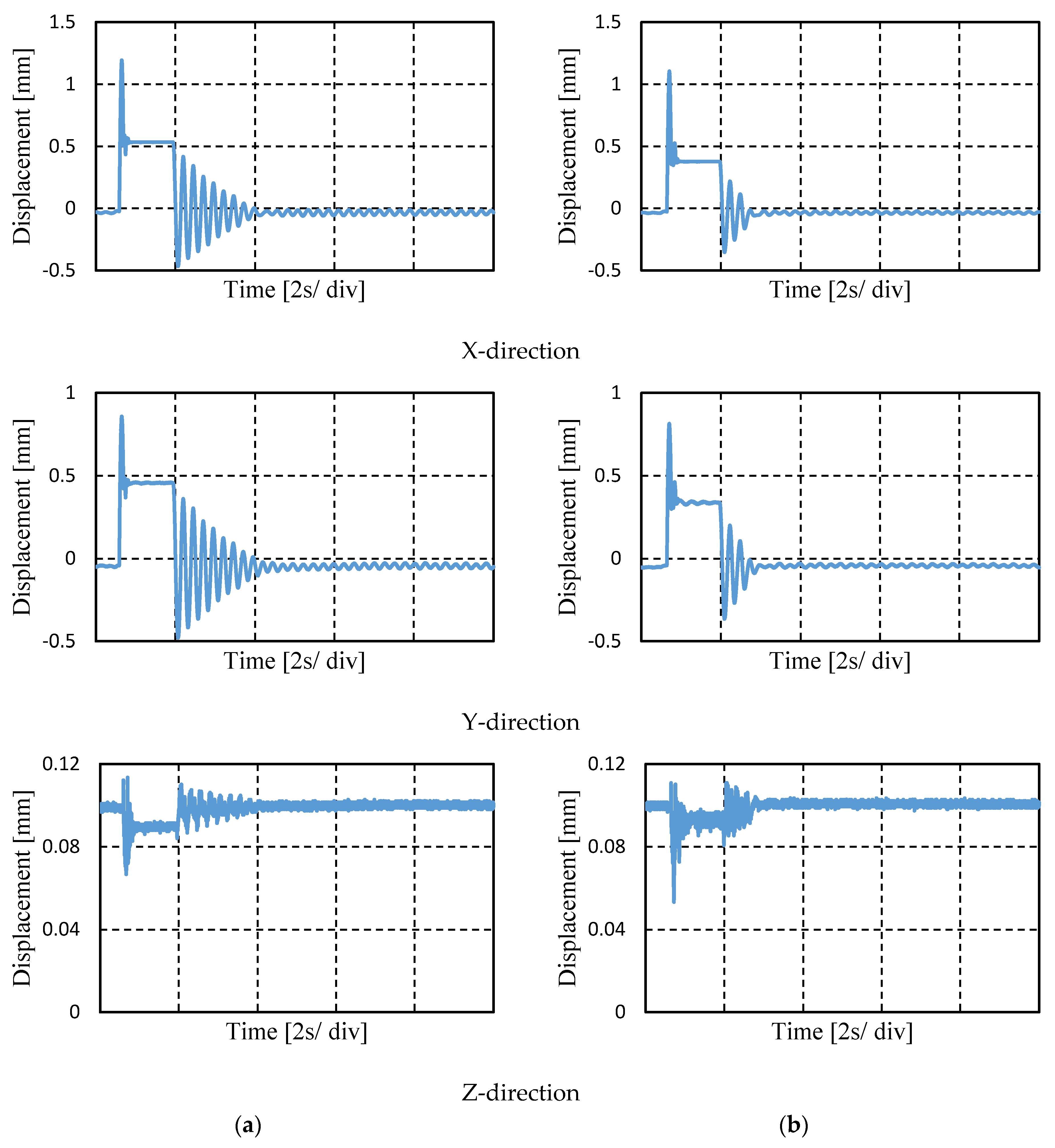
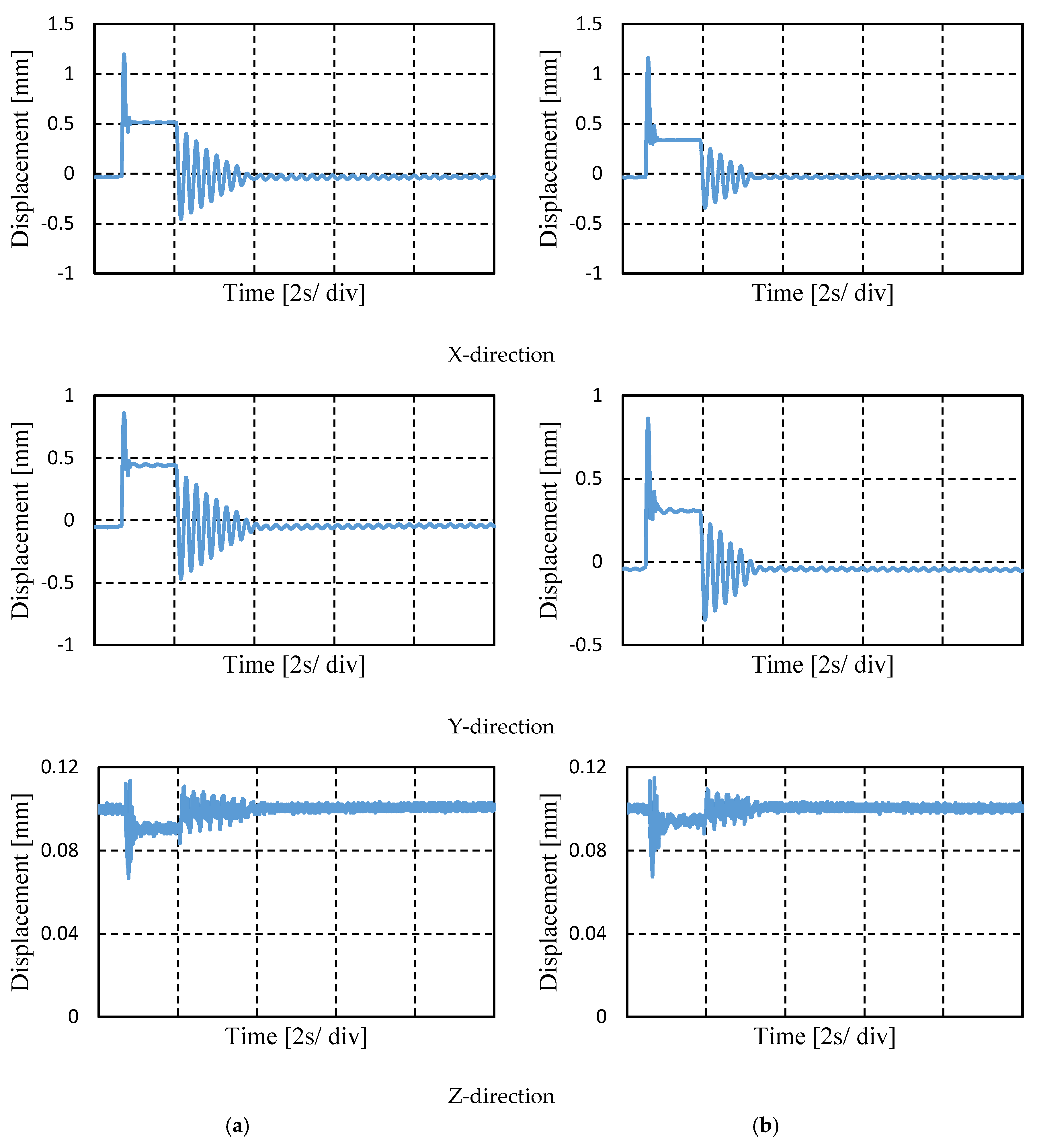
However, it has been found out that the permanent magnets get heated when control is applied. This may occur because of the large amplitude of control current that flows through the coils during control. As a result, the values are reduced to almost half of these values without affecting the balance of force.
Figure 8 shows that if balance of force is not attained, vibration occurs in the Z-direction. At first, PID control is applied, and the ball is levitated at set point 0.1 mm. Both of the EMs are assigned with the same gains, and switching stiffness control is applied with switching current, ∆
Is = 0.1 A. Due to the imbalance of force the ball moves in Z-direction with maximum amplitude of 0.03 mm, as shown in
Figure 8a. However, when the correct gain is assigned in both EMs, the amplitude of displacement reduces to 0.005 mm.