Static and Dynamic Studies of Electro-Active Polymer Actuators and Integration in a Demonstrator
Abstract
:1. Introduction
2. Materials and Methods
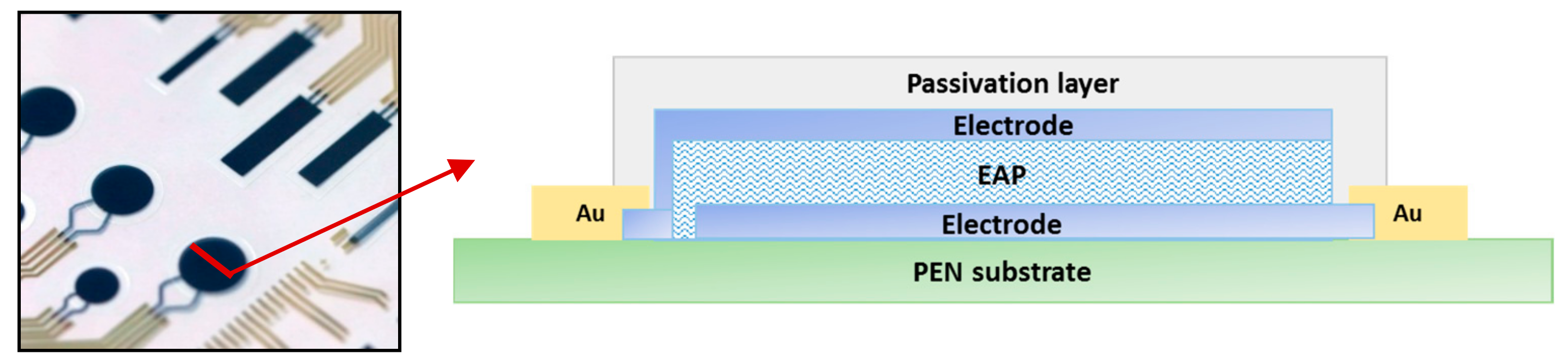
2.1. Electro-Active Polymer
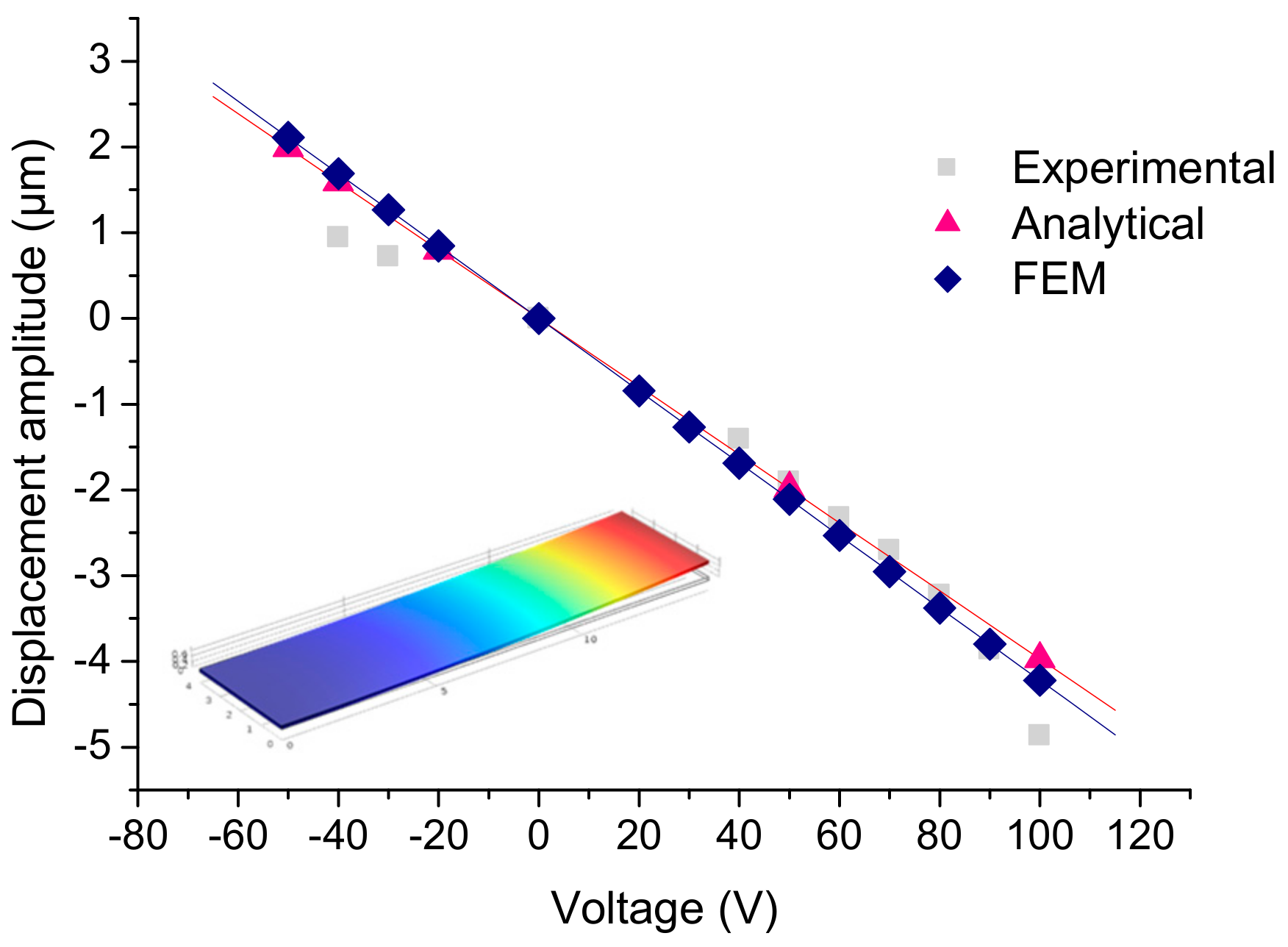
2.2. Calibration of FEM Model on Cantilever Geometry
3. Vibrotactile Circular Membrane Development
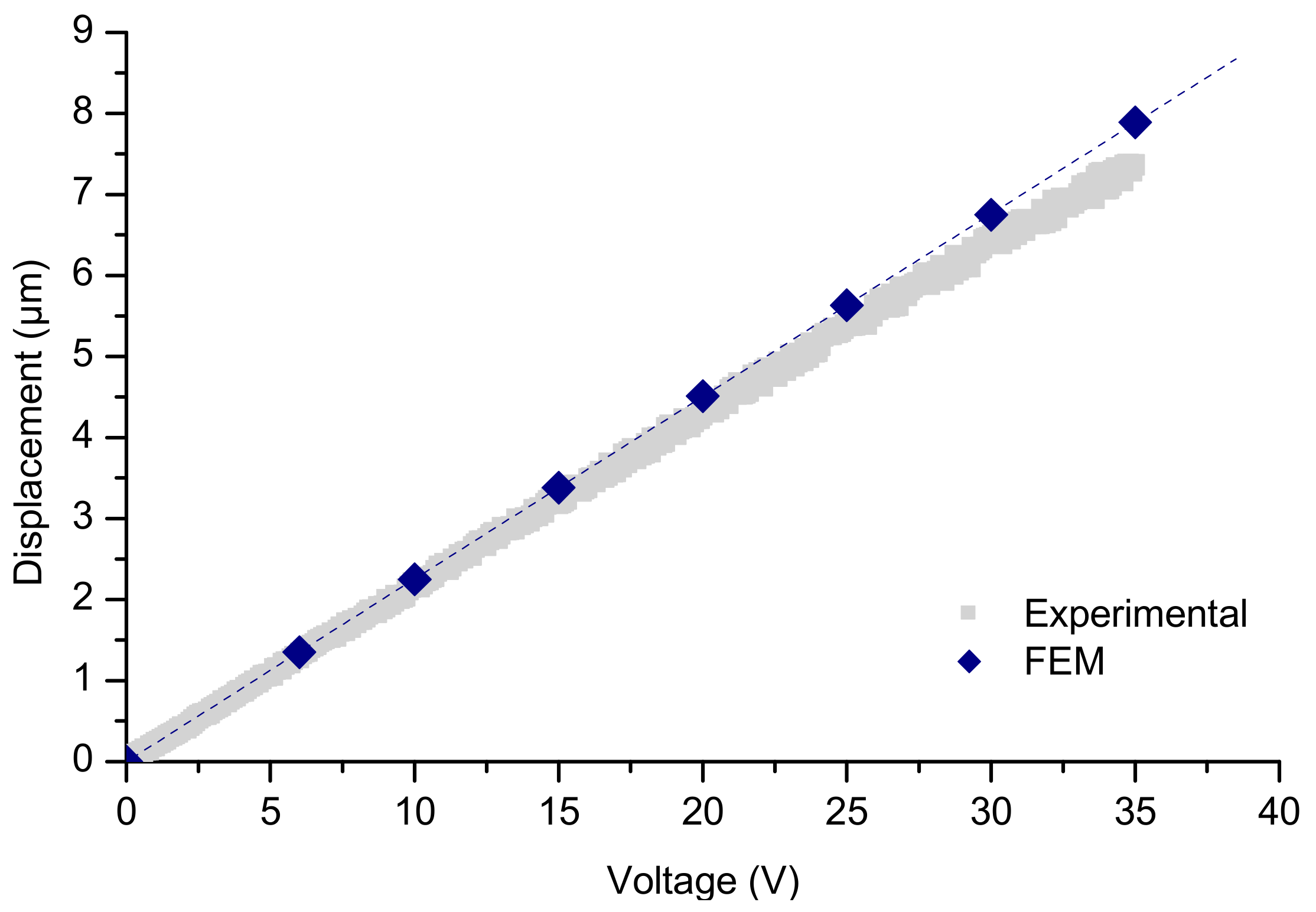
3.1. Static Study: Optimization of the Actuator
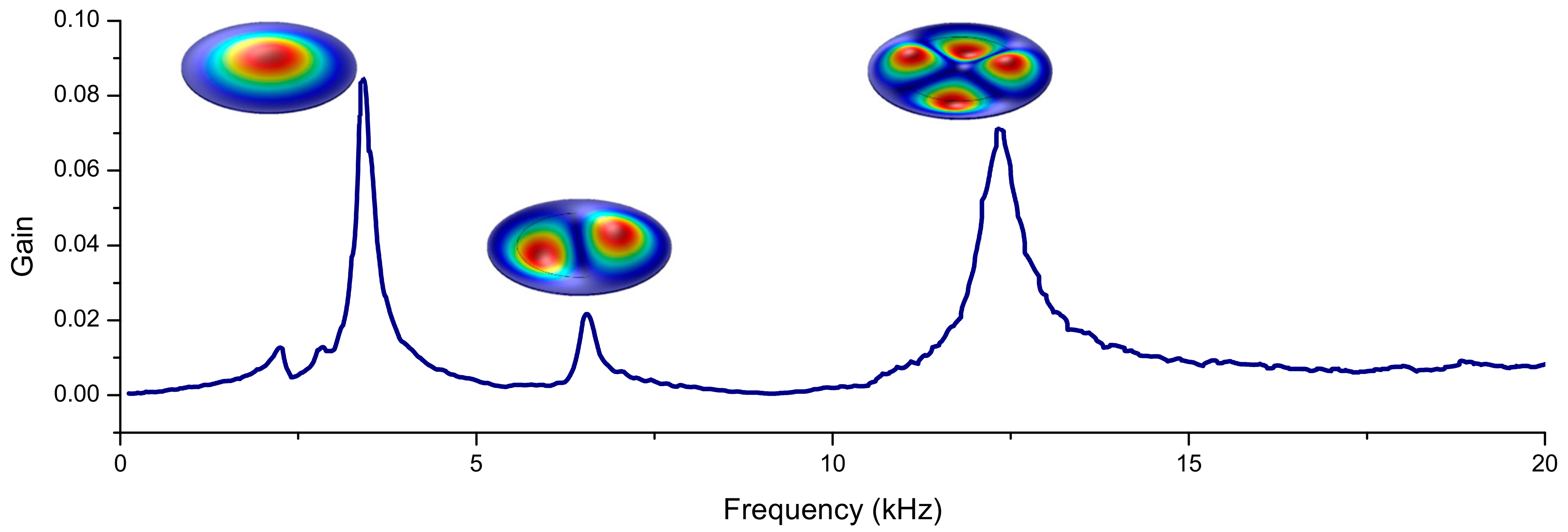
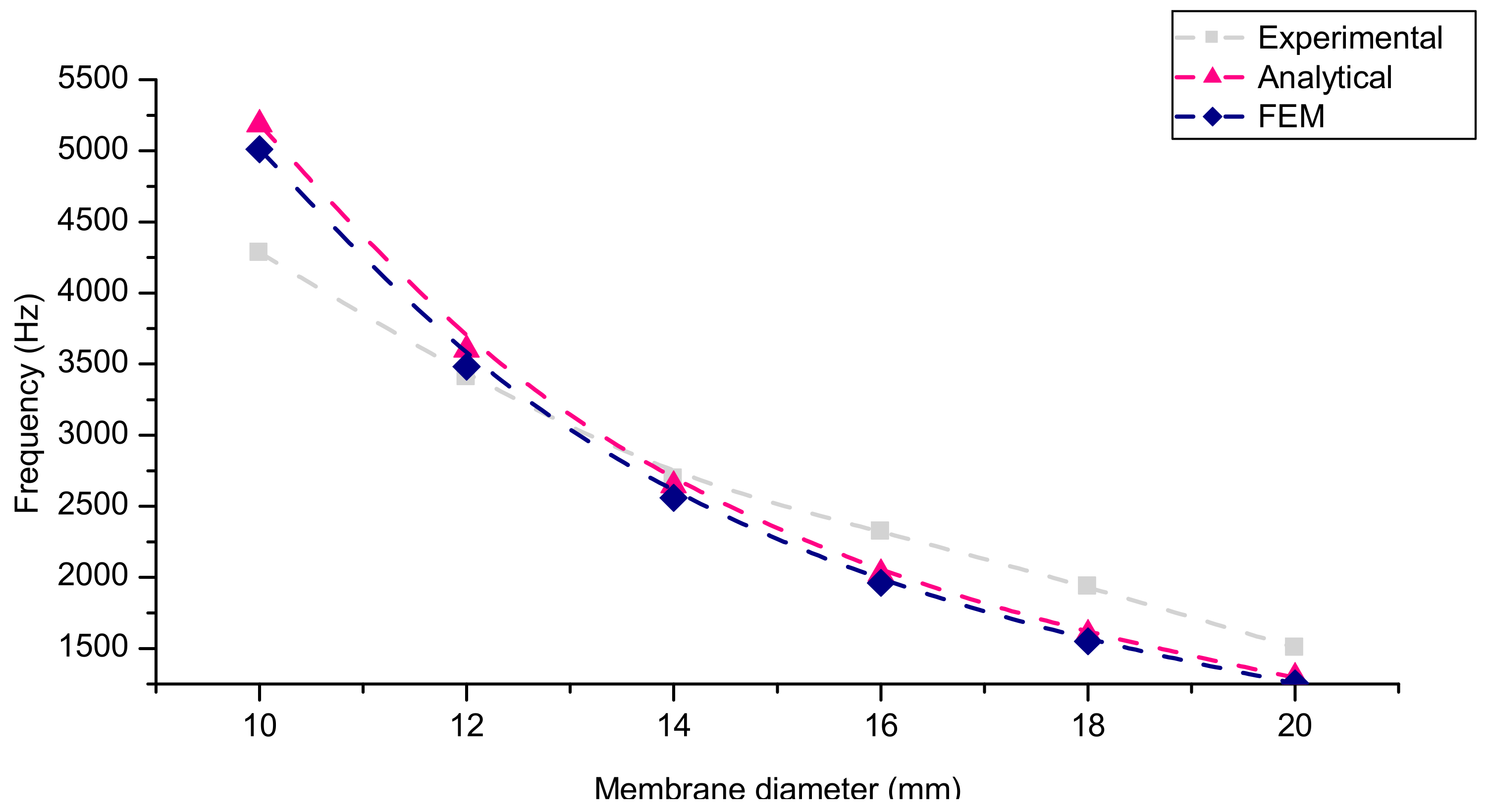
3.2. Dynamic Study: Development of Vibrotactile Buttons Based on Piezoelectric EAP Actuation
- E: Young’s modulus (Pa);
- ν: Poisson’s ratio;
- ρ: density (kg·m−3);
- t: thickness (m);
- r: membrane outer radius (m);
- λn: Eigenvalue at the n resonant mode (for the first mode, λ1 = 3.196).
3.3. Haptic Demonstrator
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Hayward, V.; Astley, O.R.; Cruz-Hernandez, M.; Grant, D.; Robles-De-La-Torre, G. Haptic interfaces and devices. Sens. Rev. 2004, 24, 16–29. [Google Scholar] [CrossRef]
- Zoller, I.; Lotz, P.; Kern, T.A. Novel thin electromagnetic system for creating pushbutton feedback in automotive applications. In Proceedings of the International Conference on Human Haptic Sensing and Touch Enabled Computer Applications, Tampere, Finland, 13–15 June 2012; pp. 637–645. [Google Scholar]
- Watanabe, T.; Fukui, S. Method for controlling tactile sensation of surface roughness using ultrasonic vibration. In Proceedings of the 1995 IEEE International Conference on Robotics and Automation, Nagoya, Japan, 21–27 May 1995; pp. 1134–1139. [Google Scholar]
- Elspass, W.J.; Kunz, A.M. Portable haptic interface with active functional design. Proc. SPIE 1999, 3668, 926–932. [Google Scholar]
- Siegel, E. Haptic Technology: Picking up Good Vibration; EE Times: San Francisco, CA, USA, 2011. [Google Scholar]
- Mastronardi, V.M.; Guido, F.; De Vittorio, M.; Petroni, S. Flexible force sensor based on c-axis oriented aluminum nitride. Procedia Eng. 2014, 87, 164–167. [Google Scholar] [CrossRef]
- Matysek, M.; Lotz, P.; Flittner, K.; Schlaak, H.F. Vibrotactile display for mobile applications based on dielectric elastomer stack actuators. Proc. SPIE 2010, 7642, 76420D. [Google Scholar]
- Lotz, P.; Matysek, M.; Schlaak, H.F. Fabrication and application of miniaturized dielectric elastomer stack actuators. IEEE/ASME Trans. Mechatron. 2011, 16, 58–66. [Google Scholar] [CrossRef]
- Ling, Q.D.; Liaw, D.J.; Zhu, C.; Chan, D.S.H.; Kang, E.T.; Neoh, K.G. Polymer electronic memories: Materials, devices and mechanisms. Prog. Polym. Sci. 2008, 33, 917–978. [Google Scholar] [CrossRef]
- Martins, P.; Lopes, C.; Lanceros-Mendez, S. Electroactive phases of poly(vinylidene fluoride): Determination, processing and applications. Prog. Polym. Sci. 2014, 39, 683–706. [Google Scholar] [CrossRef]
- Aliane, A.; Benwadih, M.; Bouthinon, B.; Coppard, R.; Domingues-Dos Santos, F.; Daami, A. Impact of crystallization on ferro-, piezo- and pyro-electric characteristics in thin film P(VDF–TrFE). Org. Electron. 2015, 25, 92–98. [Google Scholar] [CrossRef]
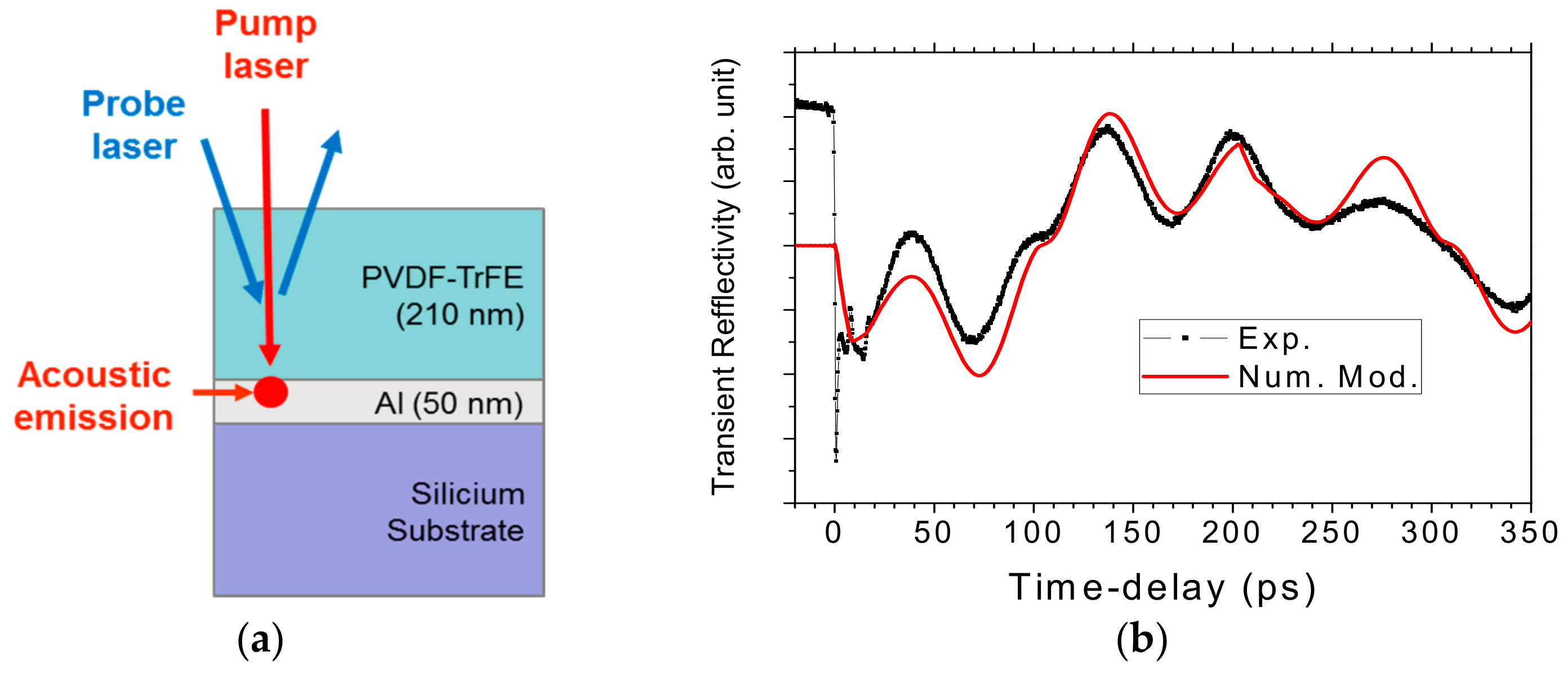
- Mante, P.A.; Robillard, J.F.; Devos, A. Complete thin film mechanical characterization using picosecond ultrasonics and nanostructured transducers: Experimental demonstration on SiO2. Appl. Phys. Lett. 2008, 93, 071909. [Google Scholar] [CrossRef]
- Devos, A.; Côte, R.; Caruyer, G.; Lefèvre, A. A different way of performing picosecond ultrasonic measurements in thin transparent films based on laser-wavelength effects. Appl. Phys. Lett. 2005, 86, 211903. [Google Scholar] [CrossRef]
- Devos, A.; Robillard, J.-F.; Côte, R.; Emery, P. High laser-wavelength sensitivity of the picosecond ultrasonic response in transparent thin films. Phys. Rev. B 2006, 74, 064114. [Google Scholar] [CrossRef]
- Thomsen, C.; Grahn, H.T.; Maris, H.J.; Tauc, J. Surface generation and detection of phonons by picosecond light pulses. Phys. Rev. B 1986, 34, 4129. [Google Scholar] [CrossRef]
- Callister, W.D., Jr. Materials Science and Engineering: An Introduction, 7th ed.; John Wiley & Sons, Inc.: New York, NY, USA, 2007. [Google Scholar]
- Defaÿ, E. Integration of Ferroelectric and Piezoelectric Thin Films: Concepts and Applications for Microsystems; Wiley: Hoboken, NJ, USA, 2011. [Google Scholar]
- Nguyen, M.D.; Nazeer, H.; Dekkers, M.; Blank, D.H.A.; Rijnders, G. Optimized electrode coverage of membrane actuators based on epitaxial PZT thin films. Smart Mater. Struct. 2013, 22, 085013. [Google Scholar] [CrossRef]
- Kelly, S.G. Fundamentals of Mechanical Vibrations; McGraw-Hill Education: New York, NY, USA, 1992. [Google Scholar]



| Propriety | Value |
|---|---|
| Elastic modulus | 3.6 GPa |
| Poisson’s ratio | 0.4 |
| Density | 1780 kg/m3 |
| Permittivity | 9.4 |
| Piezoelectric coefficient d31 | −3 pC/N |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Poncet, P.; Casset, F.; Latour, A.; Domingues Dos Santos, F.; Pawlak, S.; Gwoziecki, R.; Devos, A.; Emery, P.; Fanget, S. Static and Dynamic Studies of Electro-Active Polymer Actuators and Integration in a Demonstrator. Actuators 2017, 6, 18. https://doi.org/10.3390/act6020018
Poncet P, Casset F, Latour A, Domingues Dos Santos F, Pawlak S, Gwoziecki R, Devos A, Emery P, Fanget S. Static and Dynamic Studies of Electro-Active Polymer Actuators and Integration in a Demonstrator. Actuators. 2017; 6(2):18. https://doi.org/10.3390/act6020018
Chicago/Turabian StylePoncet, Pauline, Fabrice Casset, Antoine Latour, Fabrice Domingues Dos Santos, Sébastien Pawlak, Romain Gwoziecki, Arnaud Devos, Patrick Emery, and Stéphane Fanget. 2017. "Static and Dynamic Studies of Electro-Active Polymer Actuators and Integration in a Demonstrator" Actuators 6, no. 2: 18. https://doi.org/10.3390/act6020018
APA StylePoncet, P., Casset, F., Latour, A., Domingues Dos Santos, F., Pawlak, S., Gwoziecki, R., Devos, A., Emery, P., & Fanget, S. (2017). Static and Dynamic Studies of Electro-Active Polymer Actuators and Integration in a Demonstrator. Actuators, 6(2), 18. https://doi.org/10.3390/act6020018






