Design and Characterization of In-Plane Piezoelectric Microactuators
Abstract
1. Introduction
2. Materials and Methods
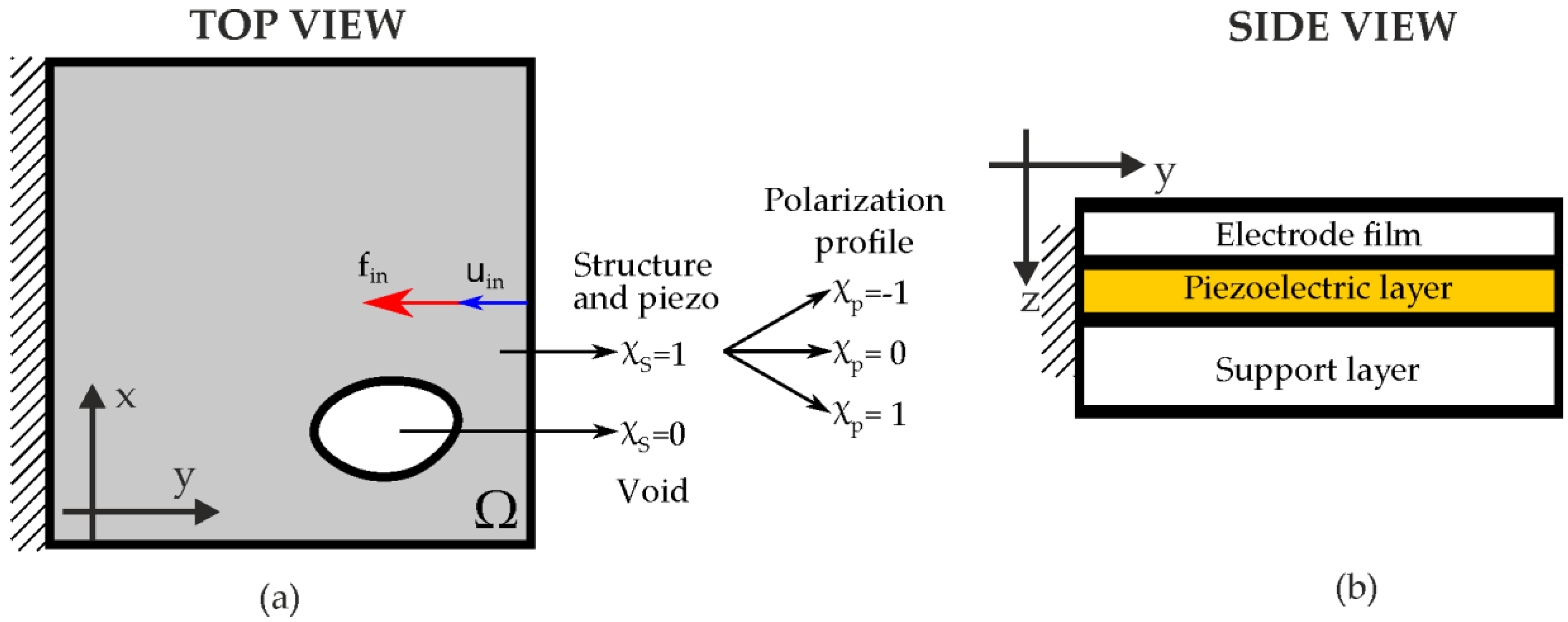
2.1. Optimal Design of the Actuators
2.1.1. Optimization Problem
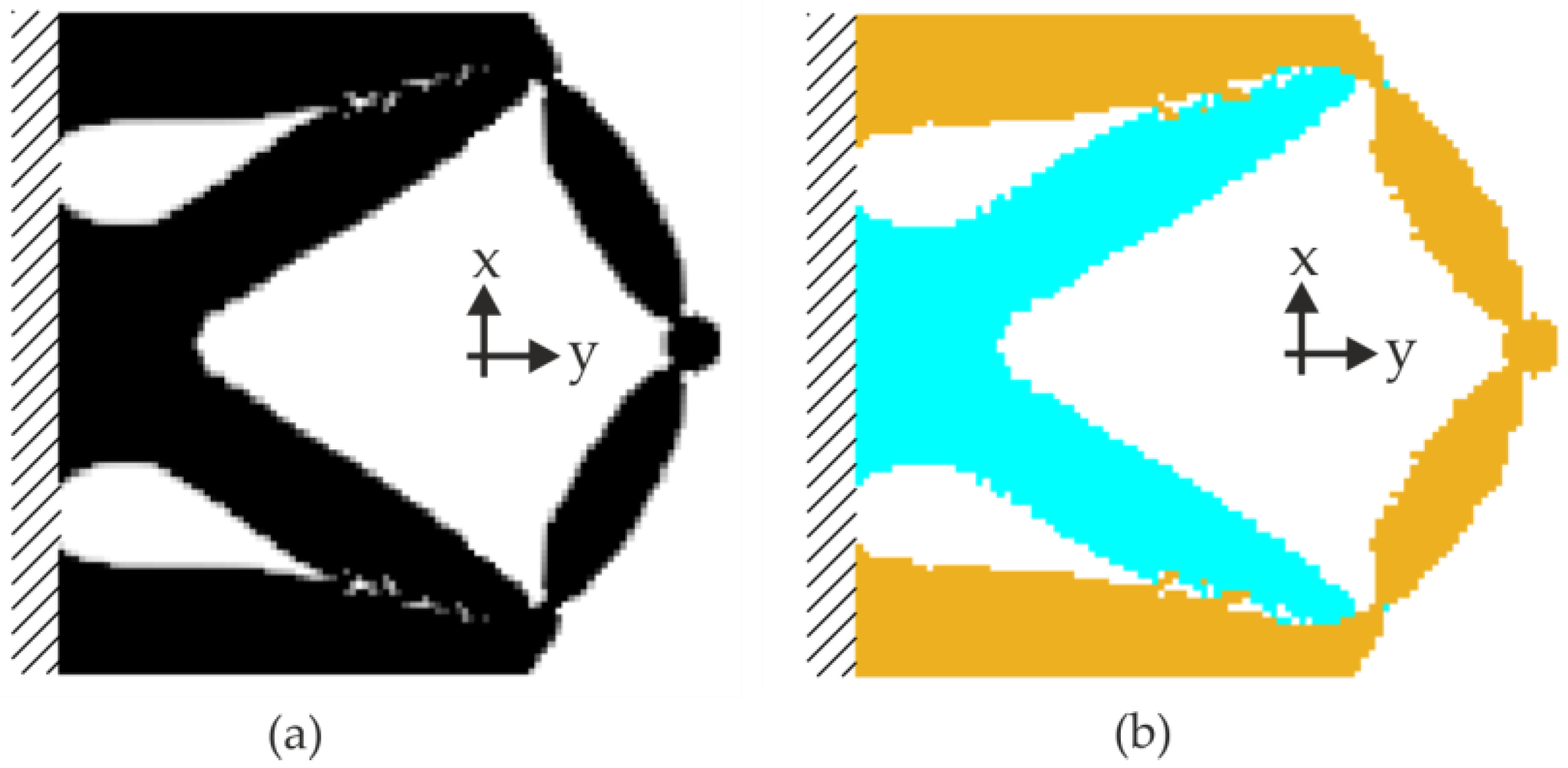
2.1.2. Numerical Examples
2.2. Final Design of the Actuators
2.3. Fabrication Process of the Actuators
3. Results and Discussion
3.1. Optical Measurements
3.2. Electrical Measurements
3.3. Analysis of the Displacement
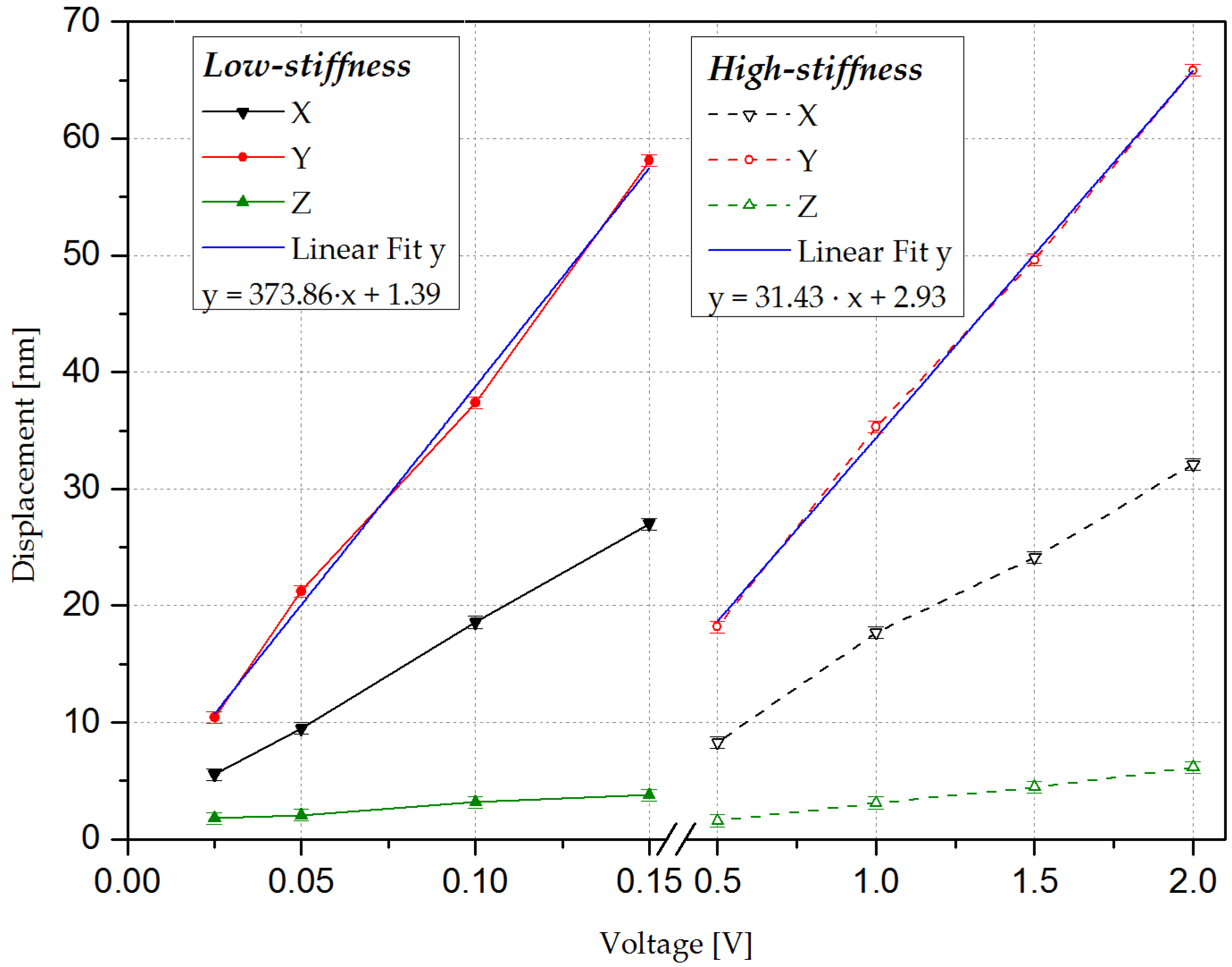
3.3.1. Analysis of the Displacement in Quasi-Static or DC Condition
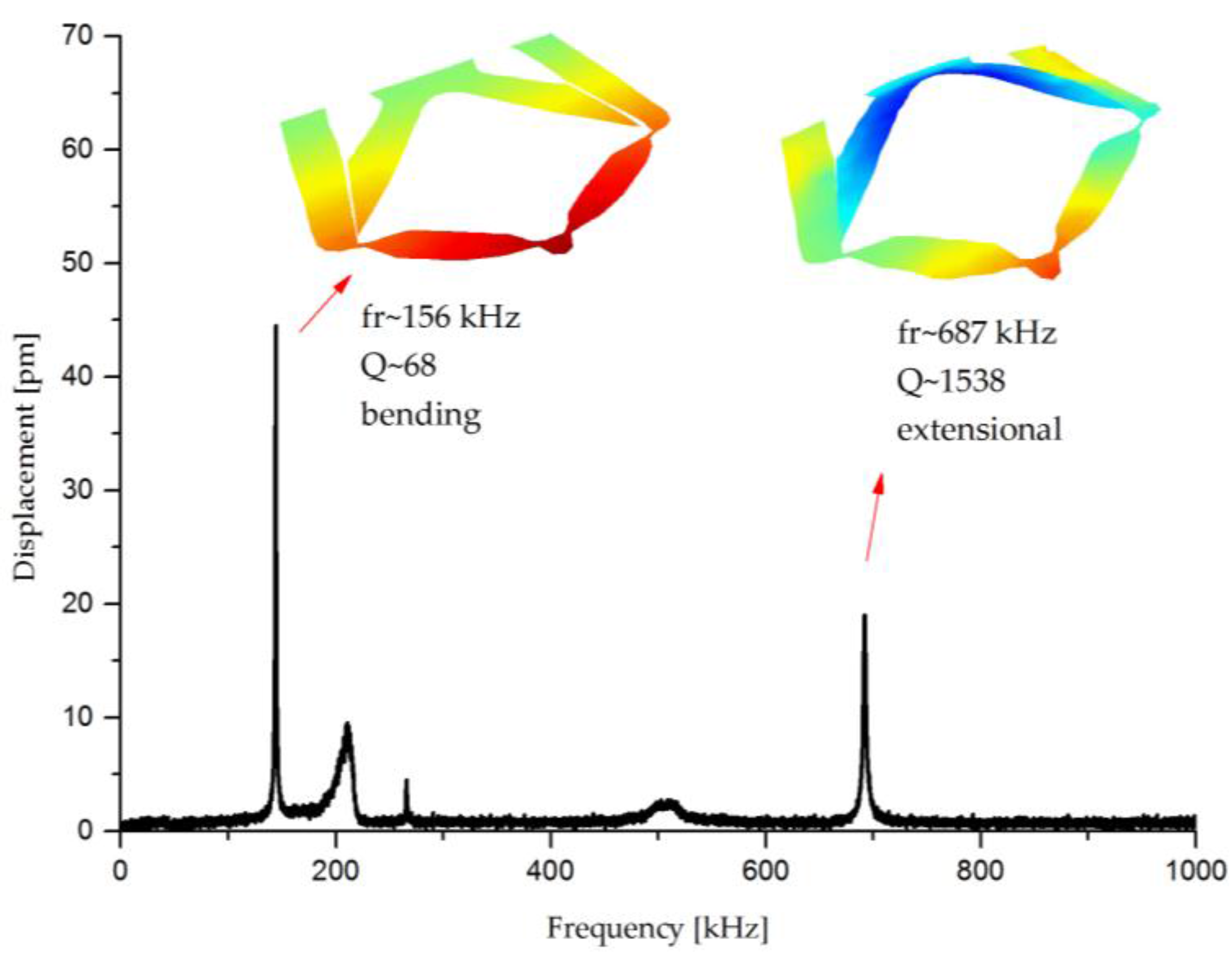
3.3.2. Analysis of the Displacement at the Resonant Frequency or AC
3.4. Analysis of the Elastic Constant
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Howe, R.T.; Muller, R.S.; Gabriel, K.J.; Trimmer, W.S.N. Silicon micromechanics: Sensors and actuators on a chip. IEEE Spectr. 1991, 27, 29–35. [Google Scholar] [CrossRef]
- Fujita, H. Microactuators and micromachines. Proc. IEEE. 1998, 86, 1721–1732. [Google Scholar] [CrossRef]
- Panchawagh, H.V.; Faheem, F.F.; Herrmann, C.F.; Serrell, D.B.; Finch, D.S.; Mahajan, R.L. Packaging of In-Plane Thermal Microactuators for BioMEMS Applications. In Proceedings of the ASME 2005 International Mechanical Engineering Congress and Exposition, Orlando, FL, USA, 5–11 November 2005; pp. 49–52. [Google Scholar]
- Eltagoury, Y.M.; Soliman, M.; Al-Otaibi, M.; Sabry, Y.M.; Sadek, M.; Khalil, D. In-plane comb-drive actuator with high frequency-displacement product for micro-optical bench applications. In Proceedings of the 2014 International Conference on Optical MEMS and Nanophotonics, Glasgow, UK, 17–21 August 2014; pp. 155–156. [Google Scholar]
- Grade, J.D.; Jerman, H.; Kenny, T.W. Design of Large Deflection Electrostatic Actuators. J. Microelectromec. Syst. 2003, 12, 335–343. [Google Scholar] [CrossRef]
- Ko, J.S.; Lee, M.L. Development and application of laterally driven electromagnetic microactuator. Appl. Phys. Lett. 2002, 81, 547–549. [Google Scholar] [CrossRef]
- Qui, J.; Lang, J.H.; Slocum, A.H.; Strümpler, R. A high-current electrothermal bistable MEMS relay. In Proceedings of the IEEE Sixteenth Annual International Conference on Micro Electro Mechanical Systems, Kyoto, Japan, 23–23 January 2003; pp. 64–67. [Google Scholar]
- Manzaneque, T.; Ruiz-Díez, V.; Hernando-García, J.; Ababneh, A.; Al-Omari, A.N.; Kucera, M.; Bittner, A.; Schmid, U.; Seidel, H.; Sánchez-Rojas, J.L. Piezoelectric in-plane microplate resonators based on contour and flexure-actuated modes. Microsyst. Technol. 2014, 20, 691–699. [Google Scholar] [CrossRef]
- Lee, F.Y.; Tang, T.L.; Fang, W. Development of a novel dual-axis large-displacement microstage using Lorentz force actuators and curved-beam springs. Procedia Eng. 2011, 25, 689–692. [Google Scholar] [CrossRef][Green Version]
- Lv, X.D.; Wei, W.W.; Mao, X.; Yang, J.L.; Yang, F.H. A linear low driving voltage mems actuator with large lateral stroke driven by Lorentz force. In Proceedings of the 2015 Transducers—2015 18th International Conference on Solid-State Sensors, Actuators and Microsystems (TRANSDUCERS), Anchorage, AK, USA, 21–25 June 2015; pp. 2117–2120. [Google Scholar]
- Leang, K.K.; Fleming, A.J. High-speed serial-kinematic SPM scanner: Design and drive considerations. Asian J. Control. 2009, 11, 144–153. [Google Scholar] [CrossRef]
- Aktakka, E.E.; Peterson, R.L.; Najafi, K. A 3-DOF piezoelectric micro vibratory stage based on bulk-PZT/silicon crab-leg suspensions. In Proceedings of the 2013 IEEE 26th International Conference on Micro Electro Mechanical Systems (MEMS), Taipei, Taiwan, 20–24 January 2013; pp. 576–579. [Google Scholar]
- Conway, N.J.; Kim, S.G.G. Large-strain, piezoelectric, in-plane micro-actuator. In Proceedings of the 17th IEEE International Conference on Micro Electro Mechanical Systems, Maastricht MEMS 2004 Technical Digest, Maastricht, The Netherlands, 25–29 January 2004. [Google Scholar]
- Oldham, K.R.; Pulskamp, J.S.; Polcawich, R.G.; Dubey, M. Thin-film PZT lateral actuators with extended stroke. J. Microelectromech. Syst. 2008, 17, 890–899. [Google Scholar] [CrossRef]
- Yoshida, S.; Wang, N.; Kumano, M.; Kawai, Y.; Tanaka, S.; Esashi, M. Fabrication and characterization of laterally-driven piezoelectric bimorph MEMS actuator with sol–gel-based high-aspect-ratio PZT structure. J. Micromech. Microeng. 2013, 23, 065014. [Google Scholar] [CrossRef]
- Luo, Z.; Tong, L.; Luo, J.; Wei, P.; Wang, M.Y. Design of piezoelectric actuators using a multiphase level set method of piecewise constants. J. Comput. Phys. 2009, 228, 2643–2659. [Google Scholar] [CrossRef]
- Chen, S.; Gonella, S.; Chen, W.; Liu, W.K. A level set approach for optimal design of smart energy harvesters. Comput. Methods Appl. Mech. Eng. 2010, 199, 2532–2543. [Google Scholar] [CrossRef]
- Grossard, M.; Rotinat-Libersa, C.; Chaillet, N.; Boukallel, M. Mechanical and control-oriented design of a monolithic piezoelectric microgripper using a new topological optimization method. IEEE/ASME Trans. Mechatron. 2009, 14, 32–45. [Google Scholar] [CrossRef]
- Khadraoui, S.; Rakotondrabe, M.; Lutz, P. Optimal design of piezoelectric cantilevered actuators with guaranteed performances by using interval techniques. IEEE/ASME Trans. Mechatron. 2014, 19, 1660–1668. [Google Scholar]
- Ruiz, D.; Donoso, A.; Bellido, J.C.; Kucera, M.; Schmid, U.; Sánchez-Rojas, J.L. Design of piezoelectric microtransducers based on the topology optimization method. Microsyst. Technol. 2016, 22, 1733–1740. [Google Scholar] [CrossRef]
- Bendsøe, M.P.; Sigmund, O. Topology Optimization; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Kögl, M.; Silva, E.C.N. Topology optimization of smart structures: Design of piezoelectric plate and shell actuators. Smart Mater. Struct. 2005, 14, 387–399. [Google Scholar] [CrossRef]
- Carbonari, R.C.; Silva, E.C.N.; Nishiwaki, S. Optimum placement of piezoelectric material in piezoactuator design. Smart Mater. Struct. 2007, 16, 207–220. [Google Scholar] [CrossRef]
- Luo, Z.; Gao, W.; Song, C. Design of Multi-phase Piezoelectric Actuators. J. Intell. Mater. Syst. Struct. 2010, 21, 1851–1865. [Google Scholar] [CrossRef]
- Molter, A.; Fonseca, J.S.O.; Fernandez, L.D.S. Simultaneous topology optimization of structure and piezoelectric actuators distribution. Appl. Math. Model. 2016, 40, 5576–5588. [Google Scholar] [CrossRef]
- Kang, Z.; Wang, R.; Tong, L. Combined optimization of bi-material structural layout and voltage distribution for in-plane piezoelectric actuation. Comput. Methods Appl. Mech. Eng. 2011, 200, 1467–1478. [Google Scholar] [CrossRef]
- Kang, Z.; Wang, X.; Luo, Z. Topology Optimization for Static Shape Control of Piezoelectric Plates with Penalization on Intermediate Actuation Voltage. J. Mech. Des. 2012, 134, 051006. [Google Scholar] [CrossRef]
- Cook, R.D.; Malkus, D.; Plesha, M. Concepts and Applications of Finite Element Analysis, 3rd. ed.; Wiley: New York, NY, USA, 1989. [Google Scholar]
- Ruiz, D.; Bellido, J.C.; Donoso, A.; Sánchez-Rojas, J.L. Design of in-plane piezoelectric sensors for static response by simultaneously optimizing the host structure and the electrode profile. Struct. Multidiscip. Optim. 2013, 48, 1023–1026. [Google Scholar] [CrossRef]
- Gibbs, G.P.; Fuller, C.R. Excitation of thin beams using asymmetric piezoelectric actuators. J. Acoust. Soc. Am. 1992, 92, 3221–3227. [Google Scholar] [CrossRef]
- Moheimani, S.O.R.; Fleming, A.J. Piezoelectric Transducers for Vibration Control and Damping; Springer-Verlag: London, UK, 2006. [Google Scholar]
- Coventor Ware. Available online: http://www.coventor.com/mems-solutions/products/coventorware/ (accessed on 3 June 2017).
- Kucera, M.; Hofbauer, F.; Wistrela, E.; Manzaneque, T.; Ruiz-Díez, V.; Sánchez-Rojas, J.L.; Bittner, A.; Schmid, U. Lock-in amplifier powered analogue Q-control circuit for self-actuated self-sensing piezoelectric MEMS resonators. Microsyst. Technol. 2014, 20, 615–625. [Google Scholar] [CrossRef]
- Kucera, M.; Wistrela, E.; Pfusterschmied, G.; Ruiz-Díez, V.; Manzaneque, T.; Hernando-García, J.; Sánchez-Rojas, J.L.; Jachimowicz, A.; Schalko, J.; Bittner, A.; Schmid, U. Design-dependent performance of self-actuated and self-sensing piezoelectric-AlN cantilevers in liquid media oscillating in the fundamental in-plane bending mode. Sens. Actuators B Chem. 2014, 200, 235–244. [Google Scholar] [CrossRef]
- Segovia-Fernandez, J.; Cremonesi, M.; Cassella, C.; Frangi, A.; Piazza, G. Experimental study on the impact of anchor losses on the quality factor of contour mode AlN resonators. In Proceedings of the 2013 Transducers & Eurosensors XXVII: The 17th International Conference on Solid-State Sensors, Actuators and Microsystems (TRANSDUCERS & EUROSENSORS XXVII), Barcelona, Spain, 16–20 June 2013; pp. 2473–2476. [Google Scholar]
- Castille, C.; Dufour, I.; Lucat, C. Longitudinal vibration mode of piezoelectric thick-film cantilever-based sensors in liquid media. Appl. Phys. Lett. 2010, 96, 154102. [Google Scholar] [CrossRef]
- Manzaneque, T.; Ruiz, V.; Hernando-García, J.; Ababneh, A.; Seidel, H.; Sánchez-Rojas, J.L. Characterization and simulation of the first extensional mode of rectangular micro-plates in liquid media. Appl. Phys. Lett. 2012, 101, 151904. [Google Scholar] [CrossRef]
- Ruiz-Díez, V.; Hernando-García, J.; Manzaneque, T.; Kucera, M.; Schmid, U.; Sánchez-Rojas, J.L. Viscous and acoustic losses in length-extensional microplate resonators in liquid media. Appl. Phys. Lett. 2015, 106, 083510. [Google Scholar] [CrossRef]
- Arnau, A.; Sogorb, T.; Jimenez, Y. A continuous motional series resonant frequency monitoring circuit and a new method of determining Butterworth-Van Dyke parameters of a quartz crystal microbalance in fluid media. Rev. Sci. Instrum. 2000, 71, 2563–2571. [Google Scholar] [CrossRef]
- Gatti, P.L.; Ferrari, V. Applied Structural and Mechanical Vibrations. CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Ho, G.K.; Abdolvand, R.; Sivapurapu, A.; Humad, S.A.H.S.; Ayazi, F.A.A.F. Piezoelectric-on-Silicon Lateral Bulk Acoustic Wave Micromechanical Resonators. J. Microelectromec. Syst. 2008, 17, 512–520. [Google Scholar] [CrossRef]




| Actuator | Simulations | Displacement y-axis (nm) |
|---|---|---|
| Low stiffness | Optimal | 27.28 |
| Final | 16.85 | |
| High stiffness | Optimal | 13.23 |
| Final | 11.22 |
| Actuator | Displacement x-axis (nm) | Displacement y-axis (nm) | Displacement z-axis (nm) |
|---|---|---|---|
| Low stiffness | 5.09 × 10−3 | 16.85 | 9.12 |
| High stiffness | 3.36 × 10−3 | 11.22 | 18.57 |
| Actuator | Vibration Mode | fr (kHz) | Q | C0 (pF) | Rs (kΩ) | Ls (H) | Cs (fF) |
|---|---|---|---|---|---|---|---|
| Low-stiffness | Bending | 156 | 68 | 95 | 2340.0 | 163 | 6.37 |
| Extensional | 687 | 1539 | 135 | 51.0 | 18.2 | 2.95 | |
| High-stiffness | Bending | 143 | 139 | 140 | 232.0 | 36.0 | 34.30 |
| Extensional | 925 | 154 | 145 | 110.0 | 2.9 | 10.10 |
| Actuator | Simulations | Optical Measurements | |
|---|---|---|---|
| Optimal (nm) | Final (nm) | Fabricated Device (nm) | |
| Low-stiffness | 27.28 | 16.85 | 12.04 |
| High-stiffness | 13.23 | 11.22 | 6.40 |
| Actuator | Vibrational Mode | Displacement/V (nm/V) | (N/V) | (N/m) | / (m/V) |
|---|---|---|---|---|---|
| Low stiffness | Extensional | 373.86 | 1.22 × 10−5 | 5.01 × 104 | 2.43 × 10−10 |
| High stiffness | Extensional | 31.43 | 4.97 × 10−5 | 2.45 × 105 | 2.02 × 10−10 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Toledo, J.; Ruiz-Díez, V.; Diaz-Molina, A.; Ruiz, D.; Donoso, A.; Bellido, J.C.; Wistrela, E.; Kucera, M.; Schmid, U.; Hernando-García, J.; et al. Design and Characterization of In-Plane Piezoelectric Microactuators. Actuators 2017, 6, 19. https://doi.org/10.3390/act6020019
Toledo J, Ruiz-Díez V, Diaz-Molina A, Ruiz D, Donoso A, Bellido JC, Wistrela E, Kucera M, Schmid U, Hernando-García J, et al. Design and Characterization of In-Plane Piezoelectric Microactuators. Actuators. 2017; 6(2):19. https://doi.org/10.3390/act6020019
Chicago/Turabian StyleToledo, Javier, Victor Ruiz-Díez, Alex Diaz-Molina, David Ruiz, Alberto Donoso, José Carlos Bellido, Elisabeth Wistrela, Martin Kucera, Ulrich Schmid, Jorge Hernando-García, and et al. 2017. "Design and Characterization of In-Plane Piezoelectric Microactuators" Actuators 6, no. 2: 19. https://doi.org/10.3390/act6020019
APA StyleToledo, J., Ruiz-Díez, V., Diaz-Molina, A., Ruiz, D., Donoso, A., Bellido, J. C., Wistrela, E., Kucera, M., Schmid, U., Hernando-García, J., & Sánchez-Rojas, J. L. (2017). Design and Characterization of In-Plane Piezoelectric Microactuators. Actuators, 6(2), 19. https://doi.org/10.3390/act6020019








