A Two-Phase Switching Adaptive Sliding Mode Control Achieving Smooth Start-Up and Precise Tracking for TBM Hydraulic Cylinders

Abstract

Tunnel boring machine (TBM) hydraulic cylinders operate under pronounced start–stop shocks and load uncertainties, making it difficult to simultaneously achieve smooth start-up and high-precision tracking. This paper proposes a two-phase switching adaptive sliding mode control (ASMC) strategy for TBM hydraulic actuation. Phase I targets a soft start by introducing smooth gating and a ramped start-up mechanism into the sliding surface and equivalent control, thereby suppressing pressure spikes and displacement overshoot induced by oil compressibility and load transients. Phase II targets precise tracking, combining adaptive laws with a forgetting factor design to maintain robustness while reducing chattering and steady-state error. We construct a state-space model that incorporates oil compressibility, internal/external leakage, and pump/valve dynamics, and provide a Lyapunov-based stability analysis proving bounded stability and error convergence under external disturbances. Comparative simulations under representative TBM conditions show that, relative to conventional PID Controller and single ASMC Controller, the proposed method markedly reduces start-up pressure/velocity peaks, overshoot, and settling time, while preserving tracking accuracy and robustness over wide load variations. The results indicate that the strategy can achieve the unity of smooth start and high-precision trajectory of TBM hydraulic cylinder without additional sensing configuration, offering a practical path for high-performance control of TBM hydraulic actuators in complex operating environments.

1. Introduction

Hard-rock tunnels play a pivotal role in energy, transportation, and major infrastructure, making efficient and safe excavation essential [1,2]. As construction targets extend to more complex geology and special operating conditions, the engineering community has explored and adopted novel cutterheads and excavation configurations to enhance excavation performance [3]. One such practice is excavation with a free-section cutterhead whose axis is parallel to the cross section; a hydraulic motor drives the cutterhead to rotate while thrust cylinders press against the rock to realize efficient rotary cutting. Under this operating condition, the rock tends to spall periodically under the cutting action, leading to pronounced cyclic fluctuations in the load borne by the thrust cylinders [4,5]. These fluctuations introduce uncertain disturbances that significantly weaken the actuator’s tracking accuracy and operational stability. The resulting control imprecision and instability will compromise construction quality and safety, calling for optimization beyond conventional strategies and the development of control algorithms tailored to such conditions [6].

For precise and stable control of hydraulic cylinders under deterministic or regularly varying loads, extensive research has focused on nonlinear modeling and disturbance compensation. Sliding model control (SMC) has increasingly become a mainstream approach. Sun et al. [7] proposed a cross-coupled SMC with a coupling surface combined with a hyperbolic-tangent function for dual-cylinder gate actuators, improving synchronization accuracy while alleviating chattering. Zhao et al. [8] addressed force control of an aerospace electro-hydraulic load simulator by introducing an improved fast variable-power reaching law within terminal SMC and combining it with a nonsingular fast terminal SMC structure, achieving finite-time convergence with reduced chattering. Yue et al. [9] employed a backstepping SMC based on extended state observer, where adaptive/compensation-function observers estimate disturbances to mitigate performance degradation due to model uncertainties. Another line of work augments SMC with neural networks or radial basis function networks to approximate unknown disturbances via output feedback and thus enhance tracking accuracy [10]. In addition, continuous SMC via the super-twisting algorithm, rotation control with improved nonlinear extended state observers, sliding-mode repetitive control, and schemes coupling unknown-dynamics estimators with SMC have been reported, all seeking performance gains through refined reaching laws, observers, or estimators [11,12]. Despite these advances, many studies assume constant or slowly varying loads; controller design often relies on known disturbance bounds or accurate plant models. Chattering is typically mitigated by boundary layers or higher-order SMC, which increases implementation complexity and makes it difficult to sustain high accuracy under highly dynamic and uncertain conditions [13,14]. Therefore, although the aforementioned control algorithm achieves high-precision tracking, it still has shortcomings such as requiring precise models, strong dependence on the bound of disturbances, and difficulty in balancing robustness and chatter suppression. These limitations make it unsuitable for the hydraulic system with uncertain loads and periodic disturbances described in this paper.

Under uncertain loading conditions, achieving precise and stable control of hydraulic cylinders becomes considerably more challenging. To address unknown load effects, Pan et al. [15] proposed a control framework that combines a compensation-function observer with backstepping SMC, enabling online estimation of lumped disturbances and compensation of external loads. Hou et al. [16] tackled parameter uncertainty arising from inertia variations during lifting or grasping by fusing stereovision with an initial-value identification algorithm, thereby realizing online inertia estimation and automatic tuning of sliding-mode parameters. For position control of single-rod electro-hydraulic actuators, Son et al. [17] employed a robust nonlinear strategy assisted by an extended state observer to achieve high-precision positioning in the presence of disturbances and model uncertainties. In underwater applications subject to hydrostatic pressure variations, Nie et al. [18] integrated a disturbance observer with SMC to attain disturbance compensation and robust tracking. Beyond these, several studies leverage methods such as unknown-dynamics estimators and compensation-function observers to improve disturbance estimation accuracy, or exploit displacement-feedback mechanisms grounded in system physics to compensate for unmodeled dynamics, ultimately enhancing precision and stability [19]. Overall, most of the above approaches presume slowly varying; their observers often require high gains that amplify sensor noise, and their adaptive capability remains limited. In addition to these drawbacks, the dynamics of the control valve itself may also lead to unstable operation of the hydraulic system. If the valve is not properly controlled, the resulting instabilities can cause the hydraulic cylinder to deviate from its desired trajectory. Consequently, for free-section cutterhead systems characterized by periodic load fluctuations and uncertainty, there is still a lack of an intelligent algorithm that can accommodate fast-varying loads and suppress chattering.

Considering the significant adverse impact of unstable and inaccurate cylinder motion on TBM tunneling performance and safety, the purpose of this study is to realize stable constant-velocity motion of TBM hydraulic cylinders under uncertainties and load variations. To address the aforementioned challenges, this study develops a state-space model of the thrust hydraulic cylinder and advances a switching control strategy based on adaptive sliding mode control (ASMC). The proposed design not only surpasses traditional single-cylinder controllers in tracking accuracy, but also markedly improves velocity stability during start-up, demonstrating strong resilience to periodically varying loads. The main contributions are as follows:

(1)

We formulate a precise state-space model of the thrust hydraulic system, and experimentally obtain the cylinder’s external load conditions and system parameters.

(2)

We propose an ASMC-based switching controller that under load fluctuations simultaneously achieves high tracking accuracy and enhanced start-up velocity stability.

The remainder of this paper is organized as follows. Section 2 details the system architecture and derivation of the state-space model for the thrust hydraulic cylinder. Section 3 designs two ASMC structures: one prioritizes reduced velocity jitter at the expense of tracking accuracy, while the other attains higher accuracy with increased velocity ripple. Section 4 integrates the merits of the two controllers by designing a switching controller that simultaneously ensures tracking accuracy and start-up velocity stability. Section 5 concludes the work and outlines future research directions.

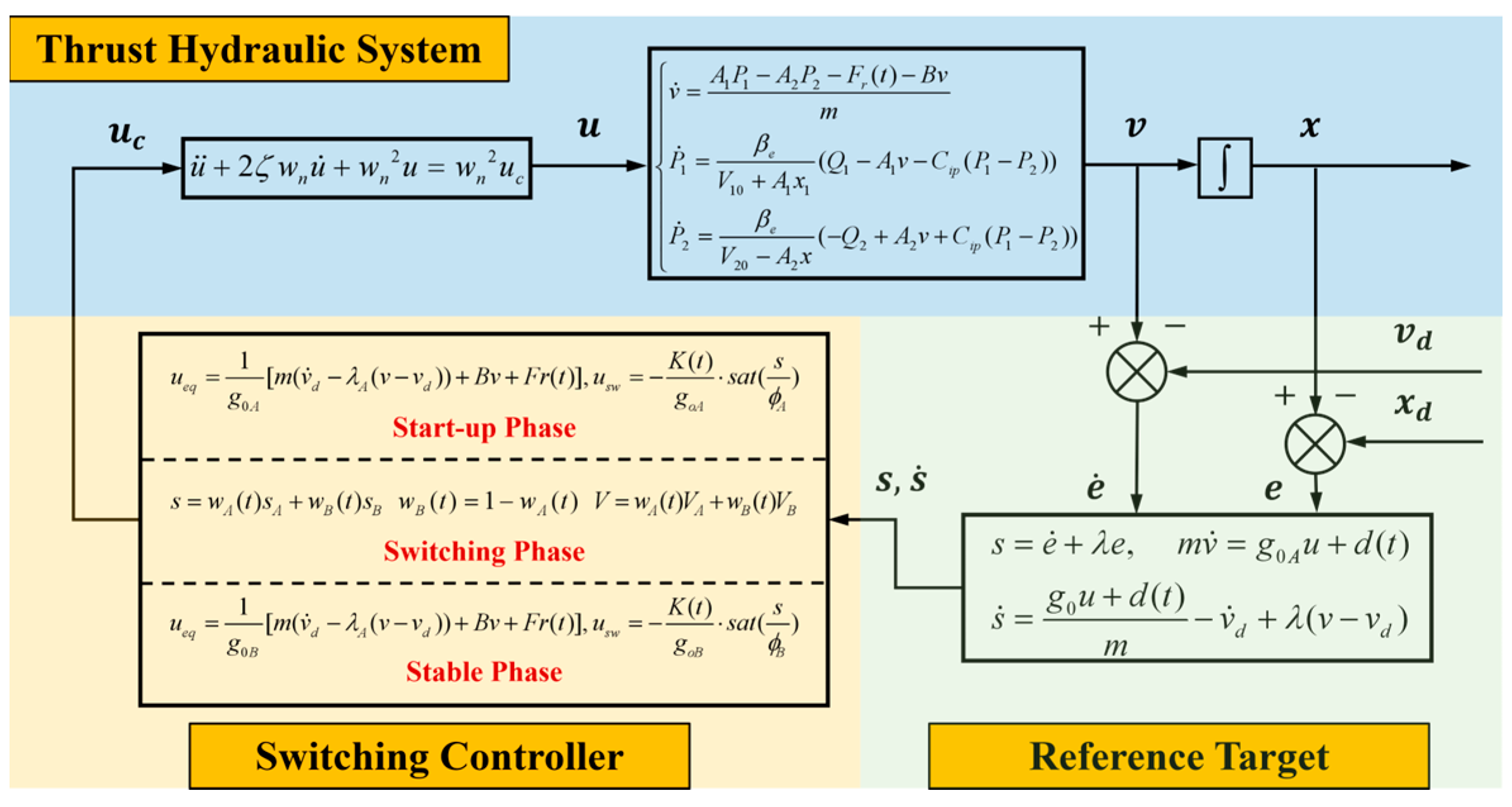
2. Introduction to the Hydraulic System and Modeling

This chapter analyzes the thrust cylinder’s hydraulic system and its components, identifies the control and controlled variables, and derives a precise state-space model of the hydraulic dynamics. To support controller design, we also perform experiments under different excavation conditions to measure external loads acting on the thrust system and identify unknown parameters. These results lay the foundation for the precise and stable control developed later.

2.1. Hydraulic System and Components

During operation of the novel free-section cutterhead, the thrust hydraulic cylinder extends to push the cutterhead against the rock ahead. As shown in Figure 1, the cutterhead axis is parallel to the excavation face and perpendicular to the tunnel axis. Rotated by a hydraulic motor and advanced by the thrust cylinder, the cutterhead periodically contacts the rock and once cracks accumulate to a critical level, the rock spalls. Throughout excavation, the thrust force balances the reaction from the rock. Because the rock’s compressive force on the cutterhead decreases intermittently when periodic cutting and spalling occur, the load on the thrust system varies in a cyclic manner.

Figure 2 depicts the hydraulic system of the thrust cylinder for the novel free-section cutterhead. It consists of three parts: (1) in the input/output part, oil is supplied from the oil tank to the hydraulic pump and then into the system; a relief valve located near the pump outlet regulates system pressure. (2) In the control part, the flow then passes through a three/four-way directional valve and into the upper hydraulic lock. By modulating the inlet/outlet openings via the command voltage, the three/four-way directional valve sets the operating speed of the hydraulic cylinder. (3) In the execution part, the hydraulic lock—comprising a check valve, a throttling orifice, and a relief valve—prevents reverse flow under load action. External fluctuating loads act on the hydraulic system through the asymmetric hydraulic cylinder.

2.2. Establishment of State Space Model

This study’s object can be abstracted as a valve-controlled asymmetric hydraulic cylinder system, with the piston separating a rod-less chamber (effective area $A_1$) and a rod-side chamber (effective area $A_2$). The state-space modeling of this hydraulic system is divided into three parts: the mechanical subsystem, the hydraulic subsystem, and the proportional-valve dynamics.

Firstly, for the mechanical part, considering the force balance of the piston along the load direction [20], the piston mechanics equation is as follows:

$$m\dot{v}=A_1{P}_1-A_2{P}_2-F_r(t)-Bv$$

(1)

where $m$ is the equivalent load mass, $P_1$ and $P_2$ are the pressures in the rod-less and rod-side chambers, $F_r\left(t\right)$ is the external disturbance load, $B$ is the viscous damping coefficient in which the friction of the piston, rod seals as well as the guideway resistance are lumped into a single linear damping term, and $v$ is the piston velocity.

The relation between piston displacement $x$ and velocity is as follows:

$$\dot{x}=v$$

(2)

Next, we consider the pressure dynamics of the hydraulic system during thrusting. The instantaneous volumes of the two chambers are as follows:

$$V_1=V_{10}+A_{1}x$$

(3)

$$V_2=V_{20}-A_{2}x$$

(4)

where $V_1$ and $V_2$ are the instantaneous volumes, and $V_{10}$ and $V_{20}$ are the initial volumes of the two chambers, respectively.

Accounting for oil compressibility and the leakage present in both the rod-side and rod-less chambers [21], the pressure continuity equations of the two chambers are as follows:

$${\dot{P}}_1={\displaystyle \frac{{\beta }_e}{V_1}}(Q_1-A_{1}v-C_{ip}(P_1-P_2))$$

(5)

$${\dot{P}}_2={\displaystyle \frac{{\beta }_e}{V_2}}(-Q_2+A_{2}v+C_{ip}(P_1-P_2))$$

(6)

where ${\beta }_e$ is the effective bulk modulus of the oil, $C_{ip}$ is the chamber internal leakage coefficient, and $Q_1$ and $Q_2$ are the inflows into the rod-less and rod-side chambers, respectively.

The hydraulic cylinder is represented by a lumped-parameter model including inertia, viscous damping, and internal leakage. Coulomb and Stribeck friction between the piston and the housing, the detailed dynamics of the pump, and pressure losses along the pipelines are omitted and interpreted as slowly varying parameters and bounded disturbances acting on the cylinder. Their numerical effects are partly absorbed into the equivalent parameters ${\beta }_e$, $B$, and $C_{ip}$ to be identified, and partly into the external load force $F_r\left(t\right)$. Thus, the present model should be seen as an idealized but practical description of the dominant pressure–flow–force coupling for the cylinder.

For the proportional valve’s flow equations, we approximate its flow characteristic as linear, so the effective orifice area $A_o$ can be expressed as follows:

$$u=\left\{\begin{array}{ll}0,& \left|\tilde{u}\right|\le u_0\\ \tilde{u}-u_0\mathrm{sgn}(\tilde{u}),& \left|\tilde{u}\right|>u_0\end{array}\right.$$

(7)

$$A_0=wu$$

(8)

where $u$ is the effective spool displacement, $\tilde{u}$ is the spool displacement, $u_0 > 0$ is the deadband width caused by the null overlap, and $w$ is the valve-port area gradient.

According to the orifice flow formula, the valve flow has two operating cases. When the spool opens in the positive direction ($u > 0$), $Q_1$ and $Q_2$ can be obtained as follows [21]:

$$Q_1=C_{d}wu\sqrt{{\displaystyle \frac{2(P_s-P_1)}{\rho }}}$$

(9)

$$Q_2=C_{d}wu\sqrt{{\displaystyle \frac{2P_2}{\rho }}}$$

(10)

When the spool opens in the negative direction ($u < 0$), $Q_1$ and $Q_2$ can be obtained as follows:

$$Q_1=-C_{d}w\left|u\right|\sqrt{{\displaystyle \frac{2P_1}{\rho }}}$$

(11)

$$Q_2=-C_{d}w\left|u\right|\sqrt{{\displaystyle \frac{2(P_s-P_2)}{\rho }}}$$

(12)

where $C_d$ is the discharge coefficient, $\rho$ is the oil density, and $P_s$ is the supply pressure.

The electro-mechanical dynamics of the three/four-way directional valve can be approximated by the following second-order system:

$$\ddot{u}+2\zeta w_n\dot{u}+{w_n}^{2}u={w_n}^2{u}_c$$

(13)

where $u_c$ is the input control voltage, ${\omega }_n$ is the natural frequency of the spool, and $\zeta$ is the damping ratio.

In this study, we mainly focus on the extension stroke of the thrust cylinder along the TBM excavation direction ($u > 0$), which is the critical phase for start-up and tracking performance. The return stroke is normally executed at low speed and with much smaller load for repositioning, and is therefore not analyzed in detail here. In principle, the control algorithm proposed later can also be applied in the reverse direction by changing the sign of the reference trajectory.

The proportional directional valve is modeled by a second-order spool dynamics and an orifice flow equation with a small symmetric deadband around the null position. The effective spool displacement $u$ is obtained by subtracting the null overlap $u_0$ from the actual displacement, and is then used to compute the metering area. Other nonlinear effects such as hysteresis, saturation, and notched spool lands, which make the “slot area-spool position” relation nonlinear [22], are not modeled explicitly. This is because the purpose of this article is to research the precise control method of hydraulic system in normal condition, during which the proportional valve core moves in the linear part. Previous studies have shown that medium-complexity, quasi-linear simplified valve models can achieve sufficiently accurate system-level results under certain conditions [23], and a large number of valve-controlled cylinder studies have also adopted the above simplified model [21,24], which proves that the simplification proposed in this paper is feasible.

To control the hydraulic system via the electro-proportional valve voltage, we select the system state vectors as follows:

$$\mathrm{x}={\left[\begin{array}{l}x\\ v\\ P_1\\ P_2\\ u\\ \dot{u}\end{array}\right]}^T$$

(14)

Combining Equations (1)–(14), the state-space model of the thrust-cylinder hydraulic system can be written as

$$\left\{\begin{array}{l}\dot{x}=v\\ \dot{v}={\displaystyle \frac{A_1{P}_1-A_2{P}_2-F_r(t)-Bv}{m}}\\ {\dot{P}}_1={\displaystyle \frac{{\beta }_e}{V_{10}+A_1{x}_1}}(Q_1-A_{1}v-C_{ip}(P_1-P_2))\\ {\dot{P}}_2={\displaystyle \frac{{\beta }_e}{V_{20}-A_{2}x}}(-Q_2+A_{2}v+C_{ip}(P_1-P_2))\\ \dot{u}=\dot{u}\\ \ddot{u}={w_n}^2(u_c-u)-2\zeta w_n\dot{u}\end{array}\right.$$

(15)

where $Q_1$ and $Q_2$ are defined piecewise by Equations (9)–(12), and the external load $F_r\left(t\right)$ is determined by the actual operating condition.

2.3. Determination of the Periodic Load Curve

During hydraulic cylinder control, different external loads $F_r\left(t\right)$ exert a substantial influence on control accuracy and stability, and thereby determine parameter selection for the control algorithm. Accordingly, we first determine the range and variation pattern of $F_r\left(t\right)$ through experiments.

Figure 3 and Figure 4 show the novel free-section cutterhead rock-breaking test bench used in this study. In the experiment, the supporting beam, fine tuning components, and cutterhead are connected into an integral assembly through hinges and flanges. The supporting beam passes through the central opening of the rack, and the hydraulic cylinder pushes the supporting beam forward, thereby driving the cutterhead advance and cutting the rock specimen. The fine tuning components are used to adjust the cutterhead motion in the vertical and lateral directions, so that the cutterhead is aligned perpendicular to the excavation face, consistent with the actual cutting condition.

The force sensors mounted behind the cutterhead are one-dimensional axial force sensors used to directly measure the cutterhead thrust during excavation. Due to the fixed connection between the propulsion cylinder, supporting beam, fine adjustment mechanism, and cutterhead, they can be equivalently regarded as a mass block. Due to the fact that the entire test bench is guided by linear guides, the direction of the cutterhead thrust is parallel to the motion of the hydraulic cylinder; at the same time, it was observed in the experiment that the swing amplitude of the cutterhead during operation does not exceed 5°. Therefore, the axial force measured by force sensors is directly regarded as the equivalent external load $F_r\left(t\right)$ acting on the hydraulic cylinder, and the error will not exceed 10% (sin 5° = 0.087), which is acceptable for this study.

By measuring the thrust-cylinder pressure under penetration depths of 3 mm and 6 mm, the external load profiles $F_r\left(t\right)$ are obtained as shown in Figure 5. To better analyze the variation of $F_r\left(t\right)$ at different penetration depths, four indicators are selected: average, maximum, minimum, and period. The indicators for each penetration depth are summarized in

Table 1. Indicators at different penetration depths.

Penetration Depth	Mean	Max	Min	Period
3 mm	29,037.16	40,994.91	18,162.57	4.96
6 mm	29,314.81	40,904.33	20,248.69	4.94

.

As shown in Figure 5, the external load variation in the thrust system is broadly similar across penetration depths. This phenomenon can be explained as follows: as the cutterhead rotates, the disc cutters act on the rock from top to bottom. After the thrust process enters a steady stage, the upper part of the rock sample is excavated more while the lower part is excavated less, and a free surface gradually develops in front of the cutterhead. Under this condition, rock failure is mainly governed by periodic spalling as the cutters pass by. As a result, in the experiment the axial cutting force level remains similar for different penetration depths, while the most pronounced character is the periodic fluctuation. The external load thus exhibits a periodic variation that is primarily determined by the rotational speed of the cutterhead, and its dependence on the penetration depth becomes relatively weak in this cutting condition.

According to Table 1, its overall trend can be characterized as oscillating about a baseline of approximately 29 kN with an amplitude of about 10 kN and a period of 5 s. In addition, due to the periodic contact of the cutters and the nonuniform spalling of the rock, small-amplitude, high-frequency ripples are superimposed. Therefore, the external load $F_r\left(t\right)$ can be summarized as the superposition of a large-amplitude, low-frequency sinusoid and multiple small-amplitude, high-frequency sinusoids. While its specific values vary slightly with geology, penetration depth, and other excavation parameters, the overall pattern remains consistent.

2.4. Determination of Unknown Parameters

The state-space model of the thrust hydraulic system involves geometric parameters, operating condition parameters, hydraulic fluid properties, and several equivalent dynamic parameters. Some of these parameters can be directly determined from the structural design of the test bench, whereas others cannot be obtained from static data alone and must be identified using dynamic experimental data. To ensure the accuracy of the simulation model, these parameters need to be determined as follows.

Based on the design dimensions of the thrust cylinder, pipelines, and pump station, as well as the specified operating conditions, parameters like effective piston areas, initial chamber volumes, supply pressure, and fluid properties can be directly obtained. In addition, part of the proportional valve’s dynamic parameters can be taken from the manufacturer’s technical documentation. The main known parameters are summarized in

Table 2. Main known hydraulic system parameter values.

Parameters	Values	Units	Physical Meanings
$m$	2000	kg	equivalent load mass
$A_1$	0.015	m2	rodless side area
$A_2$	0.008	m2	rod side area
$V_{10}$	0.010	m3	rodless side initial volume
$V_{20}$	0.025	m3	rod side initial volume
$P_s$	20	MPa	supply pressure
$\rho$	870	kg/m3	oil density
$C_d$	0.65	-	discharge coefficient
${\omega }_n$	200	rad/s	natural frequency
$\zeta$	0.8	-	damping ratio
$u_{\mathit{max}}$	0.50	mm	upper limit of valve

.

Unlike geometric and operating condition parameters, some parameters such as the effective bulk modulus cannot be directly obtained, yet they have a significant influence on the precise dynamic response of the system. To further improve the model accuracy, this study performs parameter identification for the following unknown parameters: the effective bulk modulus ${\beta }_e$, the inter-chamber leakage coefficient $C_{ip}$, and the viscous damping coefficient $b$.

The identification procedure is as follows: (1) multiple sets of experimental data are collected from the test bench, including the time history $t_e$, the cylinder displacement $x_e$, and the pressure responses in the two chambers $P_{1e}$ and $P_{2e}$; (2) the same load conditions are applied to the simulation model to obtain the simulated time history $t_s$, displacement $x_s$, and chamber pressures $P_{1s}$ and $P_{2s}$; (3) a cost function is constructed as the weighted mean square error between the measured and simulated responses, which is given in Equation (16); (4) the three unknown parameters are iteratively updated until a parameter combination that minimizes the cost function.

In the above procedure, the cylinder displacement $x_e$ is measured by a linear position sensor mounted along the piston rod, with one end fixed to the cylinder barrel and the other connected to the piston rod. The chamber pressures $P_{1e}$ and $P_{2e}$ are measured by pressure transducers installed near the inlet ports of the rod-less and rod-side chambers, respectively. All signals are synchronously acquired and used as reference data for parameter identification.

$$J=w_x{(x_e-x_s)}^2+w_{p1}{(P_{1e}-P_{1s})}^2+w_{p2}{(P_{2e}-P_{2s})}^2$$

(16)

where $w_x, w_{p1}, w_{p2}$ are weighting coefficients and their mathematical relationship is set as $w_x+w_{p1}+w_{p2} = 1$.

Considering that displacement tracking accuracy is the primary concern in controller design, this study assigns $w_x = 0.5$ and $w_{p1} = w_{p2} = 0.25$. With these weights fixed, smaller discrepancies of unknown parameters lead to a smaller value of $J$. On this basis, the ${\beta }_e$, $C_{ip}$, and $b$ are identified using a nonlinear optimization algorithm based on the least-squares criterion. The principle is that, within preset bounds for the parameters, the algorithm starts from an initial value, evaluates the accuracy of the parameters through the cost function $J$, and then iteratively updates the unknown parameters using a gradient-descent strategy so that $J$ decreases at each iteration. The iteration is terminated when both the change in $J$ and the change in the parameter vector fall below prescribed thresholds, at which point the corresponding parameter set is regarded as the one that minimizes the weighted squared error. To ensure that the identified results remain physically meaningful, lower and upper bounds are imposed on the three parameters according to engineering experience, as summarized in

Table 3. Identification ranges of unknown parameters.

Unknown Parameters	${\mathit{\beta }}_{\mathit{e}}$	${\mathit{C}}_{\mathit{i}\mathit{p}}$	$\mathit{b}$
Range of Values	0.8 × 109~1.6 × 109	1.0 × 10−13~5.0 × 10−12	2000~8000
Units	Pa	m3/(s·Pa)	(N·s)/m

.

After parameter identification, the values determined for the three unknown parameters are shown in

Table 4. Identification results of unknown parameters.

Identified Parameters	${\mathit{\beta }}_{\mathit{e}}$	${\mathit{C}}_{\mathit{i}\mathit{p}}$	$\mathit{b}$
Values	1.4 × 109	7.2 × 10−13	3200
Units	Pa	m3/(s·Pa)	(N·s)/m

. The comparison between the measured values used for parameter identification and the simulated values of the identified simulation model is shown in Figure 6. It can be seen that the simulation results are in good agreement with the measurement results, indicating that the results of parameter identification are reasonable.

3. Design of the ASMC Controller

Based on the state-space model of the hydraulic system, the experimentally determined external load pattern and identified unknown parameters, this chapter designs two ASMC Controllers and derives their control laws in detail, together with stability verification. The two controllers are then compared against a PID controller; their performances under the conditions of $F_r\left(t\right)$ are analyzed and summarized to guide subsequent optimization.

3.1. Design of the Controller A

We first design a conventional ASMC Controller (Controller A). Let the actual displacement be $x$, the reference displacement be $x_d$, the actual velocity be $v$, and the reference velocity be $v_d$. The tracking error $e$ is defined as follows:

$$e=x-x_d,\dot{e}=v-v_d$$

(17)

Letting a first-order sliding surface be $s$ [25], its expression is defined as follows:

$$s=\dot{e}+{\lambda }_{A}e$$

(18)

where ${\lambda }_A>0$ is the sliding surface parameter.

From Equation (15), a highly nonlinear relationship exists between the cylinder piston displacement $x$ and the control input. Introduce a linear gain $g_{0A}$ into the controller so that the input–output relation of the hydraulic system can be rewritten as

$$m\dot{v}=g_{0A}u+d(t)$$

(19)

where $d\left(t\right)$ includes the external disturbance $F_r\left(t\right)$, unmodeled dynamics, and modeling uncertainties.

By taking the derivative of Equation (17), the expected sliding mode dynamics can be obtained as follows:

$$\dot{s}={\lambda }_A\dot{e}+\ddot{e}={\lambda }_A(v-v_d)+(\dot{v}-{\dot{v}}_d)={\displaystyle \frac{g_{0A}u+d(t)}{m}}-{\dot{v}}_d+{\lambda }_A(v-v_d)$$

(20)

When modeling without considering external disturbances and uncertainties, setting the sliding dynamics to 0, the equivalent control $u_{eq}$ can be obtained from Equations (1), (9), (10), (18) and (19). The $u_{eq}$ is mainly responsible for controlling the known system dynamics to achieve the desired sliding surface dynamics.

$$u_{eq}={\displaystyle \frac{1}{g_{0A}}}[m({\dot{v}}_d-{\lambda }_A(v-v_d))+Bv+Fr(t)]$$

(21)

To suppress the uncertainty and disturbance effects of the system, the switching control term $u_{\mathit{sw}}$ is introduced and its formula is established as follows:

$$u_{sw}=-{\displaystyle \frac{K(t)}{g_{oA}}}\cdot sat({\displaystyle \frac{s}{{\varphi }_A}})$$

(22)

where ${\varphi }_A>0$ is the boundary-layer thickness and $sat\left(x\right)$ is the saturation function. In this paper, a smooth approximation is adopted with $sat\left({\displaystyle \frac{s}{{\varphi }_A}}\right)\approx tanh\left({\displaystyle \frac{s}{{\varphi }_A}}\right)$, where $K$ denotes the adaptive gain.

To ensure the switching action effectively compensates the uncertainty, a suitable adaptation law is crucial for enhancing robustness. The adaptive gain and its update method are given as follows:

$$K=K_A+{\eta }_A$$

(23)

$${\dot{\eta }}_A={\gamma }_{A}s$$

(24)

where $K_A$ is the base gain, ${\eta }_A$ is the adaptive term, and ${\gamma }_A>0$ is the adaptation gain. This structure increases the gain faster when sliding surface $s$ is larger, thereby strengthening robustness.

It should be noted that ${\eta }_A$ is implemented with an explicit upper bound (${\eta }_{A,\mathrm{m}\mathrm{i}\mathrm{n}}\le {\eta }_A\le {\eta }_{A,\mathrm{m}\mathrm{a}\mathrm{x}}$), which prevents unbounded growth of the adaptive gain. ${\eta }_{A,\mathrm{m}\mathrm{a}\mathrm{x}}$ and ${\eta }_{A,\mathrm{m}\mathrm{i}\mathrm{n}}$ is defined as a function of the expected operating time of Controller A:

$$\left\{\begin{array}{l}{\eta }_{A,\max }={\eta }_A(0)+{\gamma }_A{S}_{\max }T\\ {\eta }_{A,\min }={\eta }_A(0)-{\gamma }_A{S}_{\max }T\end{array}\right.$$

(25)

where ${\eta }_A\left(0\right)$ is the initial value of adaptive term, $S_{\max }$ is the limit gain, and $T$ is the expected operating time. They keep ${\eta }_A$ within the limit while also providing significant room for changing.

By combining the equivalent and switching components in Equations (21)–(25), the control law of Controller A is as follows:

$$u_A=u_{eq}+u_{sw}={\displaystyle \frac{1}{g_{0A}}}[m({\dot{v}}_d-{\lambda }_A(v-v_d))+Bv+Fr(t)]-{\displaystyle \frac{K_A+{\eta }_A}{g_{0A}}}\cdot \tanh ({\displaystyle \frac{s}{{\varphi }_A}})$$

(26)

The term $u_{eq}$ guarantees the overall stability of the system, while the introduction of $u_{\mathit{sw}}$ feeds back all errors—including model uncertainties and tracking errors—onto the sliding surface. Equations (22)–(24) enable the adaptive parameter to vary in real time according to the error feedback, thereby regulating the system and improving the control accuracy [25,26].

3.2. Design of the Controller B

As a reinforcement of Controller A, and tailored to the strong-disturbance operating regime of the novel cutterhead system, we further design an ASMC Controller (Controller B), who features a strong adaptive switching gain with a forgetting factor. The principle and structure of Controller B are essentially the same as Controller A, and its control law is given as follows:

$$u_B=u_{eq}+u_{sw}={\displaystyle \frac{1}{g_{0B}}}[m({\dot{v}}_d-{\lambda }_B(v-v_d))+Bv+Fr(t)]-{\displaystyle \frac{K_B+{\eta }_B}{g_{0B}}}\cdot \tanh ({\displaystyle \frac{s}{{\varphi }_B}})$$

(27)

where $g_{0B}$ denotes the linear gain of Controller B, ${\lambda }_B>0$ is the sliding surface parameter, $K_B$ is the base gain (with an adaptive term ${\eta }_B$), and ${\varphi }_B>0$ is the boundary-layer thickness.

To enlarge the adaptive estimate value during high-disturbance phases and let it decrease when the disturbance weakens, Controller B augments the original adaptation rate with a forgetting factor, expressed as follows:

$${\dot{\eta }}_B(t)={\gamma }_B(\left|s\right|-{\sigma }_B\eta )$$

(28)

where ${\gamma }_B>0$ is the adaptation gain and ${\sigma }_B\in \left(\mathrm{0,1}\right)$ is the forgetting factor. It is a first-order linear differential equation driven by the bounded signal $\left|s\right|$. Under the situation that $\left|s\right|$ remains bounded, this equation exists a unique bounded solution and converges to a finite steady value determined by the residual sliding variable. In the implementation, a non-negative constraint is also enforced so that ${\eta }_B$ is not allowed to decrease below zero, and practical limits ${\eta }_{B,\max }$ and ${\eta }_{B,\min }$ are imposed, leading to ${\eta }_{B,\min }{\le \eta }_B\le {\eta }_{B,\max }$ for all time. Thus, the forgetting factor mechanism does not lead to parameter drift; instead, the adaptive gain is driven towards a bounded steady value consistent with the magnitude of the residual sliding variable.

Compared with the adaptation method of Controller A, the introduction of the forgetting factor decouples the adaptive term from a purely linear dependence on sliding surface $s$. When $\left|s\right|$ is large, ${\eta }_B$ can grow rapidly; when $\left|s\right|$ is small, ${\eta }_B$ decays exponentially toward zero, thereby enhancing precision control. However, because controller parameters may vary rapidly during this process, issues such as potential instability or severe velocity ripple due to overly fast regulation can arise.

In general, the proposed two ASMC Controllers can address matched uncertainties like load force variations and parametric perturbations, which act through the same channel as the control input, and can be compensated by robust switching action. To achieve smooth control and alleviate chattering, the switching term is implemented with a boundary layer, which may subsequently introduce a small residual tracking band even for matched uncertainties. Unmatched uncertainties like neglected high-order/fast dynamics and implementation nonidealities are not explicitly compensated and thus limit the achievable tracking accuracy. Their effect is only reduced by the system-level closed-loop feedback, leading to an ultimately bounded tracking error. Consequently, the remaining error during cylinder moving stems from these two sources and greatly depends on the controller settings (e.g., feedback gains and boundary-layer width), reflecting the robustness–smoothness trade-off.

3.3. Stability Analysis

We first analyze the stability of the Controller A by selecting the Lyapunov function as follows:

$$V={\displaystyle \frac{1}{2}}{s}^2+{\displaystyle \frac{1}{2{\gamma }_A}}{\tilde{\eta }}^2$$

(29)

where $\tilde{\eta } = {\eta }_A-{\eta }^{*}$, ${\eta }^{*}$ is a constant related to the upper bound of system uncertainty; choosing ${\eta }^{*}\ge d\left(t\right)$ suffices here.

Taking the derivative of the Lyapunov function, the following expression can be obtained:

$$\dot{V}=s\dot{s}+{\displaystyle \frac{1}{{\gamma }_A}}\tilde{\eta }{\dot{\eta }}_A$$

(30)

Combining Equations (20), (24) and (26), we obtain:

$$\begin{array}{ll}\hfill \dot{V}& =-{\displaystyle \frac{K_A}{m}}s\tanh ({\displaystyle \frac{s}{{\varphi }_A}})-{\displaystyle \frac{\tilde{\eta }+{\eta }^{*}}{m}}s\tanh ({\displaystyle \frac{s}{{\varphi }_A}})+{\displaystyle \frac{d(t)}{m}}s+{\displaystyle \frac{1}{{\gamma }_A}}\tilde{\eta }{\dot{\eta }}_A\\ & \le -{\displaystyle \frac{K_A}{m}}\left|s\right|\left|\tanh ({\displaystyle \frac{s}{{\varphi }_A}})\right|+\tilde{\eta }\left|s\right|\left[1-{\displaystyle \frac{1}{m}}\tanh ({\displaystyle \frac{s}{{\varphi }_A}})\right]+{\displaystyle \frac{{\eta }^{*}}{m}}\left|s\right|\left[1-\tanh ({\displaystyle \frac{s}{{\varphi }_A}})\right]\\ & \le \left|s\right|(-{\displaystyle \frac{K_A}{m}}+\tilde{\eta }\left[1+{\displaystyle \frac{1}{m}}\right]+{\displaystyle \frac{2{\eta }^{*}}{m}})\end{array}$$

(31)

Therefore, by appropriately selecting the parameters $K_A$, ${\varphi }_A$, and ${\eta }^{*}$ to suitable values ($\tilde{\eta }(m+1)+2{\eta }^{*}\le K_A$), the controller remains stable. It should be noted that during the control phase, the adaptive parameters will constantly change. To avoid local instability, it is best to set the controller parameters to ${\eta }_{A,\max }(m+1)+2{\eta }^{*}\le K_A$.

Similarly, the derivative of the Lyapunov function for Controller B is as follows:

$$\begin{array}{ll}\hfill {\dot{V}}_B& \le -{\displaystyle \frac{K_B}{m}}\left|s\right|\left|\tanh ({\displaystyle \frac{s}{{\varphi }_B}})\right|+\tilde{\eta }\left|s\right|\left[1-{\displaystyle \frac{1}{m}}\tanh ({\displaystyle \frac{s}{{\varphi }_B}})\right]+{\displaystyle \frac{{\eta }^{*}}{m}}\left|s\right|\left[1-\tanh ({\displaystyle \frac{s}{{\varphi }_B}})\right]-{\sigma }_B\tilde{\eta }{\eta }_B\\ & \le \left|s\right|(-{\displaystyle \frac{K_B}{m}}+\tilde{\eta }\left[1+{\displaystyle \frac{1}{m}}\right]+{\displaystyle \frac{2{\eta }^{*}}{m}})\end{array}$$

(32)

In this case, by selecting suitable parameters $K_B$, ${\varphi }_B$, and ${\eta }^{*}$ to suitable values (${\eta }_{B,\max }(m+1)+2{\eta }^{*}\le K_A$), the sliding surface converges to a small neighborhood whose size depends on the disturbance intensity, and the system attains asymptotic stability.

3.4. Control Performance Analysis

We now compare the control effects of Controller A, Controller B, and a conventional PID Controller. A simulation model of the hydraulic system is constructed based on identified parameters. The external load follows the experimentally determined pattern: a baseline of 29 kN with a 10 kN amplitude and a period of 5 s, with an additional random superposition of multiple small-amplitude, high-frequency components to represent nonstationary and random load.

In order to make the comparison clear, the parameters of the baseline PID controller, Controller A, and Controller B are explicitly listed as follows. The PID gains were tuned by trial and error in simulation until a compromise between overshoot and settling time was obtained under the nominal load condition. The parameters of Controllers A and B were then adjusted from typical values so that the cylinder could start smoothly, the tracking error could converge quickly, and no severe chattering appeared in the control signal. The final parameter values used in all simulations are summarized in

Table 5. Control parameters of the PID controller, Controller A, and Controller B.

Controllers	Parameters	Values	Parameter Meanings
PID Controller	$K_p$	800	proportional gain
	$K_i$	0.1	integral gain
	$K_d$	0.0005	derivative gain
Controller A	${\gamma }_A$	10	adaptation gain
	$K_A$	30	base gain
	${\varphi }_A$	0.01	boundary-layer thickness
	$g_{0A}$	1.0 × 108	linear gain
Controller B	${\gamma }_B$	4.0 × 103	adaptation gain
	$K_B$	1.75 × 103	base gain
	${\sigma }_B$	0.05	forgetting factor
	${\varphi }_B$	0.008	boundary-layer thickness
	$g_{0B}$	7.5 × 108	linear gain

.

As shown in Figure 7 and Figure 8, Controller B yields the highest accuracy: during the initial stage (0–5 s) the error is kept within 10 mm and fluctuates violently, and subsequently the displacement error fluctuates around 5 mm. The PID Controller achieves moderate accuracy: its initial response (0–5 s) is slow, with the error rising to about 38 mm; thereafter, the tracking error remains stably oscillating around 38 mm and stays below 40 mm. Controller A does not meet the precision requirement—its error grows with piston travel; however, within 0–3 s it tracks reasonably well, keeping the start-up displacement error near 5 mm.

To further examine the system dynamics, we analyze the cylinder velocity and the spool displacement of the proportional valve under the three controllers. As shown in Figure 9 and Figure 10, the PID Controller exhibits substantial initial velocity jitter, oscillating between −0.02 m/s and 0.02 m/s; later, the oscillation settles into a high-frequency ripple around the target velocity 0.025 m/s with an amplitude of approximately 0.005 m/s. This stems from limited spool authority: after the initial phase, the spool displacement oscillates only slightly and at low frequency around 0.4 mm. In contrast, Controller B regulates velocity with high precision after 5 s by commanding small-amplitude, high-frequency spool motions near 0.4 mm, maintaining the target velocity 0.025 m/s with minimal fluctuation. However, due to the forgetting factor, the transient of velocity 0 m/s to 0.025 m/s is overly aggressive, resulting in strong control over the spool: within the first 3 s, the spool rapidly oscillates between −0.3 mm and 0.5 mm, producing sharp cylinder-velocity swings between −0.04 m/s and 0.04 m/s. Although this reduces displacement error, such violent transients can be harmful to the system. Controller A presents intermediate behavior between Controller B and PID Controller: while its tracking error becomes larger after 3 s, it achieves better start-up tracking accuracy than Controller B and PID Controller, with less severe spool and velocity fluctuations in the first 3 s.

In summary, the PID Controller exhibits large displacement-tracking errors and pronounced velocity fluctuations throughout the stroke; Controller B attains superior tracking accuracy but suffers from excessively violent spool/cylinder transients at start-up; Controller A lacks overall precision yet offers better start-up tracking accuracy and better stability than Controller B and PID Controller. Given these trade-offs, a controller that jointly ensures accuracy and stability is still required.

4. Design and Analysis of the Switching Controller

Section 3 designs two ASMC Controllers. Controller B delivers better overall performance but suffers from instability during start-up; Controller A lacks overall precision yet achieves a better accuracy and stability performance at start-up. Therefore, this chapter combines their respective strengths and proposes a switching controller, whose performance is validated by comparative tests.

4.1. Design of the Switching Controller

In the proposed scheme, Controller A is tuned with relatively small gains and a wider boundary layer, so that the start-up response remains gentle: in the first few seconds it reduces the large initial position error while keeping the cylinder velocity smooth, without pronounced oscillations under rapidly building pressures. This conservative setting, however, limits its steady-state tracking capability once the system undergoes a long-term control. Controller B is instead designed with higher gains and a narrower boundary layer to achieve tighter tracking in steady operation; if it were applied from the very beginning, the combination of large initial errors and strong feedback would generate noticeable velocity ripples and pressure fluctuations.

In order to combine the advantages of both controllers, this paper designs the following switching controller:

$$u=w_A(t)u_A+w_B(t)u_B$$

(33)

where the formulas of $u_A$ and $u_B$ are provided by Equations (26) and (27) respectively, $w_A\left(t\right)$ and $w_B\left(t\right)$ are the switching parameters for Controllers A and B, defined as

$$w_A(t)=\left\{\begin{array}{ll}1& \mathrm{when} {\mathrm{error}}_A\le 1.2{\mathrm{error}}_B or {\mathrm{error}}_A\le {\mathrm{error}}_{allow}\\ 1-{\displaystyle \frac{t-t_{switch}}{\Delta t}}& \mathrm{when} {\mathrm{error}}_A\ge 1.2{\mathrm{error}}_B \mathrm{exceeds} 0.1 \mathrm{s}\\ 0& \mathrm{when} t\ge t_{switch}+\Delta t\end{array}\right.$$

(34)

$$w_B(t)=1-w_A(t)$$

(35)

where ${error}_A$ and ${error}_B$ are the tracking error of Controllers A and B, ${error}_{allow}$ is the maximum allowable error value (set according to the system), $t_{switch}$ is the Controller switching time, and $\Delta t$ is the total duration of switching.

In the initial stage, ${error}_A\le 1.2{error}_B$ is used to ensure that the error control effects of Controllers A and B are not significantly different. At the same time, ${error}_A\le {error}_{allow}$ is used to ensure that there is a certain redundancy in the switching controller, so that fluctuations in the initial stage will not directly trigger switching instructions. At this point, Controller A takes the lead and can balance displacement accuracy and velocity stability. During the switching phase, when Controller A begins to experience accuracy issues (exceeding 0.1 s), control commands are triggered. To ensure system stability, it is recommended to switch for more than 1 s. In the final phase, the system is entirely controlled by controller B, which can achieve good accuracy. Regardless of whether a controller is currently contributing to the control action, the adaptive parameters of both Controller A and Controller B are updated simultaneously and independently according to the system state, ensuring timely adaptation.

When $t\le t_{switch}$, the Lyapunov function of the switching controller is $V = V_A$; when $t\ge t_{switch}+\Delta t$, the sliding surface is $V = V_B$. As proved in Section 3.3, both functions are positive and under appropriate parameter choices have negative derivatives, so these two phases are stable. It remains to prove switching controller’s stability during $t_{switch}<t<t_{switch}+\Delta t$.

When $t_{switch}<t<t_{switch}+\mathsf{\Delta }t$, using Equations (33)–(35), the time derivative of the Lyapunov function is as follows:

$$\dot{V}={\displaystyle \frac{\Delta t-1}{\Delta t}}(V_B-V_A)+w_A{\dot{V}}_A+w_B{\dot{V}}_B$$

(36)

From Equations (31) and (32), the Lyapunov derivatives for Controller A and Controller B can be written as follows:

$${\dot{V}}_A\le -c_A\left|s_A\right|+{\delta }_A$$

(37)

$${\dot{V}}_B\le -c_B\left|s_B\right|+{\delta }_B$$

(38)

where $c_A, c_B>0$ is a constant determined by the hydraulic system physical parameters and controller parameters, ${\delta }_A, {\delta }_B$ is a bounded term.

Substituting Equations (37) and (38) into Equation (36) yields the following result:

$$\dot{V}\le {\displaystyle \frac{\Delta t-1}{\Delta t}}(V_B-V_A)-w_A{c}_A\left|s_A\right|-w_B{c}_B\left|s_B\right|+w_A{\delta }_A+w_B{\delta }_B$$

(39)

From the inequality $\left|s\right|\le w_A\left|s_A\right|+w_B\left|s_B\right|$, it follows that

$$-w_A{c}_A\left|s_A\right|-w_B{c}_B\left|s_B\right|\le -c_{\min }\left|s\right|,c_{\min }=\min \left\{c_A,c_B\right\}$$

(40)

Combining Equations (39) and (40) gives the following formula:

$$\dot{V}\le -c_{\min }\left|s\right|+\left[{\displaystyle \frac{\Delta t-1}{\Delta t}}(V_B-V_A)w_A{\delta }_A+w_B{\delta }_B\right]$$

(41)

where since $V_A, V_B$ and ${\delta }_A, {\delta }_B$ are bounded, $\left[{\displaystyle \frac{\mathsf{\Delta }t-1}{\mathsf{\Delta }t}}\right(V_B-V_A)w_A{\delta }_A+w_B{\delta }_B]$ is bounded; moreover, since ${\dot{V}}_A, {\dot{V}}_B\le 0$, the negative term can be made dominant in the Lyapunov derivative. Hence the sliding surface is constrained within a small neighborhood during operation of the hydraulic system, ensuring overall system stability.

The control module is developed in MATLAB (R2024a), and the control block diagram of thrust hydraulic system is shown in Figure 11.

In practical applications, the proposed two-phase ASMC is implemented in discrete time on a digital controller. With a fixed sampling period $T_s$, the cylinder displacement, velocity and chamber pressures are sampled at each instant ${kT}_s$, the sliding variables and adaptive laws are evaluated in algebraic form, and the adaptive gain is updated by a simple forward-Euler step. The valve command $u\left[k\right]$ is held constant over $[{kT}_s, (k+1\left)T_s\right]$ by a zero-order hold. For the TBM thrust system considered in this paper, a sampling period on the order of a few milliseconds is sufficient to be much faster than the dominant hydraulic dynamics, so that the discrete-time implementation closely approximates the continuous-time controller analyzed above and can be realized on standard industrial digital hardware.

4.2. Analysis of the Switching Controller

This article selects the total duration of switching $\Delta t = 2 s$. We first analyze the displacement tracking of the proposed switching controller. This experiment still uses the same hydraulic system parameters and external load conditions as in Section 3.

As shown in Figure 12, the switching controller achieves good accuracy: during the initial stage, the tracking error gradually rises to about 7.5 mm; thereafter, the displacement error fluctuates around 7 mm. It can be seen that the switching controller successfully inherited the control accuracy of Controller B, while ensuring good accuracy and stability in the initial stage. We next examine the cylinder velocity and the spool displacement of the proportional valve under this control scheme.

As shown in Figure 13 and Figure 14, a certain level of velocity jitter appears at the beginning, but it is generally constrained to about 0.1 m/s, and the amplitude becomes very small in stable stage. Regarding the spool motion, high-frequency oscillations are present in the initial stage but remain within 0.1 mm in amplitude; after switching, the spool position stays near 0.4 mm with a small-amplitude, low-frequency trend overall.

As shown in Figure 15, throughout this process, the sliding surface remains stable. In the initial stage, it undergoes small-amplitude, high-frequency oscillations around zero; between switching stage, its value steadily decreases to around −1 (a bounded value); after switching, it stabilizes near −1 with small-amplitude, low-frequency fluctuations. Therefore, the hydraulic system is stable under the switching controller.

A comparison of key performance metrics between the switching controller and the three algorithms in Section 3 is given in

Table 6. Comparison of control performance of four controllers.

Performance Metrics		Switching Controller	Controller A	Controller B	PID Controller
Initial Stage	Maximum Displacement Error	6.944 mm	23.619 mm	10.320 mm	36.122 mm
	Velocity Peak-to-Peak Fluctuation	0.138 m/s	0.138 m/s	0.878 m/s	0.050 m/s
	Spool-Displacement Peak-to-Peak Fluctuation	0.202 mm	0.202 mm	0.811 mm	0.360 mm
Stable Stage	Maximum Displacement Error	7.599 mm	201.86 mm	6.455 mm	38.756 mm
	Velocity Peak-to-Peak Fluctuation	0.011 m/s	0.017 m/s	0.017 m/s	0.011 m/s
	Spool-Displacement Peak-to-Peak Fluctuation	0.028 mm	0.200 mm	0.045 mm	0.029 mm

. As shown in Table 6, the switching controller outperforms Controller A and except for slightly worse speed fluctuations in the initial stage (including switching stage) compared to the PID Controller, the switching controller’s overall performance is superior to it. Compared to Controller B, within the initial stage, the switching controller reduces the maximum displacement error by 80.7%, the velocity peak-to-peak fluctuation by 84.3%, and the spool-displacement peak-to-peak fluctuation by 75.1%, yielding better tracking and stability; after switching, its stability is still better than Controller B with the spool-displacement peak-to-peak fluctuation reduced by 37.8%, though the maximum displacement error increases by 1.1 mm compared with Controller B. In summary, while the switching controller’s accuracy after switching is slightly lower than Controller B, it achieves superior tracking accuracy and stability during start-up, leading to the best overall performance.

5. Conclusions and Outlook

This paper addresses the dual challenge of start–stop shocks and load/parameter uncertainties for TBM hydraulic cylinders by proposing a “two-phase switching ASMC” strategy. Phase I targets a soft start by embedding smooth gating/ramped start-up into the sliding surface and equivalent control to limit initial flow and pressure rise, thereby suppressing pressure spikes and displacement overshoot caused by oil compressibility and sudden load changes. Phase II targets high-precision trajectory tracking; with adaptive laws and a boundary-layer treatment, it reduces chattering and steady-state error while maintaining robustness. Based on a state-space model incorporating oil compressibility, leakage, and pump/valve dynamics, a stability analysis demonstrates bounded stability and error convergence under parameter variations and external disturbances. Simulation results show that, compared with PID Controller and single ASMC Controller, the proposed method markedly reduces pressure/velocity peaks and displacement overshoot during start-up, achieves smaller steady-state errors with faster dynamics during tracking, and remains robust under wide load changes. Overall, without additional sensing or extensive a priori identification, the method unifies smooth start-up and precise tracking for TBM hydraulic cylinders, showing strong potential for practical deployment.

Given space limitations, this study does not yet develop a systematic treatment of multi-cylinder coordination and constrained optimization. Future work will pursue engineering-scale validation under larger and more complex loads to assess generalization, and extend the two-phase switching ASMC strategy toward multi-cylinder synchronization and energy-efficiency co-optimization.