Fuzzy Active Disturbance Rejection Control for Electro-Mechanical Actuator Based on Feedback Linearization

Abstract

As an actuation mechanism for achieving precision attitude control in aircraft, the electromechanical actuator (EMA) plays a critical role in ensuring flight safety and stability. However, the EMA is subject to unmeasurable unknown disturbances that act through mismatched channels relative to the system’s control input. To address this, this paper employs feedback linearization to transform the existing model. The transformed model effectively recasts the unknown disturbance into the same channel as the control input, thereby enabling active disturbance rejection via control law design. Furthermore, to overcome the challenge of immeasurable disturbances, an extended state observer (ESO) is designed to estimate the unknown disturbance; the estimated value is then directly utilized in the control law synthesis. Subsequently, a fuzzy logic system (FLS) is developed to perform real-time online adaptation and optimization of the controller parameters. Finally, extensive simulation results are provided to validate the effectiveness of the proposed algorithm.

1. Introduction

Aerodynamic rudder servo systems regulate aircraft flight attitudes by controlling the deflection angles of control surfaces, serving as critical electromechanical systems for ensuring stable flight dynamics [1,2]. Owing to their advantages in lightweight construction, precise controllability, and cost-effectiveness, permanent magnet synchronous motors (PMSMs) [3,4,5] have been predominantly adopted as actuation mechanisms in most research and engineering implementations of aerodynamic rudder servo systems. Enhancing the control performance of PMSM-driven servo systems directly contributes to improved overall flight stability, which has motivated extensive research on advanced control architectures for electromechanical servo systems in recent years.

The three-loop PID control methodology remains widely employed in EMA system design due to its practical implementability and straightforward parameter tuning [6,7]. However, its reliance on heuristic parameter calibration by domain experts and inherent inflexibility in adaptation often leads to suboptimal tracking accuracy and disturbance rejection under complex, time-varying operational demands. To mitigate these limitations, intelligent optimization algorithms such as particle swarm optimization [8], ant colony algorithms [9], and reinforcement learning have been explored for automated PID parameter selection [10]. Nevertheless, fundamental constraints in PID-based control topologies persist, resulting in inadequate dynamic response and robustness against aerodynamic disturbances. Moreover, optimization algorithms demand non-negligible iteration time, thereby compromising real-time control performance in EMAs.

EMAs require not only rapid response to desired position commands but also robustness against unmeasurable and unavoidable external disturbances. To address these challenges, the industry typically employs robust control, neural network control, sliding mode control, and model predictive control to compensate for disturbances and achieve stable control performance. Notably, ref. [11] proposes an adaptive terminal sliding mode control strategy that establishes a characteristic model for the online identification of system inertia parameter variations, enabling adaptation to wide-ranging parameter changes while suppressing uncertain disturbances. An internal model control algorithm based on global robust regulation theory for PMSM systems subject to parameter uncertainties and time-varying load disturbances is proposed in ref. [12], demonstrating validated posit ion tracking and disturbance rejection capabilities. Significantly, refs. [13,14,15] present active disturbance rejection control (ADRC) strategies for disturbance compensation control, where observers are designed to estimate system parametric uncertainties and unknown disturbances, thereby enhancing the overall control performance.

ADRC exhibits model-independent characteristics and demonstrates strong capability in handling system uncertainties. As documented in ref. [16], a robust high-LADRC employs a linear ESO to estimate parametric uncertainties and unknown external disturbances. Subsequently, ref. [17] introduces an adaptive LADRC approach that effectively balances disturbance attenuation against measurement noise suppression. Further advancing parameter tuning methodology, ref. [18] implements the Non-Dominated Sorting Genetic Algorithm II (NSGA-II) to optimize ADRC controller parameters, thereby streamlining complex controller design while demonstrating significant enhancement in dynamic response characteristics of the EMA compared to traditional PI control.

Despite these progress, certain limitations persist in EMA systems. Crucially, the mismatched disturbance problem—where unknown disturbances enter through channels distinct from control inputs—renders conventional feedforward control algorithms ineffective for disturbance compensation via control law design. Furthermore, traditional ADRC controllers suffer from cumbersome parameter tuning procedures and lack real-time adaptability, thus failing to accommodate dynamic operational demands.

To address the aforementioned challenges, this paper proposes an ADRC strategy incorporating fuzzy logic systems for the position tracking control of electromechanical actuators. The principal contributions are threefold:

• A feedback linearization-based model transformation method is proposed to decouple uncertain disturbances into the same channel as control inputs, enabling effective compensation through control law design.
• An ESO is designed to estimate uncertainties in EMAs with its stability rigorously proven via Lyapunov stability theory.
• An ADRC control law based on the transformed model is developed, which is complemented by a fuzzy logic system featuring membership functions and rule bases. This system dynamically adjusts control gains according to EMA position-tracking errors and their derivatives, thereby enhancing tracking precision.

The remainder of this paper is organized as follows. The transformed model of EMA is developed in Section 2, and the fuzzy ADRC algorithm is designed in Section 3. Detailed hardware-in-the-loop experimental results are provided in Section 4, which are followed by conclusions in Section 5.

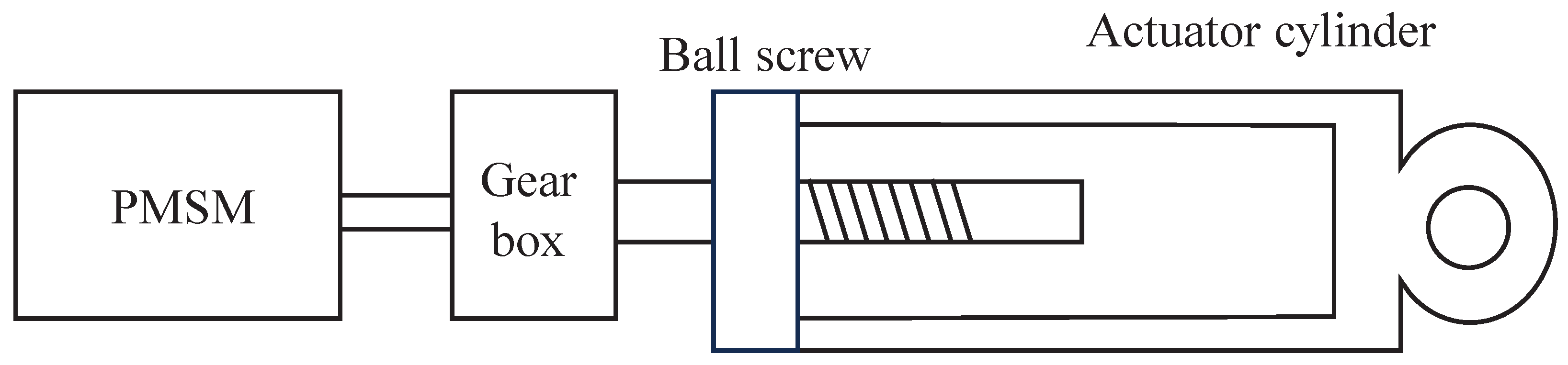
2. Electromechanical Actuator Model Development

As depicted in Figure 1, an EMA primarily consists of a PMSM and the mechanical transmission component, including the gearbox, ball screw, and actuator cylinder. The integration of these components facilitates the conversion of electrical energy into precisely controlled mechanical motion.

2.1. Model of PMSM

In the d-q rotor reference frame, the equation of mechanical motion for a PMSM describes the relationship between its rotational movement and the torque produced. This equation is expressed as ref. [2]:

$$\begin{array}{c}\hfill J_m{\ddot{\theta }}_m+B_m{\dot{\theta }}_m=T_e-T_l\end{array}$$

(1)

where ${\theta }_m$ denotes the angle of the PMSM, $J_m$ is the moment of inertia, $B_m$ represents the viscous friction coefficient, and $T_e$ and $T_l$ are the electromagnetic torque and load torque of the PMSM, respectively. When employing the control protocol of $i_d=0$, where $i_d$ denotes the d-axis stator current, the electromagnetic torque $T_e$ can be simplified and expressed as $T_e=K_e{i}_q={\displaystyle \frac{3P_n{\psi }_r}{2}}{i}_q$. Here, $i_q$ denotes the stator current on the q axis, $p_n$ is the number of pole pairs, and ${\psi }_r$ indicates the flux linkage, respectively.

2.2. Model of Mechanical Transmission Component

The motion equation and torque equation of the mechanical transmission component of the EMA can be formulated as follows:

$$\begin{array}{c}\hfill J_l{\ddot{\theta }}_l+B_l{\dot{\theta }}_l=n{T}_l-T_f\end{array}$$

(2a)

$$\begin{array}{c}\hfill T_l=K_l({\theta }_m-n{\theta }_l)\end{array}$$

(2b)

where ${\theta }_l$ is the ball screw output angular, $J_l$ and $B_l$ are the rotational inertial and viscous friction coefficients, n is the gear ratio of the gearbox, and $K_l$ denotes the stiffness of the shaft connecting the PMSM and the gearbox. $T_f$ is the external load torque of the EMA, which includes the hinge torque, rudder shaft friction torque, damping torque, and torque disturbances resulting from model parameter uncertainties. The displacement of the actuator, denoted as $d_l$, is calculated as

$$\begin{array}{c}\hfill d_l=k{\theta }_l\end{array}$$

(3)

where $k={\displaystyle \frac{P}{2\pi }}$ with P representing the pitch of the screw.

2.3. Model of Electromechanical Actuator

By integrating the PMSM model (1) and the mechanical transmission component models (2) and (3), the comprehensive model of the electromechanical actuator can be represented using the following state-space formulation:

$$\begin{array}{cc}\hfill \dot{\mathit{x}}=& \mathit{A}\mathit{x}+\mathit{B}u+\mathit{E}\epsilon \hfill \end{array}$$

(4a)

$$\begin{array}{cc}\hfill y=& \mathit{C}\mathit{x}\hfill \end{array}$$

(4b)

with

$$\begin{array}{cc}\hfill \mathit{A}=& \left[\begin{array}{cccc}0& 1& 0& 0\\ -{\displaystyle \frac{K_l}{J_m}}& -{\displaystyle \frac{B_m}{J_m}}& {\displaystyle \frac{n{K}_l}{J_m}}& 0\\ 0& 0& 0& 1\\ {\displaystyle \frac{n{K}_l}{J_l}}& 0& -{\displaystyle \frac{n^2{K}_l}{J_l}}& -{\displaystyle \frac{B_l}{J_l}}\end{array}\right]\hfill \\ \hfill \mathit{B}=& {\left[\begin{array}{cccc}0& {\displaystyle \frac{K_e}{J_m}}& 0& 0\end{array}\right]}^T\hfill \\ \hfill \mathit{E}=& {\left[\begin{array}{cccc}0& 0& 0& -1\end{array}\right]}^T\hfill \\ \hfill \mathit{C}=& \left[\begin{array}{cccc}0& 0& k& 0\end{array}\right]\hfill \end{array}$$

where the model states, input, and outputs are $\mathit{x}=[x_1,x_2,x_3,$$x_4{]}^T={[{\theta }_m,w_m,{\theta }_l,w_l]}^T$, $u=i_q$, $y=d_l$, and $\epsilon ={\displaystyle \frac{T_f}{J_l}}$ is regarded as an unknown external disturbance. Note that the variable $\epsilon$ is assumed to change slowly, such that its derivative $\dot{\epsilon }$ can be approximated as zero. The EMA model (4) can also be represented as the block diagram shown in Figure 2, and the corresponding transfer function is

$$\begin{array}{c}\hfill d_l\left(s\right)={\displaystyle \frac{F_1\left(s\right)}{G\left(s\right)}}{i}_q\left(s\right)+{\displaystyle \frac{F_2\left(s\right)}{G\left(s\right)}}{T}_f\left(s\right)\end{array}$$

(5)

with

$$\begin{array}{cc}\hfill F_1\left(s\right)=& nk{K}_l{K}_e\hfill \\ \hfill F_2\left(s\right)=& k{J}_m{s}^2+k{B}_{m}s+k{K}_l\hfill \\ \hfill G\left(s\right)=& J_m{J}_l{s}^4+(J_m{B}_l+B_m{J}_l)s^3+(B_m{B}_l\hfill \\ \hfill & +K_l{J}_l+K_l{n}^2{J}_m)s^2+(K_l{B}_l+K_l{n}^2{B}_m)s.\hfill \end{array}$$

2.4. Feedback Linearization-Based Model Transform

Upon analyzing the EMA model (4), it becomes apparent that the external load torque $ϵ$, acting as an unknown disturbance, does not align with the control input channel u. This misalignment precludes the direct application of conventional feedforward control methods for disturbance compensation. Given the affine nature of the system in (4), feedback linearization [19] can be utilized to restructure the original EMA model into a new configuration. In this transformed model, the disturbance and control input are effectively aligned within the same channel, enabling more efficient disturbance compensation. Based on the above analysis and theory of feedback linearization, the relative degree of the system is determined by differentiating the output y with respect to time until the control input u explicitly appears. The Lie derivative of a scalar function $h\left(\mathit{x}\right)$ along a vector field $f\left(\mathit{x}\right)$ is denoted as $L_{f}h\left(\mathit{x}\right)={\displaystyle \frac{\partial h}{\partial \mathit{x}}}f\left(\mathit{x}\right)$. The first derivative of the output y is given by

$$\dot{y}={\displaystyle \frac{\partial h}{\partial \mathit{x}}}\dot{\mathit{x}}=L_{f}h\left(\mathit{x}\right)+L_{g}h\left(\mathit{x}\right)u$$

(6)

Substituting the system parameters, we obtain $L_{g}h\left(\mathit{x}\right)=0$ and $L_{f}h\left(\mathit{x}\right)=k{x}_4$. Thus, $\dot{y}=k{x}_4$. Since the coefficient of u is zero, further differentiation is required. The second derivative is derived as

$$\ddot{y}=L_f^{2}h\left(\mathit{x}\right)+L_g{L}_{f}h\left(\mathit{x}\right)u$$

(7)

Calculating the Lie derivatives yields $L_g{L}_{f}h\left(\mathit{x}\right)=0$ and $L_f^{2}h\left(\mathit{x}\right)=k({\displaystyle \frac{n{K}_l}{J_l}}{x}_1-{\displaystyle \frac{n^2{K}_l}{J_l}}{x}_3-{\displaystyle \frac{B_l}{J_l}}{x}_4-\epsilon )$. The disturbance $\epsilon$ appears in this step, but the control input u is still absent. Differentiating again yields the third derivative:

$$\stackrel{⃛}{y}=L_f^{3}h\left(\mathit{x}\right)+L_g{L}_f^{2}h\left(\mathit{x}\right)u$$

(8)

Here, $L_g{L}_f^{2}h\left(\mathit{x}\right)=0$ because the expression of $L_f^{2}h\left(\mathit{x}\right)$ depends on $x_1,x_3,x_4$, while the control input vector $\mathit{B}$ only affects the $x_2$ channel. The term $L_f^{3}h\left(\mathit{x}\right)$ is derived as

$$L_f^{3}h\left(\mathit{x}\right)=k(-{\displaystyle \frac{B_{l}n{K}_l}{J_l^2}}{x}_1+{\displaystyle \frac{n{K}_l}{J_l}}{x}_2+{\displaystyle \frac{B_l{n}^2{K}_l}{J_l^2}}{x}_3+\left({\displaystyle \frac{B_l^2}{J_l^2}}-{\displaystyle \frac{n^2{K}_l}{J_l}}\right)x_4+{\displaystyle \frac{B_l}{J_l}}\epsilon )$$

(9)

Finally, the fourth derivative is obtained:

$$\stackrel{⃛}{y}=L_f^{4}h\left(\mathit{x}\right)+L_g{L}_f^{3}h\left(\mathit{x}\right)u$$

(10)

The decoupling matrix (scalar in SISO case) is calculated as

$$L_g{L}_f^{3}h\left(\mathit{x}\right)={\displaystyle \frac{\partial \left(L_f^{3}h\right)}{\partial \mathit{x}}}\mathit{B}={\displaystyle \frac{\partial }{\partial \mathit{x}}}\left(k{\displaystyle \frac{n{K}_l}{J_l}}{x}_2\right)\mathit{B}={\displaystyle \frac{kn{K}_l{K}_e}{J_l{J}_m}}$$

(11)

The term $L_f^{4}h\left(\mathit{x}\right)$ is derived as

$$\begin{array}{c}\hfill \begin{array}{cc}{L}_f^{4}h\left(\mathit{x}\right)\hfill & =k({\displaystyle \frac{n{K}_l{B}_l^2}{J_l^3}}-{\displaystyle \frac{n{K}_l^2}{J_l{J}_m}}-{\displaystyle \frac{n^3{K}_l^2}{J_l^2}})x_1-kn{K}_l({\displaystyle \frac{B_l}{J_l^2}}+{\displaystyle \frac{B_m}{J_l{J}_m}})x_2\hfill \\ \hfill & +k({\displaystyle \frac{n^2{K}_l^2}{J_l{J}_m}}+{\displaystyle \frac{n^4{K}_l^2}{J_l^2}}-{\displaystyle \frac{n^2{K}_l{B}_l^2}{J_l^3}})x_3+k({\displaystyle \frac{2B_l{n}^2{K}_l}{J_l^2}}-{\displaystyle \frac{B_l^3}{J_l^3}})x_4\hfill \\ \hfill & +{\displaystyle \frac{kn{K}_l{K}_e}{J_l{J}_m}}u+k\left({\displaystyle \frac{n^2{K}_l}{J_l}}-{\displaystyle \frac{B_l^2}{J_l^2}}\right)\epsilon \hfill \end{array}l\end{array}$$

(12)

Since all physical parameters $k,n,K_l,J_l,K_e,J_m$ are non-zero constants, it follows that $L_g{L}_f^{3}h\left(\mathit{x}\right)\ne 0$.

A critical insight from the derivation above concerns the nature of the disturbance. In the original state-space model (4), the disturbance $\epsilon$ acts on the load acceleration channel ${\dot{x}}_4$, while the control input u acts on the motor current channel ${\dot{x}}_2$, which constitutes a typical mismatched disturbance problem, which is challenging for conventional disturbance compensation. However, by defining the coordinate transformation $\mathit{z}={[z_1,z_2,z_3,z_4]}^T={[y,\dot{y},\ddot{y},\stackrel{⃛}{y}]}^T$, the system can be deduced as

$$\begin{array}{cc}\hfill {\dot{z}}_1=& z_2\hfill \end{array}$$

(13a)

$$\begin{array}{cc}\hfill {\dot{z}}_2=& z_3\hfill \end{array}$$

(13b)

$$\begin{array}{cc}\hfill {\dot{z}}_3=& z_4\hfill \end{array}$$

(13c)

$$\begin{array}{cc}\hfill {\dot{z}}_4=& b_1{x}_1+b_2{x}_2+b_3{x}_3+b_4{x}_4+b_{5}u+b_6\epsilon \hfill \end{array}$$

(13d)

with

$$\begin{array}{cc}\hfill b_1=& {\displaystyle \frac{nk{K}_l{B}_l^2}{J_l^3}}-{\displaystyle \frac{n^{3}k{K}_l^2}{J_l^2}}-{\displaystyle \frac{nk{K}_l^2}{J_m{J}_l}}\hfill \\ \hfill b_2=& -{\displaystyle \frac{nk{B}_l{K}_l}{J_l^2}}-{\displaystyle \frac{nk{K}_l{B}_m}{J_l{J}_m}}\hfill \\ \hfill b_3=& -{\displaystyle \frac{B_l^2{n}^{2}k{K}_l}{J_l^3}}+{\displaystyle \frac{n^{4}k{K}_l^2}{J_l^2}}+{\displaystyle \frac{n^{2}k{K}_l^2}{J_m{J}_l}}\hfill \\ \hfill b_4=& -{\displaystyle \frac{k{B}_l^3}{J_l^3}}+{\displaystyle \frac{2n^{2}k{K}_l{B}_l}{J_l^2}}\hfill \\ \hfill b_5=& {\displaystyle \frac{nk{K}_l{K}_e}{J_m{J}_l}},b_6=-{\displaystyle \frac{k{B}_l^2}{J_l^2}}+{\displaystyle \frac{n^{2}k{K}_l}{J_l}}.\hfill \end{array}$$

In (13), the aggregated disturbance term $\epsilon$ appears in the same channel ${\dot{z}}_4$ as the control input u. This mathematical transformation effectively converts the mismatched disturbance into a matched disturbance.

3. Fuzzy ADRC Algorithm Design

A novel control methodology incorporating disturbance compensation mechanisms is proposed herein. As depicted in Figure 3, $i_a,i_b,$ and $i_c$ represent the three-phase stator currents. $y_d$ represents the reference of displacement y. The blocks labeled $2r/2s$ and $2s/3s$ correspond to the inverse park transformation and the SVPWM generation, respectively. The control strategy consists of the following two control loops:

• In the inner loop, two proportional–integral (PI) control methods regulate both d-axis and q-axis currents to achieve reference tracking, thereby boosting the current-loop bandwidth for stringent dynamic performance specifications. Exploiting the decoupling between the d-axis and q-axis current loops controller in an FOC, the control scheme adopts $i_d^{\ast }=0$ to streamline implementation while maintaining torque regulation via $i_q$.
• In the outer loop, an active disturbance rejection control (ADRC) strategy is proposed based on feedback linearization, where the desired command current input is calculated using the state feedback of a PMSM and the estimation of disturbance from an ESO, with control law gains adaptively optimized via a fuzzy logic inference mechanism.

The architecture leverages the affine nature of electromechanical servo systems to enable separate controller–observer design via the separation principle.

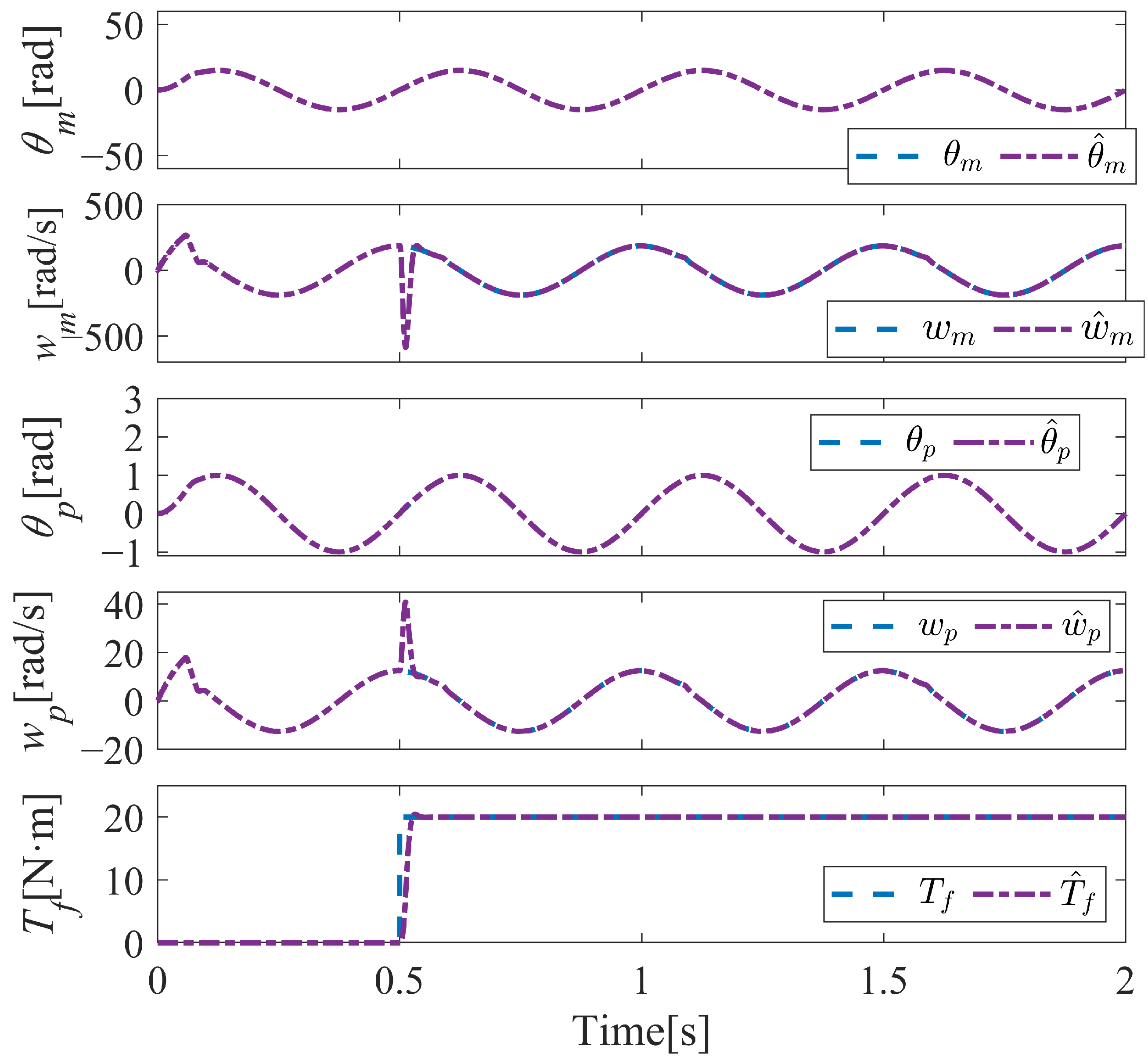
3.1. ESO for Uncertain External Torque Estimation

Due to the presence of an uncertain external load torque that cannot be precisely measured, which is treated as a lumped external disturbance acting on the system, an ESO is designed to achieve its accurate estimation. Specifically, by augmenting the disturbance as an extended state dimension to form a new state vector, (4) can be translated into the extended state equation as

$$\begin{array}{cc}\hfill \dot{\overline{\mathit{x}}}=& \overline{\mathit{A}}\overline{\mathit{x}}+\overline{\mathit{B}}u\hfill \end{array}$$

(14a)

$$\begin{array}{cc}\hfill y=& \overline{\mathit{C}}\overline{\mathit{x}}\hfill \end{array}$$

(14b)

where the state vector $\overline{\mathit{x}}$ and the matrices $\overline{\mathit{A}}$, $\overline{\mathit{B}}$, and $\overline{\mathit{C}}$ are

$$\begin{array}{c}\hfill \begin{array}{c}\overline{\mathit{x}}=\left[\begin{array}{c}\mathit{x}\\ \epsilon \end{array}\right],\overline{\mathit{A}}=\left[\begin{array}{cc}\mathit{A}& \mathit{E}\\ {\mathit{0}}_{\mathit{1}\times \mathit{4}}& 0\end{array}\right],\overline{\mathit{B}}=\left[\begin{array}{c}\mathit{B}\\ 0\end{array}\right]\hfill \\ \overline{\mathit{C}}=\left[\begin{array}{ccccc}0& 0& k& 0& 0\end{array}\right].\hfill \end{array}\end{array}$$

with ${\mathit{0}}_{\mathit{1}\times \mathit{4}}$ denoting the zero matrix of dimension $1\times 4$. The ESO is designed as

$$\begin{array}{c}\hfill \begin{array}{c}\dot{\widehat{\overline{\mathit{x}}}}=\overline{\mathit{A}}\widehat{\overline{\mathit{x}}}+\overline{\mathit{B}}u+\mathit{L}(y-\overline{\mathit{C}}\widehat{\overline{\mathit{x}}})\hfill \end{array}\end{array}$$

(15)

where $\widehat{\overline{x}}$ is the estimation of $\overline{x}$, and L is the designed observer gain vector, which can be systematically obtained through appropriate pole placement. The estimated state $\widehat{\epsilon }$ obtained from (15) is utilized to replace $\epsilon$ in the transformed model (13) to address the challenge of unmeasurable external disturbance. The stability proof for the observer is subsequently provided.

3.2. Fuzzy ADRC Based on Transformed Model

Based on the transformed model (13), exponential convergence of the system is guaranteed when the error differential Equation (16) holds ref. [20].

$$\begin{array}{c}\hfill \stackrel{⃜}{e}+k_4\stackrel{⃛}{e}+k_3\ddot{e}+k_2\dot{e}+k_{1}e=0\end{array}$$

(16)

with $k_1$, $k_2$, $k_3$ and $k_4$ denoting controller gains, and $e=y-y_d$ denoting the tracking error. The tracking error system achieves exponential stability by selecting the gain coefficient to give the eigenvalues of Equation (16) a negative real part.

Then, the following feedback control method can be designed:

$$\begin{array}{c}\hfill u={\displaystyle \frac{v-(b_1{x}_1+b_2{x}_2+b_3{x}_3+b_4{x}_4)-b_6\epsilon }{b_5}}\end{array}$$

(17)

where v is an auxiliary control variable that is designed as

$$\begin{array}{c}\hfill \begin{array}{c}v=\stackrel{⃜}{y_d}-k_4(z_4-\stackrel{⃛}{y_d})-k_3(z_3-\ddot{y_d})\hfill \\ -k_2(z_2-\dot{y_d})-k_1(z_1-y_d)\hfill \end{array}\end{array}$$

(18)

Fuzzy logic systems, which typically do not rely on precise system models or parameters, are well suited for electromechanical servo systems with inherent uncertainties. This paper employs a fuzzy logic system to perform online optimization of the control law gains for feedback linearization. Specifically, a fuzzy logic system is employed to online tune the gain coefficients $k_1$ and $k_2$ in the control law, which are associated with the error e and its derivative $\dot{e}$. Consequently, the adjusted gains $k_{1n}$ and $k_{2n}$ satisfy the following equations

$$\begin{array}{c}\hfill k_{1n}=k_1+\Delta k_1\end{array}$$

(19a)

$$\begin{array}{c}\hfill k_{2n}=k_2+\Delta k_1\end{array}$$

(19b)

where $\Delta k_1$ and $\Delta k_2$ denote the incremental adjustment values for the controller gains $k_1$ and $k_2$, respectively. Therefore, the new control law is expressed as

$$\begin{array}{c}\hfill u_n={\displaystyle \frac{v_n-(b_1{x}_1+b_2{x}_2+b_3{x}_3+b_4{x}_4)-b_6\epsilon }{b_5}}\end{array}$$

(20)

where $v_n$ is designed as

$$\begin{array}{c}\hfill \begin{array}{c}{v}_n=\stackrel{⃜}{y_d}-k_4(z_4-\stackrel{⃛}{y_d})-k_3(z_3-\ddot{y_d})\hfill \\ -k_{2n}(z_2-\dot{y_d})-k_{1n}(z_1-y_d).\hfill \end{array}\end{array}$$

(21)

The fuzzy logic system primarily comprises three components: fuzzification, a fuzzy rule base, and defuzzification. During the fuzzification process, normalization factors are first applied to map inputs and outputs to the fuzzy universe of discourse. To mitigate the exponential growth in complexity of the fuzzy rule base associated with increasing input dimensionality, only the error and its derivative are adopted as inputs to the fuzzy logic system, while the parameters to be optimized serve as the output. The corresponding fuzzification procedure is implemented as follows:

$$\begin{array}{c}\hfill d={\displaystyle \frac{d_{min}+d_{max}}{2}}+K(d^{\prime }-{\displaystyle \frac{d_{min}^{\prime }+d_{max}^{\prime }}{2}})\end{array}$$

(22)

where K denotes the normalization factor, d and $d^{\prime }$ represent the variables before and after normalization, respectively, $[d_{min},d_{max}]$ specifies the fuzzy universe of discourse, and $[d_{min}^{\prime },d_{max}^{\prime }]$ defines the physical domain. The fuzzy subsets for inputs and outputs are selected as specified in (23) with conventional triangular membership functions employed as illustrated in Figure 4 and Figure 5. This enables linguistic representation of the input–output mapping.

$$\begin{array}{c}\hfill e=\left\{\mathrm{NB},\mathrm{NM},\mathrm{NS},\mathrm{ZO},\mathrm{PS},\mathrm{PM},\mathrm{PB}\right\}\end{array}$$

(23a)

$$\begin{array}{c}\hfill \dot{e}=\left\{\mathrm{NB},\mathrm{NM},\mathrm{NS},\mathrm{ZO},\mathrm{PS},\mathrm{PM},\mathrm{PB}\right\}\end{array}$$

(23b)

$$\begin{array}{c}\hfill \Delta k_1=\left\{\mathrm{NB},\mathrm{NM},\mathrm{NS},\mathrm{ZO},\mathrm{PS},\mathrm{PM},\mathrm{PB}\right\}\end{array}$$

(23c)

$$\begin{array}{c}\hfill \Delta k_2=\left\{\mathrm{NB},\mathrm{NM},\mathrm{NS},\mathrm{ZO},\mathrm{PS},\mathrm{PM},\mathrm{PB}\right\}\end{array}$$

(23d)

As the decision-making core of the fuzzy logic system, the fuzzy rule base captures the underlying fuzzy logic relationships between inputs and parameters to be optimized. The fuzzy inference rules for $\Delta k_1$ and $\Delta k_2$ established in this work are presented in

Table 1. Fuzzy inference rules for $\Delta k_1$.

$\mathit{e}\setminus \dot{\mathit{e}}$	NB	NM	NS	ZE	PS	PM	PB
NB	PB	PB	PM	PM	PB	ZE	NS
NM	PB	PB	PM	PB	PB	NS	NS
NS	PM	PM	PM	PB	ZE	NM	NM
ZE	PM	PM	PS	ZE	NS	NM	NM
PS	PS	PS	ZE	NS	NS	NM	NB
PM	PS	ZE	NS	NM	NM	NB	NB
PB	ZE	ZE	NM	NM	NM	ZE	NM

and

Table 2. Fuzzy inference rules for $\Delta k_2$.

$\mathit{e}\setminus \dot{\mathit{e}}$	NB	NM	NS	ZE	PS	PM	PB
NB	PS	NS	NB	NB	NB	NS	ZE
NM	PS	NS	NB	NM	NB	NS	ZE
NS	ZE	NS	NM	NM	NS	NS	ZE
ZE	ZE	NS	NS	NS	NS	ZE	ZE
PS	ZE	ZE	ZE	ZE	ZE	PS	PB
PM	PB	PS	PS	PS	PS	PS	PB
PB	PB	PM	PM	PM	NM	PS	PS

, respectively.

Finally, the centroid defuzzification method is employed to compute the optimized gain adjustments for the active disturbance rejection controller based on a transformed model. This is achieved by calculating the centroid of the aggregated membership function of the fuzzy set.

4. Results and Discussion

To validate the effectiveness of the proposed fuzzy active disturbance rejection control algorithm based on feedback linearization, extensive MATLAB/SIMULINK R2023b simulations are conducted on an electromechanical actuator with its parameters shown in

Table 3. Parameters of the EMA system.

Parameters	Value	Unit
$J_m$	$2.4\times {10}^{-4}$	$\mathrm{kg}·{\mathrm{m}}^2$
$B_m$	$0.01$	$\mathrm{N}·\mathrm{s}/\mathrm{rad}$
n	15
$J_l$	$0.103$	$\mathrm{kg}·{\mathrm{m}}^2$
$B_l$	$0.01$	$\mathrm{N}·\mathrm{s}/\mathrm{rad}$
$K_l$	$1\times {10}^3$	N/m
$K_t$	$0.16$	$\mathrm{N}·\mathrm{m}/\mathrm{A}$
P	$2\mathsf{\pi }$

. The gains in the feedback linearization control algorithm and ESO are selected as $k_1=1.124\times {10}^{11},k_2=1.566\times {10}^9,k_3=3.84\times {10}^6,k_4=3400$, and $L={[-3.84\times {10}^4,3.5\times {10}^7,1.46\times {10}^3,-5.53\times {10}^6,-7.12\times {10}^4]}^T$, respectively. Note that these gains are determined using the method of pole assignment. In addition, the normalization factor K associated with input e is $0.13$, whereas that for input $\dot{e}$ is $0.001$. Regarding the outputs, the factor K for $\Delta k_1$ is ${10}^9$, and for $\Delta k_2$, it is $-4\times {10}^9$. The simulation section provides a comparison of displacement of the actuator response curves with a traditional PID and pure feedback linearization, including three typical responses (step response, sine response and ramp response) and two common disturbances (step constant disturbance and sine disturbance). Next, we provide the observation variable curve of the ESO.

4.1. Displacement Step Tracking Results

To highlight the effectiveness of fuzzy active disturbance rejection control based on feedback linearization, this section introduces 20-step disturbance torque and a sine disturbance torque at 0.5 s based on the 1 m and 0 s position step tracking. The position tracking curve and the observation curve of the ESO are presented. Regarding the position tracking curve graph, traditional PID and pure feedback linearization algorithms are provided as comparison benchmarks, which are briefly described as follows:

• Method 1: PID control method.
• Method 2: Feedback linearization method without fuzzy adaption.
• Proposed: The fuzzy ADRC method based on feedback linearization.

4.1.1. Step Torque Disturbance Results

Figure 6 shows the position response curve under step command and step torque disturbance, where the torque disturbance is set to 20 N·m and the position command is set to the initial 1 m. It can be seen that in step tracking, the fuzzy control based on feedback linearization proposed in this paper not only has a faster response speed compared to the benchmark algorithm but also a smooth dynamic process without overshoot. The steady-state error is reduced by one order of magnitude compared to the traditional PID algorithm of 0.03 cm, and its steady-state error is roughly consistent with the pure feedback linear algorithm, reaching 0.001 cm. However, the adjustment time and overshoot are both better than pure feedback linearization. When subjected to step torque interference in 0.5 s, the PID algorithm cannot resist the interference torque, resulting in a steady-state error of 0.8 cm. However, the proposed algorithm has the ability to resist interference, and the steady-state error after interference reaches 0.001 cm. However, compared with feedback linearization, the recovery ability of fuzzy control is stronger. The maximum deviation of feedback linearization from the position instruction is 3 cm, but the maximum deviation of fuzzy control is only 1.5 cm, and the recovery time and stability are stronger than feedback linearization.

The observation curve of the extended state observer is shown in Figure 7. When subjected to torque disturbance, the observed values of the system are basically consistent with the variable values of the system: the disturbance estimation of the observer can track the observed values within 0.1 s, achieve fast torque disturbance estimation, and have good dynamic characteristics. Although the observed variables of the system are affected by actual torque disturbance variables, they can all recover to normal within 0.1 s and then closely follow the system variables, indicating the excellent estimation performance of the ESO.

4.1.2. Sinusoidal Torque Disturbance Results

Figure 8 shows the position response curve under step command and sine torque disturbance, and the position command is set to an initial 1 m. When subjected to step torque disturbance for 0.5 s, the PID algorithm still cannot resist the disturbance torque, and after stabilization, it produces equal amplitude oscillations with a maximum error of 0.6 cm. The proposed algorithm has the ability to resist interference, and the steady-state error after disturbance reaches 0.008 cm. Therefore, the fuzzy control and feedback linearization under sine disturbance have the same disturbance suppression effect.

The observation curve of the extended state observer is shown in Figure 9. When subjected to sinusoidal torque disturbances, the observed values of the system are basically consistent with the variable values of the system. The disturbance estimation of the observer can quickly estimate the disturbance values, and the system variables and observed variables are basically not affected by the sinusoidal torque disturbance. This indicates that the algorithm proposed in this paper can effectively suppress small amplitude sinusoidal torque disturbances.

4.2. Displacement Sine Curve Tracking Results

A comparison of the tracking performance under a sinusoidal reference signal was conducted among the PI controller, the feedback linearization algorithm, and the proposed algorithm. The amplitude of the sinusoidal tracking signal was set to 1 m with a frequency of 2 Hz. Simulations were performed in the presence of both step disturbance torque and sinusoidal disturbance torque, respectively.

4.2.1. Constant Torque Disturbance Results

A constant torque disturbance of 20 N·m is applied. Figure 10 and Figure 11 depict the position tracking response of the system and the observation curves of the ESO, respectively, under this disturbance.

4.2.2. Sine Torque Disturbance Results

Furthermore, for the sinusoidal disturbance case, the disturbance was set as a sinusoidal signal with an amplitude of 40 N·m and a frequency of 10 Hz. The corresponding position tracking responses and the ESO observation curves are depicted in Figure 12 and Figure 13, respectively.

It can be observed that during sinusoidal trajectory tracking without disturbances, all three algorithms achieve similar convergence speeds and are able to accurately follow the command trajectory. However, under disturbance conditions, the PID algorithm exhibits significant steady-state error, while the conventional feedback linearization method shows larger error peaks and slower error recovery. In contrast, the proposed fuzzy feedback linearization control algorithm demonstrates smaller error peaks and faster error convergence when subjected to both types of disturbances. As illustrated in Figure 13, the observer can still accurately estimate the fast-changing disturbance, demonstrating its excellent robustness.

To further validate the advantages of the proposed algorithm, the tracking performance of the three methods was evaluated using the following servo tracking error metrics: the maximum absolute error (MAE), the integral absolute error (IAE), and the root mean square error (RMSE). The corresponding indices are summarized in

Table 4. Tracking error metrics in sinusoidal command.

Disturbance Types	Methods	MAE	IAE	RMSE
Constant	Method 1	0.28791	0.1009	0.1294
	Method 2	0.20551	0.03990	0.05886
	Proposed	0.19158	0.01365	0.03645
Sinusoidal	Method 1	0.30145	0.1606	0.1635
	Method 2	0.20551	0.0158	0.04167
	Proposed	0.19158	0.01361	0.03629

.

Furthermore, the tracking error indices presented in Table 4 indicate that the proposed algorithm significantly enhances the system’s disturbance rejection and rapid tracking performance for complex sinusoidal trajectories, outperforming the other compared algorithms.

5. Conclusions

To address the challenges of mismatched disturbances and parameter tuning difficulties in electromechanical systems, this paper proposes an active disturbance rejection control method integrating fuzzy logic systems with the model transformed by the feedback linearization method. An ESO is implemented to estimate unmeasurable disturbances with its convergence rigorously guaranteed via Lyapunov stability theory. Novel fuzzy membership functions and rule bases are designed to dynamically update controller parameters. The proposed control framework enables comprehensive compensation for unknown disturbances, demonstrating enhanced dynamic response and steady-state precision compared to conventional industrial control algorithms. Our future work will concentrate on the optimization of the proposed algorithm and its deployment in practical systems.