Development and Performance Validation of a Magnetorheological Damper for Passenger Cars Featuring Ball Screw and MR Brake

Abstract

This paper introduces a novel Magnetorheological (MR) damper integrated with a ball-screw mechanism (SMRB damper) that is designed to unify translational and rotational motions for enhanced automotive suspension performance. While shear-mode rotary MR dampers offer excellent responsiveness and stability, prior designs face persistent issues such as high off-state torque, structural complexity, or limited damping force. The proposed damper aims to overcome these limitations. Its design and operating principle are presented, followed by the development of a mathematical model based on the Bingham-plastic formulation and finite element analysis. To maximize damping capability, the key structural parameters are optimized using an Adaptive Particle Swarm Optimization (APSO) algorithm. Finally, a prototype is fabricated based on the optimized results, and experimental tests validate its performance against simulation predictions, demonstrating its improved potential for vibration control applications.

1. Introduction

Over the past decade, advances in vibration control have become increasingly vital for automotive suspension systems, which must mitigate vibrations to ensure safety and passenger comfort. Magnetorheological (MR) dampers have emerged as a leading solution, offering high damping force, precise controllability, and effective adaptation to varying conditions through the use of MR fluids [1,2,3,4]. Studies have focused on three primary operating modes: flow, shear, and squeeze modes. Among these, shear and valve modes receiving the most practical attention, especially for MR dampers [5,6,7]. Each mode presents distinct trade-offs: the valve mode is structurally simple and easily controlled but suffers from pressure drops and response delays; the flow mode produces large damping forces but has high initial resistance, limiting sensitivity. In contrast, the shear mode provides smaller damping forces but superior responsiveness, sensitivity, and stability, making it a particularly promising approach for advancing suspension system performance.

Several recent studies have focused on rotary MR dampers operating in shear mode. Sun et al. [8] examined a rotary MR damper integrated into a seat suspension system for heavy-duty vehicles. Their experimental results demonstrated that the damper delivered performance comparable to that of linear MR dampers. However, the structural design had not yet been optimized to improve efficiency or reduce the off-state torque at 0 A. Bai et al. [9] developed a multi-disc rotary MR damper intended for seat suspensions with a parallelogram mechanism. Although effective, this damper featured a large structure and high energy consumption, limiting its suitability to systems with fixed layouts and making it impractical for installations requiring compactness or design flexibility. Yu et al. [10] introduced a rotary MR damper employing a helical flow configuration that enabled operation in both flow and shear modes, resulting in a more compact design than traditional shear-mode dampers. Following this, an enhanced rotary MR damper comprising two passive discs and one active disc was proposed, allowing precise adjustment of damping force and stiffness [11]. Experimental validation confirmed its ability to regulate angular stiffness with clear dependence on rotational angle, torque, and current. Although the issue of low damping torque density was addressed, the device still suffered from structural complexity and manufacturing challenges. Park et al. [12] developed a rotary MR damper for low-floor vehicles with semi-active suspension. The prototype exhibited rapid response and achieved a high damping torque of 600 Nm, slightly below the simulated value of 744.8 Nm; however, the off-state torque remained undesirably high. Similarly, Zhu et al. [13] designed a compact rotary MR damper integrated with a bearing, but the output torque was found to be unstable during rotation. Ehab et al. [14] optimized a rotary MR damper for torsional vibration control, demonstrating its effectiveness. Nevertheless, the design was susceptible to a magnetic bottleneck effect and performance degradation due to temperature variation during operation. To address the bottleneck issue, Zuo et al. [15] proposed a rotary MR damper with a T-shaped rotor for seat suspension applications. Although this configuration improved certain aspects of magnetic flux distribution, it had not yet been fully optimized to enhance overall performance or reduce the brake volume. Moreover, the maximum damping force achieved for seat suspension applications was only about 320 N, indicating room for further improvement. Yang et al. [16] proposed an integrated optimization strategy for multi–MR damper systems that jointly considers material properties, damper configuration, and installation layout. The results indicate that effective seismic vibration control can be achieved with fewer dampers and improved efficiency, demonstrating the method’s potential for economical vibration mitigation in spatially irregular structures. Next, Yang et al. [17] proposed an ant colony–based cooperative control strategy for multi–magnetorheological damper systems to mitigate coupled translational–torsional vibrations in spatially irregular structures. By enabling coordinated real-time current allocation among dampers with different functional roles, the approach improves overall vibration control performance and demonstrates robustness under various seismic excitations. Several studies have proposed the use of multiple coils in MR dampers to achieve a more uniform and controllable magnetic field, thereby enhancing damping capacity and control flexibility [18]. This configuration improves MR fluid utilization and is well suited for high-performance vibration control applications. However, the use of multiple coils also leads to higher power consumption. Although numerous studies have investigated MR dampers as aforementioned, none have integrated both translational and rotational motions to enhance performance and adaptability, especially for vehicle suspension application. More recently, Le et al. [19] proposed a Screw MR Brake (SMRB) damper that integrates a ball-screw mechanism with an MR brake to enhance the damping force in automotive applications. However, the proposed structure is relatively complex, which makes manufacturing and assembly challenging. In addition, the damper has not yet been fabricated, and its performance has therefore not been experimentally validated.

To overcome this limitation, the present work introduces a new SMRB damper with simple MR brake structure that convenient for experimental works and implementation. In addition, experimental works are conducted and compared with simulated ones, with its structural design and operating principles described in Section 2. Section 3 develops the mathematical model of the SMRB damper using the Bingham plastic formulation in conjunction with finite element analysis. To further increase the damping capability, an optimization problem is established and solved using the Adaptive Particle Swarm Optimization (APSO) algorithm, as detailed in Section 4. Finally, based on the optimized parameters, experimental evaluations are conducted to assess the damper’s performance and compare it with the simulation results.

2. Working Principles and Modeling of SMRB Damper

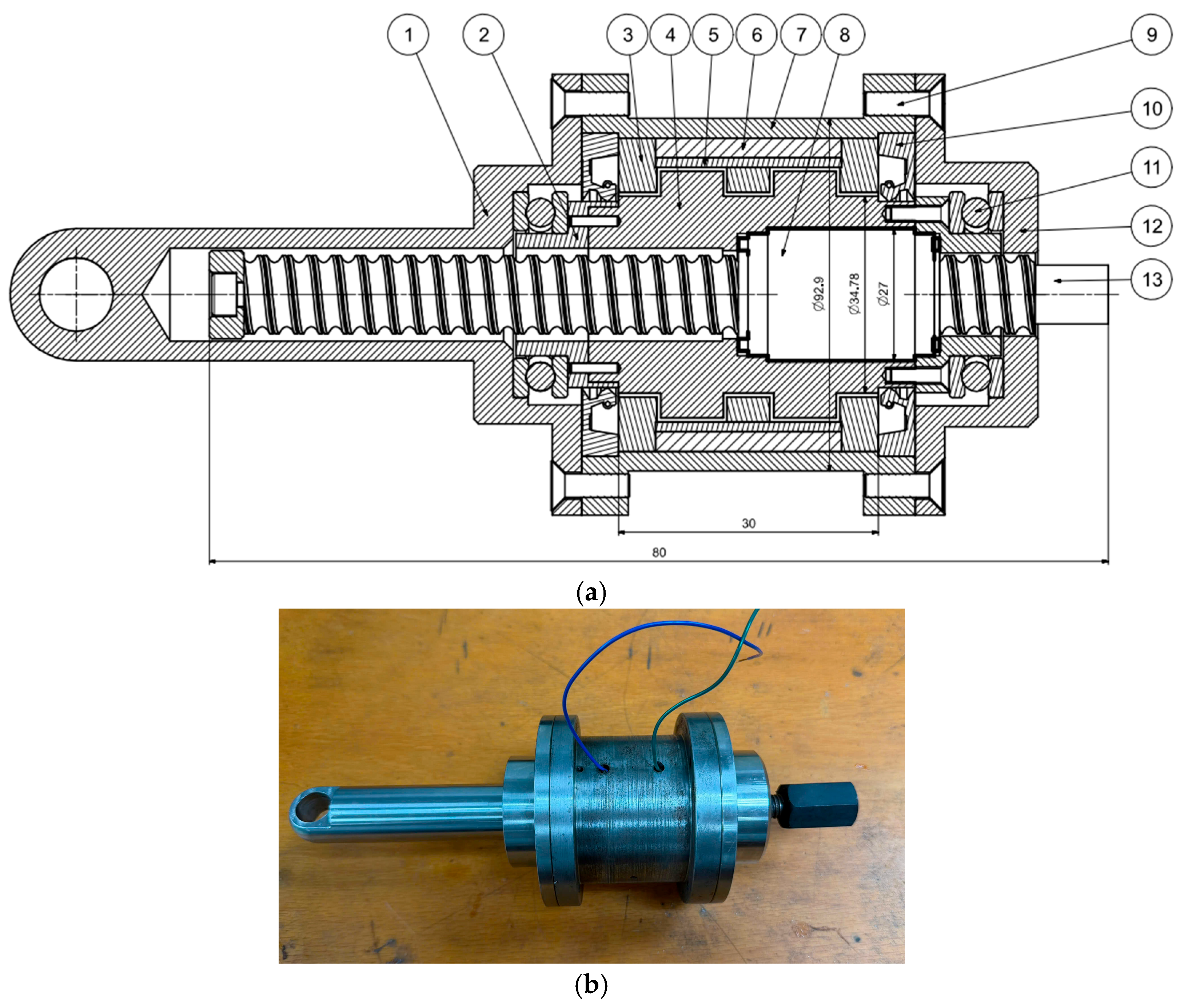
Figure 1 illustrates the structural configuration and operating principle of the proposed SMRB damper. The system comprises a ball-screw assembly, a magnetic rotor sleeve, a magnetic stator housing, and a coil positioned inside the housing. To prevent fluid leakage and ensure reliable long-term operation, the design incorporates two lip seals along with a set of thrust ball bearings. The lower cover, housing core, and upper cover are fixed and collectively serve as the stator, whereas the ball-screw nut and rotary sleeve are rigidly connected to form the rotor. When a linear force is applied to the screw shaft, as illustrated in Figure 1, it is transmitted through the ball-screw mechanism, causing the nut to rotate. Since the nut is fixed to the rotary sleeve, the sleeve rotates simultaneously, thereby converting the input linear motion into rotational motion. Both the stator and rotor components are fabricated from magnetically permeable materials to establish an effective magnetic circuit. The annular gap between the stator housing and the rotary sleeve is filled with MRF. A non-magnetic separator is mounted on the outer surface of the rotary sleeve, allowing the magnetic flux to pass through the MRF gap to generate a controllable resisting torque, while preventing direct contact between the MRF and the coil. In this design, the coil is positioned above and wound around the separator, which avoids direct magnetic interaction with the MRF and thereby simplifies assembly and maintenance procedures. When an electrical current is supplied to the coil, a magnetic field is generated, causing the MRF to produce a resisting torque that operates in a manner analogous to an MRF-based magnetic braking system. To ensure smooth and stable rotation of the rotary sleeve, thrust ball bearings are incorporated to reduce the axial force (F_a) induced by the ball-screw mechanism. Furthermore, the rotor sleeve is engineered with a double-tooth configuration, which increases the magnetic flux interaction area, thereby enhancing the torque output and improving the damper’s overall damping force capability.

Finally, the resisting torque generated by the MRF brake is transformed back into a linear damping force through the action of the ball-screw mechanism. Consequently, the proposed SMRB damper, developed based on the operating principle of an MR brake, enables efficient transformation between rotational and translational motions while providing controllable and effective damping performance.

Understanding the magnetic field distribution within the SMRB damper is essential for interpreting the behavior of the MR damper. Accurate modeling of the magnetic circuit requires detailed information regarding its geometry, material characteristics (B–H curves), mesh configuration (element type and size), applied current, and relevant boundary conditions. A simplified representation of the magnetic circuit is provided in Figure 1. The dimensional parameters are divided into three categories: design variables, which can be adjusted during the optimization process; fixed variables, which remain unchanged; and dependent variables, which are determined based on the first two groups. Specifically, the design variables include the coil thickness (h_c), the thickness of the rotary sleeve (t_f), the length and width of the teeth (L_t, L_s, and t_t), the separator thickness (t_s), the thickness and length of the housing (t_o and L_i), and the width of the MRF gap (t_g). The fixed variable is the radius of the ball screw nut (R_s). The dependent variables consist of the coil length (w_c) and the overall length and radius of the SMRB core (L_c and R_c). The outer surfaces of the housing are defined as magnetic boundaries, ensuring that the magnetic flux lines remain parallel at these edges. The magnetic circuit is analyzed using the finite element method (FEM) implemented in ANSYS 2021R1. For this purpose, a quadrilateral axisymmetric element (PLANE13) in ANSYS APDL is selected, as illustrated in Figure 2. The resulting magnetic flux density distribution and field lines obtained from the simulation are shown in Figure 3. Magnetic components such as the housing core, made of SC45 steel, are assigned their respective B–H curves to capture their nonlinear magnetic behavior, as shown in Figure 2b. Conversely, non-magnetic parts—including the copper coil and the intermediate pole constructed from non-magnetic stainless steel (Aluminum 6061)—are modeled with a relative permeability of 1.0, identical to that of air. The resistivity of the copper used in the coil is denoted as ${\rho }_{wire}=0.01726·{10}^{-6}$. Furthermore, this study employs a commercial MRF (MRF132-DG) supplied by LORD Corporation. The magnetic behavior of the MRF is characterized using its corresponding B–H curve, as described in [20].

$$B=1.91.{\mathrm{\Phi }}^{1.133}.\left[1-\exp (-10.97.{\mu }_0.H)+{\mu }_0.H\right]$$

(1)

where B is the flux magnetic density (Tesla), H is the magnetic flux intensity (A/m), $\mathrm{\Phi }$ is the volume fraction of the MRF, ${\mu }_0=4\pi ·{10}^{-7}$ is the permeability of vacuum.

To investigate the behavior of the MRF in the operating gap, the distribution of magnetic flux density, which varies spatially, must be assessed. The average magnetic flux density across the MRF gap is therefore calculated by integrating the flux along paths P1 to P7, as illustrated in Figure 3b.

The evaluation of the SMRB damper’s damping force begins with the operating principle of the ball-screw mechanism, where the axial load applied to the screw dictates the motion of the nut. This load causes the balls to roll along the helical groove, generating a torque that drives the nut’s rotation. The magnitude of this rotational motion depends on both the applied axial load and the geometry of the screw, enabling high accuracy and efficiency in power transmission. To ensure effective mitigation of external disturbances, the maximum damping force is defined to correspond to the maximum external load, thereby contributing to system stability and operational safety. The resulting motion is influenced not only by the screw’s lead angle and friction angle but also by additional resistive components. Specifically, the damping torque is produced by the MR fluid in the annular gap when subjected to magnetic excitation, along with frictional contributions from the lip seal and the thrust bearings. The relationship between the generated damping force and the corresponding damping torque is thus established based on the mechanical transformation provided by the ball-screw mechanism [22,23]:

$$T_d=F_d{D}_b{\displaystyle \frac{\tan \left(\gamma +\phi \right)}{2}}$$

(2)

$\gamma$ and $\phi$ are, respectively, the lead angle and the replacement rolling friction angle, which are determined by the following equation [22]:

$$\gamma =\arctan \left({\displaystyle \frac{p}{\pi D_b}}\right)$$

(3)

$$\phi =\arctan \left({\displaystyle \frac{2f_t}{d_1\sin \beta }}\right)$$

(4)

where D_b is the ball circle diameter, $\beta$ is the contact angle, f_t friction coefficient, p is the screw lead, and d₁ is screw inner diameter.

The damping torque produced by the MRF is evaluated under the assumption of a linear velocity distribution across the MRF gap, while its rheological behavior is described using the Bingham plastic model. Accordingly, the damping torque (T_d) of the SMRB damper can be expressed as:

$$T_d=T_{MR}+2T_{ls}+2T_{br}$$

(5)

where T_MR, T_ls, and T_br are, respectively, the friction torque of MRF, the lip seal and the thrust ball bearing (Nm).

The friction torque generated by MRF in the SMRB damper consists of two main components: the induced torque in the vertical duct (T_i) and the induced torque in the annular duct (T_j). The MRF regions contributing to the shear stress are illustrated in Figure 3b, corresponding to regions 1 through 7. These two torque components can be expressed as follows [24,25]:

$$T_{MR}={\displaystyle \sum _i{T}_i}+{\displaystyle \sum _j{T}_j}$$

(6)

$$T_i={\displaystyle \frac{\pi {\eta }_i{R}_{i+1}^4}{2t_g}}\left[1-{\left({\displaystyle \frac{R_i}{R_{i+1}}}\right)}^4\right]\mathrm{\Omega }+{\displaystyle \frac{2\pi {\tau }_{yi}}{3}}\left(R_{i+1}^3-R_i^3\right);i=1,3,5,7$$

(7)

$$T_j=2\pi R_j^2{L}_j\left({\tau }_{yj}+{\eta }_j{\displaystyle \frac{R_j\mathrm{\Omega }}{t_g}}\right);j=2,4,6$$

(8)

The induced yield stress $\left({\tau }_y\right)$ of the MRF depends on the magnetic flux density across the fluid gap and the corresponding post-yield viscosity $\left(\eta \right)$. In the MRF, the gap is determined as follows [25]:

$${\tau }_y={\mathrm{2.717.10}}^5.C.{\mathrm{\Phi }}^{1.5239}.\tanh ({\mathrm{6.33.10}}^6.H)$$

(9)

$$\mathrm{\eta }={\mathrm{\eta }}_{40}.\exp \left[{\displaystyle \frac{(1+2.43.\mathrm{\Phi }).(40-T)}{48-T}}\right]$$

(10)

where ${\tau }_y$ denotes the average yield stress induced in the MRF within the fluid gap (Pa). The parameter C is a coefficient dependent on the base fluid of the MRF, with typical values of C = 1.0 for hydrocarbon oil, C = 1.16 for water, and C = 0.95 for silicone oil. The variable H represents the average magnetic flux intensity in the MRF gap (A/m). ${\mathrm{\eta }}_{40}$ denotes the viscosity of MRF at 40 °C, T is the working temperature of the MRF ($℃$).

The friction torque caused by the lip-seal (T_s) is determined as [24]:

$$T_s=0.65{\left(2R_1\right)}^2{\mathrm{\Omega }}^{1/3}$$

(11)

The friction torque caused by the thrust bearing (T_br) is presented as [26,27]:

$$T_{br}=1.06·{10}^{-9}{d}_b^{1.83}{F}_a^{0.54}(vn)+1.6·{10}^{-5}{d}_b^{0.05}{F}_a^{1.33}{\mu }_{sl}$$

(12)

Here, R₁ denotes the outer radius of the magnetic rotary sleeve, $\mathrm{\Omega }$ the rotational speed of the nut, the thrust ball bearing friction depends on rotational speed (n), oil kinematic viscosity (v), axial load (F_a), and bearing average diameter (d_b), coefficient of sliding friction $({\mu }_{sl})$.

3. Optimal Design and Results of SMRB Damper

In this section, the optimization of the SMRB damper is addressed with respect to two key factors: achieving the required damping force and reducing the overall size. The damping force (F_d) must reach a predetermined target and is highly dependent on the damper’s geometric parameters. Accordingly, these parameters are adjusted to ensure that the desired damping force is obtained while simultaneously reducing the damper’s mass (M_d) and overall production cost. In essence, the geometry is refined to maintain adequate damping performance while minimizing structural weight. The objective function and constraints are expressed as follows:

$$\mathrm{Minimum}: OBJ=M_d=V_f{\rho }_f+V_{bs}{\rho }_{bs}+V_c{\rho }_c+V_h{\rho }_h+V_{MR}{\rho }_{MR}$$

$$\mathrm{Subjected} \mathrm{to}: F_d\ge F_{dr}=1500N$$

Here, V_f, V_bs, V_c, V_h, and V_MR denote the volumes of the sleeve, ball-screw mechanism, coils, housing, and MR fluid of the SMRB damper, respectively. ${\rho }_f,{\rho }_{sh},{\rho }_c,{\rho }_h,{\rho }_{MR}$ are represent the densities of the materials corresponding to the previously mentioned components, respectively.

It is noted that the damping force F_dr is selected as 1500 N based on the required damping force characteristics of passenger vehicle suspensions as a function of piston velocity reported by Oh et al. [28]. It can be observed that, in the low-to-moderate piston velocity range (below approximately 0.3 m/s), which is typically associated with low-frequency body motions, the required damping force lies in the range of 1000–1800 N. In particular, a damping force of approximately 1500 N corresponds to the representative operating condition for controlling vehicle body motions while maintaining ride comfort. At these operating conditions, the suspension response is dominated by low-frequency excitation related to heave, pitch, and roll motions of the vehicle body rather than high-frequency road irregularities. Therefore, selecting an MR damper with a maximum controllable force of 1500 N is sufficient to provide effective vibration attenuation without introducing excessive stiffness that could degrade ride comfort. Moreover, this force level is consistent with practical damping requirements for semi-active suspension systems, ensuring adequate control authority while remaining within the feasible operating range of MR dampers. Consequently, the selected damping force of 1500 N is considered appropriate for representing realistic suspension operating conditions in the present study.

The design variables (DVs) of the SMRB damper are defined, with the primary structural dimensions selected for optimization. These include parameters such as the sleeve thicknesses (t_f, L_t, t_t, L_c), separator thickness (t_s), coil dimensions (w_c, h_c), housing thickness (t_o), core lengths (L_i, L_o), and the MRF gap (t_g). A critical design consideration is that a smaller MRF gap increases the friction torque and consequently enhances the damping force. However, excessively reducing the gap also raises manufacturing challenges and requires higher precision during machining. Therefore, the MRF gap is selected within a practical and feasible range of 0.8–1.5 mm.

To solve the optimization problem, several conventional methods—such as Newton’s method, the Newton–Raphson technique, Sequential Quadratic Programming, and Gradient Descent—have been employed in previous studies [29,30,31]. Although these approaches can be effective in certain scenarios, they are typically sensitive to initial conditions and often converge prematurely to local optima. To overcome these limitations, the Adaptive Particle Swarm Optimization (APSO) algorithm is adopted in this work. APSO maintains the simplicity and low computational demand of standard PSO while significantly improving performance through dynamic parameter adaptation. In APSO, population diversity is assessed using the average distance between all particles and the global best position. This distance is normalized into a convergence index (Et), which serves as the basis for continuously adjusting the inertia weight and learning factors. Through this adaptive mechanism, APSO achieves an effective balance between exploration and exploitation, enabling it to avoid entrapment in local minima and enhance convergence speed toward the global optimum [32]. In the study, APSO is implemented in MATLAB 2019b and integrated with ANSYS APDL to obtain the optimal damper design. The previously defined design variables are used in the optimization process, with the maximum number of iterations set to t_max = 50 and the population size specified as N = 70. The adaptive adjustment of inertia weight and learning coefficients ensures that APSO maintains robust search capability throughout the optimization process. Specifically, for each particle t, the mean distance to all other particles is calculated as [33]:

$$d^t={\displaystyle \frac{1}{N}}{\displaystyle \sum _{i=1}^N‖x_i^t-gbes{t}^t‖},i=1,2\dots ,N$$

(13)

From these values, the maximum distance (d_max), the minimum distance (d_min), and the distance corresponding to the global best particle (d_g) are obtained. Based on them, the evolutionary factor is defined as $E^t={\displaystyle \frac{d_g-d_{\min }}{d_{\max }-d_{\min }}}$ with $E^t\in \left[0,1\right]$, which indicates the degree of convergence or dispersion of the swarm.

According to the value of $E^t$, APSO estimates the evolutionary state of the swarm, such as exploration, exploitation, convergence, or jumping out of local optima, and adjusts the learning coefficients c₁ and c₂ accordingly [33,34]. At the same time, the inertia weight is adaptively updated using a sigmoid- mapping w(E^t) function in Equation (14), so that a larger inertia weight promotes global exploration, whereas a smaller one enhances local exploitation [34].

$$w(E^t)={\displaystyle \frac{1}{1+1.5e^{-2.6E^t}}}\in \left[0.4,0.9\right]$$

(14)

Next, the adaptive evaluation of the acceleration coefficients 1 and c₂ is performed based on four evolutionary states of the swarm, namely exploration, exploitation, convergence, and jumping-out [34]. These coefficients are constrained within predefined ranges $1.5\le c_1,c_2\le 2.5;c_1+c_2\le 4$. According to the identified evolutionary state, the algorithm automatically adjusts the inertia weight as well as the acceleration coefficients c₁ and c₂ to achieve a balance between global exploration and local exploitation.

Finally, based on the obtained results, the velocity and position of each particle are updated using the standard PSO equations [32]. This process is repeated until the stopping criterion is satisfied, ensuring stable convergence and high optimization performance of the APSO algorithm.

This study employs a 24-gauge copper coil wire with a 0.511 mm diameter and a current-carrying capacity of up to 3 A. For operational safety, the current is limited to a maximum of 2.0 A. The SMRB damper design utilizes a filling ratio of 0.7. Furthermore, based on prior experimental data, an energy loss of approximately 10% is accounted for, primarily attributed to magnetic losses from hysteresis and eddy currents. Figure 4b present the objective and constraint conditions, as well as the magnetic flux distribution at the optimal solution. As shown in Figure 4a, the optimization converges at the 19th iteration. At this optimal point, the mass of the SMRB damper is reduced substantially—from an initial 2.23 kg to 1.42 kg. Meanwhile, the damping force achieves 1500.87 N, satisfying the requirement of being no less than 1500 N. Compared with the initial design, which produced a damping force of 1345.17 N, the optimized configuration results in a noticeable reduction in force output. Figure 4b further shows that the magnetic flux density within the MRF gap at the optimal design is also significantly lower than that obtained using the unoptimized parameters. Despite this reduction, the optimized structure is markedly more compact and efficient than the initial design. At the optimal point, the off-state force (Fd₀), representing frictional resistance in the absence of an applied magnetic field, is determined to be 104.51 N. The magnetic flux density along the MRF gap segments reaches approximately 0.191 T. In the region of the gap located beneath the separator, the flux density increases significantly, reaching up to 0.55 T. Owing to this higher magnetic flux density, the area beneath the separator contributes substantially to the generation of torque. The magnetic core of the optimized SMRB damper has a length of 30 mm and a radius of 46.45 mm. A comprehensive summary of the final optimal parameters and performance characteristics is provided in

Table 1. Optimal results of SMRB damper at the optimum.

Types	Design Parameter (mm)	Characteristics
SMRB damper	Coil: Width of coil wcs = 19; Height of coil hcs = 10.53 Radius and length of magnetic core: Ra = 46.45 and La = 30; No. of turns: 476 turns. Rotary sleeve: tf = 3.89; Rotor tooth width and height: Lt = 5.1 and tt = 10.6. Middle stator tooth width: b = 5.1. Separator: ts = 3.0 Magnetic housing: Length: Li = Lo = 5.2; Thickness of housing: to = 2.0; MRF gap: tg = 0.925	Mass: 1.42 kg Damping force (Fon): 1500.87 N Off-state damping force (Foff): 104.51 N Power Consumption: 28.34 W

.

From the optimized results presented in Table 1, the proposed model achieves a maximum damping force of 1500.87 N at an excitation current of 2.0 A. Under this operating condition, the power consumption of the coil is 28.34 W, indicating that the proposed damper is capable of generating a very large damping force with a reasonable level of energy consumption. For performance evaluation, these results are compared with those of the monotube shear mode MR damper reported in [35]. At the same excitation current of 2.0 A, the referenced MR damper produces a damping force of approximately 200 N with a power consumption of 18 W. Therefore, the proposed model delivers a damping force that is about 7.5 times higher, while the power consumption increases by only 10.34 W, demonstrating a significantly superior energy-to-damping-force conversion efficiency. To ensure a more consistent comparison and to investigate low-power operating conditions, the geometrical dimensions of the optimized SMRB damper are kept unchanged, while the excitation current is reduced to 0.15 A. Under this condition, the proposed damper still achieves a damping force of 217.34 N, which is higher than that of the referenced MR damper operating at 2.0 A, whereas the power consumption is reduced to only 4.21 W, corresponding to an approximately 85% reduction in power consumption compared with the 2.0 A operating case. These results clearly demonstrate that the proposed SMRB damper not only provides a substantially higher damping force at higher excitation currents, but also maintains excellent performance under low-power conditions, highlighting its clear advantages over conventional MR dampers.

Based on a comparison with study [36,37], it can be concluded that the proposed SMRB damper exhibits a clear advantage in the off-state condition, with an off-state force of only 104.51 N, which is significantly lower than the value of approximately 400 N for the MR damper. This indicates a superior ability to maintain a compliant response in the absence of excitation current, thereby enhancing ride comfort and fail-safe performance. Moreover, the SMRB damper achieves a relatively large controllable force range, with an dynamic range (F_on/F_off) of about 14.36, markedly higher than the value of 5.5, demonstrating a clearer distinction between the ON and OFF states. Nevertheless, in terms of absolute performance, the maximum damping force of the SMRB damper (1500.87 N at 2.0 A) remains lower than that of the MR damper (approximately 2200 N), while the required coil power consumption is considerably higher (28.34 W compared with 4 W). These results indicate that, although the SMRB damper performs better in reducing off-state force and improving controllability, its electromagnetic efficiency is still inferior. Overall, the comparison suggests that further optimization of the magnetic circuit and coil configuration is necessary to enhance the on-state damping force and reduce power consumption, thereby achieving a more balanced overall performance.

4. Experiments and Results

Using the optimized parameters listed in Table 1, a detailed 3D prototype of the SMRB damper was constructed in Siemens NX12, as illustrated in Figure 5. The model is divided into four main components—the inner housing, outer housing, magnetic core, and ball-screw mechanism—to facilitate straightforward assembly, fabrication, and maintenance. The complete prototype measures 110 mm in length and 75 mm in diameter, while the magnetic core has dimensions of 30 mm in length and 92.9 mm in diameter. The damper is designed for a functional stroke of 75 mm; however, to ensure operational safety and prevent potential contact that could damage the magnetic core, the maximum allowable stroke is limited to 80 mm. During assembly, the sleeve is rigidly connected to the nut of the ball-screw mechanism, forming an integrated rotor unit. The annular gap between the sleeve and the inner housing is filled with MRF. The coil is directly wound around the inner housing, whereas the outer housing functions as the magnetic yoke, completing the magnetic circuit when the field is generated inside the SMRB damper.

Figure 6 presents the experimental setup for evaluating the proposed SMRB damper. In this configuration, a crank–slider mechanism is used to generate the linear reciprocal motion, driven by a 500 W-AC motor (Wanshsin, Taiwan) with gearbox. The system can produce a maximum axial force of 2000 N at a velocity of 0.15 m/s. The excitation frequency of the test system, adjustable within the range of 0 to 0.7 Hz, is controlled using a Mitsubishi D740 frequency inverter. The damping force is measured by a PST (Keli, China) load cell (300 kg capacity), with its output signal amplified before acquisition. Together with the displacement data obtained from the LVDT sensor (Soway, China), both signals are captured through an NI-6002 data acquisition card (National Instruments, Malaysia) and subsequently processed in LabVIEW 2021. A PPW-8011 programmable power supply (Twintex, Taiwan) is employed to deliver the input current to the SMRB damper prototype. Additionally, the Denoising Wavelet feature in LabVIEW is used to suppress measurement noise, thereby improving the precision and reliability of the recorded data.

In the experimental procedure, the power supply was manually adjusted to deliver various current levels to the MR damper, allowing the corresponding damping force outputs to be observed and evaluated. Under a displacement excitation with an amplitude of 37.5 mm and a frequency of 0.5 Hz, the resulting damping force–displacement characteristics were recorded and are shown in Figure 7a. The results reveal that the damping force increases in proportion to the applied current, confirming the current-dependent behavior typical of the SMRB damper prototype. As the current rises, the damping force–displacement loops broaden symmetrically along the displacement axis, illustrating the damper’s capacity to absorb and dissipate kinetic energy effectively. The experimental data show that the peak damping force reaches approximately 1417 N at an input current of 2.0 A, which is slightly lower than the theoretical optimum value of 1500.87 N. This deviation may arise from several factors, including non-uniformity of the MRF, localized magnetic saturation, fabrication tolerances, and discrepancies between simulated and actual material properties. Despite these differences, the experimental findings validate the damper’s ability to deliver adjustable damping and efficient energy dissipation, demonstrating its suitability for applications requiring variable damping performance under diverse loading and frequency conditions.

Figure 7b presents the force–velocity characteristics of the SMRB damper, showing a pronounced increase in damping force as the input current rises from 0 A to 2 A. The curves display a nonlinear hysteretic behavior: at low piston velocities, the response is dominated by yield stress, whereas viscous effects become increasingly significant as the velocity increases. The magnitude of the damping force expands from approximately ±142 N at 0 A to nearly ±1417 N at 2 A, with a noticeable trend toward saturation at higher current levels. These results confirm the damper’s capability for controllable damping and its effectiveness in dissipating energy across a range of operating conditions.

Figure 8 illustrates the output damping force of the SMRB damper under sinusoidal displacement excitation. Across frequencies of 0.4 to 0.7 Hz at a constant 2.0 A current, the damping force exhibits only a minor increase. Notably, the shape and enclosed area of the force-displacement hysteresis loops show negligible variation with frequency. This suggests that the viscous damping component, attributable to the MRF’s apparent viscosity, contributes minimally to the total force. Instead, the damper’s dynamic response is governed primarily by the yield-stress-related shear force of the MRF. Consequently, the SMRB damper demonstrates stable, frequency-insensitive damping performance, affirming its suitability for applications requiring reliable operation across varied conditions.

5. Conclusions

In this study, a novel rotary MR damper is proposed as an alternative to conventional configurations, with the aim of enhancing performance in both translational and rotational motions while reducing initial magnetic resistance. Drawing upon an extensive review of previous research and its associated limitations, a new structural concept was formulated and further supported by the design and modeling of an MRF sealing mechanism. To improve overall effectiveness, finite element analysis was conducted, and the SMRB damper was optimized through the integration of MATLAB and ANSYS APDL using the Adaptive Particle Swarm Optimization (APSO) algorithm. The optimized model achieved a maximum damping force of 1500.87 N with a compact total mass of 1.42 kg. Following the optimization stage, a physical prototype of the SMRB damper was manufactured and experimentally evaluated to examine the relationship between the input current and the resulting damping force. The experimental findings show that the prototype produced a peak damping force of 1417 N at 0.5 Hz under an applied current of 2 A, corresponding to 94.46% of the optimal value predicted by simulations. Further tests conducted across multiple excitation frequencies confirmed a characteristic nonlinear response with pronounced hysteresis loops. These results not only demonstrate the stable and effective performance of the proposed damper but also validate the practical feasibility of the SMRB configuration for applications requiring dependable vibration control under a wide range of dynamic loading conditions.